宇宙論的問題

目次

はじめに
１. 年齢問題
２. 大規模構造
　２.１ 必要な非一様性はCDMに
３. インフレーションとダークマター
　３.１ 臨界密度
　３.２ 平坦性と地平線問題
４. ハッブル定数
　４.１ 宇宙項とハッブル定数
　４.２ 宇宙項(斥力項)
　４.３ ハッブル定数とその線型性
　４.４ Tolman Test 銀河輝度と赤方偏移
　４.５ クエーサーの赤方偏移
　４.６ ハッブルの沈黙
　４.７ セファイドとSNIa
５. それなら定常か
　５.１ 赤方偏移の原因
　５.２ アインシュタインは否定した
６. ハッブル深部領域 Hubble Deep Field
７. オルバースのパラドックス
８. 背景輻射
８.１ 2.7Kの黒体輻射
９. 銀河
　９.０ 熱死論
　９.１ 銀河の M/L 比
　９.２ 銀河の回転と渦巻の回転方向
　９.３ 銀河の回転曲線
　９.４ 天の河銀河は棒渦状?
　９.５ 銀河は重力的に球状?
　９.６ 衝撃波による恒星形成の渦巻?
　９.７ マージによる渦巻銀河形成?
１０. 短かすぎる
　１０.０１ 宇宙初期の惑星
　１０.０ メタル
　１０.０２ 銀河型の分類
　１０.０３ 恒星の HR 図
　１０.１ 恒星の光度と質量
　１０.２ HR 図と恒星進化
　１０.３ 恒星の形成と収縮過程
　10.31 方励之の重力系の崩壊時間
　10.32 形成時間が宇宙年齢に比例する
　10.33 太陽系の重力捕捉速度
　10.34 3K が重力捕捉の可能な温度
　10.35 電子の捕捉と水素原子の形成
　10.36 平均自由行程と衝突間隔
　10.37 銀河系収縮の時間
　１０.４ 宇宙の果ての銀河の光度
　１０.５ 銀河の輝度について
１１. 幻想的宇宙論 ー膨張と特殊相対論の結合ー
　１１.１ 一様等方、ハッブルの法則が成立する宇宙
　１１.２ 累積距離は有限
　１１.３ 光速物体の存在
　１１.４ 無限の重力の変動
　１１.５ 物体は速度を変えない
　１１.６ 静止無限/有限宇宙の問題
　１１.７ ニュートン力学と宇宙
　１１.８ 特殊相対論と宇宙
１２. 特殊相対論の宇宙
　１２.１ 時間と空間の混合
　１２.２ 系が対等でないときの相対性
　１２.３ 始まりのある宇宙の相対性
　１２.４ 閉じた宇宙での双子のパラドックス
　１２.５ 閉じた宇宙では特殊相対論は成立しない
　１２.６ ステンレスのナイフ
　１２.７ 銀河型間の移動は、なぜあり得ないのか
　１２.８ 絶対時間：始まりからの時間、絶対静止系：共動座標系
　１２.９ それから、考えられること
１３. 回転系
　１３.０ ニュートン力学での回転系
　１３.１ 回転をさせるのではなく、すでに回転している
　１３.２ 回転系の時空
　１３.３ Sagnac 効果
１４. 加速系
　１４.１ 一様重力系と加速系とは、原理的に区別できない
　１４.２ 加速系の光速は、より正確に解くことができる
　１４.３ 特殊相対論を使って空間短縮を導く
　１４.４ 議論
　１４.５ 光速一定の放棄は何によるのか
１６. ポアンカレの宇宙
　１６.１ ポアンカレの寓話宇宙
　１６.２ 内部は無限
　１６.３ 物体(定規)のサイズが場所による
　１６.４ 時空の変形(=計量)と不変量
　１６.５ 宇宙の果ての見え方
　１６.６ 宇宙と幾何学
　１６.７ 宇宙の内部でこの構造を知ることができるか
１７. アインシュタイン宇宙
　１７.１ 射影による g_ik
　１７.２ その他の射影
１８. ド・ジッター宇宙
　１８.１ アインシュタイン宇宙とド・ジッター宇宙の成り立ち
１９. フリードマン宇宙
　１９.１ フリードマン解
　１９.２ 空間曲率０の解
　１９.３ 空間曲率非０の解
２１. 光の廻廊
　２１.１ 赤方偏移は、宇宙膨張かドプラー効果か
　２１.２ ゴム膜の上の虫
　２１.３ 光エーテルの復活
　２１.４ 曲る光のハッブル定数
　２１.５ 遠方のハッブル定数
　２１.６ 局所慣性系と速度をもった場
　２１.７ 閑話休題
　２１.８ 閑話休題つづき
　２１.９ フリードマン解の空間曲率０のときの光エーテル的回帰について
　２１.１０ ブルータス、...
　２１.１１ 曲って戻る光？
　２１.１２ g_ik からの光速を使うと
　２１.１３ 場と速さ
　２１.１４ 背景輻射自体、存在できるのか
　２１.１５ 光の廻廊
　２１.１６ 光が戻る計量
　２１.１７ 光速が０になる計量
　２１.１８ 光速が０になる計量(続き)
　２１.１９ G,A ともに逆数でないと意味をなさない
２２. フリードマン宇宙解の計量
　２２.０ 縮小を意味する計量
　２２.１ パウリの相対性理論の付録
　２２.２ 収縮する物差し
　２２.３ 全体写像
　２２.４ 全体写像による膨張
　２２.５ 全体写像膨張は結論
　２２.６ 膨張宇宙論のふたつの思考
　２２.７ 膨脹宇宙とブラックホール
２３. 膨張宇宙の解釈
　２３.１ 選択的膨張
　２３.２ 縮小する物差
　２３.３ 質点間のひもの縮小に伴う力学現象
　２３.４ 物差しと物体
　２３.５ 縮小する物差しによる膨張は、過去の空間間隔の拡大
　２３.６ 解釈に問題
　２３.７ 計量の意味
　２３.８ あり得る膨張宇宙
　２３.９ 膨張宇宙説に対する批判のまとめ
２４. WMAP衛星の観測による宇宙の年令・運命、ほぼ結着?
　２４.１ 大規模構造がさらに遠方にも続く
　２４.２ 再イオン化時期の前倒しなど
　２４.３ WMAP の観測から 3 年目
　２４.４ 最も遠方の銀河団
２５. 重力ポテンシャルと宇宙項
２６. 宇宙膨張のポテンシャル上昇による赤方偏移
　２６.１ 重力ポテンシャルの時間経過を考慮した赤方偏移
２７. 横ドップラー効果による赤方偏移
２８. ハッブルの銀河分布
２９. パイオニア異常
３０. 特殊相対論の膨張の年齢と距離
３１. 正の曲率のある宇宙と膨張宇宙
３２. おわりに

はじめに

この文章の目的は、科学への信頼と献身である、そう言うべきほどこの文章は、批判者的文章として、多くの方々によって否定された。 それは単に、科学を批判的に論ずることが困難な作業だからであると思う。その方々のように、何も言わなければそれで終わり、 私は少しいうのを選択しただけである。現代科学は、思想をもたない国家事業である。そこには個人の作業を超えたものがある。しかし、 科学は間違うことがある。それだけでなく、一般的に正しい答えに到達するまでにあらゆる誤りを経験することがある。それゆえ科学の言説 の大半は誤りかもしれないという意識をもつ必要がある。なぜなら、科学こそ献身する価値のある仕事だからである。

ギリシャ時代にアリスタルコス(BC310-BC230)による月と地球の大きさの比、月と太陽の距離比、エラトステネス (BC276-BC196) による地球の 大きさの測定の歴史を持ちながら、永い中世に時を費し、我々は長期間、天動説を信じた。彼らからじつに 1800 年後にコペルニクスをもつ。 なぜこれほどの停滞をしたのか。そこには思想上の問題があった。数千年間の歴史時代はすでに言語の筆記をしているから、人間の特性には 現代人と明確な違いはない。歴史上の人々は肉体/精神的に現代人と同等で、どの時代の人も現代人と遜色ない批判と推論能力をもつと考える。 しかし、彼らの思考内容は現代人と全く違った。彼らに対して我々が有利であるのは、この履歴だけである。

天動説は、占星術のための惑星計算にすでに有効な精度をもっていた。しかし、天動説と地動説を判別する天体現象には、内惑星の満ち欠けがある。 水星と金星は、地球中心ならつねに太陽のこちら側だが、実際は太陽の遠近の両側にあるような満ち欠けをする。それを望遠鏡で見るだけで2世紀 からのプトレマイオスの天動説は否定できてよかったのである。J. D. バナールの "歴史における科学" によれば、望遠鏡は、眼鏡技術ができて 300年、光学機器製作が普及した 1600年頃、ガリレオに先行する誰かによって発明されたが、オランダの眼鏡店で、ある子供が偶然にレンズを通して 店の窓に設置した別のレンズをみたことによるという伝説があるという。このことの含意は、望遠鏡はそれまでそれが可能と誰も予想さえしなかった 技術であったことである。科学が変わることができたのは、そういう予期せぬ道具によってであった。

凸レンズの対物に凹レンズの接眼を組み合わせたガリレオの望遠鏡は、正立した虚像をみる仕組みであった。それはすぐに接眼レンズにも凸レンズを使う ことで対物レンズの作る上下左右逆の実像を接眼レンズで拡大して見る仕組みになって、対物レンズと接眼レンズの焦点距離の比だけの倍率を与える 点は同じだが広い視野を与える望遠鏡に変わる。ガリレオの望遠鏡は、接眼レンズから対物レンズの視角内の像が拡大されるだけであり、 倍率の高い長い望遠鏡ほど視野は狭かった。接眼レンズは、複数のレンズを組み合わせることで広視野で歪の少ない、ホイヘンス、エルフレ、 オルソスコピックなどが開発された。

凸レンズの対物レンズは、色の屈折率の違いによって像に色が付く現象「色収差」を克服するために、凸凹2枚の屈折率の違うレンズを張り合わせた アクロマート、又は3枚のレンズを組み合わせたアポクロマートの対物レンズに変わっていく。対物レンズの最終的な進化として凸レンズをやめ、 放物面の凹面鏡の反射式望遠鏡にして、色収差を完全に克服したのは、あの物理学において偉大なニュートンである(*)。光は対物鏡に垂直に反射し、 45度に配置した楕円型の平面斜鏡が90度角度を変え接眼鏡に導く。斜鏡は対物鏡への入射光を遮るから接眼鏡程度の大きさに抑え、3、4本の足に よって望遠鏡筒から支持される。その後、主鏡軸上の凸面鏡によって焦点を伸ばし、主鏡の中心に開けた接眼部をもつカセグレン型などが開発された。

(*) この対物レンズの反射鏡への変化は、良質のガラスを必要とせず、多くの面の成形が不要で、1面だけ成形すればよい点などの利点がある。 天体望遠鏡の製作について、ガラス屋さんに2枚の1cm厚程度ガラスを円形(直径10cm程度)にくり抜いてもらい、周囲の円形を研磨剤によって研く。 グラインダーなどの回転板にガラスをピッチで張り付け回転させて周囲を粗く研磨する。そして、コランダム(又はアランダム)など数100番から1000番 の研磨剤を水に混ぜ間にいれて、下のガラスを台に固定し、上のガラスを合わせた中心から数cm手前の位置に前後させながら上のガラス板を徐々に 回転させ、自身も台の回りを移動するだけで、上のガラス面を凹面に、下の相手側のガラス面を凸面に成形できる。これは、ガラスの外側の円形の 精度に依存している。さらに球面から放物面に変化させる方法も、難しい方法でなく用意されていた。この段階のガラスはまだすりガラスであるが、 水に濡らして反射した像で焦点距離を計測し面の成形の段階をチェックする。焦点にナイフエッジを使った反射パターンで球面/放物面/楕円が区別 できる。研磨剤を細かくしていき、最後に酸化鉄粉を水に解いて染み込ませた紙を挟んで研磨して透明な鏡面にする。それに銀メッキか現代では 真空中のアルミ蒸着によって鏡面化して反射鏡にできる。メッキしなくても太陽望遠鏡には使える。粗ずりまで私は小中学生で試した。焦点距離は 容易に1mまで短くなったが、それ以降の精度のよい放物面を確認しながらすりガラスを透明にする作業は恐らく何倍も大変だろうと思って諦めた。

アインシュタインが "エーテルと相対論"でいうように、一般相対論の計量場g_ikに速度特性をもたせるだけで 古典的エーテル論に戻ることを我々は警戒すべきである。遠方空間のそれを直ちに誤りとはいえないが、特殊相対論は宇宙を適用範囲から失い無限小 の領域に狭められたが、無限小の近傍だけからエーテルが排除されると理解すべきでない。一般は特殊の完全な拡張である。それは基本的に過去の 誤謬である光媒体エーテル論に戻らない。ところが宇宙論では、計量という高度な思考法を使いながら、誰もが望まずに容易に前近代的思考に陥いる。 計量場は一般の物質のように速度特性はなく、一般相対論は天動説も、CMB、局所慣性系と名を変えたエーテルも、絶対静止空間も復活させない。 トリチェリによって存在が証明された真空の中に波が存在する媒体エーテルへの傾倒は、真空充填を求める偏好であり、その根拠は合理的でない。 計量g_ikは、運動し世界線を辿れる存在ではない。磁力線の運動のように速度をもつ系、任意の座標系からみて値が違う。それでも、時空の最重要な 特性として、局所の物差しと時計とを規定し、g_ik場の全体の振舞は、重力方程式を通して実現する。

この文章は、もちろん教科書ではない。疑問には解決を伴わないかもしれないし、すでに多くの人によって解決しているかもしれない。不勉強な私が 手に余る題に手を付けただけかもしれない。しかし、もともと概念主張の強すぎる宇宙論に対して、多少の概念批判をする。それがこの小論が否定 される原因である。批判は多くの人に害を与える。概念否定は反証で行え、その通りである。しかし、概念主張される方も証拠を提出すべきである。 この小論に批判を頂く方は、最近の概念しか知らない方が多く、しかもそれを絶対不変の真理と思われている。私は最近の概念を批判するが、たった 10年前に現在と違う何が主張されていたかを知らずに、私の書く宇宙論の歴史を "99%の嘘"と言われる。その方には私の話の99%が初めて聞く、 理解不能なことなのであろう。私も多くのことに気が付いたのはここ10年以内である。

この方が知らないことに対して、私はお手上げである。まずは知りそして考えよ、である。しかし知るためには、よく考える必要もある。 知識は、入口であって中身ではない。この世界の理解において、よい事はむしろ、あいまいな発想、思い付きにある。読書は材料であって、 書かれたものを批判なしに受け入れることは、昔も今も危険である。この文章を受け売りでレポートに使ってはいけない。不用意な行為は 損失を招くだろう。しかし自ら考えることは、危険であり時間がかかるが、それだけの価値があるものである。

WMAP の結論の出し方は、宇宙論の重要なパラメタ 6 個(物質密度(Ω_m h^2)、バリオン密度(Ω_b h^2)、ハッブル定数(h)、ゆらぎ振幅(σ_8)、 光学深度(τ)、スカラー摂動スペクトル傾斜(n_s)) を同時にすべて決定する。今回、さらにパラメタの範囲が絞られたという。Ω_m、Ω_b は、 それぞれマターとバリオンの臨界密度に対する比率であり h の 2 乗に関係する。n_s= 1, r= 0 というスケール独立仮定は誤りで、 それより明確に小さいスケール指数をとる必要がある。バリオン比率は、半分の 2% になった。じつに、"98%の謎" が正しい。

なぜ、宇宙項に緩和が必要だったのか。確率過程のシミュレーションによって、膨張宇宙の時間経過のなかでゆらぎが成長して背景輻射の パワースペクトル波形その他の観測データの再現性によってパラメータを判定する、この方法では言えることが限られ、その方法論自体が 宇宙論を限定するだろう。例えば極端に言えば、定常宇宙論がこの背景輻射のまだら模様の空間パワースペクトルを説明することは不可能だろう。 しかし、定常論へのこの新たな圧迫は、宇宙論の重要な 6 つのパラメタが同時に指定されること自体に疑いを抱かせる十分な材料でもある。

背景輻射のゆらぎのパターンの空間的パワースペクトルからハッブル定数、宇宙項、密度などがすべて出るなら、それは万能の測定である。 科学の歴史は、そういうものが今日まで容易になかったことを示している。それらのひとつのパラメタにおいてさえ、他の方法の確認がない、 又は確認の歴史すらないと思う。CDM の主張も、それが何によって作られているかを言えない段階での主張は、ほとんど意味がないということ もできる。さらに、λを気軽に導入してデータにフィットしたからそれをλの存在証拠というべきではない。どうして初期宇宙論が一般相対論 でなく得体の知れないスカラー理論に頼るのか私は理解できない。すべての怪しいものを取り去った後にしか科学において答えはないからである。 データに一致すればあり得ない物質を導入し、データが要求すれば宇宙定数さえ変え、結果が欲しければ理論の枠さえ取り去る、それが宇宙論 の現状か、とさえ思う。

我々が行う判定は、大概において誤った観測、予想に基づいた仮定の上に構想された絵によって行われ、正しい結論と逆の結論がつねに論戦を 勝利してきたのかもしれない。例えば、有名な1920年の Curtis と Shapley の宇宙のサイズについての大議論である。そこでの議論は、星雲が 銀河系内天体であるという説が優勢だったが、そこには星雲が銀河内天体であることを客観的に示す、渦巻星雲の実際の回転を測定した、 van Maanen のM33等に対する観測結果があった。数年〜数十年で回転が観測される渦巻は、銀河系外にあるほど大きく遠いはずがなく、 星雲が太陽系の近傍にあることを示していた。その観測結果は、後に星雲が銀河系外天体であることを示したハッブルの論調を極めて 慎重にさせたと思う。観測が行ったことは、こういうことである可能性がある。多くの人が粛然とした気持ちになる宇宙の認識には、 批判力が低下し結果は誤りやすい。我々はつねに自明と思える基本的な物事から考える必要がある。

１. 年齢問題

そこでの細かな問題、時間のスケールが合わないこと、つまり、宇宙の年齢が球状星団の年齢を超えない問題がある。実は、これは細かな問 題などではなく、この宇宙論の歴史的欠陥であると私は思う。少なくとも現在までずっと、宇宙論はこの基本的な年齢問題を満たしていない。 アインシュタインの時代には宇宙論からくる宇宙の年齢が 15 億年でしかなかった。彼の"相対論の意味"(原題 "The Meaning of Relativity" 矢野健太郎訳、岩波書店)の"第二版への附録"によれば、彼は、このパラドックスからこの理論自体の有効性に疑問があることを述べ、

h の測定値からわれわれは、宇宙の現在までの存在期間として、1.5・10^9 年を得る。この年齢は、地殻に対してウランの壊変から得た それとほぼ同一である。これは、種々の理由から、理論の妥当性に対して疑いを起した、一つの逆説的な結果である。

この誤りは、彼の罪ではない。彼は、当時のハッブル定数 432km/s/Mpc を信用したが、この数値にどれほど精度がなかったか、10 倍ほども狂 っていた。そしてその後も、宇宙の平均密度ρだけでなく、我々はハッブル定数自体が確定できず、いまだに 2 倍の誤差を克服できない。

宇宙の年齢問題は、現在、地球の地質的年代との矛盾は解決したが、星の一生の年代で問題を残している。球状星団の中の星の年齢は、明らかに 150 億年を超えるものがある。(160 〜 190億年とされる。球状星団の中の恒星の長い年齢に対応するものは、絶対光度の小さい終末星だから、 今後も記録は更新されるだろう。) この事情はもうすこしで不整合を解消しようとしているとみるべきか、欠陥は解決していないとみるべきか。 仮にそれが解決しても、銀河形成と、新たに発見されている大規模構造の説明の不能、という問題が次にある。

２. 大規模構造

THE CfA REDSHIFT SURVEY

ビッグバン宇宙論は、3つの宇宙原理、一様、等方、定常の内、定常を捨てたのであるが、一様等方という前提から怪しいかもしれない。 星の一様等方は、銀河の発見で覆された。大規模構造が議論される前には、銀河を超える構造がないことを一様性の証拠と考えていた。 銀河は空間に与えられた指標のように一様に分布すると考えた。それは誤りだった。この銀河の一様等方も再挑戦を受けている。 大規模構造の発見は、銀河を超える構造を主張したヴォークルールのメタギャラクシーが生き返ったかに思え、宇宙論の基本的パラダイムに 疑問を投げかける。どこまでも大構造のある宇宙は、宇宙論的な定式化を拒むだろうからである(*)。さらなる大規模構造の発見に伴って、 私は私の生きている間にも、宇宙の年齢はもう 1 桁ぐらい延びるのではないかと期待している。

大規模な構造は、常識的にはサイズに比例する以上の長時間の形成時間がかかるものである。80年代の終わりに大規模構造が発見されたとき、 800億年から1000億年の時間が必要という言葉の行き交う学会会場の摸様が TV に流されていた。大規模構造は、当時、明らかに膨張宇宙論へ の反論だった。銀河が出来、それらが集合して形成するには、例えば光で 20 億年かかる構造は、10 億年より短期に出来ることはあり得ない。 それどころか、その 100 倍の時間がかかって当然である。しかし、1000 億年の形成時間は、膨張宇宙ではあり得ない長さである。

これを膨張宇宙論では、初期宇宙の数億年以内に大構造を作る。大構造ほど初期宇宙の早期にもっていき、そのことの成否を疑わない。かりに 宇宙の果てまで大構造があっても、初期の時代にあったとするであろう。膨張の間に構造形成するには、質量の非一様性の互いの重力による 収縮がその時点の膨張を超える必要がある。背景輻射は、等方一様な2.7Kの黒体輻射であって、10^-5 の程度に一様な温度(エネルギー密度) が永く宇宙膨張の証拠といわれて来た(一方、これは地平線問題という別の疑問を生むが)。もし例えば、宇宙の晴れ上がりの背景輻射の非一様性 が 10^-2 もあれば、非一様性は発達して現在の大規模構造や銀河の構造を生むのに支障がないが、10^-5 からの発達は無理なようである。そこで、 数10万年当時にもダークマター存在を仮定し、そこに大きな非一様性を有していたと仮定する。当時の物質は一様だが、ダークマターは非一様とする。

２.１ 必要な非一様性はCDMに

最近は、背景輻射の時代に背景輻射以上のゆらぎが CDM にあったと仮定して CDM で大構造を説明しようとする。存在している10^-5 の背景輻射 のゆらぎから大規模構造を説明できないから、観測できていない当時の CDM に必要なゆらぎを預ける。そのような未確認粒子に頼った仮説は、 どれほどの確かさをもつのか何をしているのか反省すべきである。CDM の素粒子としての種類、その素性に全く手がかりがないのに、何かの反応を 予想して検出器を作り、それを直接検出しようという調査が注目され、銀河系中を太陽系が進行する季節変化を捉えたという報告まである。

1999年イタリアのグループがアペニン山脈のグランサッソー山の地下に設置した装置を用いて季節変化を検出したと主張したが、追認されなかった (マーチン・リース著、青木薫訳、"宇宙の素顔"、講談社)。これで測定しようとする静止したダークマターも、それが質量を持つなら銀河系の回転 曲線にすでに出ているはずである。「季節変化」というとマイケルソン・モーリー実験のエーテル探索の残党、特殊相対論の否定論者の論理のようだ。 周囲の通常物質の運動に関係なく静止するエーテルである。220km/s+-30kmは、まるで絶対静止空間のようだ。銀河系内の太陽系の進行に独立した 銀河系に静止したダークマターを考えるのは、通常物質との相互作用が非常に小さい粒子とするからである。地球の運動と方向によって検出量が 違うほど遅い未知の素粒子を仮定するのである。それはもし発見されたら大事件となる挑戦的な試みである。それは決して確認されないだろう。 その存在すら仮定でしかないからである。(しかし、CDM の存在を仮定しても何ともならない不足分が残っていた。)

それは、物質とダークマターが乖離して存在することを仮定する。例えばニュートリノのように通常物質とほとんど相互作用しない粒子では地球や 太陽程度の厚みの物質を通過してもほとんど速度を減衰しない。ニュートリノが物質よりはるかに軽い粒子(標準理論では静止質量は0だったはずだが、 最近は小さな質量があるとする)であり、光より遅いがほとんど光速であり、ホットダークマター(HDM)という。(1987年の超新星1987Aでは 15万光年先 のマゼラン星雲からきたニュートリノが捉えられたが、光より少し先に到着した。これは爆発の中心部から超新星の物質を先に抜け出すからである。) 通常物質がほとんど停止しているため両者の運動は乖離している。高速に運動する軽い粒子は、互いに衝突することなく、互いの運動を消し去らないから、 重力収縮することは難しい。

逆に、通常物質よりもはるかに重い粒子で、通常物質と相互作用が殆どない粒子を仮定すれば、通常物質がまだ光速に近い速度で運動している時期 に速度を落し通常物質との運動が乖離するという可能性がある。これをコールドダークマター(CDM)という。通常物質とはほとんど相互作用せず、 CDM同士は互いに相互作用する(大きな衝突断面積をもつ)、物質であることが求められる。それは素粒子の衝突実験で検出されたことのない新粒子であろう。

宇宙論がそのような仮定の上に初めて説明できる新粒子を要求(予言)し、その後に新粒子が発見されるなら素晴らしいが、それほど状況はよくない。 宇宙論が望む性質の粒子が容易に存在することはなく、ダークマターはこの分野の何十年の歳月を消費した。以前のモノポール、ミニブラックホール、 タキオン探しと似ている。それほど、CDMは、通常物質から性質が違うものである。

しかし、大規模構造の形成が、大構造ほど短時間という要求は、それ自身、難しいシナリオである。現在、説明できない大規模構造を1/10の過去に 持っていけば 10 倍のサイズの構造形成が説明つくだろうか。そこには 1/10の時間しかないのである。説明が付かないとさらに1/100の過去にその 原因を求める逃げ口上のようである。それでは最終的に最初の1点に構造が必要になる。あるとき一瞬にこの宇宙全体が始まったとする考え方は、 この結果を招く。形成の説明で理論を精密化しようとしても基本的に困難がある。宇宙は、差し渡し20億光年の構造を10億年より短い時間で形成 する普通の物理であり得ないことを許さないだろう。ところがそれが現在行われている考え方なのである。

宇宙論は、恒星と銀河形成を説明するだけでなく、その100倍から1000倍の大きさの大規模構造の形成を説明する必要が出てきた、そのときからすでに 20年が経過し、問題は解決しただろうか。CDMは何かを解決せず、さらにそれ以外のλを必要とすることを知っただけである。そして大規模構造は、 宇宙の果てに近付いてきている。遠方過去において大規模構造が形成途中という進化の証拠は期待されるほどにない。 むしろ宇宙には近傍と区別しにくい時空間的均一性が勝っている。 ("Observational evidence favours a static universe" http://arxiv.org/abs/1009.0953)

例えば Large Structures and Galaxy Evolution in COSMOS at z ＜ 1.1 (http://arxiv.org/abs/astro-ph/0612384) は、COSMOS というリストの 15 万の銀河の調査である。42 の大構造(1x10^11 〜 3x10^13 (太陽質量) を検出。ダークマターを含めると 50〜100倍)。 1x10^13 をこえる大構造は、5 つある。z ＜1.1 と z 〜 2 との比較。 星生成領域の密度の分布に 2 倍をこえる大規模構造の進化はないという。

また、 Large Scale Structures at High Redshift in GOODS Field (http://arxiv.org/abs/0801.3557) は、GOODS-South 領域の過密度のカタログを提示する。z〜2.5 までの全体の領域に散布する構造に埋め込まれた様々な高密度のピークを見出した。 それらの色-等級関係の傾きは、z による明確な進化を示さない。これらの構造を形成する銀河が低密度の領域にある銀河よりもより大質量という 証拠を見出した。また、環境の密度と銀河の特性の多様性を分析し、赤色銀河の密度による分離は、低赤方偏移、高光度においてより強く、 zの増加によってより弱まることを見出したという。

(*)大規模構造に次元 D〜2 のフラクタル性があり、ほとんどの宇宙論の前提である一様、等方の宇宙原理を覆すという。 D.F.Roscoe, "Via Aristotle, Leibniz, Berkeley & Mach to necessarily fractal large-scale structure in the Universe" (http://arxiv.org/abs/0802.2889)

３. インフレーションとダークマター

重大な反証がでてくると、それを説明するために理論の枠組が違っても修正する。そのような歴史をビッグバン宇宙論はもってきた。 解決できなかった宇宙の平坦性 (どんな曲率もありえたのに、どうしてこれほど宇宙は平坦であるのか)と、地平線問題 (どうして一度も 出会っていない宇宙の別の方角が同じ性質をもっているのか）は、インフレーションを使って説明する(*)。

インフレーションの時期に宇宙は、宇宙項(斥力項、λ)によって指数関数的な膨張をし、一度光速を追い越している。だから、一度関与し た部分からの光どうしが現在再会しているとする。それによって地平線問題が説明できた。そして、インフレーションの膨大な拡大の結果 として膨張に伴って曲率を極端に下げ、宇宙の空間的曲率は完全に 0 になる。つまり、インフレーションは曲率0の宇宙を生み、 インフレーション後の膨張は、平坦を保つ臨界密度の膨張になる。これによって平坦性が説明できた。

一般相対論の重力方程式は、膨張宇宙の様態を3種類に分別する。臨界密度を超える密度の宇宙は、時空間的に閉じた宇宙であり、ある程度、 宇宙のサイズは膨張した後に時間に対称に一点に収縮するサイクロイド曲線を描く。臨界密度以下では宇宙は時空間的に永久に膨張を続ける。 両者の境目の臨界密度では平坦(空間曲率0)を保ちながら膨張を続ける。宇宙の空間的曲率と膨張のしかたは、宇宙の密度とハッブル定数の2乗 によって決まる。(18章の式(5c)参照。)

つまり、インフレーション後の空間曲率0の完全平坦を与える物質密度(臨界密度)が、インフレーションの証拠として検出されるだろうと予想された。 インフレーションは臨界密度ちょうどの平坦宇宙を約束した。インフレーションがあったなら、空間的に平坦な膨張をする臨界密度だけの質量 がある。何らかの物質、又はダークマターが存在して不足分を埋め合わせ、ちょうどの臨界密度になるだろうと信じられた。ダークマターの存在 と物質が突き止められることはインフレーション理論の予言の実証である。理論は意識される前に現実を予言し、それが後に実証されて正しさが 証明される。それが、次の継ぎはぎのために便利だからではない。

しかし、そのインフレーションが要求するダークマターがどうしても存在しない。平坦であるための臨界密度 ρ_cr に比べて物質密度ρがかなり低い。 見える物質はΩ=ρ/ρ_cr= 0.003 である。宝探しのように銀河間のガスや、褐色矮星などの物質の量が検討された。見える物質の10倍程度の質量は 銀河の腕の運動から推定される。銀河の半径 r に対する回転速度を表す、銀河回転曲線(銀河を横切るスリットのスペクトルシフト、銀河の半分の スペクトルがもう半分のスペクトルとは明かにずれていることによって知る)が、見える銀河の外側ではケプラー回転 v(r)∝ 1/√r (v^2= GM/r) で減少せず、v(r) がほぼ一定に伸びることは、銀河の外側にまで拡がる、半径に比例する質量 M(r)∝ r の存在を示す。 これらが最初のダークマターの発見であり、信頼できるダークマター存在量だが、臨界密度の 0.02(連銀河で 0.04) である。) これは現在いわれるダークマターの量とは全く違う微々たる量でしかない。

1933 年 Zwicky によってかみのけ座の銀河団の速度分散が測定され、見える銀河の質量から 80km/s が計算されたが実際は 1500km/s もあった。 これは見えない質量が輝く物質の 400 倍(現在 200-600倍とされる)もあることを示していた。銀河団内の銀河の運動からは、最大のΩ= 0.4〜0.6 の質量の存在が推定される。このツビッキーは光疲勞説を保持してきた、宇宙膨張を信じない学者である。ダークマターは彼によって半分は発見 されたといってよいが、問題は、それが何か全く不明のままなことである。

通常物質バリオン(陽子と中性子など)では、膨張論の物質形成の理論から存在量の上限(0.01＜Ω_b h^2＜0.02)があり不足する。そこで、それ 以外のダークマターが探された。通常物質でない、例えばニュートリノのような特別に軽い粒子、アクシオンなど未知の重い粒子を仮定する。 存在の可能性の殆どない(現在ある粒子どうしは互いに超対称性粒子ではないから、超対称性粒子はすでに存在確認されていないといけない。) フォティーノまで追求された。どれほどの困難がこの問題にあるかは、1992 年の小玉英雄著の"宇宙のダークマター"(サイエンス社) に詳しい。

不明の存在を仮定しても、ダークマターは 20 数% までであり、大半の不足分 70% を補うことができないと明らかになって理論の枠を外し、 宇宙項をダークエネルギーと呼んで物質密度の代わりをさせ、平坦に必要な差の分を説明させる。ただし、宇宙項は膨張の仕方を変え、宇宙の 将来の姿を変える。それはまた、宇宙年齢の矛盾に対しても、膨張論に好都合の結果を生むのである。

３.１ 臨界密度

半径70万kmの太陽の密度が1.4程度(r= 7.0 x 10^10 cm, 太陽M= 2.0x 10^33 g から密度 1.4)から、太陽近辺は、臨界密度からは極端な 物質集中をしている。太陽近傍の恒星間の物質密度は、0.1 太陽M/pc＾3 である (10 立方パーセク(pc=3.26lyr)に一個の太陽である)。 臨界密度の太陽質量単位、2.77 x 10^11 太陽M/Mpc^3(= 2.77 x 10^-7 太陽M/pc^3)と比べ、10^6倍も大きい。銀河系内側はもっと密度が 高く外側は密度が低い。太陽系の銀河系中心を半径8.5kpcで公転する速度220+-10km/sから太陽近辺までに1000億(その2倍の半径には2000億) の太陽質量である銀河系の内部密度は、1x10^11太陽M/(4π/3 x 8.5^3 x 10^9)= 3.9 x 10^-2 [太陽M/pc^3](太陽より内部) 〜 1 x 10^-2 [太陽M/pc^3]であり、これは臨界質量の10^5倍である。しかし、平均の銀河間距離を銀河サイズの100倍とみるなら宇宙の密度は銀河内部より 10^6倍も小さい。宇宙の臨界密度は、宇宙においては到達できない高過ぎるハードルであった。

宇宙の物質密度測定は、ハッブル定数の測定よりずっと難しい。アインシュタインは、曲率が正になる物質密度であることを望んだが、 それは輝かない物質の量の推定が難しいからである。一度、正の曲率と判明すれば、さらに暗黒物質が後に発見されても定性的な結果は 変わらない。その逆ではつねに結論が逆転する可能性を秘めている。しかし、事実は昔から物質は、臨界密度よりかなり少ないことが 明らかで、ミッシングマス問題と呼ばれてきた。臨界密度は、ハッブル定数の2乗と関係するから、アインシュタインの時代からいえば ハッブル定数が 1/10 になったことによって、空間曲率を0にする臨界密度は、1/100 になったが、それでもまだ物質は不足していた。

ハッブル定数の2乗と物質密度ρの関係で空間曲率が決まるから、今言われる臨界密度の4%しかないといわれる通常物質だけで空間曲率を 平坦にするにはハッブル定数の推定値を 1/5 にすればよい。これが最も単純に矛盾を解消する方法である。 (ヴァージニア・トリンブルは、すでに近くに来ている。50+40-30では20までOKのようだ。 通常 75 の 1/3.75である。) しかし、そのような矛盾解消の必要はインフレーションが約束する平坦性から来ている。

３.２ 平坦性と地平線問題

しかし、インフレーションは "平坦の地" を約束した。それは、平坦のための密度がオーダー(桁)として合っていればよいという一致ではなく、 よく測定すれば宇宙はきっと "完全に" Ω= 1 なのだ、という信念が多くの心を占有した。負の曲率を導くようにインフレーション理論の方を 現実に合わせるようなことでは十分でなかった。すでに、ダークマターCDMと宇宙項λが平坦のための不足分を埋めるために駆り出され、 ぴったり Ω＝1 が実現する宇宙が探られている。

地平線問題も、別の方向の背景輻射が始めて出会うとき、どの程度の一致をいうのかという基準がない。10^-5 は小さいのか大きいのか。つまり、 平坦性と地平線問題は、膨張宇宙説に対する、漠然とした定性的反論なり不安だったのだろうか。いや、ことの本質はそれでもない。むしろ、 インフレーションが提案された当初から解決が主張された地平線問題と平坦性問題は、それまでほとんど問題とされなかったことである。 背景輻射を取り上げたピーブルスがインフレーションがこれらを解決したという以前に、それらが宇宙論の重大な問題として膨張宇宙論を疑う議論 があっただろうか。上手な宣伝マンは、元もと問題なかったのに、こんな深刻な問題が解決すると言う。この理論はふたつの実証を携えて登場した。

実際、インフレーション理論の必要のためにダークマターが探され、未解決である。これは、事実による否定ではないか。先に平坦の事実があって ダークマターが必要とされたわけではない。空間曲率には測定の歴史はハッブルの仕事以外にほとんどないことを思い出してほしい。空間曲率は 小さいサイズで小さく現れる。宇宙的な規模に正負の曲率があっても銀河程度の規模ではつねに平坦である。身近な空間からこの宇宙の空間が 平坦とアプリオリ(先験的)に思ってはいけない。ところが、初期宇宙の理論から、背景輻射の空間パワースペクトルの 1 度程度にピークがある ことを平坦宇宙に結びつけるのは無理矢理の感である。初期宇宙の理論だけから導出される空間曲率は、測定といえる性質のものではなく演繹である。 それ以前に、遠方の銀河の分布、背景輻射と遠方銀河との間の天体などから空間曲率の測定結果を積み上げて帰納的にいうべきことである。 ハッブルは彼の後半生をその銀河分布と宇宙の曲率の測定とに捧げ、静止宇宙の場合に平坦で限りなく、膨張の場合に空間が狭くなって膨張の分だけの 曲率が必要になることを知って静止宇宙を採用した。それを誤りという後継者(A. Sandage)がそのことを伝えている(4.6参照)。

４. ハッブル定数

４.１ 宇宙項とハッブル定数

膨張の速さから始まりの時刻が求まり、現在、加速膨張しているとすると、宇宙年齢を長くできる(*3)。ハッブルの定数(後退速度 /距離)は、その逆数が宇宙年齢を決める。宇宙年齢は、ハッブル定数を 100〜50 km/s/Mpc とするとき直線的膨張(*2)で 100〜200 億年、 空間曲率が平坦に対応する減速膨張(宇宙のサイズが t の 2/3 乗に比例)では、その 2/3 の 65〜130 億年になる。

ポール・デイヴィス著の "時間について" (林一訳、早川書房)によると、ハッブル定数は、ハッブル自身の測定では、540 km/s/Mpc (メガパーセク)(1 pc= 3.26 光年)であったが、その後継者の天文学者、アラン・サンディジは、1952 年に一桁小さい 50 km/s/Mpcを採用した。 その 100万光年あたり 15.337 km/s は、光速の約 2 万分の 1、その逆数は、200 億年、減速膨張を考慮する宇宙年齢は、130 億年になる。 それに対して、ジェラール・ド・ヴォクルールは、ハッブル定数を 100 km/s/Mpc にした。その場合、宇宙年齢は、65 億年になる。 現在は、両者いずれかの派に組するか、新しい測定から 70-80 の値を使う。1994 年 10 月のハッブル宇宙望遠鏡 (HST) の測定値は、 約 80 km/s/Mpc であり、減速膨張での宇宙年齢は、80 億年である。この宇宙年齢は、すでに誤差として耐えられる範囲を超え、 抜き差しならない矛盾の状態として、ポール・デイヴィスは、アインシュタインの "人生最大の誤り" を "彼は最初から答えを知っていた" と変え、宇宙項を導入し、年齢を 2 倍以上に延長する。"時間について"から引用する。

年齢の問題は宇宙膨脹の割合が”あまりにも”速すぎるという事実から生じる。宇宙が速く膨脹すればするほど、それが圧縮された ビッグバン状態にあったのはそれだけ最近だったということになる。膨脹の割合はスピードを距離で割ったものである。ハッブル自身は、 540km/sec/Mpcという値を与えている。(中略) もっともハッブル自身は前に述べたように計算を間違えていたのだが。ハッブルの学生で 技術にたけ、献身的なアラン・サンディジは、膨脹割合の測定に生涯を捧げた。サンディジは、多くの人にはアメリカの古参天文学者と いうだけで通り、ハッブルの当然の後継者と見なされた。彼は長年、50km/sec/Mps という値を採用していた。不幸なことに、テキサス 大学オースチン校のフランス生まれのジュラール・ド・ヴォクルールに率いられた別の天文学者グループがこの数字に激しく反対し、 もっと大きな100という値を採用した。違いは決定的だった。もし50が正しければ、アインシュタイン・ドジッター宇宙の年齢はほぼ 130億歳となる。ことによると、最古の星の年齢に関する天文学者の推定は多少いい加減で、利用できる時間内に納まるのではないだろうか? だがもし、100が正しければ、宇宙はたった65億歳だということになり、矛盾は目を剥くようなものになる。

奇妙なことに、最近にいたるまで、天文学者はどちらかの陣営につく方を好み、サンディジとド・ヴォクルールの値の平均を取ろうと するものは少なかった。しかし、データに関するいくつかの注意深い解析の結果、値は今では70か80の辺りの落ち着いている。 だがもし、アンシュタイン・ド・ジッターモデルが正しければ、これでも依然、星の年齢とはうまく折りあえない (80ならば年齢は80億歳をわずかに超えると計算される)。 またしても、宇宙は自分自身のいくつかの部分よりも若いという、不合理な結論が押しつけられようとしているように見えた。

ハッブル定数は、1929 年から最近までで 1/10 になったが、1960年代から1990年代まで種々の測定でまだ、2 倍の誤差 (50〜100 km/s/Mpc) を埋められない。(これには最も信用できる距離測定、セファイド変光星の周期を標準光源にする方法の精度が2倍ほどの誤差をもつからである。) 膨脹宇宙論の最重要な定数、ハッブル定数ですらこうである。ましてガウスが夢見た宇宙の空間的曲率の測定や、物質密度ρの推定はさらに難しい。 ハッブル定数Hの2乗と密度ρの関係で曲率が決まるので、曲率と密度の不確定は、ハッブル定数の不確定の2乗ほどでて当然であり、それ以上に、 宇宙項λは存在するのかしないのかすら、全く分からないものである。(一般相対論では存在が任意であり、量子論ではその大きさが10^120 も違う。)

(*) バーデやサンディジの修正は、ハッブル定数(速度/距離)を求めるための距離測定の標準光源の問題であり、距離の過小評価だったのだから、 赤方偏移の測定の問題ではなく、ハッブル定数は0とか負の可能性はないと思う。ハッブル(1929)は、多くのデータが彼の測定データではなかったし、 当然採用すべき値も省かれたりしたが、他に不可解なデータ処理をしていない点でハッブルは信用された。それまで同じ主張をした人々と異なって とA.サンディジはいう。 4.6参照

(*1) 減速膨張
フリードマン宇宙解は、宇宙項なしの一般相対論の宇宙解であり、宇宙膨張には物質密度の影響があり、それが宇宙の時空間の有限性を決定する。 物質密度の大小によって空間的な曲率が正の有限宇宙、平坦な臨界宇宙、負の無限宇宙ができる。それらの中の臨界宇宙にあたる減速膨張では 宇宙が空間曲率 0 (平坦)となる臨界密度を保ちながら、永遠に膨張を続ける。減速膨張では重力の影響はニュートン力学的な抛物線ではなく、 宇宙のサイズが時間の 2/3 乗に比例する G ∝ t^(2/3) 宇宙になる。この減速膨張は、最もあり得る膨張と永く考えられて来た。 宇宙年齢は、ハッブル定数の逆数の 2/3 になる。

(*2) 直線的膨張
物質が一点から様々な初速をもって四散する重力を考慮しない慣性的な膨張をいう。ニュートン力学的な宇宙膨張もこれであり、フリードマン 宇宙解ではρ= 0 の極限にあり、空間が時刻に比例 (G ∝ t) する。宇宙年齢はハッブル定数の逆数である。

(*3) 現在の宇宙のサイズ G の傾きを過去に向かって直線または曲線で伸ばし時間軸との交差を宇宙の始まりとすると、減速膨張のG= t^(2/3) では始まりからの時間は、直線膨張のそれより短く2/3になる。逆に宇宙項による加速膨張は、指数関数を基本にする式であり、始まりからの 時間を長くする。例えば、f(x)= 0 の解をニュートン法で求めるときδx= -f(x)/f'(x)、x_n+1= x_n + δx を繰り返すように、ハッブル定数は、 G の傾きを G で割った G'/G 、宇宙年齢の逆数の1次推定であるといえる。G'/G= r/t から logG= r logt + C、G∝t^r。 G∝ t^r の宇宙年齢は、t= r/(G'/G)、ハッブル定数の逆数の r 倍である。

４.２ 宇宙項(斥力項)

以前に天文学者は、ダークマター問題に宇宙項を使う説には見向きをしなかった。それは禁じ手、最終手段であった。宇宙年齢の矛盾を 避ける代わり、CDM だけでなく、よほど危険な未知を登場させるからである。膨張宇宙論における宇宙項の導入は、彼が定常宇宙論のために 宇宙項を導入し、それを後に人生最大の誤りとした、当時の思想、＜余計な項を除くことが宇宙膨張の説明の成果をもたらした＞ "宇宙項なし"のフリードマン宇宙論を基本的筋書きとした宇宙論の文脈を崩す。アインシュタインは、ド・ジッター解が定常のため以外に 宇宙項を使ったことを批判し、余分な宇宙項を使用せずに宇宙膨張を導いたフリードマン解を了承した。現代の宇宙論が宇宙膨張を論じ、 しかも (変動する) 宇宙項を必要にする事は、それまでの宇宙論を崩壊させている。

2階のリッチ曲率テンソル R_ik とスカラー曲率 R から作られる、アインシュタイン曲率G_ik = R_ik - 1/2 g_ik R が運動量エネルギー テンソルT_ikと宇宙項λから求まる重力方程式、G_ik - λ g_ik= - κ T_ik では、κT_ik に -λg_ik が加わる。つまり宇宙項は、 物質のエネルギー(T_00＝物質密度ρ) κ T_00 からλ g_00 を削減する働きをもつ。λは外部パラメタとして式に入力し式はλを出力しない。 λは時空に影響し、時空はλに影響しない。宇宙項λからの影響は宇宙の一生への一方通行である。一般相対論にはλのダイナミズムは外部 であり全くの未知である。定常という宇宙原理のために0以外の値を宇宙項に設定して、ρとバランスを保つようにしたことでアインシュタイン 宇宙は非難された。ならば、自分の都合に合わせて宇宙項の時間的変動をいれるのは、非難されないのか。いや、それはもはや科学ではない。 それは重力方程式の目的である、宇宙の変動説明の主要な部分を、方程式以外の未知の存在に預ける、探求からの逃走である (参考)。

λを観測事実と思わせられている我々は、真実から最も遠いところに追いやられている。宇宙項はなぜか今だけその差の分、必要な密度差 に一致する。例えば、現在の 1/10 の時刻には、減速膨張では宇宙のサイズが(1/10)＾(2/3) であり、臨界密度は、今の 100 倍であり、 現在と等しい宇宙項では、空間を平坦にする量の 1/100しかない。あなたの都合がよい宇宙では、宇宙項は常に臨界を保つように不足分を 与えるのか。アドホック(一時的)な妥協としか見えない。

４.３ ハッブル定数とその線型性

遠方銀河からの光が赤方偏移をしている。一般的傾向として遠方ほど大きな赤方偏移があって、それが光のドップラー効果と解釈すれば、 赤方偏移は、遠方銀河の後退の速度に対応する。ハッブル(1929)によって発見された、測定から予想される比例関係、後退速度 v として 表された赤方偏移が距離 d に比例している。(ハッブル(1929)は、横軸に距離、赤方偏移を速度の単位で表して縦軸にした。)

v= H d

つまり、遠方の天体が我々を中心に我々から逃げている。何か宇宙的な疫病が流行っていて、ここが特別な恐ろしい場所のため、宇宙全体が 逃げている。遠方ほど大きな速度とは、遠方にある天体は早めに逃げ出したため、加速し速度を得たのか。遠方の速度が大きいのは、最初に 等加速度運動と思うだろう。しかし、天体の加速度運動は理由があり得ないし、我々は直接測定し得ないが、加速運動では銀河分布が一様で なく遠方ほど疎らになる(残された天体が少なくなるなら帳消しされるかもしれないが)。加速度一定で時間に比例する速度の運動では、速度は 距離の1/2乗に比例する。距離に対する速度の増加は緩くなり、ハッブル定数は遠方で小さくなる(*1)。「早目の退散」は誰のアイデアだろうか。 私はハッブル(1947)で読んだと記憶していた。訳

赤方偏移は、最も容易には地球から離れる視線方向の運動の証拠と解釈されるー星雲たちが我々から全ての方向に逃げ去っていて、 それらがより遠くに去ったものは、より速い速度をもって退いていることの証拠であると、この解釈が、膨張宇宙の理論にそれ自身、 直接に貸与している。その解釈は、全面的には受け入られていないが、我々の最も慎重な人でさえ、赤方偏移は、膨張宇宙か又は、 今まで知られていない自然の原理の証拠であることを承認する。

「それらがより遠くに去ったものは、より速い速度をもって退いていること」は、早めに退散を開始した者が遠方に高速で去っていることを 意味してはいないようだ。あるとき一斉に様々な速度で逃走をしたことを表しているととるべきだろう。これはニュートン力学的な膨張宇宙に近い。

ニュートン力学の膨張宇宙で、あるとき空間の1点から天体は一斉に爆発し、様々な初速をもった点が四散すると、爆発後は個々の粒子は速度一定で、 初速を保存する。爆発後はつねに速度の近いものが近くにあって、互いの天体の速度差は、互いの距離に比例する。つまり、ハッブルの法則の成立 する宇宙ができる。しかしそれでは、宇宙の膨張を始めた点が特別な場所になってその影響が残るだろう、宇宙の爆発の原点が不動点として宇宙の 全ての点が見るのではないか、という疑いは確ではない。それが中心から離れた点で時間が若いなら、銀河が一方に偏って見える "エッジ効果" を観測でき、この場所の宇宙のなかの位置を知ることができるかもしれないが、この一様原理を失うようなニュートン的な膨張宇宙でも光速の 観測限界を導入すればエッジ効果はないかも知れない(*3)。 我々は観測領域のなかにエッジ効果を全く見出さない(参照Virginia Trimble)。

「もしかして、どこもこのように見えるのではないだろうか」と、この空間点の特別な異常は全く正反対のことを根拠なく想像させた。宇宙全ての点が 原点である均一な膨張、宇宙のどの場所も対等な "一様" な膨張と解釈できる。この場所の特別さから、これがどこでも成立する宇宙ではないか、 この場所が特別である確率は無限に小さいと想像するのは、偉大な想像力(又は都合のよい合理化)である。空間に特別な点を設けてはいけないという 宇宙原理である。しかし膨張は、時間に特別な点を設けない宇宙原理を破棄している。

我々は子供のときから宇宙膨張をそう教えられ、銀河を表す水玉摸様のゴム風船の宇宙の写真を示された。このゴム風船を膨らませるとき、風船の表面 の2次元宇宙では、どの銀河も他の銀河が遠ざかり、遠い銀河ほど大きな速度で逃げ去るように見える。つまり距離に比例する速度は当然に思える。 それは単に、宇宙全体の膨張であるというのである。

しかし、それ以外の解釈もある。例えば、光が長時間空間を飛ぶとき、エネルギー喪失を全くしないだろうか。光の疲労説(tired light)は、距離又は飛行 時間に比例するハッブルの法則をそのまま与える。又は、宇宙は、現在まで時間の進み方だけが徐々に加速していっているのではないだろうかという、 時間加速説も光の飛行時間に比例するハッブルの法則を自然に与える。存在するにも関わらず他の解釈は、我々の世代には全く教えられず一つの解釈 だけが支配してきた。そしてその現象の発見者であるハッブルの解釈さえ無視された。膨張宇宙論の歴史は、少しく血生臭い。サンディジとツビッキー の娘の対立など、正常な学者の関係ではない。激しい思想の対立は殆ど憎悪である。そして、このような分野における思想の支配は、 工学におけるような実証によるものでなく、整合性の優位性という不明な原理をもって行われる。

我々は、もし、速度が距離に比例しないなら、逆にこの場所を特別扱いする("一様" 原理を失う)宇宙といわれ(*2)、それが方向によらないことは、 宇宙が特別な方向を持たない"等方"の表れで、そのことは時間を遡れば、宇宙が一点から膨張してきたことを意味し、我々が始まりのある宇宙に いることを示すと教えられた。

しかし、遠方までハッブル定数が一定というのは、膨張説では不合理である。赤方偏移と距離との比例関係を遠方まで保つことはできない。 光で見る遠方は過去であるから、遠方のハッブル定数は大きく、速度が距離に比例するよりも大きくなる。これは単にハッブル定数が宇宙年齢の 逆数であるから、現在の 1/2 の時刻のハッブル定数は現在の2倍であり、見られる側の時刻の空間における距離と速度の関係は、見る側の現在の ハッブル定数の関係ではないことによる。遠方のハッブル定数

このハッブル定数の線型性からの外れは、過去が現在と異なる膨張説だけに要求され、光の疲労説、時間加速には要求されない。ハッブル定数が 2倍になる現在の時刻の1/2では、速度はまだ小さいので、これを原因とする非線型は、相対論的速度合成による非線型よりも、先に(低いzで)現れる。 そのため、その違いが明確になる遠方まで線形であれば、膨張説に対する反証となる。

アラン・サンディジが 1989年(ハッブルの生誕100年)にハッブルの業績をまとめた文章、 エドウィン・ハッブル 1889-1953 ( 訳 )にいう、

ハッブルが彼の書き物の中でどこにも書かなかった中心的な重要性は、赤方偏移ー距離法則の"式"の"線形"性 である。この単純な特徴は、 標準モデルにとって最も厳しい。

勿論、速度には光速の限界があり、相対論的な速度合成の非線型がある。速度合成は v, u が光速を単位にする速度のとき合成速度は、v+u でなく (v+u)/(1+vu) である。加算は速度が光速に比べて十分小さいときの近似であり、速度が光速と比較できるほどの遠方では外れる。 また、相対速度vと赤方偏移1+zの間のドップラー効果には非線形 1+z ＝ √((1+v)/(1-v)) がある。また、遠方天体の距離推定にも非線形がある。 それら付随要因を除外しても、膨張説には固有の非線型がある。一様性と線型性は付随しない。膨張説は一様を原理にするが、線型性を満たさない。

(*1) 速度vは、退散し始めてからの時間tに比例し、距離xは時間の2乗に比例するから、v^2/x= 一定、距離xと速度vは比例しない。遠方ほど ハッブル定数が小さい。しかし、過去のあるときから物体の等加速度運動が一斉に始まったなら、ハッブル定数は時刻tに反比例する。 個々の銀河によって加速度aが違わないと銀河が天球を形成する。a分布が一様のとき、遠方ほど銀河の空間分布は疎らになる。

v= at, x= 1/2 at^2
v/x = 2/t

「遠方ほど早めの退散」は、距離大は、退散開始からの時間が長いと考え、ハッブル定数v/xは退散からの経過時間tに反比例する。tは速度vに 比例し、v^2/x 一定で v/x は遠方ほど小さい。逃げ始める時刻の違いで銀河は空間的に分布するから、加速度a= 一定でよく、銀河に分布して 与えずにすむから、時空、特に宇宙項を原因とする後退、定常的な空間膨張になる。しかし、銀河の逃走開始が時間に一定に発生するなら、 銀河分布が遠方ほど疎らになる。空間的に一様な銀河分布にするには、退散の時間分布を一様から変えるか、宇宙項が変化したとするかである。

(*2) 赤方偏移が距離の 2 次に比例するといわれた ド・ジッター宇宙も一様等方な宇宙原理から作られた宇宙モデルである。 距離に比例する速度だけが一様性を満たすのではない。彼らがそれを金科玉条のようにいうが、膨張説こそ線型性を満たさない。

(*3) ニュートン的な膨張宇宙での光速の観測限界の導入は、単に空間的距離が大きいことだけで起き、宇宙の始まりとは関係ない。そこに見える 光速に近い後退をする天体は、宇宙初期である必要はなく、宇宙の現在より若いどの段階でも距離と速度の比例関係をもつ。その比例係数、 ハッブル定数は爆発の始まりからの逆数になる。特殊相対論を導入して、光速に近い後退をする部分の時間経過の遅延が起き、宇宙初期の天体像 になる。

４.４ Tolman Test 銀河輝度と赤方偏移

日本の多くの解説のように、宇宙膨張が現在まで全く疑問の余地のない歴史をもち、それ以外の考え方、意見は現在まで成功しなかったと検討 する価値がないようにいうのは間違いで、多くの別の意見もあったし、いまもそれらは選択肢としてほとんど対等に存在する。膨張説もその中に 大きな問題を抱えている。

そして問題は、この宇宙膨張という多数意見に我々は大きく影響されてきたことである。大きなハッブル定数は、短い宇宙年齢を示し、天体の 年齢と矛盾して、宇宙膨張に対する疑問を提示するから、天体の年齢と矛盾しないようにハッブル定数測定は、(アラン・サンディジのしたように) 小さめの値に調整され、宇宙年齢を伸ばそうとする。逆に天体形成説明も、宇宙年齢と矛盾しないように短めに調整する。球状星団の年齢測定 において宇宙年齢との矛盾が起きやすく、それを避けるために(例えば宇宙項の存在を初めて観測したという High-Z グループが最初にしたように)、 球状星団の測定結果の再検討がなされる。

測定がそうして、考え方に影響されて偏っていく。このことは明確に言えないが、天体 (恒星、銀河や銀河団、大規模構造) の形成が短時間にされ、 不足する形成時間は、宇宙の初期に先送りされ、その矛盾は、物理的観測のほとんどない初期宇宙の過程に集中されていく。それでも、天体形成 時間に無理がないわけではなく、ぎりぎりあり得る最小の期間しか与えられない。しかし、宇宙全体についての仮説がより身近な天体形成の理論 と観測結果を左右することは、その逆の過程しか許されるべきことではないのではないか。

４.５ クエーサーの赤方偏移

彼によって多く発見された、銀河から放出されたようにみえるクエーサをみると、彼の説は一考に値する。それを単に異常にまれな偶然によ って視線が接近しているだけであるとして、観測を否定しようとする批判に対して、そのあり得ないほど小さな確率の割りに、その観測数が 多いことが示された。天体が生まれたとき(対生成した)物質から出る光が赤方偏移していて、天体が成熟するとそうでなくなるという仮説が 彼から出されているが、それでなくてもブラックホール周辺からの放射は、異常な強度の重力赤方偏移を持ち得ることが想像される。

我々は、銀河形成の過程を具体性をもって知ることができていない。そして、クエーサー、銀河の相互作用、活動銀河核、爆発する銀河など、 説明の付けられない現象を多く抱えたまま、単純で居心地のよい仮説を擁護するために辻褄合わせを繰り返してきた。大きな赤方偏移をもつ クエーサが遠方にあって、宇宙の初期に存在した銀河の初期形態と考えられた。しかし、宇宙の遠方はクエーサーではなく大きな赤方偏移を 示す成熟した銀河に満ちていた。そしてクエーサーは、いま、銀河の後期現象とされている。

最初、QSO は、点状の電波源(QSS)として発見された。(1959年発行第3ケンブリッジカタログで、471個の 3Cで始まる名で呼ばれる。南天は シドニーカタログがある。) 電波強度が大きく1秒以下の点状の電波源(3C48, 3C147, 3C196, 3C273, 3C286)で、可視光で対応する恒星は、 スペクトルが全く特定出来なかった。それが大きな赤方偏移3C273は z=0.16, 3C48は、z=0.37 のスペクトルとして解釈できることがわかり、 銀河系内の天体の重力赤方偏移では 10^-4 程度であった白色矮星とは桁違いに大きく、しかも、そのような天体は輻射が弱く観測できるも のでないはずであった。銀河系外天体としてみると、ハッブル定数(75km/s/Mpc) を適用すれば距離は、3C273 は、600Mpc、3C48は、1200Mpc にもなる。その場合、3C273が 13m、3C48は、16mであり、絶対等級は、銀河系の吸収を計算にいれて、-26.5m, -25m になる。これは超巨大 銀河の100倍もの光度である。実視直径が小さいから大きな距離を考慮しても実際の大きさは、1000pc, 5000pc である。

クエーサーの赤方偏移は、それが重力によるものであれば、中心天体がブラックホールや中性子星でないと起きないほどの大きさであり、も しそれが宇宙膨張とハッブル定数に従う遠方なら、超巨大銀河の100倍もの光度でありながら、3C48では光が数ヵ月程度で30%も変化した。 過去の変動も確認された。そのため、それが差し渡し 1 光年程度の実際の大きさ(銀河サイズの 10^-5) でなけらばならない。重力赤方偏移 でもドップラー効果の赤方偏移でも、時間経過の遅延は赤方偏移に伴うから、赤方偏移 z= 5 の 1 年での変光は、その場所では1/(1+z)= 1/6 年の変光である。3C9 は、z=2.012であった。ハッブル定数(75km/sec/Mpc)を適用して 3000 Mpc になる。その後、同様のスペクトルをもつが 電波源でないQSG(恒星状銀河)が多くみつかり、QSSはQSGの一時的な状態であると考えられた。

少なくともクエーサーは、銀河の赤方偏移と距離の関係から外れているだろう。その赤方偏移には重力赤方偏移による部分が大きいと思われる。 クエーサーは、銀河から生み出される卵のような銀河に付随する現象かもしれない。銀河中心のブラックホールは銀河系の中心部の恒星の周回 速度から存在が分かってきたが、銀河形成のなかでのブラックホールの役割の説明は容易でないと思うが、クエーサーは、それに関係すると思われる。

最近 H.Arp は、M31 (アンドロメダ銀河)の近辺に多くあり、付随すると考えられる、円弧状に並んだ暗い(z=1〜2, m=17.5〜20) クエーサー列 の存在、M31の短軸(渦巻の軸)上にある幾つかのクエーサー(m=16.6〜18.4, z=0.12〜1.7)を報告している "M31 and Local Group QSO's" ( arXiv 0706.3154)。いくつかは絶対等級が-23以下でないから、クエーサーと扱われず銀河 になる。最も近い渦巻銀河にも内在的な赤方偏移のクエーサーが伴うという話は、クエーサーを銀河の初期段階として、銀河進化のために遠方 にしかないという膨張説側の議論の完全な否定である。

"Dark Energy and Hubble Constant" arXiv 0712.3180) ダークエネルギー再加速の話は、 遠方銀河(z〜0.35)で測定したハッブル定数測定 (Shafieloo 2007) が、近傍の測定値(72km/s/MpcFreedman et al.2001) より小さな値(H= 65km/s/Mpc) を示しただけであり、近傍の測定もまだ多くの説(例えばアラン・サンディジや Gustav Tammann の 55km/s/Mpc)がある。

いかに精度のない測定が、さらに不可解な説に使われているのかと思う。私はハッブル定数は遠方過去には大きいはずで見掛けの減速膨張を見る、 ハッブル定数を定数とすることは、遠方では理屈に合わないと考える。 H. Arp は正しくハッブル定数を赤方偏移の関数 H(z) とした。再加速の 話は、この遠方でH0が大きいはずという説と逆方向の変化、遠方でH0が小さかったという観測である。超新星 Ia型によるz= 0.35 のハッブル定数 測定が信用できるとしても、10%程度の違いは、誤差の範囲内で一定とみなすべきだろう。しかしもし、さらにz= 2, 3までこれが定数なら、もっと 困ったことになるだろう。この論文の図1は、セファイド距離と赤方偏移上に散布した銀河にハッブル定数だけ傾斜する直線をあてることが不自然 なことを見せる。また遠方になるほど、Hが大きく、広がりも大きく、広がりの比率も大きくなることを示すように見える。

"Arguments for Hubble Constant near H0= 55" http://arxiv.org/abs/astro-ph/0106466

４.６ ハッブルの沈黙

"Observational Cosmology: caveats and open questions in the standard model", Martin Lopez-Corredoira が、ハッブルの言葉を引用していた。"it seems likely that red-shifts may not be due to an expanding Universe, and much of the speculation on the structure of the universe may require re-examination" (Hubble, E. P. 1947, PASP, 59, 153.))(*) (拙訳)

そして、NASA のサイトに公開されていた、1920年の大議論と同じ会場で行われた、宇宙のサイズについての 1996年4月の大議論は、 Shidney Van Den Bergh 。と Gustav Tammann 。との間で行われ、モデレータは、 John N. Bahcallで、招待講演を Virginia Trimble と Owen Gingerich が行っている。

そのサイトに E. Hubble の1929年の論文、 http://antwrp.gsfc.nasa.gov/diamond_jubilee/d_1996/hub_1929.html があった。( 訳 ) ハッブル(1929) は、距離に対する速度の図を提示し、その傾きが "ハッブル定数" の直線を与えたが、ド・ジッター宇宙の赤方偏移が距離の 2 乗に比例する特性を知り、その最後の段落で、(赤方偏移が距離に比例するのは、) 観測した "距離の制限された範囲を表す 1 次近似である" として、ド・ジッター宇宙の 2 次式がモデルであることを示唆している。

そして、アラン・サンディジ(AS)がハッブルの生誕 100 年記念に 1989 年に書いた文章、 Edwin Hubble 1889 to 1953 もそこにあった。( 訳 )

ハッブル(1929年)は、もし、さらに遠方を測定すれば 2 次の項が明確になることを予想していた。しかし、その後、さらに遠方の結果においても 距離に線形の赤方偏移があることが分かった。(ASによれば)ド・ジッターは、自らのモデルが現実と合わないことを認めたとされる。ハッブルは、 論文に言及はないが当時、静的宇宙解以外に、動的宇宙解の存在も知っていたと思われると、1929 年以前にロバートソンと議論したと、ロバートソン がアラン・サンディジに語った。(ルービンとサンディジの Tolman test の論文 IV のイントロから、 膨張の証拠(ルービン&サンディジ 2001 年) その原文、 The Tolman Surface Brightness Test for the Reality of the Expansion IV http://arxiv.org/abs/astro-ph/0106566 参照。) は、ハッブルの業績と膨張宇宙についての沈黙と否定を解説している。ハッブルは、宇宙膨張と宇宙の年齢について沈黙し、長年、銀河分布の研究 を続け、実証的に宇宙膨張を否定する観測結果を求めた。以下引用。

もし、赤方偏移が基本的に速度シフトによるものでなければ、...[そのときは、] 速度-距離関係は、線形であり；星雲の分布は均一である；膨張 の証拠は、なく、曲率の跡はない、時間のスケールに制限はない... 予想外の、そして、本当に驚くべき特徴は、赤方偏移が後退を計測している という追加的仮定によって導入される。速度-距離関係は、前提とされる後退の正確な量だけ、線形から離れる。分布の均一からの離反は、後退の 量に一致している。その出離は、後退の正確な量と等価な曲率によって補償される。同期性は、多くの要素の間の、背後にある必要な関係の証拠で あるにもかかわらず、それらは、その解釈の蓋然性を実質的に毀損している。膨張モデルの小さいスケール、空間と時間の両方の、は新奇であり、 その受容には、さらなる決定的な証拠を必要とするだろう。

４.７ セファイドと SNIa

ケフェウス座δ(デルタ)星型の変光星、ケフェイド(英語読みでセファイド)の変光は、光度が急激に上昇し徐々に下降する変化をする。 主系列から巨星になったときヘリウム原子の 1個電子を失った"1階電離" は光を通すが、 2個電子を失った"2階電離"は、光を吸収し、 高温になり星は膨張し冷却して "1階電離" に戻り収縮する振動をする。

スライファーがアンドロメダ銀河などの近傍の銀河のスペクトルを測定した(1912〜1914)。アンドロメダ銀河は青方偏移していたが、多くの 銀河は赤方偏移していた。1920年当時はまだ星雲が銀河系の外かどうかが議論されていた。ハッブルはセファイドを使ってそれらが銀河系の 外であることを示し、銀河系外の銀河までの距離と赤方偏移の関係を示した。ハッブル自身の 1929 年の距離と速度との係数は、500 km/s/Mpc (530) であった。星種I(青白)と星種II(赤い)の発見に伴って、対応するセファイド変光星の長周期型と短周期型があって、周期と光度の関係 が異なることが分かり、1954 年バーデによって近隣の銀河の距離は、約 2 倍に修正され、ハッブル定数は半分 250 km/s/Mpc になった。

さらにハッブルが使った銀河内の明るい星が実は星雲だったと、サンディジによる修正もなされ、ハッブル定数は 180 km/s/Mpcに小さくなった。 その後、さらにサンディジは、75 という値、70 年代半ばには 55(誤差10%)という値を出した。70 年代から 80 年代にテキサス大学のジョラール ・ド・ボークルールは、それに強く異をとなえ、100 km/s/Mps を主張した。サンディジは、遠方銀河の中にあるIa型超新星の絶対光度を標準光源 にする新しい方法を使った。カーシュナーも 55 という数値を出していた。

1994 年のウェンディ・フリードマンらによるハッブル宇宙望遠鏡によるハッブル定数測定は、乙女座銀河団の中の渦状銀河 M100 の20個の セファイドを使い、5600万光年というそれまでの測定より小さい距離と 80 km/s/Mpc というハッブル定数を出した。Ia 型超新星の輝度が 同じという仮定によって測定するサンディジの出す 50 km/s/Mpc とは大きく異なる値であった。マーク M フィリップスは、 Ia 型超新星 の明るさは同じでなく、明るい渦状銀河中では光度が大きいことを発見し、カーシュナーは 67 に数値を修正した。マーク M フィリップス 等による 20 個の超新星による結果は、60〜70 という値を出した。

1996年に遠方の距離スケールについての論戦が1920年の大議論を模して行われた。ハッブル定数に70-80近辺の大きな値を出し、宇宙定数を 持ち出すグループと、50近辺の小さな値を出すグループが対立する。
(1) ハッブル定数の歴史、ヴァージニア・トリンブル "H0: 1925-1975 信じられないほど縮小する定数"(1996)、
(2) 大きなハッブル定数、シドニー・バン・デン・バーグ "外部銀河の距離スケール" (1996) 、
(3) 小さいハッブル定数、グスタフ・A・タンマン "ハッブル定数: 論談" (1996)、
これらを読むと、いかにハッブル定数の測定が多くの作業ステップの積み重ねで作られている微妙な数値であるかを感じることができる。

標準光源は距離を知り、ハッブル定数を求めるための最重要な道具である。赤方偏移は、光のスペクトル分析によって比較的容易にその量を測 ることができるが、それとは別に距離を知る方法をもたなくてはならない。セファイド変光星の周期という方法の他には、銀河のなかの星の 最大の光度を一定とみなす方法、タリー・フィッシャー関係という中性水素HIの21cm電波の幅、銀河自体の明るさを一定とする方法、 銀河表面輝度の変化の度合、超新星II型、超新星Ia型の最大輝度、その他、重力レンズ、γ線バーストなどが使われてきた。 一般に非常に明るい現象に一定の性質を見出すことから始まる。明るくないと、大きな赤方偏移のある遠方に存在確認できない。 超新星Ia型は、遠方まで使われる光源であるが、他の方法との差が明確にある小さめのハッブル定数を導くので、 その性質を我々が十分に把握したかどうか疑われる。

遠方銀河に SN Ia を使い、近傍の乙女座銀河団の距離にはセファイド距離を使い、遠方銀河が暗い、ハッブル定数が小さい(〜65) ことから宇宙 が再び加速を始めたとする再加速の議論がある。近傍でなぜ 75 を使い、アラン・サンディジ等の SNIaによる 55 を使わないのか、それを使うと 結果が逆転するからか。2008年に亡くなった Wheelerは再加速に対する意見を、ふたつ述べられた。(1)は、超新星 Ia 型に対する過剰な依存、 (2)は、説明の単純さの欠如であった。解釈すれば、先ず宇宙項の値を現在平坦にするのに必要な値 Ωm + Ωλ = 1 にする。再加速の理由として、 宇宙項が一定なら宇宙がある大きさになれば、空間が大きくなって、宇宙項の影響が大きくなり、自動的に加速モードに入ると考えるのか。 それ以外の理由で、宇宙項自体が変動したのか。z= 0.45の時期に減速膨張から加速に変化したという理由の不明である。また現在、Ωλ= 1 - Ωm である理由がない。平坦性は測定したのか。吸収を無視している。z= 0.45にみえる約50億年前、それまで空間平坦な減速膨張(Ωm + Ωλ= 1) だったのがどうして再度、現在、Ωm + Ωλ= 1 を満たすのか。Ωλが変化したのか。Ωmの計算がどうなっているのか、私には疑問である。 遠方銀河の SN Ia によるハッブル定数測定が近傍よりz= 0.45が若干10%程度小さく測定された。ハッブル定数の歴史的な精度(近年まで約2倍の誤差) から考え、我々はどれだけの意味を、それに期待できるのだろうか。

ハッブル定数の数値は、この数十年につねに論争の種であった。それだけの為の論文が多数ある。ただの数値がなぜこれほど重要だろう。それが 正であれば膨張宇宙は変わらないから、大問題にする必要はない、量が本質を決めることなど普通ない。ところが、ハッブル定数ではそれは成立 しない。大きなハッブル定数は、短い宇宙年齢を導き、球状星団の年齢と矛盾する。小さなハッブル定数は、それ自身の観測と矛盾する。 その数値が多くの考え方の判別の土台になって、それが次の考え方に大きく影響する。大きめの定数は宇宙項を導入し、小さめの定数には必要がない。 SNIaによる遠方銀河のハッブル定数が近傍よりも小さいから再加速が99%あったと主張する説、SNIa は小さめの定数を導くから、近傍にもそれを使 えばその遠方の値より小さく再加速のアイデアの必要はないという説が対立する。

論戦は時間を必要とし世代を必要とする。プロの研究者は、その説の成否が業績であり、異なる考えを認めない固執は共通の性質である。彼らは 一般人に無縁の議論に一生かけ、データは誤りを多く含んでいて、値は違うという発表をその人の死後にじつにその直系の後継者がするという、 天文学的現象の原因は、まさに徒弟制度かもしれない。これは、学術雑誌が査読者に一方的に有利な体制をとる限り、どの分野にも起きる可能性 がある。しかし、さらに遠因としては、観測の天文学が宇宙を論じるからであろう。宇宙を違うように論じるのは宗教を異にするのと同様に、 強い対立を生む。だからこそ、論争が全てここに集中するのである。観測は、一般には宇宙論の成否を左右する客観的な証拠のように思われるが、 私の思うには、観測は実際に歴史的に主観的であり、事実を捏造することさえ多く、論理を組めず辿れない者が事実を盾にする道具である。 基本的に目的又は主張のない観測はあり得ない。そのことを知れば、天文学も少し違って見えるというものである。

局所銀河団とそれ以遠

天の河銀河系が超巨大銀河であることは、それだけで人間中心主義に見えて疑わしい。人間は特別な存在でなく人間の住む場所も特別なはずがない。 つまり、我々の銀河もアンドロメダ銀河も中位銀河にする 3 等級(15.6倍)の明るさの違いに相当する 4 倍程度の距離であればよい。局所銀河群と より遠方の銀河の距離に、現在考える距離に4倍の誤差の可能性はないのだろうか。それがあればハッブル定数は、20km/s/Mpcになり、宇宙年齢は、 減速膨張でも250億年になって全ての問題がなくなる。もしそうなら、ハッブルの時代の測定は何だったのかと思うかもしれないが、それら過去の 測定には正当な理由があったし、誤った考えと測定は訂正されるだけでよい。そして、すでに10倍の誤差が判明しているなら、あと4倍の誤差など 問題ではないのではないか。それほど正確な測定が可能と誰も期待していない。しかし、仮に私のこの夢想の証拠が発見されても最終解決ではない と私は予想する。なぜなら、それは程度の差でしかなく、問題は宇宙に年齢がある限り残るだろうからである。次の難関がすぐに現れるだろう。

５. それなら定常か

そのような不利な面は定常宇宙論にはない。定常側では変動の説明をする必要はない。 逆に定常を保つ機構の説明が必要になるかというとそうでもない。 変動が局所的現象なら、ほとんど無視すべきことだからである。 しかし、定常側が一時提案したクリエーション場は、膨張と定常の折衷案であった。 宇宙膨脹の存在を認め、定常的に膨脹するために非常に微かな物質の継続的生成を考えたのである。 そのような折衷でない、静的宇宙の定常説には少なくとも、背景輻射の説明が必要であろう。 赤方偏移の説明も必要である。膨張説は宇宙の進化として物質形成までを説明しようとしているからである。

誤りであったはずの宇宙項を使うことが許されるなら、定常で物質なしに遠方ほど赤方偏移する、 ド・ジッター宇宙でも赤方偏移は説明できる。赤方偏移に宇宙膨張と始まりは要らないことになる。 ド・ジッター宇宙は、空っぽの宇宙モデルであり、現在の物質密度ではどうなるのか、それらの説明が必要であるが。 そして ド・ジッター宇宙では赤方偏移が距離の 2 乗に比例するのであるが。

定常説が可能であっても、何も生み出さないのではないか。それは、常にデフォールトの状態、もしダメだったら、これに鞍替えすれば いいという代替案としてとっておく存在、を用意しているだけで、例えば、物質の起原を説明する、水素と重水素とヘリウムの現在の比率 を説明する方法を持たないではないか。膨張説は、パラメータを可能なかぎり調節して現実に合わせて現実の比率を「説明する」だろう。

しかし、それが何か意味のある結果を生み出しているかどうかは問題である。それはどこまで無理をするつもりかと疑わせるように思える からである。無限の温度の特異点を使えばこのように説明できるというのは、私には正常な論理に思えない。どこまでも、仮説に仮定を 積み重ねて、説得しようとする必死の行為は、なぜかと疑う。まずは、すべての仮定を一旦は捨て、現実の自らの仮説と疑わしさを認める ことである。定常説は、その蓋然性だけで生き延びている。定常説は新たなことを言わないから、間違いも生み出さない。

我々は定常説に説明性を求めることはできないのだろうか。膨張説は、必死に説明性で支持集めをする。そのうち、中学校高校の教科書に 載るかもしれない。大学の受験も膨張説を認めない限り、受からなくなってしまうかもしれない。米国の教育事情では未だに進化論が教え られない州があるというが、すでに科学的思考は、そこまで衰退したのだろうか。例えば私の娘は、月のジャイアントインパクト説を仮説 としてでなく、事実として習ったという。これは単にそれを教える人の問題ではあるが、何がどの程度の仮説であるかを明確にすべきである。 論文になったから全て受け入れるというのは、異なる考えの存在を知らない者のすることである。宇宙の起原についての研究は、基本的に 殆ど全てが仮説であることを明確にすべきであり、この分野の研究の多くは解決しないまま、次々の仮説を積み上げる(例:λ-CDM)。

最近のCMB偏光のB-mode(磁場に類する回転場)に影響した始源重力波がインフレーションを示す これには幾つの仮説が重なっているか考えてみて欲しい。私が仮説と思うのは、CMB、始源的、重力波、インフレーションの4つである。 それぞれの仮説には先に証拠が必要であり、絡まった新たな現象の提出はこれを解決しない。これがインフレーションの証拠であると きっと主張されるだろうが、ひとつの仮説の証拠を得るのに多くの仮説、前提として認めるには未解明の重すぎる仮定が使われている。 重力波はまだ地上での存在確認がない。 CMBは、ビッグバンの証拠でない。

５.１ 赤方偏移の原因

(1) 過去の時空と、現在の時空の重力ポテンシャルが異なるだけかもしれない。

これは、計量の時間的変化、ダイナミクスをいう点でフリードマン宇宙と同じだが、フリードマン宇宙が計量の空間的係数 (g_ik の i,k= 1〜3) の時間的変化であるのに対し、ポテンシャルは、計量の時間的係数 g_44 に対応するから、g_44 の 時間的変化がいる。過去からの光が低地から来る光のように赤方偏移するならば、過去の時間経過が現在からみると遅く、 これは、(4) の時間加速と同じである。ド・ジッター宇宙解も x^4 の時間的遠方で g_44 が大きいという性質をもつ。 (おっと、|g_44| 大は早送り画像である。空間的遠方で、g_ii (i=1-3) が大は、そこの物体の奥行きの平坦化である。)

(2) 遠方ほどポテンシャルが低く見える空間構造もありえる。

地球が丸いため、遠方から来る船がすべて海面より下から浮かび上がって来るかに見えるように、地球上では、全ての点 が他の点より高い地点にみえる構造をしている。空間的遠方においてポテンシャルが低い構造があれば、遠方からの光は、 赤方偏移する。x^1,x^2,x^3 の遠方において|g_44|が小さいことがこれを満たす。

(g_44とポテンシャルとの関係は、パウリの相対論では標準値 g_44= -1で Φ=0になるように、Φ= -1/2 c^2 (g_44 + 1)、 g_44= - 1 - 2Φ/c^2 と1次近似された。低地でΦは負、g_44は -1 に近いが少しだけ0に近い。しかし、g_44は時間経過 の2乗に関係し、その√がΦ比例であり、Φ/c^2= √-g_44 - 1, g_44= -(Φ/c^2 + 1)^2。)

(3) また光は長い期間飛ぶことで決してエネルギー低下を起こさないのか。

光の波長がその飛行時間によって低下する光の疲労説 "tired light" として、1929年から Zwicky が主張した説である。 その理論付けは難しいと思われる。光と粒子のコンプトン効果を使った光のエネルギー低下は、遠方画像をぼやけさせ、 低下の周波数依存が起こる。それなしに光のエネルギー低下を起こす理論も存在するが、既存の理論と合致しないという。

(4) 時間の経過が過去は遅かったかもしれない。

時間加速ともいう。これは、計量の時間的変化 (1) がその原因でもよい。 g_44 の変化を一般相対論の解とすることができれば、物差しのサイズ変化や宇宙膨張も最初から必要がないのである。

(4) 膨張宇宙ならドップラー効果以外に、過去の高密度による低い重力ポテンシャルからの赤方偏移があり得る(26章)。 このことを膨張宇宙説は、考慮していないのではないか。

(5) 遠方銀河の固有運動の積み重ねは、累積した横ドップラー効果の赤方偏移の可能性がある(27章)。 ハッブルの発見した赤方偏移は、静止宇宙の銀河の乱数的固有運動の累積による赤方偏移ではないか。

それらの異論を考えた方がよいのではないだろうか。

５.２ アインシュタインは否定した

アインシュタインはこの (1)と(4)との説を局所の時計の存在の否定であるとして斥けている。物差しの変化は受け入れ、一定でない時計は、 時計でないと考えるのだろうか(*)。いやそれだけでなく、アインシュタインは、"相対論の意味"の中に、"或る種の原子の形態は "相似" ではなく"合同" に基づいている" と、物差しのサイズ変化さえも否定するかのように読める文章を残している(**)。

膨張宇宙が光速の変化を伴うとき、それを物差しのサイズの変化か時計の変化としないなら、計量は現実とどう関わることができるのだろうか。 まさか、近年の学者のように膨張宇宙に光速の変化が伴わないとする考え方を採ったとは思えないのだが。一般相対論は、時計と物差し の変形の思想である。赤方偏移は、合同の証拠というよりは、相似の証拠というほうが当たっているように思える。膨張宇宙について、 物差しのサイズが変化してきたか、時間の経過が変化してきたと考えるしかないのではないか。そして、一般相対論によって重力赤方偏移 の効果を提案した彼は、赤方偏移がドップラー効果以外ではあり得ないと断言したのであるが、そう断言する必要はなかったと思う。

この世界は、人工的である。必ずといっていいほど人の手がかかっている。しかし、物体があれば作った者がいるというのは誤謬である。 そのように、"壷には作った人がいる。しかし、蟻塚は、誰かが作ったものではない"。これは、古代インドにおいて神概念を超えるための ウパニシャッド哲学の言葉であると思うが、物事には必ず始まりがあるというのは一種の信念でしかない。とくに宇宙に始まりがあると いうのはそれを求める思考が導くだけかもしれない。始めもなく終りもなく存在する、無始無終という概念が定常宇宙概念である。 宇宙の果てに立てば、そこからまた宇宙の果てが見えるように、どの時刻にも必ず、それより過去と未来が存在するのではないか。 それは、人間の法律が場所と時間によって自ら翻弄されたくないように、場所と時間によって物理法則が変わらないことを望むのと、 同じ希望を宇宙に托す、宇宙原理のひとつである。今から 100 年前、大半の天文学者は、この定常の概念にいた。現在の天文学者は、 それと正反対の観念の中にいて、そのことを自覚していないようにみえる。宇宙に対する evolution それをあえて変化と訳すが、 それを基本概念としている。

天文学は、観測の学問であるが、この世界、宇宙を見ることを学問領域にした唯一の学問である。それを使って世の中の役に立とうとか、 他の科学の道具になろうとか、低位を甘んじる殊勝な心がけの学問ではなく、これは、それ自身の目的によって動く学問である。そこでは、 そこに紛れ込む観念、推測、実証、証明は、実は学問の主題ではないはずである。観測という事実の集積に名を借りた哲学的主張の、 一見 "科学的表現" があり得る。ハッブルに始まるビッグバン、膨張宇宙の研究は、事実の蓄積なら天文学の主題として適切であるが、 我々が子供のころから火の玉宇宙の証拠と教わった教育を思い起こせば、基本的に概念主張の強すぎた話であったように思う。 証明のできない事象を判定をするのに足るほどの証拠というわけではないペンジアスとウイルソンの背景輻射の発見(次の項を参照)は、 それを重要視したピーブルス等の学者の問題である。

(*)彼は局所の時計の存在を原理的要請として、g_44 を一定にするようにフリードマン解を誘導したかもしれない。もし重力方程式のg_44が 変化する解があれば、空間的膨張なしに、距離に比例する赤方偏移をもたらすことができる。ポテンシャルが0から始まるなら時間的始めが必要 かもしれないが、時間的始めもなくポテンシャルがマイナス無限大から無限大に向かって増大するだけの宇宙かもしれない。それはポテンシャル が時間に関わっていると考える時間加速であり、光が飛行した時間と距離だけ、遠方の銀河の赤方偏移をもつだろう。全ての時間経過の加速に よる赤方偏移は、飛行中の光だけが過去の時間経過に取り残されて光疲労して見えるから、光疲労説とは違うが、より根本的な説明となり得る。

つまり、一般相対論の解として、空間計量の時間変化でなく、時間計量の時間変化とすると、宇宙のサイズは変化せずドップラー効果はない。 時間の関数としてのポテンシャルの上昇があればよい。空間計量の違う場所からの光は、出発当初、波長は違っても、周波数を変えない。 フリードマン宇宙の空間計量の増大は、物差しだけの縮小ではない。物差し、物体、全ての空間間隔の縮小であり、むしろ、遠方銀河は こちらに向かって来るドップラー効果の青方偏移があると考えるべきではないか。

(**)つまり、空間の間隔がなぜか変化していく宇宙として多くの人が認識するように、膨張宇宙を物差しの変化とさえ考えなかった可能性もある。 局所の時計と物差しとは、固有時、固有長の存在である。鏡の間の光の往復の時間が変動するなら、特殊相対論さえ成り立たないという否定が されるが、一般相対論はそれを乗り越えた理論だったのではないだろうか。局所には特殊がどこまでも成立するとするなら、それには局所時間 の存在も含められると思う。我々は宇宙に出たり地上に戻ったり、速度を持ったりを失ったりするとき、固有時、固有長は変化しないが、 一定の時空を基準にしてそこからみた我々の時間や物差しは大きく変化するのである。

６. ハッブル深部領域 Hubble Deep Field

写真の説明では、この若い銀河はサイズが現在の銀河のサイズの 1/10 以下だという。しかし、基本的に大半の銀河の形態は、 完全な渦巻きをしていて、どこも変わったところがない普通の銀河である。南方深部探査写真(HDFS)の中には、青い不定形の銀河 が多く含まれ、それは明らかに現在のものとは違うといってもよいが、銀河形成に 50 億年と言っていた定説は、10 億年に短縮 しないといけなくなった。

これを見ていて思ったことは、つぎの通り。もしかして銀河サイズが 1/10 に小さいのではなく、距離が 10 倍ほど遠いのではないだろうか。 将来、さらに分解能が上がれば、銀河間の空間にさらに小さな銀河が見えて来るとする。そうしたとき、それがさらにサイズの 小さな銀河であると説明するのだろうか。そもそも宇宙膨張は、重力で結合した銀河内には働かない原則ではなかったか。

銀河自体のサイズの膨張は、初めて使われる説明である。それほど初期の異常な時期か。いや、単に意外に小型の銀河が見えた ため説明に窮したのだろう。ビッグバン説では、ある距離以上の距離があってはならないため、見えるサイズが小さいものは、 現実のサイズが小さいと言わざるを得ないのである。

Hubble Deep Filed (STSCI)

Hubble Deep Filed 1996

ハッブル深部領域観測 R.E.Williams et.al.(Space Telescope Science Institute)拙訳

定常無限の宇宙では、星の間にまた星が見えて、夜空は星の表面程度の輝度をもつだろうか。いやそれほど深宇宙は透明では ないのである。深部探査が銀河だらけの図と、銀河中心方向の先がほとんど見えないことを考え併せるべきである。

そして、それほど宇宙の平均温度は高温ではないことを忘れている。光学的に見える物質の 1000 倍程度の暗い物質があれば、 宇宙の平均温度は絶対温度数度になり、これで背景輻射も同時に解決するではないか。定常状態で、温度が一ヶ所に集中する ことはないから、オルバースの杞憂は無用である。これをそのまま定常論へのパラドックスとして捉えているひとは、 宇宙はどこまでも透明で、宇宙の物質はすべて数 1000 度の表面を持っていると考えているようである。 それなら、我々の銀河中心方向は、一つの星のように光り輝いているのかと聞きたい。

ハッブル深部探索の結果は、夜空の最も暗い部分が、オルバースのいうように、遠方の銀河に埋まっていた。それらの光度は、 約 30等級であり、HST の 10 日間の露光ではじめて姿を表すほど暗いものであった。宇宙が透明なら、銀河のような大きさが 写る物体の輝度が距離で下がることはない。これは銀河間空間の塵の存在量を示しているのかもしれない。ドップラーシフトで 説明が付くのだろうか。

そこで、こういう結論はどうだろう。そう、オルバースの疑問は、解かれたのである。パラドックスは、なかった。宇宙の果ては、 どこまでも星ぼしで埋まっている。ときに閉塞感すら与える無限空間の、一種、恐るべきこのイメージが浮かび上がって来る。

このような暗い銀河に通常のスペクトルでなくフィルタを通した光度からの赤方偏移の推定がされて、それら (z= 2〜4.5) の大半がそれほど遠方の銀河ではない (z_med = 3) とされた。しかし、当時予想された銀河の密度の 3 〜 4 倍の密度であった。 遠方銀河は、小さく明るかった。 "Keck Spectroscopy of Redshift z~3 Galaxies in the Hubble Deep Field", James D. Lowenthal et al.

しかし、この種の画像は衝撃的である。それは事前に期待された画像と全く違った。研究施設と研究者の10%を所長の自由に扱う 権限が与えられ、計画が作られた。宇宙の果てを見てみようとした HDFの発案者、STC の所長 R. E. Williams は、TVで "我々は神の創造を見ている。" と言った。宇宙膨張説が出てきたとき、それ自体が宗教的神学的に見られ、科学的でないと忌避 した傾向は、米国にはすでにないのだろうか。いや、彼がそう言うのは米国の文化がそうさせているのであって、それを言いかえて 日本では、"永遠と無限をみる" というだけかもしれない。ビッグバンを説明するのに、それと正反対の言葉である "無限の宇宙" と言ってしまう NHK の番組をみても、ここには時に始まりはなく宇宙に果てはないのである。しかし、文化宗教を原因として宇宙論 が左右に振られているのではない。これは科学的な姿をとった宗教論争だったということではない。宇宙が始まりをもつかどうかに 正しい結論はひとつしかない。これからも未来永劫にである。

始めもなく終もなけれ冬銀河 (蕪村) (2007 年 3 月 31 日朝の俳句番組から。)

宇宙の果てを見る限界の能力は、地上の 5m 鏡の 23.0 等級 (60 年代) から 30 等級へと大きく変化した。この HDF 領域について ケック望遠鏡によって近赤外 28 等級までの銀河が分析された。 "Near Infrared Imaging of the Hubble Deep Field with The Keck Telescope", David W. Hogg et al., HDF 領域の銀河分類や大規模構造の研究、例： "Redshift clustering in the Hubble Deep Field", J. G. Cohen et al. が行われた。その後、NASAは、 Hubble Ultra Deep Field という後継の調査を続けている。すばる望遠鏡も HDF 領域の画像を出したがこれは、どうして、 これほどの違いが出るのか、不思議なほど渦巻銀河の全くみえない異様に殺風景なものであった。一見して対応が付かない。 分解能の不足はどうしようもないということだろう。

７. オルバース (Olberse) のパラドックス

定常で無限の宇宙では、夜空は無限の輝度になるという話がある。星の密度を一定とすると星の数は、体積に比例する。 ある半径 R の先の一定の厚さ d (d は r より十分小さいとする d≪r)の球殻を考え、球殻の体積 v は厚さ d 一定 (*) から球殻の面積 S= 4πR^2 に比例するが、放射は、距離 R の 2 乗に反比例するから、両者の影響は打ち消され、 球殻からここに届く放射が距離によらず一定になる。これを無限遠まで積分すれば無限大になる。 膨張宇宙論の入門書で、よくこの説明が使われ、これを使って宇宙の膨張の証明とする。(例えば佐藤文隆氏の"ビッグバン"(講談社) 又は、 Edward L. Wright のサイト)

この話は、何かが間違っていることを教えるパラドックスである。定常でなければ無限大にならないし、宇宙に端がある有限宇宙でも 放射が無限大になることはない。しかし、それで宇宙には始まりがあるか、または有限と結論するのは早計である。そこには数学的な 間違いがある。まず、この無限大は、物質の立体角を 0 とすることから起きている。これは、さきほどの簡単な数学に抜け落ちた部分である。 星には大きさがあり、透明でない。それが遠方の光を遮る。そのため、宇宙の明るさが無限大になることはない。 せいぜい全天が星の表面輝度で埋めつくされ、夜空は、その明るさになるだけである。これは、無限大とは全くちがう。 無限大でなくても、星の表面温度の輝度では、夜空が暗いという現実と合わないのではないか、と考える人には、次の説明が必要だろう。 つまり、星の表面輝度ではなく、全天が物質の平均温度輝度で埋めつくされるのである。

宇宙の塵埃(チリ) のために夜空が暗いという考えも、膨張説はこう否定する。"宇宙が透明でなく途中に光を遮る物質があっても夜空 が無限大(または星の表面温度)の輝度になることを妨げない。定常が無限の過去からであれば、光を遮る塵埃物質がいずれは温度を上げ、 星と同じ温度になるからである"と。それは、一部は正しい一方的な議論である。それは、塵が星の表面温度になるだけではない。 逆の流れもあるのである。

(*)球殻の厚さを一定とせず、R に比例させると、球殻の体積は R の 3 乗に比例するが、これでも無限遠までを無限個の球殻に分割 することができ、放射が距離 R の 2 乗に反比例すると、それぞれの球殻からの影響は 1/R である。これを無限遠まで積分しても やはり無限大になる。仮に放射が距離の 2 乗でなく 3 乗に反比例でも、(これを星の密度が 1/R に比例していてもと言い替えられる) オルバースのパラドックスが成立することがわかる。球殻の厚さが R に反比例するとき、球殻の体積は R の 1 乗に比例するが、 これでも無限遠までを分割でき、放射が距離の 2 (3) 乗に反比例では、球殻からの影響は、1/R (1/R^2)である。 ()の場合、ある距離 から無限遠までの積分は発散しない。オルバースのパラドックスは、このような積分の厚みの取りかたで変わるのだろうか。

もし、夜空が無限の輝度なら、一瞬で塵埃は無限の温度になる。そもそも、温度が一ヶ所に集中することは、現実の系であり得ない。 太陽光をレンズや凹面鏡でどれほどうまく集光しても、太陽表面温度を超える一点を作ることさえ我々には原理的にできないのである(*)。 そのことから、先の簡単な数学にどのような間違いが入り込んでいるかが分かってもよいのである。自然界には決して無限大は出てこない。 無限大は、マイナスの確率やエネルギー、超光速よりも問題がある。定常無限の宇宙であっても、なくても、夜空が無限の輝度となることは 絶対にない。定常無限の宇宙ではそれが起きるから、定常無限宇宙があり得ないというのは、物質の立体角を 0 にする単純化がもたらす 誤りである。絶対にあり得ないことを起こさせる力が定常無限にあるようにいう論理は、それが原理的にあり得ない宇宙であると思わせる 宣伝である。もともと物理量が無限大から開始する宇宙がどれほどあり得ようと、どのような宇宙もそれよりはましであると反論すべきである。

太陽の表面温度の輝度で全天が覆われるなら、塵はそのうち太陽表面温度になる。それは難しい理屈でなく、温度の平均化過程である。 それにかかる時定数は、小さな塵を選べばどこまでも短縮できる。しかし塵が温かくなると同時に星も冷める。全ての塵が十分に暖まる 時間を考えるなら、その間に太陽も塵の温度になる。そして塵のほうが光る物質よりもずっと多い場合、その方が優勢である。つまり、 宇宙全体で物質がどの程度の平均温度を持つかを考えたほうがよいのである。

この星の表面温度とは何度なのか。表面温度が 1 万度以上の青い星もあるし、太陽の表面の 6000 度より温度の低い暗く赤い星もある。 それら、まちまちな星の表面温度に包まれている場合でも、塵にとってある平均温度に包まれるのと等価と考えられる。塵にとって夜空 のある方向から光と熱が来て他の方向からは来ないという非等方性があっても、夜空に模様がない等方の夜空があると考えても塵の到達 する温度は違わない。それが、夜空の平均輝度のもたらす温度であり、宇宙の平均温度である。

それは、決して太陽表面温度の 6000 度ではなく、絶対温度 2.7 度程度である。宇宙は、星のように温度の高い光る物質だけでできて いるのでなく、暗い物質、塵埃のように光らない物質の方が 1000 倍も多く、それらが物質の大半を占めることが昔から知られている。 全天がその平均輝度になるとは、全天が 2.7 度の黒体輻射に満たされることである。塵は 2.7 度の温度に向かいそこに停留し、星は まだ光っている。この塵がどういう物質で出来ているかに関係なく、温度だけが定める黒体輻射を放つ。そうすると、オルバースの話は、 多くの人が余りにも明らかに主張するように定常宇宙を否定するパラドックスでなく、宇宙の背景輻射を定常宇宙が説明する話であることに、 やっと気が付くのである。

(*)温度でなく放射密度は、非焦点鏡による太陽光の絞りこみによって太陽表面を超えることができる。昔、雑誌 "サイエンス" にあった 印象深い話だった。エアコンのような熱の能動輸送は、エントロピー増大に逆らうためにエネルギーを使う。その極端な実現は、熱を集中させ レーザー光で排熱して太陽の中に入ってゆく宇宙船を書いたデイビッド・ブリンの "サンダイバー" である。普通、熱は自然に分散していき、 物体 i ごとの Q/T を合計するエントロピー Σ_i Q_i/T_i （熱量Q、温度T) は減少せず、一般に増大する。しかし、熱の能動輸送をすれば 減少できる。それは、人間の行う能動輸送を故意に自然に含めないだけだろうか、そうではない。能動輸送に使うエネルギーまで含めると 常にエントロピーは増大し、生物などの開放系は、勘定に入れない部分が常にあるから、みかけのエントロピーが減少を示すのである。 重力を含む系ではエントロピーは減少するといわれるが、本当だろうか。膨張宇宙では非平衡系であるからエントロピーが減少するといわれるが、 少しでも温度が違う物体を含むものは、すべて非平衡であり、それが特別な物理であるはずもない。全てを含む宇宙は少なくとも開放系ではない。

1758年生まれのドイツの物理学者・天文学者、ハインリッヒ・ウイルヘルム・オルベルスのグループは、火星と木星の間に惑星を探していた。 小惑星セレスの発見は、1801年イタリアのジュゼッペ・ピアッツイに先を越されたが、彼は、当時のガウスによる最小二乗法による見失った セレスの再発見 (1802年) を行った。1826年のこの人の議論によって、その名を冠する "オルバースのパラドックス" は歴史上、その時代の 考えを鼓吹するために使われてきた。特殊相対論の出たときは、これがオルバースのパラドックスを説明するとされたし、現在優勢な膨張 宇宙論は、有限時間とそれから来る有限の観測できる空間がこれを説明するとしている。

なお、無限空間でなくても、周期的な境界条件でも同様な結果になる。境界条件が熱的な反射壁なら小さな有限の閉鎖空間でも、 無限空間と同じである。それが無限の輝度を生むはずはなく、体積あたりの(有限の)エネルギー密度で満たされるだけである。 アインシュタインの定常宇宙解のような無境界有限空間は、無限の過去からの放射が回り込むので、オルバースの問題を逃れるわけではない。 アインシュタインは、このパラドックスを避けるために有限宇宙又は膨張宇宙を採用したわけではないと思うその理由を後に示そう。

私のオルバースのパラドックスに対する意見は、これを定常宇宙論によって説明すべきということである。そして、これが背景輻射が黒体輻射 をなす理由でもある。宇宙の晴れ上がり時点のプラズマの黒体輻射が赤方偏位したのではなく、現在の静的宇宙の平均温度が黒体輻射を成す。 逆に、晴れ上がりでは背景輻射における水素やヘリウムの軽元素の吸収スペクトルの非存在が説明がつかない。

多くの科学解説の典型として引合に出すのは、アイザック・アシモフの "夜はなぜ黒い？" の最後の終わり方である。時間と空間の有限性と ドップラー効果によるエネルギー低下が我々の存在を可能にしていると考える彼は、デカルトの "我思う。故に我あり！" を修正できる といって、"われあり、ゆえに宇宙は膨張する"という。我々の存在自体が膨張宇宙の証明となるというこの論理はほとんど、西洋の哲学者＝ 神学者が苦しんで行った「神の存在証明」である。この問題は、そのような論理にまでなっていくのである。

(*)宇宙の果てがあっても、その端に立てばそこはここと変わらず、ここが逆に宇宙の端になることはあり得る。宇宙に端があることは、 そこに行って端を間近に見ることではないからである。場所によらず果てが見えることは、例えば、地平の境界、地平線は、 どこにもあってどこにもないが、そこの(2 次元)空間、地面の奥行きがなくなって見える場所である。地平線までの空間は有限であった、 その外側は、それよりもずっと大きく広がっていたがそれも有限であった、というのが地球であった。有限で曲率が正であることが地平線 の存在の原因でもあった。このような地平線、宇宙の果てがあっても無限宇宙が有限とみえてしまう。

私の夜空を眺める習慣は途絶えてしまったが、天の河はたんに美意識で眺めるものではない。多くの星が実は無限の宇宙の中の太陽の ようなものと最初に知ったのは、火あぶりにされたジョルダノ・ブルーノだった。太陽地球間の距離(1億5000万km)と隣りの恒星まで の距離(1.3pc)の比率が約20万倍である。pc（パーセク)という単位が太陽地球間を基線にして角度の 1 秒の距離として定義されている。 夜空に星は、肉眼で 6000 個ほども見える。星々はまとまって、天の河をなす。それは立体的には円盤形をなし、我々の銀河系を構成 していた。それ以外の部分は空虚と思われていた時期があったし、たくさんの星雲が他の銀河系であるという理論が認められたのは、 20 世紀に入って20 数年も経ってである。(1920年の大議論では星雲の外銀河説が劣勢だった。) 隣りの恒星までの距離とアンドロメダ 銀河という隣りの銀河系までの距離の比率が 100 万倍もある。

ほんのお隣りの銀河までの距離は、太陽地球間の距離の20万倍と100万倍の積で、2000億倍の距離がある。これはほとんど想像を絶する 距離の比率である(1m 対太陽地球間の1億5000万kmと同程度である)。 しかし、太陽地球間を遠いと思う場合、これは全く実感できない。 太陽の光は、昼の明るさをつくりだし、星々のすべての光の量を合わせたよりずっとずっと明るいものであるが、 それは、地球が平均的な恒星間の中にいないからである。 もし地球が平均的な恒星間にいれば、太陽からの光と、その他の全ての星の光とは、ほぼ同程度か、他の方が大きいことになるだろうからである。 他の銀河系からの光は、 (その 1/10 の距離にある大小のマゼラン星雲は、ほとんど我々の銀河系と続いているから除外し、) もっとも近い アンドロメダ銀河だけが肉眼で観測できる銀河であり、その他の銀河がそれより暗いことも、我々が銀河系の平均距離の中にいずに、 銀河系にどっぷり浸かっているからである。もし銀河間のただ中にいれば、われわれの銀河系からの光量と他のすべての銀河系からの光量は、 やはり同程度か他の方が多いということなるだろう。

遠方の物体は、距離の 2 乗に反比例して影響が少なくなるが、同じく距離の 2 乗に比例して数が多くなるのである。 銀河系の中の星の数は、さきほどでた 2000 億という数字と一致する数が使われている。隣りのアンドロメダ銀河も我々の銀河と ほぼ規模が同じと考えると、そこからの星の光量は、2000 億倍し、そして太陽までの距離の 2000 億倍なので、 影響は、2000 億倍の 2 乗に反比例するから、太陽からの光量の 2000 億分の 1 になる。 これでは遠方は影響がないように考えるほうが正しいようにみえるだろうが、これが正しくない理由は先に説明した。 重力も、光量も距離の 2 乗に反比例する。星の輝度と重力とは、ともに、近傍と遠方の影響が同程度である。 しかし、力をポテンシャルの空間微分ととらえる重力ポテンシャルの式 -GM/R でみれば、後述するように、 地球への太陽の影響とアンドロメダ銀河の影響とは、じつに同程度になるのである。

地球に対する太陽とアンドロメダ銀河の影響が同程度とは、パラドキシカルであるが正しいのである。g_ik という計量(g_44又はg_00という 時間計量はそのままポテンシャルに換算できる量である) を物理量として、それが従う方程式、それが重力方程式である。ポテンシャルは、 確定値を持ち得ないという任意性があるが、ポテンシャルの任意性は、一般座標の任意性に置き換えられている。 重力方程式は g_ik の確定値を出さず、座標系を指定することで g_ik が確定する。地上と GPS 用人工衛星の微小の時間経過の違いの換算に、 ポテンシャルという時空の計量は、すでに実用に供されている。

ニュートンの万有引力をポテンシャルを使って表す理由は、重力という遠隔力のベクトルを使わず、空間に存在するスカラー(場) ですむだけでなく、ポテンシャルと物質、質量との関係が微分方程式 ∇^2 φ = ρ に表せ、それをポテンシャル場が従う方程式と みることができるからである。電磁気においてもスカラーポテンシャルと電荷密度の関係は、まさにこの式を満たしている。 特殊相対論ができたときニュートンの万有引力は、何者も光速を超えられないという特殊相対論の法則に違反しているので、 重力の影響の光速化が必要であった。リエナール・ヴィーヘルトの式φ= ∫ρ(x)dx/R(x,t-r/c) のように、 重力も、ある点からの過去の光円錐の時空点にある質量からの遅延ポテンシャルとして計算することができると思われた。 ポアソン方程式と、質点の運動方程式、加速度がポテンシャル勾配に比例する、d^2r/dt^2= - grad φをローレンツ不変な形式に 書き換えることが要請された。しかし、それは予想以上の書き換えになり、その作業にアインシュタインは、10 年をも要し、 最終的に、一般座標変換に不変な重力方程式を導いた。

この物理での力学的記述からポテンシャル記述への移行は、上に述べたパラドックスを招来する。それは、普通に言う オルバースのパラドックス以上のパラドックスである。ポテンシャルは距離の 1 乗に反比例するからである。

逆平方の力について、電気力は、2 からのずれが非常に小さいことが実験的証明されているが、重力の場合、それの証明はない。 galaxus 宇宙に一様に分布する。r の距離の dr の厚さの球殻からの重力のr=∞までの積分が∞になる式について、

ρdw r^2 dr/r^2 ∝ ρ∫ dw ∫ dr = ∞

我が地球上の運命は、はるか彼方の銀河系宇宙に依る。非常に離れた距離をもつ時は、事件から影響を受けないという常識と異なる。 このことは、信念でもあった。これは宇宙論 (Cosmology) における大きな Paradox である。

光は r^2 で広がる、 r^2 で弱まる以上に弱まる。吸収。重力においても、非常に大きな距離では弱まるのではないかとして、∝ e^(-αγ)/r^2

∫ e^(-αr)dr = 1/α

∝ e^(-αr)/ r^2

(α〜0) また、アインシュタイン宇宙論では、宇宙は無限でない。

∫ dr = R

ミクロに対して考えた湯川は、核子のもつ核力。e^(-ae r)/r, ae^-1 = 10^{-13} cm。

(以上原文) それからベクトル解析の Gauss の定理に移られ、力とスカラーポテンシャルの説明、 ラプラスの方程式、ΔΦ= 0 とΔΦ- ae^2 Φ= 0 → Φ= exp(-ae r)/r と説明されていた。

伏見先生は、オルバースのパラドックスを遠隔の影響のパラドックスと読んでいた。光のオルバースのパラドックスを吸収と見ていたし、 重力にポテンシャルの式の変更があるとみていた。ここに再録するのは、少し前の大学者がどのような思想をもっていたかを記したかった ためである。私は、パウリで初めてこれを勉強したのではなかった。 (Dec 30 2006)

８. 背景輻射

1965 年マイクロ波受信装置の取れない雑音に苦しんでいたペンジアスとウイルソンが発見した、宇宙からの均一のマイクロ波 (最初は 3.5K とされた)は、ビッグバン宇宙論での物質形成、膨張による非平衡過程によって水素とヘリウムの現存比率を説明する、 ガモフの"αβγ理論" (1946年)によって絶対温度約 7 度としてすでに予言されたものであったとされる。

近藤陽次著の "世界の論争・ビッグバンはあったか" (講談社)によると、定常側では、アーサー・エディントンが1926年の著書で 恒星間空間温度を銀河系内恒星の光の強度から3.2Kと推定し、1930年には、レゲナーの銀河系間空間温度 2.8 K という推定が存在したという。 その方がペンジアスとウイルソンの測定へのガモフの予言よりもずっと精度の高い予言であった。つまり、2.7 度の黒体放射を ビッグバンの証拠とする必要はないし、全く逆の解釈が昔からあったのである。

アインシュタインもそうであったように、定常宇宙説が当り前であった時代の宇宙空間の平均温度という考え方は、 近傍の空間温度を素直に測定又は推定するものであり、ビッグバン説の宇宙の晴上り神話を持ち出さなくてもよい単純さがある。 膨張宇宙論での時間に依存する温度は、晴上り時期に数1000度であった温度が、現在、数度になっていると考える。 銀河間の空間の平均温度が 2.7 度であるなら、それは、黒体輻射となって現在のマイクロ波の背景輻射となるであろう。

また、一方で平坦のためにダークマターが存在するといい、定常論を否定するためのオルバースのパラドックスにはダークマターの ない数1000度の物質の表面温度を言うのは矛盾している。数1000度の星の表面輝度は晴上り時点の温度であり、現在は数度である。 それは現在、正しい平均温度と一致している。それなら、今は 2.7 度のオルバースのパラドックスを考えるべきである。

私には昔から解けない疑問がある。ビッグバンの晴上り時期には、プラズマが一斉に結合し、水素原子を形成するのであるから、 1000倍のドプラーシフトを受けた強い水素やヘリウムの吸収スペクトルが出るはずなのに、どうして黒体放射か、という疑問である。 黒体輻射は、プラズマの放射として理解できるが、背景にプラズマが見えて、前景に水素、ヘリウムなどの原子が形成されるとき、 どうして吸収スペクトルとしてスペクトルの凹凸ができないのか。形成の時間がずれていて吸収スペクトルの幅は多少ならされても 全く凹凸が検出されないのは疑問である。どうして黒体輻射のままなのか。昔からの化学の炎色反応に類する容易なはずの現象は、 なぜ起こらないのか。太陽や恒星の表面(虹彩)で我々が最初に見出したヘリウム元素のようにである。(水素はヘリウムよりも見出すのが 難しかった。) そのような基本的な疑問がある。COBE 衛星による背景輻射の黒体からの偏差が 10^-5 オーダの発見 (1990) は、 "化学ポテンシャル" といわれた、この原子の吸収スペクトルの非存在は膨張論にとって衝撃だったはずである。 私は、永く逆に"黒体輻射だから膨張の証拠"と聞いてきたように思うが、それは全くの誤謬である可能性が高い。

晴上りの情况説明は、単純すぎるのである。また、電磁波の背景輻射だけでなく、それ以前の現象として、X 線の背景輻射、ニュートリノ の背景輻射が存在しなければならないのに、全く検出されていない。何か起源をいうには確かさが必要である。超新星爆発過程に似たような ビッグバンの過去時点の現象全てに証拠の必要がある。電磁波の背景輻射の前景にあるべき、銀河形成と超新星爆発の激しい時期には 全く証拠がないどころではなく、反証が存在するというべきだろう。暗黒時代と再電離の時期がどんどん早期に先送りされ、現在と状況 の違わない時期が宇宙初期まで広げられる。これは、宇宙膨張説に対する反論である。

ニュートリノの観測では、カミオカンデ(元神岡鉱山で純水によるチュレンコフ光の測定)で、太陽ニュートリノ問題 (太陽内部の反応から 予期されるニュートリノに対して観測される量が数分の 1 であることを確認したこと)や、1987 年に発見されたマゼラン星雲中の超新星 1987A の観測(爆発の中心部からの到達なので爆発の周辺からの光よりも 2 時間前に到達した、11個のニュートリノの検出)、さらに 8.4 x 10^32 年以上という陽子寿命の下限を求めた陽子崩壊測定が行われた。最近の観測からは、標準理論に反してニュートリノには 微小な質量があるらしく、ニュートリノの背景輻射は、かなり低速のニュートリノになる。そのため、カミオカンデの採った方式、 水の電子を弾いて水中の光速以上にしてチュレンコフ放射を見る方法では、検出できないだろう。

もしかすると、宇宙初期の低速のニュートリノが素通りしている。そうかもしれないが、ないものを探す人は、モノポール探し、 ダークマター探しと同じ徒労を経験するだろう。発見できなかったことは、単に忘れ去られ、どこが間違っていたかは、追及されないだろう。 小柴氏のノーベル賞受賞以降、ニュートリノ検出への期待によって、カムランドによる低速のニュートリノ検出の試みがされている。 2005 年 8 月の小柴氏の TV での話では、ニュートリノに質量があれば、超電導金属によって全反射できるという。そうすると、 本当に像を結ぶニュートリノ望遠鏡ができるかもしれない。

８.１ 2.7Kの黒体輻射

宇宙の晴れ上がり時点の黒体輻射のピーク温度T0からT1(T0＞T1、T1は2.7K)に赤方偏移によって変化したとき、λmaxはT0/T1倍になり、 当時の全ての波長λが比例的に伸びるなら、伸びたλに対する相対的な強度カーブは現在の2.7Kの黒体輻射と変わらない。なぜなら、 プランクの輻射法則、

hc^2/λ^5 １/(exp(hc/λkT) -1)

この関数 1/(exp(x)-1)、x= (hc/λkT) はTλ積による。つまり、λmax に対するλの相対強度分布はT0の黒体輻射と相似である。横軸λに対して 縦軸に強度をとる両対数グラフでは同じ形をシフトしたものになる。その強度は、宇宙の晴れ上がり時期の赤方偏移による波長λの伸び率 1+z に 対する銀河の表面輝度の Tolman testの議論からは後退仮説による強度は (1+z)^-4 であり、波長の伸び率の -4 乗(絶対温度の4乗)に比例し、T0 の名残りとする背景輻射の強度は、(T1/T0)^4 倍に比例する。それに対して、現在のT1の塵の黒体輻射の波長に渡る強度は、ステファン・ボルツマン 法則 E(T)∝ σT^4 から、絶対温度T1の4乗比例の (T1/T0)^4 倍である。

つまり、晴れ上がり時期の黒体輻射が後退の赤方偏移によって絶対温度2.7Kの黒体輻射になったとする輻射は、現在の2.7Kの黒体輻射とλに関する 相対強度のカーブもピークも違わない。近傍の塵の温度が絶対温度2.7Kなら、両者の輻射は区別できない。そのため、宇宙の背景輻射を宇宙膨張の 名残りとする解釈は可能だが、屋上屋である。まして、その証拠とは決していえないものである。

赤方偏移の原因を距離や時間に関係しない原因とする静止宇宙の赤方偏移では、強度は (1+z)^-1 に比例し、T0の黒体輻射の赤方偏移の名残りは、 T1の黒体輻射よりも強くでる。そのため、もし測定がそれを示すなら証拠となる。また、時間又は距離に比例する tired lightの赤方偏移では、 (1+z)^-2 に比例し、やはり、T0の黒体輻射の赤方偏移は、T1の黒体輻射よりも、強くでるだろう。現実の測定結果がそれに一致しないだろうこと は、両仮説に不利だが、遠方の銀河の赤方偏移は、事実として Tolmanテスト、銀河表面輝度の赤方偏移依存 (1+z)^-n の指数nの測定ではn= 2程度 の値が出ている。ところが、背景輻射ではn= 4を採る後退仮説は、背景輻射が静止宇宙の現在の2.7Kの塵の黒体輻射と同じ結果を与えるのである。

以前、全ての電磁輻射の最大エネルギーといわれ、背景輻射の存在は膨張宇宙の証拠といわれると、通常の2.7Kの黒体輻射より強度が大きいのだろう と我々を誤解させる。仮にそうなら、明確に現在の2.7Kの塵の温度ではない。しかしそれでも、後退仮説の赤方偏移でなく別の何かの赤方偏移かも しれない。逆に同じ大きさなら、晴れ上がりの時期の名残りとするより、まず、現在の2.7Kの塵の黒体輻射とみるべきだろう。少なくとも背景輻射は、 膨張宇宙の "証拠" とはいえない。なぜなら、それは、2.7Kの黒体輻射と寸分違わないのだから。

黒体輻射が現実世界では稀な現象だろうか。黒体輻射は、穴の開いた内側が鏡面の球体でそれは模擬され、穴に差し込んだ光が、内面の反射を繰 り返して穴に反射してこない空洞で作られる。この宇宙も内面の反射がないが、差し込んだ光は帰ってこない。内部の空間がある温度に相当する 黒体輻射に満たされることは通常の当り前の現象である。

背景輻射の測定は、太陽と月から始まって銀河中心方向など全ての高温天体を遮る必要がある。それはどこまで万全なのだろうか。少しでも高温の 物体が測定に混在すれば、マイクロ波の波長に対する放射強度は、特に短波長側で大きく測定される。我々が全ての遠方天体を知ることはないことから、 可視光で存在を知る全ての天体を遮ることはできない。例えば HSTの10日の露光で初めて姿を現したHDF領域の銀河を排除しなかっただろう。 そして、HDFのような深部銀河が全天の10%をも占めるとき、COBE/WMAPは確実な測定とはいえないだろう。

これには多少、問題があり、塵が黒体輻射になるには、粒状でなく線状の物体でないといけないという。そのため恒星間に鉄のホイスカーが塵と なっているという説がある。しかし膨張説は、背景輻射が本当に全ての背景であるという信念をどのように得たのだろう。どのように、遠方銀河 の全ての背景を取り出したのだろうか。それが近傍の輻射でないといえる証拠は、何だろうか。晴れ上り時点の水素やヘリウムの吸収スペクトル の不在を意識すべきだろう。党派性の公式見解に従い、これを疑えば全てが崩れるからと、必死に藁にすがりつくことは愚かである。

９. 熱死論

19 世紀末の熱的定常死の幻想に苦しめられたケルビン卿は、太陽の寿命をどれほど長くしても2000万年としていた。 現代のイメージの1000分の1である。寿命より、年齢が長いはずはない。彼は、地球の地質年代を疑って、それよりもずっと短い 太陽年齢と寿命を考えた。そのようなエントロピー増大による熱死論は、重力収縮による熱源だけでなく、その時代には想像も できなかった核反応という違う熱源、それまでの化学反応によるエネルギーに比べ 100 万倍を超えるエネルギーが、 すでに自然界で使われていたことが知られ、完全に無意味になった。

熱死の寿命は、6 桁、100 万倍に延びた。彼(又は当時の最高の科学者)は、それぐらい間違っていた。星は、一過性のものではない。 重い星は寿命が短く、軽い星は寿命が長い。その一生を過ぎれば宇宙に残骸を残し、それがまた新しい星の素材になる。太陽の寿命は、 100 億年を超える。太陽質量が水素で出来ていてそれがヘリウムに全て変わるなら、現在の放出エネルギーを 1000 億年続けることができる。 しかし、一旦水素が消費され、大きい重い元素になると、それを戻す仕組みを考えない場合、物質からの寿命ができてしまう。鉄にまで 変化した物質は、核の結合エネルギーだけでは、もとに戻せない。星々は終いには、核融合する水素を失い、最初からヘリウムしかない 星々になる。その後はどうするのだろうか。それは、星間の水素が恒星の 1000 倍あれば、それは 1000 億年の 1000 倍程度の未来である。

エネルギーへの変換効率なら、核融合よりブラックホールは、さらに 100 倍ぐらい高い。星が核融合マシンなら、銀河は、 ブラックホールマシンかもしれない。物質生成も可能かもしれない。ブラックホールへの物体落下で質量の5%がエネルギーとなるが、 これは、1%以下(0.7%)の核融合の効率よりかなり大きい。自転のない2体のブラックホール合体で質量の最大29%まで失われる。 自転や電荷があれば最大 65% がエネルギーになる。そういう合体を繰り返せば、100% に近付くことができる。エネルギーさえあれば、 鉄を水素に戻す吸熱反応も可能である。つまり、少量の質量を失うことで、大量の水素を生成することができるだろう。 (1g の質量を失って 100g の鉄を水素に戻せるだろう。)

物質はブラックホールに放りこんで、質量だけにしておいて、発生するエネルギーで素粒子を生み出すほうが鉄を水素に戻すより話が単純 である。しかし、物質の生成にその前の世代の物質の質量のエネルギーを使うなら、それを永遠に繰りかえすことはできない。最後には、 全ての物質が宇宙の平均温度の放射に変化するだけである。つまり、今の状況が永遠に続く方法を我々は知らないということである。 たった 100 年前に我々はそれをその 100 万分の 1 しか知らなかったのであるが、そして今もなぜかエネルギー問題は解決できずに、 我々は石油に依存した文明を未に継続し、実用核分裂炉を原子爆弾から短期間で作動させた我々が、その 50 年後の今、国家の巨額の 投資を続けても核融合炉の実用までさらに 50 年かかると言われて途方に暮れているのであるが、いま仮りに、星々を翔けるに必須の、 質量を 100 %エネルギーに変える方法を持っていたとしても、それは宇宙の永遠を保証しないのである。

銀河の寿命は、一体どれぐらいだろうか。銀河の巻き付きの謎(数億年で自転する渦巻き銀河は 150 億年からみると、 その腕の巻き付き回数が少なすぎる。)から、銀河の渦巻きの暗部にも、見える腕と同じだけの物質が用意され、 星の生成は、銀河の中央からの衝撃波によるらしい。それが渦巻の形をなすだけであるという(話を聞いた)。

数千億の星を抱える銀河の寿命は、星の寿命の何千倍もあって当然であろう(*)。銀河の寿命は、かなり長いものであろう、 しかし、永遠ではないだろう。それで定常論を捨てる必要があるわけではない。銀河にもサイクルがあるだろうからである。

それよりも、化学反応から核反応への変化と同じような、現在の我々の知らないダイナミクスも、まだ残されているはずである。 しかしそれが今説明できないことは、定常論の弱味である。熱死論を未だにそのまま信じる人はいないにしても、 エントロピー増大の熱力学第2法則のケルビン卿の強迫観念は残っている。

(*) "１個の銀河系の寿命は軽く1000 億年にはなるだろう"と、アイザック・アシモフの "夜はなぜ黒い？" にある。銀河が 1000 億の恒星 を蓄えている巨大構造であるのに、始まりのすぐそばにいるような、不規則さ不安定さを、私は全く銀河の形態に見ることができない。

９.１ 銀河の M/L 比

銀河が恒星の光だけからでき恒星の仕組みだけで発光しているなら、その寿命はその M/L 比に比例する。恒星は、恒星の発光開始から終了 までを寿命とみるが、銀河質量には恒星の暗い静かな収縮過程も含む分は、ある回の恒星に使用されなかった水素が次回に利用されるから 効率は回復する。銀河内部の光る恒星でも隠れて見えない分は、エネルギー的に寄与していると考える。核反応に寄与しない無駄な質量と してのダークマターなら寿命に寄与しない。しかし、反応生成物に別の利用方法又は回復方法があれば、寿命は長いと考えられる。

９.２ 銀河の回転と渦巻の回転方向

渦巻銀河が "巻き込む" 方向に回転しているのか、"巻をほどく" 方向に回転しているかということには永く論争があった。まず、 楕円形にみえる渦巻のどちらの縁が近いのかを知る必要があった。銀河の水平面に薄くある暗黒物質の見える銀河の場合、その側が 近いのである。ボークルールは、暗線がみえる程度に斜めの方向からみえる銀河(例えば NGC7331)を使って渦巻は、"巻をほどく" 発散しているのではなく、 "巻き込む" 台風のように収縮している方向に動いているということが分かった。論争は、ほぼ終結した。 星々は渦を描いて吹き出しているのではなく、中心に向かって落ち込んでいたのである。ところが、衝撃波説では再び中心からの 働きで渦の模様が発散していることになるが、渦の速度は "巻き込む"方向になるのではないか。衝撃波が回転速度より遅いなら 模様はあまり変わらず回転するだろうか。このような話を聞くと、我々は現在、銀河のことをほとんど知らないといったほうがよいことがわかる。

９.３ 銀河の回転曲線

但し、銀河回転曲線からのダークマターの量は、わずかであり、平坦に必要な量Ω0の 0.02倍 (近傍銀河の潮汐が重力と等しい半径 までとって 0.04)程度である。

９.４ 天の河銀河は棒渦状?

そして、ホール(F. Hohl 1971)のバー安定性の理論から、銀河の回転運動からのずれの運動エネルギーの2倍をΠとし(60km/s)、回転運動の運動 エネルギーをTとする(220km/s)とき、Π/T ＞ 5 という安定条件を満たさないことを指摘し、天の河銀河が渦巻銀河をダークマターの証拠とした オストライカー(J.P.Ostriker)と、ピーブルス(P.J.E. Peebles)の研究(1973)を、もともと天の河銀河が棒渦状なら、前提の誤りによる無意味に するだろう。

地球上で渦を描く気象現象として台風がある。北半球では空気の移動が右にそれるコリオリ力が、台風は左にそれる渦巻を描く。これは気圧勾配と コリオリ力がつり合っていると説明される。宇宙のあの規模の渦巻銀河というのは、どういう仕組みだろう。そこに気圧勾配があるはずもなく、 またコリオリ力が働く回転系の上にあるわけではない。単に円盤状をなした物質が重心の周りを回転し、中心にドレイン(排出口)があれば渦巻を 描くだろうか。回転座標系でない場合、物体の回転だけでは渦はできない。物体の速度方向を曲げるものがいる。物質を放出又は収縮するものが 回転するとき渦はでき、そのとき、渦の方向と物質の運動方向は全く一致しない。例えば、芝生へのスプリンクラーが水を放出し回転するとき、 幅一定の渦の筋では、個々の水滴は中心から外側に飛び出しているだけである。2つのアルキメデスの渦という現象として、そのような形の宇宙現象や、 SB型銀河がある。

光っているのは物質のほんの一部で、物質が全て見えていたら、回転系でない宇宙で渦巻はできないだろうか。物質が中心に落ち込む降着円盤に 渦は普通の現象である。渦巻は光る物質だけでない。しかし、最近耳にする、「重力的には銀河は球状だ」と言われると、さすがに本当かと驚き、 それはないだろうと思う。なぜなら、渦巻銀河は回転している。光学観測でもあれほどにも明確に、上下の空間になにもないと見せる渦巻銀河から、 どうやってこの結論を導くのか。(いや、この人には、これは結論ではなく、それを疑うことのない前堤なのである。そして、その前堤は、もっと 重要な前堤(ダークマターの存在)に遡ることができる。)

９.５ 銀河は重力的に球状?

質量が球対称なら、なぜ銀河は円盤状に収縮し回転しているのか。これは、CDMと通常物質の重力収縮を立て分けるのである。通常物質よりも 先に収縮したCDMは、銀河核や銀河面でなく銀河ハローまでしか収縮していないという予想によっている。外部に球状に分布するCDMは銀河内の 通常物質の重力収縮を妨げないが促進もしない。CDM自身は回転せず、通常物質の回転運動に表われ、上下運動には表われない、ということだろうか。 この面状質量による上下運動から球状に分布するダークマターはもともと測定できないのであり、そこから質量が球状であるという結論を導く のは回転からの推定が大きいからだろうが、面状質量の測定からいえることはその不足だけである。結論が先にある測定と疑われる。

９.６ 衝撃波による恒星形成の渦巻?

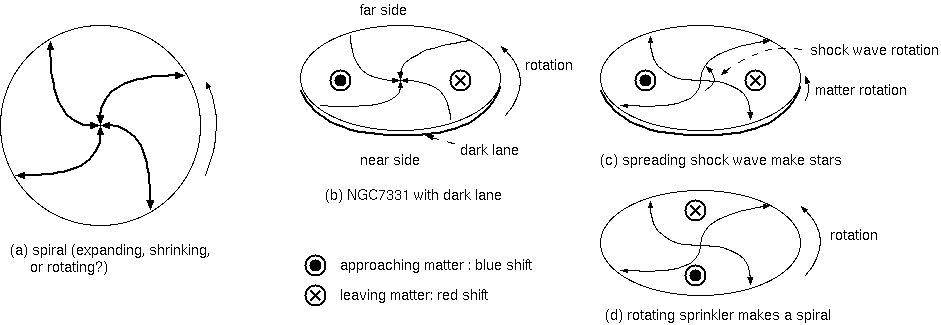
中心からの衝撃波説(図(c))は、上述のボークルールの観測(図(b))とは矛盾しない。衝撃波源の高速な回転よりも遅い同じ方向の物質回転によって 視線方向の速度(青方/赤方偏移)が決まる。剛体回転する質量に中心からつねに衝撃波が吹き出しては渦の摸様はできないから、衝撃波は、特定方向 (図では4方向)に制限して回転して出ているか断続的に出ているのである。しかし、衝撃波説では渦の摸様は内側ほど密に詰まる(巻き付く)。この説 には、渦は巻き込みが増加していき、形成からの時間を考えると渦の数が少なすぎるという、昔からあった「巻き付きの謎」(謎：反証)がある。 また、音速は温度の1/2乗に比例し圧力にはほとんど依らず非常に遅い。銀河の回転速度、毎秒200km/s程度になるのは、√(200km/340m) * 300K ＝ 23万Kであるが、銀河系内の温度はそれほど高くない。そのため仮に「衝撃波」を銀河中心からの光速の重力波とすると、それが顕著な物理的現象を 引き起こすとすることには大きな疑いがある。

９.７ マージによる渦巻銀河形成?

しかし重力収縮の結果として円盤状になる渦巻銀河は、まだ重力収縮した形態として説明可能だが、楕円銀河はどうしてその形態を続けて いられるのだろうか。数1000億〜数兆個の恒星集団である渦巻銀河より楕円銀河はずっと巨大な構造であり、これを渦巻銀河や、棒渦状銀河の ような円盤型への収縮前とするには、あまりに老齢にみえ、私には全く納得できるものがない。これにはもっと違うしくみが必要かと思う。

それよりずっと小規模な球状星団さえ私には理解不能である。少なくとも160億年という老齢とされる100万個程度の恒星集団の小さな構造が、 天の河銀河にも数100個、それ自身球状であるだけでなく、銀河の周囲に球状に分布して位置して存在している。まず、それらはなぜそれ以上 収縮せずに球状でいられるのか。個々の恒星のランダムな運動の程度の差という説明は成立しないように思う。大きなランダム運動は短時間に 消されて行き、円盤型の降着をするものである。銀河収縮のシミュレーションは、その周囲に球状星団を見出しているのだろうか。

つまり、このような小さな構造が重力収縮しないしくみ、重力の引力性を否定する、デカルトやカントの「万有斥力」のような、現在とても 扱えない不可解なものを持ち出して、定性的にそれの必要をいうべきかもしれない。一般相対論は全くそのような重力を持たないと思う。 重力方程式の宇宙定数は、質量がそれに対抗する外部的なパラメータでしかない。

我々が核反応を知る前、太陽が 2000万年を超える寿命を持てないとケルビン卿が信じたように、今我々は、太陽は核融合で熱を発生していると 信じているが、それが違っている可能性もあると考えるべきだろう。太陽の発熱の仕組が核融合ではなく物質を100% エネルギーに変えるモノ ポールとかミニブラックホールであれば、太陽の寿命は、太陽の水素の 1/10 しか核反応しないとして寿命を 1/10 にされた 100 億年でもその 10 倍でもなく、10兆年かもしれない。 http://arxiv.org/abs/nucl-ex/0602005 太陽のニュートリノ問題 が現状を報告している。

http://arxiv.org/abs/astro-ph/0411658 太陽コアの構造(O Manuel ミズリー大学) は、太陽の明るさ(SL)を理解するための測定と理論研究のフレームワークが必要という。太陽のコアに中性子星、中性子崩壊の可能性があり、 元素の質量比率が太陽系内部で、(H/L)^4.56。中心の中性子星からの中性子放射では 〜10-22MeV(＞57%SL)、中性子崩壊では nー＞H + e + anti-ν 0.782MeV (＜5%SL)、核融合では、4Hー＞He + 2ν + 27MeV (＜38%SL) という。

１０. 短かすぎる

宇宙自体の歴史が、46 億年と言われる地球の歴史のほんの数倍といわれる事も、信じがたいことである。こんな小さな片隅の石に宇宙年齢 の1/3もあてるのか。人間中心主義は、科学の歴史の中で常に破綻してきた。前世紀の間に我々の世界観の空間的スケールは、太陽系と星ぼし の世界から、数1000億の恒星を抱える銀河が数1000億あると 10^19 倍に変化した。それに対して、時間的スケールの方は、太陽という普通 の星の一生も入れないほどの短時間のままである。これを不自然に思うことから、全ては始まる。

現在、宇宙の年齢が地球の年齢より長くなり、太陽の年齢もなんとか宇宙の年齢以内に入っているが、地球を構成する物質(水素、ヘリウム 以外の元素) は、ビッグバンでは決して作ることができず、星の最期の核反応によるため、太陽は第 2 世代以降の星であるとされている (最近は第2世代でもないという)。しかし、太陽の前に太陽質量程度の前世代が入るだけで、その加算年齢が簡単に宇宙年齢を超える。 重い星の短い寿命を使えば、多世代も入るが、重い星の存在確率を使わなければならない。重い大きな星は、軽い小さな星より圧倒的に少ない。 しかも、宇宙の初期に重い星が多かったという証拠は(すぐに発見するだろうが、まだ)ない。物質が超新星爆発を経験する周期は、非常に 長いだろう。重物質の生成において、膨張宇宙説は、銀河だけでなく太陽系の生成さえ説明しないと思える。

１０.０１ 宇宙初期の惑星

その星は、近傍にあるほぼ現在の姿である。その星が宇宙初期から現在まで燃え続けたとするためには、太陽よりかなり質量の小さい星でな ければならない。ピーブルスがビッグバン説に移った理由は、メタルの少ない星があることだったという。メタルは、星間、銀河間の物質の 元素比率の話につながる重要な問題である。私には、宇宙初期の軽元素比率仮定では星間の水素以外の元素比率 0.1% が説明できないように 思うし、恒星大気のヘリウム比率 10% というのも少な過ぎるという疑問がある。

宇宙初期の恒星に惑星があったということは、それでも何かおかしいという疑問がでる。宇宙初期の星に惑星があった。その惑星は木星型と いう。通常の形成過程として恒星と惑星が同時に形成されたのなら、その惑星も、水素、ヘリウム以外を持たないのだろうが、それが惑星と して存在できるのだろうか。中心恒星の光を受けても蒸発しないで惑星の形態を保持できるのだろうか。我々の知る太陽系の惑星とかなり違 うだろうが、不可能ではないと考えるべきだろうか。これを、普通の漂流惑星(矮星)が、メタルの少ない恒星に捕獲されたとすると、惑星組 成が特別である必要はないが、星間での捕獲という低確率の事件を介在させるには、矮星や漂流惑星の比率が高い必要がある。

水素とヘリウムが宇宙の最初に比率が決まり、それ以降、ヘリウムは増加するだけであり、それ以外の重い元素は、超新星爆発によって生成 され、メタル欠乏星は、これを経ない初代だからであり、宇宙の全期間を通じた燃焼でもメタルが欠乏であるとする。元素変化は一方的な変 化であり、初期型はメタル欠乏で、後期型はメタル豊富である。この、メタル欠乏は宇宙初期という考えを疑うなら、メタル欠乏星で大質量 星は、現在決して存在しないのかということである。もしそれがあれば、メタルの少ない恒星が宇宙初期型という論理は崩れ、何か別の水素 精製過程が存在することになる。

定常説は、メタルの蒸留のような組成改変過程を、恒星一生の過程において持つ必要がある。例えば銀河の中心窩において初期型が多く、渦 巻銀河の銀河面では少ないのは、銀河面になぜかガスが多く、そこでガスから新たに星が形成されるだけでなく、この蒸留過程が銀河中心付 近で軸方向に行われるのではないか。中心窩の恒星たちが最初に作られてから、一度も再生されていない恒星であるなら、それらは暗い星で ないといけない。銀河面に近い太陽はメタル豊富型であり、比較的最近に形成されたとされるが、定常宇宙説のなかでは、渦巻銀河の構造的 な機能を使ってこの違いが説明される必要がある。我々の銀河系もガスからの恒星生成とするにはガスが少な過ぎると言われるが、楕円銀河 はガスがもっと少なく恒星生成が全て終わった後のように見えるがどうなのか、そこでも生成過程はあるのか。星の初期型を保つ浄化機能が 強力な銀河であろうか。

１０.０ メタル

"Metals and dust in high redshift AGNs", R. Maiolino, T. Nagao, A. Marconi, R. Schneider, S. Bianchi, M. Pedani, A. Pipino, F. Matteucci, P. Cox and P. Caselli , http://arxiv.org/abs/astro-ph/0603261

概要の訳：高赤方偏移(1＜z＜6.4)の活動銀河核 (AGN) の金属と塵の特性の最近の結果をまとめた。我々は、SDSS からの 5000 以上の QSO のスペクトルを使うことによって、2＜z＜4.5 の範囲の赤方偏移には、いかなる金属性の進化の証拠もない一方、光度金属性には重大な 依存関係があることを見出した。これらの結果をより少ない高赤方偏移の狭線 AGN (QSO2 と電波銀河)スペクトルによって再確認した。 金属性の進化の欠如は、宇宙的な小型化の結果 (高い赤方偏移で QSO の重いホストは急速に進化する) とする解釈と、QSO と銀河の結合 進化の選択効果結果 (ほとんどの QSO は、それらのホストの進化の後期段階で観察できる) とする解釈との両方に解釈される。 光度金属性関係は、QSO のホスト銀河の質量金属性関係の結果と解釈できるが、降着速度による関係という解釈もまた可能である。 金属性の進化の欠如は、知られる最遠の QSO (z〜6) のスペクトルにさえ観察される。結果は、特に鉄、炭素、硅素のような元素において 驚くべき結果である。それらは遅延産物であり、非常に高い赤方偏移 (z＞10) に QSO のホストの短期バーストによって形成される 必要がある。高 z QSO 中の塵の特性を初期宇宙の塵生産メカニズムの文脈で議論する。z＞4 を越え、z〜6 までに進化が観察される塵の 減光曲線は、SNe による塵生産に期待される性質によってよく説明でき、後者が初期宇宙の塵生産の主要なメカニズムと示唆される。 我々はまた、遠方 QSO に見られる膨大な塵質量生産は、SN 塵によることを現在得られる観測の制限の中で示す。最後に我々は、 塵生産の別のメカニズムとして提案された QSO 風がまた、高赤方偏移の全体の塵計算に重要な貢献をしうることを示す。

"The Age of Early-Type Galaxies at z - 1 ", Aperello di Serego Alighieri, Alessandro Bressan, Lucia Pozzetti, http://arxiv.org/abs/astro-ph/0612047

概要の訳： z 〜 1 の初期型銀河の年齢の研究、それらの質量と環境への依存性は、銀河の形成と初期進化において理解が厳しいものである。 我々は、フィールドとクラスタ環境内両者の初期型銀河 z 〜 1 の基本平面(FP)の分析から導かれる M/L 比についての最近の仕事をレビューした。 我々は銀河年齢の推定を導くのに M/L 比を使用する。我々はまた、K20 サーベイから、初期型銀河 (0.88 ＜ z ＜ 1.3 ) の標本から 高 S/N 中分解能 VLT スペクトルの集合を使用して、SSP モデルスペクトルの合致によって、独立にそれらの年齢を推定するのに使用した。 その高い赤方偏移標本による利点を梃として、同一標本の M/L 比の分析と現在の銀河形成の階層モデルの予測とから得られる年齢を比較 して結果を分析した。

z〜1 の遠方銀河とz〜0 近傍銀河との M/L 比比較において、同じ質量では近傍銀河の M/L 比が 10 倍(小型銀河)〜 3 倍(大型銀河)大きく 遠方が明るい結果である。M/L 比の進化(遠近の違い) は、小型銀河ほど大きいという。銀河年齢は、赤方偏移に依らず、その大きさに依る。 メタルの [Z/H] の大小は、赤方偏移によらず環境(クラスタ内銀河かフィールド(孤立) 銀河か) にも依らない。 FP 分析年齢と SSP (スペクトル合成モデル)年齢はあまり一致していない。という結果である。

"Metal Enrichment in Galactic Winds",Yohan Dubois and Romain Teyssier, http://arxiv.org/abs/astro-ph/0611419

概要の抄訳：観測は、銀河間の媒質にメタルが存在することの証拠を与えるが、銀河形成の標準シナリオの中では、水素とヘリウムから、 より複雑な元素への変換が関係する恒星は、銀河の外側にそれを形成しない。超新星による風とそのフィードバックが銀河間の そのような豊富さを説明する可能な解であると提案されるが、揺動する銀河乾媒質中の適切な超新星爆発モデル化は、困難と判明した等。

銀河間空間は、銀河内の超新星爆発によるメタル生成とは場所がかけ離れているが、メタルが豊富である。それを説明しようとする銀河の CDM ハーローを合わせ銀河からのアウトフローを使ったシミュレーションは、条件を合わせても結果を説明できないという。 銀河の渦巻きは、その構造を利用する放出メカニズムの発想を喚起するが、渦巻から垂直にジェットを放出するというのは過去に普通に あった現象とするのは無理があろう。いうまでもなく、それは天体現象として非常に珍しいことだからである。これはまた太陽系などの 星の生成のときのガスの冷却の説明にも使われるアイデアである( T タウリ型の時期という段階とされている)が、星の生成自体が予定 時間内には奇抜な方法でしか説明できない、時間のかかる過程であることを示していると、私には解釈できる。

初期の状態が現在と変わらないことに膨張説は、初期の時期を前倒しして対応する。再イオン化という最初に星が輝き始めた時期を z= 6 としていたのが、それ以前の銀河 (z= 6.68, z= 6.56) が見付かる。Hubble Deep Feild では進化の証拠が少ないことが分かり、 銀河形成に約 5 億年とし、WMAPの結果では再イオン化時期を 2 億年とした。日本の電波望遠鏡で赤方偏移 z= 4 - 5 の CO 分子線に よって観測される初期銀河は、CO 分子の初期からの豊富さを示しているのではないか。そうやって初期の宇宙にしわ寄せをして 行くと、その初期期間の形成の問題に無理を強いることになる。

１０.０２ 銀河型の分類

                                       Sa - Sb - Sc 
E0 - E1 - E2 - E3 - E4 - E5 - E6 - E7＜              ＞I
                                       SBa - SBb -SBc

ハッブル自身の分類による、巨大な楕円銀河(E0-E7)、渦巻銀河(Sa-Sc)、不規則銀河(I) の多くの段階を時間に対する進化として説明するには、 宇宙の時間は、余りにも短く、できたままになる(*)。それらの銀河は、それ自身の形態(偏平率)の多様性だけでなく、特徴的な内部の星々の色の 違いをもつ。一般に巨大な楕円型銀河と渦巻型のバルジは、古い星からできていて、ガスや塵がない。渦巻型の渦状枝には青く輝く若い星、 散開星団が多くあり、対称面には塵があり、真横から見られる渦巻銀河には黒い筋が見られる。現状では、銀河の進化を説明するどころではなく、 様々な形態を説明する理論がない。それらの進化による説明はあきらめられて、そのように別々に作られたとするしかない。銀河が偏平率を変 える進化はあり得ないという見解は、ダークマターが存在すれば再考できるし、 (しかし、それによって偏平率の変化は速くなるだろうか?) (光学的偏平率が質量偏平率と異なる可能性もある。)、一般的に収縮過程において偏平率は大幅に変化する事実と相反する意見である。

当時、最大の望遠鏡を使って多くの銀河を観測したハッブルによる銀河の分類は、正式にそれを主題にした論文はなく、脇せりふのように出て きたという。図を使って述べられたのは彼の本 "星雲の領土" のなかである。これには、 Edwin Hubble 1889 to 1953 参照。( 訳 )

現在、渦状枝にもその間の暗い部分にも質量は同じだけ球状に分布し、渦状を示すのは明るい星の存在量の違いであるといわれる。さらに渦巻 銀河、渦棒銀河のダークマターの存在形態が球対称とする考え方は、渦巻と回転を否定するようにみえる。内部の恒星の運動から銀河の質量分布 が面対称か球対称かは分かるが、スペクトル線がシフトするドップラー効果で回転は明らかな事実であるのに偏平は実在でないのだろうか。

(*) 現在、渦巻型銀河が銀河のマージによってできたとする衝突説のようだ。

１０.０３ 恒星の HR 図

O - B - A - F - G - K - M

恒星のスペクトル型は、恒星の組成は違わずに、数万度〜数千度までの温度の違いという1つのパラメタによって連続的に並べられる。 近傍の恒星の色温度ー絶対光度をプロットして、多くが主系列という並びにのる。

こんなことをいうと、本当に変人扱いされるのであるが、恒星の H.R. 図の線上に並ぶ主系列星でさえ、星の発生の段階として捉えたい 欲求がわくものである。並びは単に形成時の質量の違いとされる。スナップ写真に子供と大人老人が並んでいて、成長の段階はこの写真に 写っていない、形成時の質量の違いでこう並んでいる、と説明されるようなものである。私は、畑中武夫氏の "星の進化" という題名の 講演を昔、聞いたことがあるが、いま、この美しい言葉に相当するものがないことに気がつく。宇宙論のいう"進化"とは、生物学が使う "進化"という高度な概念とは無縁であり、変化程度の意味かと思う。"発生"すら否定されるとき "進化" はあり得ないからである。

アインシュタインの"相対論の意味"の "要約とその他の注意"の(6)に "恒星のスペクトル型の違いを天文学者は、恒星の均一な発展の 年齢のクラスと解釈することが多く、その過程は、10^9 年より永い時間を要する。" とある。恒星のエネルギー源が何かは、彼なしに 知られようもなかった核エネルギーの巨大さによるのであり、それ以前、太陽の年齢を 2000 万年を超えることは難しいとケルビン卿が 考えたのも当然だったのであるが、この"相対論の意味"の第 5 版が書かれた時代、原子爆弾による戦争を経験し、恒星の核融合が周知 された時に、天文学者の傾向としてスペクトル型の違いが年齢のクラスと解釈されたということは、そのような今では全く無知な誤謬 といわれそうな考え(スナップ写真の子供と大人、老人のたとえ)が、さほど無理な説ではないのかも知れないと私には考えられる。 そして星の過程は、現在の状況と同様に、当時の宇宙論の宇宙年齢 10 億年よりも永い時間を要したのである。現在、主系列を年齢の クラスとする解釈は消え去り、質量の違いとする解釈に変わり、ハッブル定数とともに宇宙年齢がアインシュタインの頃の宇宙年齢の約 10 倍になって、両方が変化して譲歩しても、やはり矛盾は解決していないようにみえる。

太陽の質量と放射から計算される太陽の寿命は、水素がヘリウムになるときに放出するエネルギー効率 0.7 % から見て、 1000億年 ある。恒星の大気には水素以外にヘリウムが10% 程度含まれている。内部には、もっと多くのヘリウムがあると思われる。 ビッグバンで水素、ヘリウムができるなら、恒星大気だけでなく、10% のヘリウムは最初からどこにもあって、恒星での反応に大きく 影響することになる。恒星で水素がすべて反応するのではなく、恒星の水素の 10% 程度までが反応するとして、太陽の寿命はむりやり 100 億年に短縮される。仮りに太陽が 1000 億年の寿命をもっていても、150 億年の宇宙の年齢と矛盾するわけではない。寿命が年齢より 長いのは自然である。それにもかかわらず、オーダー(桁数)的な問題があると思われたのである。太陽が地球のような恒星でしか出来ない 重物質の惑星をもつため、第 2 世代以降の恒星であるとされるが、(前述したように、最近では、第 2 世代でもないらしい。第 3 世代 以降のようだ。) その形成に要する時間の問題は大きい。 最初からそれらには無理がある。星の寿命のオーダーより宇宙の年齢が短いのであるから。

１０.１ 恒星の光度と質量

星の内部は、核融合がそのエネルギー源であり、表面において 6000 度程度の温度をもつから、内部ではそれよりも高温、高圧であって 核融合の反応素材と反応生成物である、水素原子核、ヘリウム原子核、そして電子は、原子を形成せず、ばらばらの状態のプラズマ状態である (*)。 プラズマ状態は良導体であって、光を通さないとされる。星のエネルギーは、ニュートリノ以外は直接の放射ができず、中心から表面まで 熱は散乱された伝導と対流によってゆっくり伝播する。太陽の場合、中心の変動が表面に伝わるのに半径 70 万キロを 10 万年がかかるという。 これは、じつに 7km/year、20m/day、1m/hour という遅さである。

太陽の発熱は、P-P 反応(陽子と陽子反応)という核融合反応によって起こり、その反応に最低限必要な 1000 万度という温度は、太陽の中心 付近にしかないと思われている。1000 万度は、6000度の 1000 倍以上も大きく、後述の温度と半径のほぼ反比例関係を使えば、核反応の起き る領域は、太陽の半径の 1/1000 程度の半径でしかない。太陽よりずっと質量の大きい星では C-N-O サイクル(炭素、窒素、酸素を使って 循環する反応) という、より高い温度、数億度の必要な核融合反応が行われていると考えられている。それは、P-P 反応よりさらに中心で しか行われない反応である。

絶対等級Mから質量を計算する式 m= 3.89*10^(-0.1194M) (mは太陽質量(2x10^33gr)を単位にする)は、表面温度を無視しているのだろうか。 ステファンの法則 5.71*10^-5 T^4 erg/sec/cm^2 から、光度は、温度の 4 乗比例である。10 倍の温度比をもつ O 型と G5 型は、10^4 倍 も違い、さすがに O 型は例外としても、F0型〜K0型の間でも 3.6 倍の違いがある。それなら上式は、全く意味をなさない。そうでなく、 質量が半径(表面積)と温度を決めると考えると、上の式に意味を与え、それは、HR 図上で一本の線になる。つまり、これは主系列を説明する かもしれないが、同じ光度の様々な温度をもつ、主系列以外の赤色巨星、超巨星、準矮星、白色矮星を説明しない式である。 m= 3.89*10^(-0.1194M)と、絶対等級の式、M= -2.5log(L/(4πr^2))+C から、光度と質量の関係は、L∝(m/3.89)^3.35。 星の寿命は、τ∝m/L からτ∝m^-2.35 となる。

主系列星の性質が均質であるから、質量を与えると星のサイズと表面温度が自動的に決まると考えて、半径と、表面温度は、どのように 質量に依存するのだろう。R∝m といわれるのはどの程度正しいのだろうか。 R∝m では、2 倍の質量は 2 倍の半径である。光度の質量依存 3.5 (または 3 〜 4.5) は、どのようにもたらされた推定だろう。累乗の 3 〜 4.5 (3〜5 という数字も見掛ける) は、大きな不確定さである。

形状とサイズからは、星が球体とすると、体積は半径 R の 3 乗に比例し、放射の出口にあたる表面積は R の 2 乗に比例する。そのため 体積あたりの出口は、サイズに逆比例する。つまり、大きい星は、体積あたりの発生エネルギーは小さくても表面で同じ放射密度が保てる。 同じ表面温度の星は、体積あたりの発生エネルギーは、1/R に比例する。

半径の質量依存を k とし、半径が 質量の k 乗 に比例する (R ∝ m^k) ならば、星の平均密度ρは、ρ∝ m^(1-3k) である。小さい星と その半径 2 倍の大きい星の質量比が 8 倍未満 (k＞0.333) のとき、大きい星の平均密度が小さい星の平均密度より小さく、サイズと密度 の逆転が発生する。また、同じ表面放射密度では表面積に比例する発生エネルギーが必要であるから、質量比が 4 倍より小さい(k＞0.5) とき質量あたりの発生熱が大きくなり、大きな星が小さい星よりも短命になる。

表面温度の質量依存を j とし、T ∝ m^j (j ＞0) とすると、L∝T^4 R^2 から、光度の m 依存は、半径の m 依存の 2 倍と Tの m 依存の 4 倍、 L ∝ m^(2k+4j) となる。これで、2k+4J= 3.35(3.5) とすると、k= 1 では、j= 1.35(1.5)/4= 0.3375(0.375)、T∝m^0.3375 (0.375) だが、 デネブと太陽の間では、R= 40, m= 16.5 から、k= 1.32, j= 0.1775、R ∝ m^1.32、T∝ m^0.1775 になる。

定常的発熱 W を外に伝導する恒星内部の半径 r の温度 T(r) を考える。熱の流れが温度勾配に比例する J = -λ grad T と、 流れの発散がその点の時間的な温度変化を与える熱の保存式(連続方程式) div J = -Cv dT/dt とがあって、両者から熱伝導方程式、 Cv dT/dt = λ∇^2 T (Cv: 熱容量、λ: 熱伝導率、ラプラシアン∇^2= div grad) ができるが、定常状態では J = -λ grad T だけを使う。温度が r だけによる球対称な T(r) として、J = -λ dT(r)/dr になる。

気体の熱伝導率λは、気圧には依らず、原子分子の速度である温度の 0.5 乗に比例する。さらに 0.5 乗よりも 0.6 乗が使われる。 最初、熱伝導率を一定、λ= 1 として考え、その後、T^0.6 を使う。基本的考えは、温度の勾配に比例する熱伝導 J(r) と面積(r^2比例) の積が一定の熱の流れ W であり、熱の通路の断面積が半径の 2 乗に比例するから、流れ密度 J は、1/r^2 に比例する。そしてそれは、 温度 T(r) の微分である。

J(r)= W/(4πr^2)= -T(r)'

dT= -(W/4π) dr/r^2

T(r)= (W/4π)1/r + c

T(r) は、内部点温度が半径に反比例する部分と小さい c の和である。λ= T^0.6 を使うと左辺の dT が変わり、

T^0.6 T(r)'= -W/(4πr^2)

T^0.6 dT= -(W/4π) dr/r^2

(1/1.6) T^1.6 = (W/4π)1/r + c

T(r)= [1.6((W/4π)1/r + c)]^1/1.6

表面の r= r1 で T(r1)= T1、という境界条件をもたせ同じ表面温度では、1/r に比例する式(とその変種)であり、r=0 で発散 するため中心付近では何もいえないが、1/2 の半径の場所に約 2 倍(2.06)の温度である。小さい星と 2 倍大きい星があって、 大きい星の中に小さな星のサイズの核を考えるとその温度は、表面の約 2 倍の温度である。表面温度の等しい大きな星の内部は、 小さな星の内部温度より温度が高く、恒星の中心からの距離にほぼ反比例する。これは、中心だけから熱が発生し、熱の流れが 定常で半径によらないと仮定し、熱伝導率の温度依存性を 0.6 乗とした恒星内部の単純な熱伝導による方法がもたらす。

距離は、数 100 パーセク以内の恒星では 3 角測量できるが、距離によって精度は低下する(*1)。遠方の恒星の距離は、ケフェウス型変光星 (セファイド)以外、距離推定の方法がない。1910 年 G.リービットによる小マゼラン雲中のセファイドの測定から周期と光度(絶対等級)の関係 ( 2 倍の周期に 1.7 倍の光度(-0.6m)) がわかったように、その恒星が距離の判っている星団に属すと仮定できればそれによる。 距離には多少の不正確さが残る。さらに恒星の半径の直接測定は干渉性で恒星の半径を求めると昔聞いたが最近はどうするのか(*2)。 距離よりもずっと不確かであろう。恒星の内部の推定には、光度と半径とが必要であり、光度の決定にはもちろん距離がいる。 距離があればみかけの等級を 10 pc の距離に置いたときの等級 (絶対等級) に換算し、スペクトル型のデータとともにスペクトル型ー 絶対等級 (H.R 図)にプロットできる。

もし、太陽と表面温度が等しく半径が 2 倍の恒星は、表面積が 4 倍であるから光度が 4 倍、そして体積は、8 倍である。もし、恒星の 平均密度が等しいなら、質量 8 倍と、放射 4 倍とから、寿命は、質量/光度(M/L 比)であり大きい星が小さい星の 2 倍になる。 もし、大きい星の平均密度が小さい方のちょうど 1/2 とすると、質量比が放射比と等しくなり寿命は等しくなる。現実が、両者の間にあれば、 大質量星が小質量星より一般に寿命が長くなるが、これは普通に言われることの逆である。 半径が 2 倍大きい星の寿命を小さい星の 1/2 にしようとすると、密度を 1/4 として質量を小さい星の 2 倍まで小さくするのである。 それは、2 倍の半径の星が 2 倍の質量、R ∝ m の関係であるが、1/4 の密度の星に全体で 4 倍の発熱させるのである。体積は 8 倍だから、 体積あたりの発熱量は 1/2 だが、質量あたりの発熱は、2 倍である。このことは、密度が低くても温度が高ければ反応速度は大きいという 激しい温度依存性 ∝ T^15 があるから、少しでも温度が上がれば不可能ではないが、その任意さは、R∝ m を導く"ためにする"議論かも しれない。大きな星の重力は、小さな星より密度の高い内部を想像させる (それは、R ∝ m^0.333 以下に対応する。) という常識から乖離した結論を要求しているとみることもできる。

光度が質量に比例する以上に増加して初めて質量の大きい星は寿命が小さい。その光度の質量依存性に 3.5(3.35)乗という数字がある。 光度 L ∝ m^3.5 なら、寿命τ= m/L ∝ m^-2.5 となる。しかし、この 3.5 とかをまだ説明できていない。要するに、サイズの増大とともに 面積よりも体積が増大し寿命は長くなる一般的なスケール則は、恒星において成立しないと十分に納得できるかである。

(*1) ヨーロッパ宇宙機構 ESA のヒッパルコス (Hipparcos) 衛星 (1989年8月〜1993年 6月) は、約 12 万個の恒星の年周視差を 1/1000 秒角 精度で測定した。その精度では 1000 pc までしか測定できず (1000 pc での誤差は 100% である)、100 pc で 10 %程度である。予定の 静止軌道移行に失敗し、近地点 500 km 遠地点 3 万 6000 km という超楕円軌道になったため、測定計画全体が修正され、出版(1997年) された測定結果の信頼性にも疑問が多く提出された。133 pc 程度のプレアデス星団の距離にさえ議論がある。
http://arxiv.org/abs/astro-ph/0408370
http://arxiv.org/abs/astro-ph/0412093
http://arxiv.org/abs/astro-ph/0505431)

(*2) 1995年のHSTの観測によってオリオン座の左上肩の赤色巨星 Betelgius と変光星クジラ座ミラ(Mira) 星の直接像が得られている。 APOD の Archiv の 2007年2/21などにある。

伝導方程式からの T(r)∝ r^-1 と、ステファンの放射の法則からの表面温度 T(r)∝ r^-0.5 とが異なる累乗をもつことは、 前者は、恒星内部の熱伝導の内部温度であり、後者は、同じ放射を実現するための表面温度であって、式の意味は、違うが表面温度で両者を 併用すると、光度が恒星表面の半径 r を決める式になる。T= (W/4π) 1/r を、T^4 (4πr^2) = W に代入し、(W/4π)^3 = r^2、r= (W/4π)^3/2。 半径は、放射の 1.5 乗に、T は、放射の -0.5 乗に比例し、H-R 図上では右上りの線であり、この考え方の現実性はないと思われる。

恒星の質量について、温度と圧力とがどう密度をもたらすかを考えてみよう。密度ρ(r)は半径に依存するとすると、ボイル・シャルルの法則 PV = nRT で、 n/V= ρ/m 密度を原子量mで割ったものであるから、P= ρ/m RT である。体積 V 一定のときのように圧力 P が温度 T に比例 する場合にρは T との関係を失い、密度 ρ(r) 一定になる。

仮りに P が T の 2 乗に比例するとき、ρ(r)∝ r^-1 になるがそのとき、恒星の質量 M は、M= 4π∫r^2ρ(r)dr の 0〜r1(表面)の積分であり、 M ∝ 2πr1^2。質量が半径の 2 乗に比例になる(M ∝ 2π r^2)。これからは、M∝ L^3、L∝ M^0.333 となる。

密度ρ一定なら、質量は半径の 3 乗比例である。M ∝ r^3, r∝ L^(3/2) から、M∝ L^(9/2)、L∝ M^(1/4.5) となる。両者ともに、光度が質量の 1 乗よりも小さい累乗になるため、大きな星は寿命が長いという結果になる。L ∝ m^3.5 を求めたいのに、この結果は、累乗がその 1/10 である。

しかし、圧力 P(r)と密度ρ(r)とを、より正確に考える方法がある。恒星では圧力勾配と重力がつり合うという考え方である。 面積あたりの力である圧力 P(r) の勾配が面積あたりの重力とつり合い、重力は、ρ(r)と、中心から半径 r までの質量 M(r) との両者に比例する。

dP(r)/dr= G M(r)ρ(r)/r^2 (1)

M(r) は、dM= 4πr^2ρ(r)dr の 0〜r の定積分である。

M(r)= 4π∫r^2ρ(r) dr (2)

T は、発熱を決めれば単独に求まっているから、P が求まれば、ρ= m P/T からρが求まり、Mも求まる。発熱は P と T から決まる。 発熱も含めて P, T, M, ρは、一気に全て求めることできるだろうが、これは、解析的に解くことが難しい式であると思う。

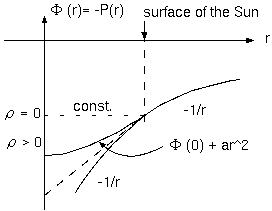
ボイル・シャルルの法則 PV＝nRT と V=一定 なら、PとTは比例する。温度は熱伝導から、T(r)∝ 1/r。しかし、圧力Pは、重力＝圧力勾配から、 重力ポテンシャルに比例する(Φ∝-P)。太陽外部とΦの値が連続し、内部が空洞ならポテンシャルは一定(const.)である。太陽内部のΦとPは図の -1/r (太陽内部で質量が一点に集中しているときのポテンシャル) と内部のΦがρ一定の2次関数 (ar^2+Φ_center)との間と予想できる。ある面を 境に重力が不連続ならその面の粒子に発散/収縮が起きるからあり得ないとして、太陽表面で重力が連続(ΦだけでなくΦの勾配も連続)とすれば、 中心のΦは表面のΦの1.5倍になる。

Φ_center= 1.5 x Φ_surface

この関係を全ての一様密度の星の、表面と中心のポテンシャルに期待するのは、余りに制限的であり、現実性はないかもしれない。この制限は、 重力方程式が計量の2階微分まで使用し、2階微分まで有限であることを要求するからであり、重力は空間的に連続である。但し、表面外だけに 重力がある空洞星を重力方程式が認めないのでない。重力不連続を生む厚さ0の空洞星は存在しないが、厚さがあればあり得る。

１０.２ HR 図と恒星進化

昔、考えられたのは、これを時間的並びとするものである。つまり、星の進化の流れをそのままに見るものだとする。 それは、主系列の左上から右下へ、青く耀く早期星から赤く暗い晩期星への変化である。この早期星、晩期星という言葉は、いまも使われる。 この考え方は、興味深く、星の進化のありさまがそのまま図になっているなら、これほど分かりやすいことはない。 存在分布が時間的分布で、集合平均が時間平均である。星の進化の過程はすべて見えていることになる。 ところが、HR 図が現在の存在分布のスナップショットでしかないなら、星の進化がこの図と関係ないという考えも可能になる。 星は、この図の上に現れ消えるだけで、存在分布は、星の進化の上の安定期しか見ないとするのである。そしてその考え方では、 この存在の分布図に現れないほどに急速な、又は暗い進化の過程があるということになる。図に存在しないものを利用するこの考え方は、 正しいのだろうか。図に見えているものを存在の変化と見ないのは、基本的な誤りかもしれない。

昔の星の進化説は、主系列の左上から右下への進化であり、青く明るい星から赤く暗い星への変化である。温度が高い青く若い星が、 徐々に歳老いた赤く暗い星になるとする。それは、なにか自然の生物の加齢の過程と一致するものであるが、過程は燃料終了とともに終わる。 それでは、過程は1段階であり、水素の核融合によってヘリウムができ、ヘリウムの次の過程がないことになりそうだ。 主系列星以外の、例えば赤色巨星から青色巨星までの列は、はっきりと別の並びになっている。それが説明できない。ヘリウム以降の変化も 主系列星の中で起こっているとしては、それらの系列間の質的変化を持ち得ないのではないか。

逆に、主系列が右下から左上への進化なら、弱く赤く暗い星が、中心温度を徐々に増大させて青く耀きその最期を遂げるという変化である。 これは、質量が増えるように思えるから否定されるのだろうか。質量推定の方法を調べたほうがよい。主系列中の青い星は、本当に赤い星より 質量が大きいのか。主系列は、質量一定の直線よりも多少左上がりとされるが、それが確かなら、主系列を左上にいくのは、星が核反応によって 光と熱を放出しているのに、なぜか質量を少々増加させているということになる。温度上昇は、水素がヘリウムに変化し、ヘリウムがその他の 元素に変化する反応が徐々に並行して進行するという説明になる。核反応の過程は、連続的と考えることになるが、そうすると、青い散開星団は、 実は歳老いた星たちの集合であり、球状星団の星々は若いものになる。これは、常識のひっくり返しである

一般の考えは、水素からヘリウムに変わる融合を利用した主系列は、そのうち中心核にヘリウムが溜り、中心核は収縮し外側の水素殼は膨脹し、 ヘリウムを融合する反応が始まるのは、赤色巨星になるときであるとする。中心核は、全体の10万分の1のサイズになるという。 主系列から赤色巨星までの変化は、非常に急速で HR 図に現れないなら、それを確認する方法もないことになるが、いままさに変化している星を 見付けてもよいのではないか。その後の超新星爆発現象による巨星から白色矮星への変化が捉えられるようにである。 この考え方のモデルシミュレーションで散開星団の HR 図が再現されるというが、本当だろうか。

１０.３ 恒星の形成と収縮過程

物質が用意されたとしても、前世代の超新星爆発から今の太陽系が形成されるまでの収縮に必要な期間を考えると、太陽系が第 2 世代という 確信は、なくなる。散乱した微細な原子、分子を結合するには、サイズの小ささから重力でなく、光圧が最も強い引力を与える。宇宙空間の 光圧は弱い。太陽系の原子分子の集合過程は、通常の星が光を放つ期間よりもオーダーとして、十分長い期間が必要に思える。物理的な過程 は一般に、発散は短時間で、収縮過程は長期である。数年間土中に幼年期をすごし成虫で数週間しかいない蝉のように、恒星は物質のサイク ルからみると、核融合に点火して光る期間はその一部ではないかと思う。これは光るのを待つ通常物質ダークマターの量に関係する。

太陽質量の水素がヘリウムに変わるエネルギーと現在の太陽のエネルギー放出率からみた寿命は、1000 億年である。太陽の質量 2*10^33 gr の水素がヘリウムに変わるエネルギー効率 0.7% と現在の太陽のエネルギー放出率 4*10^33erg/sec からみた寿命は、E= mc^2 から、erg と gr と cm/sec で、2*10^33*0.007*(3*10^10)^2/4*10^33 = 3*10^18 sec = 10^11 年、1000億年となる。

これが宇宙の進化説からは、宇宙進化のスケールより大きいため、恒星の全ての水素がヘリウムに変わるのでなく、恒星の中心核だけが ヘリウムに変るとして太陽の寿命を 1 桁下の 100 億年にする。それほどに恒星の効率を低く見る必要はないのではないか。 さらにヘリウム以降の反応の期間もあって、それを極端に短く見積もりすぎではないか。その根拠も全くないのに、現在が太陽の活動の中期 であり、最も活発に反応しているとされるが、他の期間は、もっと緩やかだとするだけでも寿命はもっと長くなる。

輝く物質の N 倍の通常物質ダークマターがあるとき、物質が恒星を経る周期は、星の寿命の N 倍であろう。これは、単純な算数だが、 もしも定常を前堤にして、すべての物質が循環するとするなら、時間平均が集合平均に一致するエルゴード仮定が満たされない理由はない。 そうすると、前世代の超新星爆発は、そのぐらいの昔となる。太陽の寿命が星の物質平均の輝く期間の代表になるかどうかは不明であるが。

恒星の収縮過程では、超新星爆発で飛散した物質は、その重力ポテンシャルの井戸を出ると速度が落ちるだろう。さらに物質が互いに衝突して 相対速度を落し、ガスの中心の重力に捕捉される。それから、さらにぶつかり合って速度を落し、中心に落下し塊を作る。 稀薄なガスが重力中心を見いだす重力捕捉速度を次のように考える。ガスの塊が周辺よりもΔρだけ密度が高いとすると、重力ポテンシャル -GM/R = -4π/3 GΔρR^2、これが、-v^2/2 より大きく √(8π/3 GΔρ) R ＞ v の場合にガス塊は重力捕捉される。 v= √(8π/3 GΔρ) R を重力捕捉速度とすることができる。

10.31 方励之の重力系の崩壊時間

それ以前に、太陽系のもとになるガスの半径を 50 AU とするのは常識的に小さすぎるだろう。それは、現在の惑星系の大きさである。ガスの半径 を、隣の星までの距離の半分、約 0.6pc = 120000 AU とすると(1pc=21万AU)、半径 R は、2400倍、密度ρは、1.38x10^10分の1にも小さくなる。 そして収縮時間が 1/√(Gρ) に比例すると、それは 11.7万倍になり、57 年は、6.67 x 10^6 年になる。5桁も値が違うが、どちらが正しいのか。

そして、銀河系の質量を10^11Ms(太陽質量)とし、銀河系の半径を1.24x10^4pcとしている。密度は、3.5x10^-24(g/cm^3)から、収縮時間は 6.6x10^7年と書かれている。じつに、銀河系形成にはビッグバンからの時間は不足することをこの数段落で示そう。銀河系の質量を銀河系の 周辺まで考慮し1兆個の太陽質量とする。太陽系への収縮の質量比とサイズ比だけで銀河系の収縮時間を見積る。天の河銀河系は、特別に大きな 超巨大銀河とされ、これ以上に大きなアンドロメダ銀河と両者より小さな矮小銀河からなる局所銀河団という集団に属していて、他の銀河より 密集しているから、銀河系に収縮する以前のガス雲の大きさの間隔を現在のアンドロメダ銀河までの距離程度、100万pc と仮定する。これは 先の(現在の)銀河系の半径1.25万pcの80倍のサイズであり、特に不自然な仮定ではない。すると、太陽系に対して質量が 10^12倍、半径が10^6倍で、 ρ∝M/R^3は、10^12/10^18= 10^-6 から、銀河系の収縮時間は太陽系の収縮時間の 6.67 x 10^6 年の t∝1/√ρ=1000倍、6.67*10^9年、67億年 になる。これは銀河系の円盤状の形態への重力収縮時間を考えたものではなく、その周回速度で半径Rから中心への直進するだけの時間であり、 実際にそれで収縮できるはずがない短期間への見積もりである。

アンドロメダ銀河と銀河系の間隔は、両者がすでに数10億年接近を続けているから、形成前のガス雲を少し大きく見た方がよいと2倍にすると、 それだけで密度は1/8になり、収縮時間は √8= 2.8倍になる。それは、67億年の 2.8 倍、187.6億年である。銀河系の質量を10倍しない昔の 数字を採用して1000億太陽質量とすると密度はそれだけで1/10になり、収縮時間は√10 = 3.16 倍、593億年となる。繰り返すが、これは実際の 銀河系の形成時間ではない。銀河系の質量による質点の円運動速度を使って半径を横切る時間である。銀河が現在のような円盤状の形態に収縮し、 渦巻を形成するのに要する時間は、これの何倍あれば可能なのか、私は容易に見積もることができない。実際の収縮時間を求めるには、どのような 考察が必要だろうか。複雑な思考も必要だろうが、我々に必要なものは何よりも時間である。銀河は決してビッグバンからの時間に入らないと 判定してよいのではないだろうか。

10.32 形成時間が宇宙年齢に比例する

ρ∝ 1/R^3= 1/t^2、

それゆえ、銀河の形成時間は、宇宙年齢に比例する。

t_g ∝ 1/√(Gρ) ∝ t

銀河形成時間が宇宙年齢に比例するとは、どういうことか。現在、宇宙年齢が137億年では67〜600億年かかる銀河形成は、半分の宇宙年齢63億年では 半分の33〜300億年でできる。1/4の年齢では 16-150億年、1/10では 6.7-60億年、1/100では0.67-6億年、仮に銀河の収縮時間を67億年として宇宙年齢 に2つ入るとすると、後にできた銀河ひとつを残して、前半の期間にまた2つ入り、同じことはどこまでも繰り返せる。こうして宇宙年齢のなかに銀河を 無限に作り出せる。67〜593億年に臆することはない。銀河は無限の過去から無数に形成された姿を示す。こうして膨張説は、過去の永遠を模擬する。

膨張は無限を模倣する

これは、膨張説の過去は密度ρが高いため構造形成が速いことからくる。初期宇宙は重力による天体力学を高速化でき、無限大の密度からの膨張を 使えば何でも可能、時間まで自由かとみえる。無限の過去が必要なほどの現実の宇宙の様相を目前にして膨張説は有限の時間内でそれを模倣する。 しかし、必要なのは現実が膨張説の宇宙年齢より長期を示していることを知ることである。注意すべきは、現在とその状態はそのまま、どれだけ 遡っても、物理法則のない特異点以外のどの時点も、銀河形成時間が宇宙年齢以内にはとても入らないことである。矛盾は決して解消していない。 それなら現在の宇宙をよくみて、物語を作るのは止めるのがよい。膨張は無限を模倣しているだけである。

また、方励之の挙げたこの話の不思議さ、なぜ、収縮前のサイズの代わりに収縮後のサイズを使って、収縮に要する時間を極端に小さくするのか。 それは、膨張説の欠点を隠すためか。銀河の構造形成が膨張説を否定するからか。いや、収縮前のρを導くために、現在の収縮後のサイズを使うの である。それは、ρ(ago)＝ρ(now)x R^-3 であり、ρ(ago)＝ρ(now)x t^-2 である。膨張説は、膨張を前提にした計算をする。質量が一定で、 (収縮前のρ)＝(収縮後の体積からのρ) と考えるのは、収縮前にどれだけの体積から収縮したかを全く消し去る。つまり体積が変らない。これは、 収縮の過程ではなく、膨張に取り残された部分が相対的に収縮してみえるというだけである。その体積内の粒子の相互作用が考慮されないから、 普通、重力収縮とはいわないだろう。そのとき宇宙の膨張から局所的に逃れ静止状態になっただけである。そのような方法で、現在の美しい銀河が できるだろうか。

それは、渦巻銀河の構造を、粒子が互いに相対速度を打ち消し合う衝突を経て、重力だけによって収縮した後に、それによる発熱を放散し、質量は 分布を変えて元のサイズよりずっと小さな円盤状に収縮し、打ち消されず残された平均角運動量で回転すると考える、カントとラプラスからの古典 的な重力収縮による構造形成とは違うものである。そして、太陽の回転と全ての惑星がほぼ近い面内で同じ方向に軌道運動する太陽系の形成は銀河 の円盤状の形成過程と完全に整合した小型版と理解できる。それよりサイズが 10^5 倍も大きい1回転するだけでも数千万年〜数億年かかる円盤状の 渦状構造、ガスが冷却し重力収縮し光熱を放散する恒星と銀河の形成過程と、膨張説のこのみせかけの相対収縮とは、余りにも乖離した考え方である。

太陽系でも、銀河系でも、超銀河団でも、現在の収縮した又は未完成の状態のρを収縮前のρに使って、銀河形成と太陽系形成との各過程が現状の 実現にうまくいくように現在の値を使う。そんなことをすれば、例えば、太陽系や銀河系の大きさが現在と10倍も100倍も違っても、全く同じように 実現できてしまうが、それでいいのか。それはこうすればこうなるというだけの、不正処理ではないだろうか。根拠のある正当な処理だろうか。

また、1/√(Gρ) のρは周囲を超える密度差Δρにすべきで、 1/√(GΔρ) である。そのとき、背景輻射の時期の温度の均一さ (Δρ/ρ)＜2x10^-5 を質量の均一さとみると、それは構造形成時間を√5万= 223倍にする。背景輻射の均一さは、昔からCOBEまで、宇宙膨張の証拠と言われたが、これは 一方的な意見だったのであり、よく考えると全く逆で、実際は膨張説に有利な結果ではなかった。それが現在、彼らがλ-CDM説を採用する理由である。

現存する銀河と大規模構造を説明しなければならない。大規模構造はその後、冷たいダークマターCDM存在を仮定し、それがすでに晴れ上がり時点で 偏っていたという仮定をいれて、さらにダークエネルギーという新しい言葉に変えた宇宙項λを仮定しなければ、説明できなかった膨張説に困難な 存在である。ところが、彼の論点はそうではなく、表題の "超銀河団いまだ完成せず" であり、彼の計算する380億年という超銀河団の収縮時間 (本当の収縮時間、構造形成にはもっと長期が必要。周回速度で中心にいくだけの時間、太陽が57年で収縮するような話だからである。) は、 宇宙が始まってからまだ来ていないということだけである。太陽系の話に戻ろう。

10.33 太陽系の重力捕捉速度

温度からくる粒子速度を考えると、温度 T のとき、質量 m の粒子の速度は 3/2 kT (1自由度に 1/2 kT) の平均運動エネルギーをもつ。 ボルツマン定数 k= 1.3806 x 10^-16 [erg/K]、陽子、電子の質量、m_p= 1.6726 x 10^-24 [gr], m_e= 9.1093 x 10^-28 [gr] を使うと、 粒子速度は、v= √(kT/m) で、陽子のとき v_p= 0.9x10^4 √T [cm/sec/K] である。電子の速度は、質量の√に反比例して√1836.1= 42.85倍大きい。陽子の速度は、T= 300 Kの常温で 1.56 km/sec、現在の背景輻射の温度 T= 3K で 156 m/sec であり、太陽系の重力捕捉速度 より大きい。太陽系が、水素ガスから始まるのには、現在の背景輻射温度ですら、重力捕捉速度を超えている。

10.34 3K が重力捕捉の可能な温度

宇宙膨脹の非平衡を仮定することによって、これが容易になるとは思えない。宇宙膨脹の中での収縮は、さらに困難で時間がかかると思うべきである。 なぜなら、ある永い時間をかけて、膨脹が局所的に停止した領域ができても、それはまだ収縮ではない。仮にある空間の部分の内部粒子(物質)の 四散する速度を0にできても、まだ粒子は同じ位置で互いに接触せずに静止する。それ以降の収縮過程は、この静止から開始しなければならない。 膨張の時間反転の収縮にはその速度変化は2倍である。つまり、膨張宇宙の重力収縮は前期過程をさらに増やすだけである。膨張宇宙が初期に収縮 していたから収縮が容易という理由はない。初期の収縮状態は位置は同じだが速度が逆である。地球上でボールを投げ上げるとき、上昇と落下とは 違う状態である。ボールの上昇は頂上に届いてから落下が始まる。そして、膨張宇宙の全ての質量は、簡単に停止しない脱出速度をもつボールである。 膨張から脱落させることは普通できない。速度停止の相対的収縮は、塵の座標系(共動座標系)からみたもので、我々の通常の物理の成立する系から みれば、膨張宇宙での重力収縮は、静止宇宙の重力収縮よりも、困難で多大な時間がかかる逆向きの変化である。

さらに、それがビッグバンから現在までの1/10、1/100の時刻に起こるなら、そのときの宇宙の平均温度は、(直線膨張では)絶対温度27度、270度 であり、(t^2/3 の臨界膨張では、放射温度T_r＝ 1/R＝ 1/t^(2/3) から4.64*2.7=12.5K, 21.54*2.7=58.16K)絶対温度12.5度、58.2度であり、 ガスは、そこまでしか冷却しない。輻射の光圧は現在より大きいため収縮に有利であるが、冷却の底辺となる周囲温度が高いために収縮過程は 現在の宇宙よりも困難で長期だろう。

(*) 重力捕捉のポテンシャルは、-M/R 比例で R^2に比例、重力捕捉速度の2乗 v^2 がポテンシャルに等しいから、vはRに比例する。 大質量星のガス温度は高い(M∝T^1.5)。宇宙初期の恒星質量は大きかったといえるかもしれない。(寿命が短かったかはいえない。) 臨界膨張 R∝t^2/3 では、T∝1/R∝t^-2/3 だから M∝ T^1.5 は、1/t比例である。しかし、密度ρを考慮すれば、-M/R ∝ρR^2、 v∝R√ρ、T＝v^2 からρR^2= T、形成される恒星質量 M∝ρR^3∝T√(T/ρ)＝T^1.5 ρ^-0.5 である。ρ∝ t^-2から、恒星質量は、 M∝ T^1.5 t ∝ 1 である。初期宇宙の恒星質量は、ρを考慮しないとき大きいが、ρを考慮すれば、現在と変わらない。

10.35 電子の捕捉と水素原子の形成

衝突の運動エネルギーが13.6eV以下で、陽子に電子が電気的に捕獲され水素になる。それ以前はプラズマ状態で、電子は陽子に衝突しても反発される。 捕獲されると水素原子になって、Lymann系列(n=1)、Balmer系列(n=2)、Paschen系列(n=3)の、それぞれ、 紫外線(m= 2,3,4,5,...の波長 122, 103, 97, 95, 94nm)、 可視光(m= 3,4,5,6,... = 656, 486, 434, 410nm)、 赤外線(m= 4,5,6,.. = 1875, 1282, 1094nm)の帯域に対応する光を吸収/放出をする。(n=1,m= 2)はLyα、(n=1,m=3)はLyβ、(n=2,m=3)はHαという。 古典物理では加速度運動する電荷は電磁波を放って急速に軌道が落下するはずが原子内電子は安定軌道をもち、軌道を変えるときだけ特定の波長の 光を吸収/放出する。電子の波が軌道上に定在する速度の逆数が n= 1,2,3,...である軌道のエネルギーが、-1/n^2 に比例する。また原子の軌道半径は n^2 に比例する。軌道間のエネルギー差が、1/λ= ν/c= R (1/n^2 - 1/m^2) (R= 1.097 x 10^7 [m^-1] リュードベリ定数) の波数(1/波長)になる。 エネルギーと周波数は波数に比例する。基底軌道と自由電子とのエネルギー差(n=1, m=∞)が、13.6eVである。水素原子を中性水素とも H I といい、 電離した水素、陽子プラズマを H II という。中性水素 H I 領域は陽子電子のスピンの並行、反並行間の移動によって21cm電波を発生する。

1eV は1万1600Kに相当し13.6eVは温度にして 15万7800Kである。その温度からプラズマは水素原子に姿を変え始め、その下数1000Kまでに水素になる。 途中、水素原子2個がエネルギー差 4.47eV (5万2000K)に相当する速度で分子を形成する。軌道のエネルギー差には電磁波の出入が対応するが、 粒子の結合は一般に発熱反応である。これは、膨張宇宙の空間膨張に伴って低下してきた周囲の温度低下を妨げる。水蒸気が液体の水に凝結する とき100度C、液体の水が氷になるとき氷点の0度Cを保つように温度変化の停滞時期が考えられる。水素原子比率が増大する停留と、水素分子比率が 増大する停留の2つの時期(*)があるはずである。それらの温度は、15万7800Kと5万2000Kである。

電子速度が大きいとき、電子捕捉と光の放出は、紫外線のn=1への捕捉であろう。速度が下がれば、n=2も、n=3もあり得る。捕捉が確かでないほど 大きいnと半径(n^2)の大きい軌道への落ちこみは、どこまでも長波長であり得るから、自由電子と区別できず、つねに存在し得る。電子がある速度 もって陽子に衝突するとき、どの軌道に落ちるかは、最小のnが最大の確率で起きるだろう。

(*) R＝t＾2/3の膨張での 1100 倍の温度の時期は、いつなのか T＝1/R ＝t＾(-2/3) から、T^3= t^-2, √(1100＾3)＝3.65 x 10^4, 137x10＾8 年/ 3.65 x 10^4= 37.5 万年。

13.6eV= 15万7800K の温度は、いつなのか 15.78x 10^4/ 2.7= 5.84 x 10^4, √(5.84x10^4)^3= √5.84^3 x 10^6 = 14.1 x 10^6, 137 x 10^8 / 14.1 x 10^6 = 9.7 x 10^2 年(970 年頃)である。

このような16万Kに近い高いエネルギーをもつ水素原子形成、宇宙の晴れ上がりの温度が3000Kと言われる温度の50倍とは一体どういうことだろう。 時間にして、970年/38万年は、1/400である。膨張宇宙説は、晴れ上がりに大きな幅の時間を持たせているのか。それは、13.6eV/n^2 というエネルギー がn= 1,2,3,...においてあるから、13.6eV から可視光線の赤色 0.3eV までを晴れ上がりに考えるからであろう。

そして、膨張宇宙で特徴的な、それがいつの黒体輻射の名残であるか分からないという特性、いつの晴れ上がりなのか、2.7K は3000Kの黒体輻射の 波長をを1100倍にしたものか、16万Kの黒体輻射の波長を5.5万倍したものか全く分からないという特性と関係している。膨張宇宙の波長スペクトルは、 つねに全ての温度で黒体輻射なのである。現在残るその強さは現在の2.7Kの黒体輻射と全く同一である(そのため疑わしく膨張証拠でないのだが)。 完全な晴れ上がりは、0.3eVでよいが、晴れ上がり始めるのはすっと前で、晴れ上がりの中心温度は、16万Kであり、中心時刻は、970年である。

黒体輻射の波長は、過程の半分の中心時刻から50倍にも伸び、Lα、Lβ、Hα、Hβなどの暗線スペクトル線は幅広い時間平均によってなだらかにされ、 平均によって正確な黒体輻射だけが残るということだろうか。そういう説明を考えないと晴れ上がりになぜ水素の暗線が見えないのか説明できない。 つまり、2x10^-5の正確さをもつ晴れ上がりは、970年にあり、その時期の温度の10万分の2の空間的一様さなら、ダークマターなしに現在の大規模構造 を作ることが可能だろう。つまり、宇宙黒体輻射が形成される時刻は400倍、温度は50倍、違っているのかもしれない。

10.36 平均自由行程と衝突間隔

初速をv0とし、最終速度をv1とするとき、log_r (v0/v1)= N なら N 回の衝突が必要だが、それぞれの時間間隔は、 τ0= L/v0, τ1= L/v0r, τ2= L/v0r^2, ... , L/v0r^N という等比数列となるから、それらの総和は、Στi 〜 L/v1/(1-r)、 r と v1 だけによる。太陽系の場合、先ほどの密度と最終速度v1= 100cm/sec とするなら L/v1 = 10＾14 sec = 3 x 10^6 yr の 1/(1-r)倍になる。

恐らくは、中性水素に変ってからの時間が長いだろう。それは、陽子と電子の衝突は、結合する可能性が高く反撥係数が低くr= 0とみなしてもよい。 中性水素原子も水素分子に反応するので反発係数は低い。結合反応は、粒子速度からその結合エネルギー分を光に変換して、粒子速度を落す。

水素原子同士、水素分子同士は基本的に反応しないので反撥係数は高いが、r=1 ではない。衝突で少し高い電子軌道に遷移し光を放出して戻ることで 速度を落すことができる。しかし、下方の軌道に落ちれば、その1つ上の軌道までのエネルギー差以上のエネルギーをもつ速度しか削減できない。 例えば、基底状態(n=1) に下がれば、次の軌道までのエネルギー差が大きく(紫外線の122nmに相当する)が速度として大きくそれ未満の速度を消す ことができない。これは、Lyα(n=1, m=2)では 1/n^2 - 1/m^2 は、13.6eV(n=1,m=∞) の 3/4 (10.2eV)の温度11万8000Kに相当する速度 31.2 km/secである。次に、n=2 とその上の軌道との Hα (n=2, m=3)では 1/n^2 - 1/m^2 は、(1/4-1/9)*13.6=1.89eV= 2.17万K= 13.27km/secである。 これは太陽系の収縮前のガスの速度に近い。そこから中性水素ガスは、粒子衝突において速度を落すことが難しい。

しかし、それ未満の速度に対応する温度でも、速度削減は不可能ではない。なぜなら、温度から粒子速度はつねにマックスウェル分布をして高速粒子は、 僅かながら、つねに存在するからである。そのとき r= 1 ではなく、それに近い値になる。もし、最終速度 1m/sec が達成されるまでの中性水素の 反発係数が、r= 0.99 なら 3億年、r= 0.999 なら 30億年になる。Hαの速度v= 13.27km以上は削減されそれ未満は保存されるとして、分布の比率 から反発係数rを求めると、周囲温度3k,30K,300Kでのr= (m/2πkT)^3/2 exp(-mv^2/2kT) のexpの運動と温度比率だけについてみれば、 3K では 10^4 30Kでは 10^3, 300K では 10^2、3000Kで10 である。それらの exp は、3000K でも exp(-10)であり、r= 1 - 1/2万20000 であり、 600億年になる。

10.37 銀河系収縮の時間

銀河系収縮の最終速度を太陽系の重力捕捉速度、100m/sec とするなら、銀河系の形成と太陽系形成は連結して考えることができる。その場合、 銀河系形成の L/v1 は、太陽系形成の 5000/100 = 50 倍の時間になる。1.5 x 10^8 yr = 1.5 億年の 1/(1-r) 倍になる。r= 0.9 なら 15億年、 r= 0.99 なら 150億年、r= 0.999 なら 1500億年である。

原始銀河系ガスの半径230kpcの重力捕捉速度は、651 km/sec であり、これに対応する温度は、5200万度である。この温度自体は、 銀河団の内部にあるX線を放射するガスの存在が確認されているから、意外でもないが、この温度では、稀薄なこのガスは、 プラズマ状態であり、水素原子を形成しないだけでなく、重力収縮して銀河や、恒星を形成するのでなく、核融合を起こして 発熱する温度である。この温度より十分小さくても問題がないわけであるから、この温度である必要はないのだろうか。そうではない。 現実の温度が低ければ、現実の銀河系より小さな矮小銀河を生むだろうし、これより高い温度では、より巨大な銀河を生むだろう。

現在、太陽系には恒星が耀き、太陽風によってガスは吹き飛ばされてしまって、そのガスはないとされる。 太陽半径 6.960 *10^10 cm と、太陽質量 M= 1.989 * 10^33 g を使って、物質の量が変わらず、ρR＾3一定から太陽系のもとのガス密度を 計算する。太陽平均密度を 1.4(g/cm^3)とし、太陽半径を半径 0.5pc の球体に拡げると 1.4/(1.5*10^13/7*10^5)^3= 1.4/(2*10^7)^3= 1.7*10^-22 これは、現在の値 (恒星間ガスは 5〜8 x10^-25g/cm＾3)より3桁大きい。太陽が近傍恒星より大きめを考慮し半径を 1pc に拡げても 2.2* 10^-23 となり、まだ2桁大きい。昔はガスがあったと考えるべきか。ガス不足は、太陽風による太陽周辺だけの局所現象ではない。

銀河中心からの衝撃波によって、点火期間は、加速できるかもしれない。しかし、恒星の収縮過程が恒星の寿命よりずっと短時間という説 には、根本的な無理がある。ビッグバンからの時間に間に合うには、数億年で収縮しないといけない。46億年前の太陽系完成までの残りの 時間をすべて収縮期間に充てることはできない。以前 50 億年と言われ、今20〜10億年になった、銀河形成の同様な永い期間と、物質を 用意する超新星爆発サイクル期間が必要だからである。宇宙の初期に重い星が多く、超新星爆発による世代交替が速かったという証拠はない。 天文学は、ビッグバンからの時間に収容することを要求され、急がされている。時間がかかりそうな過程を、非常に容易に通過するように する。そうでもしないと、とてもその時間にはいる訳がないからである。最近はその矛盾が早期の時期に集中し、恒星形成、銀河形成を 圧縮している。

2003年9月28日、放送大学の"宇宙の観測"(講師は川辺良平氏)で、最近の恒星の始まりの考え方を知った。ガスは分子雲を形成する (10万〜100万年)。原始星を形成する(1万年〜10万年)。ダスト円盤(デブリ円盤)と両極へのアウトフロー放出をするＴタウリ型星を形成する (1000万年〜2000万年)。そして主系列星になる(＞1億年)。という昔よりさらに急速な恒星形成を考えるのである。 Ｔタウリ型という独得な天体を、すべての恒星の形成の段階と考えるかどうか疑問だが、(というか、とてもそんなことは信じられないが) このように急速な恒星形成を考えなければならなくなった理由は、いわずもがなである。

１０.４ 宇宙の果ての銀河の光度

(1)宇宙の果ては、銀河間の塵によって 99% 覆われているのかもしれない。塵による減光は、距離に比例する等級変化が 1.25 等級/Gpc になり、すこし大きすぎる。銀河系や、アンドロメダ銀河は、数ある銀河のなかで、超巨大銀河(-19 等以下)に属す。中位の銀河は、 アンドロメダに比べ5〜3等級暗い。深部探査の銀河達を中位銀河とみなすと、29.3〜27.3等級になる。予測からの誤差は、0.7 〜 2.7に減る。 4Gpc の塵による減光を 2 等級とすると 0.5等級/Gpc、銀河内太陽近辺の光の減衰 0.5等級/3kpcに比べて、約 6 桁少ない。

それ以前のハッブルの測定、銀河の分布が一様で、宇宙が透明とするときのゼーリガーの式、等級 m+1 までと等級 m までの銀河の個数比 N(m+1)/N(m)= 3.98 (1等級差は、2.512倍、距離比は√2.512。個数比は距離の3乗、(2.512)＾(3/2)= 3.981) からの偏りが微小で偶然的から、 塵の密度は、10^-31〜10^-32 g/cm＾3 を超えず、"わが恒星系の主平面ちかくでの星間ガスよりは、100万倍も薄いことが必要。"に合う。

(2)普通の宇宙原理からいって、銀河系やアンドロメダ銀河を超巨大銀河とせずに平均的な銀河と考えるか、深部探索で見えた銀河達が平均よりも かなり明るいものと考えると、 5等級の差に戻ることになり、宇宙の果てが5等級、100倍光度が低下する距離、つまり10倍宇宙の果てを 遠ざけることが合理的になる。ハッブル定数を 1/10 にし、宇宙の始まりの時期を10倍過去に伸ばす大変なことになるが、 銀河系とアンドロメダ銀河以遠の銀河の距離推定に使った道具を疑うだけですむ。

(3)宇宙が平坦でなく、曲率が正で空間的に閉じている場合、遠方の光は、宇宙自体の凸レンズ効果で距離の２乗に反比例よりも明るくなるし、 反対に曲率が負であるなら凹レンズで遠方が暗くなる。宇宙が透明で空間曲率が正なら、ある距離まで空間が拡がるが、それより先は空間が 狭くなり、遠いほうが明るくなる。そして最大距離には一点からの光が収斂する、対極点がある。対極点の存在は、宇宙の光学に異常な性質を 帯びさせるはずで、定常有限宇宙のオルバースのパラドックスを生む。アインシュタインの定常宇宙にもこの問題は残る。 現実の宇宙においてこのような性質は、全く確認されていないし、曲率が負であることが、宇宙の果てを暗くさせる。 曲率が負であることが減光の理由かもしれない。

(4)ドップラーシフトも、塵なしに遠方の光度を下げる。遠方では光の速度に近づくに従って、際限なく光度低下をもたらす。 銀河のスペクトル型(F2〜G4)がシフトされ、可視光領域に入るものが変わることで光度が変化する。 しかし、宇宙の果ての銀河が、本当にどの程度遠方かによる。銀河の赤方偏移の値があれば、議論できるだろうが、 スペクトルが得られたわけではない。

1995 年からのハイゼットチームによる40〜70億光年の50個ほどの銀河での超新星爆発の赤方偏移と明るさの比較で、予測より平均 25% 暗い ことから斥力項の存在を確認したとする話と比べれば、大きな誤差であり、説明は容易でありうる。彼等は、たった25%の誤差から斥力項を 結論する。塵の関与分、赤方偏移自体の減光分の計算もしない。

１０.５ 銀河の輝度について

1929年ハッブルと1929年 ヒューメイソンによって遠方銀河ほど大きな赤方偏移があることが分かった。 ハッブル自身、宇宙膨張の考えは持っていず、"赤方偏移は宇宙の膨張によるものではないと思われるから、宇宙構造の考察の多くは再考が 必要だろう。" と述べたことは、よく知られている。彼の次の世代がそれを膨張の直接の結果と思ったのである。 一般相対論が宇宙膨張を説明し、その他の説明は、正統の理論からそれほど受け入られなかった。ドップラー効果以外に赤方偏移をさせる 代替理論は多くあり、重力赤方変移、時計的宇宙論、可変質量仮説、慣性の誘導、時間の加速、不完全光伝播 (tired light説)がある。

tired light 説について、銀河間の媒体による光子のエネルギーの損失というアイデアは、1929年 Zwicky によって示唆され、彼によって 長く防御された。ネルンストNernstは、1937年に輻射が光エーテルによって吸収されるという仮定のモデルを開発した。20世紀の半ば Zwicky は、tired light 仮説が発展できるように手入れをした。しかし２つの問題があった。１）φ-bath は光源からの光のコヒーレンス を汚し、遠方の物体がぼける。２）散乱現象は光のエネルギー損失が周波数に依存する。Vigier は、真空を共変超流体として扱うメカニズム を提案した。これは上の２つの欠点を持たない。また、インコヒーレント・ラーマン散乱は、同じくドップラー効果をエミュレートする。

(中略)

遠方銀河の明るさには、 Hubble と Tolman による Tolman test がある。赤方偏移が宇宙の膨張によるのか、他の原因によるのか判別できる のである。銀河が本当に速度をもって後退している場合、銀河の輝度は、I = const - 4 log(1+z) + 0.4 K そうでない場合、 I= const - log(1+z) + 0.4 K という。実際の測定は非常に難しい。最近は、Sandage によって 1991 年と 2001 年に報告が出されている。 2001 年の Lubin と Sandage とは、(1+z)^-n の n を測定から求め、Ω_M = 0.35, Ω_Λ = 0.65 のモデルでは R-band では、n = 2.28+-0.17, I-band では、n = 3.06 +-0.13 とし、静的宇宙では、 R-band では、n = 1.61+-0.13, I-band では、n = 2.27 +-0.12 とした。 宇宙の進化分を加算して n = 4 になるとし、tired light では進化分が加算できないし、加算は正であるべきで tired light は否定されたとした。 これに対して、著者は、n = 1 (静的宇宙), n = 2 (Tired Lightでは、視線方向以外にもう一方向にでるので 2 という。)に近く、 銀河の進化の分が常に正にでるという根拠はないとして静的宇宙と、tired light の可能性を否定すべきでないと主張している。

(以上、引用)

Tolman test が容易でないのは、遠方銀河は、フィルタを通した幾つかの画像でしかなく、それの赤方偏移も粗い推定であり画像も小さいので 面積も正確でないからであろう。絶対等級が等しい銀河があって、等しい大きさを持ち、静止している場合、ユークリッド空間で、赤方偏移が ないとき、距離によって光度は、距離の 2 乗に反比例して低下するが、銀河像の面積も同じ比率で小さくなるから輝度は変らない。輝度の変化は 次によってもたらされる。(0) 空間の曲率による輝度の変化。(1) 銀河間の塵による輝度の低下。(2) 赤方偏移による輝度の低下 1/(1+z) である。 光のエネルギーが周波数に比例することから周波数の低下がそのままエネルギーの低下になる。(3) 赤方偏移が後退の速度によるドップラー効果 であるとき、これは違って来るのであろう。

特殊相対論のドップラー効果は、光源が速度 v をもって遠さかるとき、ν'= ν√(1-v^2) /(1+vcosθ) θは、視線方向の後退速度 v との角度、 θ= 0 では、ν√(1-v^2)/(1+v) = ν√((1-v)/(1+v))、側方向では、ν'= ν√(1-v^2)= ν/γ になる。赤方偏移の直接のエネルギー低下だけ でなく、後退速度の本当にある場合、どうして (1+z)^-4 比例だろうか。赤方偏移自体の減光が、(1+z)^-1。ハッブルの法則があれば、 距離が (1+z) に比例し、光度は、距離の 2 乗に反比例するから (1+z)^-2 。速度は、さらにエネルギーを削減し、その分が (1+z)^-1 これらを掛けて、(1+z)^-4 であろうか、これでは、銀河の輝度でなく光度になるが、(1+z)^n は、光度の話で輝度ではないようだ。 Sandage らの論文はざっとみると、50km/Mpc という自分主張のハッブル定数を使って、4 部に別けた大部の論文を使って膨張説を主張する。 値が観測と最も近い Tired light を"10σ"で排除されたとする論理。それは膨張の証拠へ危機感を示している。Lubin と Sandage の Tolman test の論文は、arXiv で読むことができる。

The Tolman Surface Brightness Test for the Reality of the Expansion. I http://arxiv.org/abs/astro-ph/0102213
II http://arxiv.org/abs/astro-ph/0102214
III http://arxiv.org/abs/astro-ph/0106563
IV http://arxiv.org/abs/astro-ph/0106566

１１. 幻想的宇宙論 ー膨張と特殊相対論の結合ー

そこではローレンツ短縮で、すべての物体が平たく奥行きがなくなり、宇宙の内側には薄い殻ができる(*)。 その距離に近付くのには無限の物体が折り重なり畳み込まれている。（これは特殊相対論的）それでも物体が無限に質量を増しているので、 ある物体がその境界に近付くとき、宇宙に激しい重力の衝撃を与える。（これも特殊相対論的）重力は全てのものに即時に(?)働くので、 いかにその衝撃は大きくとも、地球に乗っている人には全く感ずることはない。（これはニュートン力学）

これは、特殊相対論と膨張宇宙を結合した異常な幻想である。このような殻の宇宙は、有限でありながら無限の物体を詰め込むことができる。 これは空間が負の曲率をもったロバチェフスキー宇宙だろうか。後述するように、アインシュタインの定常宇宙も殼をもつ宇宙である。 宇宙論には証明がいらない。明確な観測からの反証があれば消えるだけである。宇宙論は、実験ができない。そこに求められるのは科学としての 整合性だけである。

(*) 周辺短縮は、随分と忘れられた効果である。私は、この若年の幻想の周辺短縮を、アイザックアシモフの"夜はなぜ黒い？" というオルバースのパラドックスの解説(アシモフの科学エッセイ(3)"時間と宇宙について"山高昭訳、ハヤカワ文庫)によることを再発見した。

"さて、宇宙の膨張を前提とすると、オルベルスの仮定はどんな影響をこうむるだろう? (中略) その "ハッブル半径" は、120億光年だと考える ことができる。だが、これでもオルベルスの矛盾(パラドックス)は一蹴されない。アインシュタインの理論の要求するところによれば、銀河系 が観測者に対して速く運動すればするほど、それらは運動の方向に沿ってますます短くなり、ますますわずかな空間しか占めないようになるから、 ますます多数の銀河系を収容する余地ができることになる。事実、半径 120 億光年という有限な宇宙の中にさえ、依然として無限の数の銀河系が 含まれていて、その(紙のように薄い)銀河系の大多数が "宇宙球" の最外層の数マイルに存在しているかもしれないのである。"

じつは、これらが無限ではないことがすぐにわかる。次ページ以下を参照。

１１.１ 一様等方、ハッブルの法則が成立する宇宙

そこでは最初の爆発がどこから開始したか知ることができるだろうか。この宇宙のどの点もその点から開始したと判断するのではないだろ うか。どこから見ても物質はその点を中心に四散し、距離に比例した速度で逃げていくからであり、全ての点はもとは同じ場所にあったか らである。全ての点は、静止した宇宙の空間的中心点のようにみえる。その意味で、この宇宙は一様等方の宇宙原理をもっている。こうして、 最初の爆発がどこで起きたかは特定できない、又は、全ての場所で起きたと思うのではないだろうか。それに対して、いつ起きたかは実に 明確である。速度は全て距離に比例するから、全ての距離は、速度で割ると一定の時間を生み出す。それがハッブル時間、"宇宙年齢"である。 これは、ハッブル定数(＝速度/距離)の逆数である。しかし、宇宙の全てが見えるなら、中心から外れた点が銀河の分布から端であること (エッジ効果)を知ることができるかも知れない。さらに、光速より速く後退する点からの光は到達しないとして、見えないことにする。

もし、この宇宙に爆発的膨張以外に何もないとすると、現在存在する、天体の固有運動が説明できないことになるが、それは時間に比例する 天体間の相互作用によるとして、この単純なモデルではそれは扱わず、物質は決してぶつからないとすることができる。この物質以外の光は、 天体間を駆け巡る。物質からつねに光は出るとする。遠方の天体の速度は距離に比例して、実際に後退する。それによってドップラー効果が 発生する。ある遠方からの光の波長の比を 1+z として表すと、周波数＝エネルギーは、(1+z)^1 だけ低下する。そして、1+zが√((1+v)/(1-v)) に比例する(vはc単位)。特殊相対論のドップラー効果は、相対速度vで決まる。それ以前、光源の運動では 1+v に比例し(＜2)、観測者の運動 では 1/(1-v) に比例するとしていた、実に折衷的な幾何平均になっている(!)。

この宇宙では、ニュートン力学で物質が直進するだけでなく、光も一定の速度で直進する。そして、特殊相対論によって光速は、物質の速度限界 としてある。現在の我々が受ける全ての影響は光速以下であるとすると、現在の時空点は、過去の光円錐をもつ。そして、宇宙の膨張は、考えら れる0から無限大の速度までのうち、光速以内の膨張円錐内だけが現実に見え、観測可能である。そして光速の膨張円錐が宇宙の半径と宇宙の果 てをつくる。つまりこの宇宙は、膨張による円錐と過去への光円錐というふたつの円錐構造をもち、その内部からできている。円錐は、3次元空 間を2次元に制限して時間を加えたイメージであり、空間3次元的には球状の光の爆発または拡散とその後の現在への収縮である。この場合の我々 の目にはいる光は、実際に遠方を逃げる物体から出てきたものであり、宇宙の最初の爆発点の光ではない。光エーテル論の膨張宇宙では最初の光 がもどって来ることがあるのとは違っている。

この膨張円錐内部を現実の宇宙としてみるなら、ここからみる宇宙は有限であり、宇宙の果てに近い遠方銀河は光速に近い速度をもって後退し、 物体は無限に薄くローレンツ短縮を受けている。周辺短縮はその点から見ても同じく存在するだろう。宇宙の周辺からみると我々のいるこの場所 も周辺短縮を受けて平坦であると考えられる。そして、後述する、ポアンカレ宇宙、アインシュタイン宇宙、ド・ジッター宇宙は、周辺短縮した 有限サイズの宇宙である。ド・ジッター宇宙は、4 次元的な有限宇宙である。さて、フリードマンの膨張宇宙は、周辺短縮があるのだろうか。

An Interpretation of Milne Cosmology
Introducing the Dirac-Milne universe
Do we live in Dirac-Milne unverse?
Milne-Eddington Solutions for Relativistic Plane-Parallel Flows

１１.２ 累積距離は有限

速度が宇宙の果てまで直線的に増加する膨張宇宙とする。(光で見る過去の光円錐ではなく、現在の空間断面であり、距離 r と速度 v とは、 どこまでも比例する。) v= x= r/R (v:光速単位の速度 R:宇宙の半径、r:中心からの距離) の膨張宇宙で物体の厚みがローレンツ短縮 1/γ= √(1-x^2) を受ける。中心から R までの累積距離は、γを積分して、

∫_0^1 γdx= ∫_0^1 dx/√(1-x^2) = [Arc sin(x)]_0^1 = π/2。

積分は発散しない。この膨張宇宙の特殊相対論的ローレンツ短縮による重畳は、奥行きが発散しない。1 パーセクの一里塚と途中の一里塚 の数の比は、約 1.57 倍である。そのため、光のオルバースのパラドックスは発生しない。

なお、過去の光円錐でも発散しない。速度と距離の関係は v= x/(1-x) となるから、1-v^2= 1 - x^2/(1-x)^2= (1-2x)/(1-x)^2、 ∫_0^1/2 γdx= ∫_0^1 dx/√(1-v^2) = ∫_0^1/2 (1-x)/√(1-2x) dx = 1/4 ∫_0^1 (1+u)/√u du= 1/4 ∫_0^1 {u^(1/2)+u^(-1/2)} du = 1/4 [2/3 u^3/2 + 2 u^1/2]_0^1 = 2/3

∫_0^1 dx/√(1-x^2)= ∫dx/y は、直径に対する半円周。この種の積分で∫_0^1 dx/(1-x) (=∫_0^1 dx/x)は、残量に比例した消費だから発散。 ∫_0^1 dx/(1-x^2) は、さらに発散する。 ポアンカレ宇宙、参照。 またブラックホール ds^2= (1-A/r) dt^2 - dr^2/(1-A/r) - r^2dΦ^2 の地平面 A の外側 R (R＞A) から A までの累積距離 ∫_A^R dr/√(1-A/r) は、 ∫_A^R dr/√(1-A/r) = A ∫_0^(1-A/R) dx/(√x (1-x)^2) = A [1/2(1-x) + 1/2 ln(x/(1-x))]_0^(1-A/R) から、 定積分範囲がAを含むなら、そこで不定積分が-∞であるから必ず発散する。

この積分が収束するためには、膨張の存在による有限宇宙が必要条件であるが、十分条件ではない。ローレンツ短縮の逆数のγの式だけに依る のである。有限宇宙でも積分が収束する保証はなく、この式が異なるだけで無限にも有限にもなり得ることは、例えば、ポアンカレの有限宇宙 が無限の内容を持ち得る。直線的膨張でなく減速膨張では、有限に留まるかどうか確かでない。この積分は、すでに有限であるが、ドップラー 効果による光のエネルギー低下はまだ考慮されていない。

１１.３ 光速物体の存在

つまり、宇宙のしくみを特殊相対論のエネルギー原理より上に置く必要を感じるのである。宇宙しくみは、特殊相対論の無限大のエネルギーの 局所発生の困難に優先すると仮定しなければならない。そこに微小な物体が存在し得るとするだけでその仮定が必要になる。微小な物体も、 そこに置くだけで質量が無限大になる。このようなエネルギー無限大に平気でいることは、宇宙論以外では決してしないことと思う。特殊相対論 の質量とエネルギーが等価でかつ無限大であるから、それを実現することは有限宇宙の質量エネルギーの全てを使ってもできない。それが膨張 だけによって起きるのである。これは、膨張の最初に無限大のエネルギーを使うから、これ自体を不可能ということもできない。

ある距離まで光速の1/2、その2倍の距離では光速、この単純なことがこのような内容を孕むから、膨張宇宙は何でもありの困りもの、という 想いになる。宇宙にそれを許すのは宇宙が無限の大きさも質量も許すからである。これがニュートン力学と特殊相対論の組合せに特有のもので、 フリードマン宇宙には同様の困難がないと理解する方法はないと思われる。ただ、場の理論では特異点の存在の問題になるだけであり、困難は 薄まって感じられるだけである。

ここで注意すべきであるのは、この宇宙には、光のオルバースのパラドックスはないが、光速物体の質量は無限大になるから重力のオルバース のパラドックスが光とは別の原因で発生すると考えられることである。

１１.４ 無限の重力の変動

いくつか、困難を前にして、この宇宙の存在し得ない理由を考えてみよう。現実に振動はないから、これは否定しないといけないと考えることは できるだろうか。ニュートンの引力のように重力は一瞬では来ないとしても、最初の爆発だけを置くのでなく、もし、全ての空間に連続した膨張 (定常膨張) があるとしなくても、光と同様にこれはすでにここに来ていなければならない。光も初期宇宙の様子を伝える膨張の光円錐からの光 は常にくる。これは、現実に物体が飛び去って、それから光が発したのである。しかし、その宇宙の果ては、特殊相対論で時間経過が少ないため に、宇宙年齢の 1/2の時刻であるのに、その物質は初期宇宙の時刻をもっている。光の到達時間からの宇宙年齢は、我々の場所の物質の経過した 宇宙年齢の1/2であり、宇宙の実測の空間半径は、宇宙年齢の 1/2 の光速倍であるという特徴がある。また、光のエーテル論と比べて背景輻射の 強さは弱いのではないかと予想される。光エーテル論では、光が弯曲して還ってくるという特徴があり、初期の宇宙の爆発がそのまま全ての場所 に戻るとき、光速より大の初速の物質の内側向けの光から発した光が戻ることから、凸レンズ効果が高いように思われるのである。

宇宙の果ての重力の変動は、地球に乗った我々には知ることができないだろう。なぜなら重力自体は、地球も我々も同様に等しく受ける加速だから である。重力の空間微分をした潮汐作用だけが、自由運動をする物体が検知できる重力効果である。時間的に変動しない近傍天体からの潮汐効果は、 距離の 3 乗に反比例する。そのため、宇宙の果てのような遠方天体からの潮汐は、ポテンシャル、重力、潮汐と 2 段階に減衰したものだろう。 どの程度の減衰かといえば、最も近い恒星との距離の比で１段階に 40億倍である。太陽の距離との比ではその20万倍、１段階に800兆倍程度である。 それらは近傍の潮汐とは全く違うと考えなければならない。重力の時間的な変動は受ける場所の違いで検知できることもあるだろう。もしそれが 平面波なら、時間差による変動の振動があり得るかもしれない。しかし、その大きさ自身小さいので時間的変動の検知は難しいことがわかる。

１１.５ 物体は速度を変えない

あるとき、0 から無限大までの速度をもって、ある場所から宇宙が爆発的に膨張をしたとする。それ以降は、全ての物質は速度を変えずに、 等速直線運動、慣性的な運動をしている。そういう仮定のもとの直線的膨張は、重力による減速も無視している。光速の速度をもった物質は、 ずっとそれを保ち続ける。だからその場合、物体が宇宙の半径を出てゆくということもない。この場合、宇宙の半径は、光速をもった物体の 位置であり、宇宙の半径も、光速で拡がり続けるということになる。物質とそれとは、同じ光の速度で遠ざかっている。光速の壁を超えて向 こう側に行くということも、あり得ないのである。

光速の壁を物質が超えて外へ出て行くというのは、光速が一定でなく時間的に減少している宇宙か、物質が加速をうけている宇宙である。 逆に減速膨張の宇宙では、光速の壁の外側から物質は内側に姿を表すことになる。ニュートン力学の直線膨張宇宙では、特殊相対論の光速の壁、 宇宙の果ては、同じ物質が常に占めているので、変動はない。よろしい。これでひとつ明確にこの幻想を打ち破ることができた。そこを物体が 横切らない限り、無限の重力の変動の問題は発生しない。その場合でもそれは、その場所の任意の運動による加減速によってすぐに発生しえる。

１１.６ 静止無限/有限宇宙の問題

しかし、ニュートン力学の宇宙の広さが無限であれば、重力も無限だから、我々は互いに無限の力を与えあってしまう。それがまた別の面 で不合理になる。ニュートン力学の無限宇宙は、無限量の重力の相互作用を導き、ここの一点には、無限の重力があらゆる方向から重ね合 わされる。力は方向と大きさをもったベクトルだから全方位重ねると消え、ランダムな擾乱だけが残る。もちろんそれも、無限に累積する という問題をもつが、ポテンシャルはスカラーであり、そのまま加算されてマイナスの無限大になる。しかも、ポテンシャルは距離の 1乗 に反比例する。一様な密度ρの宇宙では、ポテンシャルは、距離に2乗に反比例である重力や光の量と比べて、容易に無限大に発散する。 これは、無限の広さの宇宙が任意の点の物理量を無限大にして、局所の物理法則を不可能にする。

無限の物質をもつ宇宙は、一瞬で(重力の光速伝達なら違うが)で成立を危うくする。質量は、重力という物理量になって手近の物体に作用 するから、宇宙の質量が無限であれば、それが有限の距離ならもちろん、無限の彼方にあっても一様に分布すれば、物体に作用する重力は、 オルバース無限大になる。そこでと、ニュートン宇宙は無限でないと仮定すると、その問題は出ないが、有限の物質は有限時間内に一点に 収縮するという問題をもつ。

有限の星の集団は、重力のために安定できない。最初にほぼ静止していても、それはどこかに中心を作って収縮し始め崩壊する運命をもつ。 全体もそうだが、局所もその外側によらず成立する。ニュートン力学での重力発生は、ある球形のなかに球状に分布する全質量は、中心の 重心に質量が集中して存在するのと同じ働きをする。ひとつの星にとって、他の全ての星との万有引力の相互作用は、自分以外の宇宙全体 の重心との重力相互作用による運動をする。星々の運動エネルギーは、実際の衝突しさえしなければ、位置エネルギーの分を引き受け、星 の拡がり全体が収縮によって運動エネルギーを増す。そのとき、全体の形態を崩すほどの変形は起きないだろうが、その歴史のなかで、全 体の星の集団のなかの小さい質量の星ほど、先に弾き飛ばされ集団から蒸発する。衝突や、ニアミスなどの運動量の交換において、小質量 の物体ほど運動エネルギーを多く与えられ脱出できるからである。

そのような運動において、全てがランダムな運動を保って存在することはできない。しかし、それは永遠を保証しないということであり、 この一瞬の世界が成立しないということではない。星の集団は、大きければ大きいほど収縮に時間がかかり、その寿命も長いだろうという ことになる。無限の大きさのとき、どうなるかを考えなければである。

１１.７ ニュートン力学と宇宙

特殊相対論は宇宙では成立しない。きみの国の法律はここでは通用しない、ここにはここの法律がある。そういうことがないように、法則が宇宙 一般に成立するように宇宙原理を使う。宇宙の果てもここと平均的には何も区別できない。宇宙に特別な場所はない、そういう一様性の宇宙原理 がある。そして、ある空間的な方向だけが特別ということもない等方性である。一様等方の宇宙原理である。宇宙の果てにここと同じ法則を要求 する。法則は、時間と空間に依存しない。時空依存の法則は、法則の名に値いしないとする。一様等方時間不変が法則を法則とするために誰もが 認める原理であろう。それゆえ、宇宙の果てには特殊相対論は通用しないという言い方は許されない。そこでも、ここと同じ特殊相対論が成立す るだろう。局所的には。

１１.８ 特殊相対論と宇宙

だから、宇宙のような重力の大きく影響するサイズでは、特殊相対論は、無意味になったと否定されるべきだろうか。それより大きな領域の法 則に従うと考える。平坦な時空では特殊の成立する大きな領域が存在してもよいとするし、いままでの特殊で考えた成果は、ほとんどそのまま 移行できると考えるのである。

特殊相対論は、局所にしか適用しない。だから宇宙論には関係ない? そうだろうか。それだからと我々は速度場のエーテルを認知してしまうの だろうか。または、膨張宇宙論では、計量が変動する式を目の前にしていながら、計量が変動しないような座標系を物理的現実とみてしまうの か。また、特殊相対論の規則を無視して光速に近い速度をもつ物体、光速物体、又は光速以上の物体の存在が出てくると考えることは正しいの だろうか(*)(**)。

彼等はこう言うだろう、宇宙の果て、そんなものは問題ではないと。 それは、彼等がそれより深刻な問題に満たされているだけのことかもしれない。 宇宙の果てがどう見えるかなど関係ない、座標依存なものを気にすることはない、という反論さえあった。 計量が系によって違うから重要でないという、そうだろうか。宇宙の果ては、どこからもみても存在し場所に依らないだろう。 それがどうあるかは、むしろ自明である。ここと同じ物理法則が成り立つ、というのは一様等方の宇宙原理である。 どう見えるか、どうここに影響するか、という問題しか宇宙論には存在しないと、私には全く逆の感想を与えるのである。

(*)遠方銀河の Ia 型の超新星の光度変化曲線の時間遅れが (1+z) に比例するという観測は、赤方偏移が宇宙膨張によるという説に有利とする 結果であるが、これには特殊相対論を使っている。

(**) 宇宙にニュートン力学を使うだけで批判されるが、それしかないとき、アインシュタインが一般相対論を提案し定常宇宙論を出す前に人々 が何をどう考えたかは、重要であると思う。現在は、ニュートン力学だけでなく、特殊相対論も、宇宙論から排斥されているかにみえる。問題は 人々の思い込みの強さである。よく考えると特殊相対論は、もともと膨張宇宙論とあまり相性がよくない。全てのものに始めが存在すると、慣性 系の対等の基本的な条件である互いに速度をもった系同士に相対的な時間経過の差は存在しえず、絶対的な時間経過の差しか存在し得ないように みえるからである。そして、さらに背景輻射は、絶対静止座標系が存在することを示しているかのようである。膨張宇宙では、たとえ物理法則が 等しく同じであっても、絶対静止系が他の系と少なくとも区別できる系である。それらは、宇宙が特殊相対論を否定すると理解し古典的エーテル 論に人々を引き戻す原因になる。少なくとも我々は、エーテル理論に戻る必要はない。特殊相対論のほうがどれだけ良いかを考えるべきである。

１２. 特殊相対論の宇宙

１２.１ 時間と空間の混合

ニュートン力学では、時間と空間はそれぞれ別個のものであり、空間は全てのものを入れ、時間は全ての事象を均一に記述する パラメタであった。場所によっても系によっても事象の時刻と時間経過に違いはなかった。時間と空間とは系によって違うもの ではなかった。物理現象から隔絶していて影響を受けない絶対的なものであった。しかし全ての慣性系は、ガリレイ変換におい て対等であった。

宇宙には、一様(特定の場所はない)、等方(特定の方向はない)、定常(宇宙は永遠に続き、現在は特別ではない)であることが 求められた。時間的、空間的な無限には、夜空の暗さについてのオルバースのパラドックスが昔から疑問を提示していた。 無限に広がる空間に質量が一様に分布して存在する宇宙は、力学的に安定ではなく、それを永遠に同じ状態に保ち、定常性を 満たすことは難しい。ニュートン重力より基本的であるはずの (距離に反比例する) 重力ポテンシャルは、光のオルバースの パラドックス以上のパラドックスをもつ。ニュートン力学の一様な物質密度は、容易にポテンシャルの無限大をもたらす。 そのような困難があったにしても、一様、等方、そして定常の宇宙は強く要求される前提なり、原理であっただろうと思われる。

特殊相対論によって時間と空間とは、別々のものではなく一体のものになった。ある系がみる空間は、別の系では時間と空間が 混合したものである。光速に近いロケットに乗れば、乗員の時間の経過は小さくても遠方に行くことができ、極端に言えば、 宇宙の果てまでも人の一生もかからずに行けるのである。速度を持った系の同時刻(空間)は、別の系からみるとその系の前方が 未来に傾斜している。そのため、加速時に前方の到着の直前の時刻と同時刻になるから、機内の時計より外部時計が経過しない のである。150 億年後の宇宙の果ては、高速なロケットの座標系では現在であり、同時刻の空間である。

１２.２ 系が対等でないときの相対性

高速な系の時間は経過しないので、150 億年を人の一生にも満たないで通過するロケットの系では、時間は、宇宙が始まってから 数十年しか経っていないし、150 億年後かもしれない宇宙の終末がそのロケットには数十年後に訪れることになる。ロケットは、 地上よりも時間が経過しない。そして、その逆がない。宇宙の始まりを受け入れると、ニュートン力学でも、特殊相対論でも対等 であった慣性系は、このように事実上対等でないものになる。

宇宙の始まりの存在は、それに対する速度の計測できる絶対静止座標系の存在を保証してしまった。絶対静止系は、宇宙の場所に 依存して各点に存在する。それが実際に確認されている。 COBE衛星、WMAP人工惑星の背景輻射に対する太陽系の速度は実際に存在し、 背景輻射の変動量は、地球の速度の成分が最も大きく、その成分を除去して初めて10^-5 の範囲にはいる。エーテルの風はこうして 再発見されたのか。そうかも知れない。しかし、エーテルを再確認するよりも重大かも知れないことは、絶対静止系が実質的に再認識 されたことと言えるのではないだろうか。

時間経過について、全ての物体、物質が宇宙の始まりを同時に経験したなら、速度の違う物体の年齢に多義性は許されない。 ある系では時間が経過し、他の系では時間が経過していない。ただそれだけである。特殊相対論にいう逆がない。端的に言えば、 特殊相対論の慣性系の対等は、宇宙膨張説によってすでに思想的に根底的に崩されてしまったのである。絶対的な静止座標系とそれに 対する速度、そして絶対的な時間が宇宙を支配している。相対性の観念は、人間の平等に対応するように系の対等性によって当然のご とく保証されると思っていたのに、ローレンツ短縮を受け、時間経過の緩慢さを受けるのは、動く一方だけということだったのか、 ということである。これこそ、特殊相対論から遡ってエーテルの風によってローレンツ・フィッツジェラルド短縮を受けるということ の意味である。時代はこうも変わった。

１２.３ 始まりのある宇宙の相対性

宇宙の空間的曲率が負である、密度 0 から空間曲率が 0 になる臨界密度までの低い密度では、最初から無限の宇宙が膨張してもおかしくない。 密度が臨界密度より高ければ、ある時に膨張が収縮に転じる。その場合、有限の空間的サイズには有限の時間が対応する。それは、質量による 空間曲率がないと宇宙は閉じられないからである。それ以前の特殊相対論の宇宙は、質量から重力への、すなわち時空への影響を考慮しない 理論であったから、宇宙は当然ながら平坦であり、開放系と考えたと想像できる。フリードマン宇宙で時間に依存する宇宙のサイズ G は 臨界密度を超えるときサイクロイド曲線を描いて膨張し収縮する。ちょうど臨界質量の平坦宇宙では 時間 t の 2/3 乗の関数となる。 それは、直線的膨張ではなく多少の減速膨張の曲線である。この減速膨張が宇宙論で永く蓋然性をもつとして採用されてきたものである。

しかし、この宇宙の地平線は空間弯曲のために発生した地平線ではなく、膨張がもたらす限界であり、宇宙の始まりが見えるための 限界である。ゴム風船のサイズが現在の 1/1000 程度のとき、プラズマから原子を形成する "宇宙の晴れ上がり時期" の最初の光が、 ゴム風船が膨らんで、もう一度各点に帰還していると考えている。宇宙膨張を認めるホーキングの数学的説明の全くない本にも、この 洋梨型の光の帰還が美しいカラーで描かれ、これが宇宙膨張説の基本的思考方法であることを示していた。この共変エーテル、一般 エーテルという美しい名前は、一般相対論の計量が速度をもち、それが光の媒体となるという考えであり、光エーテル理論の一種である。 遠方の光速を 1 - (距離に比例する媒体速度)とする方法では、計量 g_ik を使う意味がない。しかし、それ以外に問題として、 光が戻る方法がそれ以外にはないことである。計量と光速の正しい扱いでは光の経路はこちら側に曲らず、帰還しないと考えられる からである。

１２.４ 閉じた宇宙での双子のパラドックス

特殊相対論の時空の一体化によって、時間だけ有限で空間的は無限とか、空間的に有限で時間的に無限というのは、存在しなくなった。 特殊相対論の時空、特殊相対論の成立する宇宙は、ユークリッド幾何学のように、時間的にも空間的にも開いた宇宙を前堤としている。 ミンコフスキー時空は、局所の平坦さを指定するだけでなく、その位相幾何学的な構造を指定をしているのである。

アインシュタインの定常宇宙のように、時間方向には定常であるが、空間的には閉じたシリンドリカル(円筒)宇宙では、慣性系が引返す ことなく再会するので、双子のパラドックスが再燃し困難を生み出す。そのため、そのような時空構造には、絶対静止系が存在するという ことになり(光を前後方に出して同時に受けるのが静止系である。)、特殊相対論の前堤のひとつを覆えす。物理法則は、どの慣性系も対等 を根拠に特殊相対論が成立したのに、大局的には成立せず絶対静止系が存在するというのは、整合した考えとは思えない。絶対静止系の 存在だけで局所の特殊相対論が否定されるわけではないが、特殊相対論の前堤であった座標系の間の対等性なしに特殊相対論を成立させる ことはできない。それは、ローレンツ変換をどのように導いたかを思い返せばよい。慣性系の対等を利用したはずである。

そのように前堤を否定する結論を得た場合に採るべき方法は、結論の否定である。それを支えてきた前提を取り去ればよいということではない。 慣性系の対等という前堤を変化させることは、この上もなく重大な結果を招く。"そのような宇宙では、絶対静止系以外は時間の経過が遅く、 ローレンツ短縮しているが、絶対静止系だけが時間経過が正しく、物差しも正しい" という結論を受け入れることができるだろうか。なぜなら、 それでは、局所的にも特殊相対論を成立できず、特殊相対論を抛擲するからである。閉じた空間とそれを導いた一般相対論は、特殊相対論を 転覆させるのだろうか、という疑問である。

双子のパラドックスの兄と弟が、ロケットで出発した兄の引返しなしに再会するとき、弟は兄より老けているだろうか。老けているなら、 兄は移動系で弟は静止系である。移動系は時間経過が遅い。しかしこれは、もはや慣性系が対等でないことになり、相対論の前提を壊し、 そして、老けていないなら、時間は運動によらないことになり、これも相対論以前の時間の絶対性を復活させる。対称性のあるときは後者 と推定できる。そして、静止系が区別できる条件では、前者の結果になると推定できる。そして、いずれもが破壊的な結論を導くのである。

１２.５ 閉じた宇宙では特殊相対論は成立しない

2つの人工衛星の系は、慣性系ではなく、重力のある中の局所慣性系である。ふたつが対等であるという対称性から両者に時間経過の差がなく、 特殊相対論の双子のパラドックスの時間差がないことが明らかである。相対速度があっても特殊相対論は成立しない場合があると理解すべき だろうか。しかしその説明は明確でない。対称性を使って否定してもそれ以上の説明に進めないからである。

それは、重力と潮汐力のある時空であるから特殊相対論は成立しない、と説明すべきことだろうか。そうでもないようである。それは、 どこまでも平坦に近い場合でも同じ結論になるからである。その極限である円筒宇宙の場合、特殊相対論が成立する宇宙だろうかと考える。 そしてそこにそれが成立しないと認めるなら、その成立しない原因は、宇宙の閉構造と考えることができる。

局所慣性系どうしが離れたとき、それはもう局所のできごとではないから成立しないのだろうか。重力のある時空は、もはや一般相対論でしか 扱えないものであり、特殊の範囲ではないからなのか。一般の局所に成り立つ法則は離れたところに成立しない可能性はある。しかし、 それは円筒宇宙では違う。円筒宇宙ならどこでも平坦なミンコフスキー時空であり特殊相対論が成り立たなければならない。

"特殊相対論の時空は、重力がないことが前提であったと同様に、開いた時空構造が前堤にあった。閉じた時空では、特殊相対論は成立しない。" というのは、ひとつの解答であろう。空間の曲率を論ずることのできない理論には空間的に閉じた宇宙は、存在しない。しかし、適用できない と逃げて矛盾を避けることは、十分に正しいのだろうか。逆にそれなら、そのような閉じた平坦な時空に適用されるのは、どういう理論かと疑う。 それは、古典的エーテル理論に戻ることを必要とされているのだろうか。依って立つのは一般相対論であるなら、一般相対論は、局所慣性系間 には特殊相対論が成立するとするならこの考えも十分疑わしい。しかしさらにいえば、一般相対論が、局所慣性系間には特殊相対論が成立する ということにも、疑いを持つべきかもしれない。それは一般相対論が保証しないのに勝手に期待したことかもしれない。

１２.６ ステンレスのナイフ

一様(homogenity)とは、どこも特別な場所がないことであり、宇宙に中心を持たせないことである。どこから見ても宇宙は同等にみえるだろう。 等方(isotropy)は、特定の空間的方向を特別にしないことである。そのためには宇宙全体が回転しないことを必要とする。そして、どの時点も 特別でない、他と区別できない時間的な一様性を望むならば、定常(steady state)または静的(static)な宇宙を仮定するだろう。宇宙膨張説は、 この定常性を捨て、ある時点から宇宙が始まったとする考え方であり、それ以前が存在しない境界をもつ。その考え方では現在の宇宙には宇宙 年齢以上の例えば 1000 億年という時間経過を経た物体の存在はただひとつも許されない。宇宙年齢以上の年齢をもつ小物体は、それだけで 宇宙開闢の反証となるからである。例えば人類以前にムー大陸に過去の人種がいたとするような考え方を否定するのにその時代の遺物としての ステンレスのナイフひとつも存在しないではないかという。確かに我々は、数億年前のステンレス製のナイフを持たないだろう。それは、 宇宙論においてもそうだろうか。その証拠を持たないことが確実であるかは、十分考えるべきことである。通常我々は、ステンレス素材である ことだけでそれが古いことを疑ってしまう。それは例えば、球状星団ではないだろうか。それは、銀河自体かもしれない。

球状星団は、青い生まれたての散開星団よりはずっと規模の大きい、数100万の恒星が中心近くの恒星密度は大きく周辺は疎らであるような、 そのこと自体非常に不思議なのだが、球状分布をした天体である。そのなか大半の恒星は互いにランダムな運動を残しているから、偏平な形態 にはならなかったと考えられる。星団全体としての無回転を示す縦横比、偏平率が 1 である。球状星団のなかの恒星は大抵、古い赤色巨星である。 (マゼラン星雲のなかには、青色、白色の巨星からなる球状星団が見付かっている。何かによって説明可能だろうか。)その球状星団でのH.R 図は、 主系列の左上部にあるはずの青色、白色の恒星はすでに寿命を終え右に移動して、上部が右に曲り広がった H.R 図をなしている。恒星進化の理論 のもたらす球状星団の年齢は、150億年から200億年までとされる。それらは宇宙の年齢よりも長期の時間を経過した天体という矛盾の証拠を突き 付けるナイフであるが、その時間の矛盾は 2 倍ほども大きくはない。

銀河については、我々は銀河の様々な形態を 100 年前から知っているにもかかわらず、その進化の理論を全くと言ってよいほど持っていない。 多様な銀河の形態、見掛けの偏平率が進化で形成されたものではなく、楕円銀河は、楕円として生まれ、渦巻銀河は、渦巻のまま生まれたと 言われる。それらの偏平率の大きな違い、みかけの縦横比である偏平率が楕円銀河で 0〜7 に分類される。渦巻銀河ではその偏平率は、10 以上 にもなる。そして、偏平率を違える時間的進化自体存在しえないとまでされている。しかし、我々は、一般に質量が重力によって収縮集合する とき、角運動量保存によって、質量の分布が球状分布からしだいに偏平な分布に変わることを知っている。例えば、太陽系の惑星の軌道が ほとんど全て同じ平面内に存在することを誰も疑問には思わないのは、そのような知識があるからである。物体どうしがランダムな運動から 衝突によって互いの相対速度を失って、それぞれの速度を平均化していくには、非弾性衝突とか、摩擦のような過程が必要である。 その相対速度を無くす相互作用の過程を通して、球状の分布は、残された角運動量の保存のために偏平な渦巻型の分布になるのである。 銀河の偏平率を大きく変える物理過程は存在しない、といういい方は、理屈に合わないことのように思えるだろう。

１２.７ 銀河型間の移動は、なぜあり得ないのか

太陽の半径は 70万km、その200倍の太陽地球間の距離が 1.5 億 km、その20万倍の 30兆km が 1pc である。最も近傍の恒星までの距離、1.3 pcは、 39 兆km、太陽の半径の 4000万倍もある。その 2 乗の断面積の比率 1.6 x 10^15 は、銀河系の恒星数、2 x 10^11(2000億) より 4 桁も大きい。 銀河どうし 1 万回衝突しても、ほとんど素通りし、恒星は、1 回衝突するかどうかという程度である。銀河を構成する恒星は、このように互い に極端に離れているために衝突しない。それらが本当に衝突するとか、恒星半径の数倍のところをニヤミスするかでない限り、それらの間の 重力による相互作用は、恒星が共通の重心の周りを双曲線軌道を描くだけの弾性的衝突であり、互いの相対速度の減少はない(*)。

これは、恒星の固有運動による衝突においてもいえる。仮りに恒星間距離を 4 光年、恒星の固有運動の平均速度を 100 km/sec とすると、 恒星が恒星間距離を行くのに要する時間は、4 年 x 30万 km/100km = 12000 年である。そのとき、非弾性衝突をする確率、1/(1.6x10^15) を考えると、衝突の平均時間間隔は、12000 x 1.6 x 10^15 年 = 2 x 10^19 年であり、現在言われる宇宙年齢、1.37 x 10^10 年の 10 億倍 である。恒星が非弾性的な衝突を繰り返して、銀河が球形から円盤型に分布を変更するために、各恒星が 1〜 1000 回の非弾性衝突をするの には 10^19〜 10^22 年、宇宙年齢の10億倍〜1兆倍必要である。これが多くの人が銀河の形はできたまま、と結論する理由である。形を球から 円盤に変えるのにはガスであればこのような長時間は必要としないと思う。 そこでどうだろう。宇宙膨張説の時間が短かすぎるだけで、銀河 の存在自体がそのような短期の宇宙生成を否定していると考えてみてはどうだろうか。

ついでにこれは、ジーンズの太陽系生成における恒星接近説、私は子供のときこれを読んだのだが、これがあり得ないとされる理由でもある。 恒星のすぐそばを他の恒星がかすめて通過したことで、物質が両方の恒星から取り出される。それによって惑星が形成されたという説である。 この説の利点は、惑星の角運動量を大きくできることである。ラプラスの惑星形成説では、中心恒星が質量の大半を、惑星が運動量の大半を 担うことができないとされる。

英国の天文学者のジーンズによる銀河間の進化の理論(楕円銀河から渦巻き銀河への変化)は、楕円銀河と渦巻銀河の中心窩がガスであるという 仮定が誤りであり、恒星の集合であることがわかって覆され、顧みられることがない。しかし、宇宙膨張の発見者であり、銀河の分類を行った ハッブルでさえ、まだ銀河の系列を進化に関係したものであると考えていた。銀河の様々な形態をそのほとんどまま生まれたままの違いである ということ(不規則銀河 I から逆向きにSc, Sb, Sa という変化は推測されている。) には、すこし疑問をもつべきではないだろうか。

楕円銀河は、一般に赤色の恒星で構成されていて巨大である。どうしてそうなのだろう。不規則銀河には、青い恒星でできた不規則銀河と そうでない不規則銀河がある。宇宙が一回きりの膨張でできたなら、青い恒星をもつ不規則銀河から、通常の渦巻銀河の渦状枝まで変化した とする方向の方が正しそうに思えるかもしれないが、そういう青から赤への変化だけでは、多様な銀河の形態を説明することはできないであろう。 渦巻型(S)に対して SB型はどうしてバーをもつのか。バーをもつことの解析は、バー安定性の話としてある(我々の天の河銀河がバーをもたない 渦巻であることはダークマターが必要な理由のひとつであった。)が、巨大な楕円銀河は、全く別なのだろうか。どうして銀河変化の第 1 印象 である逆向きの変化(楕円から渦巻の方向)を基本にできないのか、重力収縮は、一般に楕円から円盤ではないか。そのような疑問が解決されない。 (重力収縮には時間が足りないのである。)

色々と想像はできる。渦巻銀河は、常識的には一旦渦巻になると楕円や球形には戻れないだろう。つまり、方向は楕円から渦巻であろう。 楕円銀河はガスを失っているし内部恒星は老齢のようだが、形は若いという年齢不詳さである。近くの球状星団のように詳しく調査できないが、 球状星団と同じ理由で老齢かも知れない。その場合、楕円という単純な形態を重力崩壊なしに保つ理由が必要だろう。これを球状星団以上に不 思議に思うのはその規模の大きさで、一般の渦巻型よりも遥かに大きいからである。楕円銀河が渦巻よりも規模が大きいことは、収縮によって 楕円から渦巻になるなら正常である。逆向きに質量を増やすのは難しい。

(*)もちろんこれは、銀河どうしの衝突によって銀河全体の形態が互いに大きく乱されるという、多くの数値シミュレーションを否定しない。 銀河は、衝突によって形を変えることができる。しかし、恒星間の接近遭遇なしには、ここで必要とする意味の変形である偏平率の増加はない のではないか。球状分布した楕円銀河どうしの接近遭遇によって、現在の安定した平坦な渦巻に変化することは少し都合が良過ぎないか。 もちろん、昔から相互作用する銀河は多く知られている。それらは相互作用自体が奇異だったのであり、渦巻と楕円銀河の変換に利用しようと は誰も考えなかったのである。良く見る整った渦巻は、それらの衝突が収まったあと、どれだけ時間経過すればできるのだろうか。

１２.８ 絶対時間：始まりからの時間、絶対静止系：共動座標系

そしていま、流行遅れの「局所慣性系」の代わりにさらに昔の、これを否定するために特殊相対論が苦労をした、「絶対静止空間」が もつ共通の始まりからの時刻を伴ってそれによって我々は縛られている。その時刻が本当にあったのかを疑うものはいない。「宇宙の 始まる前」をいわず、「本当に始まりはあったのか」ではなく、「なぜ宇宙が始まったか」という無意味な言葉が放送される。この「 なぜ」の答えは、より深い原因を指すだろうか。又は、科学の芽のない、答えのない神学かもしれない。生命が偶然の確率では決して できない、地球環境は銀河系を探してもない、宇宙に人類はユニークかもしれない、なぜこれほど宇宙は平坦なのか、なぜ地平線の向 うにも同じ風景が拡がっているのか、なぜこれほど人類は孤独なのか、これらの問いは人間中心主義に陥る、思想の病的状態である。 現象は必ずそれを説明する理論を求めるが、もちろん問い自体は解でない。問いは答えと離れすぎて、解が多数存在するか、解がない か判然としない。もしかしてこれは、正反対の答えが対等に主張できる問題かもしれない。また、一部はユダヤ的選民思想、残りは創 造への讃美のようだ。宇宙論は宗教との戦いに敗れ、その奴隷となったのか。

軽薄なのは、科学の計算依存である。計算で何が安心なのだろう。確かなことを求めるのに計算が役に立つだろうか。さらに可視化と いうプレゼン技術に頼る。λ-CDMシミュレーションで 1億の銀河の動きを「ニュートン力学で」重力計算をしてできる大規模構造形成 の画像を人に見せる学者に問いたい。なぜ共動系がニュートン力学なのか。計量変化は考えないのか。共動系の力学は系に対しての距 離と速度は、時間とともに小さくなり、物体は速度に比例する抵抗をもった媒体のなかにあるような動きをする。これはニュートン力 学ではない。

１２.９ それから、考えられること

一般相対論からみれば特殊相対論は、ガリレイ領域という、平坦な時空の局所慣性系間でしか成り立たない法則とする。 特殊相対論では物体が速度を得て光速度になるには、無限のエネルギーが必要なのに、一般相対論からの宇宙論では、 空間自ら膨張する場合、光速制限も平気で無視し、特にエネルギーを必要としないとするが、確かだろうか。

そのとき宇宙の辺縁の光速物体は、重力効果をもたないのか。 それは、時空の速度であり、自分で稼いだものでないから身に付かないのか。 重力効果が後方には伝われないだけだろうか。

それより先に、物体が速度を得て、光速の近くに達する場合、その重力効果はどうなるのだろう。 見る慣性系によってブラックホールであったり、なかったりしては困るので、ないという予想はあるが、 速度がエネルギー密度に関与することは、確かである。誰か明確に答えを与えているだろうか。

時空の膨張宇宙の中で、ある大きな初速で船を進めると、船と周囲の物体との相対速度は、段々落ちていくのか、 それとも、その場所に行くことで船が速度を得て相対速度は保たれるのか。光との類推からエネルギーを失って、 周りとの相対速度を失うという方がありそうである。しかしそれでは、時空の膨張をいう必要があるのだろうか。

考えなくてはならないことは多い。明確であることは少ない。

１３. 回転系

１３.０ ニュートン力学での回転系

ニュートン力学では回転系は、遠心力とコリオリの力で説明される。その系の中で回転は知ることができる。静止物体は、軸からの距離 による遠心力をうけ、速度をもった運動物体は、その点の速度と系の回転との外積のコリオリの力を受ける。遠心力は、半径と角速度の 2 乗に比例する加速度 rw^2 であり、コリオリの力は、速度と角速度の外積 v x w に比例する加速度、両者の式が違うからその特性は、 一見違うようにみえる。しかしよくみると、両者は、同じ力を分解しているだけである。 遠心力とコリオリの力 また、太陽地球系のような地球軌道に同期する回転系での平衡点に ラグランジュ点と言われるものがある。

特殊相対論では、回転系では円周方向の速度が光速になる距離の宇宙の半径ができ、それに近づけば宇宙の周囲は、無限に延びる必要がある。 回転系は、アインシュタインが一般相対論へ進むのに重要なステップをなす思考実験であった。回転系では、周辺空間の幾何学が違ってくる。 回転系の各点は、半径方向には速度をもたず、円周方向に速度をもつ。そのため円周方向にローレンツ短縮があり、回転系の上の円周方向に おいた物差しは慣性系からみて短縮し、半径方向には短縮しない。外(慣性系)から見た円形の形が保存するので、円周は半径の円周率倍でなく、 それより長い。回転系の半径と周囲の比率は、よく間違われる。これは、コズミックストリングの線状の質量の重力による円周の削減とは逆である。

アインシュタインの"The Meaning of Relativity"(英語版) では "The General Theory of Relativity" の章の始めの方に円周と直径の関係を U/D＞π と明記しているのに、その矢野健太郎の訳、"相対論の意味" (岩波書店)では、U/D≠π と改ざんされている。アインシュタインの 最高に良い本なのに残念である。また、後藤憲一の"相対論"(共立全書)では、その29章"一様に回転する座標系"では、 "円周と半径の比は、 2π/√(1-r^2w^2/c^2)＜2πとなり、2πより小さくなる。"と誤っている。立派な内容の本なのにこの部分は台無しである。また、今枝国之助、 今枝真理の"ブラックホール物理学" ブルーバックス(講談社)も同じ誤りをしている。一般向けの本でも、M・ボルンの本や、 ランダウ・ジューコフの本では、もちろん間違っていない。

物理とは、時代による変化のない対象をあつかう分野である。それゆえに後生に誤りが分かりやすく、指摘を受けやすい分野である。 気を付けなければならない。流行や風俗や技術の分野では少々の誤りも何十年も経って後の世から指摘されることは決してないだろう。 物理は、時代が変わっても同じことを繰り返し考え尽くす。自らの思考形成に大いに役立ち、有り難かった本に対してさえ、余計な批判を してしまうのはそのためである。

１３.１ 回転をさせるのではなく、すでに回転している

考え方を変え、これから円盤を回転させるのではなくて、すでに円盤は回転しているとする。それより良いのは、回転している台の上で 円を描くことである。コンパスか紐かで、回転台の上で円を描く。この円は、回転系の外の静止系から見ても、やはり円形である。 しかし、回転台の上で円周にそって置かれた物差しは短縮し、半径方向に置いた物差しは短縮しない。こうすれば回転系では円周直径比 が円周率より大きいと理解できる。

座標系が回転するとは、(x,y,z)と(x',y',z')とが座標軸の z と z' を共通にして、x'軸とy'軸が、x,y 平面上を回転するだけである。 そこには、硬い床でなく変形可能な軟らかい床を考え、さらに床さえないほうがよい。z' 軸からの距離と回転の角速度とによって存在する、 その点の接線速度がある限界、光速に近付くと、円周方向のローレンツ短縮は、どこまでも短縮の度合を進める。限界距離では、 回転と逆方向に移動する物体は存在を許されるが、静止物体が存在できない。そのように、回転系は、有限半径 (r＜ c/w) のその果てに 無限の周囲を抱える世界である。そこは、球状の星ぼしが薄い円盤となって放射状のフロッピーケースにように詰め込まれた世界である。

１３.２ 回転系の時空

速度をもった系の物差しが他の系からどう見えるかという特殊相対論によって考えると、(中心が静止した)回転系を静止系からみた幾何学は、 半径 r の場所にある微小な 3 方向の物差し (dr, dl, dz) は、r に垂直な円周方向の速度 v= w x r によって 1/γ= √(1-r^2w^2) 倍のローレンツ短縮とγ倍の時計の遅れを受ける。(γ= 1/√(1- v^2) ≧ 1) 角速度 w をもつ回転系の半径 r の場所の時空は、 円周方向に短縮し時計の遅れがある。

ds^2 = g_rr dr^2 + g_ll dl^2 + g_zz dz^2 + g_tt dt^2

において、g_ll と g_tt とが短縮や時計の係数を表す必要から影響を受ける。半径(r)方向と軸(z)方向とは回転による影響がなく、 g_rr = g_zz = 1 であるが、l 方向の係数 g_ll がγ^2 になる。時計の遅れは、時間係数 g_tt が -1 から変化しその絶対値が (1/γ)^2 倍に小さくなる。

ds^2 = dr^2 + 1/(1 - r^2 w^2) dl^2 + dz^2 - (1 - r^2 w^2) dt^2

１３.３ Sagnac 効果

特殊相対論では、動く系は、その前方の同時刻を未来にするので、回転系では静止点同士の時計の合わせ方に問題がでる。 光をやりとりし、系内の点どうしが同時刻を使って、任意の閉曲線で時計合わせをすると、一順すると同じ場所の違う時刻になる。 同時刻は、螺旋を描いて閉じない。そのため、円周上で同時刻に止まろうしても、無限の過去から合意しないとできない。

同じ半径の円周上の点の時間経過は等しいから、a 点から光を送り、b 点で反射して a 点に戻す、b 点で反射した時刻と同時刻なのは、 a 点の送受の中央の時刻として時計合わせをする。同じ半径の円周上進行方向に a から b とすると、a と同時刻は、b の(静止系から みた) 未来である。これは進行方向に a, b, c, d ...と並んでいても、その方向に未来が同時刻になる。ところがこれは、円周上で一巡 できる。...の後に a がもう一度出てくるとき a 点の同時刻は a 点自身の未来になる。これは、同時刻という意味の破壊であり、局所 因果性を壊して時間が周期的になるわけではないが、同時刻＝空間が大局的に何かまずいことになっているのである。

回転の存在は普遍的で、地球、太陽系、銀河系も全て回転物体であるが、宇宙自体の回転は、星ぼしの見え方が異様になるはずであり、 現実の宇宙は、全体として回転をしていないとされる。回転円盤のどの点もその点での回転が等しく存在するから、回転宇宙は、 どの場所も回転の中心とする一様性をもつが、軸方向が特別であるから等方ではないのか。いや、軸の位置からの距離によるから 一様でもないだろう。

アインシュタインのいたプリンストン高等研究所にともにいた数学者、論理学の完全性と自然数を含む命題の不完全性定理で有名な ゲーデルによる、一般相対論のゲーデルの回転宇宙解(1949)があり、一順する時間軸ができてしまうという。マッハの原理からは、 宇宙全体の物質がすべてある軸のもとに回転している宇宙というのは、静止宇宙と同じである必要があるのではないか。そうでないなら マッハの原理は、一般相対論に保たれていないことになる。

１４. 加速系

一様な重力が、加速度系と原理的に区別できないとする。高いところの光源からの光は、低いところに達するまでに系が速度を増しているため エネルギーを獲得する。そのため、上方からの光は青方偏移する。連続的にこれが起こるためには、ばかげたことに重力場では時間の経過速度 が場所によって異なるという必要がある。局所点の時間の経過速度は、その点の光速と同一視できる。場所による光速の違いは、屈折率の違い のように、重力による光の湾曲をもたらすと予想した。そして太陽の側の光線の折れ曲がりを計算し、その後の一般相対論のもたらす、 重力による光の折れ曲がりの 1/2 の折れ曲がりを導びいた。時間経過は、実に物体の存在する場所の物体にエネルギーを与える場、 重力のポテンシャルに直接に関係するものであった。

重力のポテンシャルが、時間の経過と、光速というスカラーによって表されるこの単純な理論は、どこで失敗したのか、どうして重力理論は、 一般座標変換というとんでもない数学を持ち出さなくてはならなかったのか、このことは、ほとんど説明されない。そして理解が難しい。 この初期の論文は、ナイーブな物理的な思考方法のお手本と考えられるほどに、物理的な常識を壊して行く。時間経過の速さが場所の関数である。

重力でなく重力ポテンシャルがその時空点の時間経過の速さを決める。重力は、より実在的な重力ポテンシャルの勾配でしかない。地球の中に 穴を掘れば、穴の中では次第に重力は減少していくが、ポテンシャルは低下し続け、地球の中心では重力がなく、ポテンシャルでは最低点、 時間経過の最遅点である。未来の超高密度物質で作った球殻内には重力がないが、低い重力ポテンシャルが時間経過を遅らせる。 SF の時間停滞場(ステイシスフィールド)というのは重力ポテンシャルだけによって可能なのである。

もし重力が時空のテンソル理論でなく、より理解の容易な電磁気のような 3 次元ベクトル解析で表されるものであったら、どれだけ楽だった ことかと考える。一様等方の解が宇宙論であり、球対称場の解がブラックホール解である。そういう最も容易な条件における数種類の解しか 存在していない一般相対論は、十分にこなされた理論とは、私には思われない。電磁気での遅延ポテンシャルを扱うようなニュートン力学と 一般相対論の橋渡しの近似的解が欲しい。この初期の論文は、その問いに答えているかもしれない。

１４.１ 一様重力系と加速系とは、原理的に区別できない

重力はすべての物体、物質に等しい加速度を与える。ニュートン力学は、重力を加速度で表現する。z のマイナス方向に g の 重力加速度をもつ静止系と z 方向に加速度 g をもつ加速系とは、ニュートン力学的に同一である。アインシュタインは、これ を一歩押し進め、一様な重力の静止系 K が重力のない加速系 K' と "原理的に" 区別できないと仮定する。この同一性の厳密 な要求は、時空間の考え方の枠組を壊す結論をも辞さない。その仮定は、絶対速度を否定した特殊相対論と同様に、絶対加速度 を否定する理論になるという。

高所からの光は、低地に達するまでに系が速度を増してエネルギーを獲得するため、上方からの光は青方偏移する。高さ h だけ違う 上の a 点から下の b 点に光を投げるとき、これを加速系に置き換えると、a 点から b 点まで光が飛ぶ間に、b 点が光が来る z 方向 に速度をもつため、ドップラー効果によって b で受ける光は、青方偏移する。逆に b 点から a 点に光が飛ぶときその間に a 点が 光から逃げる方向に速度をもつため a 点で受ける光は、赤方偏移する。

持続的にこれが起こるためには、"表面的には、ばかげたことだが"、重力場では時間の経過速度が場所によって異なる必要がある。 時間経過の速度の差は、重力加速度 g と高さ h の積 gh 重力ポテンシャル差によって生ずる。局所の時間の経過速度の遅れは、 光速の低下をもたらす。光速の違いは、屈折率の違いのように重力による光の弯曲をもたらす。太陽の側を通る光の重力弯曲を計算し、 0.83 秒角を出す。それは、その後の一般相対論の導いた、重力による光の折れ曲がりの 1/2 であった。

時間経過は、実に重力ポテンシャルに直接に関係するものであった。重力は、より実在的な重力ポテンシャルの勾配でしかなかった。 重力でなく重力ポテンシャルがその時空点の時間経過を決める。直接測定できる物理量でないとされてきた重力ポテンシャルに 時間経過が比例するという結論には驚きを禁じ得ない。

ニュートン力学では重力ポテンシャルφは、全体としてある一定値シフトしても物理的にはなんら影響を受けない仮想的な量であった。 ポテンシャルはその差にしか意味がなかった。ところが、時間経過が (1 + φ/c^2) に比例するという結論は、φの大きさを直接使う。 例えば、φに -c^2 以下を与えると、時間経過が 0 以下になり、物理的に許されないようにみえるが、それはいま、ブラックホールの 事象の地平面を表すと解釈できる。彼は、その考察を 1 次近似と明言している。その式は、ポテンシャルの微少変化の範囲の式であるが、 以下の考察は、彼がより精密な結果を考察して、そのままこの理論から一般相対論まで発展させてもよかったように思えるのである。

普通にはこのスカラーのポテンシャル理論は、失敗した理論であるとされ 10次元の計量 g_ik に置き換えた理論にしない限り、解決し 得なかったと理解されているが、この理論で彼が行った考え方の変化は、(1)時間経過が時空の関数である、そして(2)光速が時空の関数 であることを明確に示したことである。その両者ともに、一般相対論の原理として採用されてきた考え方である。この理論は、 一様な重力をもつ系を加速系に置き換えることで、ニュートン力学の道具だけから上の 2 つの結論を導いたのであるが、 この重力系＝加速系という原理に対して特殊相対論を導入することで、さらにもう一歩、先に進むことができるのである。

１４.２ 加速系の光速は、より正確に解くことができる

ν/ν0= 1 + v/c = 1 + gh/c^2 (1)

光速 c は、時間経過に合わせて、場所によって異なる。φ= gh とすると、

c= c0 ( 1 + φ/c^2 ) (2)

アインシュタインの論文では式(3)としてある、この(2)式は、一種異様である。ひとつの式の中に 4 つの光速がある。φを割る分母に光速が 2 つあり、ab 間の通過時間 h/c の分母の光速とドプラーシフトの比率 v/c の分母の光速とである。c0 という不明な光速と、最後に計算結果 の光速 c がある。分母の 2 個の c は、結果の c と一致しない。(φ= 0 か c = ∞でないと c = c0 ではない。) ポテンシャルは質量当たり のエネルギーであるから、右辺の分母側の c^2 は、ポテンシャルの次元合わせのためかもしれない。

しかし、光速がその場所のポテンシャルの関数であることをこの (2) 式ほど明確に示すものはない。特殊相対論の光源の速度に依らない光速、 座標系によらない光速から、光速に対する考え方が大きく変わったのである。(2) 式によれば、光速は、場所によるポテンシャル φ(x) に比例 して低下し、ある低さ φ(x)= -c^2 になると光速が 0 になる。それを超すと光速が負になる。

この式につけたアインシュタインのコメントは、"光速一定の原理は、この理論に従っても、通常の相対論の基礎をなす形式とは異なる形式でよく 保たれているのである。" という不思議なものであった。そのことは、とても文章どうり受け取ることはできない。特殊相対論の最も不変な 時空の特性であった光速が場所 (と時間)の関数でしかないとき、光速一定の原理は、徹底的に解消されたというべきことである。この式の基本的 な重要性から次の考察を行った。1 次近似でなく、a 点から b 点まで光が到達する間の光速も、結果の光速と一致させて微分方程式によって 解くことができる。すなわち、

最初から高さによって光速が違うという考え方による計算をすれば、一様な重力下の光速は、(2) 式よりも正確に解くことができるのである。 下方向を x の正として a から b への到達時間 T は、1/c(x) を a から b まで空間で積分(線積分)した T= ∫_a ^b dx/c(x)、である。 b 点での速度を v= gT とすると、ドップラー効果は、v/c0= g/c0∫dx/c(x) であり、光速を c(x)= c0 - v = c0 - g∫dx/c(x) とすると、 この両辺を微分した微分方程式 c'(x)= -g/c(x) は、変数分離し c(x)c'(x)= -g、c(0)= c0 として、

c^2(x)= c0^2 - 2gx

φ= -gh とすると、

c(x)= c0√(1 + 2φ/c^2) (3)

式 (3) は、ドップラー効果には 1 次近似が使われているが、途中の光速の変化に対応したことによって (2)よりも精度の高い式である。 (2) は、(3) の φ≪ c^2 における 1 次近似である。(3) によると、一様な重力の下の光速は、x により、その 2 乗がポテンシャルに比例して低下し、 ある低さφ(x)= -c^2/2 で光速が 0 になる。それを超すと光速が虚数になる。特異になる低さが式 (2) とは異なってその 1/2 であること、 特異な面より下では光速が負ではなく虚数であることが異なっている。しかし、どこまでも続く一様な重力というのは物理的にありえないから、 この結果も不思議ではないだけでなく、加速系＝一様重力系では、下方のある距離に地平面ができ、光速が 0 とか虚数になる事象の地平面より 下の現象は、永遠にこの場所に影響することがないことと解釈できる。上方の時間経過と光速は (その 2 乗が距離に比例してだが)、 どこまでも大きくなる。加速系の描写は、特殊相対論の双子のパラドックスの弟が遠方でロケットを反転するとき、地球時間が急速に経過する 情景と類似している。双子のパラドックスでは、加速度と距離に比例した時間経過速度だったので、少し違うが。

c(r)= c0 - v = c0 - GM/r^2∫dr/c(r)

a 〜 b の積分範囲は r の向きと逆だから微分方程式、

c(r)'= GM/(r^2 c(r)) - (GM/r^2)'∫dr/c(r)

を得る。第 2 項を小さいとして無視するなら、(3) の導出と同様に変数分離し c(r)c(r)'dc = GMdr/r^2 から c(r)^2= -2GM/r + const、 r→∞で、c→c0 をいれ、c^2(r)= c0^2 - 2GM/r から、

c(r)= c0√(1 - 2GM/rc0^2) (4)

この式は、(3) にニュートンポテンシャル φ(r)= -GM/r をいれたものと一致する。一様重力の場合と同じく光速 c(r) の 2 乗がポテンシャル の 2 倍に関係して低下し、ある半径で光速が 0 になり、それより内側で光速が虚数になる。一般相対論とこの結果とは、地平面の存在とその半径は、 等しいが、光速は、一般相対論のシュワルツシルツ解の光速、

dr/dt= c0(1- 2GM/rc^2) (5)

と比べるとその変化の影響は 1/2 乗である。この論文の考察には、何が欠落していたのか、時間の計量 g_00= (1-2GM/c^2r) は、 この論文で時間経過としてあるが、半径 r 方向の空間計量 g_11= 1/(1-2GM/c^2r) がなかった。光速 (ds=0 を与えたときの dx/dt) は、 √(-時間計量/空間計量) = √(-g_00/g_11) であるから、時間計量だけでは 1/2 乗しか反映しないのである。 この論文の考察に欠落していたものは何か、それは、驚くべきことに特殊相対論である。次項では特殊相対論が正確な重力による空間短縮を 導くことを示す。

アインシュタインのこの論文の以降の計算を簡単に説明を追加しておくと、光速を半径の関数 c(r) として求めたあと、この c(r) で太陽の 側を通過する光線の曲りを計算した。原点を太陽、光経路(y 軸に平行な直線)と太陽との距離を d とし、光線の曲りは、波面中の光速の 傾きの経路上の線積分であるから、光経路上の点の太陽からの距離を r とし光速の r 方向の微分 dc(r)/dr の x 成分を経路にそって積分する。 ∫(dc(r)/dr)cosθds であるが、この論文では、dc/dr = (1/c^2) dφ/dr であり、光速の r 方向の微分は重力と同じ式になり、 その x 方向成分の積分となる。s = r sinθ= d tanθ から ds = d/cos^2θ を使って、距離の2乗に反比例と、 cosθと線分s 方向の 線積分のビオサバールの式と同じ形の定積分になり、∫(kM/r^2) cosθds を sでは -∞〜∞、θでは -π/2〜π/2で定積分する。 ∫(kM/r^2) cosθds = kM∫dθ/r = (kM/d)∫cosθdθ= (kM/d)[sinθ] = 2kM/d

１４.３ 特殊相対論を使って空間短縮を導く

1/γ= √(1 - v^2/c^2)= √(1 - 2GM/rc^2) (5-1)

であり、一般相対論のシュワルツシルト解の無限遠からみた重力による半径方向の短縮比率と一致する。

重力場のある静止系を加速系に置き換える。加速系上に静止点 a, b 点があり、a 点を離れた物体が b 点に到達するまで、b 点が加速する。 重力加速度中の落体の加速が系の加速に置き換わり、a 点で離れた物体の慣性系がみる加速系の x 位置の速度 v(x) は、前項の計算と同様に v(x)= gT = g∫_a^b dx/v(x) を x で微分して、v(x)'= g/v(x) の微分方程式を変数分離して、v{x)v(x)'= g、 v{x)^2 = 2gx、 v(x)^2 = v0^2 + 2gx = v0^2 - 2φとなり、ニュートン力学の -PE が KE に加算される式になる。この速度のローレンツ短縮は、v0= 0 とすると、

1/γ= √(1 - (v/c)^2) = √(1 + 2φ/c^2) (6)

であり、光の ab 間通過時間の系の加速による速度のドップラー効果からくる光速の低下 (3) と等しい。それは、なぜか。

重力場の物体の落下を、加速系での物体の放出に置き換え、自由落下物体の慣性系から見て加速系上の静止物体にローレンツ短縮と時計の遅れがある。 特殊相対論の時計の遅れとローレンツ短縮とは逆数で、時計の遅れが γ倍のときローレンツ短縮比率 1/γである。(3) の光速の低下は、 時計の遅れの逆数である。それゆえ、ローレンツ短縮比率と等しい。光の落下のドップラー効果による時計の遅れが、自由落下速度による 特殊相対論の時計の遅れと等しいのは、加速系の時間経過という同一の物理現象だからである。結果が違ってはいけない。

しかしそれは、十分な説明ではない。同じ現象でも違う考え方で解くと違う式をもたらすものである。式が同一となるには理由がある。 重力のある系でも加速系でも、静止した 2 点間で、光と物体とをやりとりするとき、両者の時間経過の比が存在し一致する。その理由は、 c^2 と v^2 がともに上下の ab 間のポテンシャル差 2gx を持つからか。γが速度による質量エネルギーの増加率であることだろうか。

光の落下によるドップラー効果で場所による時計の遅れを説明したことは、物体の自由落下の速度で説明することもできたわけであり、 アインシュタインがこの論文で使わなかった特殊相対論だけを使ってすむ話だった。しかも、特殊相対論では、時計の遅れとローレンツ短縮は、 常にペアで表れる現象であるから、もし、アインシュタインが彼の特殊相対論をこの問題に使う気になっていれば、 当然、もう片方の空間短縮にも着目せざるを得なかったものであろう。

1/γ= √(1 - 2GM/rc^2) (7)

であり、これは、無限遠から見たシュワルツシルト解の半径方向の空間短縮と等しい。時計の遅れは、その逆数 γ= 1/√(1 - 2GM/rc^2) である。光速は空間/時間であり、短縮と時計の遅れの両者から、

c(x)= c0 (1 - 2GM/rc^2) (8)

一様な重力は、加速系と原理的に区別できないとして、加速系上の静止点の速度による特殊相対論のローレンツ短縮と時計の遅れから シュワルツシルト解の空間短縮と時計の遅れそして光速を導くことができたようだ。

空間短縮を物体の慣性系からみて速度を獲得した加速系上点のローレンツ短縮で説明できるのは、重力＝加速系仮定を使用した結果であり、 逆に加速系上のその位置からみれば、自由落下物体側のローレンツ短縮も同等に相対的に起きる。互いに相手の短縮をみるのは加速系上点と 落下物体との間の特殊相対性である。上述の (5-1) の偶然にみえた合致、一般相対論の重力短縮が自由落下物体のローレンツ短縮と一致する ことは、重力＝加速系仮定と特殊相対性で説明される。

このアインシュタインの初期論文の光速が時計の遅れと同じであるために、光速が一般相対論におけるそれの 1/2 乗であることは、 空間の重力による短縮、空間短縮を考慮しなかったためである。光速はスカラーではなく、空間計量が方向によって異なるような空間異方性 があると方向によって速度が違ってくるのである。例えば、質点の側の計量は、半径方向に大きくなり、それに垂直な方向は変化しないため、 光速は半径方向と球面内の方向とで違ってくる。この論文に問題があるとすれば、空間の異方性を考慮しなかった点にあるのであり、 "一様な重力の静止系と重力のない加速系とが原理的に区別できない" という仮定が間違いだったわけではないと思う。

質点の側の時空の光景を描くことができる。質点近くの観測者は、半径方向の距離が長いと見る。遠方の静止した観測者からは、逆に質点の 側の物体が平坦化、薄膜化してみえる。ブラックホールに物体は落下して最後は凍結して永遠に停止する際に、後から落ちる物体が前の物体に ぶつからない理由がそこにある。薄くなって降り積もり、後からの分を受け入れるのである。自由落下物体と重力に踏ん張る物体とは、等しい 比率で平坦化しているという、一般相対論の質点の側の時空の光景が初等的に再現される。

１４.４ 議論

(1) 加速系でのドップラー効果は、相対速度から発生するものであるが、重力による赤方(青方)変移は、速度差がない。重力を含む系で速度を獲得 するのは、系ではなくその中の物体である。重力系を、加速系に全く区別できないとする仮定は、この間の類似性を原理的合同性に格上げする ことで、重力系の時空記述を試みている。

加速系での速度差のドップラー効果が重力系に置換されたとき、時間経過の違いを系内点に持ち込んだ。時間経過が場所によって異なるならば、 静止点間でドップラー効果と同じ現象が観察される。時間経過比率がドップラー効果比率であることは、静止点間であるから継続的にドップラー 効果を得るため正しい。その比は、 v1 を光が通過する時間の加速による速度として 1 + v1/c である。

それに対し、光でなく物体の自由落下での時計の遅れは、物体の位置する場所のポテンシャルの変化である。その終端速度の特殊相対論的な 時計の遅れが最初のドップラー効果による時計の遅れと一致するのは偶然なのかという疑問がある。後者の時計の遅れは、慣性系からみた 加速系上の物体の時間経過である。式からは、一致する理由がないかにみえる。 v2 を自由落下中の加速による速度として、時計の遅れは、 γ= 1/√(1- (v2/c)^2) であり、v2 は、上記の v1 よりはるかに大きい別の値である(v2 ≫ v1)。

(2)慣性系からみると光速は場所によって変化しないが、加速系では光速が場所に依存するとして、その場所の光速を c(x)= c0 + v(x) とした。 加速系の光速を露わに使った。とくに光速に見る側の速度を加算すること、c(x)= c0 + v(x) は、乱暴である。重力があるとき光速が変化し、 時間の経過も変化すると考えるのに対して、慣性系からみたときは、光速が変化しない代わりに、空間短縮で説明することはよい方法だろうか。

(3)加速系で、場所によって光速が異なることを使うときの光速と、結果の光速が異なっていること。ab 間を光が通過する間にb が速度をもつ。 v= gT = g∫_a^b dx/c(x) を微分した、微分方程式 c'(x)= v'(x)= -g/c(x) が満たすのは、c(x)= c0√(1 + 2φ/c^2) これが加速系の空間短縮 を考慮しない時間経過に比例した光速であり、重力系の遠方から見た光速とは異なっていた。空間短縮と時間短縮の両者を考慮して正しい光速 を出すことができたように見える。しかし、自然が種々の光速を使い分けることはない。さらに式は統一的に扱われるべきである。

加速系を a 点で物体が離れた時点から t 秒後 a 点での並進慣性系 (x',y',z',t') からみると、加速系 (x,y,z,t) の静止点のもつ速度 v= gt による局所ローレンツ変換は、 dx'= γ(dx - v/c dt), dt'= γ(dt - v/c dx), 1/γ = √(1-(v/c)^2) 加速系の物差しの目盛の短縮 dx'/dx は、dt'= 0 をいれて dx'/dx = 1/γ、時計の遅れは、dx= 0 をいれて dt'/dt =γである。 これが、φ= -1/2 c^2 (g_{4,4}+1),　g_{4,4}= -1 - 2φ/c^2 にまでどう継るのか不明である。

(4) 最後に完全な否定。重力による計量とローレンツ変換の関係をより明確に扱うべきである。任意の計量は、座標系を選択すれば空間的な 異方性と時間経過になる。一般変換は、速度をもった局所のローレンツ変換に空間異方性を、後から掛けて遠方からみることであるなら、 局所の計量をその局所で知ることはできない。重力による空間圧縮を局所ですれ違う慣性系のローレンツ短縮で説明することは無理ではないか。

(5) 加速系と重力をもつ系は、例えば慣性系からみたとき、加速系が速度を増して動き、重力系は静止しているという違いは明らかである。 1 g の加速系は、1 年もすると宇宙の果てを目指して光速に近い速度で進んでいるのに、1 g の重力系はそうではなく、地上に止まっている。 両者が同一であるはずはない。これは、どこか間違った議論だろう。加速系においても加速系の系内の点は静止している。系内の静止点は、 互いの速度をもたないのに加速の方向に一方的なドップラー効果をもつ。そのことについて、加速系と重力系で同一というのである。

加速系と重力系を同一とするのは系内の現象についてであり、系外の遠方からの光や物体の現象は別ということである。加速系では星々は後方 から横に回り込んで進行方向の前方に集合し、星々の見え方が違ってくる(光行差)が、重力系ではそういうことはない。少なくとも定常である。 両者の同一性は、系内現象に限定されるだろう。また、加速系を側でみる慣性系は存在するが、一様な重力の系が存在し得ないから重力系の側 には微小な局所慣性系しか存在しない。両者の(局所) 慣性系、静止点から離した物体が同じ振舞をすると仮定し、そして、その局所慣性系から みた両者の系も同じと仮定することも問題なさそうである。遠方の星々からみた両者の系は、遠方の星からの光が違って見えるように違うだろう。 局所慣性系と遠方の慣性系の違いである。

加速の方向が x のとき、時刻 0 で a 点から離れた(局所)慣性系からみた加速系の速度は gt であるが、その各点が速度をもつために、ローレンツ 短縮や、時計の遅れがでる。a 点からの距離 x = 1/2 gt^2 の√に速度が比例する。a 点からの時刻 t は、それに比例するからである。

速度の 2 乗は、エネルギーの単位であり、加速系の各点の加速方向の距離とエネルギーが比例する。後方にエネルギー 0 の距離ができ、前方は どこまでもエネルギーが延びるという非対称の構造ができるのは、このエネルギーに関係している。

問題は、加速系の距離がローレンツ短縮を考慮された距離だろうかということである。 a 点を離れてからの時間 T は、慣性系上の時計であり、 相手側の静止した一個の時計は、時計の遅れを起こすが、原点が速度 v= gT ですれ違う相手の場所の累積時間 T' は a 点を離れてから多くの 時間を経過している。 (T'＞T) 向かい側の場所の a 点からの累積距離 X' は、ローレンツ短縮のために系内距離は大きい。 (X' ＞ X)

なぜなら、局所ローレンツ変換、

dx'= γ(dx - v dt),
dt'= γ(dt - v dx)

に dx= 0 をいれ、 dx'= -γv dt, dt'= γdt から、

T'= ∫dt'= ∫γv dt、
X'= ∫dx'= ∫γdt。

γ倍を微分時間と微分距離に掛けて、すれ違う加速系の点の距離と時間経過は、その積分である。

１４.５ 光速一定の放棄は何によるのか

上空で、1 m の水平方向の往復に 1 秒かかる光速をストップウオッチで測定しているとする。ストップウオッチの針がある位置に来 たとき光が到着する。地上と上空で時間経過が違い、そのストップウオッチの針の周り方が地上からみて 2 倍速く、その時計は、 0.5 秒でその回転をするとする。そのとき、そのストップウオッチの針がある角度になって光が到着することが地上からみても同じ とすると、0.5 秒で 1 m を往復するように、上空の光速が 2 倍速くないといけない。

もし、光速だけが場所に依らず地上でも上空でも一定とすると、ストップウオッチの針の位置と光の到着が違わなければならない。 そしてそれは、上空の局所事象を変えることになる。つまり、上空での時間計測が 2 秒に変わらなければならないが、それは 1 秒 であった。この局所事象、局所計測は、どう遠方から眺めても、相対論がそれを変えることができないこととするのである。 (1 m の距離が変ればそれは光速に影響するが、一様な重力では水平方向の物差しは変わらない。垂直方向は違って来る。)

つまり、局所の時間経過に局所の光速が比例して初めて局所事象が保存される。地上からみて、上空の出来事はすべて高速化される とみるべきで、上空の光速だけそのままということはあり得ない。ある点の光速は、時間経過と物差しのサイズに比例し物差しが方向 に依存するとき光速も方向によって違うと考えられるのである。

特殊相対論は、他の系の時間と空間(時間経過、物差の長さ)を変化させるが、同じ系の中の物差し時計を変化させない。 その系の中での長さと時間の計測は、固有時、固有長として別の系からみても変わらない不変量である。一般相対論では、 非線形の座標系変換を採り、局所がそれぞれ違って座標変換され、g_ik という係数が掛かった不変量の式をもつ。局所の計測は、 座標変換によらない不変量 ds^2 として保存されるのである。

１６. ポアンカレの宇宙

非ユークリッド幾何学の話は、平行線が唯一つ存在する、存在しない、又は無数に存在するユークリッド幾何学、ロバチェフスキー幾何学、 そしてリーマン幾何学を対比し、それらの依って立つ公理は、いずれが正しいかどうか判定できず、それらはただ便利さのうえで選ばれる。 それらが現実の宇宙のなかでいずれか検証することはできないという考え。そこで、星の視差による検証可能性の議論が否定的にでてくる。

宇宙の空間的曲率の判定が恒星程度の距離によって可能でないことは、現在の後知恵として明らかであるが、彼は、それを原理的な不可能性 として議論している。この本のなかにアインシュタインの "幾何学と経験" の議論のもとではないかと思われる考えがあった。 第 2 部第 4 章空間と幾何学の "非ユークリッドの世界" にある球状有限宇宙の話である。

(勿論、ポアンカレは、特殊相対論と一般相対論に大きく貢献をしただけでなく、その他の多くの分野、特に最近は複雑系、カオスの学問に 業績を残したことが知られるようになった、当時の最高の知識人であった。)

１６.１ ポアンカレの寓話宇宙

この仮想の世界では、大きい球に閉じ込められていて、この世界は温度は一様でなく、中心がもっとも温度が高く、 中心から遠ざかるにつれて温度が下がり、この世界を包む球面に達すると絶対温度が 0 になる。

この温度の変化する法則は、限界をなす球面の半径を R として、中心からの距離を r とする場所の絶対温度は、 R^2 - r^2 に比例する。

そこではあらゆる物体は、等しい膨張係数をもつ。どの定規の長さも絶対温度に比例する。 物体は、そこに置かれるとすぐにその温度に熱平衡になる。

これらの仮説は、矛盾しないし、想像できないものはない。そうすると、運動する物体は、限界の球面に近付くと しだいに小さくなるに違いない。

この世界は我々の用いる幾何学の見地からは有限であるが、この世界のなかにいる住人にとっては、 無限の広がりをもった宇宙になる。

(中略)

さらに、この世界の光は、その屈折率が R^2 - r^2 に反比例してさまざまに屈折する媒質の中を通過すると仮定しよう。 この条件のもとでは、光線は、直線ではなく、円弧となることがわかる。

(引用終了)

１６.２ 内部は無限

まず、どうして R^2 - r^2 という 2 次なのか。例えば、R - r という 1 次式に物差しのサイズが比例する場合、この世界の住人に とって宇宙は無限にならないのかもしれない、との予想は外れた。限界球面 R までの距離 x = R - r に物差しが比例する 1 次式 であっても、住人にとっての限界球面までの距離、∫dx/x の 0 から R までの定積分は、無限大に発散する。

R
∫ dx/x ⇒∞
0

物体が中心から遠方にいくに従って 2 次元的な占有面積は、より速く 2 乗で減少し 0 に漸近するし、物体の体積は、 3 乗で 0 に近付く。そのため、その面積、体積をもとに計測する宇宙の体積は、より速く発散するだろう。 R^2 - r^2 に物差しが比例する 2 次式では、さらに容易に発散するだろう (∫_0^R dx/x^2 ⇒∞)。 しかし、住人が無限の宇宙を感ずる有限宇宙のために物差しのサイズの変化が 2 次である必要はないのである。

１６.３ 物体(定規)のサイズが場所による

ds^2 = dx^2 + dy^2 + dz^2

そして、特殊相対論のローレンツ変換が知られ、速度をもった剛体の変形の法則、ユークリッド距離の式に、時間間隔の 2 乗 を引いたものが、ローレンツ変換によって変わらない不変の時空間隔であるとするミンコフスキーによる定式化があった。 そしてそれは、時間が虚数軸なら 4 次元ユークリッド空間になる。

ds^2 = dx^2 + dy^2 + dz^2 - dt^2

ミンコフスキーの時空間隔をもつ特殊相対論の扱う時空は、一様等方な、平坦な時空であり、それは、時空が重力によって変形した、 平坦でない時空の幾何学では異なることを理解する必要があった。曲った時空での幾何学として、非ユークリッド幾何学が必要となる。 そこでは平坦な時空と何が違うのかというと、最も基本的な不変の時空間隔、ユークリッド距離が成り立たないことから始まる幾何学の 再編である。そこでは、剛体は変形なしに平行移動もない。この世界の住人にとって中心から遠方に移動することは、縮小を伴うのである。

１６.４ 時空の変形(=計量)と不変量

つまり、相対論は、物差と時計の変化、時空の変形を表す法則である。時空(=剛体)の変形、弯曲、膨張、縮小を 記述することが相対論の目的である。特殊相対論によって速度をもった時空が変形を受け、物差の縮小や、時計の 間隔の変化が起きた。それは一般的な常識からは遠く想像もつかないものであった。(しかし、基本的な事象間隔は、 虚数の時間を追加しただけの 4 次元ユークリッド距離だった。) 同様に一般相対論では時空の変形が質量の存在から起き、 それが重力の本当の姿というのである。

特殊相対論の座標系中の時間測定、座標系中の長さ測定が他の系からどう眺めても変えられないように、 剛体と時空間隔は、固有時、固有長の存在に置き換えられる必要があった。一般相対論において不変量は、 時空のある一点の事象が、他の点からどのように非線型に写像され変形しても保存される量であり、 それは遠方からの観測によらない局所の事象間隔であり、曲がった時空での剛体の移動の法則である。

ds^2 = g_ik dx^i dx^k

ポアンカレのこの球状有限宇宙は、アインシュタインの "幾何学と経験" で応答されたように思える。 そして彼の定常宇宙にとって重要なヒントだったのではないだろうか。 次に述べる、アインシュタインの球状有限の定常宇宙は、R^2 - r^2 を計量 g_ik の平坦 δ_ik からの偏差の分母にもつ。 ただし、g_ik が R^2 - r^2 に反比例するとき、物差しの長さはその 1/2 乗に反比例するから、 このポアンカレの宇宙の半分程度の歪である。 そして分子側に、x^ix^k があって、それが物を奥行き方向に平坦化させるのであるが(*)。

(*) アインシュタイン定常宇宙の計量、g_ik= δ_ik + x_i x_k/(R^2-r^2) から、その宇宙の中心からの累積距離は、x= r/R とし、 ∫_0^R √g_11 dx= ∫_0^R √{1 + x^2/(1-x^2)} dx = ∫_0^R dx/√(1-x^2) は、発散しない。

１６.５ 宇宙の果ての見え方

それを知るためには中心以外にいればよい、という意見は当たらない。宇宙を見る位置としては中心以外の地点はないからである。 球状の有限宇宙というとき、それは宇宙を外から見ることではない。宇宙を外から見ることは不可能である。住人の視点は、つねに 中心の視点であり、宇宙を外から見る視点は、ありえないものである。

宇宙を我々が見るとき、中心に我々の銀河系があって、中心から外れた所に遠方の銀河がある。その遠方銀河からみると、そこを中心 とする宇宙がみえて我々の銀河系は、遠方にあるだろう。しかし、見え方の様相は、ここから見た宇宙と基本的に違うものではない と思われる。宇宙の任意の一点から眺めた宇宙の像は、どこから眺めても多少の偶然的な違いはあっても基本的にはほとんど同じ像 であろう。

1992年、ブラジルのリオから南に少しいったアングラ・ドス・ライスという観光地での MPEG 会議に参加したとき、激しい一週間の 会議の終わりの週末に真っ暗な静かな内海の海辺にでて夜空を眺めた。しばらくすると目が慣れてきて南半球の星ぼしが見えてくる。 そこで見たのは全くなじみのない星座である。ここはブラジルで日本とは地球の反対側だから人間が逆さに立っているだけではない。 星空さえも違うのである。それは、まるで遠方の星系にいって迷ったかような幻想を抱かせる。 そして友人が持参した小さな双眼鏡で眺めた南半球でしか見えない球状星団は、それまで一度も経験することのなかったものであった。 その夜空は、多少きらめく星団と星雲が多いように見えるが、北半球の夜空と同程度に暗いのだろう。宇宙原理と仮定すべき一様性と 等方性。それは、宇宙を数学的に扱うための方法である。そして問題は、3番目のそれを我々が捨て去ったと思っている定常性なのである。

１６.６ 宇宙と幾何学

ポアンカレの宇宙で、この歪を測定しようと移動して自らのサイズ変化を測定しても無駄である。観測者は、つねに宇宙 の中心にいる。しかも、持ち運んだ物差で測定しても結果は変わらない。宇宙の有様は、遠方の見え方によって判断する 以外の方法はない。宇宙はこの図のように、遠方に歪みを持つことが基本的に起こりえる。この静的宇宙では宇宙を同時刻 の空間で切断した像と、宇宙の果てを光でみる像が同じであるから、この宇宙の住人は、この図そのままの宇宙を見るのである。 この宇宙では一様に分布する遠方の銀河が平坦な空間よりも多く小さく見え、距離と面積の2乗、距離と体積の3乗の関係 からの偏りがあるだろう。

この宇宙では不変の空間間隔は、ds^2= (R^2/(R^2-r^2))^2 dr^2 であろう。中心から r の場所の計量、g_ii(i=1〜3)= (R^2/(R^2-r^2))^2 であって r が大きくなると、g_ii (i=1〜3) がともに同じく大きくなり、物が平坦化でなく等方的に 小型化する。そして、r → R で、g_ii → ∞に発散し、物体は無限小になる。

１６.７ 宇宙の内部でこの構造を知ることができるか

さて、この宇宙の直接の距離 r を測定する方法がない場合も、この宇宙の様子を知ることができるだろうか。 dx= R^2/(R^2 - r^2) dr のとき、距離 r までの物差の累積距離 D(r) は、

D(r)=∫_0^r dx= ∫_0^r R^2/(R^2 - y^2) dy = R/2 ln |(R+r)/(R-r)|

である。（D(r)＞r、r→R で D(r)→∞である。）この宇宙の住人が、r を知らず、D しか知らないとき、この宇宙が遠方で 歪んでいることを知ることができるだろうか。D を半径とする球面の面積 4πD^2 は、D の増大が緩いので、S(r)の g_ii 倍 よりも小さい。そのため、r を知らなくても、この宇宙の様子を知ることができる、と考えることができる。 これは、ポアンカレに反論できたのかもしれない。

１７. アインシュタイン宇宙

G_ik= R_ik - 1/2 g_ik R

G_ik - λ g_ik= - κ T_ik

物質の全エネルギー運動量テンソル T_ik がそのまま、時空のアインシュタイン曲率 G_ik を与えるというのが、一般相対論の 重力方程式である。ここで数学的に導入が任意な宇宙項(斥力項)、λ g_ik の項を導入するのは、定常宇宙が宇宙項λと物質密度μ_0 の引力 のバランスを要請するからである。これを縮約したスカラーの式 R + 4λ = κ T をみれば、任意の物質密度に対してそれに対応するλ を与えると宇宙は平衡し定常となる。宇宙は、空間的に球的で有限、時間的に定常な4次元円筒世界となる。

g_ik= δ_ik + x^i x^k/( a^2 -(x^1)^2 -(x^2)^2 -(x^3)^2 ) 　(i,k= 1,2,3)

g_i4= 0, g_44= -1

とおけば、

R_ik= -2/a^2 g_ik,　R= -6/a^2,　G_ik= 1/a^2 g_ik　　(i,k= 1,2,3)

R_i4= R_44= 0

となる。これから、

T_44= μ_0 c^2　他の T_ik= 0,　T= -μ_0 c^2

λ= 1/a^2 = 1/2 κμ_0 c^2 = 4π k μ_0 / c^2

彼には定常であることが前提であったため、0 でない物質密度と宇宙項が必要であった。λ= 0 を与えると物質密度 μ_0= 0 となり、 宇宙の半径 a は無限になる。これよりは、0 でない物質密度をとる有限宇宙の方を合理的と考えた。

λをいれると物質密度 0 の重力方程式には g_ik 定数という一般解(λと物質のないとき T_ik= 0, R_ik= 0, R= 0, G_ik= 0 から、 真空は、平坦なミンコフスキー時空になる。)がなくなり、g_ik= 0 という特解だけになり、物質の存在しないとき、場すら存在しない というマッハの原理に合う。その場合、光も真空中を伝播できず、時計や物差しも存在しない。それがλの重要な意味と考えられた。

１７.１ 射影による g_ik

定曲率空間を表現するために n+1 次元ユークリッド空間中の n 次元超球面上の点を赤道面 x^(n+1)= 0 に平行射影する。 ユークリッド空間、

ds^2= Σi= 1〜n (dx^i)^2 + (dx^(n+1))^2

の中に半径 a の n 次元超球面を考える。

Σi=1〜n (x^i)^2 + x^(n+1)^2 = a^2

これを使って、x^(n+1) を消去する。x^(n+1) = √((a^2 - Σ(x^i)^2 ) から、

dx^(n+1) = 1/2 ((a^2 - Σ(x^i)^2)^(-1/2) d(Σ(x^i)^2) = -Σ(x^i dx^i) / √(a^2 - r^2), r= Σi=1〜n (x^i)^2

ゆえに、

ds^2= Σi=1〜n (dx^i)^2 + (-Σ(x^i dx^i))^2 / (a^2 - r^2), r= Σi=1〜n (x^i)^2

これから、

g_ik= δ_ik + (x^i x^k)/(a^2- r^2), r= Σi=1〜n (x^i)^2

が得られる。4 次元ユークリッド空間中の 3 次元超球面が我々の空間ならば、この図の高さ方向 x^(n+1) が時間であり、 変動する宇宙を示すものであるが、射影によって次元を減らして x^(n+1) をなくし平行射影の結果を空間とする。 時間は別に定常とする。この射影は、半径 a (赤道)で特異になる。この宇宙の超球面の面積は、射影の面積の 2 倍であり、 有限から有限への写像である。無限空間を閉じ込める有限空間ではない。

１７.２ その他の射影

x^i = r/r' x^i', r^2 = Σ(x^i)^2, r/r'= |x^(n+1)|/a = a/√(a^2+r'^2)

という変換で得られた座標系では、r' を r と書き直し、

ds^2= a^2/(a^2+r^2) Σ (dx^i)^2 - a^2/(a^2+r^2)^2 (Σ x^i dx^i)^2 となる。

また、北極 x^k= 0, x^(n+1)= a から南極の外接面への射影は、北極だけが特異となり、 Stereographic projectionと言われる。 これも有限から無限への写像である。 ds^2= 1/(1+r^2/4a^2)^2 Σ(dx^i)^2 という g_ik を与え、形を変えない同形写像 (conforming transform)である。これは、アインシュタインが"幾何学と経験"のなかで言及した写像であるが、 彼の定常宇宙で使われたのは平行射影であり、周辺の計量は全く異なるものになる。 平行射影では赤道近辺の射影された剛体球は奥行きが短くなり平べったくなるが、 ステレオグラフィックでは逆に北極近辺の射影された剛体球が遠方において巨大化する。

１８. ド・ジッター宇宙

g_ik= δ_ik + x^i x^k/(a^2 -(x^1)^2 -(x^2)^2 -(x^3)^2 -(x^4)^2) 　(i,k= 1,2,3,4; x^4= ict)

T_ik = μ_0 = 0, λ = 3/a^2

これは、4 次元 "擬球" 状世界である。アインシュタインは「 a^2= Σ(x^i)^2 で特異だから、これは物質のない宇宙のモデルではなく、 殻のある宇宙のモデルである」とこれを批判した。しかし彼自身の定常モデルも空間的果てで特異である。これらの宇宙解は、一様なのは密度 μ_0であり、計量 g_ik は一様等方ではない。宇宙の中心の時空がミンコフスキー的であり、遠方はそうでない。宇宙の中心部と周辺で g_ik が異なり、方向にも依存する。どの点も対等という空間的一様等方性は g_ik にはない。g_ik のδ_ik との差が中心からの距離に斉次 (x^i と x^k との積に比例)である。このとき g_ik dx^i dx^k において等方性をもつと考えられる。任意の点からみた遠方の時空の様子、 宇宙の果てが計量 g_ik を使って表現される。ここでは誰もが中心から宇宙をみる。どの点も対等にこのような g_ik 構造をみるのである。

アインシュタイン宇宙は、定常かつ静的宇宙であり、膨張もないのに周辺短縮している。同様にド・ジッター宇宙にも周辺短縮がある。 アインシュタイン宇宙は、3 次元空間、ド・ジッター宇宙が 4 次元時空という超球の次元の違いしかないからである。両方の宇宙とも 空間の係数 g_ii (i= 1〜3) が周辺で大きい。両宇宙とも中心からある方向、x^i に離れると g_ii は、最初、距離の2乗に比例して大きくなり、 距離 a の宇宙の果てに近付くと分母が 0 に近付き、g_ii が無限大に発散する。g_ik は時空の間隔(又は剛体)の不変式 ds^2= g_ik dx^i dx^k の係数(感度)だから、両方の宇宙とも、宇宙の果てには奥行き方向に薄くなった殻のような周辺世界をもつのである。

ド・ジッター宇宙は、時間軸を虚数 (x^4= ict) にするから球状でなく擬球状である。斥力項λの働きは反発であり物質がないため収縮要素がない。 過去未来の時刻 t の半径 √(a^2 + c^2t^2) は、現在の半径 a よりつねに大きく、中心から半径 a の脇を通過する光と中心との距離のようである。 無限大から a に縮まり、現在反発し、また無限大に拡大するハイパーボリック(擬球状、双曲)な宇宙であり、これほど動的な宇宙を静的宇宙とするのは、 時空の一様性からの解だからである。

時間を虚数軸にするこの式の時間計量 g_44 は普通の計量の符号のような -1 の近辺でなく、1 の近くである。 g_44= 1 - (ct)^2/(a^2 +(ct)^2 - r^2) は、 質点の周りのポテンシャルφ= 1/2 c^2 (g_44 -1), g_44 = 1 + 2φ/c^2 で表すと、φ= -1/2 (ct)^2/(a^2+(ct)^2-r^2) の分母から、 空間的遠方 r には上に凸の 3 次元逆パラボラ底のように端で落ちる散逸壁のポテンシャルをもつといえる。ただし、普通φは、 g_44 と 1 次の関係ではなく、√g_44 と 1 次の関係である。そして時間経過は、√g_44 に関係する。

(１) 光で見る時刻 t の点の距離を r= ct (光円錐)と近似すると、単純な分母一定の g_44= 1 - (ct/a)^2、 g_44＜1 となり、1 との 差が t^2 に比例するから、時間経過√g_44 の逆数 1/√(1-(ct/a)^2)= 1+z の赤方偏移 z も、t^2 に比例する。距離に比例でなく 距離の 2 乗に比例する赤方偏移となる。ct= +- a の時刻は特異であり g_44= 0。これは、始まりと終りをもつ宇宙である。

(２) 時間的領域((ct)^2 ＞ r^2) では分母が大きく赤方偏移の程度が小さい。宇宙の半径、√(a^2 + c^2t^2) は、過去未来で大きく、 現在は最小の a である。つねに収縮し反発し膨張に転じる宇宙である。

(３) 空間的領域は、r が √(a^2 + c^2t^2) に近付くと分母が小さくなり、分数は大きくなる。r^2＝ a^2 + c^2t^2 で特異である。 その外側 r＞a は、g_44＞1 であり、そこからの光が中心に届くなら青方偏移する。

(ド・ジッター宇宙の赤方偏移が距離の2乗比例というのは、俗説の可能性がある。J.A. Peacockによると Weyl(1923)が線形と明らかにしたという。もしそうなら、これはド・ジッター宇宙に対する誤った理解であったことになる。)

１８.１ アインシュタイン宇宙とド・ジッター宇宙の成り立ち

R_hijk + α( g_hj g_ik - g_hk g_ij )= 0

これを縮約して、R_ik +(n-1)αg_ik= 0

さらに縮約して、R= -n(n-1)α

アインシュタインテンソル G_ik も超球中では、次の値をもつ。

G_ik= (n-1)(n-2)/2 α g_ik

超球の射影の g_ik をもつことで、超球上の等曲率を確保し、上の R_hijk + α( g_hj g_ik - g_hk g_ij )= 0 が成立する。 その縮約した上記の3式に n= 3 を入れれば、R_ik= -2αg_ik, R= -6α, G_ik= α g_ik. (α= 1/a^2) が出る。

G_ik - λg_ik = -κT_ik は、(α-λ)g_ik = -κ T_ik となる。αとλが同じ値をとるとき、 T_ik = 0 となる。 塵埃の質量運動量テンソル T_ik は、3次元においてすべて 0、T_44 = ρ、 T= -ρ を仮定すると、宇宙項は、αと一致させ、 λ = αとすると、R + 4λ = κT から α= 1/2 κρ、半径 a は密度の関数、a = √(2/κρ) となる。

また、上記の3式に n= 4 を入れると、R_ik= -3αg_ik, R= -12α, G_ik= 3αとなり、G_ik - λg_ik = -κT_ik は、 (3α-λ)g_ik = - κT_ik となる。これに T_ik= 0, T= 0 とするための λ = 3αを入れると物質のないド・ジッター宇宙解がでる。

アインシュタイン宇宙解 (α-λ)g_ik = -κ T_ik の α-λ が 0 でないときと、 ド・ジッター宇宙解 (3α-λ)g_ik = - κT_ik の 3α-λ が 0 でないときとは、ともに T_ik が値をもつが、宇宙解を与えるだろうか。 4次元的 (3α-λ)g_ik = - κT_ik は、自然な解釈を許さないかを考えると、物質の圧力を導入し T_11= T_22= T_33= p とし、T_44= u (p, u ともに正) T= 3p - u から、3α-λ= κ(3p - u) を与える。アインシュタイン解の(α-λ)g_ik = - κT_ik は、 α-λ= κ(3p - u) を与えるがそれらが解と言えるか不明。

１９. フリードマン宇宙

(R_ik - 1/2 g_ik R)+ Λ g_ik +κ T_ik = 0 ...(1)

"拡張された重力方程式の第二項、宇宙定数Λは、理論を複雑にし、論理的簡単さをかなり減ずるものである。物質の有限平均密度の導入が 避けられないことから起こる困難によってのみ妥当とされる。フリードマンはこのディレンマから逃れる方法をみいだした。"

”三次元に関して等方的な四次元空間”の章で、物質の平均密度ρと、計量場の一定を捨てる場合、空間的一様等方の前提は、 四次元的宇宙の中心を通る全ての測地線を軸とする回転について不変から、四次元的球対称と考える。通常の4つの座標でなく、 x^1〜x^3 が不変で、x^4 だけが変わる時間的な線、中心を通る粒子の測地線を、中心からの距離と時間とを等しいとし、

ds^2= (dx^4)^2 - dσ^2, 　dσ^2= γ_ik dx^idx^k　(i,k= 1〜3) ...(2)

γ_ik= γ_ik0 G^2

γ_ik は、時間による正の係数 G を除いて同じ三次元の定曲率の計量とする。さらに、線素がユークリッド的になるように x^1 〜x^3 を採り直して、

γ_ik0= A^2 δ_ik

ds^2= (dx^4)^2 - G^2 A^2 ( (dx^1)^2 + (dx^2)^2 + (dx^3)^2 ) ...(2)

と表す。G を時間 x^4 だけの関数。A を r だけの関数 (r^2= (x^1)^2 + (x^2)^2 + (x^3)^2) とする。

A= 1/(1+ z/4 r^2) (z= 1 球状、z= -1 擬球状、z= 0 ユークリッド空間) ...(3)

１９.1 フリードマン解

G_{i,k}= (z/G^2 + G'^2/G^2 + 2 G''/G) G＾2 A＾2 δ_ik = 0 　　(i,k= 1,2,3)
G_{4,4}= -3(z/G^2 + G'^2/G^2) = -κρ .......(4a)
G_{i,4}= 0

G は、時間 x^4 の関数で、宇宙の質点間の計量的距離の相対的測度。z/G^2 は、ある x^4 の空間的曲率、G'/G がハッブル膨張を表す。

(z/G^2 + G'^2/G^2 + 2 G''/G) = 0 .....(5)
(z/G^2 + G'^2/G^2)= 1/3 κρ

辺々引いて、

G''/G + 1/6 κρ = 0 ...(5a)

Gとρは正であるから G"は負で減速膨張であることが分かる。G は、極小や、変曲点をもたず、ρが 0 でない限り G に定数解はない。

１９.２ 空間曲率０の解

2h' + 3h^2= 0 ...(5b)
3 h^2= κρ

h からρを推定する。h= 432km/sec/Mpc = 4.71・10＾(-28)、κ= 1.86・10^(-27) から、ρ= 3h^2/κ= 3.5 ・10^(-28) g/cm^3 空間の曲率は、ρと h の関係のつぎの式で与えられる。

z/G^2 = 1/3 κρ - h^2 ...(5c)

空間曲率 0 のとき、ハッブル定数は時間に反比例する。h= 2/3t ...(6)

(アインシュタインの使ったハッブル定数は現在の10倍大きい。密度と宇宙の空間的曲率には、h^2 が関係し、h が10倍の誤差をもつとき 密度ρと曲率 z/G^2 の関係は 100 倍違ってくる。上のρの値は、G.C.マクヴィティ(1939)の "ρ＜10^-27 g/cm^3, おそらくρ〜 10^-29 g/cm^3" という推定より１桁大きい。アラン・サンディジのハッブル定数を使うと、ρ〜 10^-30 g/cm^3 と、さらに１桁小さくなる。)

ここでアインシュタインは、次のように述べる。" h の測定値からわれわれは、宇宙の現在までの存在期間として、1.5・10＾9年 を得る。 この年齢は、地殻に対してウランの壊変から得たそれとほぼ同一である。これは、種々の理由から、理論の妥当性に対して疑を起したひとつの 逆説的結果である。"

１９.３ 空間曲率非０の解

z + 2GG" +G'^2= 0 ...(5d)

t を G の関数と考え u= G'= 1/t', G"= (1/t')'(1/t')=u'u (ここで t, u の'はGによる微分)。z + 2 uu'G +u^2 = 0 または、z + (Gu^2)'= 0 (ここで ' はGによる微分である)。これをGで積分し、zG + u^2G = G0 (G0は正の定数)ゆえに、

(dG/dt)^2= u^2 = (G0-zG)/G ... (5h)

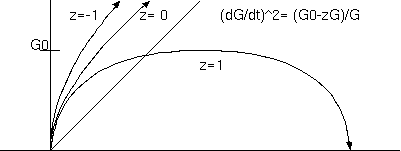
(5h)から、曲率が正 (z= 1) のときは、(dG/dt)^2= (G0-G)/G という、サイクロイドの微分方程式になる。曲率が0のときは、 (dG/dt)^2= G0/G から(*)、G= a t^(2/3), a= (9/4 G0)^(1/3)。宇宙年齢は、t= 2/3 (G/G')、ハッブル定数の逆数の 2/3 である。

曲率が負 (z= -1) のとき (dG/dt)^2= (G0+G)/G、Gは 0〜∞まで単調増加である。その中の ρ= 0 の極限は、(dG/dt)^2= 1、 曲率が消滅しユークリッド的、直線膨張に変わる。

(*) ((dG/dt)^2= G0/G は、dG/dt= a/√Gを変数分離し、√G dG= a dt、2/3 G^(3/2) = at + b、G= (3/2(at+b))^(2/3)+ c、 t=0 で G=0, t=1 で G=1 を使えば G= t^(2/3)である。)

ρとGの関係は、質量が保存されるなら ρ∝ G^-3 であるが、(G"= -1/6κρG は、G"∝-1/6κG^-2となる。) 宇宙論の場合、重力場の エネルギーは、質量と比較できるほど大きいため、そうとは限らないと思う。クリエーション場など無くても、空間が拡がっても薄まらない 斥力項がある場合のインフレーションではρ一定の膨脹すら考えることができる。

熱力学の断熱膨脹は、密集でエネルギーが高く、気体は、圧縮するのに仕事が必要である。ところが、重力による密集では逆に密集が エネルギーが低い状態であり、密集することによって仕事をさせることができる。断熱膨脹では粒子が稀薄になるだけで温度が下がるが、 それは粒子が外部壁に仕事をするからであった。物体がポテンシャルの高い場所に進むとき速度を失い粒子温度が下がる。これは、 ポテンシャルの空間的傾斜に仕事をしたのである。宇宙膨張では空間的な外部がないので外部壁はない、(ド・ジッター宇宙でないから) ポテンシャルの空間的傾斜もない。その体積だけが増大するとき温度と質量はどうなるのか。温度が下がる理由はないようにみえるが、 一般には温度が G に反比例するとされる。

フリードマン宇宙解について、アインシュタインの不満は、一定の大きさがないこと、その短期であることも問題だった。そして、最も 困るのがどのような条件でも特異点が避けられないことだった。これについては、相対論の意味(の拙訳) の"第2版への付録ー宇宙論的問題についてー"にならぶ各章をざっとみて頂きたい。アインシュタインのこれらの問題に対する真剣さが 伝わってくる。彼は三度条件を変えてそれが避けられないことを示した。なぜそれほどまでに特異点が問題でそれを避けたいのか、現在 では誰もそれを理解しないだろう。殆どの人はそういうものと思い、暢気に神のつくりたもう宇宙には原初があるものと思うかも知れ ない。最近では物理学者が、それについて"光あれ"などという言葉を口にするのを見てしまう。しかし、「相対論の意味」を読まずに 相対論を宇宙論を知った気にならないでほしい。明らかに、アインシュタインはそういう態度ではないからである。

２１. 光の廻廊

２１.１ 赤方偏移は、宇宙膨張かドプラー効果か

もし、光の赤方偏移を空間膨張による波長の拡大で説明するなら、現在の宇宙の果てに見える過去の物体は静止し、光が飛んでいる間に 膨張して赤方偏移したのである。その場所は、近傍から宇宙の果てまで移動したのではなく、最初からその遠方にあったことになる。 これは、膨張を否定するわけではなく、その広さが最初からあったことを意味するだけであり、その点はそこから膨張して今はその２倍 近く遠くをほぼ光速で遠ざかりつつあるとしてよい。これは、また有限宇宙を否定するわけでもない。宇宙の果てより宇宙の半径が十分 大きければ、問題ない。しかしこの解釈は、フリードマン宇宙は、初速がゼロの膨張でないことから反論を受けると思う。

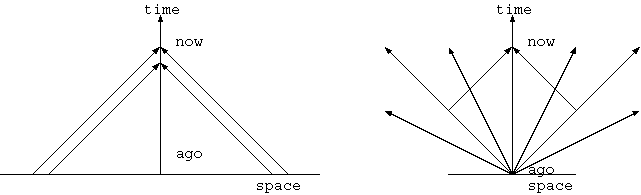
それに対して、赤方偏移をドップラー効果とし、今見える宇宙の果てがほぼ光速で遠ざかる物体のドップラー映像とするなら、もし、今 見える宇宙の果てが最初から遠方にあってほぼ光速で遠ざかっていたとするなら、ハッブル定数が、始りからの時間の逆数ではなくなり、 フリードマン宇宙(または膨張宇宙)の原則と矛盾するようだ。そこで、それらの物体がここの近傍からほぼ光速で広がり、宇宙の果てに 到達してからここまで光が届くなら、この場所の宇宙の始めの原点から広がる、膨張による事象の地平線の光円錐と、この場所の現在の 観測点に収斂する光円錐の交わる円（実は球面）が宇宙の果てであり、この場所の宇宙年齢は、宇宙の果てからの光の到達時間の 2 倍 となり、普通に言う、宇宙年齢が宇宙の果てからの光の到達時間に等しいこととは、異なる結論になる。これは、”簡単に宇宙年齢を2 倍にする方法”である(21.7, 30)。 (杉本大一郎氏は、現在の地平線が 2ct の距離にあるとするが、年齢を 2 倍にはしない。("間違いだらけの物理概念"(丸善)参照。))

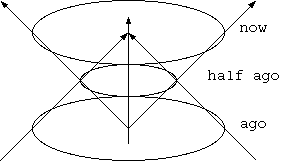
佐藤文隆氏は、宇宙膨張で時間的に見える領域が拡大し、宇宙の果てに外から物質が入り込むという説明を TV で話されたことがある。 それは、最初から遠方の宇宙が存在し、時間とともにその観測可能な領域がちょうど光速で広がるとするのだろうか。もしそうなら、 それは少なくとも彼のいわれるようにその場所が最初、この１点にあって、ある時期にはここから 数 cm にあった、というものではない と思われる。一点からの膨張では宇宙の始めから広がる光円錐領域である宇宙の果ては、時間的に変化しないからである。(直線的膨張 なら、宇宙の果てには、いつまでも同じ模様が見えているはずである。減速膨張なら外から物体が境界を越えて入ってくるかも、しかし 根拠が不明。いや、氏は単に始まりからの時刻が経てば観測空間が拡がらないといけないという意味で言われただけかもしれない。)

それらは、宇宙に光速一定を適用した宇宙と光の議論である。特殊相対論的な宇宙の像である。そこでは光は直進する。これを一度、 放棄してみよう。過去には物差しが小さく、光速が遅かったとするとどうなるか。まず、光速が宇宙の始まりからの時間に比例するとき、 光経路 x(t)を求めたい。

dx/dt= c(t)= at

距離をx、時刻をt(始0現在1)とし、光速c(t)はxの時間微分、境界条件 x(1)= 0, c(1)= -1 とすると、光の経路は、x(t)= -1/2 t^2 + 1/2 と簡単にでる。xは光の経路であって、宇宙の果てのようでもある。xとは t^2 に比例する放物線で2乗拡大する宇宙、パラボリック宇宙に なり、宇宙の果てからの光の到達時間は、直線の光の 2 倍かかる。宇宙の果ては最初から遠方にあり、見える領域が時間とともに拡大する 宇宙である。ハッブル定数は、時間に反比例し、その逆数の 2 倍が宇宙年齢になる。そして、この宇宙では光は戻らず、背景輻射がない。

次に単純な関係、宇宙のサイズ x に光速 c(t)が比例するとすると、

dx/dt= c(t)= ax

宇宙が一定の比率だけ拡大するのに一定の時間がかかり、宇宙は、無限の過去からの指数拡大のインフレーションになる。ハッブル定数は、 文字どうり、時間的定数である。いつ見ても宇宙は同じように膨張している定常膨張宇宙である。この宇宙も光が戻らず背景輻射がない。 両者とも宇宙の年齢を延ばすが、まだまだ粗雑で、これを宇宙とはいえないだろう。これらは、光速が大きい理由を宇宙年齢に比例させ、 宇宙のサイズに比例させただけで、微分方程式に仮定する c(t)= at, c(t)= ax の物理的根拠や現実性が見えないからである。

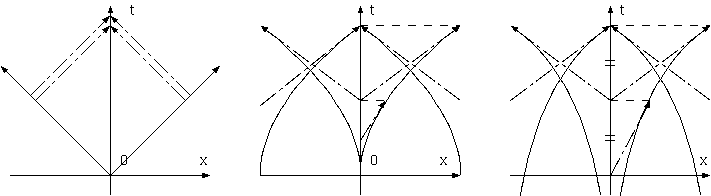
(*) 前の20章のように、光が飛んでいる間に波長を伸ばすのは、宇宙の塵を結んだ膨張する各点を静止とする共動座標でのことで、 通常の物差しの変化しない座標系に変換するとドップラー効果になるだけの話だという説明がある。 "Interpretation of the cosmological metric" http://arxiv.org/abs/0803.2701

２１.２ ゴム膜の上の虫

しかしこの描像は、膨張するゴム風船上を虫が這うのとは、まだ異なっている。相対論 FAQ のいう、”２匹の虫が同じところから時間 をおいて同じ方向に出発すると、その間隔が時間とともに広がる”という性質がない。（FAQ によると、これが宇宙の膨張による光の 赤方偏移であり、ドップラー効果による説明は、その１次近似という。この説明も訳の分からないもので、光の膨張とドップラー効果 は採る座標系が違うという説明が必要だったのだが。）つまり、この虫の這うイメージは、光速一定でなく、光速が光の媒体に対して 一定である。これを図示したのが下図の右(b)である。遠方の光速は媒体の広がる速度が差し引かれ遅い。近傍で45度 の傾きになるためには、虫のスタート時点は、昔に遡る必要がある。

しかし、光速度が媒体に対して一定というのは、特殊相対論以前の光である。どの観測系から見ても光速一定というのが特殊相対論であ り系の中で光速を時空の関数とするのが一般相対論である。光エーテルの復活がこの膨張宇宙論に本当に必要かどうかは、疑問である。 そうすると系によって光速が違い、局所においても特殊相対論が成立しないように思うが、それでよいのかどうか。FAQの答えを書かれた かたは、マイケルソン・モーリー実験をどう解釈し直すのだろうかと、腑に落ちない。

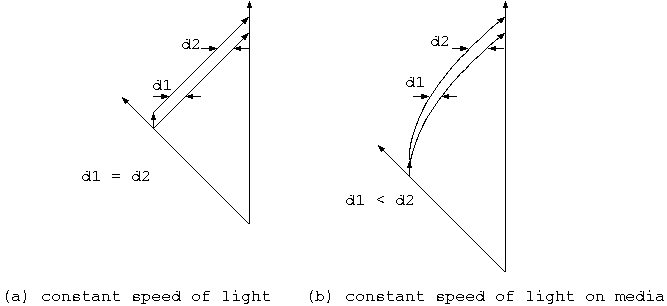
FAQ に従って、宇宙の果ての光の出発時点は、更に古い可能性がでる。風船上の虫の光の経路は、現在のこの場所を (x、t)= (0, t0)とし、 距離 x に比例する空間膨張で光速が低下するような、光エーテルを考えてみよう、

c(t)= dx/dt= x - 1

とする微分方程式は、

x(t)= 1 - exp(t-t0), c(t)= -exp(t-t0)

光の経路は、下図になる。距離 1 からの光の到達には、無限の時間がかかり、宇宙の始まりからある程度膨張してから虫(光)がスタート したとしても、どの程度過去からの光か特定できない図になる。しかしこれは、距離による光速低下を固定した定常的な空間構造であり、 膨脹宇宙とは、まだかなり違う。

２１.３ 光エーテルの復活

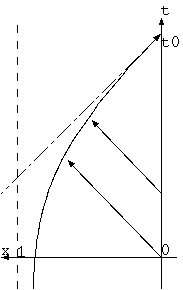
x/t

によるものである。なぜなら、原点から初速vを保存して発散する点の座標 x は、x_i = v_i t であるから、v_i= x_i/t (i= 1,2,3))。 膨脹宇宙の各点の位置 x で速度が決まるのではなく、x/t でその速度が決まるとする。光速 c(t) を媒質速度 x/t - 1 として、

c(t)= dx/dt= x/t - 1

この微分方程式は (u= x/t とおき、dx= u dt + t du を、dx= (u - 1)dt へ代入。du= -dt/t から、u= -log|t|+C、x= -t(log|t|+C)。 x(1)= 0 から、C= 0)、

x(t)= - t log |t|

という解をもつ(下図)。

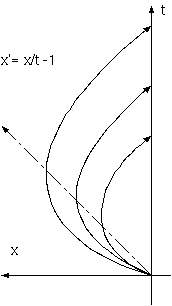
光は、ぐるりと曲って来る。光線は、原点(t,x)= (0,0)から発し、広がってまたもとの位置、x= 0 の t 軸に戻る。これが我々が見る光 である。宇宙の果てと見ているものは、この場所の、どこの場所でもある原点の光である。光は、一度その宇宙の果てより外側まで行って、 外側から地平線を越えて入ってきて、そのあと原点に帰って来る。光は、この曲線上の途中から発生してもよい。それは、最初からの光 と重なってくるだろう。

宇宙の果てに x(t)= t という地平線があり、その外側は媒質速度が光速以上であり、粒子はこちらに向かえない。それらの粒子からの 光は、最初しばらくは、こちらに向いたまま、向うに進むことになる。x= t では、媒質速度がちょうど光速を打ち消し、ここからみる 光速は 0 となる。すべての光の曲線の頂点は、x= t に乗っている。地平線を光が通過するのは、地平線が粒子的地平線であり、粒子は それを越えられないが、光にとっては違うからである。光はそこにしばし止まり、地平線が光速で逃げ過ぎるのを待って、こちらに向か い始める。宇宙の果ては、現在の 1/e の時刻の t= x= 1/e の大きさである。

この光の経路は、現代の膨脹宇宙の考え方に最も近いようだが、このモデルは単純に宇宙の各点は一点から直線的に膨脹するとするニュ ートン的な膨脹宇宙である。x/t の 1 以上、光速以上の膨脹も最初から存在する。粒子的領域は地平線を越えては来ないが特異な原点 以外では一度も関係のない光が地平線から入ってくるため地平線問題が存在する。この宇宙モデルも、現代的な膨脹宇宙に近く、その 問題点も備えているようだ。

宇宙の果てと宇宙年齢の関係がこのモデルでは、明確である。宇宙年齢を150億年としてその 1/e (e=2.71828182..)、宇宙の果ては約50数 億光年先でしかない。 光は、少なくともそれよりも近いどこかで発したのである。その地平線は、今はさらに遠くに膨脹し、ちょうど150億光年先にある。しかし、 もし、宇宙の果ての地平線が 150 億光年先なら、今は宇宙年齢 400 億年であり、現在の地平線は、400億光年さきになる。 これは ”簡単に宇宙年齢を e 倍にする方法”である。ハッブル定数(速度/距離)の示すのはどちらなのだろうか。距離の推定が正しければ、 それは宇宙の果てが 150 億光年であり、宇宙年齢に関する推定が正しいならそれは宇宙年齢が150億年である。宇宙の果ての距離と宇宙年齢 に同一の数字を使うのは、何か考えがあるのだろうか。球状星雲の年齢などから、宇宙年齢〜150億年のほうが正しい。距離を宇宙の果て まで明確にいう方法はない。この2倍やe倍の関係は、私はまだ聞いたことがないが、私は間違ったのだろうか。頂点の最大距離を目でみる方法 はないし、曲がる光(方向と速度の変わる光)には、光速*時間=距離の関係はないだろう。

２１.４ 曲る光のハッブル定数

光経路上で、速度 x/t と距離 x は、現在から昔に遡ると、地平線までは線形ではないが単調な対応で、速度と距離はともに上昇する。しかし、 地平線は x の最大点であり、そこから外側では、t→0 で x→0、x/t= -ln|t|+C →∞ であり、距離は下がり速度は増えるので、ハッブル定数 は、地平線付近からさらに増加する。このハッブル定数の遡及による変動は、光線経路に沿うための見掛の変動であり、膨脹の時間的変動ではない。

もしも、現在の近傍でハッブル定数を正しく求められるなら、その逆数は正確な現在の宇宙年齢を示すだろう。しかし、銀河の固有運動のために 赤方偏移は、近傍では正確でなく、遠方ほど精度が向上するという性質をもつ。一方、距離の測定は、事情が逆で、セファイドの周期、Ia型超 新星の明るさ等、絶対等級を知る道具は、当然、それが見える範囲しか測定できない。そこで、できるだけ光度の大きい標準光源によって、 遠方まで測定する。そのため距離と速度の両者を使うハッブル定数は、適当な距離で固有運動を超える赤方偏移が明確に存在するほど遠く、 距離推定の方法と組み合わせられるほど近い必要がある。

ハッブル定数は、赤方偏移と距離の一定の関係として、それが測定できる距離よりも、さらに遠方に適用できると考えられた。しかし、深宇宙の 赤方偏移までハッブル定数が使えるという自信は、多くの天文学者は持たない。大規模構造の考え方では、数十億光年まで距離と赤方偏移の線形 関係が成立すると考えているようであるが。

例えば、見えている光が過去であることを全く考慮しないハッブル定数(点線)と、宇宙の果てから直線的に来る光のモデル(一点鎖線)と、この モデル(実線)との 3 者はどれほど違うかを考えよう。見えているものを現在とするハッブル定数は、現在 t0= 1 とすると H= 1/t0= 1 であり、 速度は距離に比例する(v= x)。宇宙の果てからの 45度の光経路(光速一定)では、時刻 t= 1-x の過去の期間を測定する。v= x/t= x/(1-x) は、 x に比例するよりも遠方で大きい。

さらに、曲った経路モデルは、もっと過去の大きなハッブル定数を測定する。ハッブル定数が 1/t であること、H= v/x = 1/t は変わらないから、 この空間(点線)測定に比べ、45 度直線光モデル(一点鎖線)は、地平線までの遠方で 2 倍まで大きなハッブル定数、そして、この曲った経路の モデル(実線)は、e (=2.71828182..)倍まで大きなハッブル定数を測定することになる。

もし、現実がこの曲線モデルであって、それを空間方向の測定とか宇宙の果てからの直線光、と誤認するなら、ハッブル定数の測定値は、実際 より大きく(宇宙年齢を実際より短く)誤認することになる。これの補正は、宇宙年齢の矛盾を多少とも緩和する方向である。

２１.５ 遠方のハッブル定数

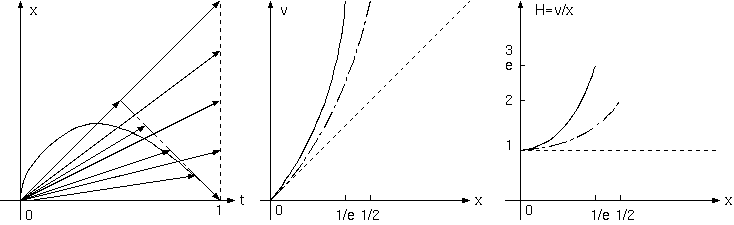
ハッブル定数の逆数は、距離を速度で割った時間を表し、それは、膨張を始めてからの時間、宇宙年齢である。そのため過去のハッブル 定数は、現在より大きかった。ハッブルの "定数" は、時間の関数であり、はるかな深宇宙では速度が距離に比例しない。それは、単純 な理由である。速度 v と距離 x の比であるハッブル定数は、見られる側の時空点の(過去の)時刻 t に関係し、みる側の(現在の) 時刻 1 ではないからである。

ここから遠方まで宇宙が膨張した遠方をみることは、過去の遠方からここまで光が戻ってくることである。光が -45 度の x= 1-t の経路 をやって来るとする直線光モデル(前項の図の一点鎖線)では、遠方銀河の距離 x と速度 v をプロットすれば直線から外れていく。 時空の各点で、x= vt の直線的膨張をするとき、過去の光円錐上 (x= 1-t) では、速度 v、x、t、H は互いに次のように表せる。

時刻 t= 1-x = 1/(v+1)

距離は、x= 1-t = v/(v+1)、

速度は、v= x/(1-x)= (1-t)/t。

ハッブル定数は、H= v/x = v+1 = 1/t = 1/(1-x)

直線の光では地平線の無限大の赤方偏移 v= 1 は、t= x= 1/2 にある。このとき、速度 v と特殊相対論のドップラー効果の赤方偏移(1+z) には、v= ((z+1)^2-1)/((z+1)^2+1)と、1+z= √((1+v)/(1-v))の関係がある。

2006年6/28、ビッグバン(放送大学 進化する宇宙('05)) (杉山直氏) は、ハッブルの測定した距離の 100 倍(z= 1、赤方偏移による波長の 延びが (z+1)= 2倍、v/c= 0.6)程度の距離まで直線に乗ることを強調し、"ハッブルは正しかった" と発言をされたが、(この言葉は2重に 間違って元に戻っている。そもそも1929年のハッブルは、赤方偏移が距離の2乗に比例するド・ジッター宇宙を意図していた。その後も彼は、 宇宙膨張説、後退仮説を取らなかった。) ここでの話は、もっと遠方で直線から外れるという話である。時刻の逆数であるハッブル定数は遠方ほど大きい。この要素を無視すると、 直線膨張であっても過去ほど膨張が激しいという見かけの減速膨張を見てしまう。また、距離 x= v/(v+1) は、x= v より小さいので遠方 銀河が明るくなる方向である。

これは z= 1 程度までの測定で、遠方銀河が暗すぎるという方向の観測と、過去に速度が小さかったとして宇宙項の存在による解釈がなさ れることとは、整合しない。(銀河の M/L 比からは遠方が逆に明るいという結果もある) 逆に、遠方まで厳密に ハッブルの法則が成り立つためには、次の(1)〜(4) のいずれかであればよい。

(1) 光速が無限大で光は即時に来ている。遠方も t= 1 ならハッブル定数は 1 になるが、光速の有限性が確認されて数百年もたつ。光速は 高い精度で測定されてきたから、この説は除外してよいだろう。

(2) 光速が有限かつ一定で、観測がすべて過去の光円錐であること x= 1-t を認め、その上で距離 x に比例する速度 v (x= v) を仮定すると、 v= 1-t、速度が時間だけの関数となる。距離に比例するように見えた後退速度 v は、実は、時刻 t だけによって変化していて、宇宙全体が 一様に最初光速で後退し、それから宇宙年齢によって後退速度は線形に減退し、現在 0 である。これは、時間加速説に近い。

(3) 遠方までハッブル定数が一定 (v= Hx が H= 1) を満たし、dx/dt= v - 1 なる光エーテル速度場の光経路は、v を x で置き換えた dx/dt= x - 1 という微分方程式(境界条件 t= 1 で x= 0, x'= -1)から x(t)= 1 - exp(t-1) であり、 21.2 に図示 した指数的経路である。光の経路が指数的な宇宙では、光が出発点に戻らないから背景輻射が存在しない。ハッブル定数は、文字どおり時 間的定数であり、宇宙の年齢との関係はない。

(4) 共動座標の計量 ds^2= dt^2 - a(t)^2 dx^2 を認め、a(t)= t (直線的膨張) であるなら、光経路xの微分である光速は dx/dt= -1/t から光経路は、x= -log(t) になり、外に曲がる(光が直線よりも遠方から来る)曲線だが、a(t)dx を dx' に置き換え ds^2= dt^2 - dx'^2 の計量に移る宇宙的座標変換をすると、光経路 x に t が掛かり、x'= xt に、光エーテル論が導く経路と全く同じ光経路 x'= - t log(t) になる。媒体速度は、v= x'/t = a(t)x/t = x、速度は距離に比例し、ハッブル定数は宇宙の果てまで定数である。しかし、v= x になるのは、 a(t)= t の直線膨張だけであり減速膨張ではできない。(間違いのようだ。v = x' でないとハッブル定数が定数ではないようだ。)

２１.６ 局所慣性系と速度をもった場

光源の速度が光速に加算されないことは、色々な光源からの光も、遠方からの光も局所で同等であるという必要があったからであった。 光の遠方での速度は、それほどは重要ではなく、それを統一する必要はないとする考えかたがあるのも事実である。それなら、光は遠方 では、光源ではないが光の媒体の速度が光速に加算されるとするのは、正しいことだろうか。これは、正しいとも間違っているとも実証 されていない。遠方では、光速一定は実証されていないとすべきだろう。

いや逆に、場所によって速度なしに時計の進みの違うことが実証されているといった方がよい。時間の進みが異なれば、光速も違って当 然である。しかし基本的にエーテルの存在が無意味になった後で、同じような空間に属性を持たせるものは、局所においても光は媒質に 対して速度をもつとする考えを復活するのではないか。そうすると、特殊相対論は、根拠を失い、その損失は大きい。これは、大きさの 違いではない。局所と宇宙に違う法則が働くこと自体が疑問である。天体と地上が同じ法則で動くことをニュートンは見出したのである。

アインシュタインは、"エーテルと相対論"で、この新しい(計量)エーテルについて、速度の概念はこれには 適用できないといった。宇宙膨脹では、計量(メトリックテンソル) g_ik の場に速度の概念を適用したことにおいて、"我々はただ、動き の状態をエーテルに帰属させることから自らを防御しなければならない。" という彼の考えから逸脱し、誤りを発展させたのかもしれない。

２１.７ 閑話休題

宇宙の果てからの直進光、この宇宙の果ては、原点から時間が経っていないこと：
宇宙の果ては原点から光の速度に近い速度で飛び去っている。その場所は、宇宙の始まりの時刻を止めている。だからそこに至る時間を 考えなくてもよい。という反論。特殊相対論を膨脹宇宙に適用しようとするのは、めずらしく貴重である。しかし、光の速度に近い速度 で移動する物体は歳をとらないが、それをみる我々が歳をとるのである。原点から宇宙の果てまで物体が移動するのに必要な宇宙年齢の 1/2 の時間は、宇宙の中心から眺めるこちら側に存在する経過時間である。 (特殊相対論には同時刻が定義できる。A-B-Aと光を往復させ て、Bで光が反射する時刻と同時刻なのは、光がAを出てからAに帰るまでの中央の時刻とする。宇宙の果てと同時刻になるのは、ここの宇 宙年齢の 1/2 の時刻である。*)

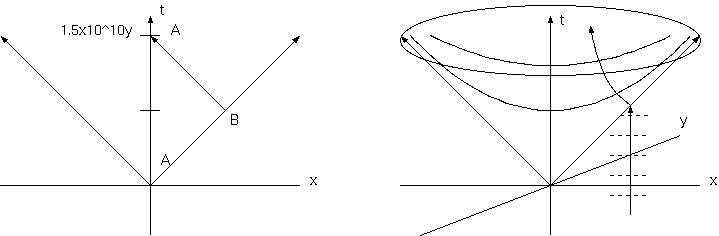
膨脹宇宙の泡の中では、空間は双曲面をしている。泡の中の空間は無限ということについて：
1999 年の 4 月の日経サイエンス、佐藤勝彦氏訳の Martin.A.Bucher、David.N.Spergel の "Infration in Low-Density Universe" は、 新しいインフレーション理論、オープン・インフレーションの考えを紹介している。その中で、擬真空から眞の真空に変る、２段階目の インフレーションを行う、光速で膨脹する泡の中の空間が無限という話である。泡の膨脹開始時点からの経過時間は、膨脹の円錐に そって時間が経たないから、同じ経過時間を結んだ双曲面が空間になる。それは、無限の広さをもつ負の曲率の空間になるという。

これは、宇宙の果ての特殊相対論的な議論と解釈でき、不思議な感動を与える。膨脹宇宙の周辺での宇宙膨脹からの局所経過時間をτとする。 v= x/t, γ=1/√(1-v^2), τ= t/γ= t√(1-v^2) = √(t^2-x^2), τ^2= t^2 - x^2 から、 局所経過時間τ一定をむすんだ超曲面は、負の曲率の双曲面をなし無限の広さをもつ。

過去の閉ざされた方向には現実に地平線があったように見えても、実際的に空間が無限というのは、光に近い速度で飛んでも 空間に限界や周期性をもたないことである。この未来の方角への光線は、膨脹宇宙では、もとより無限であった。 原点から同時刻を結んだ双曲面が無限空間とは、どういう意味があるのかは難しい。その意味を体験できるのだろうか。 ここで真直と考えている座標軸は、遠方では膨脹宇宙の円錐に沿って曲っているかもしれない。 内部の時間は外からその泡に入ってからの経過時間であり、外からみると各時点で有限の泡であり、外から入ることができるが、 出ることができないというから、少なくとも、光エーテルによる曲った光のモデルではないようだ。

２１.８ 閑話休題つづき

この泡、光速で広がる暗い泡を爆発させてビッグバンを体験させるというこの最終兵器が原理的にも可能でないことを祈る。 この描像は、少し怖いことかもしれない。この宇宙が 2 度目のビッグバンというのだろうか。それは、実証可能な仮説だろうか。 外から入ってきた物質が短期間の高温を経験して生き残れるのだったら、それは、実証可能である。ビッグバン以前の物質の存在が その実証になる。そして、もし実証されたなら、このビッグバンは、自然現象だったかもしれないが、誰かの最終兵器だったかも しれないことになる。人工的なビッグバンは、作った本人もその場から逃げ出すことができないから、兵器というよりは、宇宙の近隣を 光速で拡大しながら破壊する自爆装置である。それは、宇宙の殆んどすべてを捨て周りの迷惑を顧みない自暴自棄も極端な話である。 そこから宇宙は真っ新の様相で始まるのである。人類は、単細胞生物を 30 億年経験し、多細胞になって 6 億年にしかならない。 みずからそこまでの破壊を受けたと理解することはまずないだろう。そういうひとときの幻想を導く話である。

速度 v= x/t で移動する宇宙の周辺の経過時間τの1/γの短縮の比率は、周辺宇宙の奥行のローレンツ短縮の比率と同じである。 その逆数γを距離 x にある間隔 dx に掛算して積分すると、∫γdx= ∫1/√(1-(x/t)^2) dx= ∫t/√(t^2-x^2) dx これは x＜t では、 arc tanh(x/t)= 1/2 ln((t+x)/(t-x)) であり、t が x に近づくとどこまでも大きくなる。 これが、特殊相対論的膨脹宇宙の周辺短縮、宇宙の果てに無限の物体が薄くなって畳み込まれているという描像である。

２１.９ フリードマン解の空間曲率０のときの光エーテル的回帰について

dx/dt= c(t)= rx/t - 1

x'= rx/t - 1 を解くには u= x/t とおくと、もとの式は、x'= ru - 1、dx/dt= ru-1、 dx= (ru-1)dt、になり、 x= ut、dx= udt + tdu をつかうと (ru-1)dt= udt + tdu、変数分離し、 ((r-1)u-1) dt = t du、dt/t= du/((r-1)u-1)、ln|t|= 1/(r-1) ln|u- 1/(r-1)|+c、 u= c t^(r-1) - 1/(1-r)、x= ut= ct^r - t/(1-r)、これは、すでに x(0)= 0 をみたす。x(1)=0 から c= 1/(1-r)。

x= 1/(1-r) (t^r - t)、

時間微分、x'= r/(1-r) t^(r-1) - 1/(1-r) は、 x'(1)= -1 をみたす。 r= 2/3 では、x= ct^(2/3) - 3 t、x(1)=0 から c= 3 をいれ、光経路は、

x= 3(t^(2/3) - t)

時間微分は、x'= 2 t^(-1/3) - 3 となる。

地平線で光が止まる光の頂点は、dx/dt= 0 から、x/t= 1/r をつかい、t^(-1/3)= 3/2, t= (2/3)^3 となる。x= 3(t^(2/3) - t) に代入すれば、佐藤文隆の"ビッグバン"での "膨脹因子 a(t)= 4/9 での引き返し" という説明と一致する。

２１.１０ ブルータス、...

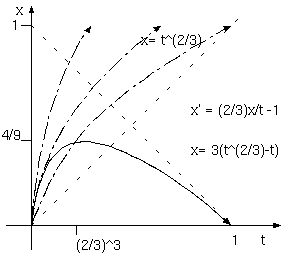
"量子と実在"、ニック・ハーバート著、はやし・はじめ訳、白揚社 p.23からの引用。

"イギリスの指導的物理学者、かの高名なウイリアム・トムソンのちのケルビン卿が、マイケルソン・モーリーの実験の数年後に語った 次の言葉は、物理学者の一般的な態度を示すものであった。 "私たちにとって確実なことが一つある。それは、光エーテルの実在性と 物質性(substantiality)である。""

この言葉は、当時の学者にどれだけ先見性がなかったかを示す逸話であるが、これが膨脹宇宙論では文字通りの復活を果している。

２１.１１ 曲って戻る光？

曲って戻る光は、空間的な曲がりではない、時間と距離の図での曲がりは、速度変化である。石を真上に投げ上げ、真直に落ちてくるように、 時間軸を横に取った図の曲線は、対称的な抛物線とちがい、登りよりも墜ち方が緩やかである。向うへ進んでいた光がこちらに向かいだす、 方向転換かともとおもうと、それも方向転換ではなく、光速より速い物体からのこちら(内側)向きの光が、しばらくは向うに引っ張っていかれて いたのが、空間(?)が光速以下になると、こちらに向かい出すのである。

この光の引き返し現象は、本当にあるのだろうか。例えば、ニュートリノに質量があれば、それを追い越す系があるから、右巻き左巻きのスピンの ２種類ができると習った。光だけは、系が追い越せないものだった。系とは、特殊相対論で速度の違う慣性系の意味である。異なる場所に行くこと を、系を次々乗り替えるというのは、まるで速度をもった慣性系がその空間に所属してるようだが、 系の乗り換えであるから、粒子は、遠方に行っても加速されるわけではないようだ(*)。

光は、系に対する速度を変えず、エネルギーと運動量を波長を延ばして下げる。それがどこまで下がっても、到達するというのは、どうしてだろう。 ブラックホールの事象の地平線のように、光が越えられない境界でないのはなぜだろうか。それは、どこでも系に対する速度が光速という仮定 だから、少なくとも少しは系を乗り換えて、何とかはい上がってやって来ることができる、ということだろうか。 ブラックホールの事象の地平線の内部から外に向かった光が引き返すのと、仕組はどう違っているのか。

粒子がその場所に行っても系の乗り換えだから加速されないなら、宇宙膨脹の中で、ある場所から光速に近い速度で飛びだした宇宙船は、 周囲との相対速度を徐々に落し、そのうち停止するということのようだ。粒子は、停止してしまうとそのあとは、系を乗り換えられない。 なぜなら、停止しているからである。その場に停止したままである。これでは、まるで速度に比例する抵抗のようだ。 粒子の性質がそれなら、もし、ニュートリノに質量があるなら、粒子の地平線を越えられず、光の背景輻射はあっても、 それ以前のニュートリノの背景輻射は存在しないということか。

(*) 測地線の物理にあるように加速の項は存在する(2017 6/8)。

２１.１２ g_ik からの光速を使うと

光速は、g_ik 自体から計算できる。膨脹宇宙の各時点の g_ik から、各時点の光速を使えば、光エーテル的描像よりもましな方法で、 曲った経路の光が計算できるかもしれない。それが同じ結果になるか調べる必要がある。そう思って、やってみると全く逆の結果になった。

ds^2= dt^2 - (GA)^2 (dx^2+dy^2+dz^2)

フリードマン宇宙の計量の式に空間的間隔 dl= √(dx^2+dy^2+dz^2)を使い、ds=0 をいれると、dl/dt= 1/(GA) が光速。 空間的曲率が 0 のとき、G の従う微分方程式、(dG/dt)^2= G0/G から、G∝ t^(2/3) である。 光速は、c(t)= t^(-2/3) とすると t= 1 で c(t)= 1 を満たす。光速 c(t) から光の経路 x(t) の求出は、単純に dx/dt= -c(t)= -t^(-2/3)、 x(t)= -3t^(1/3) + C である(C は任意定数)。 光が現在この場所に来ていること x(1)= 0 を使い、

x(t) = 3(1 - t^(1/3))

となる。この光の経路は、45度の線に見える距離の 3 倍の距離から来る逆方向に曲った光の経路である(下図)。この光の経路は、フリードマン宇宙の 計量の時間変化、G の増大を字義どおり使用し、光速の時間的変化としたもので、宇宙膨脹という解釈を必要としないし、物差の縮小という 解釈もいらない。なにより光エーテルを使用しない。しかし、膨張宇宙的結論とは、全く違う結果になっている(*)。 この経路は、直線的な距離よりも遠い所から来ているため、光の減衰が多くなる現象を説明することができるかもしれない。

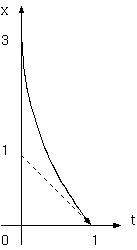
(*) 物差しの縮小の解釈には合致している。光速が昔大きかったから、光は、光速一定の場合の距離より 3 倍遠方から来る。 当時の物差しで測れば違うが、それは計量変化を無視する系である。

２１.１３ 場と速さ

ある時空点の g_ik 場を速度をもった系だとするのは、電磁気で力線を物質的実在とみて、電磁場の速度を考えるのと同様に、 怪しい方法であろう。ある系で磁力線があって、それを速度 v で横切る電荷の系では、磁力線が速度 -v で横切っているとみるわけではない。 電荷は電場を見ているのである。電磁場は観測系によって変換されるから、場の速度とは、一種、混乱した概念である。 g_ik 場も観測系によって異なるから、それに速度を与えるのは同様の問題がある。 電磁場が系によってローレンツ変換されるように、g_ik もローレンツ変換される訳ではない。 g_ik は変換方法を表す不変式の係数である。 しかも、局所慣性系では、g_ik は、g_00= 1, g_11= g_22= g_33= -1 というミンコフスキー時空の標準値である。

物質の移動は、光円錐の中だけで、光の移動ですらこのように制限されるという光円錐を、曲がる光の膨張宇宙に書き込めば、 次のようになる(下図)。それらの光円錐は、媒体の速度によって、吹き流しのように、色んな方向を向いている。 時空点に、小さな光円錐を描くのはすべて、一般相対論の光エーテル的理解であるといって良いのかもしれない。

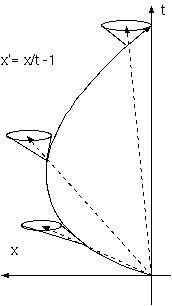
ある時空点を通過する光は、均一でどこから来た光も等しい性質をもつ。その時空点の全ての局所慣性系は、その光とは光速の関係にあるが、 互いに光速までの全ての速度をもつ。それゆえ、その系の速度をその点の光の速度(これを遠方から知ることができるとして、)から光速を 引いて与えることはできない。その時空点に唯一の速度を与え、その時空点の標準的な静止系を設定するのは、特殊相対論的に誤りである。 (それは、その時空点の全ての局所慣性系は、大きな速度の可変性があるのに、唯一であること、この見方では全ての局所慣性系からみて光速一定 は成立できないだろうと思われる点である。)

光エーテルを認めるなら、特殊相対論を否定することになり、マイケルソン・モーリー実験を説明できなくなり、物理は一からやり直しになる。 2種類の曲がった光経路の光エーテル的描像、dx/dt= rx/t - 1 (r= 1, 2/3) では、ある時空点の光速を、その時空点の媒体速度 rx/t と 光速 1 の差で与えている。光速 1 は、この場所からみた光速をそのまま、遠方の局所に適用している。 順序としては、媒体速度を先に与え、光の経路がそのあとに求まる。

そうではなく、遠方過去の光速を g_ik 自体から先に与え、光経路を求めたのが、dx/dt= -c(t)= -t^(-2/3)、x(t)= 3(1 - t^(1/3))である。 それは、全く反対の性質の光経路になる。より遠方の空間からの光の経路にみえる。しかし、これが宇宙の膨張や収縮を表している訳ではない。 光エーテル的概念では、光経路 x(t) があると媒体速度は、dx/dt + 1 になるが、光経路 x(t) の微分 dx/dt に先与の光速 c(t) を加算した 媒体速度 dx/dt + c(t) は常に 0 である。局所光速は 1 だが、ここから見るその時空点の光速は 1 ではなく、計量から直接に求まる。

２１.１４ 背景輻射自体、存在できるのか

光が曲って戻って来ているとするとき、最遠の距離は、宇宙年齢の 1/2 の距離よりも短い。直線的膨張 x= vt において光の経路は、 x= -t ln|t| であり、dx/dt= 0 の時刻と距離は、1/e である。これは、50.4 億光年になる。減速膨張 x= t^2/3 では、光の経路は、 x= 3(t^(2/3) - t) となり、光が曲る頂点は、t= 8/27, x= 4/9 である。137億年にいれると 60.89 億光年の場所になる。

最初光は、光速より速い後退場所からこちら向きに出て、こちらに向かっても向うに進んでいて、あるとき速度を失いこちらに向かい出す。 虫が膨張する風船の上を進むように光が媒体に対して速度をもち、媒体が x/t の速度をもつという考えは、特殊相対論以前の 光エーテル論 である。物質は光速に制限されても慣性系は光速に制限されないという考え方は、光を追い越す系を容易に設定する。その系からみると 光が逆進するということさえ使っている。光の運動量が系によって逆転するためには、光速の系から見た止まった光のエネルギーが 非ゼロでないといけない。この考え方はほとんど無謀な、特殊相対論の成果のすべてを放棄する試みである。ここからみると遠方の光の 速度は、一度止まりこちらに向かう、その地平線の近傍の系からみると問題がないが、ここからみたその停止した光とは一体、何だろうか。

特殊相対論的にみれば、この光の経路の頂点 x/t= 1 (又は x/t= 3/2)は、現在の我々から光速で飛び去っていた場所であり、そこからの ドップラー効果が無限大である。光速にどこまでも近い場所では時間経過がなく、そこよりも先からの光は、来ることができない。 光の経路は、(一般相対論で仮に曲ったとしても、) そこで途切れその先を考えることができない。その外からは光だけでなく全ての影響 のない因果の地平線である。その場所に僅かな質量でも存在させるのには無限大のエネルギーが必要であるから、それは仮に有限宇宙 とすると有限の質量しかもたない宇宙全体を使っても不可能なことであり、有限宇宙には存在しえないなにかの幻影であろうといえる。

重要なことは、現在の 1/1000 程度の時刻の晴れ上がり時点の背景輻射が見えるためには、原点近辺の光が戻ることが必要なことである。

２１.１５ 光の廻廊

そのような計量の場所の例として、例えば、ブラックホールの事象の地平面がある。ブラックホールの半径方向の計量は、∞になり、 時間方向の計量は 0 になる。そこでは、半径方向の物差しは長さが 0 になり、時間の経過は無限に遅くなり、光速度が 0 になる。 しかし注意すべきは、光がそこで方向転換はしないことである。光が方向転換をする計量とは一体あり得るのだろうか。 全くないのでないか、そのために必要なことは何か、について考える。

その時点以前とその時点以降で時間の経ちかたが逆転すること。その場合、その時刻で時間軸が折れ曲がる必要があり、 一般座標変換が折れ曲がりのない滑らかな写像であるという原則を崩す。g_ik の時間微分が連続でないということになる。 また、それは、空間軸についても言え、空間軸に折れ曲がりを必要とするものも存在しないと考えてよい。 ある場所までの空間が折れ返すと、光は、そこで反射するように戻ってくるだろうが、その時空の一点において、 光の逆転を期待するのは、g_ik の微分可能性から排除できる。光がそのまま戻って来るというのは、ブラックホールの地平面が そうであるように時空の特異面であるが、それよりもさらに存在し得ない特異性を要求するのである。

折れ曲がりでなくて、光は、時空を使ってぐるっと回って来ているのであり、ある時空点による反射ではない、ということでは ないだろうか。それでは、光がぐるっと回って来るためには、その場所の時空は、計量はどうであればよいのだろうか。

２１.１６ 光が戻る計量

光円錐がそこでは、ある時刻より前では、外側に向かっていて、ある時刻ではちょうど円錐の近い側面がこちらの時間軸と平行 であって、それからすこし時間が経過すると光の円錐はこちらに向かい、光は時間空間図の上でぐるっと回って来る。それが、 膨張宇宙説の光の回廊の描像であろう。そこに必要なものは、時空のゆっくりとした傾斜だけであり、特異性は必要でないよう に考えられる。近くから発した光がある地点より先に届かないという意味では特異であるが、局所に特別なものは不要である。 そこでは、ds= 0 という光の経路は、時空間の座標変換によって、こちらの時間軸に平行であるだけである。光の進路の空間軸 と時間軸だけの2次元 (dx, dt) を考え、局所からミンコフスキー時空 (dx', dt') への変換において、

dx'= a dx + b dt
dt'= c dx + d dt

とし、変換後の ds^2 を

ds^2= dx'^2 - dt'^2

として上の変換を代入して、

ds^2= (a^2-c^2) dx^2 + 2 (ab - cd) dxdt + (b^2-d^2) dt^2

２１.１７ 光速が０になる計量

g_11= a^2 - c^2, g_14= 2(ab - cd), g_44= b^2 - d^2 である。dx,dt が 0 でなく ds^2= 0 なら光が存在すると考え、例を探す。

a = c, かつ b = d は、g_ik を恒等的に 0 とし、ds^2= g_ik dx^idx^k という不変式を成立させない。物差し、時計の存在 できない時空であるから、除外してもよいだろう。

b = d で、a != c なら、g_ik が恒等的に 0 ではなく、計量として存在し得るのではないか。g_44 = 0 であれば、光速が 0 になる。 これは、特殊相対論で慣性座標系が光速度をもつローレンツ変換に相当し、(γ= 1/√(1-v^2) を除外した疑似)ローレンツ変換、

x'= x - vt
t'= t - vx

に v= 1 をいれると

x'= x - t
t'= t - x

となり、a= 1, b= -1, c= -1, d= 1 の上の変換に相当する。それはあり得ないローレンツ変換であるが、一般の局所の変換として 何ら問題のない変換ではないか。時空の変換は場所、時間とともに徐々に滑らかに変化していって、局所の変換が光速の慣性系に 相当するローレンツ変換でもよい。しかし、 g_11= a^2 - c^2= 0 になるので、光速 √(-g_44/g_11) は 0/0 の不定であり、0 ではない。 これは、局所慣性系が光速で飛び去る時空である。そこでの時間と空間は、ミンコフスキー時空に変換後に同じものの符号違いになる。 ということは、そこには時計と物差しの区別のないものしか存在しないことを意味し、それは、この変換に対して疑いを抱くに十分である。

２１.１８ 光速が０になる計量(続き)

は、光速 u= dx/dt= 0 をもつには、b= +-d であればよい。

(a^2 - c^2) u^2 + 2 (ab - cd) u + (b^2 - d^2) = 0

は、a^2= c^2、ab != cd なら 1 次方程式、解は、u= -(b^2-d^2)/2(ab-cd)。a^2 != c^2 なら 2 次方程式、解は、 u= (cd - ab +-|bc - ad|)/(a^2 - c^2)、u= (d - b)/(a - c) 又は -(b + d)/(a + c)。u= 0 を満たす a,b,c,d は、あり得る。

v を残して、上の疑似ローレンツ変換の光速を求めると、a= 1, b= -v, c= -v, d= 1 であるから、v!= 1 では a^2 - c^2 = (1-v^2) != 0 になり、bc-ad= v^2 - 1 であるから、v＜1 では bc-ad＜0, v＞1 で bc-ad ＞0 である。u= +-|v^2-1|/(1-v^2)= +-1、 疑似ローレンツ変換の局所光速は+-1 である。v= 1 のときに光速不定。γは、v= 1 で無限大になるから、γを含めた局所ローレンツ変換、

dx'= γ(dx - v dt)
dt'= γ(dt - v dx)

は、dx' dt' の両方が無限大になる。この数学的な特異性は、ここからみた地平面にだけにある。しかし、地平面で光が反射する とはまだいえない。こちらから地平面に進んでいった光がそのまま先に行き、向うからの光がこちらに来るだけかもしれない。 光速で飛ぶ地平面を文字どうり事象の地平面とするなら、向うからなにも来ないから、光はこちらから進んで反射するか、地平面 は完全黒体面でないといけない。局所慣性系の速度になんら制限がなく、地平面は事象の地平面ではないという立場をとるなら、 光は地平面を越えて行き来する。計量の場に局所慣性系の速度を関連付ける光エーテル理論なら、地平面が飛び去る向うからの光 を受け入れるだろう。

しかしながら、この議論で抜け落ちているのは、実際のフリードマン宇宙の計量が、それを満たしているかどうかである。それは、 実に怪しい。それは例えば電磁場を自由に配置してよいなら可能なことも現実に物理的に存在を決めるマックスウエル方程式の解か どうかによって現実性をみる必要があるようにである。

２１.１９ G,A ともに逆数でないと意味をなさない

空間計量 g_11 には、G^2 A^2 という係数がかかっているが、G は時間の関数で時間とともに増大するもの A は空間の関数であり、

A= 1/(1+ zr^2/4) z= 1(球状), -1(擬球状), 0 (ユークリッド的平坦)

となっている。時間的計量 g_44 には固定的値 -1 が取られていて、それが 0 になることはない。だから、光速を 0 にするためには、 空間側の係数 g_11 が ∞ になる必要があるが、それは、A が擬球状であるときの r= 2 の場所である。そのとき空間的計量 g_ii は ∞になる。宇宙は周辺短縮し、r がそれを越えると A は符号が反転するが、A^2 しか計量にはでてこないので、問題があるわけではない。

その場合、宇宙の周辺で光速が 0 になる条件が満たされているが、それが光の廻廊になっているかどうか怪しい。むしろ、宇宙の原初 の光の回帰は、光エーテル的解釈に依る、とみるほうが理解が容易である。もともと、フリードマン宇宙の計量の式は、物差しの縮小 する式であり、宇宙膨張の式ではないから、その式をまともにとっても得るところは少ないのかもしれない。

A の球状、擬球状も逆転しているようにみえる。宇宙がある大きさの限界をもつものを球状と呼ぶのは、通常の習慣である。A の大きさに おいて限界を持つのを球状、∞にするのを擬球状としている。AとGは空間計量をその2乗に比例させ、AとGは、物差しのサイズの逆数を 意味している。G が増大するとは、空間の物差しの縮小である。A が∞になるとき(擬球状でr= 2 のとき) 周辺空間の物差しの微小化に よって空間的限界を与えるのである。それに反して、球状の場合の-∞〜∞までの∫ A dr が 2πを与えることが示されるがこれは、 物差しの大きさに積されるものであるから、G と A とともに、その逆数でないと、その意図するものにはなっていない。

そのような計量の意味の取り違えによって GA がその逆数でしかないとき、時間的関数 G がどのようになるか、例えばそれが空間的曲率 が正のとき、サイクロイドの微分方程式を与えるなどを議論してもさほどの意味のない議論である。

２２. フリードマン宇宙解の計量

２２.０ 縮小を意味する計量

g_44= -1, g_11= g_22= g_33= (GA)^2

(GA)^2 は、時間的に変化する空間的計量である。曲線の空間的グリッド、メッシュを考えるとき、空間的計量の大きいところでは メッシュ間隔が狭い。GA が小さかった過去には、空間的メッシュは大きかった。物差しは計量 g_ik の逆数の平方根、1/GA に比例するから、 過去の剛体の物差しが大きかったということになる。これは、過去の世界がすべて小さかったという、常識的イメージの逆である。 この計量の意図したと思われる常識的な膨張宇宙、過去の小さい世界では物差しも小さかったというイメージは、実際には成立しない。 物差しは過去には逆に大きかったとなると、膨張宇宙は表現しようもない。ある時刻の宇宙の空間的サイズの測度という G も、 そのまま受け取ることができない。その逆数が宇宙のサイズに比例する。G の膨脹は、実は宇宙の収縮であると私には思える。

例えば、宇宙の晴上り時期の水素原子は、宇宙のサイズが現在の 1/1000 のときのものだとするが、物差である水素原子が現在の 1000 倍に大きいということで、宇宙の膨脹を考えることはできるだろうか。それは、物差ごとに物体が収縮してきたと表現すべきことがらであり、 膨脹してきたということではない。光が空間を飛んでいる間に空間が膨脹して、光が数 1000 度の黒体放射から、2.7 度の黒体放射に変化した、 とする話は、もともと水素原子が大きかったから、波長も長かったとするならまだ理解できる。

このように、式がその意図に反する理由を理解するのは難しい。しかし、言えることは、計量の意味を本気で考える人はいなかったと いうことであろう。アインシュタインも、このフリードマン宇宙を認める際に、天文学の膨張の発見が先にあった。 観測が理論を導く流れがあるとき、理論の細部の不備は無視される。

それにもまして重要な点は、この計量を導く際、４次元空間の一様等方でなく、３次元空間の一様等方を採用し、４次元空間を球対称にとり、 時間を半径とし、３次元超球面を空間としたことである。それは、有限無境界空間を前提に入れることである。この前提では、無限空間は、 無限の未来にしかない。時間的に閉じない場合に初めて空間的無限が存在する。最初に無限の空間を置くことはできず、宇宙解を４次元球対称解 に限定する。このことは、この部分の数学的扱いを知って初めて明らかになる膨脹宇宙論の基本的思想であり、それ自体に疑いを持つ以外には 否定できない事項である。

もともと粗雑な比喩であると思っていた、ゴム風船の上の虫は比喩ではなかった。彼等は、この宇宙を脹れつつあるゴム風船であると 本気で考えているのである。時間軸が宇宙の中心からの距離なら、空間の大きさは、単調に時間の関数として決まるのが普通の答えである。 G がサイクロイド解を得たりするのは話としておかしいのではないだろうか。

２２.１ パウリの相対性理論の付録

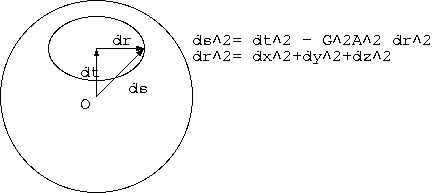
ds^2 = R(t)^2 dσ^2-(dx^4)^2, x^4 = ct

と書かれているが、アインシュタインの "相対論の意味" との重要な違いとして、 "x^1, x^2, x^3 が R(t) を単位としてその座標値を 与えることに相当(*)"しているとし、"g_44= -1 なので、光速は一定" と解説している。空間距離dσがR(t)を単位としていて、その後に R(t)^2 を掛けるから、空間距離をR(t)を単位にしないもとの単位に戻すと、

ds^2= dσ^2-(dx^4)^2 ,x^4 = ct

となり、R(t)が消え去る。R(t)が何であってもこの式がミンコフスキー空間を導くから、膨張宇宙論で光速が一定という(*)。これの意味 は普通、局所慣性系に移って光速一定であり、元の共動座標系で光速一定ではない。これを不明確に光速一定(**)とする。

問題は、グローバルに光速一定とすると宇宙膨張が一般相対論の重力方程式の解だった計量と関係を失うことである。R(t)が数学的に任意 になり、宇宙の計量的な物理的現実と関係をなくす。それは、大きさに比例する単位という考えが原因である。"空間の膨張に追随する物体 については、空間座標 x^1, x^2, x^3 は一定である。"という、空間座標を共動座標として、膨張宇宙論の計量の式を全く無効にし、R(t) が計量の式から消え去る。これは、数学的な詐術であり物理の処理とは思えない。何のためのR(t)だったのか。少なくとも、もとのフリー ドマン計量の式と異なる意味になっている(***)。

これで膨張宇宙論は、収縮する物差しという概念から解放され、ミンコフスキー空間を導くから、膨張宇宙論で光速が一定となる。これは、 膨張宇宙論の秘密であろう。そして、宇宙的な光速一定と空間の膨張という概念に遊ぶことができるのである。空間の速度、光エーテル的 な説明もこれによって正当化できる。なるほど、こういうことだったのかと納得できる。共動座標系がR(t)を空間計量にもって、dlが最初 からR(t)を単位にするなら、本来的に単位を掛けて一定である。

しかし、これはパウリの誤解かもしれない。フリードマン宇宙の膨張解の計量が、彼の言うような共動座標の意味なら、共動座標からみる と宇宙の膨張も収縮も物質の移動としては存在しない。計量の意味が物差しの縮小だけなら、共動座標からみる縮小する物差しは、もとの 座標からは、一定の物差し、共動座標での光速の縮小が、もとの座標で光速の一定となる。つまり、ミンコフスキー空間でのニュートン力 学的な物質の飛散する膨張宇宙を意味するのである。それは、一般相対論の正しい解だろうか。どのような膨張の仕方 R(t) も、もとの空 間の物差し時計に影響できないのである。これは塵と空間を分離し、R(t)は塵の運動だけを説明し、残りの空間をミンコフスキー的とする かのようである。

(*) W.パウリ "相対性理論" 内山龍雄訳、講談社、付録19宇宙論的問題(p.350)参照。共動座標系の計量 g_ii= (GA)^2 (i=1-3)を無視する 物差し一定の物理的根拠のない系で光速を一定とするのは、正しくない。実際その系では光速は一定でなく、空間を直進せず戻ってくる。 (参照)

(**) その結果、|p|R＝一定(pは質点の運動量、 p=mv/√(1-v^2/c^2)といい、R/λ＝一定(λはドブロイ波長λ= h/p)、という。さらに、光速 一定であるから、上の単位を用いると、νR＝一定、つまり、共動系で周波数がRに反比例するという。しかしこれは、g_44= -1 と合わない。 彼は系を行き来して混乱している。正しくは計量から直接に、局所で光速一定、共動で光速変動、局所と共動の両方で周波数は不変である。 これによると、共動系では運動量もエネルギーも保存しない。共動系では空間間隔が減少するから速度が減少し、エネルギーや運動量が減少 する。塵が速度0でずっと静止するのは、運動量保存ではない。塵よりもっと細かい塵が塵でないというのではなく、共動系の塵に対しての 速度だけが落ちる。まるで空間に局所系との間の抵抗があるように。そうして、誤りは混乱と謎を再生産する。局所系はエーテルのようだ。

(***) 空間計量は、局所の物差しが時空的遠方からどう計測されるかを表し、時間計量(重力ポテンシャル)は、局所の時計がどう進むかを意味していた。 局所の時計や物差しが局所で計測できないのは当然である。時計と物差しに対して速度をもった慣性系からみて起きる特殊相対論の時計の遅れと 物差しの短縮は、その系の上の時計や物差しでは決して分からない。太陽の周りを毎秒30kmで進む地球の軌道速度を自ら検出しようとしたのは、 エーテルに対する速度が計測可能と考えた相対論以前の物理の誤りであった。この慣性系に対応するのが一般相対論では一般座標系の局所の時計 と物差しである。その空間に浮いた塵の上の時計と物差しは、局所でミンコフスキー系をみて特殊相対論が局所で成立するが、時空的遠方の時計 と物差しがどうなるかを考えるのに、局所的な変換を与える不変量の式の係数である計量 g_ik を使って、計量についての重力方程式を解いて 密度一様の宇宙解の計量を求める。つまり、解は、計量でありそれ以外でない。重力方程式は、すでにミンコフスキー的でない計量を与えている。 それゆえ、空間がミンコフスキー計量であるはずがない。局所と大局を通る光は違う光ではないが、局所を通る光が時空遠方から計測して違って いるのである。光速は一定でない。

２２.２ 収縮する物差し

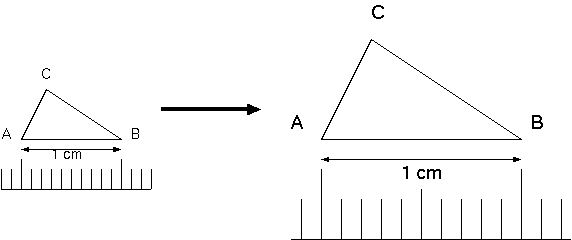
図は、膨張している三点の銀河の空間座標を書いているとしよう。その間隔 AB は、ある過去の時点に 1 cm であった(左図)。 そして、時刻が約 2 倍になり、物体の間隔が 2 倍になったが、この共動座標では、1 cm のままである(右図)。 パウリの言うように "空間の膨張に追随する物体については、空間座標 x^1, x^2, x^3 は一定である。"という、その単位が膨張する 座標系に乗っている場合、これは、物差しの縮小する宇宙と言えるかどうか、図を見て考えて頂きたい。

このような事態が起きるほどに、膨張宇宙の計量概念は、希薄である。空間的に配置され(共動座標からは)大きさの一定であるこの 3 角形以外に本当の物差しがあるわけではない。別に固定の物差しがあって、それは、一般相対論とは別の、"それより基本的な" 量子力学の法則で動くからと考えるのは、相対論の計量の解釈としては最悪である。物体のサイズを決める原子が不可解な波動関数で あっても、この座標上に現象として表れるときには時間空間の計量に支配される。この図のように、物差しである原子は、膨張すると 理解されるべきである。(それは、フリードマン宇宙の計量の式の意味するところ：物差しの縮小には反している。) そうでなければ、それは計量というものを全く誤解していることを表している。 実際の原子が、この共動座標に協力して動く理由はない? 共動座標は勝手に人間がとった座標であり、物理現象を支配しない? そうだろうか。それなら、宇宙の膨張は、物理的根拠を全て失うのではないだろうか(*)。

空間的距離 dl^2= dx^2 +dy^2 + dz^2 に、R(t)=GA の 2 乗の係数を掛け、それが不変量 ds^2 を構成するとき、

ds^2= R(t)^2 dl^2 - dt^2

膨張宇宙の共動座標での dl が R(t) を単位とする数値(物差しによる測定値)でしかないなら光速一定のミンコフスキー時空になることは、 正しい。しかし、dl は拡大する物差しである。この図のように dl が膨張するときそれは、全く誤った処理である。物差し dl 自体が R(t) に比例するのであり、反比例ではない。この混乱は、膨張宇宙の計量の式に物差しの縮小の式を使ったことによる。もともと、 膨張宇宙の計量の式は、間違っていて物差し膨張の式、

ds^2= dl^2/R(t)^2 - dt^2

を使わなければならなかった。共動座標の中にこの物差し拡大の式があれば、共動でない座標系では、dx= dl/R(t) とおけば ds^2 = dx^2 - dt^2 というミンコフスキー時空になってもよい。パウリの説明に反論したのは、"dl が R(t) を単位とする" と言って R(t)dl を一定とすることである。そこでは、dl は短縮していく物差しであり、理屈は 2 度間違って元に戻っている。 R(t)= GA は、その逆数が使われるべきである。そしてフリードマンの求めた G の時間変化が正しい結果とすると、その逆数が 宇宙のサイズの測度になり、フリードマン宇宙は、収縮宇宙論であったことになる。

(*) 計量が天体力学にしか関係しないという見方に私は反対する。時計と物差しが全てを支配するという見方なしに相対論の理解はできない。

２２.３ 全体写像

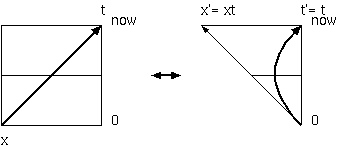
このグローバルな座標変換、写像という考えに通常の減速膨張の x'= xt^(2/3) をいれると、x'= (1-t)t^(2/3) であり、その結果は、多少 違ってくるが、違いは大きくはなく本質的でもない。t= 0 と t= 1 で x= 0 は変わらず、最遠点が過去に寄って t= 2/5 となるだけである。

膨張する系、共動座標で計量が ds^2= G(t)^2 dl^2 - dt^2 であり、それを dl が G(t) を"単位"として全ての計量が無視され、結果的に我々の みる系で光が直進するという話とは、これは違う理解のしかたである。左側の光の直進する座標系は、共動座標でなく、じつは局所慣性系の つもりだろうか。局所慣性系では光は直進するが、ある点の局所慣性系と別の点の局所慣性系とは実際 "系の速度" が違っているから、グロ ーバルな単一の系として光が直進する系を仮想しても、それは、ある点の近辺の計量を遠方に延長しただけではないか。 また、計量の G(t) の消去は、dx の換算でできるが、それは局所変換としては可能だが、宇宙全体に行なうことはできないのではないか。

２２.４ 全体写像による膨張

局所慣性系の速度は、それが光エーテル論的な問題点を含んでいたが、このグローバルな系のマッピング、写像という考え方では、時空間の系 から系への直接的なグローバルな写像によって光の経路が決まるから、局所の光速に影響するエーテルの風のような考え方を必要としない点が 優れている。しかしその経路は、本当の経路を各時空点での光速から微分方程式の解として求めたものではなく、一定のミンコフスキー時空の 光の直線経路を単に過去で空間方向に縮小しただけである。過去の局所の光速は縮小された光速であるはずが、これではそうではない。過去の 空間がグローバルに縮小されることには、あまり物理的な根拠もないように思えるが、計量は、局所の変換を与え、それは積分されて、全体の 写像になる。計量は時間だけに依存するとする(GAのGだけを使う)と、全体写像は、ある時刻の空間全体のサイズの縮小になっても不思議ではない。

それなら、上の図の全体の変換が、宇宙の真の姿を表しているかというと、それは、まだまだ疑問がある。まずは、どうして膨張かということ である。計量が物差しの膨張ではなく、縮小であること、過去の光速が小さかったのではなく、過去の光速は、大きかったという計量の時間変化 を全体写像するとき、どうして膨張を先与としてマッピングするのだろうか。そこに合理的理由が見出せるだろうか。しかし、膨張を先与の知識 とする人を責めることはできない。私を含めてほとんどの人がそうであったからである。

２２.５ 全体写像膨張は結論

x'= xt^(2/3)= 3(1 - t^(1/3))t^(2/3) = 3(t^(2/3) - t)

この変換された光経路の曲線の最遠点は dx'/dt'= 2t^(-1/3)-3= 0 から、t= (2/3)^3 の時点、 その距離は、x'= 3(2/3)^2 - 3(2/3)^3= 4/3 - 8/9= 4/9 である。宇宙論の光の戻りの経路と一致した。

膨張宇宙説の基本は、局所慣性系が速度をもつ光エーテル論かと思ったが、そうではないかもしれない。光エーテル論を理由とした膨張宇宙論への 私の批判 は、その重要な根拠を失ってしまったかに見える。光エーテル論から来るものが現代膨張宇宙論の結果と一致する からといって、膨張宇宙論の考え方が光エーテル論に依って立っているとの私の予断は、このような結果を招いた。しかし、全く同じ光経路を導く 2 つの全く異なる考え方が存在することは予想できなかったし、それにはより基本的な理由があると思われる。これの計量の意味はもちろん逆転して いるが、それを除けば、計量の局所変換を一様に宇宙全体の非線型写像に適用した、一種、美しい方法であることに気がつく。

２２.６ 膨張宇宙論のふたつの思考

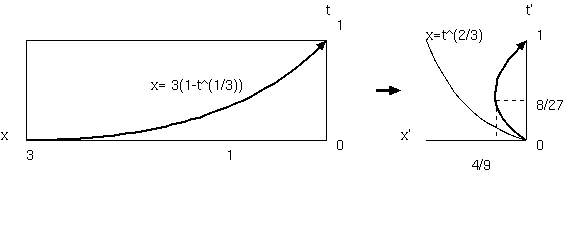
(1) 共動座標系で計量を求め、 ds^2= G(t)^2 dl^2 - dt^2 は、G(t)の増大は、物差しの縮小する宇宙を表す。 物差しに比例して光速も縮小するから、ここでの光経路は、直線よりも3倍遠方から光がやってくる縮小宇宙である。

(2) それを物差し一定の座標系に換算する。無限小の変換では、dl' = G(t) dl によって、ds^2= dl'^2 - dt^2 から、局所的には光速一定の宇宙に見える。 しかしそれは、局所だけでなく宇宙全体も変換する。 x'(t)= G(t) x(t) として、過去の宇宙は小さかったとする膨張宇宙ができる。

(1)によって G(t) を求めて、それを直接に物体一般、物差しの縮小宇宙と解釈せず、宇宙空間の膨張と解釈するには、(2)の換算が必要である。 (2)は、重力方程式の成立する合理性をもつ座標系ではない。そのため、(2) によって光速一定という Pauli (又は内山龍雄)の説明は誤りというべきである。 光の経路は、(1) による 3 倍の距離から近傍にくる光経路 x(t) を、宇宙膨張、過去の宇宙空間が小さかったとする (2) の換算によって、 曲ってもどる経路 x'(t) に変換されてできている。

物理的事項は、(1) でしか動いていない。上述の (1) の問題、計量が膨張でなく縮小であることは、しばし措き、(1) は、フリードマン計量 の物理的な座標系である。それに対して (2) は、物理と関係のない換算宇宙、いわば幻想である。 (2) の換算系に物理を求めても誤りを招く。 その例が光速一定という見解である。この系では局所的に光速一定にみえるが、光速一定どころか、光が、空間を直進し、停止し、反転して戻る という非物理的な行動をする。光が反転して戻るような宇宙は、光速一定とはいえない。そこに膨張するゴム風船上の虫が生まれる。

両者の系は、決して対等ではない。一般座標系が対等に表現できることは、計量を無視した換算系を考えることではない。(2)は、計量の時間変化 を否定して現在の大きさと等しいとする系である。一般相対論の計量を使いながら、それを否定する系(2)に不用意に移り、現実の物理とみてそれに 物理的な説明を付けようと、不合理な現象を作りだす。それが "ドップラー効果"、"空間膨張"であり、"光エーテル"、"速度場"と同じ光経路を導く。 私は、21.15 光の廻廊 で共動座標系の計量から光が戻ると思ったが、そうではなく(2)の換算によって、光が戻るのである。

注意することは、 (1) の与える空間計量 G(t) が膨張/収縮のどちらでも、(2) を使えば同じ結論にできることである。仮に(1)が事実とは逆に 重力方程式に従って物差しの膨張する計量を与えたとしても、そのとき、宇宙が膨張しているから、宇宙は後退しドップラー効果(又は空間膨張) による赤方偏移があるという説明ができる。物差しの縮小を逆手にとって、(2) を使った宇宙膨張という一般的な解釈は、物差しと力学的存在で ある物体を乖離させる誤った理解であり、特殊相対論の短縮のローレンツによるエーテル力学的解釈と類似する。 (1)を直接に受け入れるなら、宇宙が一点に収縮するという宇宙認識を持たなければならない。

２２.７ 膨脹宇宙とブラックホール

ブラックホール解では、極座標表示の角度θとφ方向の計量は影響を受けず、時間tと中心からの距離rが影響を受ける。 事象の地平線の内側では、(1-2GM/r)が負になるため、t と r の役割が入れ替わり、空間的なブラックホール中心からの距離が 外の世界の時間の役割をして、物体は不可避的に中心に進む。

ds^2= (1-2GM/r) dt^2 - 1/(1-2GM/r) dr^2 -r^2 dθ^2 -r^2 sin^2θdφ^2

これを極座標でなく直交座標(t,x,y,z)で書くと、次になる。

ds^2= a^2 dt^2 - b^2 (dx^2 + dy^2 + dz^2)

a= (1-GM/2r)/(1+GM/2r),　b= (1+GM/2r)^2

dt^2 の係数 g_00 を 1 に正規化すると、

ds^2= dt^2 - (1+GM/2r)^6/(1-GM/2r)^2 (dx^2 + dy^2 + dz^2)

これは、フリードマン宇宙解の光速 (1/GA) を (1-GM/2r)/(1+GM/2r)^3 とするのと同じである。右辺の G は、重力定数であり、 (1/GA) の G は、フリードマンの宇宙サイズである。同じ文字を使ったが別物である。フリードマン宇宙解では、この空間係数は、 空間的距離に依存する項Aと時間に依存する項Gの積であるが、ブラックホール解では、中心からの距離 r にだけ関係する。 (注意5)

(注意5) この時空の光速は、-a/b= -(1-GM/2r)/(1+GM/2r)^3 である。r が 0 に近付き k= GM/2r が 1 を超えて大きくなると光速は、 -a/b= (k-1)/(1+k)^3 〜 1/k^2 から、r の 2 乗に比例して小さくなる。これは、フリードマン宇宙解の光速 (1/GA) が空間係数 GA の時間に依存する項 G の増大とともに減少するのと同じである。ブラックホール解では、空間係数 b が中心からの距離 r の 2 乗 に反比例する。また、時間経過を決める時間係数 a が変化することがフリードマン解とは違うことである。 a は、r が大きい値から 0 にまで変化するとき 1 から下り、r= GM/2r のとき 0 を通過して、-1 に近付く。ブラックホールの地平面の内側では、時間経過が 逆転している。空間係数 b は、1+GM/2r の 2 乗であるから、GM/2r＞1 では、2^2 から無限大まで増大する。物差の大きさは 1/b ∝ r^2 である。そこの物差しで計測した中心までの距離は 1/r であり中心までの距離は、中心に近付くにつれて大きくなる。

違いは、宇宙解には物質密度ρがあることである。ブラックホール解では、中心にだけ質点があり、それ以外の部分に物質密度を考えない。 たしかに条件の違いはある。条件の違いがなく解が違うなら、少なくともいずれかが誤りである。それでは、ρ= 0 のフリードマン宇宙解は、 なぜブラックホール解と違うかというと、それは、中心質量が 0 だからである。ρ=0 でも違いがあるといえる。

膨張宇宙解とブラックホールの内側とは、時間反転の様にみえる。一点に収束するのではなく、一点から拡大する膨張宇宙と似るのは、 ホワイトホールであるが、それらは、同じ解の時間反転でしかない。しかし、問題はそれでなく、これは、同じ方向の現象なのである。

ブラックホールの時空の地平線の内部では r が 0 に近づくと GM/2r＞1 となり、 a は -1 に近づき、 b は 1/r の２乗に比例して大きくなる。 これは、宇宙膨脹で (GA)^2 の G が時間関数として大きくなるのと同じ方向である。 このことは、前章に述べた宇宙膨脹が実は収縮であることから理解できる。 ブラックホールの内部では r に比例する物差の収縮がある。 それは曲率0の宇宙膨脹では物差が t^(2/3) に反比例して収縮することと似ている。

膨張宇宙とブラックホールの内側を同一視するのは、通俗 SF か初心者のイメージと笑われることが多いが、 笑って思考停止するのは止めたほうがよい。それらは実は殆ど区別できないからである。

ρ_c0 = 3H_0＾2/8πG

であり、1.88x10^-29h^2 g/cm^3 (h=0.5〜1) となっていて、話は合っている。そこで、もうひとつの密度を考える。これは、 ブラックホール (BH) の密度である。BH は、質量に比例するシュワルツシルト半径 R= 2GM/c＾2 をもつから、 密度は、半径の -2 乗に比例する。BH の密度は、

ρ = 3c＾2/8πG R^-2

である。これは、見覚えのある式で、先ほどの宇宙の臨界密度の式が ρ_c0 = 3H_0＾2/8πG だから、

H_0 = cR^-1

ならば、これは全く同じ値になる。小玉さんの本ではこの半径 R をホライズン半径 cH_0＾-1 という。 つまり、膨張宇宙論の臨界密度は、BH の宇宙サイズの場合と変わりがない。宇宙が閉じるかどうかを決める臨界密度は、 それが BH となる密度と全く同じである。

アインシュタインの定常宇宙論では、一様な密度σを先に与えて、a= √(2/κσ) から宇宙の半径 a= κM/4π^2 が決まる。 この半径は、その BH の半径とは違っている。κ= 8πG/c^2 だから、a= 8πMG/c＾2/4π^2 = 2GM/(πc^2) となる。 BH 半径の式の 1/π の半径である。

しかし a= √(2/κσ)の a^2= 2/κσ に σ= M/(4πa^3/3) をいれると a^2= 2*4πa^3/3/κM から κM= 8πa/3、上の半径の式 a= κM/4π^2 でなく a= 3κM/(8π) になる。これは、私の計算間違いだろうか。κ= 8πG/c^2 をいれると、a= 3GM/c^2 となり、 BH の半径の 1.5 倍となる。

２３. 膨張宇宙の解釈

"Interpretation of the cosmological metric" http://arxiv.org/abs/0803.2701

もうひとつは、通常の平坦な時空から遠方を眺める座標系である。共動座標系の拡大を換算をすればこの場所からの距離と速度から光は 周波数が一定でも波長が延びるドップラー効果に換算できる。距離を換算するだけで特殊相対論のミンコフスキー座標系になり、光速一 定の特殊相対論が成立する。この系では天体が速度をもって逃げ、赤方偏移は特殊相対論的ドップラー効果である。距離と速度の関係は 最初比例的だが、速度が大きくなって相対論的になり、光速に対応する半径に近付くと共動系に静止する銀河はローレンツ短縮で奥行き が短くなって薄く折り重なって、ある半径で赤方偏移が無限大に上昇する。そのため、ハッブル法則は同時刻空間でさえ線形でない。 この系は共動系の距離の換算系であり、近傍の座標を遠方に直線的に延長した接平面であり、一種の幻想であるが、前の塵の系(共動系) と比べ、我々の現在見聞きする宇宙であり、この局所慣性系によって我々は宇宙の果てを見ている。

先のひとは、これらふたつの座標系、共動系と局所慣性系の混乱が膨張宇宙論の全てのパラドックスのもとであって、両者の分別をすれば、 何の問題もないという論調であるが、この人の結論の要旨を表にした TABLE 1 のようには共動座標系には線形のハッブル法則はない。 座標に静止する点に速度はないからハッブル定数は0である。その系に光速を越える速度は存在はしないだけでなく、そもそも銀河の速度 が存在しない。その系に宇宙の拡大はない。座標系の速度という不明な概念で理解すべきではなく、そこにあるのは銀河である。

この人の説明は、非常に明晰で単純だが、共動系での空間計量の増大をそのまま宇宙サイズの増大と解釈する問題がある。静止宇宙論の 宇宙の果てや、ブラックホールの地平面の外の近傍では、我々が通常みる平坦なミンコフスキー座標に変換するとき、空間計量の大きな 場所は、どう捉えられたかを想起すべきで、それは空間サイズの小さな部分と扱われた。そのように、フリードマン宇宙の共動座標系上 の変化としては物差しと空間間隔、銀河間隔の縮小であり、宇宙は縮小していなければならないが、これをどうするのだろう。

共動座標系での空間間隔の縮小を意味するG(t)の増大、それがなぜ宇宙膨張なのだろう。それは、本当に正しい計量の解釈なのだろうか。

まず、膨張と共に動く系からみれば、物体が縮小することがその意味であるというが、不変量 ds^2= g_ik dx^i dx^k が意味するのは、 g_ii(i=1-3)が働くのは、これを表す共動座標系からみてではなく、別のミンコフスキー系に座標変換するときに効果をもつのであり、 共動座標系からみて縮小するのでなく、ミンコフスキー系からみて、共動座標系の全ての空間間隔 dx^i が縮小するのである。これは、 全く違うことである。これでは、ミンコフスキー系からみて、宇宙が膨張するとは全くいえない。どうしてこれほど、解釈が違うのか。 それはもともとのフリードマンの宇宙解の空間計量のGを宇宙のサイズを表すということから始まる。

膨張とともに動く共動系では、膨張が見えない。その系で計測する空間間隔 dx^i は、変化しない。そこで時間間隔の変化を記述する のではなく、空間間隔の変化を記述して、この共動座標系の性質だけを表現しようとしている。座標系とは、物体、剛体よりも堅いも ので、剛体さえ支配するものを考えた相対論の思考法からは外れている。むしろそれは物理的存在でない系として伸縮自在の軟体で、 物体から逃れた独自の座標系だけの力学的性質をもったエーテル存在になってしまった。それは物理的な2次的存在で、電場磁場の力線 のように、それに速度を与えてはいけないものではないか。ミンコフスキーがエーテルに対していうように、4次元時空連続体のなかに 世界線をもつとはいえないものである。物体に世界線を記述させることこそ座標系の働きである。ここでは、物体から離れて、それが ふらふらとする仕方を記述する物理になっている。それでは、すでに何かをそれは間違ったために幽霊化したのである。

膨張宇宙の計量の意味は、誰にとっても謎である。それは単に、フリードマンのG逆数バグであって、ハッブルの法則の前にこのバグも 無視されたのだろう。アインシュタインが最初フリードマン宇宙を基本的に間違っていると判断したというのはこれが原因だろう。 フリードマン計量は、G はその逆数の増大が空間間隔の増大を意味しない。物体剛体から離れ、任意性のある座標系が膨張するという こと与えるため物体の縮小を与え、それで系の膨張を説明しようとする。そこでは物体が縮小していく、だから共動系は大きくなって いく、という思考方法は正しそうで間違っていることを示したい。ミンコフスキー系に変換するとき計量は働くのであり、共動座標上 の全ての空間間隔が、ミンコフスキー系に座標変換するとき、ミンコフスキー系からみて縮小してきていることを意味しているのである。 そうすると膨張宇宙でないから現実と異なるという反論には、膨張宇宙に一致する解があり得ることを示そう。

２３.１ 選択的膨張

電磁気力と重力は、距離の 2 乗に反比例して無限まで到達する力である。磁場はそれほどでもないが、荷電粒子が自由に移動できる 良導体といってよい真空の宇宙では、電場と電荷の偏りは小さく、電磁気力は、この巨大なスケールでは重要でないと考えられる一方、 重力はスケールに依らず、銀河間にも大きな重力がある。いやむしろ、銀河間から宇宙全体までの最大のスケールでは重力以外は重要 でないと思われる。そのような巨大なスケールにおいて重力で結合した物体間には膨張が働かないという説明は、若干違うと思う。

そのため、銀河間空間だけが膨張するというのは、正確でない。宇宙の膨張は、普通なら吊合っている銀河の渦巻を拡大してもなんら 不思議ではない。銀河自体も、膨張してよい。しかし、膨張が太陽系のスケールにもあるとすると、46 億年前の太陽地球間の距離が 現在の 2/3 であり、地球の受ける太陽輻射が 2 倍以上現在より大きく、地上の温度は、宇宙膨張を正当化できないほど高温になる。 (そのため、選択的膨張が、解決策として出て来たのではないだろうか。)

フリードマン解は、宇宙項（斥力項）を含まない重力方程式から作られている。そのため、空間の膨張は、ほとんどニュートン力学で 天体が四散すると同様に、空間それ自身の慣性をもった膨張のようにみえる。膨張は初速として最初からあって、宇宙全体の重力による 減速だけを受ける。膨張は力を及ぼし合わない物体間にはそのまま現れ、力を及ぼし合う物体間には、その間の力の存在によって膨張 の初速が減速され膨張が止まるように考えられた。これが、"空間の選択的膨張" という考えかたである。これは正しいのだろうか。

選択的膨張について、"物差しが膨張して、すべてが膨張しては膨張でなくなるのではないか" という意見には、膨張は現在の物差しとの 比較であると答える。フリードマン計量の式は、過去の物差しの 1 m と現在の 1 m が違うことをいう。また、"過去の時間や空間をそば に持ってきて比較し、確認する方法がない" として、その議論自体を疑う意見には、我々は、過去の宇宙しか見ることができない。遠方 銀河の赤方偏移という現象が先にあって、その説明が必要なのであると答える。また、一般相対論の計量は、空間的に離れた点の計量 (物差しと時計) を論じて、時間的に離れた過去の計量を論じることを禁じる理由はないと思うのである。

ds^2 = dt^2 - G^2A^2 (dx^2 + dy^2 + dz^2)

である。そこには物質や強度による選択的要素が全くない。同じ力が弱いところに大きく現れるのでなく、強度が強いところに強く、 弱いところに弱く働く、強度に関係なく(最終的には力に関係ない)物差ごとひっくるめて長さが変化する、アインシュタインの "幾何学と経験" にある "剛体球の変化" であると思える。

ある剛体が過去にあるとき上の式で、それを局所慣性系に移すとき ds を不変として ds^2 = dt^2 - (dx^2 + dy^2 + dz^2) となる。 GA が小さい過去に物差しを含めた物体の空間的大きさ (dx, dy, dz) が変化したという式である。しかもよく考えれば、この式は、GA が小さい分、距離が大きかったという式でありその逆ではない。一般に膨張宇宙とされるフリードマン解の g_ii (i= 1〜3) の増大は、 計量の意味からは物差しを含めた空間の膨張ではなく、縮小する宇宙を表している。

そのことは、ローレンツ短縮の原因が特殊相対論以前、ローレンツが考えたような静止エーテルの中を進むことによる圧縮が原因でなく、 速度よる座標変換であったように、(アインシュタインは、エーテルの力学的圧縮の研究を尊重する文章を残し、彼によって初めて明確に された特殊相対論の中心的な考えかたの座標変換をローレンツに敬意を払って "ローレンツ変換" と呼んだ。)、特殊相対論の物差しと 時計の変化は、速度をもった座標系間を移るときに起きる座標変換であり、その系にある物体には何の力もかからずに、別の慣性座標系 からみると単に長さが違っている。しかもそのとき、物体とその上の物差しはともに短縮する。それは、別の系の観測が物体に影響を与 えないという原理に還元された(*)。

特殊相対論には、そういう常識があるのに、宇宙膨張にはまだエーテル力学的な "速度場" という考えかたが強い。一般相対論における 計量の変化も、その場所の物差も含めて物体の大きさが単に変化することである。ある時空点の物差しと時計は、別の時空点、例えば 現在からみて空間的物差しが違うだけである。そのことを想起させる必要があるほど、膨脹宇宙説は、風化、俗説化してしまったようである。

(*) それを原理化できない面がある。というのは、それはローレンツ変換が並進慣性系の認識論であって、この膨張宇宙解はそれが認識論 ではなく、宇宙の進化論であるからであるということである。系の乗り換えは、物体にとって瞬時にできるのが並進慣性系であったが、 この宇宙論では、共動系から局所系への変換は即時ではなく時間の経過を伴うと考えるからである。その時間に宇宙は内部を変形させ、 質量集中させる現象を起こすことを問題とできない。過去の共動系から現在の局所系への変換であるからである。

２３.２ 縮小する物差

膨張宇宙の説明として、現実の物体の物差しの代表である原子が縮小していき、原子の発する光の波長も時間経過に伴って縮小していく。 そして質量をもった星や銀河は、慣性があり、静止物体は静止を続け、速度をもった物体は速度を保持して存在するから、星の大きさは、 物差しの原子が縮小すれば比例的に縮小するが、星の間の距離はそのままである。これを変化する縮小物差しを使って測定すれば、物差し や恒星の大きさは変わらずに銀河の間隔が膨張していくように測定される。これが、膨張宇宙の、縮小する物差による説明である。

時空の計量の質量との関係を説明する重力方程式は、万物を説明する方程式である(又はあった)。現在、それをさらに原理から説明する 物理的過程が存在すると考えるかもしれないが、量子力学がなかった当時、決してそうは考えなかった。物差しの原子が縮小し、原子の 発する光の波長もそれに従って縮小していき、光速も比例して縮小する、そのような時空全体がどうあるかを問題にしたのである。

天体間の距離が変らず、物差しだけの縮小があれば、そこには、現象として力が現れる。例えば物体間に重力でなく物質のひもがあるとする。 ひもの原子が縮小すると、ひもはその強さ (ばね定数) に従って張力をもち、その両端の物体を引きつける。そのため、ひもによって結合 した両端の物体の間隔は、物差しの縮小の影響を受けそれに比例して縮小するから、縮小する物差しからみて、空間の膨張の影響を受けない。 結合していない質量間は、そのままの間隔を保ち、縮小する物差しからみれば、膨張していく。これが空間の選択的膨張を説明する。

２３.３ 質点間のひもの縮小に伴う力学現象

物体間の重力の結合は、距離の 2 乗に反比例する引力が大まかなばねとして存在し、引力は両端の質量に比例するからほぼ均一な膨張を 作りだす。しかし、両端質量は、密度がほぼ一定であれば距離の 3 乗に比例するから、引力は距離の 6 - 2= 4 乗に比例するし、その ばね定数は負である。それは、構造形成のもとになる不安定性といえそうだし、現実の不均一性をよく説明するようにも思える。

しかし、これは本当の話だろうか。こんな複雑な仕組みを相対論は用意したのだろうか。時空的遠方の物差しとそこにある物体間の距離 とは区別されただろうか。時空的遠方のグリッドの細かさが物差しの小ささであり、そこで物体は物差しと共に短縮したり伸長したので はないか。物体が剛体が物差しが、そこに置くとそのように縮まる、それが不変量の意味である。一体、この解釈は、何が行われたのだ ろうと思う。

まず、局所と大局の境界が不明確である。太陽地球間、銀河系内、銀河系と隣りの銀河とはまだ局所で、遠方銀河間は大局で、どこから が局所でないのか。それらの間に明確な境界はなく、空間の曲率のように遠方に徐々に表われるのだろうか。そうではない、これは空間 による効果Aではない、時間的な変動Gの話である。そのとき局所慣性系という言葉は、空間的な近傍でなく、時間的な近傍、局時の意味 である。変化が時間的間隔にほぼ1次程度の関係だから、効果は短時間にも精密に測定すれば検出可能(2次以上では無理)であろう。

例えば、極端に局所の地球と月の間の距離は、非常に精密に計測できる装置(レーザー光線の反射のための直角3面鏡)がアポロ計画によ って設置され、地球と月の間の距離は月の軌道の楕円性によって10%程度の増減があり皆既日蝕と金環日蝕が発生するが、38万kmが年間 3.5cm上昇しているという。これの原因は、地球の潮汐と自転運動からつねに月の前方からの引力が大きいために月が加速されると月の ジャイアントインパクト説(38億年の重爆撃以前の記録がないため可能性が残る)から解釈されているが、上昇に必要なエネルギーは、 それより何桁も小さい地球の自転は持ち得ないし持ち得なかったと思う。もし宇宙が膨張していて、地球と月の間も膨張していて、その 間光速が不変なら、月の上昇が約110億年という宇宙年齢を示すものになる。それはかなり良好な一致である。地球と月の配置がいつから であっても、宇宙膨張がそのまま比例的に局所に影響するなら、それは宇宙膨張の局所での最初の確認になる。光の波長と光速は空間計 量に合わせて伸縮するから共動座標では計測されず、局所慣性系ではそれは天体間の膨張として計測可能である。

この天体の膨張をみる局所慣性系は、物差しと光速が一定で運動量保存とエネルギー保存が成立するが、なぜか天体の距離 r が変化して、 時間的遠方に保存則が成立しない。共動座標では物差しが縮小する速度低下があり、運動量は1次、エネルギーは2次で低下する。 重力で結合した天体の軌道運動のつり合い位置である半径は2次でエネルギーmv^2/2が低下するからr= GM/v^2はむしろ2次で大きくなる。

縮小する原子によって誘起される力によって結合状態にある物体間は、さほど膨張せずに、その他は膨張するという仕組みは、ひもが 構成するばねの中心位置の縮小がこの共動座標上で起きることを必要とする。天体の慣性による運動は、この共動座標系によって乱さ れず、重力ばねだけが中心位置を変更する必要がある。それは、物質によるひもで考えることが容易だが、重力による引力では起こり 得ないかもしれない。

２３.４ 物差しと物体

フリードマン宇宙の膨張の説明に、力学関係をそのなかに残すのは、特殊相対論のエーテル解釈と同様に無駄な概念によって作られたもの のようにみえる。特殊相対論の座標系は、"剛体" であるが、一般相対論の座標系は、"軟体動物" という。物体が剛体であっても座標系が 軟体動物のように変形する。特殊においても座標系は短縮せざるを得なかったが、一般では幾何学すら違ってくる。回転させると剛体でさ えも変形する。又は剛体は回転できない。そのような座標系が物体の強さ硬さに関係のないものであることは慣性系と同じであろう。

２３.５ 縮小する物差しによる膨張は、過去の空間間隔の拡大

物差しと物体間隔が乖離しない拡大縮小では、常に物体と間隔が比例的である。縮小の場合、宇宙は縮小をし、過去に大きな宇宙をみる。 共動座標からは宇宙の大きさは一定であるが、通常の物差し一定の座標系を使って過去をみるときは縮小してきているのである。物体は向か ってくるので遠方の天体からの光は、赤方偏移ではなく青方偏移する。逆に膨張の場合、物差しを含めて物体と空間が膨張すれば、過去の物差 しと、宇宙サイズは小さく波長は伸びる。しかしその場合も、塵に静止した光の送受信点では、遠方過去からの光も、近傍では近傍の光と区別 できない光速になり、遠方の光は空間的に伸びる。現在の物差しを延長してそのまま過去を見る通常の座標の場合、宇宙は膨張しているから、 遠方銀河が距離に比例して遠ざかる相対速度をもち、それによる特殊相対論のドップラー効果の赤方偏移がある。

しかし、通常のフリードマン宇宙で物差しが縮小するから宇宙が膨張すると赤方偏移を説明し、ここでは、その逆数の計量変化で宇宙が膨張 するから赤方偏移が説明できると主張している。実際は、二者択一で、一方が成立すれば他方は完全に誤りである。どちらが誤りなのか明確 にできないのでは、解決にならない。

フリードマン解は、空間計量 g_11〜g_33 = G^2A^2 が時間経過に伴って大きくなる式であり、時間計量 g_44 の時間変化ではない。 もしこれが重力ポテンシャルに直接関係する g_44 の変化ならば、時間経過の速度の違いから過去のエネルギー全てが現在からみると 弱まってみえる赤方偏移があり得るが、そうではない。フリードマン解の示すことは、物差し (1/√g_ii = 1/(GA) に比例する)の縮小と、 それに伴う光速(√(-g_44/g_ii) (i= 1〜3)) の縮小である。ガウスの曲線座標系の空間的グリッドは、過去において大きく開いていた。 そもそも、これは膨張ではない。縮小という現象である。

計量の意味を本気で考え、正確に捉えることは難しい。宇宙論の学者で、フリードマン計量をそのまま使っている人は、恐らくいない のではないだろうか。そのままでは膨張宇宙の説明にならないからである。例えば、Zeldovich という有名な学者の後継者の宇宙初期の 重力波の優れた説明的な論文 L.P.Grishchuk "Relic Gravitational Waves and Cosmology" (arXiv:gr-qc/0504018 v1 5 Apr 2005) では、最初に提示する式に、

ds^2 = a＾2(η)[-dη^2 + (δ_ij +h_ij )dx^idy^j]

という式を使う。この式でηは時間のパラメタであり、スケール因子 a(η) は、空間計量だけでなく、時間計量にも乗算されている。 [ ] 内の式の (δ_ij + h_ij ) は、ミンコフスキー空間からの誤差が小さいときに g_ij の代わりに使う式である。[ ] 内は、ηを時間 ct としているなら、dx^i dx^j は 1- 3 の空間だけに渡るもので、g_01, g_02, g_03 の項は省略されている。[ ] 内がミンコフスキー 時空に近い形であり、その外に a が乗算されて ds の不変式になっている。

Pauli の相対性理論によると、一般相対論が出たとき、ノルドストーム (Nordstöm) の理論は、ds^2= φΣ(dx^i)^2 であり、光速は 特殊相対論の光速と等しく太陽の側の光の折れ曲がりはない、一般相対性原理に従っていないと Pauli は批判したのであるが、この式も、 a() を掛ける場所が違っているため、a() は、ノルドストームの式のφに相当するかたちになっている。ノルドストームの式と同様に 光速が変化しないことを意味する。この計量は、どのようにして導かれたのだろうか。(通常の教科書では、フリードマン宇宙の膨張因子 a(t) は、空間側だけに掛かる。)

この式の場合のスケール因子 a(t) の意味は何だろう。a が時間につれて大きくなると仮定し、空間的距離から時間的距離を引いた差、 特殊相対論の不変量(時空間隔、固有長、負なら固有時)が a^2() 倍されて保存されるというこの式の意味は、時空間隔の縮小である。 時空間隔= 0 である光は、a(t) の影響を受けない。(これは、まだ、膨張宇宙論の欲する式ではないように思う。)

２３.６ 解釈に問題

力の大きさでなく移動できるかであるというなら、力と膨張の容易さ、つまり強度が関係するだろうか。そのような膨張は頑丈な強い所 には、大きく働かず結合の弱い所に大きく表れるという、力学的膨張である。時空の性質としての膨張とは違う。相対論の本質は座標変 換であって、その力学的解釈は、ローレンツ短縮をエーテルからの力による圧縮と考えた時代への先祖帰りのように思う。空間そのもの、 座標系が膨張収縮するとき、物体の弱さと強さに関係なく、剛体ですらそれに伴うのである。座標系は人間の設定であって、現実の物体 が座標系に伴う必要がないからそれは違うかというと、いや、特殊相対論の速度をもった系から見た空間の座標変換も、物体と直接関係 ないということで同じであり、物体と空間とをひっくるめて全て短縮したのである。

物差しが膨張収縮するとき、見る場所でなく見られる問題の場所の物差しと物体とは、同期するのである。物差しだけが膨張収縮して その同じ場所の物体と空間が、取り残されるということはない。それは、今言った選択的膨張に繋がるからである。それなら、膨張宇宙の 空間計量、Gの増大は、宇宙のサイズの逆数の増大、空間の収縮を表すのである。フリードマンは、空間計量の増大する不変量の式を 物差しの収縮と強引にいって宇宙膨張を表すということが可能だったが、物差しだけの変化はあり得ないとすると、この不変量の式は、 宇宙膨張ではなく、宇宙の収縮の式である。

物差しの縮小が宇宙の空間の膨張の言い替えという考えは根拠がない。フリードマン宇宙の G が臨界密度より上でサイクロイドを描くこ とも、その逆数の縮小していく物差しからみれば、一定のサイズのものがサイクロイドを描くことになる。しかし、宇宙のサイズ G が その逆数の物差しの変化によるなら、宇宙のサイズの変化は、"実際の" 宇宙のサイズが変化しないことに依存している。それを膨張とい うのは言葉の意味の崩壊である。そして、物差しと物体のサイズが乖離することは相対論にはない。

物差しと空間が縮小していっても、現在の通常の座標系からみると、過去の空間が大きくなってきたのであり、ドップラー効果に一致する のではないかという反論も違うと思う。それでは遠方の銀河は接近して来て、赤方偏移とは逆の青方偏移を導いてしまう。問題はどこに あったのかと考えると、膨張宇宙論の計量の式自身にあったのだろう。空間計量の増大を宇宙サイズの増大としたことにあったと考えられる。

２３.７ 計量の意味

ds^2= g_ik dx^i dx^k

の書き方が変わっているので、一般の人には何が何だか分からない。dx^i は、i= 1,2,3 で空間間隔 dx, dy, dz を表し、i=4(又は0)で時間間隔 dt を表す。G, A が出てくる、次の式の方がもう少し普通に近い。

ds^2= dt^2 - G^2A^2 dl^2

dl^2= dx^2 + dy^2 + dz^2

この式は、膨張宇宙の式だろうか。Gの値だけが現在と過去とで違う(現在G=1過去G＜1)とする、ds は不変量で dt が過去と現在で等しいなら、 過去のdlにGAが乗算されて、現在の dl'になる dl'= GA dl。そのとき G＜1 なら dl'＜dl である。dl'= GA dl は、不変量 ds による等式に 表す単純な座標変換である。空間間隔 dl が現在からみて、どう見えるかを表す、過去の dl と現在の dl' との大小関係である。過去の dl は 過去の G 倍され、係数G(＜1)によって縮小され、現在の空間間隔 dl' になる。つまり、過去の dl は大きかったという式である。

まず、G(t)の膨張をそのまま空間の膨張と考え、これを宇宙膨張の式と考えることは誤りである。この式は不変量の式である。それには楕円の 式を思い出してほしい。x 方向に横長な楕円の式は、x方向の係数が小さい。ある方向の空間計量の増大は、その方向の物体の縮小である。

計量の増大が物差し物体の縮小を意味すると理解しても、「拡がる塵(＝銀河)が静止してみえる共動座標系からみて、物差しも物体も縮小する」 が一般的な認識であるが、「物差しの縮小は、共動座標系の膨張である。」「共動座標系が膨張するから、物差しが縮小する。物差しの縮小は、 当然、共動座標からみているわけだから、縮小でよい。」という見解は、次のように、比較の対象も比較の相手も違っているのである。

計量の式は本来、共動座標系上の静止点間の距離dlの、現在の dl'との比較である。現在のdl'から見て過去のG(t)＜現在のG(1)だから、過去 の空間間隔dlに縮小率(G(t)＜1)をかけ、縮小して現在のdl'に等しいのであって、共動座標の空間間隔、物差しを他と比較しているのである。 何か別の物差し例えば原子のサイズの共動座標上の空間間隔を基準にした比較ではない。

現在又は他の時空(例えばミンコフスキー計量)に変換するとき空間計量 g_ik (=G^2)を係数として、現在の時空をからみる過去の空間間隔dl (これは銀河間距離、太陽地球間、月地球間、人間のサイズ、原子のサイズ、全て)が過去に大きかったという式である。過去の共動座標上の 空間間隔dlを対象とし、それを別の時空の間隔に比較するのに不変量を介在させる。通俗概念では、比較される対象である物差しdlは、すでに その座標系の空間間隔でない、何か別もの例えば不明な原子のサイズに変えられ、しかも比較の相手が共動座標に変わっている。このような、 両方の入れ換えは、意味の完全な逆転である。

ここまで考え、やっと膨張認識が誤りと分かる。多くの本がこれを膨張と書いた。ds^2= g_ik dx^i dx^k がいかに理解を拒む式であったかを これは示している。このような一般相対論の最も根幹の式の誤解は、非常に性質が悪い。相対論の方法を殆どを放棄させる考え方に多くの人が 影響を受け、この式をそのまま膨張宇宙と認識した人々が、この誤解を解明するには、どれほどの労力と回り道が必要だろう。

誤解は、dx が共動座標系と関係を失った何か一定の物差しがあってそれが共動座標系の力学を記述するという観念である。共動座標系は、塵が 浮かぶ系として任意に人間が設定したものであるから、逆にそれだけが計量によって表現される対象と考えている。物差しとして物体全てを包括 して剛体すら変形させ全物体を支配するとは理解しない。座標系が物体から遊離した座標系だけが計量によって大きさを変えると考え、座標系は、 銀河間の空間だけを扱い、局所には標準的なミンコフスキー計量をつねに与えると考える。そのため、宇宙はつねにミンコフスキー的で、空間だ けが膨張すると考える人が大半である。

座標系が物体までを支配するものと認識しないから、特殊相対論の前、ローレンツ短縮を見出したローレンツが短縮にエーテルの力学的説明を考 えたようになる。それはアインシュタインによって相対速度のもたらす座標変換 "ローレンツ変換" と分かって解決した。それが特殊相対論の最 も重要な特徴であった。膨張宇宙で局所の物差しと天体間の物差しを別にして、その間に座標変換が行われ、局所と大局が特殊の慣性系の間の座 標変換と対応して考えられる。そうするとき天体力学は、我々の卑近な物体の物差しとは全く関係がないものとして扱われるが、逆にその間の力 学的な力の働きが必要となる。膨張には、力学的説明、空間に慣性があるとか、初期速度があるとか、それ以外に膨張する性質があるとか、電磁 気力や重力で結合した物体間には働かないとか、混乱し基本的に誤った説明が必要になる。しかし他方、局所と大局の座標変換は、物理的な意味 のない単なる物差しの換算として扱われるが、時間による物差しの大小関係Gだけでなく、局所からみると宇宙の周辺のローレンツ短縮も表われる はずであり、空間的周辺による空間計量Aの影響もある。我々のもつ基本的解釈が真実から余りに遠くて、それを理解することができない。

パウリの付録のいう、dl が GA を単位にするという言い方は、さらに強力な誤解を与える。まず、ある過去の共動座標の空間間隔は dl であり、 GA dl ではない。確かに dl が、過去の小さな G(t) を単位に記述されているなら、単位をかけて本当の大きさになり現在のdl'と等しいだろう。 しかしそれでは、dlが「G(t)を単位にする」とは、dlがまるでその単位の数値のようで、元の式のもつ意味、長さdlと現在の長さdl'との大小関係 自体を壊す。GAを乗算して過去の計量がつねにミンコフスキー計量になり、過去と現在の空間間隔は一致して、計量の意味を失うことである。

この式は、過去と現在の空間間隔 dl の大きさを示し、dlは例えば1mという長さが、G(t)＜1の例えば0.5が掛けて現在の1mに等しい。これを、過去 の1mはG(t)を単位するというと、まるで、dlが50cmを単位にした数値2だから、G(t)=0.5を掛けて現在の1に等しいという意味になって、計量を物差 しの大小でなく、単なる単位系の換算に矮小化する。相対論の基本的思考方法である物差しの変形の思想は、これによって徹底的に失われ、現代人 は、ほとんど元の物差しと時計の意味も忘れたようだ。私は、dlがGを単位にもつなら、Gを掛けるのでなく、逆に G で割らないとミンコフスキー 計量に変換できないと思う。なぜなら、dl に既に G が掛かっているなら G で割る必要があるからである。

膨張宇宙の解釈のこのような破産状態では、宇宙論だけでなく、1つの重力源の周囲の計量でさえ「どうして物差しと時計が、重力に関係するのか 理解できない」と言いだすかもしれない。時間計量g_00がそれに対応する、ニュートンの重力ポテンシャルも実感を失い、アインシュタイン自身が 計量をポテンシャルと呼んだことも知らず、一般相対論はポテンシャルと関係ないといいだす。重力方程式とポアソン方程式との関係もアインシュ タインが述べていたと知らず関係ないと言い張り、相対速度による物体の変形と時計の遅れの特殊相対論さえも失うかもしれない。それでなくても、 膨張宇宙論は、光エーテル論に浸り、絶対静止空間のような宇宙を見、さらにその真意としては、神の宇宙開闢の証拠を求める信仰的な動機に根ざ しているかもしれないと疑われることをしている。彼らの文言をみて感じるのは膨張論の危うさはなぜかという疑問であり、この分野が公平さを保 つことの難しさを実感しない者達の特徴として宇宙論者がその危険さに余りにも鈍感でありかつ、無防備であることである。

２３.８ あり得る膨張宇宙

そこでこの解釈を膨張宇宙にするのは、時間を逆転して、現在から特異な時刻まで、宇宙は拡大する位相にあるとする。これなら、 宇宙は過去にゆっくりと有限サイズから有限の時間を経て、又は密度が臨界以下では1点から無限の過去を経て、現在のサイズになって いて、これから暫くは膨張位相にあるとするのである。これだと、膨張宇宙だから過去からの光は赤方偏移する。元の普通の解釈の フリードマン宇宙解も、収束の一点に収束する時刻をとることもできたが、膨張の位相を採っただけである。この逆数のGでは膨張の 最後の瞬間には無限大に発散し、それから先は分からない。宇宙項のないフリードマン解は常にG''＜0 だから、その逆数のこの宇宙 はつねに加速膨張である。

その代わり未来は有限である。未来には空間が無限大に発散する特異の時刻をもつ。特異点は、過去でなく未来にあるので、そこから の光は来ないし、見えない。そして、どれだけの未来にそれが起きるかの推定が必要かもしれない。それでも、ハッブル定数の逆数が それを表すだろうか。G'/G はハッブル定数ではなく、Gの逆数が宇宙のサイズであるから、観測されるハッブル定数は、Gの逆数の微分 とGの逆数の比((1/G)'/(1/G)= -G'/G^2 *G= -G'/G= -H) となる。ハッブル定数の逆数は、宇宙年齢ではなく、そのまま特異な時刻への 残された時間を表している。

それはフリードマン宇宙の通常の解釈、「空間だけが膨張していく」や「我々が小さく縮小していく」という理解ではない。「物体を含 めた全ての空間間隔が膨張発散する」のである。過去には物体が空間間隔が全て小さかったである。これがフリードマン解の時間の関数 G(t)をそのままにして、宇宙サイズは1/Gとする解釈によって膨張宇宙にする方法である。この宇宙は膨張する、あと暫くは、である。 残された時間は、ハッブル定数の逆数＝普通の解釈の宇宙年齢に等しいから、少なくとも65億年程度はある。それをハッブル定数の測定 の歴史の拡がりから、100億年〜150億年にすることができるが、これは宇宙年齢でないから、球状星団の年齢によって上限を広げること はできない。今のところ宇宙項は、必要がないので考慮しない。すでに加速膨張であり根拠なく導入すべきでないが、宇宙項も関係しな いわけではない。正の宇宙項は宇宙の余命を伸ばさず、むしろ短縮させ、負の宇宙項は寿命を伸ばすだろう。

時間は負の値で示すのが便利である。直線膨張 x= t に対応するのは、x= -1/t である。臨界密度での平坦な空間を保つ、x= t^(2/3) に対応する膨張は x= (-t)^(-2/3) であろう。これは、現実の時間軸を反転するという変わったことをしているのではない。モデルの 位相と時間の符号を現実の現象に合わせて選択するだけである。これには、恐らく「最初の解釈が宇宙の開闢を示していたのに、これ では宇宙の終末を示して、現実に合わない」という反論があるだろう。まさに、必要は物理も生み出す、世も末である。宇宙の開闢を 示して世界の成立を説明すると考えてきた宇宙膨張は、宇宙の終末を示して世界を説明するならば、フリードマン解に実際に整合する。

しかし、これを受け入れ難く感ずるのは、どのように解釈が不明であっても、膨張という疑わしい事実を最も端的に説明する仮説として 多くの人々がフリードマン解を受け入れて来たからであり、それに対して、その解釈に基本的なバグがあると指摘しても、Gを逆数に時間 を反転にした話を、すでに式に対して信用を失った人々は直ちに納得しないだろう。それによって膨張宇宙の何が変わり、どういう現象 が予言できるのかを示さない限り、式の整合性だけでは説得性がない。違いは、この宇宙に見える過去の宇宙が始まりの余韻(CMB)でなく、 我々の宇宙が無限又は無限に近い過去をもつことであり、そのことによってどう違うかが課題である。これは過去と遠方が無限にどこま でもある静止宇宙に近い膨張宇宙である。そして、未来の有限/無限は、宇宙の果ての見え方に違いはないだろう。

膨張とポテンシャル

フリードマン解のいずれの解釈も、宇宙膨張を記述するのに膨張によって座標値が変化しない共動系、膨張が見えない系を使って不変量 ds^2 を導く。空間係数 g_ii (i=1-3)を時間関数G(t)と空間関数A(l)との積に分けるが、共動系では空間間隔 dl^2= dx^2 + dy^2 + dz^2 が変化しない。ds^2= dt^2- (GA)^2 dl^2 の ds が不変量であることを考え合わせるとこれは元もと矛盾ではないか、これが空間計量の 変化に対応して、時間計量であるポテンシャルもそれに対応して変化しないと不変量dsを保てないのではないか？ いや、これの成立を考 えると dl がその座標系の物差しの目盛の示す数値、座標値とは考えず、座標系の目盛の間隔を別の系からみた長さであったのである。 前言「元もと矛盾」は誤りであり、それは私が否定した、空間の選択膨張と縮小物差しという通常の解釈に強く結合している。もしも、 dlが(Gを単位にする)共動系の座標値であれば実際にdlは不変であり、dsは不変量だから、Gは変化できないという矛盾を示している。

つまり、共動系では空間計量変化があり得ず、そこにポテンシャル変化だけがあり得ると考える必要はない。フリードマン解が時間計量 g_44の変化をもたない共動系で表現されているが、ポテンシャル変化がない理由もない。膨張からくる質点からの距離増大に伴うニュー トン力学的なポテンシャル上昇が表される座標系のほうが、よりニュートン的である。それはニュートン力学に合致し、ポテンシャル記 述に合う座標系であろう。アインシュタインが定常宇宙論と宇宙項を導いた、一般相対論の宇宙論的考察(1917) の ds^2= B dt^2 + A dl^2 のAとBの2変数を、計量全てに時間的変動がないため、B= 1 としたのが定常宇宙論、膨張宇宙には2変数の 必要はなく1変数で十分だから B= 1 としたのがフリードマン解とすると、AとBの関係をニュートン力学的に制限して1変数にすれば、 より現実的な解になるかもしれない。考えられる変数変換におけるヤコビアン√-g = 1 = √A^3B (g= |g_ik|)を一定に保つこと、B∝ A^(-3) は強過ぎ、B∝A^-1なら、ポテンシャルΦ= 1/Rが距離に反比例する。重力方程式はどの座標系でも成立するが、座標系の選択は 解を容易にする。

２３．９ 膨張宇宙説に対する批判のまとめ

(2) 歴史的に後退仮説のハッブル定数は誤差が大きく、天文学等に大きな影響を与えた。
当初、ハッブル定数の逆数であるハッブル時間が10億年でしかなく、地球の放射性物質や恒星の進化の理論にも矛盾した。それらの矛盾を避けるため ハッブル時間は、ボーデ、サンディジによって何度も延長されてきた。現在、ハッブル定数は当初の1/10以下になったが、その測定は多くの仮定に 基づくため確定が難しく、学者によって2倍程の違いを解決できない論争の源であった。例えば、恒星の進化の理論による球状星団は160億年と言われてきた。 形成時間が長いどの現象にも問題を起こしたが、主に銀河の形成理論には、ダークマター、ダークエネルギーなど、新たな仮説が必要となった。 宇宙認識を複雑に仮説的にし困難を引き起こした。後退仮説のハッブル定数は、始まりのある宇宙であり、宇宙年齢は、全ての天体の形成時間を制限し、 説明に影響し、その相手と調停を必要とした、疑わしい概念である。

(3) さらに、フリードマン膨張宇宙の空間計量の認識(空間計量を宇宙のサイズにする)は正しくなく、実際は逆数である。
空間計量の増大は、全ての空間間隔、銀河間距離、物差しの縮小を意味する。宇宙膨張を実現するには空間計量の増大でなく縮小を望むべきである。 空間計量g_iiと物差し(dx^i)^2(i=1-3)の積和が不変量である。元々、塵の漂う系をモデルにする膨張宇宙では、空間計量は、全物理現象に働き、 空間膨張するなら銀河間空間だけでなく全ての空間間隔が膨張する。銀河間隔ではない別の物差しを使い、銀河間隔が膨張するということはない。

それまでのアインシュタイン宇宙やド・ジッター宇宙がもつ一様性を担保する有限の超球面を仮定し、その射影の無限遠の空間計量の大は、物差し、 物体、物体間隔の小であり、宇宙の周辺で物体が平坦化し、厚みを減らしていると解釈され、それを殻のある宇宙という言い方がされた。 フリードマン宇宙は、それまでの計量の定常という前提を捨てた拡張であったが、彼の空間計量の理解は逆数である。宇宙の大きさが計量に反比例 でなく比例するように解釈している。

彼の空間計量と宇宙のサイズとの間の解釈は、空間計量が近くの銀河間隔を物差しにして、仮想的な全宇宙のサイズを逆数にみるとしてこれを理解するの ではないか、近傍の銀河(物差し)の膨張は宇宙の縮小であり、物差しの縮小が宇宙の膨張である。しかし、これは銀河間距離の縮小である。その場合、 物差しの逆数が宇宙のサイズであり、空間計量に比例するのである。しかし、物差しはなぜ、宇宙のサイズの逆数であるのか、仮想的な宇宙サイズが 一定だから、物差しの縮小が、宇宙のサイズの膨張として相対的に捉えることができるという、基本的な矛盾を含んだ解釈ではないか。それは何か 不変量の仮想的宇宙サイズに対して、物差しのサイズの縮小を、宇宙サイズの膨張と理解しようとするのであり、計量の基本式でそれらの積が不変量 であることと関係する。正しそうでありながら矛盾である。物差し＝銀河間間隔の縮小は宇宙膨張ではない。物差しの拡大が宇宙の拡大である。

彼の計算結果が正しいとして、アインシュタイン宇宙、ド・ジッター宇宙とも整合する計量の理解を使い、空間計量の時間変化で宇宙膨張を説明するには、 空間計量の縮小が必要で、現在がその位相(負の時刻)であって、(物質密度の測定が反論するが)物質密度が臨界密度より大きく、我々の宇宙が空間計量が サイクロイド型の拡大縮小をする振動宇宙の必要があるが、その場合、宇宙は、140億年前からの膨張宇宙ではなく、140億年後の宇宙の無限拡大をする 発散宇宙であり、これは彼の解釈では、空間計量の0への収束、特異点への崩壊であるが、それでよいのか。彼がよくても、空間計量をそのまま宇宙のサイズ とすること、我々はそういう解釈の膨張宇宙を、受け入れるのは難しい。これは論理の途中の処理における破綻であり、前提の破綻ではない。 途中の処理が正しくないと、前提のチェックまでいかない。大きな計算ミスのような論理矛盾がある論文をどう評価するのかという問題である。

(4) g_ikの時間的増大を認めると、不変量ds^2は、 g_ikの変動を含めることができるから、時間的な不変量とはいえないのではないか。
このことは、定常な空間解を求めるときも、空間的な不変量でなくなっていることに対応しているから、不変量を単なる基準にするだけの 拡張に伴う正しい処理の可能性はあるが、時空間的に不変でないものの基準としての不変量の正当性を疑う。

(5) 基本的に特異点の存在が問題である。"相対論の意味"のなかで、アインシュタインも、特異点を避ける試みを3度行い、失敗している。 また、ホーキングも示したように、重力方程式の偏微分方程式の解が、全ての測地線が通過する特異点をもつということには概念的不満がある。 偏微分方程式は、全ての時空点において計量の2階までは微分可能という条件を課すものであるが、膨張解はそれを満たさない。 また、全ての測地線が通過する(膨張の初期の)点は計量を0にするのではなく、物差しのサイズが0になるために、無限大にすべきである。 これは、意図した結果が正しく実現できていないことだろう。逆数にできてしまって、それが正しいと認識している。アインシュタイン宇宙と、 ド・ジッター宇宙でも、観測される宇宙の周辺で無限大の計量を与えるが、そのようにである。

(この章、2019/7/1)

２４. WMAP衛星の観測による宇宙の年令・運命、ほぼ結着?

物質は4%、ダークマター23%、残りの73%はアインシュタインの宇宙定数(ダークエネルギー)とする。ハッブル定数は、71 (68〜75)。 宇宙は平坦(曲り方3%以下)で、加速膨脹を続け、800 億年後の宇宙のサイズが現在の100倍になるという。最初の天体形成は、誕生から 2 億年というのには驚く。宇宙の温度分布図だけから、宇宙定数の存在と大きさが決り、宇宙の年令を確定できるという。

150億年のなか太陽系形成 50 億年、銀河形成 50 億年ならまだ余裕があるようにみえた。銀河形成に 10 億年と言われてもまだ 可能に思えた。しかし、最初の銀河が光りだす、再イオン化時期が最初の 2 億年なら、すべての大構造をその後にするしかないようにみえる。

基本的に宇宙定数は他に存在の証拠は全くない(*)。 インフレーション理論の存続のため、平坦性を前堤にして、長い間多くの研究者 を悩したダークマターの不存在のつけを、不確かな宇宙項のせいにしただけである。それによって、どうして宇宙の年令が確定したというのか。 平坦であるための物質の欠損分を宇宙定数に割り当てると、年令が伸ばせ、ほぼ無矛盾な宇宙年令が計算できるというだけのことである。 都合がよすぎる。ダークマターを約束し、それが嘘だったインフレーションも責任を取らされず再び安泰なのか。ダークマター探しを させられた研究者は、ダークエネルギーはどうするのか。それは、物質ではないから探しようがない確かめようのない仮説である。 そういう論理は、そろそろ見限ったほうがよい。

その前堤である平坦の証拠(宇宙の曲率測定)が、背景輻射の乱れの分布では無理があり、これを宇宙定数の測定とすることは到底できない。 これは、NASAの見解でなく、朝日に解説された方の論だが、これを"宇宙論の議論を終息させ、宇宙論を推測から精密科学にした"とは、 よくも言ったものである。ものごとを逆に言うしかないのは不幸な状態である。NASAは、10 年を経過せずに、宇宙の年齢がやはり 2 倍も違いますというのは、精密科学とは逆の状態ではないだろうか。宇宙論は、数学モデルを使った整合性だけを求める理論の取捨選択 でしかない。そういう科学であること、そういう科学の段階を示している。それゆえ、これで確定ではないと思う。数年後に我々は、 さらにどのような奇想天外な結論を聞かされることになるのかと全てにおいて白紙の状態で期待して待つべきだろう。

(*) 1995 年からハイゼットグループの測定による、遠方の超新星から予測した明るさよりも約 25% 暗かったことから、宇宙定数の存在 を初めて測定したという報告があるが、その結論は確定的ということはできない。遠方銀河のIa 型の超新星のドップラー効果(速度)と 明るさから、宇宙膨張が 50 億年前までは、減速膨張でそれ以降は、加速膨張と言われるが、遠方銀河が時刻を遡ることによる効果だけ でなく、銀河間の塵の影響も全く考慮せずに、25% の減光が加速膨張の証拠というのは言いすぎだろうと判断する。

Attila Mészáros, "On the Reality of the Accelerating Universe" http://arxiv.org/abs/astro-ph/0207558

２４.１ 大規模構造がさらに遠方にも続く

インフレーションがあって宇宙を平坦としてダークマターを仮定し、その3倍の宇宙項(斥力項)を用いる以外の、宇宙年齢を満たし 背景輻射の空間周波数分布(パワースペクトル)を説明できる初期宇宙論はないということである。質量を増やすとゆらぎの形成が高速になる。 それでも、晴れ上がりの10^(-5)のゆらぎからは、大規模構造は作れない。だから当時の見えない DM に、より大きいゆらぎを与える。

大規模構造も、赤方偏移からハッブル定数を使い距離を当てはめただけのデータでしかない。本当に大規模構造は、そのような距離を 持っているのか、それだけの過去の光だろうかと疑う。赤方偏移は事実であるが、それ以外はすべて仮定と推定である。 それがドップラー効果なら後退仮説であるが、後退それ自身の証拠はない。超新星の輝度変化に赤方偏移と同程度の時間遅れをみるのは それが物理現象全般の時間遅れを起こす縦ドップラー効果と思える現象ではある。しかし、反対に赤方偏移を後退速度と関係ない現象と みる学者もいる。赤方偏移が宇宙膨張と速度を反映したものでなければ、赤方偏移による大規模構造も意味をもたない。

2005-9-27 NASA 最遠の巨大銀河

(注意7) 2006年7月27日の朝日コムに "宇宙の「大規模構造」、早期から　すばる望遠鏡で観測" という見出しで次の記事が出ていた。 " 地球からペガサス座の方向に、光の速さで約１２０億年もかかる遠い領域をすばる望遠鏡（米ハワイ島）で観測したところ、現在の 宇宙を形作る泡が集まったような大規模構造が既に存在していたことが分かった。東北大や京都大、愛媛大、国立天文台などの共同研究 チームが２７日、発表した。宇宙は約１３７億年前に誕生したと考えられており、観測したのはまだ１７億年しかたっていない段階。 これほど早い時期の宇宙に大規模構造が見つかったのは、初めてという。（時事）"

2007年07月23日 朝日コム "最も遠い銀河を発見　地球から約１３０億光年" という見出しの次の記事があった。

"　地球から１３０億光年以上も離れた「最も遠い銀河」を見つけたと、米欧の観測チームが発表した。従来の「記録」は、 日本の国立天文台などがすばる望遠鏡で見つけた約１２８億８０００万光年先の銀河。宇宙誕生は約１３７億年前と考えられ、 今回の発見が事実なら、誕生直後の宇宙を知る重要な手がかりとなる。

　発表したのは、米カリフォルニア工科大と英仏などのチーム。ハワイの米ケック望遠鏡で、星の形成が続いている「先例のない遠さ」 の六つの銀河を観測し、地球からの距離を割り出した。リーダーのリチャード・エリス同工科大教授は 「宇宙誕生からわずか約５億年後の銀河」という。

　光が銀河団などのそばを通る際、巨大な重力で進路が曲がる「重力レンズ」効果を利用。６個の銀河の光は、地球との間にある銀河団 による重力レンズ効果で約２０倍に増幅されるといい、これを３年間かけて解析した。ただ、エリス氏は「疑い深い人たちは、 さらなる証拠を求めるかもしれない」と、発見に異論が出る可能性を認めている。

　宇宙は誕生からしばらく星のない「暗黒時代」が続き、その後、星や銀河の形成が始まる「宇宙の夜明け」を迎えたと考えられている。 最初の銀河の形成は宇宙誕生から数億年後とされ、日本も含めて各国が「より古い銀河」の発見にしのぎを削っている。 これまでの「最遠銀河」を観測した国立天文台チームの家正則・教授は「重力レンズという新しい方法で得られた非常に大きな成果。 ただ、とても暗いので確認作業が重要になるだろう」と話している。"

２４.２ 再イオン化時期の前倒しなど

地上のケック望遠鏡や、すばる望遠鏡は、分解能では１世代前のハッブル宇宙望遠鏡に劣るが、明るさでは勝っているからスペクトル 分析能力は高い。HST ではできなかったスペクトル分析ができる。再イオン化時期を 2 億年とすると、 z= 137/2 = 60 である。 (Lyman A. PAGE (0306381)の WMAP の紹介では、Z= 20。) それは、再イオン化時期を前倒して以前言っていた z= 6 を 1 桁上げ、 ギャップを短縮する話である。銀河は、実はもっと前から存在していて、もっと大きな構造もあったという方法で、膨張宇宙を無効化 しているのだろうか。

２４.３ WMAP の観測から 3 年目

WMAPデータを満たすのは、初期ゆらぎが Power law スペクトルを伴う断熱を仮定し、スケールインデックスがハリソン・ゼルドビッチ ・ピーブルズのスケール不変スペクトル(Ns=1, r=1) の 1 よりはっきり小さいときの DM であるとした。3 年前に保証していた scale-invariant は間違いで、さらに λ は必要不可欠でなくなった。再イオン化時期は、3.6 億年に 2 倍に戻している。

WMAP 3-year を元にした様々な議論が始まった。例えば、2 程度の楕円性があることの議論、 大規模構造の追跡性としてのCMBの楕円性 これは、今の空間パワースペクトルでは表せないパラメタであり、双曲空間での測地線混合によるのではとする。 宇宙項と質量の同期は、宇宙項が質量密度とリンクしているという説(0607085)。等方曲率の話、東大のニュートリノ質量の上限 2.0eV の話、余剰次元による 2 次 Kalzua Klein 粒子によるCDMの量推定、Hybrid インフレーション理論の話がある。 インフレーション理論への制限の話(0605338)、大角度(low-l)相関がある問題(0605135)。CMB から宇宙の最小半径を 24Gpc とする話 (0604616)、弱い4重極のオッカムの剃刀の話(0604410)、MOND の話(0312570)。

結局、宇宙項なしでも WMAP のデータに一致するではなく、宇宙項なしの方が一致するのである。 2003 年 2 月の WMAP の最初の 1 年の結果の報告 astro-ph/0302209 では、この結果に一致するのは λCDM であると言い切っていた。宇宙論をλ+CDM に制限したという自信をもった言い方だった。 3 年後の報告では宇宙項は必要でないという。これを信じて "96%の謎" という表題の本を書いた人、そのような受け売りを読ま された読者は、被害者である。観測は怖いもので、どのような推測や操作ミスも入り得る。観測は責任を取らない。数年後の否定 にも咎められず、それを本人すら意識しない。そのような現代科学の姿勢を、我々は失望をもって知るのである。

そして、WMAPの報告を受け売りする日本では、なぜ主流の説だけを全く問題がないように主張するのだろうか。この階級社会では自分 が主流に属していることを示さないと生きられないのか。自ら主流を任じるなら傍流の考えに寛容であるべきなのに決してそうでない。 そういう弱い考え方が誤解を招く表現をさせる。正しいことでも一方的、天下り的説明で済ませてしまうと反発を生む。また、他の考え 方に対する口を極めた攻撃は、見識ある人格を損ねるものである。

２４.４ 最も遠方の銀河団

東大数物連携宇宙研究機構などの研究グループは１０日、地球から約９６億光年離れた銀河団を発見したと発表した。(中略) 銀河団は、赤色を帯びた銀河で構成されることが多い。赤い銀河では新しい星の誕生がほとんどなく、成長が止まっているという。 今回観測された銀河団にも赤い銀河が多く、光を放った９６億年前に既に成長を止めていたことになる。(後略)

最も遠い銀河団発見＝宇宙誕生から１０億年−すばる望遠鏡で・国立天文台など (2012/04/24-18:03時事ドットコム)

国立天文台などの研究チームは２４日、すばる望遠鏡（米ハワイ島）を使った観測で、これまでで最も遠い１２７．２億光年先に、 銀河が集まる銀河団を見つけたと発表した。約１３７億年前の宇宙誕生から１０億年に満たない時期の「原始銀河団」の発見は、 宇宙の構造が形成される過程を解明する手掛かりになるという。(中略) 宇宙には、銀河団のように銀河が集中する場所が点在し、 相互につながった網目状の「大規模構造」があるとされる。宇宙誕生直後の物質分布のわずかなむらがこうした構造をもたらした とされるが、形成過程の解明には、遠方の銀河団の観測が必要になる。(後略)

2年間で最も遠い銀河団が96億光年先から127.2億光年先になった。その理解は難しい。

２５. 重力ポテンシャルと宇宙項

F(ρ1 + ρ2)= F(ρ1) + F(ρ2)

地球の表面で、中心向きの重力 F(ρ)があるなら、逆に一様に物質が分布している中の空洞の表面の重力は、-F(ρ) だろうか。 空洞表面には空洞表面に中心から外側に向く重力があることになる。

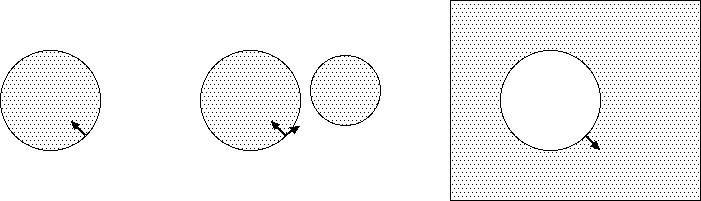
ところがこれは、よく知られているように、球対称の質量分布では、中心から半径 r の点への重力は、 r より内側部分の質量が全て中心に集中している重力と同じであり、 r より外側は、打ち消しあって関係ないという、ニュートン力学の常識とは、相容れない。

この疑問を解くため、次のように考える。空間的に一様なρのもたらす重力は、球対称に中心から r の点で、r に比例する重力になる。 半径 r の球の質量が、r^3 に比例し、重力は距離の２乗に反比例するから、r に比例する。これは、ばねの力学になり、１次元的には 単振動である。それなら空洞表面の重力は 0 であり、人が空洞に中心を上にして立つことはない。そして、これで解決だろうか。

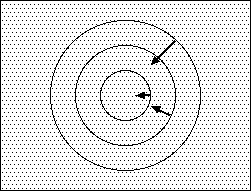
そうではない、一様なρのとき、どこかを宇宙の中心にすることに必然性はない。どの点を中心と考えても、現実的な力学を与えると いうことは、あり得ない。これは、宇宙の一様等方の前堤とは関係なく、それ以前の問題である。

しかし、重力は、なにものにも吸収減衰されず、その影響がそのまま届くとされる。オルバースのパラドックスの重力版は、無限大の破綻 に出会う。半径 r の一定厚さの球殻の質量は、r の２乗に比例し、距離の２乗に反比例する重力は、r によらず同じ大きさで中心に影響する。 これを r= 0 から無限まで積分すると発散する。もちろん、完全な球対称なら、中心への重力は、ベクトルが打ち消しあって0となり、 積分しても0であるが、打ち消しは、球殻内の質量の一様性によるので、それからのずれは、どこまでも積算され発散する。

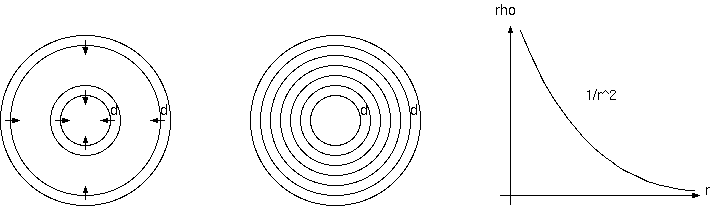
重力をスカラーの空間的傾斜(勾配)で説明しようとする重力のポテンシャル GM/r は、球殻が一様でも打ち消し合いはなく加算される。 半径 r の球殻の質量(r^2 に比例)が及ぼすポテンシャルは、r^2 と 1/r の積で、r に比例する。これは、r=0から無限遠までの積分をする 以前に、無限遠の球殻のもたらすポテンシャル自体が無限になる。ポテンシャルを破綻させないために、ρ一定を捨て、周辺宇宙の密度を 減少させると、ρ(r) ∝ 1/r で球殻の影響は、r に関係なくなり、有限になるが、積分は発散する。ρ(r) ∝ 1/r^2 でも影響は、1/r であり、 まだ積分は発散する。1/r^2 よりも急速に密度が減少するとき、初めて積分が発散しなくなる。つまり、そのような条件に入らない 一様密度の無限宇宙には、厳密なニュートン力学の適用はできない。

重力のポテンシャルが遠方で有限なら、統計力学の法則に従って星の散逸現象がいつまでも続き、定常でなくなる。逆に遠方でどこま でもポテンシャルが上昇するなら、遠方の星の運行は、高速に見えなくてはならない。これは、現実と合わない。遠方銀河の赤方偏移 を説明するには逆であって欲しい。基本的に、現実の宇宙で星の分布が遠方で疎らということは、ありそうもないことである。

C.ノイマン、ゼーリガーによる、Φ= Aexp(-r √λ)/r という指数関数的ポテンシャルを導入すれば、この困難が避けられる。 φ= exp(-ar)/r のとき、φ'= -(a+1/r)φ、φ"= (a^2+2a/r+2/r^2)φ、lim r→∞ φ"= a^2φであるから、それは、ポアソン方程式 ΔΦ= 4πkμ_0 の代わりにΔΦ-λΦ= 4πkμ_0 を導入することに対応する。この式では、一様密度μ_0に対する一様ポテンシャル Φ= -4πkμ_0/λ が存在できる。

このことは、一般相対論の重力方程式でも同じであり、斥力項のない重力方程式では、星の散乱をくい止め、星の速さが速く見えない 無限遠の境界条件は設定できない。それゆえ、宇宙に有限性を採り入れ、G_ik - λg_ik = -κT_ik(縮約して、R+4λ= κT ) という、 共変性に触れず、エネルギー運動量テンソルの保存則を崩さない斥力項λが導入された。それは定常性以外の理由では、正当化され得 ないものであった。彼がワイルに宛てた葉書では、"ド・ジッター宇宙は、任意の2点は、互いに遠ざかり、その速さはどこまでも速く なる。準静的な世界が実現しないなら、宇宙項などお払い箱だ。" とある。

指数関数入りのポテンシャル Φ= Aexp(-r √λ)/r は、距離の関数が異なるだけで、質量Mについて線形なので、重力場の線型性をもつ。 しかし恐らく重力も、一度効果を与えたら消え去る量子でできていて、通常物質では、ほとんど透明ながら、物質は重力を幾らかは遮ると みるべきだろう。重力場に線型性はなく、その式は、光の遮蔽のような質量による重力遮蔽があるだろう。

質量自体もエネルギーである。ポテンシャル中の質量もエネルギーである。無限遠から来た質量は、ポテンシャルの低下分だけ加速され 動質量が増える。質量は、周りの質量のために増加する。質量の一部は周りの影響であり、m には M の分が含まれる、マッハの原理である。 ポテンシャルエネルギーを質量に換算して、m= m0(1 + GM/rc^2) これをニュートン重力の式にいれると、F= GMm0/r^2 + (GM)^2m0/r^3c^2 これを r で積分し重力ポテンシャルは、Φ= -GM/r -1/2 (GM/rc)^2 となる。しかし、Mの2次項がある重力の式は、物質による重力の遮断 ではなく、逆に重力の相乗効果である。付加項が元の式と同符号であるから、ρ一定の宇宙の重力ポテンシャルの発散は解決しない。(*)

光のオルバースのパラドックス "夜空はなぜ暗いか" が無限大に発散しないのは、星が点光源でなく、0でない視角度(立体角)をもつからである。 ある半径の一定の厚さの球殻は、一定の光量を加算するのではなく、星の輝度(光量/視角度)の一定の面積(立体角) ds を加算しようとするが、 すでにその r までの星の存在する角度分 ∫ds は、その外側からの光を遮り、塞ぐ。積分は、そこまでの星の立体角に、一定の面積 ds *(全立体角 - そこまでの立体角∫ds) を加算し、∫(ds/dr)(4π-∫ds)dr になる。その無限遠までの積分は、有限である。夜空は、星々の 輝度で埋めつくされるだけである。星ぼしの輝度は、太陽表面の数1000度ではない。光を遮るすべての物質の平均温度、黒体温度は、 絶対温度2.7度である。この光のような関係が、重力にもあるだろうか。

2.7度の黒体輻射が説明できたとしても、赤方偏移は説明できるだろうか。斥力項が物質密度より大きい場合、g_44の大きさが周辺で大きく ド・ジッター宇宙のような行動をし、赤方偏移をする。ド・ジッター宇宙は宇宙の大きさが変化しても、物質密度=0が不変だから定常の枠 にいれることができる。密度が時間的に変動するなら定常とは言えない。

深い重力井戸の中で時間経過が 1/2 に緩やかであるとき、ニュートン力学の F = ma という力と加速度の関係はどうなっているのか。 時間は慣性質量の逆数で、慣性質量 m が大きくなって加速度が小さいとみるのだろうか。 特殊相対論の相対運動では時間経過の低下には質量の増加が伴っていた。重力ポテンシャル低下による時間経過の低下は、それと違って 質量も低下するのだろうか、謎である。 相対運動では、F= ma は、速度に垂直な力は、ローレンツ変換で 1/γ に弱まり、加速度は、1/γ^2 に弱まっていた。横質量はγ倍、 速度が小さく時間をγ倍かけないと同じだけ変位しない。速度は、1/γ、横変位は 1 のままであった。

物体は、集合するとエネルギーを増やす、それを質量に換算すると、質量を増やすという上の解釈、 これは、エネルギーは質量と等価であり運動エネルギーも質量に換算できるからであるが、 それに対して、重力現象においても全体の質量、エネルギーは変化しないという考えもありえる。 運動エネルギーが発生した分だけ、ポテンシャルの低下した場所にいるとき質量又はエネルギーが低下しているのではないか。 無限遠の平坦な時空からあるポテンシャルの地点に物体を持ってきて物体が運動エネルギーを得るのは、そのポテンシャル低下分を 埋め合わせているに過ぎないのかもしれない。引力によって結合すると物体は発生する運動エネルギーを散逸させれば一般に軽い。 物体が結合するとき、取り出す運動エネルギーの分(重力ポテンシャルの低下分)だけ質量欠損する。 それは、水素よりもヘリウムの方がより強く物質が結合し、質量欠損分を核融合エネルギーとして取り出すのと同じである。 重力ポテンシャルは、質量と慣性を決めているのかもしれない。これは、周囲の質量が物体の質量を減らすことになり、 マッハの原理の逆になるが、そのことが宇宙的な場合のポテンシャルの発散を防ぐかもしれない。 そうすると、二物体が遠くから近付くだけで、質量を増やすということはなくなる。しかし、物体が収縮して質量を減らすのなら、 遠方から物体がブラックホールに落ちるとき、地平線では質量が0になり運動エネルギーだけになるのではないか。 質量が全て0になるなら、地平線では運動エネルギーも0になる。これではブラックホールは得るものがないという不都合なことになる。

つまり、物体の集合において、次の3説があり得る。

(1)運動エネルギーの分だけ増加する説(質量は不変)。これは常識的説だがなぜ増加するのかが理解できない。 物体は配置によって質量を変えるものではないのではないか。

(2)運動エネルギーの分、質量が減っているという説(全体エネルギーは不変)。質量がポテンシャルエネルギーの低い場所にいるだけで 低減しているのではないだろうか。運動エネルギーを加算した全体のエネルギーは一定とする考え方である。

(3)質量は不変で光速の低下によって物質のエネルギー mc^2 が減る説。 c をその場所の光速とする。 （全体エネルギーが不変)慣性を決める質量は変化せずに、ポテンシャル低下に伴う光速の低下によって静止質量のエネルギーが 低下しているのではないか。

２６. 宇宙膨張のポテンシャル上昇による赤方偏移

ある質点 i から任意の位置の点xのポテンシャルは、質量に比例し距離に反比例する φ_i = -G M_i/R_i 。質量が不変で間隔が変化する とき多質点からのニュートン重力ポテンシャル φ = -GΣM_i/R_i は、各質点 M_i からの距離、R_i の膨張によって、時が進むにつれ、 負値の絶対値が小さくなり 0 に近付き、値は上昇する。宇宙膨張があればニュートン重力ポテンシャルφは、宇宙の大きさの指標 a(t) に反比例して時間変化する。物体間の距離の拡大によるポテンシャル上昇は、ニュートン力学の枠内で容易に理解できる。

そして、過去において、距離 R_i が小さかったためにφが低かったことから、過去の時間経過の遅れが存在すると考えられる。 ポテンシャルと時間経過の速さの関係、ポテンシャルφの低い時空点の時間経過は高地より遅い。過去に時間経過が遅い場合、 過去からの光は、低地からの光と同様に赤方偏移する。ポテンシャルφの時間経過への影響は、アインシュタインの 1911 年の論文、 "光の伝播への重力の影響について" によって解明された。一様な重力が加速系と原理的に区別 できないとすると、時間経過は、ポテンシャルφに直接に関係し、1 次近似で (1 + φ/c^2) に比例する。

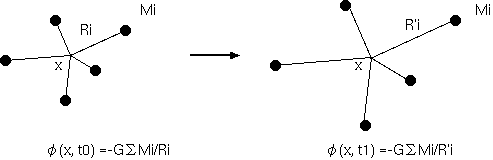
そのため、この赤方偏移が存在すれば、この赤方偏移は、膨張速度ではなく、その時間積分である過去と現在の宇宙のサイズ比によって 大きさが決まる。それに対してドップラー効果は、光を発したときと受けるときの相対速度で決まる。仮に膨張しても現在停止し相対速度 がなければ、ドップラー効果はなく、ポテンシャルの赤方偏移はあることになる。この宇宙のサイズに直接時間経過が関係するために 赤方偏移が起きるという考えは、光の波長が空間の膨張に合わせて伸びるという考えと宇宙膨張比がそのまま影響する点が類似する。 光の波長が伸びるという考え方では、過去に 1/2 の物体間から現在の距離にサイズが 2 倍になれば、赤方偏移(1+z)も 2 倍、物体間距離が 1/1000 の過去からの光は、1000 倍に伸びる。これは、速度と違う位置ということから起き、ドップラー効果とは質の異なる現象である。 しかし、ニュートン・ポテンシャルを介する点で、空間膨張に光の波長が比例するという考えとは異なる考え方である。

一般相対論の計量 g_ik を使うフリードマン宇宙の膨張は、宇宙の大きさの変化、空間計量 g_ik (i,k= 1-3) の時間的変化であって、 時間計量 g_44 の時間的変化ではない。それは物差しの時間的短縮からくるものである。空間的距離の増大からくるニュートンポテンシャルの 時間的変化による赤方偏移の説明は、g_44 の時間的変化であるから時間加速と同じものになる。

しかし、時間計量 g_44 とポテンシャルとの間には、直接に換算できる関係があって、ニュートンポテンシャルが困難を抱えるなら、 一般相対論も同じ発散の困難さを抱えるのである。それを避けるために、アインシュタインの空間的に有限の定常宇宙は、密度によって 大きさが決まっていたし、フリードマン宇宙も密度が臨界値以上では時間的にも空間的にも有限であった。一様な密度で無限の宇宙は、 密度 0 で宇宙項 0 という特別な状態以外、静的に存在し得ないし、密度 0 は、現実的でもない。

もともと無理なニュートン力学で宇宙を考える意味は何かというと、宇宙の基本的特性がニュートン力学と違わない場合、 ニュートン力学が一般相対論の結論のさらに単純なモデルとなり得ることであろう。ポテンシャルの発散の問題のように、 我々が一般相対論の結論を採り入れた、常識的に言われる幾つかの特性は、むしろニュートン力学の宇宙論の特性であって、 一般相対論でなければ言えない、というものではないのである。

同じ時刻を表すのに時刻 t とは別の時刻τを考え、t の関数である時間経過の速さ f(t) は、t のτに対する変化率 dt/dτであるとき、 これらの関係は、dt/dτ= f(t) という微分方程式になる。最も単純な例として、時間経過の速さが t に比例し、現在 t= 1 で両時刻が 等速 dt/dτ = 1 とすると、f(t)= t となり、微分方程式 dt/dτ= t は、τと t の関係、τ= ∫1/t dt = ln(t) + C を導く。 現在 t= 1 が τ= 0 にあたるが、t= 0 の時刻は、τでは無限の過去 τ= -∞ になる。

より現実的なポテンシャルを介在した時間経過への関数 f(t) は、宇宙膨張が直線的膨張で R_i ∝ t、φ∝ -c^2/t (現在時刻 t0≫1) とすると、f(t) は、1 次近似の (1) (1 - 1/t) 又は、より正確な (2) √(1 - 2/t) であり、 (1)は、dτ/dt= t/(t-1)、τ= ∫t/(t-1)dt = t + ln(t-1) + C 、(2) は、dτ/dt= √(t/(t-2))、τ= ∫√(t/(t-2))dt = √(t(t-2)) + C それらは、現在時刻の近く t0≫1 では興味深いものではないが、(1) では、時刻 t=1 がτの無限の過去になり、(2)では t= 0,2 間でτが虚数になる。

現在の時計からみて過去の時計が遅いとき、現在の時計のきざみを過去に延長して時間軸にきざみ、過去の時間を現在の時計で計る。 現在の時計のきざみで過去を測るのが 137 億年とするなら、本当に物質が経験したかもしれない過去の時計のきざみの累積時間は、 決して 137 億年のままでない(上の考えではそれより短い)と考えられる。しかしこの話には、一般相対論の重力方程式で初めて与えられた 物差しと時計の変形の物理的根拠がないように思う。

これは、時間の伸び方とは逆であるが、空間的距離において、物差しが場所によって伸縮していて、各場所の物差しの累積的距離を もって距離を計るなら、ある場所からある点までの距離が無限ということがある。ブラックホールの外部の場所から事象の地平面まで の距離は、途中の一里塚の間隔が短縮していて、一里塚を数える距離( 累積距離 )は、無限になる。そのような、 離れた時空点の計量の扱いがニュートン力学とポテンシャルによる時間遅れから発生することは、驚くべきことではないかと思う。

ふつう天体から距離が離れるとき、運動エネルギーは位置エネルギーに変化し、物体は速度を落とす。一様なポテンシャルの時間的変化では 物体の速度を落とさずにエネルギーが増加する。このことは、あり得ないことのように見えるが、質点間が増大するだけで起きることである。 時空図は通常、時間軸を上向きに取る。そのことは、ポテンシャルの上昇を意味している訳ではないが、それと符合している。

ポテンシャルを、その勾配が重力である空間的現象だけと考えるのは、過去の天体配置のポテンシャルが言えなくなる。過去と現在の物理法則 を違え法則の不変性を保てない。(ポテンシャルによる時間経過の変化は、小さいから無視できるだろうか、次項で大きさを考察する。)

天体間隔が慣性によって止まっているなかで物差しだけが縮小すると考える膨張宇宙の解釈では、空間計量だけの変化に伴って、時間計量も 変化する。つまり、空間計量だけの変化であるフリードマン計量があり得ないことになる。このように物差しと天体間隔に同時的な変化を 認めないと矛盾を招く。"共動座標系"という言葉の意味もそれを指している。 (宇宙のサイズ(空間計量)が説明の逆数にみえる問題は残っている。)

２６.１ 重力ポテンシャルの時間経過を考慮した赤方偏移

(dy/dx)^2= (1+cosθ)/(1-cosθ)= (2-y)/y .....(1)

位置エネルギーが運動エネルギーに変わる運動、天体からある距離で速度v＝0で放たれた質点が天体に向かう自由落下は、1次元なので 楕円運動ではないが、天体との距離r(t)はサイクロイドになる。Φ0= -GM/r0(速度v=0のr値をr0)として、

1/2 v^2 = GM/r + Φ0 ....(2)

天体質量Mとニュートン重力定数Gの積GMを1にし、r=2の頂点で速度v=0のとき、

(dr/dt)^2 = 2/r - 1　(r＜2) .....(3)

これは、角をpとする半径1のサイクロイドである。 t= p-sinp, r= 1-cosp, 速度は dr/dt= (dr/dp)/(dt/dp)= sinp/(1-cosp)。 ∵ (dr/dt)^2= sin^2 p/(1-cosp)^2= (1-cos^2p)/(1-cosp)^2= (1+cosp)/(1-cosp)= (2-r)/r= 2/r - 1。

v^2= 2GM/r + C の C＜0 のときサイクロイドである。フリードマン解の物質密度ρ＞ρ_critのとき、膨張速度dr/dtの 2乗の運動エネルギーは、天体間の重力ポテンシャルになって、宇宙のサイズr(t)はサイクロイドを描く。 C＞0 では (dr/dt)^2= 2/r + 1 の単調増加関数であり、C= 0 の 臨界状態 v^2= 2GM/r では、 r(t)∝ t^(2/3)の解、r(t)= c t^(2/3) (c= (2GM x 9/4)^(1/3)) をもつ。 ∵ r(t)= ct^(2/3) なら v= c 2/3 t^(-1/3), v^2= c^2 4/9 t^(-2/3) = c^3 4/9 1/r

これは、時間計量g_44 (標準値で-1) とポテンシャルΦ＝-GM/rとの関係と式が同じであるが、rの範囲が(3)とは相補的である。

-g_44= 2Φ/c^2 + 1 .....(4)

g_44= 2/r - 1　(r＞2) .....(4-1)

r=∞のとき標準値のポテンシャルを1とする時間経過の速さを表す。GPSの高度での時間合わせは、ポテンシャルと時間経過の関係を使用する。 時間経過は√-g_44= √(1-2/r) (r＞2) であり、低地からの光の赤方偏移にはこの式が使える。地上から光を発し高みに達するまでの時間は0 ではなく、ポテンシャルと時間経過の関係は、太陽系の端、銀河の端までも成立するだろう。そして、それが100億光年までも成立するなら、 膨張をみる系では後退のドップラー効果以外に、過去の密集した宇宙の時空点の、現在とのポテンシャル差も赤方偏移の原因となるだろう。

ドップラー効果の赤方偏移 1+z= √(1+v)/(1-v) に重力ポテンシャルからくる時間遅れを乗算する。時間経過は√-g_44= √(1-2/r) (r＞2) であり、 ポテンシャルからくる赤方偏移はその逆数である。これは、臨界膨張速度vとして 2/r= v^2を使うときの特殊相対論の時間遅れγと等しい。

1/√(1-2/r)= 1/√(1-v^2)= γ ....(5)

ドップラー効果と時間遅れの両方の積の赤方偏移は、

1+z= √(1+v)/(1-v) / √(1-v^2) = 1/(1-v) ......(6)

であり、 vの増大とともにドップラー効果√((1+v)/(1-v)) との違いは大きく、v〜1の近辺ではドップラー効果√(2/(1-v))の2乗に近い値 (の1/√2倍)になる。逆に赤方偏移1+zから後退速度vを求めるときは、例えば 1+z= 1000の後退速度は、

ドップラー効果だけ考慮した 1+z= √(1+v)/(1-v) からは v= 1- 2 x 10^-6 だが、
ポテンシャル効果も考慮した 1+z= 1/(1-v)       からは v= 1- 10^-3  になる。

２７. 横ドップラー効果による赤方偏移

横ドップラー効果は小さいからあり得ないという印象は、直ぐに否定できる。横ドップラー効果は、後退による赤方偏移よりも効果が小さいが 限界はなく、固有運動が光速に近付くと、後退仮説と同じくやはり無限大の赤方偏移(z→∞)まであり得る。

遠方銀河の横方向の運動があれば、すでに検出されて然るべきだろうか。例えば、天の川銀河の直径10万光年というその大きさを考えれば、 銀河系外の天体の横方向速度を横ドップラー効果以外に単独に検出することは難しいことが分かるから、この効果が見過ごされている可能性がある。

横方向速度がもたらすローレンツ短縮が見られないという疑問は、光で見る球体のローレンツ短縮は、速度の前面が側面に回転して見えるだけで、 球体として見られることが知られている。ローレンツ短縮は光によって見られる効果ではない。

横ドップラー効果は、速度の2乗に関係し光速近くになって急に発生するから、距離に比例しないのではないかという疑問は、ランダムな運動の 累積の速さの期待値は、累積の平方根に比例するという効果によって打ち消しあうことができ、後述するように、かなりの線形関係をもたらす。

固有運動による赤方偏移は、後退仮説と違って、基本的に宇宙の始めを考える必要がなく静止宇宙論になる。無限の過去から宇宙がランダム運動 をする銀河に満ち、銀河間の相対速度が光速の近くに達していると考えることは、我々にとって新鮮な考え方である。この考えにおいても、 ハッブル定数は、後述のように存在を許されるが、ハッブル時間、宇宙の年齢には結び付かない。そして、"速度場" のようなエーテル仮説をとる 必要がない。しかも、この考え方は、赤方偏移の原因として未知の物理的過程を考える必要がない。横ドップラー効果は、特殊相対論の最初から 明確にされよく知られた効果である。それゆえ逆に疑うべきは、この考えは誰もがもはや熟慮ずみであって、明確に否定できる要素があるのでは ないかということである。そこで、この考えの長所、短所を考えよう。

z+1 = √((1+β)/(1-β))

と表される。横ドップラー効果は、

z+1= γ= 1/√(1-β^2)

であり、β= v/c の2乗に関係する。

例えば、z= 1 の赤方偏移 (z+1= 2倍の波長の伸長)は、後退速度では、v/c= 3/5= 0.6 に対応し、横速度では、v/c= √3/ 2= 0.8660 に対応する。 大きな赤方偏移においての話であるから、0.6 があり得て、0.8660 があり得ないということはない。

横ドップラー効果は、距離によるランダムな速度の加算を使うので、後退仮説とは明らかに違って速度が距離に比例せず、その√に比例するから、 一見、赤方偏移が距離に比例するハッブルの比例関係を満たさないかのように見えるが、βの 2 乗の関係がそれを打ち消し、距離の小さい間は、 z が距離に比例する関係が得られる。

後退では、β= Hx であるとき、

z+1= √((1+Hx)/(1-Hx))

であるが、横速度は、距離の√に比例するから、

β= √(H'x)

これを z+1= γ= 1/√(1-β^2) にいれると、

z+1= 1/√(1-H'x)

である。この式は、後退仮説のドップラー効果の式と分母が等しく、赤方偏移の効果を約2倍にする分子側の項がないことだけが違う。 全体としても大して違いはなく、この仮説が整合するかもしれないと思われる。(Jun. 16 2007)

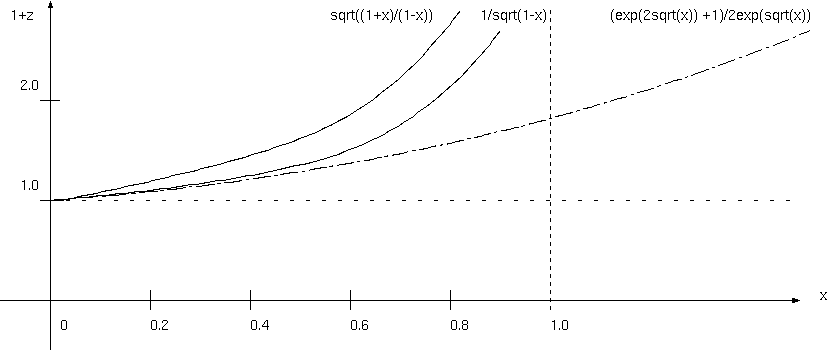
横ドップラー効果は、遠方銀河の赤方偏移分布が後退と違って、より広くなる。それによって検証/反証可能かもしれない。 銀河の固有運動が青方偏移までの範囲に拡がり、距離に対する赤方偏移分布が広すぎて、観測に合わないことはあり得ることであるが、 逆に、後退仮説では銀河の固有運動を小さく見るから、現実の距離に対する赤方偏移の拡がりを説明できない可能性もある。

また、相対論的、速度加算の定理を使い、u,v の加算を (u+v)/(1+uv) とすると、光速制限が起き、上図の 0＜x＜1 の空間制限がなくなる。 y= √x として、u=dv とし、dv/dy= lim_(dv⇒0) ((v+dv)/(1+vdv) - v)/dv= 1 - v^2、微分方程式 dv/dy= 1- v^2 から、dv/(1-v^2)= dy、∫dv/(1-v^2)=∫dy、1/2 ln |(1+v)/(1-v)|= y+c、(1+v)/(1-v)= e^(2y)、 v= (e^(2y)-1)/(e^(2y)+1)= (e^(2√x)-1)/(e^(2√x)+1)。1+z= 1/√(1-v^2)= (e^(2√x) +1)/2e^√x= cosh(√x)。 1+z は、広範囲に直線的になる(図参照)。

横速度の 2 乗が後退速度と同じ働きをして、赤方偏移と距離の線形の関係が保たれる。ハッブル定数 H が赤方偏移を後退速度に換算する 測定値であるから、後退仮説と比べて効果が約 1/2 に小さいことは、H' の値に反映されるだけで測定に隠れてしまう。速度分布が 0 を 中心とする標準偏差σの 3 次元ガウス分布のとき、その縦横ドップラー効果は、中心をσにおく分布となるかどうかが問題のようである。

銀河の距離に対する赤方偏移において、固有運動によって、赤方偏移の標準偏差の距離に伴う増大(∝√距離)が実現される。後退仮説の始 まりのある一様な宇宙では固有運動の距離による累積を通常考える必要がない。空間的相互作用は膨張のために少なく、膨張座標系からの 固有運動は空間依存でない。さらに、光でみる場合、遠方は過去であり宇宙年齢が若く相互作用時間が短い遠方では固有運動はむしろ減少 すると考えられる。それに対し、この説では固有運動の拡がりは、時間に依存せず、距離だけに依存する。それゆえ、距離に対する赤方偏 移の拡がりは、むしろ拡がり過ぎる可能性がある。3次元の速度分布は、正から負まで中心が0のまま距離の1/2乗で拡がり、その縦横ドップ ラー効果の結果としての赤方偏移の分布がどうなるかは簡単に予想できない。

２８. ハッブルの銀河分布

log N(m) 〜 0.6 m

の意味を考える。星のみかけの等級 m は、1 等星と 6 等星 (5 等級差) の明るさ L の比を 100 倍と決めたから、

m= -2.5 log L + c

である。L は、距離 r の 2 乗に反比例し、10 pcの距離においたときの等級、絶対等級 M を使って表すと、

m= 5 log r + M - 5

そして、逆に距離 r [pc] は、m - M によって決まり、

r= 10^(0.2(m-M)+1)

である。等しい絶対等級 M の銀河が空間に一様にあれば、あるみかけの等級 m までの銀河は、距離 r 内に存在し、その個数 N(m) は、r^3 に比例する。

N(m)∝ r^3 = 10^(0.6(m-M)+3)

log N(m) 〜 0.6 (m-M)

0.6 m は 5 等級差に 10^3= 1000 倍の個数を意味する。近傍の１等星までのシリウス、カノープスから始まる 12個から 6 等星までの星の数は 12000個になり、約 6000個といわれる可視恒星数と誤差 2 倍程度で合う。明るい恒星の分布は太陽系近傍の恒星の一様な分布を反映し天の河銀河 の構造を示さなかった。銀河の空間分布においても、もし、銀河間宇宙がどこまでも透明で、銀河が等しい明るさであれば、みかけの等級 m まで の個数には、個数の対数と暗さの対数である等級との線形関係、log N(m)〜 0.6 m が推定できる。 (*)

銀河に 2 種類の M が混合している場合、みかけの等級 m になるための 2 種類の距離 r(m-M) があって、体積が異なる。そして両者の存在密度 が任意であるとしても、両者とも m の変化に対して log N(m)〜 0.6m であるからといって、両者の和 N(m) が log N(m) 〜 0.6m とはいえない。 N(m)= N1(m) + N2(m), log N1(m)= 0.6m + c1, log N2(m)= 0.6m + c2 であるとき log N(m)= 0.6m + c1+c2 ではないからである。

みかけの等級 m の存在確率は、P(m) = P(M) P(d(m-M)|M) として、P(M) を銀河の絶対等級 M の存在確率とし、距離によって M が m になる 条件確率 P(d(m-M)|M) (実際は距離と m-M によって M 自体にはよらないだろうから、条件確率である必要はなく、独立の確率でよい。)の積 として表される。積の log は和であり、log N(m) = log P(M) + log P(d(m-M)|M)、この考察では、P(M) がそのまま影響を残し、それ以外の項 が 0.6(m-M) であることを示す。

(2) 宇宙膨張の影響。ハッブルの発見した、距離に比例する速度があれば 0.6 を変える。赤方偏移は、ν'= ν √((1-β)/(1+β)) 〜 1-β のエネルギー低下であり、βが距離 r に比例すれば遠方を暗くする。これは単純に距離の 3 乗に明るさが反比例するなら、log N(m) 〜 0.4m であるがそうではなく、r が 1 に近付いて初めて大きな効果をもたらす。r を宇宙の果てを1として現在のハッブル定数を宇宙の果て まで使うと、L ∝ {√((1-r)/(1+r))/r^2} であり、m-M= 5 log(r) -5 -1.25 log {(1-r)/(1+r)} であり、これから r を m-M によって表し、 N(m)〜 r^3、log N(m)〜 3 log r を m-M によって表すことができる。 (**)

(3) 曲率の影響。負の曲率をもつ宇宙では遠方が広く N は大きくなるのだろうか。0.6 は、宇宙が曲率をもたないことを意味するのだろうか。 距離 r 内の体積が r^3 より大きい場合、N(m) が単純に増加すると考える場合、曲率がこの 0.6 を変える。球の体積∝ r^3 だったから、 0.2m の 3 倍の 0.6m だったわけであり、これが 3-α であれば、0.2(3-α)m になるだろう。

正の曲率では遠方が狭いが、凸レンズ効果で個々の銀河は大きく見えるため明るい。負の曲率では遠方が広いが銀河個数の多い分、小さく 見え光度が低い。遠方がどこまでも明るい宇宙は、この場所に光を集中する宇宙になるのでありえない。オルバースのパラドックスがもつ 一様宇宙原理は、曲率によらず NL 積一定であろう。ある距離 r までの領域が境界表面積 S(r)= r^(2-α) をもつとき、曲率αは、S に 影響するだけで、境界を行き来する光の密度は、r によらず、ここ(r=0)と等しいから、銀河の個数 N が面積 S に比例するなら、銀河の 個々の明るさ L は 1/S に比例する。曲率は、この 0.6 を変えないと思われる。

(4) 銀河間の塵を考えて銀河間宇宙が透明でない効果は、銀河の分布で打ち消すことができる。しかし、これは一様性を崩し、この 場所を特別扱いする宇宙になる。少なくとも 10^-31〜10^-32 g/cm^3 以下である必要がある。という議論がある。

銀河の絶対等級の存在確率は、他の方法で確認することができるだろうし、宇宙膨張のドップラー効果が、ハッブルの銀河分布を容易に説明せず、 最終的にハッブルは、決して宇宙膨張を認めなかった。彼の発見による銀河の赤方偏移と距離の関係は、彼が赤方偏移に速度の単位を使ったため、 宇宙膨張と直に理解されたが、そのことは外ならぬ彼にとっては理解不能だったのである。後半生をかれは、地上の最大の望遠鏡 Wilson 山の 2.5 m 鏡を使って銀河の分布測定に一生を捧げた。これは決して容易でない問題を含んでいた。現代がこれを格段に超えた立場にいるかどうかである。

この項の考察を訂正した。N(m) は、等級 m の個数ではなく、等級 m までの個数であった。ゼーリガーは、1860 頃に銀河が空間に 一様に分布し銀河間の光の吸収がないとすると、等級mとm+1[まで]の数の比は、N(m+1)/N(m)= 10^0.6= 3.98 〜 4 を示した。 N(m) は空間の半径 r の 3 乗に比例し、N(m)∝ 1/L でなく ∝ (1/L)^1.5 であり、log (m) 〜 0.6m でよい。(2008年9月25日)

(*)アンドロメダ銀河の等級が+4.3これが5等級程度なら、10等級までは1000個、15等級までは100万個、20等級までは10億個である。1950年代 からの地上の5m鏡の限界は23等級であり、宇宙の銀河総数を数1000億と聞くが、HSTが30等級を限界とすると銀河の個数は1000兆個にもなる。
(**)個々の光子のエネルギー低下と、時間間隔が拡がりから、ドップラー効果の2乗の影響で(βをvと書き換えて)、(1+z)^2= (1+v)/(1-v) で暗く なる。見掛けの等級は、m'= 2.5log((1+Hr)/(1-Hr)) + 5 log(r) + M - 5、距離rが赤方偏移比率 (1+z)だけ遠い r'= r*√(1+Hr)/(1-Hr)) ように みえる。そのため、log N(m) は (1+z)の3乗だけ小さくなる。(2012年4月22日)

２９. パイオニア異常 (Pioneer anomaly)

この現象は 1998年から報告され、その解析に JPL は、いまだに力を割いている。パイオニア10号は木星の側を過ぎて、 11 号は木星と土星に接近し、海王星の側を過ぎて太陽系外に出ていった。太陽系外に初めて達した物体の正確な位置測定の分析から、 ある距離を超えて太陽光圧の加速が 4 x 10^-8 cm/s^2 程度になって現象が明確になった。10号の後半のデータと、11号のデータから 太陽方向への一定の加速度が検出された。独立の異なる 3 つの解析プログラムがほぼ同じ結果を出している。

原因として、通常の推進剤ガスの洩れ、アイソトープ Pu 電力源の熱の洩れの非等方性等、太陽系のカイパー帯の塵の密度 による抵抗などが検討され、除外されてきた。さらに、太陽からある程度の距離 (20-70AU) 離れてから場所に依らない、 ほぼ一定の加速度であることから、全く新しい物理現象の発見かもしれないと思われている。

距離の 2 乗に反比例でない新しい物理的な機構による重力的な原因によるか、定常的な青方偏移であるから、宇宙の赤方偏移を 引き起こす原因となる時間経過の加速が原因かもしれないとされる。時間加速を正確に理論付けることができるか、また独立に 再確認されることが必要である。

全体のデータが再検討されようとしている。加速度の方向が1)太陽方向、 2)地球方向、3)速度の逆の方向、4)回転軸の方向 であるかを現在分離できない (これらは、現在ほぼ同じ方向になっているから) ので、これを分離できるよう 10 号 11 号 の前半のデータの検討がなされようとしている。1)であれば重力的、2)であれば時間的、3)であれば抵抗的、4)であれば系統的 誤差の可能性がある。それでも解消しないなら、このパイオニア異常の目的だけの探査機を打ち上げる計画が作られるという。

パイオニア異常を説明しようとする多くの物理学の提案がある。arXiv のサイトの検索で abst に Pioneer anomaly で検索すると 2008年8月26日現在、117の論文が出る。このなかで、一般相対論による宇宙論を否定する J. C. Hodge の "Scalar potential model progress" http://arxiv.org/abs/0704.0487 は、このパイオニア異常の大きさが ニュートン力学から一般相対論による修正の量よりも 2 桁も大きいという。 これに、解決すべき標準的な宇宙論の問題点として次が挙げられていた。

(1) ダークマターとダークエネルギーの特別な導入の必要、(2) パイオニア異常、(3) 原子以下の粒子の観測と不両立、(4) 重要なパラメタに 微調整の必要、(5) 銀河と銀河クラスタのスケールの観測に不両立、(6) セファイド星を使用した銀河間の距離Dと銀河中心赤方偏移 z の D＞10Mpc の貧弱な相関、 (7) 観測と両立する銀河と銀河クラスタの進化モデルの欠如、(8) マッハ原理の適用の欠如。 その他、標準モデル支持者がそれらの証拠を含むデータの解釈を拒否するものとして、(1)離散的 z、(2)銀河に隣接するQSO、(3)マージで なく放出による銀河形成、(4) z がドップラー効果以外の内在的原因、があるという。

多くの新しい物理法則の提案が登場するなかで、忘れられた項の提案として未解決の減速が特殊相対論のγによっているという話があった。 http://arxiv.org/abs/0910.1641 JPLが特殊相対論の質量増加による減速を考慮してい ないなら、単純な解決である。

３０. 特殊相対論の膨張の年齢と距離

(*)光速制限があっても140億年前に静止した140億光年先の物体が存在する(静止又は乱数的運動)宇宙では、この問題は起きない。一点から の宇宙膨張では、ある面の先に光速未満の速度の物体はひとつもないという地平面がある。(膨張光円錐の外側は、物体速度が光速以上であ るから存在しない、又はそこからの光は到達できず検知できないという、不確かな領域になる。)

膨張と特殊相対論を結合した、光でみる宇宙の姿は、140億年の歴史を、70億年に短縮して見せる。これには、初期宇宙の早送りがある。 光速に近い宇宙の周辺は、時間が殆ど経過せず、例えば最初の40万年のマイクロ波背景輻射がある。それより近い手前の速度の遅い部分は、 そこに飛んで行くまでの時間経過がもう少しあって、1000万年後とか1億年とかの姿を示す。距離と時間の図では、特殊相対論の一定速度の 光は、傾き -1 の直線 (x=1-t) であるが、その上に宇宙が始まってからの時刻(t')の目盛を振ると、その目盛の間隔は一様ではなく遠方と 近傍とで違う。これは、赤方偏移とは逆に、遠方で時間経過が速い早送りである。光はそれらの場所を通過するとき、各点の物体の時刻は 全て別であり、光は一定の速度でそれらの姿を拾いあげるだけである。各物体からの光は、時間経過が遅い赤方偏移を示すが、物体間の年代は 早送りする。その早送りの程度は初期で大きく、近傍の現在に近付くと現在と同じ速さになる。そして全体で、140億年の歴史を70億年に 短縮する。こうして、膨張宇宙と特殊相対論とで考える宇宙の見え方は、140億年の時間と70億光年の距離をもつ。

光速に近い速度のロケットが出発し、半光年先のロケットから通信を受ける。地上では、ロケットが地球から半光年先まで行くのに半年余り かかり、電波が半光年先から戻るのに半年かかるから、半光年先の通信を受けるのは約1年後である。相対論の時計の遅れによって、連絡の 内容は、地球を出発してすぐの事情である。速度の違うロケットを10台同時に出発させ、0.1c, 0.2c, 0.3c,....0.9c,最後は0.99cとしよう。 1年後に全ロケットからの通信を受けると、速いロケットからは出発後すぐの事情が通信され、遅いロケットからは最近の事情を知らせる通 信である。10台の通信の時刻の並びは均等でない。t= 1-x, v= x/t, から t= 1-vt, t= 1/(1+v). これに t'/t= (1+z)^-1 = √(1-2x)= √(1-v)/(1+v)を掛けて t'を得る。

時刻 t' は、0.861, 0.745, 0.643, 0.553, 0.472, 0.395, 0.322, 0.249, 0.166, 0.051 である。
前隣との差、0.139, 0.116, 0.102, 0.090, 0.081, 0.077, 0.073, 0.073, 0.083, 0.115 である。

近傍から 0.7c までの7台の時刻は狭まっていく。これは同時に受信する電波の送信時が異なり、近傍でロケット間の距離が離れていること による。近傍では約1年分、遠方では約半年分の速度の違いがロケット間隔となるから 2 倍も違う。しかし、0.7c より遠方の 0.8c, 0.9c, 0.99c では再び疎らになる。図をみれば、そこでは遠方ほど距離間隔は狭くなっているが、隣りのロケットとの時刻の間隔は開いていく。

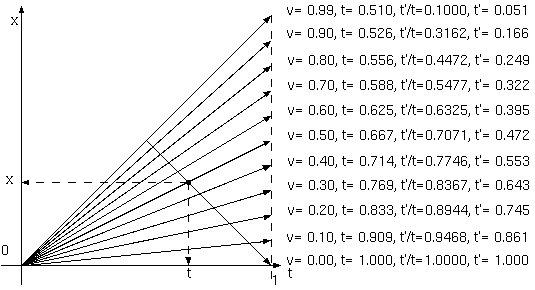
光でみる宇宙像の距離xには、光速からくる時刻 t= 1-x がある。そこ (x, t) の物体の後退速度は、(直線的膨張では) v= x/t = x/(1-x) である。それによるドップラー赤方偏移は、後退速度が直線的膨張で不変なら、始まりからの時間経過も赤方偏移と同じ比率 (1+z)^-1 で 小さくなる。そのため、その物体は、時刻tとは別の、より短い始まりからの固有時刻 t'= t/(1+z) をもつ。

特殊相対論のドップラー効果は、(1+z)= √((1+v)/(1-v)) = √((1+x/(1-x))/(1-x/(1-x))) = 1/√(1-2x) であり、距離 x と赤方偏移 (1+z) との関係は線形ではなく、距離が1/2に近付くと (1+z) は無限に大きくなる。時間経過はその逆数 1/(1+z)= √(1-2x) であり、x が 1/2 に 近付くと 0 に向かう。光でみる距離 x の天体の固有時刻は、t'= t/(1+z)= (1-x)√(1-2x) であり、その変化率 dt'/dx= (3x-2)/√(1-2x) は、x が 1/2 に近付くと無限大に向かう。つまり、視線上の天体の固有時刻の間隔は遠方1/2に近付くと無限に密になる。これが初期宇宙の 早送りである。宇宙の周辺物体は、光速に近い速度で後退し、それらの物体の空間的厚さは、1/γ倍に薄いが、光で見る距離 x の天体は、 後退のドップラー効果 (1+z) ほども詰まっている。

奥行きが浅くなって薄膜化した層を貫いてくる光は、薄膜化によってそこを早く過ぎ、その場所の人のみる局所の光より速いのではないか、 という疑問は、薄膜間の時刻が大きく違うことによって、それが局所光と同じ光速と理解できる。また、ある方向にみえる時間原点からの像は、 時刻の違うものが重なって見え、同じ物体の時系列の表示のように思うが、その間に光が届くのであるから、それらは別の物体の違う時刻の 重なりであり、同じ物体の時間変化ではない。背後の層は速度が大きく遠くまで行った物体、手前の層は速度が小さく遠くまで行かなかった 物体である。

３１. 正の曲率のある宇宙と膨張宇宙

もしも、我々の住む空間が球面のように正の曲率をもった3次元空間であったら、その体積の増分である球面4πr^2は、どこまでも増加はしない。地球 上の最短距離の大円である、北極から出る経線が、最初直線的に拡がり赤道近辺で平行で南半球では間隔を再度短縮して南極で交わるように、我々の 宇宙の辺境の大きさの増加はどこかに上限をもち、それを過ぎて減少するだろう。ある距離より遠方の銀河は、数が少しずつ減少する、とともに、 個々の銀河がそれより近い銀河より大きく見えてくる。この逆転した遠近法は、我々がまだ経験しないものである。ある距離より先が拡大される 球面宇宙では遠近は大小で判断できず、大きさがあって不透明な天体の掩蔽から判断するしかないようになる。

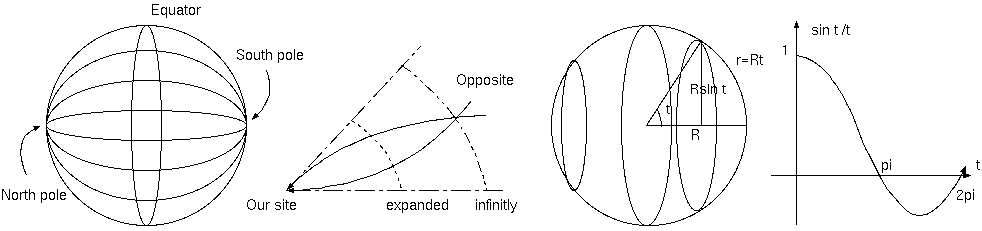
正曲率による光線の歪曲は、画像のぼやけもない一種の自然の望遠鏡であって、遠方にいくに従って拡大される図は、最後には拡大率が無限大になっ て1点からの光が全天を占めるようになる。日本を通る全ての大円がブラジルで交差するように、ここから始まる全ての光線が交差する対蹠点があって、 逆にそこからの光がここで全天を占める。先の点は、ここの反対位置というだけであって宇宙の特別な点でないから、そこからの光が再び集まって焦 点を結んでも平均的な明るさである。対蹠点に光を遮るものがなければ、その先にまた縮小していく銀河の列が見えるだろう。しかし、それらがその 点より手前の物体の上下左右前後逆転を示すことから、対蹠点の先の像であることがわかる。宇宙がどこまでも透明なら、光線は、一度対蹠点に収束 して、再び対蹠点の対蹠点の元の点に収束する。銀河は対蹠点の先は縮小していってさらに再度の対蹠点である元の位置まで再度拡大していく。光線 の収束は、そのまま遠方像における拡大である。この正曲率をもつ宇宙は、その外を知ることができない閉じた有限の体積をもつ空間である。物質は 光線をその方向に曲げる。一様に質量の満ちた空間は、この正の曲率の空間になるのが自然である。この宇宙を静止させるのに斥力項(λ)が必要だった。

遠方までの距離rを、空間の曲率半径Rとする円弧にとり、垂線の長さと角度Θ= r/R の円弧との比 sinΘ/Θ が、曲率による遠方空間の1次元縮小率 である。距離 r=πR/2 のΘ= π/2 で sinΘ= 1 の縮小率は 2/π、そのとき空間の拡がり方の極大であり、そこから r=πR まで増分は減少し最後 に1点になる。宇宙の体積は、V= ∫4π(rsinΘ/Θ)^2 dr の 0〜πRの積分である。

V= ∫4π(rsinΘ/Θ)^2 dr = 4πR^2∫sin^2(r/R)dr = 2πR^2∫{1-cos(2r/R)}dr = 2πR^2[r- R/2 sin(2r/R)] = 2 π^2 R^3
0〜πR

膨張宇宙も、遠方の拡がりは、距離の2乗に比例する球面で拡大していくようにみえて、上限があって、ある所で空間の拡がり方が極大になり、それ より先は拡がり方が減少してくる。速度 v= x/t の直線的膨張では遠方は、光が直線 x= 1-t 上をくる時間の遡及によって縮小する。光線経路と同じ 視線角度のサイズは、 t(1-t) であり、遡ると最初、増大するが極大(t= 1/2 で1/4)を過ぎ、さらに遠方で小さくなる。これの実証は全くないと思う が、膨張宇宙ではある距離より先の遠方の銀河は、拡大して見えるはずである。この自然の望遠鏡は、最後には全天が宇宙の1点に交差する。そこは、 時でいえば宇宙の始まりであり、場所で言えばどことは言えない場所で、宇宙の果てに見えていながら、元はどの場所とも同一だった点である。

静止宇宙では過去は現在と本質的に違いがないため、遠方が過去であることに意味がないが、宇宙の進化を考える膨張宇宙では、過去は現在とは違う。 膨張宇宙の遠方は、光線を遡るとどこに向かっても他に行き場のない、そこから全ての光線が発生した点に収束する。遠方は、空間曲率でなく、過去 が狭い宇宙であることによって光が逆に収束し、そこは拡大してみえるのである。膨張宇宙にも空間曲率の影響はあって、膨張と曲率の両方の影響を 受けるだろう。しかし我々は、この膨張宇宙の拡大した銀河像を意識しただろうか。HDFの赤方偏移が z= 3 とか 4 とかいう銀河は、実際に通常銀河 のサイズの1/10に小さいというが、それらは拡大して見えているから、見えるよりさらに実際は小さいのだ、という話を聞かない。

初期銀河は、現在の銀河より巨大な銀河であるという話を聞くが、それは共動座標で言っているかもしれない。共動座標は、塵が留まる座標であり 膨張を知らない座標であり、拡大鏡をもたない。現在の1/10の時刻でも共動座標では同じサイズであるが、光は現在の10倍速いということだろう(*)。 昔は物差しも含めて大きかったという計量認識では、初期の物体は原子サイズからして大きい。光速もそれに比例して大きいから、拡大鏡はない。 我々は単に縮小している。今の物差しでみると過去は物差しが大きいから波長は長い。

正曲率の静止宇宙では、その対蹠点が特異でない普通の空間の場所であるのに比べて、膨張宇宙のこの点は、特異点であり、影響が大きい一方でその 点の物理量の計算が不可能な点であって、数値的シミュレーションは、この時空点にどこまでも近い点が計算できるがその点だけは避けて行われる。 とりあえず、その特異点の温度が無限であるのに、そこからの凸レンズである宇宙は、この場所を焦がすこともなく、時空間全てに焦点を結んでいる。 いつ、どこから見ても、全天に原初の光を見る。少なくとも球面宇宙よりは膨張宇宙のほうが、オルバースのパラドックス度が高い。そこが普通の温 度である対蹠点からの光に比べて、膨張宇宙では無限の温度の特異点からの光であるからである。どう分けて無限の温度は、全時空点に有限の温度を もたらすのだろうか。無限は無限に分割して初めて有限になり得る。それに比べて有限静止宇宙は、無限静止宇宙と同等の困難であり、通常のオルバ ースのパラドックスである。

(*) 例えば直線的膨張で、光速が時間の逆数に比例する共動座標の宇宙を考えると、
c(t)= -1/t
なら光の経路 x(t) は、光速の積分で、x(1)= 0 だから、
x= -log(t)
である。共動座標から通常の座標へ変換するには、空間座標 x を t 倍して、
x= -t log(t)
通常の座標での光の経路が出る。光速は、局所的には c(t)= -1/t を t 倍すれば -1 の一定だが、大局的には間違いである。光が先にいって戻 ってくるこの通常の座標系で光速一定であるはずがない。光経路 -t log(t) を、tで微分すると、通常座標で光エーテル論の式となる。
x'= (-t log(t))'= -log(t) -t/t = -log(t) - 1 = x/t - 1

しかし我々は、それよりもずっと手前の遠方銀河の拡大の現象を見ない。背景輻射を証拠というには、現存する銀河と背景輻射との間の銀河を余りに も知らない。宇宙が膨張宇宙か空間曲率かの区別は、赤方偏移の存在だけにある。遠方は曲率が空間縮小する。過去は膨張が空間縮小する。それらは 殆ど類似した見え方である。

正曲率のある宇宙は、凸レンズのようだからといって、そのために特に宇宙が明るい訳ではない。凸レンズの焦点に明るい天体がくれば、その輝度が 拡大され広く全天に見えてとても明るくなるが、その確率はとても低い(この銀河系内の近辺の恒星間の大きさ、1.3pcと恒星の大きさ、太陽の半径は、 4000万倍あり、面積では1.6*10^15にもなる(*)が、この焦点に入る確率は体積比の6.4x10^23である。しかも、相手が銀河中にあ る確率も小さい)。それの逆に、負の曲率のある宇宙では、遠方の物体が小さくみえるが、やはり、それによって宇宙が暗いわけでもない。その現象は いつまでもそのまま続く。それらと比べて、膨張宇宙は特別である。球面宇宙の凸レンズと比べると、焦点には無限の明るさの特異点があって、我々 はそれを全天にずっと見ているから、我々は焼き尽くされて当然かもしれないが、この特異点を全天に見るのは一点でなく宇宙全体である。しかも、 特異点は最初の一瞬だけ無限の明るさであるのに、宇宙の全年代に渡ってそれを全天にみる。エネルギーを空間に分けるだけでなく時間にも分けている。

背景輻射の強さについて、数1000度の黒体輻射が、約1000倍にドップラーシフトすれば、絶対温度2.7度の黒体輻射になる。太陽表面のような輝度が、 暗黒の弱さになることは、輻射のエネルギー密度は、10^-12 = (1+z)^-4 だろう。ステファンの法則から黒体輻射の強さは、T^4 比例であるから、 アラン・サンディジの銀河表面輝度の後退説が (1+z)^-4 と話が一致するが、ステファンの法則と T ∝ t^-1 を認めただけである。(1+z)∝ t なら、 銀河輝度が (1+z)^-4 となる。(現在の太陽のエネルギー放出率 4*10^33erg/secと、ステファンの法則 5.71*10^-5 T^4 erg/sec/cm^2)

背景輻射を晴れ上がりの時期の黒体輻射の後退によるドップラーシフトは、それまであり得ると理解されていた現在の2.7K黒体輻射と区別できない。 区別できない輻射に一方の解釈を押しつけ、膨張の証拠と強く主張したのは、天文学者の罪である。2.7Kの黒体輻射と比べて現実の輻射強度が明らか に違うなら証拠にできるが、後退仮説以外では違ってきて、銀河表面輝度の (1+z)^-n は結果からは、n=2 程度(tired light)である。

ずっと点灯している灯火から、宇宙年齢 t に比例する距離だけ離れた場所で受ける面積当たりの放射エネルギーは、空間の広さ∝ t^2 から、∝t^-2 だが、あるとき空間の一点から様々な速度で爆発したニュートン的膨張は、最初の瞬間以外は光がなく、空間にエーテル的な光が戻る仕組み、何らか の光の回廊がなければ膨張宇宙には背景輻射は存在しない。膨張宇宙は光の回廊に大きく関係している。膨張宇宙がもし、温度 T ∝ t^-1 なら、温度 からくる放射エネルギー ∝ t^-4である。宇宙の体積∝ t^3の直線膨張なら、全体の放射エネルギー∝ t^-1で減少する。直線的膨張でなく減速膨張 a(t)= t^(2/3) では、体積∝ t^2、放射全体エネルギーは、∝t^-2減少。宇宙のある領域が、放射エネルギー不変を要求するなら、T∝t^-1 では体積 の t^4 膨張が必要である。温度 T∝t^-b として、放射エネルギー∝ t^-4b、体積∝ t^3c なら、放射エネルギー全体は、t^(3c-4b) から b= 3c/4 のとき一定である。

集中する質量のただ中に入り、そこから質量が四散することを使う重力加速(重力カタパルトなど)のように、一様な ポテンシャルの時間変化によって、加速された宇宙船が駆動なしに高速のまま遠方に達し四散する質量を追い抜くと弱い減速を受け、全体としては、 重力加速できる。これはエネルギー保存に反するように見えるが、エネルギーは、周囲の質量の減速によって供給される。膨張宇宙でも同様に、 ポテンシャルの時間的上昇にはエネルギー供給を必要とするように見える。ポテンシャルは、その空間的2階微分が物質密度である(▽^2Φ= -ρ) というだけでは、絶対値を求めることができず、それが差しか意味のないポテンシャルの仮想性であった。空間的に一様な密度ρからポテンシャルΦ は値を定められず、それを決めるにはλ項が必要である(▽^2Φ +λΦ= -ρ)。一般相対論はポテンシャル(を含めた計量場)を実在的にしたが、 Φの時間変化は挑戦的である。しかし、電磁ポテンシャルは、空間/時間の関数であった。そうでなければ波動方程式(□φ= 0, □A= 0)を持てず、 電磁波(□B= 0, □E= 0)も存在しえなかったであろう。

物差しを含めて天体間隔が縮小すると、遠方過去の大きな宇宙が光で見るすぐ背後を光速に近い速度でここを目指して急速に迫って来ているから、 ドップラー効果によって、赤方偏移とは逆の青方偏移が起きるべきだろう。ポテンシャルから考えても、過去が大きな天体間隔をもつなら、現在 よりポテンシャルが高く、それによって起きることは青方偏移である。ドップラー効果やポテンシャルが赤方偏移になるためには、逆に宇宙全体 が本当に膨張する必要がある。フリードマン宇宙解は、説明すべき赤方偏移を前にしてその逆を示した。空間計量g_iiが膨張宇宙のサイズにあたる かのように扱われた。空間計量が増大しては物差しは縮小する。赤方偏移を説明するには物差しが逆に拡大する計量、又は、時間計量が時間によって 変化する、ポテンシャルが上昇する計量を導くべきだった。

これは、物差しだけが縮小して、物差しからは空間が拡大してみえることによって飛行する光の波長が伸びると解釈されているが、これでは光は 物差しでなく空間側に付着するかのようである。全てが伸縮するという理解では光は飛行中に物差しと同じだけ比例的に伸縮し、元の場所の空間 計量の痕跡を消す。波長も周波数も偏移を示さない。観測点では遠方過去からの光も近傍の光と同じ光速をもち、元の周波数が同じなら観測点の 空間計量に合わせて波長が伸縮して同じ波長に変わる。継続的に光の周波数が送る側と受ける側で違って原子のスペクトル線が偏移するためには、 ドップラー効果か、両者の間に時間経過(時間計量)の違いが必要である。局所の観測点の空間計量の変動自体も、空間と同時に光が伸縮するから LIGOは重力波を検出できないだろう。

３２. おわりに

（９）最後の、しかし重要な注意：ここに用いられた意味での宇宙の年齢は、放射性金属から見出された地殻の年齢をたしかに超えていなければ ならない。これらの金属による年齢の決定は、あらゆる点からみて信用しうるものであるから、もしここにのべた宇宙論的な理論が、このような 結果と矛盾することが判ったならば、この理論は直に不可とされる。この場合に対しては、私は何等合理的な解答を見出すことができない。

宇宙論は、90 年代初期に問題にされた宇宙の年齢問題、大規模構造問題、CDM+インフレーション論の問題も解決することなくこの 10 年間に さらに切迫した重大さとなった。94 年にハッブル宇宙望遠鏡によってもたらされた、深部探索の映像はより根源的である。ここ数年、予想した ように失われた質量は、宇宙項に代行を求める。あまりに当然のように広言されるビッグバン宇宙論に欠落した論理、隠蔽された事項、又は行き 詰まりを意識してこの文章を作った。膨張宇宙論に対する批判は正当に扱われないが、海外には多くの参考文献を使用した包括的な説明論文がある。

Observational Cosmology: caveats and open questions in the standard model (拙訳)
Observational evidence favours a static universe
Sources of cosmic microwave radiation and dark matter identified: millimeter black holes (m.b.h.)
Rapid dust production in submillimeter galaxies at z>4?