目次
1.ティティウス・ボーデの法則
2.尽数関係(Resonance)
3.ラグランジュ点
4.ポテンシャルからの説明
5.L4, L5 について
6.回転系のポテンシャル
7.ティティウス・ボーデ法則の導出は、可能か
8.月のジャイアント・インパクト説
1781 年ハーシェルは、天王星を発見。1801 年小惑星セレス発見、パラス、ジュノー、ベスタ等の小惑星。 空欄であった位置が埋まった。1846 年海王星発見。この法則からかなり離れていた。1930 年冥王星発見。 今度はこの法則に合っていた。このような整数関係を説明する何ら明確で有効な物理的説明がない。 しかしながら、惑星運動の自公転の整数関係は、これ以外に沢山発見されている。
------------------------------
軌道半径 n 4+3x2^n
------------------------------
水星 0.3871 4
金星 0.7233 0 7
地球 1.0000 1 10
火星 1.5237 2 16
小惑星 2.721(avg2.65)3 28
木星 5.2026 4 52
土星 9.5549 5 100
天王星 19.2184 6 196
海王星 30.1104
冥王星 39.5404 7 388
8 772
------------------------------
太陽系の惑星や衛星の運動の公転や自転の周期の整数関係の現象を尽数関係 (Resonance)、とよぶ。天空の共鳴現象である。 その原因は、太陽系の生成から現在までの長期間の惑星間重力による抵抗のような効果であろう。 太陽系の質量の 99.9% は、太陽が担い、角運動量の大半は、惑星が担うという。 太陽重力だけではこのような現象は決して起きないから、惑星間の重力が惑星の軌道と自転に与えた影響がどれほどかを示すと理解される。
惑星運動にとって整数比のハーモニクス、調和関数が何らかの抵抗のない周期関係になっていて、長い時間を経て惑星運動が そこに落ち着いた現象と考えられる。自転と公転の整数関係は、惑星の潮汐力による惑星の変形の結果、恐らくエネルギーの 小さい自転の方が調整した結果であろう。しかし、一般にこれらは、十分に説明できる現象ではない。
上記の Web には太陽系の惑星、衛星の尽数関係が多数、挙げられている(下の表)。 大抵は、整数関係にある方が安定であるために整数比に落ち着いたのであろうが、 小惑星、土星の環の分布では整数関係が避けられている例 (3),(9),(10)がある。 これはどうして、逆に働いたのだろうかと思う。(5)のトロヤ群は、ラグランジュ点である。
(1) 月の自転と公転 = 1:1
(2) 水星の自転(58.65d) と公転(87.97d) = 2:3 (水星の昼夜は、176d)
(3) 小惑星カーウッドの空隙、小惑星帯に、木星の公転周期と 2:1, 5:2, 3:1 がない。
(4) 小惑星ヒルダ群、木星の公転周期に対して 3:2 の公転周期の小惑星群
(5) 小惑星トロヤ群、木星と1:1 の公転周期(太陽、木星を辺とする正三角形の頂点)
(6) 木星の公転周期(11.86y)と土星の公転周期(29.44y) = 2:5
(7) 木星の衛星イオ、エウロパ、ガニメデの公転周期= 1:2:4
(8) 木星の 4 大衛星ガリレオ衛星(イオ、エウロパ、ガニメデ、カリスト)の自転と公転周期= 1:1
(9) 土星の環のカッシーニの空隙:衛星ミマスの公転周期の1/2、エンケラダスの1/3、テティスの1/4 の公転周期。
(10)土星の環のマクスウェルの空隙:ミマスの公転周期の1/3
(11) 土星の衛星ティティスとミマスの公転周期= 2:1
(12) 土星の衛星ディオネとエンケラダスの公転周期= 2:1
(13) 土星の衛星タイタンとハイペリオンの公転周期= 15.945d:21.277d= 3:4
(14) 海王星(164.774y)と冥王星(247.796y)の公転周期= 2:3
(15) 冥王星の自転公転、衛星カロンの自転公転周期= 1:1:1:1 (互いに同じ面を向ける。)
(16) 太陽の活動周期11年は、木星の公転周期(11.86y)とほぼ等しい。
(17) 金星の自転周期(240.02d)と地球の公転周期(365.24d)= 2:3
(18) 金星地球の会合周期(584.0d)と地球火星の会合周期(779.9d)= 3:4
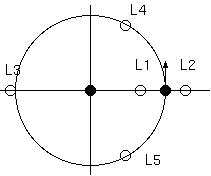
太陽地球関係でラグランジュ点 L1 は、地球から太陽に近づいた位置であり、その場所の本来の軌道速度はもっと速いが、 太陽重力から地球重力が逆方向で差し引かれ、地球と同じ公転周期をとる場所である。

遠心力と重力のつり合い、質量 M とその公転半径 r によって、軌道速度 v= rw と角速度 w が決まる。 rw^2= GM/r^2 から、 w^2= GM/r^3 (1) (v^2/r = GM/r^2 からは、v^2= GM/r である。)
L1 の太陽からの半径を R とし Rw^2 = GM/R^2 - Gm/(r-R)^2 と (1) から
RM/r^3 = M/R^2 - m/(r-R)^2
各項を R^2/M 倍し、R/r= k (k は 1 に近い1未満の値) とおくと、
1 - k^3= m/M k^2/(1-k)^2
(1 - k^3)(1-k)^2/k^2 = m/M
(1-k)^3 (1+k+k^2)/k^2 = m/M
1-k が小さい値であり、それを簡便に求めるため、(1+k+k^2)/k^2 を 3 と近似して、
1-k = (m/3M)^1/3 、
つまり (L1 までの距離)/(太陽までの距離)は、地球太陽質量比の1/3 の1/3乗となる。
ラグランジュ点 L2 は、地球から太陽と逆方向にある。そこからは、地球と太陽とが同じ側にあり、太陽と地球の重力が加算され、 その位置の本来の軌道速度より速い、地球と同じ公転周期をとる場所である。L1 の地球重力の符号が反転するだけで、 式はそのまま利用でき、おなじ近似を使うと地球から L2 の距離は L1 と同じになる。
ラグランジュ点 L3 は、太陽を挟んで地球の点対称(より少しだけ遠い)の位置である。地球公転軌道上は、一応どこも地球と同期した 軌道をとることができるが、地球重力の影響で、地球の近傍には地球に吸い込まれる傾きがある。吸い込まれない唯一の場所が L3 である。 L3 が公転軌道より少し遠いのは、太陽重力に地球重力が加算されるからである。 その差の距離は、w 一定とすると、(1) から r が M の1/3 乗に比例するから、2 倍の距離の地球の太陽重力への加算の影響は m/4M であり、m/4M の1/3乗程度か。
L1 の距離は、太陽質量 M= 1.989 x 10^33 g、地球質量 m= 5.972 x 10^27 g の比は、M/m= 3.3305 x 10^5 (33.305 万倍)、その3倍、 3M/m= 0.9991 x 10^6 (100万) の1/3乗は、(3M/m)^1/3 = 99.96 である。太陽までの距離 R_s= 1.496 x 10^11m の 1%、150万 km は、 月の距離の約 4 倍である。L3 は、(4M/m)^1/3 = 109.98、L3 と反地球位置との距離は、0.9% で 135 万 km になる。
さて、太陽重力と地球重力そして地球公転系のポテンシャルを地球公転軌道面上に考える。軌道面に垂直な方向には、物体が面から外れると 面内に引き戻す重力が働く安定性があると考えられる。
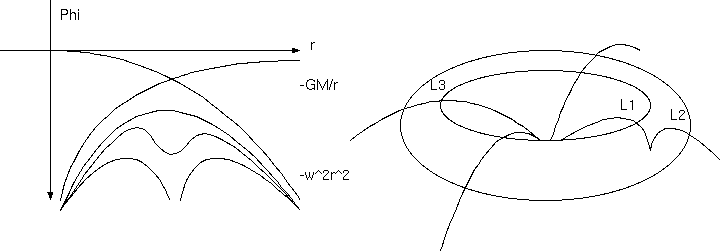
地球の重力がないときは、太陽からの半径 r だけによる点対称で、太陽中心の大きな漏斗に、 公転回転から来る半径の 2 乗に比例する下向きの放物面を加算し、 それを Phi 軸を中心に回転させた面を考えるとドーナツの表面のような上に凸な面ができる。 公転軌道上ポテンシャルは同じ高さで、軌道を内外に外れるとポテンシャルが下がり、潮汐力を表わす。
φ= - GM/r - w^2 r^2
これに地球の重力ポテンシャルを表す小さな漏斗を地球の位置に加算すると、
φ= - GM/|r-r_M| - Gm/|r-r_m| - 1/2 w^2 r^2
ドーナツ表面に小さな凹みを与え、公転軌道上にも地球からの距離によるポテンシャルの低下ができる。 ポテンシャルは、点対称から太陽と地球とを結ぶ直線についての線対称に変わる。 ポテンシャルの平坦点である無重力点がその線上にある。 ドーナツ面の地球重力による凹みの前後にふたつの頂点 L1、L2 の無重力点ができ、 軌道上で最も地球から遠い点 L3 にも無重力点がある。 これで L1〜L3 は説明できる。L4、L5 はどう説明するのだろう。
M、m を 1 辺にする正三角形の頂点 A に試験質量 m' (m'≪ M,m) を置くとき、回転系 w に m' は静止する。
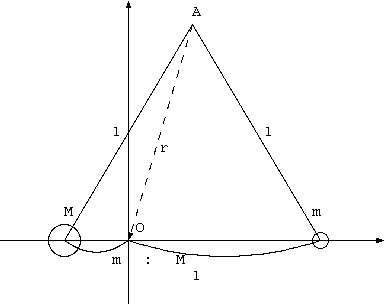
重心を O とすると、Mx = -m/(M+m) l, mx = M/(M+m) l
(1) m' に働く重力 F= F1+ F2、|F1|= GMm'/l^2, |F2|= Gmm'/l^2 は、原点 O の方向をもつ。
Aの座標は、
Ay= √3/2 l,
Ax= (1/2 - m/(M+m))l = (M-m)/2(M+m) l,
r^2= Ax^2 + Ay^2= ((M-m)/2(M+m))^2 + 3/4 = (M^2 + m^2 + Mm)/(M+m)^2 l^2 = (1 - Mm/(M+m)^2) l^2
Ay/Ax= √3 (M+m)/(M-m)
F1x= -1/2 GM/l^2 m'
F2x= 1/2 Gm/l^2 m'
F1y= -√3/2 GM/l^2 m'
F2y= -√3/2 Gm/l^2 m'
Fx= F1x+F2x= -1/2 G/l^2 (M-m)m'
Fy= F1y+F2y= -√3/2 G/l^2 (M+m)m'
Fy/Fx= √3 (M+m)/(M-m)= Ay/Ax (QED.)
(2) A 点の重力の大きさは、その点の遠心力に等しい。(|F| = r w^2 m')
M, m 間の重力は GMm/l^2、MO での w の遠心力は、M m/(M+m) l w^2 = GMm/l^2 から、 w^2= G(M+m)/l^3
F^2= Fx^2 + Fy^2 = G^2/l^4 ((M-m)^2+3(M+m)^2) m'^2/4
= G^2/l^4 (M^2 + m^2 - 2Mm + 3M^2 + 3m + 6Mm) m'^2/4
= G^2/l^4 (M^2 + m^2 + Mm) m'^2
r^2 を使って、
= G^2/l^6 (M+m)^2 r^2 m'^2
|F|= G(M+m)/l^3 r m'
w^2 を使って、
= r w^2 m' (QED.)
この結果は、M と m の大きさの比に依らない。さらに、m' の (m'≪M,m) という仮定も必要ないようだ。 "これは、3 体問題ではないか?、上の(1)(2)の計算の結果が m' に依らないことは分かるが、最初、2 体の重心を使って 2 体の回転 を仮定しておきながら、その結果が m' の大きさに依らないというのは、矛盾しているのではないか?" と思うかもしれないが、 (m'≪M,m) という仮定は、単純化のために余計な制限を入れただけである。その説明は次で十分であろう。
ニュートン重力は、相手と自らの質量の積に比例するから、複数の相手側の線形加算が出来る。クーロン力が電場の概念を使うことが できるのと全く同様にニュートン重力にも場の概念とポテンシャルの概念が使える。ニュートン重力は、重ね合わせのできる線形場である。 スカラーポテンシャルも加算可能である。
物体 C への物体 A からくる(重力的)影響と物体 B からくる影響は、独立に計算して加算できる。A からの(重力)場 Ea とBからの場 Eb があって、AB 両者からの場 Eab はベクトルの和 Ea + Eb であり、ポテンシャル φab は、和 φa + φb である。物体 C の値は、 それらの場の計算から完全に分離していて、C の位置の場の計算には使わない。C の量 m' は、力とエネルギーを求めるとき最後に乗算する。 現実に表れる力は、Fab= m' Eab であり、位置エネルギーは、m' φab である。
つまり、場に影響を与えなかった試験質量 m' がどのような大きさに変わっても、同じ結論になる (正 3 角形の頂点には、遠心力と 重力のつり合う点、実効ポテンシャルの勾配が 0 の点がある) ことは、場はそれ以外の物体で作られ、それ自身の量を場には考慮する 必要がない、という場の分離の原理がニュートン重力において完全に有効であることによる。3 番目の質点の場所のポテンシャルは、 最初の 2 個の質点の質量によって決まる。
つまり、任意の大きさの3質量は、正3角形を保って重心の周りを剛体回転できるのである。
を∇φ= 0 について解くことが L1 〜 L5 を求めことである。
φ= -GM/√((x-x_M)^2 + y^2) -Gm/√((x-x_m)^2 + y^2) - 1/2 w^2 (x^2+y^2)
を dφ/dx = 0 と dφ/dy = 0 の連立で解けばよい。
それよりもずっと簡単なのが、実効ポテンシャルの等高線を表示して同期回転系の様子を見る方である。 上式を画素毎に計算し整数化して奇偶で黒白表示する。重心を原点にして中央少し左に太陽、右に地球があり、 それらは距離に反比例するポテンシャルの鋭い凹みである。回転系の遠心力は、遠方での落ち込みとして画面周辺に表れる。 両者の和でドーナツ状のバンクができ、右の一部が地球の影響で欠けている。L1, L2 は地球の両隣りにある (等高線の連結として見える鞍部)。L3 も微かに見分けられる。L4、L5 は、バンクの右半分にある広い丘状の盛り上がりである。 この図では、太陽:地球の質量比を 40:1 に取って地球質量の影響を誇張している(l= 1, G= 1, M=100, m= 2.5)。 中央の星型模様は、ポテンシャル傾斜が大きいため等高線間隔が画素より細かいときに出る無意味なモアレである。 作成、表示プログラム

回転系の"実効"ポテンシャルは、その勾配は、回転系の静止物体が受ける力を表している。速度を持った物体は、 ポテンシャル勾配だけでなく、コリオリの力をも受ける。それは、電磁場中の電荷の運動とほとんど同じである。 (電荷運動では、質量と電荷が別物だが、回転系力学では質量しかない。) 電荷は、ローレンツ力 F = q(E + v x B) によって力を受ける。回転系の w が磁場に相当し、公転面に垂直な一様な磁場の中の 電荷運動に相当する。回転軸と速度の両方に垂直なコリオリ力はつねに公転面内にあって、運動の方向を変えるが速さを変えない。 そのため、遠心力は、重力とともにポテンシャルに含めて扱えるが、コリオリの力は、速度に依存する磁場のように別に考える必要がある。
回転系での物体の外力のないときの運動は、等速直線運動ではなく、コリオリ力によってその半径が速度に比例し、その周期が速度に依らず 回転系の周期に一致する円運動になる。緩やかな速度をもった物体は、回転系の周期と同じ周期の小さな円を描き、その近辺から移動しない。 L4、L5 は、ポテンシャルの広い丘であり、静止物体の安定点とはいえないが、物体が小円を描きその近辺に留まる動的安定性があると思われる。 ポテンシャルに傾きがあればその動的安定の小円もドリフトするかもしれないという気もするが、頂点を含む円なら安定かもしれない。
4.では L4, L5 の説明が付かなかったのに、ここで L4, L5 がポテンシャルの頂点になる理由はなにか、と再考する。 それは、4.では太陽と地球が重心から左にずれることを考慮しなかったためだろうか。太陽と地球が左にずれれば、 ドーナツ状のバンクの右側が高くなり、ポテンシャルの頂点ができても当然かもしれない。
この法則がニュートン力学に重力伝達速度を導入するだけで説明できるというのは、驚くべきことである。 重力の伝達時間を考慮するとニュートン力学的天体力学は成立しなくなると、私は理解していた。 通常、惑星の整数関係は、惑星間重力の互いの影響が原因とされる。
この惑星の重力量子化の結果は、0.4 + 0.3 x 2^n を説明するものではない。エネルギーがボーア型の 1/n^2 比例(または n^2 + n/2)、 そのため半径が n^2 に比例し、周期が n^3 に比例する修正されたティティウス法則を導出しようとしている。
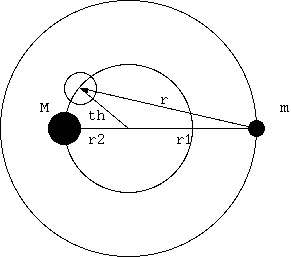
太陽 M と惑星 m は、剛体回転をしているとする。重心から惑星、太陽の距離をそれぞれ r1, r2 とし、m がτだけ過去の M (θ= ωτだけずれた位置)から重力を受けると、
F= GMm/r^3 r (1)
r= r_M(t-τ) - r_m(t),
r_m(t)= r1{cos(wt)+ i sin(wt)},
r_M(t)= -r2{cos(wt-τ)+ i sin(wt-τ)},
r= [-r2 cos(wt-τ) -r1 cos(wt)]+ i[-r2 sin(wt-τ)+ -r1 sin(wt)],
Fr= -(r2 cos(wτ)+r1)GMm/r^3,
Ft= r2 sin(wτ)GMm/r^3,
がでる。惑星 m の運動方程式は、半径の加速度変動と遠心力が Fr であり、
mr'' - mrθ'^2 = Fr, (2)
mrθ'' + 2mr'θ'= Ft, (3)
角運動量 L = mr^2θ'とし、
1/r dL/dt = 1/r d/dt (mr^2 θ')= Ft = r2sin(wτ)GMm/r^3,
wτ= kπ で Ft= 0。τ= r/c 程度で、k=0 以外の値をとることはできないから、無次元数 g を導入し、 τ= gr/c とする。
E= mv^2/2 - GMm/r = -G^2M^2m^3/(2L^2) (9)
E= -mπ^2 c^2 k^2 /(2g^2) (11)
となり、ボーアの式、
E= -1/2 m (αc)^2 /n^2
に合わせるために重力の微細構造定数α_g を考え、
E= -1/2 m (α_g c)^2 /n^2
とすると、g= k^2 g_1, g1= π/α_g になり、
E= -1/2 m G^2M^2m^2/hbar 1/n^2
1/n^2 に比例するエネルギーになる。
hbar= 2 G M m g_1/c (12)
となり、m に依存する。
r_n= h^2n^2 /(2πGMm^2) (15)
に量子化される。惑星間の重力伝達速度を光速とすると、惑星周期に影響するほどの量子化効果がでるはずもない。 それをむりやりボーアの式にするため、光速遅延要素 g を作り出して、それが量子化される式にもっていく。 結果的に量子化によって光速を 1/(k^2 g_1) に遅くしている。
ティティウス・ボーデの法則からみると、小惑星帯に対応する惑星として、ひとつの惑星が存在してもよいことを示している。 そこには最初から惑星が形成出来なかったのか、それとも、過去に惑星が存在したが後に何かの原因で破壊された残骸なのだろうか。 小惑星が熱を受けていない炭素質コンドライトであるから、前者の可能性が高いが、小惑星の総質量は惑星には到底及ばない程度の量でしかない。 地球に向かってきて地球から月を放り出したという、"ジャイアント・インパクト説" の衝突をした火星大の惑星の正体だろうか。 月が地球の衛星としては大き過ぎ、月が鉄のコアを持たず、月の岩石の組成が地球のマントルの組成と等しく、月の比重が小さいことを 説明するにはこの説が有効だった。
しかし、現在の月の軌道面は、太陽系の諸惑星の軌道面に余りにも近い。地球に衝突した天体は、存在しないか、少なくとも太陽系外起源では ないだろう。太陽系外からの衝撃が原因なら、月の軌道面を太陽系の天体のそれとは違うものにするだろう。太陽系内に原因を求めると、 太陽系の惑星のどれかがなぜか大きく移動してきて地球に衝突したとするしかないが、惑星がありそうな場所にないのは小惑星帯である。 地球軌道の L4, L5 から来たという説は、同じ軌道に複数の惑星ができた例がないし、L4, L5 はそこから移動しないラグランジェ点である。 地球に衝突した惑星は、地球に一体化したのだろうか。つまり、衝突をした惑星は、存在したとしても、どこからきて、そしていま、 どこにいったのか、そして、そのような天文学的な事件の、頻度への疑問である。
太陽系の惑星形成において地球と同時に月も形成されたという "兄弟説" のもつ問題より少ないのだろうか。同時形成において衛星の組成が その兄の惑星の組成より軽いのは当然である。月の軌道面が太陽系の軌道面に近いこと、円形に近い軌道をもつ。衝突による形成では、 放り出された月が最初から形をなしていれば長い楕円軌道を描くだろう。それが完全に破壊された円盤から再び集結したとしなければ円形 の軌道を持たないだろう。また、衝突では月の軌道は地球の近くになる。それが徐々に登っていったとする。現在も月は登っているというが、 運動量を失って地球に近付くと思う逆である (*)。地球の 23.5 度の自転軸の傾きは大きいが、月の自転は、公転と同期し 地球に同じ面を向け、地球の公転との傾きが小さい(5°)。少なくとも、月の軌道、軌道面、自転軸、地球の軌道、軌道面には過去の激しい衝突の痕跡がない。
それに比べて冥王星は、海王星の衛星であったものが、何かの影響で弾き飛ばされたような軌道を持っている。海王星の軌道と交差する長い 楕円軌道をもつし、冥王星の軌道面は太陽系の惑星の軌道面から大きく(17°) 外れている。さらに自転軸も(天王星と同じだが)ほとんど横倒し である。そして、大きな衛星カロンをもつことが分かった。地球に対する月の異常な大きさから衝突説が出てきたものである。 現在は、冥王星と海王星は、公転周期に 2:3 の尽数関係があるために互いに近付かない。
惑星公転周期の位相ロックの可能な説明としては、惑星相互の重力による影響であろう。惑星が近傍にくれば、相互の重力は余計にそうする だろう、ということである。ふたつの惑星が太陽の同じ側にあるとき、相互の引力が位相の遅れた惑星を引きつけ位相を進ませ、位相の進んだ 側の惑星を遅らす。そうして同期軌道にしようとする。近傍にくるのが惑星にとって数回に 1 回であっても同様と考えることができそうである。 近傍にきたときの影響がほとんどであるからである。しかし、そのような説明は、尽数関係が両者を近付けないようにしている海王星と冥王星 では成り立たないようにみえるが、位相のロックは完全でなく誤差があるから過去には位相が逆で近傍に来ていたかもしれない。 尽数関係は、過去に両者が近付いたためできるものである。その尽数関係が惑星衝突の原因だったかもしれない。
ティティウス・ボーデの法則は、軌道半径に関するものであるが、木星、土星、天王星、海王星の軌道半径は、天文単位(AU)で、5,10,20,30 であり、1:2:4:6 の整数比に近い。軌道半径よりも公転周期は、より惑星間の配置に影響する。尽数関係は木星と土星の公転周期には 2:5 、 海王星と冥王星に 2:3 がある。整数の関係は、火星までの惑星に 2:5:8:15 の比率、木星以降に 2:5:14:28:42 の周期比率である。 木星以降の惑星では火星までの 8 (地球)にあたる土星と天王星の間が欠けている。
水星 0.241 2 金星 0.615 5 地球 1.000 8 火星 1.881 15 小惑星 2.41-8.81 ? 木星 11.86 2 土星 29.46 5 天王星 84.01 14 海王星 164.79 28 冥王星 247.74 42
(Apr. 17 2008)
ティティウス・ボーデの法則は、軌道半径が 4+3x2^n (nが整数)で表されるが、ケプラーの第3法則の軌道半径と周期との関係 r^3 w^2= GM がある。周期 T∝ (4+3x2^n)^1.5 は、実は、周期2倍の関係を表すだけかも知れない。とくに火星までは。
水星 金星 地球 火星 小惑星 木星 土星 天王星 海/冥王星 ? (4, 7, 10, 16, 28, 52, 100, 196, 388, 772)^1.5 =(8, 18.52, 31.62, 64, 148.16, 375.0, 1000, 2744, 7643., 21450.0) =(0.253 0.586 1 2.024 4.68 11.86 31.62 86.78 241.71 678.4) [年] (0.241 0.615 1 1.881 ? 11.86 29.46 84.01 247.74 ? ) 実際[年]、(Sep. 26 2015)
伏見康治、中井真藏著 "演習 力学", 共立出版株式会社, 現代物理学演習講座 1, 昭和 34 年初版, p. 64 を引用すると、
[例題 1] 3 個の質点が互いに万有引力によってひきあっているとき、次の二つの定常解が存在することを示せ。(三体問題)
1) 正三角形解。各点が常に正三角形の頂点にあって(|r_2 - r_1|= |r_3 - r_2| = |r_1 - r_3| = r)重心のまわりに定角速度ω
ω^2 = kr^-3 (m_1 + m_2 + m_3)
で回転している。
2) 直線解。各質点が一直線上に固定されていて、同時に定角速度で重心のまわりを回転する。
(以上引用)。ラグランジュ点 L1, L2, L3 は、三体問題の直線解、L4, L5 は、正三角解である。 正三角形解が 2 つあるのは、正三角形の頂点が一辺の両側にあるから当然であり、 直線解が 3 つあるのは、2 点を決める直線上に 3 領域あるからである。 実効ポテンシャルの図は、それ以外に解がないことも示すようである。
(July 3 2008)