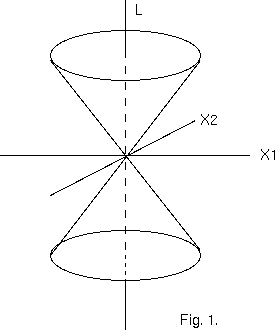
目次
前相対論の物理の時空
特殊相対性の理論
一般相対性の理論
一般相対性の理論(続き)
第2版への付録 ー"宇宙論的問題" についてー
付録2 非対称場の相対論
個人の経験は、事象の系列のなかに配置されて我々に姿を現わす; この系列のなかで我々の記憶する単独の事象は、"以前"と"以後"と の判定規準に従って順序付けられて現れ、そして、それらは、それ以上分析できない。それゆえ、その個人にとって私-時間、又は 主観的時間が存在する。これは、それ自身、計測できないものである。確かに、私は、後の事象に前の事象より大きな数を付けるように 事象に数を添えることができる;しかし、この添付の性質として、全く任意であり得る。時計を手段として事象の順序を比較して、 私が定義できるこの添付は、与えられた事象の系列の順序を時計によって供給される。我々は、時計によって何かを理解するが、 それは数えられる事象の系列を用意し、後述する他の特性をもつのである。
言語の助けによって異なる個人は、ある程度、彼らの経験を比較することができる。そのとき、異なる個人のある感覚の知覚は、 互いに対応している一方、他の感覚の知覚は、そのような対応が確立できないことを見出す。我々は、異なる個人に共通のそれらの 感覚知覚を現実とみなし、それゆえ、ある尺度で、非個人的とすることが習慣付けられている。自然科学、そして、それらの最も 基本的な物理は、それらの感覚知覚を扱う。物理的な物体の概念、特に剛体は、相対的にそのような感覚知覚の一定の複合体である。 時計は同じ意味で、また物体であり系であるが、それが数える事象の系列が、その全てが等しいと見なし得る要素(訳注:時間間隔) によって形成されているという追加的特性をもつ。
我々はいま、我々の空間の概念と判定に立ち来る。経験と我々の概念との関係に厳しい注意を払うことは、ここでまた不可欠である。 Poincaré は、彼の本、"科学と仮説(La Science et l'Hypothese)" に与える言及のなかで、明確に真実を認識していたと私には思える。 剛体に我々が知覚できる全ての変化のなかで、我々の体の自発的運動によって打ち消し得るものは、それらの単純さによって印される; Poincaré は、これらを位置の変化と呼ぶ。単純な位置の変化によって我々はふたつの物体を接触させることができる。幾何学に基本的な、 合同の定理は、位置のそのような変化を支配する法則をとり扱わなければならない。空間の概念にとって次のことは本質的にみえる。 物体 B, C, ... を A まで持ってくることによって、我々は、新しい物体を形成できる;それを我々は、物体 A を延長するという。 そうして物体 A を延長し我々は、ついに何か他の物体 X まで接触するようになる。全ての物体 A の延長の全体を "物体 A の空間" と呼ぶ ことができる。そのとき、全ての物体は、"(任意に選んだ)物体 A の空間" のなかにあることは正しい。この意味で、我々は抽象のなかに 空間をいうことはできず、"物体 A に所属する空間" だけをいうことができる。地球の地殻は、我々の毎日の生活において物体の相対的な 位置を判定することにおいて、非常に支配的な役割を果たしているために、確かに弁護できない空間の抽象的な概念を導いた。 この致命的な誤りから我々自身を解放するために "参照物体" 又は "参照空間" だけについていうべきである。 これらの概念の洗練は、一般相対論を通してだけ必要となることを、我々は後に見る。
前相対論の物理では理想的剛体の構成法則は Euclid 幾何に整合しているということが仮定されている。これが何を意味するかは、 次のように表現できる:剛体上に印された 2 点は、間隔を形成する。そのような間隔は、我々の参照空間に相対的に静止 にさせることが多種多様な方法によって可能である。もしいま、この空間の点が、座標値 x_1, x_2, x_3 であるといえ、その間隔 の 2 端の座標値の差、Δx_1, Δx_2, Δx_3 が間隔のどの方向においても同じ次の 2 乗和を与えるなら、
(1) s^2 = Δx_1^2 + Δx_2^2 + Δx_3^2
そのとき、参照空間は、ユークリッド的 (Euclidean) であり、座標値は、デカルト的 (Cartesian) という(*)。この仮定を無限小の 間隔に制限しておけば、実際には十分である。この仮定に含まれているものには、むしろ特別でないために、それらの基本的な重要性 のために我々が注意をしなくてはならないものがある。最初に、理想的な剛体が任意の仕方で動かし得ると仮定されている。第2番目に、 理想剛体の方向に対する行動は物体の素材や、位置の変化に独立であることが仮定されている。それは、ふたつの間隔が一度一致すれば、 それらはつねに、どこにおいても一致するという意味においてである。これら両仮定は、幾何学において、とくに物理測定において 基本的重要性をもち、経験から自然に起きる; 一般相対論において、それらの有効性は、天文学的大きさと比較して無限に小さい 参照空間と物体だけにおいて仮定される必要がある。
x_ν= a_ν + λ b_ν
我々は、ユークリッド幾何の直線の全ての特性をもつ線を得る。特に、直線上に間隔 s を n 回置くことによって長さ n・s の間隔を得る ということが容易に出る。長さは、それゆえ、直線に沿って単位測定棒を手段として実行する測定の結果を意味する。後に明らかになるように、 長さは、直線のそのように、座標系に独立であるという重要性をもつのである。
我々はいま、特殊相対論と一般相対論のなかで類似の役割を果たす、一連の思考に来りくる。我々は問う:我々が使ったデカルト座標 以外に、他の等価な座標はあるだろうか? 間隔は、座標系の選択から独立である物理的な意味をもつ; そして、我々の参照空間の 任意の点から敷かれた、全ての等しい間隔の終点の軌跡として、我々が得る、球状の表面も同様である。もし、x_ν と x'_ν (νは 1 から 3) を我々の参照空間のデカルト座標とするなら、そのとき、その球状表面は、我々のふたつの座標系のなかで次式によって表される。
(2) ΣΔx_ν^2 = const
(2a) ΣΔx'_ν^2 = const
(2)と(2a)が互いに等価であるために、どのように x'_νが x_ν によって表されなければならないか? x_ν の関数として表された x'_ν に関し、Δx_νの微小値への Taylor の定理によって、我々は次を書くことができる。
Δx'_ν= Σ_α ∂x'_ν/∂x_α Δx_α + 1/2 Σ_αβ ∂^2 x'_ν/∂x_α∂x_β Δx_αΔx_β ...
もし、我々が (2a) をこの式で置き換え、(1)と比べるなら、x'_ν が x_ν の線形関数でなければならないことを見る。もし、それゆえ、 我々が次を置けば、
又は、
(3a) Δx'_ν = Σ_α b_να Δx_α
そのとき、方程式 (2) と (2a) の等価性は、次式で表される。
(2b) ΣΔx'_ν^2 = λΣΔx_ν^2 (λは、Δx_νから独立)
それゆえ、λが定数でなければならないことが出る。もし、我々が λ= 1 と置けば、(2b) と(3a) は、次の条件を与える。
(4) Σ_ν b_να b_νβ= δ_αβ
ここで、α=β又はα≠βに従ってδ_αβ=1 又は 0 である。条件 (4) を直交性の条件、変換 (3), (4) を線形直交変換と呼ぶ。 もし、我々が s^2 = ΣΔx_ν^2 が、全ての座標系で長さの自乗に等しくあるべきと規定するなら、そしてもし、我々がつねに同じ 単位の物差しをもって測るならば、そのとき、λは、1 でなければならない。それゆえ、我々の参照空間のなかで、ひとつのデカルト 座標系から他へ、それによって渡すことのできる線形直交変換は、唯一である。我々は、そのような変換を適用するなかで、直線の式 が直線の式になることを見る。(3a) を逆転して、両辺に b_νβ を掛け、全てのν' によって総和すると、我々は次を得る。
(5) Σ b_νβ Δx'_ν = Σ_να b_να b_νβ Δx_α = Σ_α δ_αβ Δx_α = Δx_β
同じ係数 b は、また逆のΔx_νの置き換えを決定する。幾何学的に b_να は、x'_ν 軸 と x_α 軸間の角の余弦である。
人は普通、幾何学をその概念と経験の間のどのような関係からも分離していると学ぶことが習慣付けられている。純粋に論理的であって、 原理的に不完全である経験主義から独立であるものを切り離すことには利点がある。これは、純粋な数学者の満足である。 彼は、公理から彼の定理を正しく、すなわち、論理的な誤りなしに演繹できるならば満足する。 ユークリッド幾何学が真であるか否かという問いは、彼の関心にない。しかし、我々の目的のためには、幾何学の基本的概念を自然の 対象に関連させることが必要である; そのような関連なしには幾何学は物理学者にとって無価値である。物理学者にとって、幾何学の 定理が真であるか否かについての問いに関心がある。この視点からユークリッド幾何学が定義から論理的に導かれた単なる演繹を超える 何かを断言することは、次の単純な考察から見られるであろう。
空間の n 点の間には、n(n-1)/2 の距離 s_μνがある。これらと、3n の座標値との間には我々は次の関係をもつ。
s_μν^2 = (x_1(μ) - x_1(ν))^2 + (x_2(μ) - x_2(ν))^2 + ...
これら、n(n-1)/2 の方程式から 3n の座標値が消去されてよい、そしてこの消去から s_μνには少なくとも n(n-1)/2 - 3n の方程式 が残るであろう(*)。一方、s_μνは、測定できる量である。そして定義から互いに独立である。これらの s_μνの間の関係は、 必ずしも先験的 である必要がない。
s^2 = ΣΔx_ν^2
もし、K_(x_ν) と K'_(x_ν) がふたつのデカルト座標系であるなら、そのとき、
ΣΔx_ν^2 = ΣΔx'_ν^2
右辺は、線形直交変換の式のために左辺と恒等的に一致する。右辺は、左辺の x_ν を x'_ν に入換えただけが異なる。これは、ΣΔx_ν^2 が線形直交変換に関して不変量であるという言明によって表現される。ユークリッド幾何にある、そのような、全てのそのような量は、 明らかに客観的な重要性をもち、線形直交変換に関する不変量によって表すことができたように、デカルト座標系の特定の選択に独立である。 これが、不変量の形式を支配する法則を扱わなくてはならない不変量の理論が、解析幾何学において重要である理由である。
幾何学的不変量の2番目の例として体積を考えよう。これは、次で表現される。
V= ∫∫∫ dx_1 dx_2 dx_3
Jacobi の定理を使って我々は、次の式に書くことができる。
ここで、最後の積分の被積分は、x'_ν の x_ν に対する関数的な行列式であり、これは (3) によって、置き換えるする係数、b_ναの行列式 |b_μν| と等しい。式(4)から、もし、δ_μαの行列式を形成するなら、行列式の乗算定理によって、
(6) 1= |δ_αβ|= |Σ_ν b_να b_νβ|= |b_μν|^2 ; |b_μν|= ±1
もし、我々が自ら制限し、それらの変換を行列式 + 1 をもつ(*)(座標系の連続的な変化からくるものだけ)とすれば、そのとき V は不変量である。
不変量は、しかしながら、デカルト座標の特定選択に独立に我々が与え得る唯一の形式ではない。ベクトルとテンソルは、他の表示形式である。 現在の座標値 x をもつ点が、直線上にあることを次式で表示しよう。
x_ν - A_ν= λ B_ν (νは 1 から 3)
一般性を制限することなく、我々は次を置くことができる。
Σ B_ν^2 = 1
x'_β - A'_β = λ B'_β
ここで、我々は、次を置いた。
B'_β= Σ_ν b_βν B_ν ; A'_β= Σ_ν b_βν A_ν
これらは、第2番目のデカルト座標系 K' に関する直線の方程式である。それらは、元の座標系に関する方程式と同じ形式をもつ。 直線は、それゆえ、座標系に独立な意味をもつことが明らかである。形式的に、これは、量 (x_ν - A_ν) - λB_ν が間隔の成分Δx_ν と同様に変換されることによる。3つの量の組は、どのデカルト座標系にも定義され、間隔の成分と同様に変換され、ベクトルと呼ばれる。 もし、ひとつのデカルト座標系でベクトルの3成分が消滅すれば、全ての系で消滅する。なぜなら、変換の式が斉次であるからである。 我々は、このように幾何学的表現の言及なしに、ベクトルの概念の意味を得ることができる。直線の式のこの行動は、直線の式が線形 直交変換に関して共変であると表現できる。
我々はいま、テンソルの概念を導く幾何学的実体があることを短く示す。P_0 を2次の表面の中心、P を表面の任意の点、ξ_ν を座標軸上 への間隔 P_0P の投影とする。そのとき、表面の方程式は、
Σ a_μν ξ_μ ξ_ν = 1
このなかで類似の場合も、我々は総和の記号を省略し、2度現れる添字について総和を実行すると理解する。 我々はそうして、表面の式を次のように書く。
a_μν ξ_μ ξ_ν = 1
量 a_μν は、選択されたデカルト座標系に関して、与えられた中心位置について、表面を完全に決定する。 線形直交変換のξ_νへの変換の知られた法則 (3a) から、我々は、容易に a_μν の変換法則を見出す(*):
この変換は斉次であり、a_μνについて1次である。この変換のために、a_μνを 2 階 (2重の添字をもつから) のテンソルの成分と呼ぶ。 もし、テンソルの全ての成分 a_μνがどれかのデカルト座標系について消滅するならば、それらは、他の全てのデカルト座標系に関しても 消滅する。2次の表面の形と位置は、このテンソル (a) によって記述される。
より高階(添字の数)のテンソルも解析的に定義できる。ベクトルを階数1のテンソルとみなし、不変量(スカラー)を階数0のテンソルとみなす ことは、可能であり、かつ利点がある。この点に関して、不変量の理論の問題は、次のように定式化され得る:どのような法則に従って 与えられたテンソルから新しいテンソルを形成することができるか? 我々は、後にこれらの法則を適用できるようにするために、これらの 法則をいま考察する。最初にテンソルの特性、線形直交変換によって同じ参照空間のなかでひとつのデカルト系から他への変換に関する特性 について扱う。法則は次元数から全体として独立であるから、我々はこの数を n として残し、最初には不確定とする。
定義 もし、ある対象が n 次元参照空間のなかのすべてのデカルト座標系に関して n^α の数の A_μνρ... (αは添字の数) によって 定義されるなら、これらの数は、α階のテンソルの成分である。ただし、変換法則が次式であるなら。
(7) A'_μ'ν'ρ'... = b_μ'μ b_ν'ν b_ρ'ρ .... A_μνρ...
注意 この定義から次が出る。もし、(B),(C),(D) がベクトルであるとき、
(8) A_μνρ... B_μ C_ν D_ρ...
は、不変量である。逆に、任意選択のベクトル(B), (C) に式(8)が不変量を導くことを知るなら、(A)のテンソル性が推定できる。
(9) A_μνρ... ± B_μνρ... = C_μνρ...
証明は、上に与えられたテンソルの定義から出てくる。
乗算 階数αのテンソルと階数βのテンソルから、階数α+βのテンソルを得ることができる。最初のテンソルの全ての成分に 第2番目のテンソルの全ての成分を掛けることによって:
(10) T_μνρ...αβγ... = A_μνρ... B_αβγ...
縮約 階数α- 2のテンソルを階数αのテンソルから、ふたつの確定した添字を互いに等しく置き、そしてこの単独の添字について総和する。
(11) T_ρ... = A_μμρ...(= Σ_μ A_μμρ...)
証明は、
A'_μμρ... = b_μα b_μβ b_ργ ... A_αβγ... = δ_αβ b_ργ ... A_αβγ... = b_ργ ... A_ααγ...
(12) T_μνρ...α= ∂A_μνρ.../∂x_α
線形直交変換に関して新しいテンソルがテンソルからこれらの演算ルールに従って作られる。
テンソルの対称特性 テンソルは、それらの添字のうちふたつ μ、ν に関して、μ, νを交換した結果の両成分が互いに 等しいとき対称、等しく反対符号のとき、反対称(訳注:skew-symmetry "斜対称"は、"反対称"と意訳する) と呼ばれる。
対称状態: A_μνρ= A_νμρ
反対称状態: A_μνρ= -A_νμρ
定理 対称又は反対称の特性は、座標選択から独立であり、そこに重要性がある。その証明は、テンソル定義の式からくる。
特別テンソル I. 量、δ_ρσ (4) は、テンソル成分である(基本テンソル)。
証明 もし、変換の式 A'_μν= b_μα b_νβ A_αβ の右辺で、我々が A_αβ を、量 δ_αβ (それは、α=β,α≠β に従い1, 0) に置き換えれば、我々は次を得る。
A'_μν= b_μα b_να = δ_μν
II. 全ての添字対に関して反対称テンソル(δ_μνρ...)であって、次元数 n に等しい階数をもち、その成分が +1 又は -1 であり、 それがμνρ... が 123... の偶奇の置換に従うものがある。
証明は、上で |b_ρσ|= 1 を証明した定理の助けによって出る。
これら、数少ない単純な定理は、不変量の理論から前相対論の物理と特殊相対論の方程式を築くための装置を形成する。
我々は、前相対論物理のなかで、空間中の関係を指定するために、参照物体又は参照空間、そして、それに加えてデカルト座標系が 必要であることを見た。デカルト座標系を、それぞれが単位長をもつ棒によって形成された立方体的な枠組と考えることによって、 我々はこれらの概念の両者を融合してひとつにすることができる。この枠組の格子点の座標値は整数である。基本的な関係、
(13) s^2= Δx_1^2 + Δx_2^2 + Δx_3^2
から、そのような空間格子の構成員は、全て単位長であることが出てくる。時間のなかの関係を指定するために我々は、標準時計を加え、 デカルト座標系の又は参照座標系の、いわば、原点の位置に置くことを必要とする。もし、事象がどの場所で実行されても、その事象と 同時である原点にある時計の時間を指定すればすぐさまに、我々は、それに 3 つの座標値 x_ν と時間 t を割り当てることができる。 それゆえ、我々は、以前には個人のふたつの経験の同時性だけに関係していたのであるが、遠方の事象の同時性の言明に客観的意味を (仮想的には) 与えることができる、そのように指定された時間は、我々の参照空間のなかの座標系の位置に全く独立であり、それゆえ、 変換(3)に関して不変量である。
前相対論の物理の法則を表す方程式系は、ユークリッド幾何学の関係をもつと同様に、変換(3)に関して共変であると仮定される。 空間の等方性と一様性は、この方法で表される(*)。 我々はいま、より重要な物理の方程式のいくつかを、この視点から考察する。
(14) m d^2x_ν/dt^2 = X_ν
(dx_ν)はベクトルであり; dt、そしてそれゆえ、1/dt もまた不変量である; こうして、(dx_ν/dt) はベクトルである; 同じ方法で (d^2x_ν/dt^2) がベクトルであることを示すことができる。一般に、時間に関する微分操作は、テンソル特性を変えない。一方、m は 不変量(階数0のテンソル)であり、 m (d^2x_ν/dt^2) は、ベクトル、又は、階数 1 のテンソルである(テンソルの乗算の定理によって)。 もし、力 (X_ν) がベクトル特性をもつなら、同じことが差分、(m (d^2x_ν/dt^2) - X_ν) についても成立する。これらの運動方程式は、 それゆえ、参照空間のなかの全ての他のデカルト座標系においても有効である。力が保存される場所の場合、我々は (X_ν) のベクトル 特性を容易に認識できる。なぜなら、ポテンシャルエネルギーΦが存在し、それが粒子相互の距離だけに依存する、そしてそれゆえ不変量である。 力のベクトル特性、X_ν= -∂Φ/∂x_ν は、そのとき、階数 0 の微分についての一般的な定理の帰結である。
1階のテンソル、速度を乗算して、次のテンソル方程式を得る。
m (d^2x_ν/dt^2) - X_ν) dx_μ/dt = 0
縮約とスカラー dt による乗算によって、我々は運動エネルギーの方程式を得る。
d(mq^2/2) = X_νdx_ν
もし、ξ_νを質点と空間に固定された点の座標の差とすれば、そのとき、ξ_νは、ベクトルの特性をもつ。 我々は、明らかに d^2x_μ/dt^2 = d^2 ξ_ν/dt^2 をもつ、粒子の運動方程式が次式に書けるように。
m (d^2ξ_ν/dt^2) - X_ν = 0
この式をξ_μで乗算して、次のテンソル方程式を得る。
(m (d^2ξ_ν/dt^2) - X_ν) ξ_μ = 0
左辺のテンソルの縮約をとり、時間平均をとれば我々はビリアル(virial)の定理を得るが、それについてさらに考察はしない。添字の 交換をして続く引算をして、我々は、単純な変換をして、モーメントの定理 (訳注:角運動量の時間微分が力のモーメント) を得る。
d/dt [m (ξ_μ dξ_ν/dt - ξ_ν dξ_μ/dt)] = ξ_μ X_ν - ξ_ν X_μ
A_μ= 1/2 A_στ δ_στμ
もし我々が、2 階の反対称テンソルに、上に導入された特別な反対称テンソルδを掛け、そして 2 度縮約すれば、その成分がテンソルの成分と 数値的に等しいベクトルが結果する。これらは、いわゆる軸性ベクトルであり、右手系から左手系への変換において Δx_ν と違う変換をする。 3 次元空間で 2 階の反対称テンソルをベクトルとみなすことは、絵のような美しい利点があるが、対応する量の正確な性質を再現しない。 そのため、それをテンソルと考えるほうがよい。
我々は次に、連続媒体の運動方程式を考察する。ρを密度、u_ν を座標と時間の関数とみる速度の成分、X_ν を単位質量あたりの体積力、 p_νσ を x_ν 増加方向のσ軸に垂直な表面上の歪力とする。そのとき、領域の運動方程式は、ニュートンの法則から、
ρ du_ν/dt= - ∂p_νσ/∂x_σ + ρX_ν
ここで、du_ν/dt は、座標 x_νをもつ時刻 t の粒子の加速度である。もし、この加速を偏微分係数で表現するなら、我々はρで割って次を得る。
(16) ∂u_ν/∂t + ∂u_ν/∂x_σ u_σ = - 1/ρ ∂p_νσ/∂x_σ + X_ν
我々は、この方程式がデカルト座標系の特別な選択によらずに成立することを示さなくてはならない。(u_ν) は、ベクトルであり、それゆえ、 ∂u_ν/∂t もベクトルである。∂u_ν/∂x_σ は、2階のテンソル、∂u_ν/∂x_σ u_τ は、3階のテンソルである。左辺の第2項は添字σ,τ の縮約からの結果である。右辺の第2項のベクトル特性は明らかである。右辺第1項も、やはりベクトルであるためには、p_νσがテンソルの必要がある。 そのとき、微分と縮約によって ∂p_νσ/∂x_σ が結果する。そして、それゆえ、ベクトルである。それはまた、スカラーの逆数 1/ρの乗算の後に おいても同じである。その p_νσは、テンソルである。そして、それゆえ、次の式に従って、変換する。
p'_μν= b_μα b_νβ p_αβ
は、この式を無限小の4面体で積分するメカニズムで証明される。p_νσ= p_σν それゆえ、歪テンソルが対称テンソルであることは、 モーメントの定理を無限小の平行6面体に適用することによって証明される。以上述べたことから、上で与えたルールの助けによって、 その方程式が空間のなかの直交変換(回転変換)に関して共変であり; そして、その式が共変であるためには、式のなかの量がそれに従う ルールも変換されなくてはならないことも明らかになる。
(17) ∂ρ/∂t + ∂(ρ u_ν)/∂x_ν= 0
は、前述のことから、取り立てての議論は、必要ない。
我々はまた、歪成分が物質の特性に依存する式の共変性をテストする。そして、共変性の条件の助けを伴って、圧縮性粘性流体の場合のこれらの式 を立てる。もし、我々が粘性を無視するなら、圧力 p はスカラーであって、流体の密度と温度だけに依存するだろう。そのとき、歪テンソルの貢献は、 明らかに、次である。
p δ_μν
ここで、δ_μνは、特別な対称テンソルである。この項は、粘性流体の場合にもまた存在するだろう。しかし、この場合には圧力の項もあり、u_ν の空間微分に依存する。我々は、この依存性を線形と仮定する。一方、これらの項は、対称テンソルでなければならず、入ってくるのは唯一、
α (∂u_μ/∂x_ν + ∂u_ν/∂x_μ) + β δ_μν ∂u_α/∂x_α
であろう。(なぜなら、∂u_α/∂x_αは、スカラーである。) 物理的理由(すべりのない)から、全ての方向に対称的な拡大が仮定される。 すなわち、もし、
∂u_1/∂x_1 = ∂u_2/∂x_2 = ∂u_3/∂x_3; ∂u_1/∂x_2, etc., = 0
であるとき、摩擦力は現れず、そのことから、β= -2/3 α であることが出てくる。もし、∂u_1/∂x_3 だけが 0 と異なるなら、 p_31= -η∂u_1/∂x_3 としよう。それによってαが決定される。我々は、そのとき、完全な歪テンソルのための次式を得る。
(18) p_μν= p δ_μν - η[(∂u_μ/∂x_ν + ∂u_ν/∂x_μ) - 2/3 (∂u_1/∂x_1 + ∂u_2/∂x_2 + ∂u_3/∂x_3)δ_μν]
空間の等方性(全方向の等価性)からくる、不変量の理論の人間的な価値は、この例から明らかとなる。
∂h_3/∂x_2 - ∂h_2/∂x_3 = 1/c ∂e_1/∂t + 1/c i_1
(19) ∂h_1/∂x_3 - ∂h_3/∂x_1 = 1/c ∂e_2/∂t + 1/c i_2
....
∂e_1/∂x_1 + ∂e_2/∂x_2 + ∂e_3/∂x_3 = ρ
∂e_3/∂x_2 - ∂e_2/∂x_3 = - 1/c ∂h_1/∂t
(20) ∂e_1/∂x_3 - ∂e_3/∂x_1 = - 1/c ∂h_2/∂t
....
∂h_1/∂x_1 + ∂h_2/∂x_2 + ∂h_3/∂x_3 = 0
i は、ベクトルである。なぜなら、電流密度は、電荷密度に電荷の速度ベクトルを掛けたものとして定義されるから。 最初の3式から、e は、ベクトルとして見なされることが明らかである。そのとき、h は、ベクトルとして見なすことが できない(*)。それらの式は、しかしながら、h を 2 階の反対称テンソルとみなすならば、容易に解釈できる。 従って、我々は、h_1, h_2, h_3 の代わりに、それぞれ、h_23, h_31, h_12 と書く。h_μνの反対称性に注意を払って、 (19), (20) の最初の3式は、次の形式に書くことができる。
(19a) ∂h_μν/∂x_ν= 1/c ∂e_μ/∂t + 1/c i_μ
(20a) ∂e_μ/∂x_ν - ∂e_ν/∂x_μ = + 1/c ∂h_μν/∂t
e, h に対比して、同じ型の対称性をもつ量として、角速度がある。 発散の方程式は、次の形式をとる。
(19b) ∂e_ν/∂x_ν= ρ
(20b) ∂h_μν/∂x_ρ + ∂h_νρ/∂x_μ + ∂h_ρμ/∂x_ν = 0
最後の方程式は、3 階の反対称のテンソル方程式である( h_μνの反対称性に注意を払えば、どの添字対に関しても、 左辺の反対称性は、容易に証明できる)。この記述は、通常のものよりも自然である。なぜなら、通常の記述と違って、 それがデカルト左手系を、右手系だけでなく、符号を変えずに適用できるからである。
1. 時間は絶対的である; 事象の K' に相対する時間 t' は K に相対する時間と等しい。もし、即時的信号を遠方に送ることができるならば、 そして、もし、人が時計の運動状態がその速度に影響を受けないことを知るならば、そのとき、この仮定は、物理的に正当と認められるだろう。 なぜなら、そのとき、時計は、ひとつひとつが類似で、同じく規制され、K と K' 系に渡って分布でき、それらに静止して、それらの表示は、 系の運動状態から独立しているだろう; ひとつの事象の時間は、そのとき、その直ぐ近傍の時計によって与えられるだろう。
2. 長さは絶対的である; もし、間隔が K に相対的に静止して、長さ s をもつなら、そのとき、それは、 K 系に相対的に運動する K' 系に 相対しても同じ長さ s をもつ。
もし、K と K' の軸が互いに平行であるなら、これらふたつの仮定に基づく単純な計算が、変換の方程式を与える。
(21) x'_ν= x_ν - a_ν - b_ν t
t'= t - b
この変換は、"ガリレオ変換(Galilean Transformmation)"として知られる。時間で 2 回微分して、我々は、次を得る。
d^2 x'_ν/dt^2 = d^2 x_ν/dt^2
x'_ν^(1) - x'_ν^(2) = x_ν^(1) - x_ν^(2)
2 点間の距離の不変性は、2乗と加算からの結果である。このことから容易に、ニュートンの運動方程式のガリレオ変換(21)への共変性がでる。 こうして、物差しと時計に関するふたつの仮説を作るなら、古典力学が特殊相対性の原理へ合致するようになる。
しかし、このガリレオ変換への平行移動の相対性を建てようとする試みは、電磁現象に適用されるとき失敗する。マックスウェル・ローレンツ (Maxwell-Lorentz) の電磁方程式は、ガリレオ変換に関して共変でない。特に我々は、(21) によって、K を参照する光線がもつ速度 c をもつ ことは、参照する K' の方向に依存して、異なる速度をもつことに注目する。K の参照空間は、それゆえ、その物理的特性によって、それ (静止エーテル) に相対運動するその他の全ての参照空間と区別される。しかし、全ての実験は、参照物体とする地球に対して相対的な電磁現象 と光の現象が地球の移動速度による影響を受けないことを示した。これらの実験の最も重要なものは、マイケルソンとモーリー(Michelson and Morley) の実験であり、知られていることを想定する。特殊相対性の原理の有効性は、電磁現象に関しても、疑いをもつことは難しい。
他方、マックスウェル・ローレンツ方程式は、運動物体中の光学の問題の扱いにおいて、その有効性を証明した。他の理論は、光行差、運動物体 中の光伝播(フィゾー(Fizeau))、二重星の現象観測(ド・ジッター(De Sitter)) の事実を満足に説明しなかった。マックスウェル・ローレンツ 方程式の帰結、真空中に光は速度 c で伝播すること、少なくとも確定したひとつの慣性系 K に関しては、証明されたと見なされなければならない。 特殊相対性の原理に従って、我々は、この原理の真実性を、全ての他の慣性系についても、また仮定しなければならない。
これらの考察の全てから、空間と時間のデータは、物理的現実であり、単なる架空でない重要性をもつ; 特にこれは、座標系と時間がはいる 全ての関係に成立する。例えば、(21)の関係である。それゆえ、ひとつの慣性系 K からそれに対して動く別の K' へ我々がそれによって移る 真の変換方程式は何かと問うという意味だけでなく、それらの方程式が真か偽かを問うという意味もある。これが光速一定の原理と特殊相対性 の原理によって、独特に設定されることを示されるだろう。
この目的に向かい我々は、空間と時間とは、すでに示された方法で、ふたつの慣性系 K, K' に関して、物理的に定義されたと考える。さらに、 K のひとつの点 P_1 から別の点 P_2 へ真空を通して光線を渡す。もし、r が 2 点間の測定された距離ならば、そのとき、光の伝播は、次式を 満たさねばならない。
もし、我々がこの式を2乗し、r^2 を座標差 Δx_ν で表せば、この式の代わりに我々は次のように書ける。
(22) Σ(Δx_ν)^2 - c^2 Δt^2 = 0
この式は、K に相対する光の速度の一定性の原理を定式化する。光線を発する源の運動が何であれ、成立しなければならない。
同じ光の伝播は、K' に相対的に考察できる。その場合も、光速一定の原理が満たされねばならない。 それゆえ、K'に相対的に我々は、次式をもつ。
(22a) Σ(Δx'_ν)^2 - c^2 Δt'^2 = 0
式、(22a) と (22) とは互いに、K から K' への変換に関して相互に整合的でなければならない。これをもたらす変換を、ローレンツ変換 (Lorentz Transformation) と呼ぶ。
(22b) Δx_1^2 + Δx_2^2 + Δx_3^2 - Δt^2 = 0
すなわち、もし、ふたつの与えられた事象(光線の放出と受容)を我々が参照する慣性系でそれが満足すれば、全ての慣性系に関して方程式 が満足するということである。最終的に、ミンコフスキーとともに我々は、実数の座標値 l= ct の代わりに、虚数の時間座標を導入する。
x_4= il= ict, (√-1 = i)
そのとき、光の伝播を定義する方程式は、ローレンツ変換に関して共変でなければならないが、次になる。
(22c) Σ_(4) Δx_ν^2 = Δx_1^2 + Δx_2^2 + Δx_3^2 + Δx_4^2 = 0
この条件は、つねに満足する(*)。もし、我々がより一般的な次の条件を満足していれば。
(23) s^2= Δx_1^2 + Δx_2^2 + Δx_3^2 + Δx_4^2
(24) x'_μ= a_μ + b_μα x_α
ここで、αに渡る総和は、α= 1 から α= 4 までに拡張される。(23), (24) の式をみれば、もし、我々が、次元の数と実数性の関係を無視するとき、 ローレンツ変換は、ユークリッド幾何の平行移動と回転変換に恒等的に定義されていることが分かる、我々は、また、係数 b_μα が次の条件を 満足しなければならないことを結論することができる。
(25) b_μα b_να= δ_μν = b_αμ b_αν
一方、x_νの比が実数であるから、a_4, b_41, b_41, b_43, b_14, b_24, そして b_34 は純虚数、それ以外の全ての a_μ と b_μα が実数である ことが出る。
特別なローレンツ変換 もし、座標値のふたつだけが変換され、そして、もし、新しい原点を決めるだけの a_μ が消滅するなら、我々は、 (24) と (25) の形の最も単純な変換を得る。そのとき、我々は、添字 1, 2 について、(25) の関係が与える 3 つの独立な条件のために、次式を得る。
x'_1= x_1 cos Φ - x_2 sin Φ
(26) x'_2= x_1 sin Φ + x_2 cos Φ
x'_3= x_3
x'_4= x_4
これは、x_3 軸周りの(空間)座標系の空間のなかの単純な回転である。前に学んだ (時間の変換のない) 空間のなかの回転は、ひとつの特別な場合 として、ローレンツ変換に含まれる。添字 1, 4 については、我々は同様な仕方で、
x'_1= x_1 cos Ψ - x_4 sin Ψ
(26a) x'_4= x_1 sin Ψ + x_4 cos Ψ
x'_2= x_2
x'_3= x_3
x'_1= x_1 cos Ψ - il sin Ψ
l'= -ix_1 sin Ψ + l cos Ψ
一方、K' の原点、すなわち、x'_1= 0 については、x_1 = vl でなくてはならないから、これらの最初の式から、
(27) v= i tan Ψ
そして、また、
(28) sin Ψ= -iv/√(1 - v^2)
cos Ψ= 1/√(1 - v^2)
そうして、我々は、次を得る。
x'_1= (x_1 - vl)/√(1 - v^2)
(29) l' = (l- v x_1)/√(1 - v^2)
x'_2= x_2
x'_3= x_3
これらの式は、よく知られた特殊ローレンツ変換を形成する。それは、一般的な理論では 4 次元座標系の虚数角の回転と表現するものである。 もし、我々が通常の時間 t を光時間 l の代わりに導入するなら、そのとき、(29)のなかで、l を ct に、v を v/c に置き換えなければならない。
ΣΔx_ν^2 = 0
が、慣性系の選択に独立である重要性をもつことが出る; しかし、ΣΔx_ν^2 の量の不変性は、これから決して出てこない。 この量は、係数を伴って変換されるかもしれない。これは、(29)の右辺に係数λが掛かるかもしれないことによるのであり、そのλは v に依存できる。 しかし、我々がいま示すように、相対性の原理は、この係数が 1 から異なることを許さない。我々は、その軸の方向に運動する剛体の丸い円筒をもつ ことを想像しよう。もし、その半径が静止状態で単位の測定棒で測定されて、R_0 に等しいとするとき、運動中の半径 R は、R_0 と異なるかもしれない。 相対論は、参照空間に関する物体の形態が、その参照空間に相対的なその運動に独立であるとは仮定しないからである。しかし、空間の全ての方向は、 互いに同等でなければならない。R は、それゆえ、速度の大きさ q に依存してよい、しかし、その方向に依存してはならない; R は、それゆえ、q の偶関数でなければならない。もし、円筒が K' に相対的に静止しているなら、それの側面の方程式は、
x'^2 + y'^2 = R_0^2
もし、我々が(29)の最後の2式を一般化して書くならば、
x'_2= λx_2
x'_3= λx_3
そのとき、円筒の側面は、K を参照して次の式を満足する。
x^2 + y^2 = R_0^2 /λ^2
要素λは、それゆえ、円筒の側方向の短縮を表し、このように、上から v の偶関数だけであり得る。
x''_1= λ(v)λ(-v)x_1
....
....
l''= λ(v)λ(-v) l
いま、λ(v) は、λ(-v) と等しくなければならないから、そして、我々は全ての系で同じ測定棒を使うことを仮定しているから、 K''の K に対する変換は、恒等変換でなければならないということが出てくる (一方、λ= -1 である可能性は考える必要がないから)。 (訳注:λ(v)= 1 という言明が省かれている。) これらの考察において、不可欠であることは、測定棒の行動がそれらの以前の運動の履歴に依らないという仮定である。
運動する測定棒と時計 確定した K の時間 l= 0 において、整数 x'_1= n で与えられた点の位置は、K に関して x_1= n √(1 - v^2) で与えられる;これは、式 (29) の最初の式から出てきて、"ローレンツ短縮" を表わす。K の原点 x_1= 0 に静止する時計、その鼓動が l= n で特徴付けられるものは、K'から観察されたとき、次の式によって特徴付けられる鼓動をもつだろう。
l'= n/√(1 - v^2)
これは、式 (29) の2番目から出てきて、その時計は、K' に対して静止した場合よりも、ゆっくりと進むことを示す。これらふたつの帰結は、 必要な変更を加えれば(mutatis mutandis)、全ての参照系にとって成立し、独創的なローレンツ変換の物理的な内容を形成する。
速度の加算定理 もし、我々が相対速度 v_1 と v_2 をもつ、ふたつの特殊ローレンツ変換を結合するならば、そのとき、 ふたつの分離したローレンツ変換の代わりをする単独のローレンツ変換の速度は、(27) に従って、次で与えられる。
(30) v_12= i tan(ψ_1 + ψ_2)= i (tan ψ_1 + tan ψ_2)/(1 - tan ψ_1 tan ψ_2) = (v_1 + v_2)/(1 + v_1 v_2)
不変量 s^2 は、次元の数を軽視しても、対応するユークリッド幾何学の不変量から、次の点で異なっている。ユークリッド幾何学のなかでは s^2 は、 必然的に正である; それは、関係する 2 点が一緒になるときだけ消滅する。一方、次の式の消滅から、
s^2= ΣΔx_ν^2 = Δx_1^2 + Δx_2^2 + Δx_3^2 - Δt^2
そのふたつの時空点が一緒になると結論することはできない; 量 s^2 の消滅は、ふたつの時空点が真空中の(in vacuo)光信号によって 結合できるという、不変な条件である。もし、P が 4 次元空間のなかで x_1, x_2, x_3, l によって表現される点(事象)なら、そのとき、 光信号の手段で P と結合できる全ての "点" は、s^2= 0 の円錐上にある (図 1. と比較せよ、図は、次元 x_3 が抑圧されている)。 "上" 半分の円錐は、P から光信号を送れる点ででき; "下" 半分の円錐は、そこから光信号を P に送れる "点"を含むだろう。 円錐表面によって囲まれた内部の点 P' は、P とともに、負の s^2 を与える; P'P と同様に PP' もミンコフスキーに従って時間性である。 そのような間隔は、速度が光速よりも小さい運動の経路になり得る要素を表す(*)。この場合、慣性系の運動状態を適切に選ぶこと によって、l 軸を PP' の方向に引くことができる。もし、P' が "光円錐" の外部にあれば、PP' は、空間性である; この場合、慣性系の 適切な選択によって Δl を消滅させることができる。
(*) 光の速度を超える物質の速度は、特殊ローレンツ変換 (29) の根号表式 √(1 - v^2) から、可能でない。
任意の慣性系のなかにある x_1, x_2, x_3, x_4 の 4 つの量で指定される物理的実体、A_ν は 4 元ベクトルといって、成分 A_ν をもつ。 もし、A_ν がそれらの実数性と変換特性との関係で、Δx_ν に対応するならば;それは、空間性か時間性である。16 の量 A_μν は、 そのとき、2 階のテンソルの成分を形成する。もし、それらが次の方法に従って変換するならば。
A'_μν= b_μα b_νβ A_αβ
このことから、A_μν が変換特性と実数性特性に関して、ふたつの 4 元ベクトル (U), (V) の成分 U_μ, V_ν の積と同様に振舞うこと が出てくる。全成分は、添字 4 を一度だけ含むと純虚数であり、それ以外は実数である。3 階と高階のテンソルも同様な方法で定義される。 これらのテンソルの加算、減算、乗算、縮約、そして微分の演算は、全体として、3 次元空間のテンソルの対応する演算に類似している。
我々はいま、マックスウェル方程式 (19a), (19b), (20a), (20b)に戻って、次の記述法を導入する(*):
(30a) Φ_23, Φ_31, Φ_12, Φ_14, Φ_24, Φ_34
h_23, h_31, h_12, -ie_x, -ie_y, -ie_z
(31) J_1, J_2, J_3, J_4
1/c i_x, 1/c i_y, 1/c i_z, iρ
そして、Φ_μνは、-Φ_νμに等しくなければならないとする慣習に従うなら、そのとき、マックスウェル方程式は、次の式に繋げられる、
(32) ∂Φ_μν/∂x_ν= J_μ
(33) ∂Φ_μν/∂x_σ + ∂Φ_νσ/∂x_μ + ∂Φ_σμ/∂x_ν = 0
(30a) と (31) から代入によって容易に検証できるように。
e'_x= e_x, h'_x= h_x
(34) e'_y= (e_y - v h_z)/√(1-v^2), h'_y= (h_y + v e_z)/√(1-v^2)
e'_z= (e_z + v h_y)/√(1-v^2), h'_z= (h_z - v e_y)/√(1-v^2)
もし、K に関して磁場 h だけが存在して電場 e がないとき、K' に関しては e' も存在して、K'に相対的に静止した電荷 に作用するだろう。 K に相対的に静止した観測者は、この力を、ビオ・サバール (Biot-Savart) 力または、ローレンツ (Lorentz) 電動力と呼ぶ。それは、 それゆえ、あたかも、この電動力が電場の強さと融け合って、単独の実体になったかのように現れるのである。
(35) k= ρe+i×h
ここで、i は光速を単位とする、電気性の速度ベクトルである。もし我々が、(30a), (31) に従ってJ_μ, Φ_μ を導入すると、我々は、 その表式の第1成分として次を得る。
Φ_12 J_2 + Φ_13 J_3 + Φ_14 J_4
テンソル (Φ) の反対称性のために、Φ_11 が消滅することをみれば、k のその成分は、4次元ベクトルの最初の3つの成分は、次によって、
(36) K_μ= Φ_μν J_ν
そして、第4番目の成分は、次で与えられる。
(37) K_4= Φ_41 J_1 + Φ_42 J_2 + Φ_43 J_3= i(e_x i_x + e_y i_y + e_z i_z) = iλ
それゆえ、単位体積あたりの力の4次元ベクトルが存在し、その最初の 3 成分 k_1, k_2, k_3 は、単位体積あたりの動質力(ponderomotive force) 成分であり、その4番目の成分は、単位体積あたりの場の仕事率に√-1 を掛けたものである。
(36) と (35) の比較は、相対性の理論が形式的に電気性場の動質力 ρe と、ビオ・サバール力又はローレンツ力 i×h とを統合することを示す。
質量とエネルギー 4元ベクトル、K_ν の存在と意味から、重要な結論を描くことができる。電磁場がしばらくの間その上に作用する物体を想像しよう。 象徴的な図(図. 2)では、Ox_1 は、x_1 軸を表すと同時に、3 つの空間軸 Ox_1, Ox_2, Ox_3 の代わりをする;Ol は、実数の時間軸を表す。 この図のなかに有限の広がりの物体が確定した時間 l に間隔 AB によって表現されている; 物体の全体としての時空存在は、帯で表現されていて、 その境界がどこも l 軸に45°未満傾いている。時間の断面 l= l_1 と l= l_2 との間にあって、それらまでは拡がらない帯の部分を影付けしている。 これは、時空多様体の部分を表していて、そのなかで電磁的な場が物体に作用する、又はそのなかに格納された電荷に作用しそれらへの作用が物体に 伝達される。我々はいま、この作用の結果として、物体の運動量とエネルギーにおいて実行される変化を考える。
我々は、その物体において運動量とエネルギーの原理が有効であることを仮定する。運動量変化、ΔI_x, ΔI_y, ΔI_z エネルギー変化、ΔE は、 次の式で与えられる。
ΔI_x = ∫_l0^l1 dl∫k_x dxdydz = 1/i ∫ K_1 dx_1 dx_2 dx_3 dx_4
......
ΔE = ∫_l0^l1 dl∫λ dxdydz = 1/i ∫ 1/i K_4 dx_1 dx_2 dx_3 dx_4
4 次元体積要素が不変量であり、(K_1, K_2, K_3, K_4) が 4 元ベクトルをなし、影付きでない部分の積分が何も貢献しないから、境 l_0 と l_1 の間 の積分がそうであると同じく、影付き部分以上に拡がった 4 次元積分は、4元ベクトルとして変換する。それゆえ、ΔI_x, ΔI_y, ΔI_z, iΔE は、4元 ベクトルを形成することになる。それらの量自身はそれらの増分と同じ方法で変換されると予期できるから、我々は、4つの量の総計、
I_x, I_y, I_z, iE
自身が、4元ベクトルの性質をもつと推定する; これらの量は、物体の瞬間的な状態(例えば、l= l_1)に対するものである。
-ds^2= dτ^2 = -(dx_1^2 + dx_2^2 + dx_3^2) - dx_4^2 = dl^2(1 - q^2)
が、物質粒子の運動を表す4次元線の無限に短い部分に対する、不変量であることを注意する。不変量 dτ の物理的重要性は、容易に与えられる。 もし、我々の考える接線方向をもつように時間軸が選択されるなら、又は他の言葉では、もし我々がその質点を静止に変換すると、dτ= dl である; これは、それゆえ、質点と同じ場所に静止した光秒時計によって測定されるだろう。我々は、それゆえ、τを物質粒子の固有時と呼ぶ。 dl とは違って、dτは、それゆえ、不変量であり、光速と比べて小さい速度の運動では、実際的に dl と同等である。こうして我々は、
u_σ= dx_σ/dτ
が、dx_νと同様に、ベクトルの性質をもつことを見る; 我々は、(u) を速度の 4 次元ベクトル(短く、4 元ベクトル)と呼ぶ。 その成分は、(38)によって、
(40) Σu_σ^2 = -1
の条件を満たす。
我々は、その通常の記述では次式であるこの4元ベクトルが、
(41) q_x/√(1-q^2), q_y/√(1-q^2), q_z/√(1-q^2), i/√(1-q^2)
3次元では次式で定義される、物質粒子の速度成分から形成できる唯一の4元ベクトルであることを見る。
q_x= dx/dl, q_y= dy/dl, q_z= dz/dl
我々は、それゆえ、
(42) (m dx_μ/dτ)
I_x= mq_x/√(1-q^2)
(43) .....
E= m/√(1-q^2)
我々は、事実、これらの運動量の成分が、光のそれと比べて小さい速度では古典力学のそれらに一致することを認識する。 大きな速度では運動量は、速度に線形よりも速く増え、光速に接近するとき無限に大きくなるように増加する。
(43)の最後の式を静止した(q= 0)物質粒子に適用すれば、静止した物体のエネルギー E_0 がその質量に等しいことを見る。 我々が秒を時間の単位にとるならば、次を得るだろう。
(44) E_0 = mc^2
質量とエネルギーは、それゆえ、本質的に似たものである;それらは、単に同じことの違う表現である。物体の質量は定数ではない; そのエネルギー変化とともに変化する(*)。我々は、(43) の最後の式から q が 1 の光速に接近するとき E が無限に大きくなることを見る。 もし、我々が E を q^2 の累乗に展開するなら、我々は次を得る。
(45) E= m + m/2 q^2 + 3/8 mq^4 + ....
この展開式の第 2 項は、古典力学の物質粒子の運動エネルギーに対応する。
(46) K= d/dl (mq/√(1-q^2))
この方程式は、電子の運動のために H. A. ローレンツによって以前に採用され、β線の実験で偉大な精度で正しいことが証明されたものである。
電磁場のエネルギーテンソル 相対性の理論の開発の前、エネルギーと運動量の原理は、電磁場について微分形式で表現できることが 知られていた。これらの原理の4次元形式は、エネルギーテンソルの重要な概念を導き、それは、相対論のさらなる開発のために重要である。
もし、単位体積あたりの力の 4 元ベクトルの次の表式のなかで、
K_μ= Φ_μνJ_ν
場の方程式、(32) を使って、J_ν を場の強さ Φ_μν を使って表して、いくらかの変形の後、場の方程式 (32) と (33) を繰り返し適用して、 次式を得る。
(47) K_μ= - ∂T_μν/∂x_ν
ここで、我々は、次の書き方をした(*)。
(48) T_μν= - 1/4 Φ_αβ ^2 δ_μν + Φ_μα Φ_νβ
k_x= - ∂p_xx/∂x - ∂p_xy/∂y - ∂p_xz/∂z - ∂(ib_x)/∂(il)
(47a) ............................................................
............................................................
iλ= - ∂(i s_x)/∂x - ∂(i s_y)/∂y - ∂(i s_z)/∂z - ∂(-η)/∂(il)
または、虚数を消去して、
k_x= - ∂p_xx/∂x - ∂p_xy/∂y - ∂p_xz/∂z - ∂b_x/∂l
(47b) .......................................................
.......................................................
λ= - ∂s_x/∂x - ∂s_y/∂y - ∂s_z/∂z - ∂η/∂l
後者の形式に表現したとき、我々は、最初の3式が運動量の原理を述べることをみる; p_xx ... p_xz は、電磁場のマックスウェルの歪であり、 (b_x, b_y, b_z) は、場の単位体積あたりのベクトル運動量である。(47b) の最後の式は、エネルギー原理を表現し、 s がエネルギーの流れのベクトル、ηは、場の単位体積あたりのエネルギーである。事実、我々は、(48) から、場の強さの実数成分を 導入することによって、電磁力学からよく知られる次式を得る。
p_xx= -h_x h_x + 1/2 (h_x^2 + h_y^2 + h_z^2)
-e_x e_x + 1/2 (e_x^2 + e_y^2 + e_z^2)
p_xy = - h_x h_y - e_x e_y
p_xz = - h_x h_z - e_x e_z
(48a) .............................................
.............................................
b_x= s_x = e_y h_z - e_z h_y
.............................................
.............................................
η= + 1/2 (e_x^2 + e_y^2 + e_z^2 + h_x^2 + h_y^2 + h_z^2)
我々は、(48) から、電磁場のエネルギーテンソルが対称であることに注目する;これと次の事実は、結合している。 体積あたりの運動量とエネルギーの流れは、互いに等しい (エネルギーと慣性の関係である)。
(47c) ∂T_μν/∂x_ν = 0
保存原理への一般的表式 我々には避け難く、全ての他の場合もエネルギーの空間分布は、対称テンソル T_μν で与えられ、この完全な エネルギーテンソルがどこでも (47c) の関係をみたすという仮定を作ることになる。少なくとも我々は、この仮定によって積分型エネルギー原理の 正確な表式を得るのをみるであろう。
空間的に制限のある閉じた系を考えよう、4 次元的にその外部でT_μνが消滅する帯で表すことができる。(47c) の空間的断面に渡る積分をとる。 T_μν が積分の境で消滅するから、∂T_μ1/∂x_1, ∂T_μ2/∂x_2 そして ∂T_μ3/∂x_3 の積分が消滅して、我々は、次を得る。
(49) ∂/∂l {∫T_μ4 dx_1 dx_2 dx_3} = 0
括弧の内部は、全体系の運動量の表式であり、i 倍されて、系の負のエネルギーと一緒にして、(49)が積分形式で保存原理を表すようになる。 これが正しいエネルギーの概念と保存の原理を与えることは、次の考察からみることができる。
(*) この知識の欠如を救済する試みが荷電粒子を固有の特異点として考慮することによってなされた。しかし、私の意見では、これは物質構造の 本当の理解の放棄を意味する。外見だけの解に満足するよりも、我々の現在の不可能性を受け入れるほうが、私にはずっとよいと思える。
水力学的方程式 我々は物質が電気的な荷電粒子によって出来ていることを知っている。しかし、これらの粒子の構成を支配する 法則を知らない。力学的問題を扱うのに、我々は、それゆえ、古典的力学のそれに対応する、物質の不正確な記述を使用せざるを得ない。 物質の実質の密度σと水力学的圧力とは、その上にそのような記述が基づく基本的概念である。
σ_0 は、物質に対して動いている座標系を参照して推定する、ある場所の物質密度としよう。そのとき、静止の密度σ_0 は不変量である。 もし、我々が任意の運動をする物質を考え、圧力を無視するなら(真空中の塵、粒子のサイズと温度を無視して)、そのとき、エネルギーテンソルは 速度成分 u_ν、と σ_0 にだけ依存するであろう。我々は、次のように置き、T_μν のテンソル特性を保存する。
(50) T_μν= σ_0 u_μ u_ν
ここで、u_μ は、その3次元表現を(41)で与えた。事実、(50)から、q= 0 については、T_44= -σ_0 (単位体積あたりの負のエネルギーに等しい) であることが出てくる。それは、物質とエネルギーの等価原理に従い、上に与えたエネルギーテンソルの物理解釈に従わねばならない。 もし、外部の力(4次元ベクトル K_μ)がその物質に作用するなら、運動量とエネルギーの原理から、次式が成立しなければならない。
K_μ= ∂T_μν/∂x_ν
我々は、この式が、すでに得られたと同じ物質粒子の運動法則を導くことを示す。空間に無限小の拡がりをもつ物質を想像しよう、すなわち、4次元 のひもである; そのとき、ひも全体を、空間座標 x_1, x_2, x_3 に関して積分することによって、我々は次を得る。
∫ K_1 dx_1 dx_2 dx_3 = ∫∂T_14/∂x_4 dx_1 dx_2 dx_3 = -i d/dl {∫σ_0 dx_1/dτ dx_4/dτ dx_1 dx_2 dx_3}
∫σ_0 dV dl = ∫σ_0 dV_0 dτ
そして、それゆえ、また、
∫σ_0 dV = ∫σ_0 dV_0 dτ/dl = ∫dm i dτ/dx_4
もし、我々が右辺側を前者の積分の左辺に置き換え、dx_1/dτ を積分記号の外に置けば、次を得る。
K_x = d/dl (m dx_1/dτ) = d/dl (m q_x/√(1-q^2))
我々はそれゆえ、エネルギーテンソルの一般化された概念は、我々の以前の結果に一致することを見る。
(51) T_μν= σ u_μ u_ν + pδ_μν
静止では、物質の密度、または、単位体積のエネルギーは、この場合、σではなく、σ - p である。なぜなら、
-T_44= -σ dx_4/dτ dx_4/dτ - pδ_44 = σ - p
他に力のない場合、我々は次をもつ。
∂T_μν/∂x_ν = σ u_ν ∂u_μ/∂x_ν + u_μ∂(σ u_ν)/∂x_ν + ∂p/∂x_μ = 0
もし、我々がこの式に u_μ (= dx_μ/dτ) を掛け、μ の総和をとれば、(40)を使って我々は次を得る。
(52) - ∂(σ u_ν)/∂x_ν + ∂p/∂τ = 0
ここで、我々は、∂p/∂x_μ dx_ν/dτ = ∂p/∂τ とした。これは、連続の方程式であり、古典力学の式から dp/dτ だけ異なる。 それは、実際的には、消滅するように小さい。(52) を観察して、保存原理は次の式をとる。
(53) σ du_μ/dτ + u_μ dp/dτ + ∂p/∂x_μ = 0
その式の最初の3添字については、明らかにオイラー方程式に対応している。(52), (53) の式は、古典力学の水力学の方程式に1次近似で 対応することは、一般化されたエネルギー原理のさらなる確認である。物質(またはエネルギー)の密度は、テンソル特性をもつ(とくに対称 テンソルを構成する)。
慣性の原理を物理の要石とみなす限り、この立場は、確かに正当化される唯一のものである。しかし、普通概念のふたつの深刻な批判が存在する。 第1番目には、それは、それ自身作用するが、作用されることのない、あること(時空連続体)を思考する科学の思想の様式に反している。 これが、E.マッハ(Mach) が力学のシステムにおいて、空間を作用の原因として除去しようと試みをすることを導いた理由である。 彼に従えば、物質粒子は、非加速的な運動を空間に相対してするのではなく、宇宙の他の全ての質量の中心に相対してする; この方法で、ニュートンとガリレオの力学に対比して、力学的な現象の原因の系列は閉じられる。 媒体を通した作用の現代理論の制限のなかにおいて、この概念を開発するために、慣性を決定する時空連続体の特性が、電磁場に類似する 空間の場の特性と見なされなければならない。古典力学の概念は、これを表現する方法を与えない。この理由のため、その解として E.マッハの試みは、現在の所、失敗している。我々は、後にこの観点に戻って来るだろう。 第 2 番目として、古典力学は、互いに非均一な運動をする参照空間への相対性の原理の拡張を直接に求める欠乏症を呈している。2物体の 質量比は、力学では互いに基本的に異なるふたつの方法によって定義された;最初には、それらの間に同じ動機の力が与えられるときの互い の加速の比として(慣性質量)、次には、同じ重力場のなかでそれらに作用する力の比として(重力質量)。 全く異なって定義された、これらふたつの質量の等価性は、事実、非常に高い精度の実験によって確認された(エトベッシュ(Eötvös)実験) が、古典力学は、この等価性に何も説明を提供しない。しかしながら、この数値的一致がこれらふたつの概念の現実の性質の等価性に 還元され割り振られた後にだけ、科学は正当性を完全にすることは明らかである。
(慣性質量)・(加速)= (重力場の強さ)・(重力質量)
加速が物体の性質から独立であることは、慣性と重力質量の間に数値的一致があるときだけである。いま、K を慣性系としよう、 互いにまた他の物体から十分遠い質量は、そのとき、K に関して加速から解放されている。我々はまた、これらの質量を、K に関して 均一に加速している座標系 K' に参照させる。K' に相対的には、全ての質量は等しく平行な加速をもつ; K' に関しては、それらは、 あたかも、重力場が存在し、K' が加速されていないかのように行動する。 いまのところ、そのような重力の "原因" についての問いを俯瞰すれば、それは後に我々を占有するだろうが、この重力場が現実のもの であると我々が考えることを妨げるものはない。すなわち、K' が "静止" していて、重力場が存在するという考えは、K だけが "許される" 座標系であって重力場はないという考えと同等に考え得るものである。 座標系 K と K' の完全な物理的等価性の仮定を、我々は "等価性の原理" と呼ぶ。この原理は、明らかに、慣性と重力質量の同等性の法則 に深く結合していて、互いに非均一的運動をする座標系への相対性の原理の拡張を意味している。 事実、この概念を通して、我々は、慣性と重力の性質の統合に到着する。なぜなら、それを見る我々の方法に従えば、同じ質量が慣性だけ の作用のもとにある(Kに関して)、又は慣性と重力の結合した作用のもとにある(K'に関して)、のいずれとも表れることができるからである。 慣性と重力のそれらの性質の統合によって数値的な等価性を説明できる可能性は、私の信ずるところによれば、遭遇する全ての困難も、 この進歩と比較すれば小さいと考えなければならないような、そのような古典力学の概念に対する優越性を相対性の一般理論に与える。
等価原理は、ガリレイ領域を扱うのに、我々が等しく非慣性系、すなわち、慣性系に相対して加速と回転から自由でないような座標系、 を使用してよいことを要求する。もし、我々が、さらに、ある座標系への選別に客観的な理由についてのいらいらする問いから完全に 離れようとするなら、そのときは、我々は、任意に運動する座標系の使用を許さなければならない。この試みを真面目にしようとする とすぐに、我々は、特殊相対論によって我々がそこに導かれた時間と空間のあの物理的解釈との相克に出会うことになる。 なぜなら、K' をその z'軸が K の z 軸と一致して、後者の軸の周りに一定の角速度で回転している座標系としよう。K'に相対的に静止 する剛体の構成は、ユークリッド幾何学の法則に従うだろうか? 一方、K'は慣性系ではないので K' に関する剛体の構成の法則を、また、 自然法則一般についても、我々は、直接には知らない。しかし、我々は、慣性系 K に関して、これらの法則を知っている。そして我々は、 それゆえ、K'に関しての式を推定できる。 K' の x'y' 平面の原点の周りに円とこの円の直径を描くことを想像しよう。さらに、我々が 互いに等しい多数の剛体棒を与えられていると想像しよう。我々は、これらを K' に相対的に静止している円の円周と直径にそって順次 直列に並べることを想定する。もし、U を円周にそったこれらの棒の数、D を直径にそった数とすると、そのとき、もし、K' が K に相対的に 回転していないなら、我々は次をもつ。
U/D = π
しかし、もし、K' が回転するなら我々は違う結果を得る。K の確定した時間 t において我々は全ての棒の端を決定することを考えよう。 K に関して、円周上の全ての棒は、ローレンツ短縮を経験する。しかし、直径上の棒は、この短縮(それらの長さにそった!)を経験しない。 それゆえ、次式が出てくる。
U/D > π
我々が考察してきた場合は、表面の2次元的扱いで説明した場合と類似する。後者もまた、単純な計量的意味をもつ表面(例えば楕円体の表面) の座標系を導入することは、不可能である。一方、平面上でデカルト座標、x_1, x_2 は、単位測定棒によって測られた長さを直接に意味する。 ガウスは、彼の表面の理論のなかで、この困難を乗り越えた。連続の条件を満たす以外は全く任意な曲線座標を導入し、そして、その後にだけ、 これらの座標値が表面の計量的特性に関係しているとすることによって。 類似の方法によって、我々は、一般相対論に任意の座標値、x_1, x_2, x_3, x_4 を導入する、時空点を一意に数値化し、隣接する事象が隣接 する座標値に関連する;それ以外、座標値の選択は任意である。もし我々が、そのようなどの4次元座標系にも有効である形式を法則に与える なら、すなわち、法則を表現する方程式が任意の変換に関して共変であるなら、我々は、その最も広い意味において相対性の原理に忠実である。
ds^2 = dX_1^2 + dX_2^2
もし、我々が任意の曲線座標値 x_1, x_2 をその表面に導入するなら、そのとき、dX_1, dX_2 は dx_1, dx_2 によって線形に表現できる。 そのとき、表面のどこにおいても、我々は次の式をもつ。
ds^2 = g_11 dx_1^2 + 2 g_12 dx_1 dx_2 + g_22 dx_2^2
ここで、g_11, g_12, g_22 は、表面の性質と座標の選択によって決定される; もし、これらの量を知るなら、そのとき、その表面上に どのように剛体棒の網の目が敷かれ得るかをも知るのである。言葉を替えれば、表面の幾何は、ds^2 のこの表式に基づくことができ、 それは、平面幾何が対応する表式に基づくのと正確に同様である。
物理学の4次元時空連続体のなかに類似の関係がある。重力場のなかで自由落下する観測者の直近傍において、重力場は存在しない。 我々は、それゆえ、つねに、時空連続体の無限小の領域をガリレイ的とみることができる。そのような無限小領域には、それを参照すれば、 特殊相対論の法則が有効であると我々がみなすべき、慣性系(空間座標 X_1, X_2, X_3 と時間座標 X_4 をもつ)が存在する。 我々の単位測定棒と時計によって直接に測定可能な量、
dX_1^2 + dX_2^2 + dX_3^2 - dX_4^2
または、その負の、
(54) ds^2= - dX_1^2 - dX_2^2 - dX_3^2 + dX_4^2
は、それゆえ、ふたつの隣接する事象(4次元連続体のなかの点)に対する一意に決定される不変量である。持ち寄り重ねるとき互いに等しい 測定棒と、持ち寄るときその速度の等しい時計とを、我々が使用するならばである。このなかには、ふたつの測定棒の相対的な長さ、ふたつの 時計の相対的な速度は、それらの以前の履歴から原理的に独立である、という物理的な仮定が不可欠である。しかし、この仮定は、確かに経験 によって保証されている;もし、それが成立しなければ、鋭いスペクトル線はあり得ないだろう。なぜなら、同じ元素の単独原子は、確かに同 じ履歴を持たない。そしてなぜなら、ー単独原子の以前の履歴に依存する相対的可変性を仮定してーこれら原子の質量または固有の周波数が かつてずっと互いに等しかったと想定することは理屈に合わない。
(55) ds^2 = g_μν dx_μ dx_ν
関数 g_μν は、任意に選択された座標系に関して、時空連続体の計量関係、そしてまた重力場をも記述する。特殊相対論におけると同じく、 我々は、4次元連続体のなかで、時間性と空間性の線要素を区別しなければならない; 導入された符号の変化のために、時間性の線要素は実数の、 空間性の線要素は虚数の ds をもつ。時間性の ds は、適切に選ばれた時計によって直接に測定することができる。
以上述べたことに従って、一般相対論の定式化には、不変量の理論とテンソルの理論の一般化が必要であることが明らかである; 任意の点変換 に関して共変である方程式の形成についての問いが持ちあがる。テンソルの一般化された計算は、相対論よりもずっと以前に数学者達によって 開発された。リーマン (Riemann) は、ガウス (Gauss) の任意次元の連続体の一連の考察を最初に拡張した; 予言的視点をもって、ユークリッド (Euclid) 幾何学の一般化の物理的な意味を見た。そして、とくにリッチ(Ricci) とレビ・チビタ(Levi-Civita) とによって、テンソルの計算の 形式での理論の開発が続いた。ここで、このテンソル計算の最も重要な数学的な概念と演算を短く提示する。
(56) A'^ν= ∂x'_μ/∂x_ν A^ν
これら反変ベクトル以外に、共変ベクトルも存在する。もし、B_ν が共変ベクトルの成分なら、これらのベクトルは、 次の規則に従って変換される。
(57) B'_μ= ∂x_ν/∂x'_μ B_ν
共変ベクトルの定義は、共変と反変ベクトルがともに、次の方式に従って、スカラーを形成することによる方法も選択できる。
Φ= B_ν A^ν (νに渡って総和する)
なぜなら、我々は次をもつから。
B'_ν A'^ν= ∂x_α/∂x'_μ ∂x'_μ/∂x_β B_α A^β = B_α A^α
とくに、スカラーΦの微分 ∂Φ/∂x_α は、共変ベクトルの成分であり、座標微分とともに、スカラー ∂Φ/∂x_α dx_α を形成する; この例から、我々は、共変ベクトルの定義がどれほど自然であるかを見る。
(58) A_μ'^ν= ∂x_α/∂x'_μ ∂x'_ν/∂x_β A_α^β
テンソルは、線形直交変換の不変量理論と同様に、同じ階数の同種の性質のテンソルの加算と減算によって形成できる。例えば、
(59) A_μ^ν + B_μ^ν = C_μ^ν
C_μ^ν のテンソルの性質は、(58)によって証明される。
テンソルは、線形直交変換の不変量理論と同様に、添字の性質を保存して、乗算によっても形成できる。例えば、
(60) A_μ^ν B_στ = C^ν_μστ
証明は、変換の規則から直接に出てくる。
テンソルは、異なる性質のふたつの添字に関する縮約によって形成できる。例えば、
(61) A^μ_μστ= B_στ
A^μ_μστのテンソル性質は、B_στ のテンソル特性を決定する。証明ー
A'^μ_μστ= ∂x_α/∂x'_μ ∂x'_μ/∂x_β ∂x_δ/∂x'_σ ∂x_t/∂x'_τ A^β_αδt = ∂x_δ/∂x'_σ ∂x_t/∂x'_τ A^α_αδt
これによって、テンソルの代数的な特性に対する全ての本質的なことは、言い終えた。
基本テンソル dx_ν の任意選択における ds^2 の不変性から、(55)に整合する対称性の条件と関連して、 g_μν が 対称共変テンソル(基本テンソル)の成分であることが出る。様々な g_μνに対応して g_μν の行列式 g を作り、そしてまた、 余因子を g で割ろう。これら余因子を g で割ったものは、g^μν で記述し、そして、その共変の性質は、まだ知られていない。 そのとき、我々は、次をもつ。
(62) g_μα g^μβ= δ_α^β= 1 (if α=β), 0 (if α≠β)
もし、我々が無限小の量(共変ベクトル)を形成するなら、
(63) dξ_μ= g_μα dx_α
g^μβを掛け、μに渡り総和して、(62)を使って、次を得る。
(64) dx_β= g^βμ dξ_μ
dξ_μの比は任意であるから、そして、dx_β も dξ_μ と同様にベクトルの成分であるから、g^μν は、反変テンソルの成分(*) (反変基本テンソル)であることが出てくる。δ_α^β (混合基本テンソル)のテンソル性質は、それゆえ、(62)によって続いてくる。 我々は、基本テンソルによって、共変添字の性質のテンソルの代わりに、反変添字性質のテンソルを導入したり、その逆もできる。例えば、
A^μ= g^μα A_α
A_μ= g_μα A^α
T^σ_μ= g^σν T_μν
dx'_α= ∂x'_σ/∂x_μ ∂x'_α/∂x_β g^μβ dξ'_σ
上でなされた言明は、これから出る。なぜなら、(64)によって、我々はまた dx'_α= g^σα' dξ'_σ を持たねばならず、両式は、 どの dξ'_σ の選択にも成立しなければならないからである。
∫dx_1 dx_2 dx_3 dx_4 = dx
は、不変量ではない。なぜなら、ヤコビ(Jacobi)の定理によって、
(65) dx'= |dx'_μ/dx_ν| dx
しかし、我々は、dx を補正して不変量にすることができる。もし、我々がその量の行列式を形成するなら、
g'_μν= ∂x_α/∂x'_μ ∂x_β/∂x'_ν g_αβ
我々は、行列式の乗算の定理を2回適用して、次を得る。
g'= |g'_μν| = |∂x_ν/∂x'_μ|^2 . |g_μν| = |∂x'_μ/∂x_ν|^-2 g
我々は、それゆえ、次の不変量を得る。
√g' dx' = √g dx
それにも関わらず、一般の場合のテンソルの不変量の微分演算は、最も満足に認識される、次の方法でレビ・チビタ(Levi-Civita)とワイル(Weyl) によって導入された。(A^μ) を反変ベクトルとし、その成分が、x_ν の座標系に関して与えられているとしよう。P_1 と P_2 を、 連続体のふたつの無限近傍点とする。点 P_1 を囲む無限小領域にとって、質量を考慮する我々の方法に従って、それに関して連続体が ユークリッド的な X_ν の座標系 (虚数の X_4 座標をもつ) が存在する。A^μ_(1) を点 P_1 でのそのベクトルの座標値としよう。点 P_2 に ベクトルを引き、X_ν の局所系を使って、同じ座標値をもつ (P_2を通る平行なベクトル) ことを想像せよ。そのとき、この平行ベクトル は、P_1 にあるベクトルと移動とによって、一意に決定される。我々は、この操作を、その一意性は後に示すが、ベクトル (A^μ) の 無限近傍点 P_2 への平行移動と呼ぶ。もし、我々が P_2 点でのベクトル (A^μ)と P_1 から P_2 への平行移動によって得るベクトルと のベクトルの差を作れば、我々は、ベクトル (A^μ) の与えられた変位 (dx_ν) に対する微分と見なすことのできるベクトルを得る。
(67) δA^ν= -Γ^ν_αβ A^α dx_β
我々は、さらに、Γ^ν_αβ が、添字αとβに関して対称でなければならないことを言うことができる。なぜなら、我々は、局所座標の ユークリッド系の助けによる表現から、要素 d^(1) x_ν の2番目の要素 d^(2) x_ν に沿う移動と d^(2) x_ν の d^(1) x_ν に沿う移動と によって同じ平行四辺形が描かれると仮定できるからである。我々は、それゆえ、次を持たねばならない。
d^(2) x_ν + (d^(1) x_ν - Γ^ν_αβ d^(1) x_α d^(2) x_β)
= d^(1) x_ν + (d^(2) x_ν - Γ^ν_αβ d^(2) x_α d^(1) x_β)
上述のことは、この式から右辺の総和の添字αとβを交換して出る。
量 g_μν は、連続体の全ての計量特性を決定するから、Γ^ν_αβ をも決定しなければならない。 もし、ベクトル A^μ の不変量を考えるなら、すなわち、その大きさの2乗、
g_μν A^μ A^ν
が不変量であり、これは、平行移動によって変化しえない。我々は、それゆえ、次をもつ。
または、(67) によって、
(∂g_μν/∂x_α - g_μβ Γ^β_να - g_νβ Γ^β_μα) A^ν A^μ dx_α = 0
括弧内の式の添字μとνに関する対称性のため、この式が (A^μ) と d_ν の任意選択にも有効であることは、括弧内の式が添字のどの組合せ にも消滅するときだけ可能である。添字μ,ν,αの周期的交換により、このように全部で 3 つの方程式を得て、そこから、Γ^α_μνの対称の 特性を考慮に入れて、次を得る。
(68) [μν, α]= g_αβ Γ^β_μν
ここでクリストッフェルに従って、次の省略記号を用いた。
(69) [μν, α]= 1/2 (∂g_μα/∂x_ν + ∂g_να/∂x_μ - ∂g_μν/∂x_α)
もし、(68)に g^ασ を掛け、αに渡って総和すれば、次を得る。
(70) Γ^σ_μν= 1/2 g^σα (∂g_μα/∂x_ν + ∂g_να/∂x_μ - ∂g_μν/∂x_α) = {μν, σ}
ここで {μν, σ} は、第 2 種クリストッフェル記号である。このように、Γ の量は、g_μνから導かれる。 式 (67), (70) は、これからの議論の基礎となる。
dA^μ - δA^μ= (∂A^μ/∂x_σ + Γ^μ_σα A^α) dx_σ
も、またベクトルである。これは、dx_σの任意選択の場合であるから、次式、
(71) A^μ_;σ= ∂A^μ/∂x_σ + Γ^μ_σα A^α
がテンソルであることが出る。我々は、これを1階のテンソル(ベクトル) の共変微分と呼ぶ。 このテンソルを縮約して反変テンソル A^μの発散を得る。このなかに我々は、(70) に従って、次をみなければならない。
(72) Γ^σ_μσ= 1/2 g^σα ∂g_σα/∂x_μ = 1/√g ∂√g/∂x_μ
もし、我々がさらに、次を置くなら、
(73) A^μ√g = A^μ
これはワイルが1階の反変テンソル密度(*)と呼ぶ量である。そこから、
(74) A= ∂A^μ/∂x_μ
は、スカラー密度であることが出る。
Φ= A^μ B_μ
を不変に残すような方法で影響すべきこと、そして、それゆえ、
A^μ δB_μ + B_μ δA^μ
が、どんな値を (A^μ) に割り当てても消滅するという規則である。我々はそれゆえ、次を得る。
(75) δB_μ= Γ^α_μσ B_α dx_σ
これから、我々は、(71)を導いたと同様な過程によって、共変ベクトルの共変微分に到達する。
(76) B_μ;σ= ∂B_μ/∂x_σ - Γ^α_μσ B_α
添字μとσの交換、そして引算によって、我々は、次の反対称テンソルを得る。
(77) Φ_μσ= ∂B_μ/∂x_σ - ∂B_σ/∂x_μ
(78) A_στ;ρ= ∂A_στ/∂x_ρ - Γ^α_σρ A_ατ - Γ^α_τρ A_σα
テンソルの共変微分の一般的な法則を明確に見るため、類似の方法で導かれるふたつの共変微分を書き下す。
(79) A^τ_σ;ρ= ∂A^τ_σ/∂x_ρ - Γ^α_σρ A^τ_α + Γ^τ_αρ A^α_σ
(80) A^στ_;ρ= ∂A^στ /∂x_ρ + Γ^σ_αρ A^ατ + Γ^τ_αρ A^σα
形成の一般法則は、いま、明らかになる。これらの式から、理論の物理的応用において興味のある他のいくつかを導こう。
もし、A_στが反対称であるなら、我々は次のテンソルを、
(81) A_στρ= ∂A_στ/∂x_ρ + ∂A_τρ/∂x_σ + ∂A_ρσ/∂x_τ
それは、全ての添字の対に反対称であるが、周期的交換と加算によって得る。
A^στ が反対称の場合、我々は (80) から、τとρに関する縮約によって、次を得る。
(82) A^σ= ∂A^στ/∂x_τ
一般の場合、(79) と (80) から、τとρに関する縮約によって、我々は、次の式を得る。
(83) A_σ= ∂A^α_σ/∂x_α - Γ^α_σβ A^β_α
(84) A^σ= ∂A^σα /∂x_α + Γ^σ_αβ A^αβ
リーマンテンソル もし、我々が連続体の点 P から点 G に伸びる曲線が与えられたなら、そのとき、P に与えられたベクトル A^μ は、平行移動によって G までその曲線に沿って動かすことができる。もし、連続体がユークリッド的 (より一般的に、座標の適切な選択に よって g_μν が一定である) ならば、そのとき、その移動の結果として G に得られるベクトルは、P と G を結ぶ曲線の選択に依存しない。 しかし、そうでないとき、結果は移動の経路に依存する。この場合は、それゆえ、ベクトルは、もし、それを点 P から閉じた曲線に沿って運び、 再び P に達するならば、ΔA^μ (その方向に、その大きさでなく) の変化を被る。我々は、いま、このベクトルの変化を計算する。
ΔA^μ= §δA^μ
閉曲線の周りのベクトルの線積分へのストークスの定理のように、この問題は、無限小の線の大きさをもつ閉曲線の周りの積分に還元できる; 我々は、この場合に限定しよう。
我々は、最初に、(67) によって、
ΔA^μ= -§ Γ^μ_αβ A^α dx_β
このなかで Γ^μ_αβ は、積分経路上の可変点 G にあるこの量の値である。もし、我々が次のように置き、
ξ^μ= (x_μ)_G - (x_μ)_P
P における Γ^μ_αβ の値を ~Γ^μ_αβ で表すと、そのとき、我々は、十分な精度をもって、次をもつ。
Γ^μ_αβ = ~Γ^μ_αβ + ∂~Γ^μ_αβ/∂x_ν dξ_ν
さらに、A^αを ~A^α から P から G への曲線に沿った平行移動によって得られた値としよう。いま、(67)によって、容易に証明できるのは、 A^μ - ~A^μ が1次の無限小であり、一方、曲線が1次の無限小の大きさをもつから、ΔA^μ は、2次の無限小であることである。それゆえ、 もし、我々が次のように置いても、2次のオーダーの誤差しかない。
A^α = ~A^α - ~Γ^α_στ ~A^σ ~ξ^τ
もし、我々がこれらの値、Γ^μ_αβ と A^α を積分に導入して、我々は、2次より高次の全ての量を無視して、次式を得る。
(85) ΔA^μ= -(∂Γ^μ_σβ/∂x_α - Γ^μ_ρβΓ^ρ_σα) A^σ §ξ^α dξ^β
1/2 §(ξ^α dξ^β - ξ^β dξ^α)
この 2 階の反対称テンソル f^αβ は、その曲線で区切られた表面要素を、大きさと位置で特徴づける。もし、(85) の括弧内の式が添字α とβに関して反対称なら、我々は、そのテンソル特性を (85) から結論できるだろう。我々は、 (85) の総和の添字αとβとを交換して、 結果の式を (85) に加算することによって、これを達成できる。我々は、次を得る。
(86) 2ΔA^μ= - R^μ_σαβ A^σ f^αβ
ここで、
(87) R^μ_σαβ= - ∂Γ^μ_σα/∂x_β + ∂Γ^μ_σβ/∂x_α + Γ^μ_ραΓ^ρ_σβ - Γ^μ_ρβΓ^ρ_σα
R^μ_σαβ のテンソル特性は、(86)から出る; これは、4階のリーマン曲率テンソルであり、その対称性の特性についてさらには踏み込む 必要がない。その消滅は(選ばれた座標系の現実性に関わらず)、連続体がユークリッド的であることの十分条件である。添字μとβに関して リーマンテンソルを縮約すれば、我々は、次の2階の対称テンソルを得る。
(88) R_μν= - ∂Γ^α_μν/∂x_α + Γ^α_μβΓ^β_να + ∂Γ^α_μα/∂x_ν - Γ^α_μνΓ^β_αβ
最後の2項は、もし、座標系が g= 一定であるように選ばれれば消滅する。R_μν から、我々は、次のスカラーを形成できる。
(89) R= g^μν R_μν
δ(dx_μ/ds) = - Γ^μ_αβ dx_α/ds dx_β
左辺は、d^2x_μ/ds^2 によって置き換えされ(*)、我々は、次を得る。
(90) d^2x_μ/ds^2 + Γ^μ_αβ dx_α/ds dx_β/ds = 0
もし、我々がふたつの点の間の、次の積分の停留値を与える線 (測地線) を見出すならば、我々は、同じ線を得る。
∫ds 又は、 ∫ √ (g_μν dx_μ dx_ν)
力の作用しない物質粒子は、慣性の原理に従って直線上を均一に運動する。特殊相対論(実数時間座標をもつ)の 4 次元連続体のなかでは、 これは、現実の直線である。一般(リーマン的)不変量の理論の概念系のなかで意味のある自然で、すなわち、最も単純な、直線の一般化は、 最も真直な線、または測地線である。従って我々は、慣性と重力だけが作用する物質粒子の運動が次の方程式で記述できると、等価性の 原理の意味で、仮定しなければならない。
(90) d^2x_μ/ds^2 + Γ^μ_αβ dx_α/ds dx_β/ds = 0
事実、この方程式は、もし、重力場の Γ^μ_αβ の全成分が消滅するならば、直線の式に還元する。
どのように、この方程式がニュートンの運動方程式に繋がっているか? 特殊相対論に従って、g^μν と同様に g_μν も慣性系に関して 次の値をもつ (実数の時間座標と ds^2 の適切な符号の選択によって)。
-1, 0, 0, 0 (91) 0,-1, 0, 0 0, 0,-1, 0 0, 0, 0, 1
運動の方程式は、そのとき、次になる。
d^2x_μ/ds^2 = 0
-1, 0, 0, 0 (91a) 0,-1, 0, 0 0, 0,-1, 0 0, 0, 0,-1
これらの値は、集めて次の関係にできる。
g_μν= -δ_μν
2次までの近似では、我々は次を置かなければならない。
(92) g_μν= -δ_μν + γ_μν
ここで、γ_μν は、1次のオーダーの小ささとみなされる。
そのとき、我々の運動方程式のふたつの項は、1次のオーダーの小ささである。これら 1 次のオーダーより相対的に小さい項を我々が無視する なら、次を置かなければならない。
(93) ds^2 = - dx_ν^2 = dl^2 (1 - q^2)
(94) Γ^μ_αβ= -δ_μσ [αβ, σ] = -[αβ, μ] = 1/2 (∂γ_αβ/∂x_μ - ∂γ_αμ/∂x_β - ∂γ_βμ/∂x_α)
(90a) d^2x_μ/dl^2 = ∂/∂x_μ (γ_44/2)
この方程式は、重力場のなかの物質粒子のニュートンの運動方程式に一致する、もし、我々が (γ_44/2) を重力場のポテンシャルであると 特定するならば; これが許されるかどうかは、当然、重力の場の方程式に依存し、すなわち、それは、この量がニュートンの理論の重力 ポテンシャルと同じ場の法則を、1 次近似とかまで満たすかどうかに依存している。(90) と (90a) を眺めると、Γ^μ_αβ が、重力場 の強さの役割を実際に果たしていることが分かる。これらの量は、テンソル特性を持たない。
式 (90)は、物質粒子への慣性と重力の影響を表している。慣性と重力の結合は、(90)の左辺全体が (座標系のどのような変換に関しても) テンソルの特性をもつが、分離して採られたふたつの項は、テンソルの性格をもたないという事実によって形式的に表れている。 ニュートンの方程式との類似性によって、最初の項が慣性を、第 2 の項が重力を表しているとみなすことができる。
ΔΦ= 4πΚρ
が模型として役に立つに違いない。この方程式は、重力場が質量をもった物質の密度ρからくるという発想にその基礎をもつ。それは、 一般相対論においてもそうでなければならない。しかし、我々の特殊相対論の研究は、物質のスカラー密度の代わりに、我々が単位体積あたり のエネルギーのテンソルをもつということを示した。後者のなかには、重さのある物質のエネルギーのテンソルだけでなく、電磁的エネルギー のそれも含んでいる。我々は、実に、より完全な分析のなかで、エネルギーテンソルは、物質を表現する暫定的手段としてだけみなし得るとい うことをみた。現実に物質は、電気的に荷電粒子からできていて、それ自身、電磁場の部分、事実、主要な部分、とみるべきものである。 それは、単に状況説明として、我々が集中した荷電の電磁場の十分な知識をもたないこと、それが我々に、暫定的に、理論を提示するときに このテンソルの真の形式を未決定に残すことを強いた、ということである。この視点から、まだ未知である構造の2階のテンソル T_μν を 導入することが現在適切であり、それらは、電磁場のエネルギー密度と重さのある物質のそれとを暫定的に結合する;我々はこれを、 "物質のエネルギーテンソル" と、次下において呼ぶ。
我々の以前の結果に従えば、運動量とエネルギーの原理が、このテンソルの発散の消滅 (47c) の言明によって表現された。一般相対論において、 我々は、それに対応する一般共変方程式が有効であると仮定しなければならない。もし、(T_μν) が物質の共変エネルギーテンソルを示し、 T^ν_σ がそれらに対応する混合テンソル密度なら、そのとき、(83) に従って、我々は次が満たされることを要求しなければならない。
(95) 0= ∂T^α_σ/∂x_α - Γ^α_σβ T^β_α
物質のエネルギー密度だけでなく、重力場のエネルギー密度もまた、与えなければならないことを想い出されなければならない。そうして、 物質だけの運動量エネルギー保存原理をいうことがあり得ないようにする。数学的にはこれは、(95) の第 2 項の存在によって表される。 それは (49) の形式の積分方程式の存在を結論することを不可能にする。重力場は、エネルギーと運動量を "物質" に伝達する。そのなかで それは、それに力を働かせ、エネルギーを与える; これが (95) の第 2 項によって表現されている。
これらの条件の最初のふたつは、ポアソン方程式から自然に取って来る。一方、全てのそのような微分テンソルは、リーマンテンソルから代数的に (すなわち、微分なしに) 形成できるということが数学的に証明できるため、我々のテンソルは、次の形でなければならない。
R_μν + α g_μν R
ここで、R_μν と、R は、(88) と (89) によってそれぞれ定義される。さらに、3番目の条件は、αが -1/2 の値をもつことを要求することが 証明できる。重力場の法則として、我々は、それゆえ、次の方程式をもつ。
(96) R_μν - 1/2 g_μν R = - κ T_μν
式 (95) は、この式の帰結のひとつである。κは、定数を表し、ニュートンの重力定数に結合している。
以下では私は、むしろ含まれる数学的方法ができるだけ少ないものを使って、物理的視点から興味のある、理論の特徴を示す。 最初に、左辺の発散が実際に消滅することを示さなければならない。物質のエネルギー原理は、(83) によって、次式に表現される。
(97) 0= ∂T^α_σ/∂x_α - Γ^α_σβ T^β_α
ここで、T^α_σ = T_στ g^τα √-g
類似の操作を (96) の左辺に適用すれば、恒等式を導くだろう。
g_μν = g^μν = - δμν = -1 (if μ=ν), = 0 (if μ≠ν)
そして、それを使えば、g_μνと g^μν の1次の微分が消滅する。 我々は、この点で、左辺の発散が消滅することを検証する。この点で Γ^α_σβ の成分が消滅するから、 次式の消滅だけを証明しなければならない。
∂/∂x_σ [√-g g^νσ (R_μν -1/2 g_μν R)]
(88) と (70) をこの式に導入して、我々は、残された項は、g_μνの3次の微分が入ったものであることをみる。一方、g_μνは、 -δ_μνと置き換えされ、我々は、最終的に互いに打ち消し合うことを容易にみることのできる、少数の項だけになる。 一方、我々の形成したものは、テンソルの性格をもつから、その消滅は、他の全ての座標系にもまた証明され、他の全ての4次元点にも いえる。物質のエネルギー原理 (97) は、こうして、場の方程式 (96) のひとつの数学的帰結である。
方程式 (96) が経験と整合するかどうかを学ぶために、我々は、何よりも先に、それらが1次近似としてニュートン理論を導くかどうかを 見出さねばならない。この目的のために、我々は、これらの方程式に、様々な近似を導入しなければならない。我々はすでに、 ユークリッド幾何学と光速の一定性の法則が、ある程度の近似で、惑星系のような非常に広い領域で、有効であることを知っている。 もし、特殊相対論のなかのように、我々が4番目の座標を虚数にとれば、これは、我々が次を置かねばならないことを意味している。
(98) g_μν= - δ_μν + γ_μν
ここで、γ_μν は、1 と比べて非常に小さい値であって、それゆえ、我々は、γ_μν の高次の累乗とその微分を無視できる。もし、 我々がこれを行えば、我々は、重力場の構造、又は宇宙的大きさの計量空間について、何も知り得ず、代わりに我々は、近傍質量の 物理的現象への影響を知ることになるだろう。
この近似を行う前に、我々は、(96)を変換する。我々は、(96) に g^μν を掛け、μとνとで総和して、g^μνの定義からくる関係を 観察することによって、
g_μν g^μν = 4
我々は、次の式を得る。
R= κ g^μν T_μν = κT
もし我々が、この R の値を (96) にいれると、我々は、次を得る。
(96a) R_μν= -κ(T_μν -1/2 g_μν T) = - κT*_μν
-1/2 (∂^2γ_μν/∂x_α^2 + ∂^2γ_αα/∂x_μ∂x_ν - ∂^2γ_μα/∂x_ν∂x_α - ∂^2γ_να/∂x_μ∂x_α)
又は、
-1/2 ∂^2γ_μν/∂x^2_α + 1/2 ∂/∂x_ν(∂γ'_μα/∂x_α) + 1/2 ∂/∂x_μ(∂γ'_να/∂x_α)
そのなかで、次を置いた。
(99) γ'_μν= γ_μν - 1/2 γ_σσ δ_μν
我々は、いま、式 (96) がどの座標系にも有効であることを注意しなければならない。我々は、すでに我々が選択した座標系を特別にして、 考慮する領域のなかで g_μνが一定値 -δ_μνから無限小しか違わないようにしている。しかし、 この条件は、座標のどの無限小変化においても満たされて残っていて、γ_μνが従うべき 4 条件はまだ存在する。ただし、これらの条件が、 γ_μνの大きさのオーダーの条件に相反しない限りである。我々は、いま、座標系が次の 4 関係式を満たすよう選択されたと仮定するー
(100) 0= ∂γ'_μν/∂x_ν = ∂γ_μν/∂x_ν - 1/2 ∂γ_σσ/∂x_μ
そのとき、(96a) は、次の式を取る。
(96b) ∂^2γ_μν/∂x_α^2 = 2 κ T*_μν
これらの方程式は、電磁力学で慣れた遅延ポテンシャルの方法によって解くことができ; 我々は、容易に理解できる記述を得る。
(101) γ_μν= -κ/2π ∫T*_μν(x_0, y_0, z_0, t - r)/r dV_0
(102) T^μν= σ dx_μ/ds dx_ν/ds
ds^2= g_μν dx_μ dx_ν
ここで、σ は、静止の密度、すなわち、重さのある物質の密度である。普通の意味の、単位測定棒の助けによって測定され、そして、物質に 伴って運動するガリレイ座標系を参照したそれである。
我々は、さらに、我々の選択した座標のなかで、もし我々が g_μν を -δ_μνに置き換え、次式のようにしても、相対的に小さな誤差しか 生まないことを見る。
(102a) ds^2= - Σ dx_μ^2
場を生成する質量が、我々が選択した疑似ガリレイ座標系に相対的にどれほど急速に運動しても、以前の開発は有効である。 しかし、天文学では、我々は採用した座標系に相対した質量の速度が、光速に比してつねに小さい、すなわち、我々の時間の単位の選択では 1 に比べて小さいものを扱わなくてはならない。我々は、それゆえ、もし、(101) のなかの遅延ポテンシャルを通常の(非遅延)ポテンシャルに 置き換え、そして、場を発生する質量に対して、次式を置けば、ほとんど全ての実際的な目的に十分な近似を得る。
(103a) dx_1/ds = dx_2/ds = dx_3/ds = 0, dx_4/ds= (√-1 dl)/dl = √-1
0, 0, 0, 0, (104) 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-σ,T については、我々は、値 σ を得て、最終的に T*_μν の値は、次である。
σ/2,0, 0, 0, (105) 0,σ/2, 0, 0, 0, 0,σ/2, 0, 0, 0, 0,-σ/2,我々は、こうして(101)から次を得る。
(101a) γ_11= γ_22 = γ_33 = -κ/4π ∫σdV_0/r,
γ_44 = +κ/4π ∫σdV_0/r,
一方、他の γ_μν は、消滅する。これらの式の最後には、式 (90a) との関連で、ニュートンの重力理論を含んでいる。 もし、我々が l を ct に置き換えれば、
(90b) d^2x_μ/dt^2 = κc^2/8π ∂/∂x_μ ∫σdV_0/r
我々は、ニュートン重力定数Κが、我々の場の方程式に入っている定数κと次の関係をもつことをみる。
(105) Κ= κc^2/8π
それゆえ、Κの知られる数値から、次が出る。
(105a) κ= 8πΚ/c^2 = 8π.6・67.10^-8/(9.10^20) = 1・86.10^-27
いま、我々の結果から、測定棒と時計の行動を判断できるために、我々は、次のことを見なければならない。等価性の原理に従って、 ユークリッド幾何学の計量関係は、適切な運動状態 (自由落下、そして、回転なし)にある、無限小の大きさのデカルト座標系に関して 有効である。我々は同じ言明を、これらに相対的に小さな加速をもつ局所座標系に対して、そしてそれゆえ我々が選択したひとつ に関して静止であるような座標系に対してすることができる。そのような局所系に対して、我々は隣接2点の事象に次をもつ。
ds^2= = - dX_1^2 - dX_2^2 - dX_3^2 + dT^2 = -dS^2 + dT^2
ここで、dS は、測定棒によって直接に測られ、dT はその系に静止した時計によるものである; これらは、自然に測定された長さと時間である。 他方、ds^2 は、次式によって有限領域に採用される座標値 x_ν によって知られる。
ds^2 = g_μν dx_μ dx_ν
我々は、自然に測定された長さと時間を一方にして、対応する座標値の差を他方とし、それらの間の関係を得る可能性をもつ。 空間と時間への分割は、ふたつの座標系に関して一致するから、我々が ds^2 へのふたつの表現を等しいと置くとき、我々はふたつの関係を得る。 もし、(101a) によって我々が次を置けば、
ds^2= -(1 + κ/4π ∫σdV_0/r) (dx_1^2 + dx_2^2 + dx_3^2) + (1 - κ/4π ∫σdV_0/r) dl^2
我々は、十分に近い近似で、
(106) √(dX_1^2+ dX_2^2+ dX_3^2)= (1 + κ/8π ∫σ dV_0/r )√(dx_1^2+ dx_2^2+ dx_3^2)
dT= (1 - κ/8π ∫σ dV_0/r ) dl
1 - κ/8π ∫σ dV_0/r
我々の選択した特定の座標系は、この長さが場所にだけ依存し、方向に依らないことを保証する。もし、我々が異なる座標系を選べば、これは そうならずに、我々がどのような座標系を選んだとしても、剛体の構成の法則は、ユークリッド幾何学のそれには一致しない;言葉を替えれば、 我々は、座標値、Δx_1, Δx_2, Δx_3 を単位測定棒の端に対応して、どの方向を向けても、関係、Δx_1^2 + Δx_2^2 + Δx_3^2 = 1 をつねに 満たすように、座標系を選択することはできない。この意味で、空間はユークリッド的ではなく、"曲がっている" のである。 上の関係式の2番目から、単位時計 (dT= 1) のふたつの脈動の間の間隔は、我々の座標系に使われる単位では、次の "時間" に対応する。
1 + κ/8π ∫σ dV_0/r
従って、その近傍にある重さのある物質の質量が大きくなればなるほど、時計の速さは、遅くなる。我々は、それゆえ、太陽表面によって作られた スペクトル線は、地上で作られた対応する線と比較して、それらの波長の約 2.10^-6 だけ、赤い方向に移動すると結論する。最初、理論の この重要な帰結は、実験と相反するかにみえた; しかし、過去数年間に得られた結果は、この効果の存在をさらに確かそうにさせるようにみえ、 そして、理論のこの帰結が次の数年間以内に確認されるだろうことを疑うことは、ほとんど出来ない。
実験的にテストできる、もうひとつの重要な理論の帰結として、光線の経路を扱わなければならない。一般相対論においても、光速がどこでも 等しいのは、局所慣性系に相対してである。この速度は、我々の時間の自然計測において 1 である。一般座標における光の伝播の法則は、 それゆえ、一般相対論に従って次の式で特徴付けられる。
ds^2 = 0
我々の使う近似まででは、そして、我々が選択した座標系では、光速は (106) に従って、次の式によって特徴付けられる。
(1 + κ/4π ∫σdV_0/r) (dx_1^2 + dx_2^2 + dx_3^2) = (1 - κ/4π ∫σdV_0/r) dl^2
光の速度 L は、それゆえ、我々の座標値では、次によって表現できる。
(107) √(dx_1^2+ dx_2^2+ dx_3^2)/dl = 1 - κ/4π ∫σ dV_0/r
α= ∫_-∞^+∞ 1/L ∂L/∂x_1 dx_3
積分を実行して我々は、次を得る。
(108) α= κM/(2πΔ)
この屈折の存在は、その量が太陽の半径に等しいΔにおいて 1.7''は、1919年に英国日蝕遠征隊によって注目すべき正確さで、確認され、 そして、1922年の日蝕の際に、より正確な観測データを得るための最も注意深い準備がなされた。注意されなければならないことは、 これもまた、座標系の我々の任意選択によって影響されない理論的な結果であることである。
静的な場の場合、ds^2 は、次の形式を持たねばならない。
(109) ds^2= -dσ^2 + f^2 dx_4^2
dσ^2= Σ_1-3 γ_αβ dx_α dx_β
ここで、最後の式の右辺の総和は、空間変数だけに渡る。場の中心対称性は、γ_μνに次の形式を要求する。
(110) γ_αβ= μ δ_αβ + λ x_α x_β
f^2, μ そして λ は、r= √(x_1^2 + x_2^2 + x_3^2) だけの関数である。これら 3 つの関数のひとつは、任意に選ぶことができる、 なぜなら、我々の座標系は、先験的に、 完全に任意であるから; なぜなら、次の置き換えによって、
x'_4= x_4
x'_α= F(r) x_α
(110a) γ_αβ= δ_αβ + λ x_α x_β
この方法で g_μν は、ふたつの量、λと f によって表現される。これらは、r の関数として決定されるべきもので、それらを式 (96) に代入し、(109) と (110a) から最初に Γ^σ_μν を求めた後、我々は次をもつ。
Γ^σ_αβ= 1/2 x_σ/r (λ x_α x_β + 2 λ r δ_αβ)/(1 + λr^2),
(110b) Γ^4_44 = Γ^α_4β = Γ^4_αβ= 0, (for α,β,σ= 1,2,3)
Γ^4_4α= 1/2 f^-2 ∂f^2/∂x_α, Γ^α_44= -1/2 g^αβ ∂f^2/∂x_β
これらの結果の助けによって、場の方程式は、シュワルツシルト(Schwarzschild)解を与える。
(109a) ds^2= (1-A/r)dl^2 -[dr^2/(1-A/r) + r^2 (sin^2ΘdΦ^2 + dΘ^2)]
ここで、我々は次を置いた。
(109b) x_4= l, x_1= rsinΘsinΦ, x_2= rsinΘcosΦ, x_3= rcosΘ, A= κM/4π
M は、太陽質量を示し、座標の原点の周りに中心対称的に置かれる; 解(109a) は、この質量の外側だけに有効であり、そこでは T_μν が全て消滅する。惑星運動を x_1 - x_2 平面上に取ると、そのとき、(109a) は次式に置き換えなければならない。
(109c) ds^2= (1 - A/r) dl^2 - dr^2/(1 - A/r) - r^2 dΦ^2
d/ds (x_α dx_β/ds - x_β dx_α/ds) = 0
または、もし、我々が積分して、結果を極座標表示すれば、
(111) r^2 dΦ/ds = constant
(90)からμ= 4 について我々は次を得る。
0= d^2l/ds^2 + 1/f^2 ∂f^2/∂x_α dx_α/ds dl/ds= d^2l/ds^2 + 1/f^2 df^2/ds dl/ds
これから、f^2 を掛けて、積分して、我々は次を得る。
(112) f^2 dl/ds = constant
(109c), (111) そして (112) のなかに、我々は、3つの方程式を 4つの変数、s, r, l, Φ の間にもち、4変数から惑星運動が古典力学と 同様に計算できる。これからの最も重要な結果は、惑星回転と同じ意味の楕円惑星軌道の永年回転であり、1 回転あたりのラジアンの累積は、
(113) 24π^3 a^2/(1-e^2)c^2T^2
ここで、a= 惑星軌道の長軸[cm]、e= 離心率、 c= 3.10^10 真空中の光速、 T= 回転周期 [秒]である。
この式は、100年間 (ルベリエ(Leverrier)以来)知られ、理論的天文学がこれまで満足に説明できなかった、惑星水星の近日点の運動の説明を与える。
(114) Φ_μν= ∂Φ_μ/∂x_ν - ∂Φ_ν/∂x_μ
第2のマックスウェル方程式系は、そのとき、テンソル方程式で定義され、次から結果する。
(114a) ∂Φ_μν/∂x_ρ + ∂Φ_νρ/∂x_μ + ∂Φ_ρμ/∂x_ν = 0
そして、最初のマックスウェルの方程式系は、テンソル密度関係式で定義される。
(115) ∂F^μν/∂x_ν= J^μ
ここで、
F^μν= √-g g^μσ g^ντ Φ_στ
J^μ= √-g ρ dx_μ/ds
もし、我々が電磁場のエネルギーテンソルを(96)の右辺に導入するなら、我々は、(96)の結果として、発散を取ることによって、J^μ= 0 の特別な場合に (115)を得る。この一般相対論の図式に電気的理論を包括することは、任意であり満足できないと多くの理論家から考えられた。 我々は、また、この方法によって要素的な電気的荷電粒子を構成する電気的平衡を理解することはできない。重力場と電磁場が論理的に別個の 構造で入らない理論がはるかに好ましい。H. ワイル(Weyl)と最近は Th. カルツア(Kaluza)がこの方向に沿った独創的なアイデアを提出した; しかし、それらに関して、私は、基本的な問題の真の解にそれらが我々を近づけることはないと考える。 私は、これにさらに立ち入らず、いわゆる、宇宙論的問題の短い議論を与える。 なぜなら、これなしには一般相対論に関する考察は、ある意味で不満足に残るからである。
もし、宇宙が疑似ユークリッド的であるなら、そのとき、マッハ(Mach)は、彼の思想、慣性が重力と同様に物体間のある種の相互作用による という考えにおいて、全体として間違っていたことになる。なぜなら、この場合、適切な選択の座標系において、g_μνは無限遠で特殊相対論 におけると同様に定数になるだろうし、一方、有限の領域のなかで g_μν は、座標の適切な選択において、有限領域の質量の影響の結果 として、これらの定数値から少量だけ異なるであろうからである。そのとき、空間の物理的特性は、全体として独立ではなく、すなわち、 物質から影響を受けないわけではなく、それらは全体として、すこしの程度であるが、物質から条件付けられるからである。そのような、 双対性の概念は、それ自身としてさえ、満足できるものではない;しかしながら、それに反対するいくらかの物理的な議論が存在し、我々はそれを考察する。
宇宙が無限で、無限遠ではユークリッド的であるという仮定は、相対論的視点からは、複雑な仮定である。それは、一般相対論の言語のなかで、 4階のリーマンテンソル R_iklm が無限遠で消滅しなければならない。それらは、20 の独立な条件を与える一方、ただ 10 個の曲率成分 R_μν だけが重力場の法則に入っている。それは確かに、そのような遠隔の制限を、何らの物理的基礎なしに仮定することは満足できないことである。
1. 物体の慣性は、重さのある質量が近傍に積み上げられるとき、増加しなければならない。
2. 物体は、近傍の質量が加速されるとき、加速力を経験しなければならない。そして事実その力は、その加速と同方向でなければならない。
3. 回転する空の物体は、その内部に、回転と同じく運動物体を屈折させる "コリオリの場" を発生しなければならない。半径方向の遠心場も同様である。
我々は、マッハの着想に一致して期待されるこれら 3 つの効果が、それらの大きさは非常に小さいため、それらの実験室内での確認が考えられない にも関わらず、我々の理論に従えば実際に存在することを示す。この目的のために、我々は、物質粒子の運動方程式 (90)に戻って、式 (90a) でなされた近似よりも、いくらか先に進んだ近似を実行する。
最初に我々は、γ_44 を1次のオーダーの小ささと考える。重力の影響のもとに運動する質量の速度の 2 乗は、エネルギーの式に従って、 同じオーダーである。それゆえ、我々の考慮する物質粒子の速度だけでなく、場を発生する質量の速度も同様に、オーダー 1/2 の小ささと みなすのは論理的である。我々はいま、場の方程式 (101) と運動方程式 (90)、その考慮する項については、(90) の第2項のなかの速度に 線形なものに限り、起きる式のなかの近似を実行する。 さらに我々は、ds を dl に互いに等しいとは置かず、より高次の近似に対応して、次のように置く。
ds= √g_44 dl = (1 - γ_44/2) dl
(116) d/dl[(1 + γ_44/2)dx_μ/dl]= - Γ^μ_αβ dx_α/dl dx_β/dl (1 + γ_44/2)
(101)から、我々は、探した近似までに次を得る。
-γ_11= -γ_22= -γ_33= γ_44= κ/4π ∫σdV_0/r
(117) γ_4α= - iκ/2π ∫σdx_α/ds dV_0/r
γ_αβ= 0
ここで、(117)では、αとβは、空間添字だけを示す。
(116)の右辺で我々は、1+γ_44/2 を 1 に、-Γ^μ_αβ を[αβ, μ] に、置き換えることができ、それに加え、この近似の程度には、 我々が次を置かなければならないことを容易にみる。
[4 4, μ]= -1/2 ∂γ_44/∂x_μ + ∂γ_4μ/∂x_4
[α4, μ]= 1/2(∂γ_4μ/∂x_α - ∂γ_4α/∂x_μ)
[αβ,μ]= 0
ここで、α, β, μは、空間添字を示す。我々は、それゆえ、(116)から、通常のベクトル記述で、次を得る。
d/dl [(1+~σ)v] = grad ~σ + ∂A/∂l +[curl A, v]
(118) ~σ= κ/8π ∫σ dV_0/r
A= κ/2π ∫σ dx_α/dl dV_0/r
運動方程式 (118) は、いま、実際、次を示す。
1. 慣性質量は、 1 + ~σ に比例し、そして、それゆえ、重さのある質量が試験物体に近付くとき、増加する。
2. 加速された質量の同符号で試験物体に作用する誘導作用が存在する。これは、項 ∂A/∂l である。
3. 物質粒子で、回転する空洞物体のなかの回転軸に垂直に運動するものは、回転を意味する(コリオリ場)屈曲を受ける。
上述の回転する空洞物体のなかの遠心作用も、サーリング(Thirring)(*) によって示されたように、理論から出てくる。
宇宙的大きさの g_μν 場の満足な概念のためには、星ぼしの相対速度が光速に比べて小さい事実は、重要に思える。これから、座標を適切に選べば、 g_44 が宇宙で、少なくとも物質のある宇宙の一部でほとんど定数である、ということが出る。さらに、宇宙の全ての部分に星ぼしが存在するという仮定 は、自然に思えて、g_44 の非一定性は、物質が連続的に分布せず、単独の天体や天体系に集中している状況だけによると我々が思ってよいようにみえる。 もし、我々が、宇宙の全体としての幾何学的特性の何かを学ぶために、物質密度のそして g_μν の、これら、より局所的な非均一性を無視したいなら、 実際の物質分布を連続的な分布に置き換えることも、さらに、この分布に均一密度σを割り当てることも、自然であると見える。この想像する宇宙のなか で、全ての点と全ての空間方向は、幾何学的に等価である; それの空間に関してのその拡張は、一定の曲率をもつだろう、そしてその x_4 座標に関して 円筒的であろう。宇宙が空間的に有限であり、そしてこのように、我々のσの一定性の仮定に従って、一定の曲率をもち、球状または楕円的である可能性 は、特に満足すべきに思える; なぜならそのとき、一般相対論の立場からは非常に不便である無限遠の境界条件は、閉じた空間へのはるかに自然な条件 に置き換えられるからである。
すでに述べたことに従って、我々は、次を置くべきであろう。
(119) ds^2= dx_4^2 - γ_μν dx_μ dx_ν
ここで、添字μ,ν は、1 から 3 までだけを走る。γ_μν は、一定の正の曲率をもつ3次元連続体に対応するような、x_1, x_2, x_3 の関数であろう。 我々は、いま、そのような仮定が、重力の場の方程式を満たし得るかどうかを、調べなければならない。
x_1^2 + x_2^2 + x_3^2 + x_4^2 = a^2
dx_1^2 + dx_2^2 + dx_3^2 + dx_4^2 = ds^2
x_4を消去して(**)、我々は次を得る。
ds^2= dx_1^2 + dx_2^2 + dx_3^2 + (x_1 dx_1 + x_2 dx_2 + x_3 dx_3)^2/(a^2 - x_1^2 - x_2^2 - x_3^2)
x_ν の 3 次以上の項を無視して、我々は、座標の原点の近くでは次を置くことができる。
ds^2= (δ_μν + x_μ x_ν/a^2) dx_μ dx_ν
括弧のなかは、原点の近くでの多様体の g_μν である。g_μν の1次微分と、それゆえ、Γ^σ_μν も原点で消滅するから、 この多様体の R_μν の計算は、(88)によって、原点では非常に単純である。我々は、次をもつ。
R_μν= -2/a^2 δ_μν = -2/a^2 g_μν
関係式 R_μν= -2/a^2 g_μν は、一般共変であるから、そしてその多様体の全ての点は、幾何学的に同等であるから、この関係は、 全ての座標系で成立し、多様体のどこでも成立する。4次元連続体との混同を避けるために、3次元連続体に関する量をギリシャ文字で表して、 我々は、次を置く。
(120) Ρ_μν= - 2/a^2 γ_μν
我々は、いま、場の方程式 (96) の我々の特別な場合への適用に進む。(119)から、我々は、4次元多様体への次を得る。
(121) R_μν= Ρ_μν (添字 1 から 3),
R_14= R_24= R_34= R_44= 0
T^μν= σ dx_μ/ds dx_ν/ds
しかし、それに加えて、我々は、次のように物理的に確立できる圧力の項を加算しなければならない。物質は、荷電粒子から構成される。 マックスウェル理論の基礎の上ではこれらは、特異性のない電磁場と理解することはできない。事実と整合するように、同符号の電荷をもつ 要素間の互いの斥力にも関わらずに、単独の電気的粒子が互いに成立することができるように、マックスウェル理論に入らないエネルギー項を 導入する必要がある。この事実に整合するために、ポアンカレ(Poincaré) は、これら粒子の内部に、電気的斥力とつり合う圧力が存在 することを仮定した。しかしながら、この圧力が粒子の外部で消滅すると主張することはできない。我々はこの状況に整合するならば、 我々の現象論的提示では我々は圧力の項を付け加える。しかしながら、これは、水力学的圧力と混同されてはならない。それは、物質内部の 力学的関係のエネルギー存在を助けるだけであるから。従って我々は、次を置く。
(122) T_μν= g_μα g_νβ σ dx_α/ds dx_β/ds - g_μν p
我々の特別な場合、それゆえ、我々は次を置かねばならない。
T_μν= γ_μν p (μ,ν= 1-3)
T_44 = σ - p
T = - γ^μνγ_μν p + σ - p = σ - 4p
場の方程式 (96) が次式に書けることを見て、
R_μν= -κ(T_μν - 1/2 g_μν T)
(96) から、我々は次の式を得る。
+2/a^2 γ_μν= κ(σ/2 - p) γ_μν
0= -κ(σ/2 + p)
これから、次が出る。
(123) p= -σ/2
a= √(2/κσ)
もし、宇宙が疑似ユークリッド的であるなら、そしてその曲率半径がそれゆえ無限大なら、そのとき、σは、消滅するだろう。しかし、宇宙の物質の 平均密度が実際にゼロであることは不可能である; これが、宇宙が疑似ユークリッド的であるという仮定に反対する、我々の第3番目の議論である。 また、我々の仮説的な圧力が消滅できるということも可能に見えない; この圧力の物理的性質は、我々が電磁場のよりよい理論的知識をもった後に 正しく認識されるだろう。(123) の第 2 式に従えば、宇宙の半径 a は、物質の全体質量 M によって、次の式で表される。
(124) a= Mκ/4π^2
幾何学の物理的特性への完全な依存は、この式によって、明白になる。
1. 相対論の立場からは、閉じた宇宙を仮説することは、宇宙の疑似ユークリッド構造の無限遠における対応する境界条件を仮説するよりも、 はるかに単純である。
2. マッハの表明した着想、慣性の物体相互作用への依存は、1次近似まで相対論の方程式に含まれている; これらの方程式から、慣性が 少なくとも部分的には質量間の相互作用に依ることが出る。それによって、マッハの着想は可能性を得る、慣性が部分的に相互作用に依存し 部分的には空間の独立特性であるということは、不満足な仮定であるが。しかし、マッハのこの発想は、空間的に制限された有限宇宙にだけ 調和し、疑似ユークリッド的な無限宇宙には対応しない。認識論的な立場からは、物質によって完全に決定される空間の力学的特性をもつ ことのほうが、より満足でき、そしてこれが閉じた宇宙の場合にだけある。
3. 無限の宇宙は、宇宙の物質の平均密度が消滅するときにだけ可能である。そのような仮定は論理的に可能とはいえ、 宇宙に物質の有限の平均密度があるという仮定と比べて、それはより少ない可能性でしかない。
最初の一歩の前進は、光源の位置の(負の)重力ポテンシャルによるスペクトル線の赤方偏移の存在の結論的な表示である (p.92を見よ)。この実証は、その平均密度が水の 10^4 倍のオーダーを超える、いわゆる "矮星" の発見によって可能になった。そのような星 (例えば、シリウスの暗い伴星) では、質量と半径とが決定でき(*)、この 赤方偏移は、理論によって太陽での約 20 倍の大きさと期待され、そして実際に期待された範囲にあることが実証された。
次の一歩の前進は、短く言及するが、重力物体の運動法則に関係する。理論の初期の定式化のなかでは、重力を受ける粒子の 運動法則は、重力場の方程式に追加する独立の基本的な仮定として導入されたー式 90 をみよ、それは、重力粒子が測地線を 運動することを主張する。これは、ガリレオの慣性法則の "本物" の重力場が存在する場合への仮説の移行を構成する。 任意の大きな重力的質量の場合に一般化された、この運動法則は、空の空間の場の方程式だけから導くことができることが示された。 この導出に従えば、運動法則は、場がそれを発生する質点の外側のどこにも特異性のない条件を含められることになる。
3番目の歩みは、いわゆる "宇宙論的問題" に関係し、ここで詳細に考察されるだろう。ひとつには、その基本的重要性からであり、 部分的にはまた、これらの質問の議論が決して終結しないからである。また、現在のこの問題の扱いのなかには、最も重要な基本的 な視点が十分に強調されていないとの印象を私が逃れられない事実によって、私は、より正確な議論の必要を緊急に感じるのである。
その問題は、次のように大まかに形式化できる:恒星に対する我々の観測のおかげで我々は十分に次のことを確信している。すなわち、 恒星の系は、無限の空の空間に浮かぶ島に類似してあるものではなく、存在する質量の全体量の重力中心のようなものが存在するもので もない。むしろ、我々は次のことを確信する必要を緊急に感ずる。空間にある物質の平均密度が存在し、それがゼロではないことである。
それゆえ、問いはもち挙がる:この仮説、経験から示唆される仮説は、一般相対論とどのように和解するのか?
上記の条件は、その問題を確定的なものにするには、決して十分ではない。最も単純かつ最も根本的な特殊化は、次の条件であろう: (自然に測定された)物質の密度ρは、(4 次元的)空間のどこでも同じである。計量は、適切な座標選択によって、x_4 に独立で、 x_1, x_2, x_3 に関しては、一様であり等方である。
私が最初に最も自然な理想化された大規模な物理空間の記述であると考えたのはこの場合である;それはこの本の 103 -108ページに扱われている。この解への反論は、負の圧力の導入が必要であることであり、それには物理的正当性が存在しない。 その解を可能にするために、私は、独自に方程式に新しい項を導入し、上述の圧力の代わりにした。それは相対性の視点からは許されるものである。 重力の方程式は、こうして拡張された:
(1) (R_ik - 1/2 g_ik R) + Λ g_ik + κ T_ik = 0
ここで、Λは、宇宙的な定数("宇宙論的定数") である。この第2番目の項の導入は、理論の複雑さを構成し、論理的な単純さを深刻に減損する。 その導入は、ほとんど避けられない物質の有限の平均密度の導入によって作られる困難によってだけ正当化できる。 いずれにしても、我々が注目できるのは、ニュートン理論にも同じ困難があることである。
数学者フリードマンは、このディレンマ(*)を逃れる方法を見出した。彼の結果は、その後、ハッブルによる星系の膨張(距離に伴って均一に増大する スペクトル線の赤方偏移)という驚くべき確認を見出すに至った。次下は、本質的に、フリードマンのアイデアの表出以外の何ものでもない:
我々は、いま、宇宙が空間的にいって、どこでも等方的である状態に数学的な形式を見出さなくてはならない。(4次元的)空間の 全ての点 P を通して粒子のある経路が存在する (それは以降、短く "測地線" と呼ばれるだろう)。 P と Q をそのような測地線の無限に近いふたつの点としよう。我々は、そのとき、場の表式が P と Q とを固定する任意の座標系の回転に 関して不変であることを要求しなければならない。これは、どの測地線のどの要素についても有効であるだろう(*)。
上の不変の条件は、測地線全体が回転軸上にあることと座標系の回転にその2点が不変に残ることを意味する。これは、測地線の3重の無限の 周りの全ての座標系回転に関して解が不変であることを意味する。
簡潔さのために、この問題の解の演繹的な導出に私は立ち入らない。しかしながら、直感的に明らかであるのは、3次元空間にとって、 線の2重の無限の周りの回転のもとに不変である計量は、本質的に (適切な座標選択によって) 中心対称の型のものであろう。 そこでの回転軸は、動径の直線であり、その対称性の理由は測地線である。一定半径の表面は、そのとき、一定の(正の)曲率の表面であり、 それは、どこでも(動径の)測地線に垂直である。こうして我々は、不変の言語によって次を得る:
測地線に直交する表面の類が存在し、これらの表面のそれぞれは、一定の曲率の表面である。これら測地線の類のどのふたつの表面の間に 含まれる切片も等しい。
注意 このように直感的に得られた場合、類の表面が一定の負の又はユークリッド的(ゼロ曲率)であり得る限り、それは一般的なものでない。
我々が興味のある 4 次元の場合も、全く類似している。さらには、計量空間の慣性の添字が 1 であるとき、本質的な違いは存在しない; 唯一の違いは、時間性として、動径方向を選ばなくてはならないこと、それに対応して、類の表面内の方向は、空間性であることである。 全ての点の局所の光円錐の軸は、動径線上にある。
その上の x_1, x_2, x_3 が一定で x_4 だけが可変である時間性の線として、我々は、粒子の測地線を、中心対称の形態のなかで中心を通 る直線に選ぶ。x_4 を、さらに、中心からの計量距離に等しいとしよう。そのような座標のなかで、計量は次の形式をとる:
ds^2= dx_4^2 - dσ^2
(2) dσ^2= γ_ik dx_i dx_k (i,k= 1,2,3)
dσ^2 は、球状超平面のひとつの上の計量である。異なる超平面に属するγ_ik は、そのとき、(中心対称性から)全ての超平面の上で、 x_4 だけに依存する正の係数以外は、同じ形式をとるだろう:
(2a) γ_ik = γ0_ik G^2
ここで、γ0 は、x_1, x_2, x_3 にだけ依存し、G は x_4 だけの関数である。そのとき、我々は次をもつ:
(2b) dσ0^2= γ0_ik dx_i dx_k (i,k= 1,2,3)
は、3次元のなかで正の曲率の確定した計量であり、全ての G において同じである。
そのような計量は、次の方程式で特徴付けられる:
(2c) R0_iklm - B(γ0_il γ0_km - γ0_im γ0_kl)= 0
我々は、座標系 (x_1, x_2, x_3) を線要素が同形的にユークリッド的になるように選ぶことができる:
(2d) dσ0^2= A^2(dx_1^2 + dx_2^2 + dx_3^2) すなわち、γ0_ik= A^2 δ_ik
ここで、A は、r (r^2= x_1^2 + x_2^2 + x_3^2) だけの正の関数。方程式に代入して、我々は、A に次のふたつの方程式を得る。
(3) -1/r (A'/Ar)' + (A'/Ar)^2 = 0
-2A'/Ar - (A'/A)^2 - B A^2 = 0
最初の式は、次によって満足し:
(3a) A= c_1/(c_2 + c_3 r^2)
ここで、定数は、さしあたり任意である。
(3b) B= 4 c_2 C_3/ c_1^2
定数 c について我々は、次を得る:もし、r= 0 で、A が正でなければならないなら、そのとき、c_1, c_2 は同符号である。 3 つ全ての定数の符号変化は、A を変化させないから、c_1, c_2 を共に正にできる。我々はまた、 c_2 を 1 にできる。さらに、正の係数 は、つねに G^2 に組み込むことができ、我々は、また一般性を失うことなしに、c_1 を 1 にできる。こうして、我々は次を設定できる:
(3c) A= 1/(1 + cr^2), B= 4c
いま、ここに3つの場合がある:
c>0 (球状空間)
c<0 (擬球状空間)
c=0 (ユークリッド空間)
座標の相似変換(x_i' = a x_i ここで、a は定数)によって、我々はさらに、最初の場合に c= 1/4, 第2の場合に c= -1/4 を得る。
3つの場合それぞれに、我々は次を得る:
A = 1/(1 + r^2/4); B= +1,
(3d) A = 1/(1 - r^2/4); B= -1,
A = 1; B= 0
球状の場合、単位空間(G=1)の "円周" は、∫_-∞^+∞ dr/(1 + r^2/4)= 2π であり、単位空間の "半径"は、1 である。 3 つ全ての場合で時間の関数 G は、2質点間の (空間断面で測った) 距離の時間変化の尺度である。 球状の場合、G は、時間 x_4 の空間の半径である。
要約 我々の理想的な宇宙の空間等方性の仮説は、次の計量を導く:
(2) ds^2= dx_4^2 - G^2A^2(dx_1^2 + dx_2^2 + dx_3^2)
ここで、G は、x_4 だけ、A は、r (r^2 = x_1^2 + x_2^2 + x_3^2) だけに依存する。ここで、
(3) A= 1/(1 + z/4 r^2)
そして、場合の違いは、それぞれ z= 1, z= -1, z= 0 によって特徴付けられる。
(4) (R_ik -1/2 g_ik R) + κT_ik = 0
空間的等方性の仮定に基づいた、計量の式を置き換えることによって、我々は、計算の後に次を得る。
R_ik -1/2 g_ik R = (z/G^2 + G'^2/G^2 + 2G''/G) GA δ_ik (i,k=1,2,3)
(4a) R_44 -1/2 g_44 R = -3 (z/G^2 + G'^2/G^2)
R_i4 -1/2 g_i4 R = 0 (i= 1,2,3)
さらに、我々は、 "塵" のために物質のエネルギーテンソル T_ik には、次を持つ:
(4b) T^ik = ρ dx_i/ds dx_k/ds
それに沿って物質が運動する測地線は、それに沿って x_4 だけが変化する線である; それらの上に dx_4= ds である。我々は次をもつ。
(4c) T^44= ρ
だけが 0 でない成分である。添字を下に下げて、T_ik の唯一の非消滅の成分は、
(4d) T_44= ρ
これを考慮して、場の方程式は、次になる:
(5) z/G^2 + G'^2/G^2 + 2 G''/G = 0
z/G^2 + G'^2/G^2 - 1/3 κρ= 0
z/G^2 は、空間断面 x_4 = const の曲率である。G は、どの場合も、時間の関数であるふたつの物質粒子の計量距離の相対的尺度。 G'/G は、ハッブル膨張を表す。A が式から抜け落ちる。要求される対称性の型の重力の方程式の解があるべきため、そうでなければならない。 両式を引算し、我々は次を得る。
(5a) G''/G + 1/6 κρ= 0
一方、G とρは、どこでも正でなければならないから、G'' は、ρが消滅しない場合、どこでも負である。G(x_4)は、このように、 最小値も、変曲点も、持ち得ない;さらに、G が定数という解は、存在しない。
(5b) 2h'+3h^2= 0
3h^2= κρ
ハッブル膨張 h と平均密度ρ の間の関係は、2番目の式で与えられ、ある程度、経験と比較できる。少なくとも大きさのオーダーに関する限りでは。 膨張は、10^6 parsec に対して 432 km/sec として与えられる。もしこれを我々の使う測定の系(cm は、単位の長さ; 時間の単位は 1 cm を通過する 光の時間)で示せば、次を得る:
h= 432・10^5/(3.25・10^6・365・24・60・60) ・ (1/(3・10^10))^2 = 4.71・10^-28
一方、さらに、(105a を見よ) κ= 1.86・10^-27 であるから、(5b) の 第 2 式は、次をもたらす:
ρ= 3h^2/κ= 3.5・10^-28 g/cm^3
この値は、大きさのオーダーにおいて、天文学者の推定(質量と可視恒星、恒星系の視差を基にしている)と何かの一致をもつ。 私は、ここに例として、G. C. マックビティー(McVittie) を引用する。(Proceedings of the Physical Society of London, vol. 51, 1939, p. 537) "平均密度は、確かに 10^-27 g/cm^3 より大きくなく、そして、より確からしいのは 10^-29 g/cm^3 のオーダーである。"
この大きさの決定の非常な困難さのために、私はこれをさしあたりの満足な一致と考える。一方、量 h は、ρより正確に決定されるから、 観測できる空間の構造の決定がρのより正確な決定と連携されるという主張は、多分、誇張はない。なぜなら、(5) の第2式のために、 空間曲率は、一般の場合、次式で与えられるからである:
それゆえ、式の右辺が正であれば、空間は、正の一定曲率をもち、有限である;その大きさは、この差と同じ正確さで決定できる。 もし、右辺が負なら空間は無限である。現在、我々がこの関係から空間(x_4= const の断面)の非消滅平均曲率を演繹できるほど、 ρは十分に決定されない。
我々が空間曲率を無視する場合、(5b)の第1式は、x_4 の初期値の適切な選択の後、次式となる。
(6) h= 2/3・1/x_4
この式は、x_4= 0 に特異性がある。そのため、そのような空間が負の膨張をもち、時間が x_4= 0 の上に制限されるか、又は、 それが正の膨張をもち、x_4= 0 から存在を開始するかである。後者の場合が我々が自然のなかに実感を見出すものと一致する。
測定された h の値から、我々は、世界の今までの存在の時間 1.5・10^9 年を得る。この年齢は、地球の地殻についてのウラニュウム の崩壊から得たものとほぼ同程度である。これは、パラドックス的な結果であり、それによって理論の有効性に疑いを起こす、ひとつ の理由以上のものである。
次のような問いが起きる:現在の困難は、現実的には無視できる空間曲率という仮定のもとに起きたものである。 それは、適切な空間曲率の導入によって除去できるのだろうか? ここに、 G の時間依存を決定する (5)の最初の式が使用されるであろう。
(5) zG^-2 + (2G''/G + (G'/G)^2)= 0
zG^-2 + (G'/G)^2 -1/3 κρ = 0
曲率は、z= 1 について正、z= -1 について負である。これらの式の最初は積分可能で、我々は最初にそれを次の形式に書く。
(5d) z + 2GG'' + G'^2 = 0
もし、我々が x_4 (= t) を G の関数と考えるなら、我々は次の式をもつ:
G'= 1/t', G''= (1/t')' 1/t'
もし、我々が u(G) と 1/t' を書けば、我々は次を得る:
(5e) z + 2Guu' + u^2 = 0
または、
(5f) z + (Gu^2)' = 0
これから、我々は単純な積分によって次を得る:
(5g) zG + Gu^2 = G_0
または、我々は、u= 1/(dt/dG) = dG/dt と置くから、
(5h) (dG/dt)^2 = (G_0 - zG)/G
ここで G_0 は定数。もし、(5h) を微分し、G'' が (5a) のため負を考慮すれば、我々がみるように、この定数は、負ではあり得ない。
G は、0 ≦ G ≦ G_0 の区間に残る。G は、次のようなスケッチによって、量的に与えられる:

半径 G は、0 から G_0 まで立上り、そして再び連続的に 0 に落ちる。空間断面は、有限 (球状) である。
(5c) 1/3 κρ - h^2 >0
(b) 負の曲率をもつ空間
(5h) (dG/dt)^2 = (G_0 + G)/G
G は、t に伴い G= 0 から G= +∞ まで増加する (又は、G= ∞ から G= 0 まで行く)。このゆえに、dG/dt は、単調に +∞から1まで、次のスケッチに描かれたように減少する:
これは、そのとき、収縮なしの連続的な膨張の場合である。空間断面は無限であり、我々は次をもつ。
(5c) 1/3 κρ- h^2 <0
(訳注: (c) 曲率のない空間)
平坦な空間断面の場合、以前の章で扱われた、ふたつの場合の間に位置し、次の式に従う:
(5h) (dG/dt)^2 = G_0/G
この非消滅曲率の場合の研究の結果は、次のことを結果としてもたらす。すべての非消滅("空間")曲率には、消滅曲率の場合と同じく、 そこで膨張の始まった G=0 である初期状態が存在する。このゆえに、これは、そこでは密度は無限であり、場は特異である、断面である。 そのような、新しい特異性の導入は、それ自身、問題と思える(*)。
さらには、空間曲率の導入による膨張の開始からの時間間隔への影響と、固定値 h= G'/G への低下は、大きさのオーダーにおいて無視 できることが明らかになった。この時間間隔は、(5h) から初等的計算によって得られるが、我々はここでそれを省略する。 我々は自身を、ρ消滅の膨張空間の考察に制限しよう。これは、前述のように、負の空間曲率の特別な場合である。(5) の2番目の式は、 次をもたらす(最初の項の符号の反転を考慮して)。
G'= 1
このゆえ、(x_4 の適切な初期点によって)
G= x_4
(6a) h= G'/G = 1/x_4 ...
こうして、この極端な場合も、膨張の継続期間において空間曲率の消滅する場合(式(6)をみよ)と係数が1である以外、 同じ大きさのオーダーの結果をもたらす。
式 (6) に関連して言及した疑い、すなわち、現在観測できる星と星系の開発に、これがそのような驚くべき短い継続時間を与えることは、 それゆえ、空間曲率の導入によって除かれない。
人は、例えば、その粒子が互いに静止した塵から、ガスの分子のように互いに相対的なランダム運動をする粒子の塵に、置き換える ことができるだろう。そのような物質は、断熱的な圧縮に抵抗をするだろう。それはその圧縮に伴って増加するだろう。 これが無限の圧縮の生起を妨げることができるのではないだろうか? 我々は、次に、そのような物質の記述の変更が上の解の主要な性質を、何も変化させることができないことを示す。
(7) T^uv = mσ dx^u/ds dx^v/ds
は、不変量の意味をもつ(群れのエネルギーテンソル)。もし、多くのそのような群れがあれば、我々は、それら全ての総和によって、 次式を得る:
(7a) T^uv = m Σ_p σ_p (dx^u/ds)_p (dx^v/ds)_p
この式に関連し、我々は、ローレンツ系の時間軸を選び、T^14= T^24= T^34= 0 とすることができる。さらに、系の空間回転によって、 T^12= T^23= T^31= 0 とし、さらに、粒子ガスを等方的にすることができる。これは、T^11= T^22= T^33 = p を意味する。これは、 T^44= u と同様に不変量である。次の不変量:
(7b) J= T^uv g_uv = T^44 - (T^11 + T^22 + T^33) = u - 3p
は、このように u, p によって表現される。
T^uv の表式から、T^11, T^22, T^33 そして T^44 は、全て正であることが出る; それゆえ、同じことが T_11, T_22, T_33 そして T_44 にも真である。
重力方程式は、いま、次になる:
(8) 1 + 2GG'' + G'^2 + κT_11 = 0
-3G^-2(1 + G'^2) + κT_44 = 0
最初の式から、ここにもまた (T_11>0から)、G''がつねに負である。そこでは、T_11 項は、G と G' が与えられたとき、G''を減少させる ことしかできない。
このことから、質点のランダムな相対運動の考慮は、我々の結果を基本的に変化させない。
(2) 宇宙への空間的 "等方性" の要求だけがフリードマンの形式を導いている。それは、それゆえ、疑いもなく一般的な形式であり、 宇宙論的問題に適している。
(3) 空間曲率の影響を無視して、人は平均密度とハッブル膨張の関係を得る。大きさのオーダーについて、経験的に確認される。
人はさらに、膨張の開始から現在までの時間について 10^9 年の大きさのオーダーの値を得る。この短い時間は、恒星の発展の 理論のそれと一致しない。
(4) 後者の結果は、空間曲率の導入によっても変化しない; 星と星系の互いのランダム運動の考慮によっても、それは変化しない。
(5) スペクトル線のハッブルの偏移をドップラー効果以外の方法による説明を幾人が試みている。しかしながら、既知の物理的事実 のなかに、そのような概念の支持はない。そのような仮説に従えば、ふたつの星、S_1, S_2 を剛体棒で結合することができる。もし その棒に沿った光の波長の数が、時間に伴ってこの方法で変化すべきならば、単色の光を S_1 から S_2 へ送り、そして反射して S_2 に戻すと、異なる周波数(S_1の時計で測定して) で到着できることになる。これは、局所で測定される光速が時間に依存することを意味し、 それは、特殊相対論にさえ反することになる。(訳注1) さらに、S_1 と S_2 の間を行き来する光信号は、"時計" を構成することになるが、 S_1 にある時計(例えば原子)と一定の関係にないことを注意すべきである。これは、相対性の意味での計量が存在しないことを意味する。 これは、相対性がもたらした全てのそれらの関係の理解を失うことを意味するだけでなく、それは、また、ある種の原子的形態は "相似" に関係するものではなく、"合同" に関係しているという事実に一致しない (鋭いスペクトル線、等)(訳注2)。
上記の考察は、しかしながら、波の理論に基づいており、そして、いくらかの上記の仮説の支持者は、光の伸びの過程を全体として波の 理論に従ってでなく、コンプトン効果に類似する仕方にあると想像している。散乱なしのそのような過程を仮定することは、我々の現在 の知識の視点からは正当化できない仮説を構成する(訳注3)。それはまた、元の周波数から相対的な周波数シフトの独立性の理由付けも 失敗する。このゆえに、人は、ハッブルの発見を星系の膨張と考える以外ないのである。
(訳注1) すでに一般相対論は、特殊の結論をいくつか克服した。例えば、同じ系のなかの異なる場所の時計の時計の進行は自由になった。
S_1とS_2を往復する光による局所の時計が "S_1にある原子時計と一定の関係にない" というのは理由のない憶測であり、局所の時計の進行
は一致するだろうから、それは、"相対性の意味での計量" を否定しない。さらに、同じ系のなかの異なる時間の時計の進行は自由であろう。
特殊相対論でも、時計を移動させるとき、時計の速度に合わせて時計の進行は変化するだろう。計量の時間係数 g_44 の時間的変動があれば、
"局所で測定される光速が時間に依存し、特殊相対論にさえ反する" ことになるが、それを理由にして否定することはできないと思われる。
(訳注2) フリードマン宇宙の計量は、g_ii (i=1,2,3) の時間的変動だから、"合同"でなく、"相似" に関係するようである。
(訳注3) コンプトン散乱は、散乱角が 0 のとき、電磁波の波長の変化を見ない。Δλ= λ(1-cosΘ)。もし、Θ= 0 でΔλが少しでも
あれば、光は、荷電粒子に正面衝突するときもエネルギーを低下することになる。
理論的疑いは、膨張の始まりの時に、計量が特異に、密度ρが無限になるという事実に基づいている。これに関連して次を注意すべきである: 現在の相対論は、物理的現実を計量場(重力)を一方とし電磁場と物質を他方にする分割に基にする。現実には空間は、恐らく均一の性質をもち、 現在の理論は、制限された場合にだけ有効なのであろう。場と物質の大きな密度の場合、場の方程式とそれらに入る場の変数さえも現実の意味を もたないであろう。人はそれゆえ、場と物質の非常な高密度には方程式の有効性を仮定してはならず、人は "膨張の始まり" が数学的な特異性を 意味しなければならないと結論してはならない。我々が認識すべき全ては、方程式がそのような領域まで連続してはならないことである。
この考察は、しかしながら、"世界の始まり" が、現存する星と星系の発展の視点から、それらの星と星系がまだ個別の実体として存在しなかった、 始まりを現実に構成するという事実を変えるものではない。
(7) しかしながら、理論に要求される動的な空間の概念を有利にする、いくらかの実証的な議論がある。その比較的高速な崩壊にも関わらず、 そして、ウラニウムの創成の不可能性が認識できるという事実にも関わらず、どうしてウラニウムは、まだ存在するのか? なぜ、空間は、夜の空を 白熱する表面にみえさせるだけの放射に満たされないのか? これは、現在まで静的な世界の視点からは満足な解答を見出せない古い問いである。 しかし、この型の問いに立ち入ることは、議論を余りの遠くへ導いていく。
(8) 与えられた理由により、我々は、その短い "人生" にも関わらず、膨張宇宙を真面目に受け取らなければならないように見える。 もし、人がそうしたとき、主要な問いは、空間が正又は負の空間曲率をもつかどうかになる。これに対して我々は、次の注意を付け加える。
実証的観点からは、判断は煮詰まって、表式 1/3 κρ - h^2 が正(球状の場合) か負(擬球状の場合) かの問いになる。これは、最重要の問いと 私にはみえる。実証的な判断が、現在の天文学の状態において、不可能とは見えない。h (ハッブル膨張) は、比較的よく知られている一方、 全ては、可能な限り高い正確さをもつρの決定に懸かっている。
世界が球状であるという証明が与えられることは想像可能である(それが擬球状であると人が証明できることは、想像しにくい)。これは、 人がつねにρの上限でなく下限を与えることができるという事実による。これは、天文学的に観測できない(非放射の)質量がρのどれだけの 比率を占めるかについて、我々がほとんど意見形成できないためである。これを私は、いくらか、さらに詳細に議論したい。
我々は、多くの個別の星を含み、十分な精度で静止した系であるとみなせる天文学的な物体、例えば、((年周)視差が知られた)球状星団を 考察する。スペクトルから観測できる速度から人は重力の場を(蓋然的仮定の下に)決め、それによって、この場を発生する質量を決めること ができる。そうして計算された質量と星団の可視星のそれを比較でき、それらの重力を発生する質量が星団の可視星の質量をどれだけ 超えているかの少なくとも粗い近似を見出すことができる。人は、こうして特定の星団について ρ_d/ρ_s の推定を得ることができる。
一方、非放射星は、平均的に放射星より小さいから、それらは、星団の星との相互作用によって、平均的に大きな速度をもつ傾向がある。 こうして、それらは、大きな星よりも、星団からより速く"蒸発"するだろう。そのため、小さな天体の相対頻度は、星団内部ではその外部 と比較して小さいであろうと期待できる。人は、それゆえ、(ρ_d/ρ_s)_k (上記の星団の密度の関係)のなかに、空間全体の ρ_d/ρ_s の下限を得ることができる。人はそれゆえ、空間の質量の全体平均密度の下限を次によって得る。
ρ_s[1+(ρ_d/ρ_s)_k]
もし、この量が 3h^2/κ より大きければ、人は空間が球状の性質をもつと結論できる。他方、私は、合理的に信頼できるρの上限決定を 考えることができない。
(9) 最後に重要なこと:宇宙の年齢は、ここで使われた意味で、放射性鉱物から見出された地球の堅い地殻の年齢を確かに超えなければならない。 これら鉱物による年齢の決定は、あらゆる側面で信頼できるから、ここで提示した宇宙論的理論が、もし、それらの結果に何か反論を見出すなら、 それは、反証されたのである。この場合、私は、何も合理的な解を見ない。
我々は、複雑さを増す例のなかに含まれる概念と方法を提示する。我々自身を 4 次元場に制限しながら、これらの例の過程のなかで、我々は、 順次、関係する概念を導入するであろう。
最初の例: スカラー波の方程式 (*)、
Φ_,11 + Φ_,22 + Φ_,33 - Φ_,44 = 0
ここで系は、"ひとつ" の場の変数のただ "ひとつ" の微分方程式で構成されている。我々はΦが点 P の周囲のテーラー級数展開されると仮定する (それにはΦの解析的性質を前提にする)。そのとき、その係数全体でその関数が完全に記述される。n 次の係数(Φの点 P での n 階微分)の個数は、 4・5...(n+3)/1・2...n (略号 (4, n)) に等しく、もし微分方程式がそれらの間に何かの関係を含まなければ、これらの全係数は自由に選択できる。 方程式が2階だから、これらの関係は、方程式の (n-2) 階微分によって見出される。我々は、こうして n 次係数に (4, n-2) の条件を得る。 自由に残された n 次係数の数は、そのため、
この数は、どの n でも正だから、もし n より小さい次数の全自由係数を固定すると、n 次係数の条件は、すでに選んだ係数を変更せずにつねに満 たすことができる。
同様な論理が数個の方程式のある系に適用できる。もし、自由な n 次係数の個数が 0 より小さくならないなら、我々はその方程式系を 絶対的に連立 という。我々は自身をそのような方程式系に限定する。物理学で使われる全ての系は、この種類である。
いま、式(1)を書き直し、我々は、次をもつ。
(4,n-2)= (4,n) (n-1)n/(n+2)(n+3)= (4,n) (1 - z_1/n + z_2/n^2 +...)
ここで、z_1= +6 である。
もし我々が n の大きな値に制限するなら、括弧内部の z_2/n^2 等の項は無視できる。そして、我々は(1)に対して近似的に次を得る
z 〜 (4,n) z_1/n = (4,n) 6/n ........(1a)
我々は、z_1 を"自由係数"と呼び、我々の場合、値 6 をもつ。この係数が大きくなればなるほど、相応する方程式系は弱くなる。
Φ^is_,s= 0; Φ_ik,l + Φ_kl,i + Φ_li,k = 0
Φ^ik は、次を助けにして、反対称テンソルΦ_ik の共変添字を上にあげた結果である。
-1, 0, 0, 0,
η^ik = 0, -1, 0, 0,
0, 0, -1, 0,
0, 0, 0, 1,
これらは、6つの場の変数のための 4 + 4 の場の方程式である。これら8つの方程式の間にはふたつの恒等式がある。場の方程式の左辺を それぞれ、G^i, H_ikl と書けば、恒等式は次の形式をもつ。
G^i_,i≡ 0; H_ikl,m - H_klm,i + H_lmi,k - H_mik,l = 0
この場合、我々は、次を推論する。
6つの場の成分のテーラー展開は、次の個数の n 次係数を与える。
6(4, n)
8(4, n-1)
これらの条件は、しかしながら、互いに独立でなく、8 つの方程式の間には、ふたつの 2次の恒等式が含まれる。それらは、(n-2) 階の微分、
2(4, n-2)
個の代数的恒等式を場の方程式から得られた条件の間にもたらす。n 次の自由係数の個数は、それゆえ、
z= 6(4,n) - [8(4,n-1) - 2(4,n-2)]
z は全ての n に正である。方程式系は、こうして "絶対的に連立" である。もし、我々が右辺の要素 (4,n) を抽出し、 上と同じく大きな n に拡張し、我々は近似的に、次を得る。
z= (4,n) [6 - 8n/(n+3) + 2(n-1)n/((n+2)(n+3)) ]
〜 (4,n) [6 - 8(1-3/n) + 2(1-6/n) ]
〜 (4,n) [0 + 12/n]
ここでは、z_1 = 12 である。これは、この方程式系がスカラー波の方程式の場合(z_1= 6)より、いくらか場を強く決定しないことを示す。 両方の場合で、括弧内の定数項が消滅する状況は、4変数のどの関数も自由に残さない事実を表現している。
R_ik= 0; g_ik,l - g_sk Γ^s_il - g_is Γ^s_lk = 0
R_ik は、Γ だけを含み、それらに関して 1 次である。我々は、ここで g とΓを独立な場の変数として扱う。2番目の方程式は、 Γを1次の微分として扱うことが便利であることを示す。そのことは、次のテーラー展開、
Γ= Γ0 + Γ1_s x^s + Γ2_st x^s x^t + ...
がΓ0が1次、Γ1が2次などと我々が考えることを意味する。従って、R_ik は、2次と考えなければならない。これらの方程式の間には 4つのビアンキ(Bianchi)の恒等式があり、そして伝統的に採用された結果としては、それらは3次であると考えられる。
一般共変性の方程式系には、自由係数の数えあげにおいて、本質的に新しい次の状況が現れる:単に座標変換によって次々現れる場は、 その同じ場の単なる異なる再現であるとみなすべきであるという。それに相応して、g_ik の n 次係数の
10(4,n)
の部分だけが本質的に異なる場を特徴付けるのを助ける。それゆえ、実際に場を決定する展開係数の個数は、我々がいま計算しなければ ならないある量だけ削減される。
次の g_ik のための変換法則において、
g*_ik= ∂x^a/∂x^i* ∂x^b/∂x^k* g_ab
g_ab と g*_ik とは、事実同じ場を表す。もしこの方程式を x* に関して n 回微分すると、人は、4つの x の関数のx*に関する全ての (n+1) 回微分が g*展開の2次係数に参入することを知る;すなわち、4(4,n+1) 個数は、場を特徴付ける役割をもたないことが表れる。 どの相対性の理論においても、人は、それゆえ、 n 次係数の総個数から、4(4,n+1) を、理論の一般共変性を計算にいれるために、 差し引かなければならない。 n 次自由係数の数え上げは、こうして次の結果を導く。
10(4,n) + 40(4,n-1) - 4(4,n+1)
場の方程式(10個は2次、40個は1次)は、それらに次の個数の条件を与える。
N= 10(4,n-2) + 40(4,n-1)
我々は、しかしながら、この数から N個の条件の間にある、次の恒等式の個数を差し引かなければならない。すなわち、(3次の) ビアンキの 恒等式からくる、
4(4,n-3)
このゆえに、我々はここに次を見出す。
z= [10(4,n)+40(4,n-1)-4(4,n+1)] - [10(4,n-2)+40(4,n-1)] + 4(4,n-3)
(4,n) の要素を再び抽出して、大きな n においては近似的に、
z〜 (4,n) [0+12/n] こうして、z_1= 12.
ここにまた、z は、全ての n に正であり、上述の定義の意味で系が絶対的連立である。空の空間の重力の方程式がそれらの場を、 電磁場の場合のマックスウェル方程式と、ちょうど同じ強さで決定するということは、驚くべきことである。
ニュートン後の物理学の基礎の発展のなかで、どのような革新が慣性系の克服を可能にしたのであろうか? 全ての最初に、それは、 ファラデー(Faraday)とマックスウェル(Maxwell) による、場の概念の導入、そしてそれに続く彼らの電磁理論である。又はより正確に いえば、独立なそれ以上還元できない基本的概念としての場の導入である。現在判定できる限りにおいて、一般相対論は、場の理論 としてだけ理解できる。現実の世界が質点で構成されていて、それらの間に作用する力の影響のもとにそれらが運動するという見方に 人がとらわれていたとしたら、それは、開発できなかったであろう。ニュートンに等価原理から慣性質量と重力質量の等しいことを 説明しようと人が試みるなら、彼は必然的に次のような反論に答えなければならないであろう: 加速座標系に対して物体は、重力天体 に対してその表面に近くにいるのと同じ加速を経験するということは、確かに正しい。しかし、前者の場合、どこにその加速を作りだす 質量があるのだろうか? 相対性の理論が場の概念の独立性を前提にしていることは明らかである。
いま、概観した一般相対性の設立に不可欠な数学的理論の発展は、リーマン計量が一般相対論とこのような慣性の忌避が基礎とする基本 的概念とみなされるという結果をもった。のちに、しかしながら、レビ・チビタ(Levi-Cività) は、慣性系を避けることを可能にし た理論の要素が、無限小の移動場 Γ^l_ik であると正しく指摘した。それを定義する計量、又は対称テンソル場 g_ik は、移動場を決定 する限りの単に間接的に慣性系の忌避に関連する。以下の考察は、これを明確にするであろう。
ひとつの慣性系から他のものへの移動は、線形の変換によって決定される(特定の種類の)。もし、ふたつの任意の距離の点 P_1 と P_2 とに、それぞれ、ベクトル A1^i と A2^i があり、その対応する成分が互いに等しい(A1^i= A2^i)、この関係は、許される変換のなかで 保存される。もし、次の変換の式のなかで、
A^i* = ∂x^i*/∂x^a A^a
係数∂x^i*/∂x^a が x^a から独立なら、ベクトルの成分の変換式は、場所に依らない。異なる場所 P_1, P_2 にあるベクトルの成分の 等しさは、慣性系に制限すれば、不変性の関係である。しかしながら、もし、慣性系の概念を捨て、任意の連続変換を許し、∂x^i*/∂x^a が x^a に依存するようにすると、ふたつの異なる空間点に添付されるベクトルの成分の等しさはその不変性の意味を失い、異なる点の ベクトルは、このようにもはや直接に比較できない。この事実のため、一般相対論では、もはや単純な微分で与えるテンソルから新テンソル を作れず、そのような理論のなかでは全体として不変性の形成がずっと少ない。この不足は、無限小移動場の導入によって治療される。 それは、無限小近傍点でのベクトルの比較を可能にするから、慣性系を置き換える。この概念から開始し我々は、後続において注意深く 目的に要不要を調合して、相対性の場の理論を提示する。
δA^i= -Γ^i_st A^s dx^t ....(2)
ここで、Γは、x の関数。他方、もし、A がベクトル場なら、(x^t+dx^t)での の (A^i) の成分は、A^i+dA^i に等しく、そこでは(*)、
dA^i= A^i_,t dx^t
これらふたつのベクトルの隣接点 (x^t+dx^t)での違いは、そのとき、それ自身、次のベクトルであり、
(A^i_,t + A^s Γ^i_st)dx^i≡ A^i_t dx^t
ふたつの無限小接近点のベクトル場の成分を結合する。それが以前、慣性系が与えたこの結合を結果するから、移動場は慣性系を置き換える。 括弧内の表式は、A^i_t は端的にいって、テンソルである。
A^i_t のテンソル特性は、 Γの変換法則を決定する。我々は、最初に次の式をもつ。
A^i_k*= ∂x^i*/∂x^i ∂x^k/∂x^k* A^i_k
両方の座標系に同じ添字を使用するのは、それが対応する成分を参照することを意味しない。すなわち、x と x* における i は、 独立に 1 から 4 までを渡る。いくらかの実例の後に、この表記が方程式をかなりより透明にする。我々は、いま、次の置き換えをする。
これは、Γ* から出発して、元の系 x に関して、元の座標系の量とその微分だけを含む方程式を導く。この方程式をΓ* について解き、 人は望みの変換式を得る。
Γ^i_kl*= ∂x^i*/∂x^i ∂x^k/∂x^k* ∂x^l/∂x^l* Γ^i_kl - ∂^2x^i*/∂x^s∂x^t ∂x^s/∂x^k* ∂x^t/∂x^l* ....(3)
ここで、(右辺の)第2項は、いくらか単純化でき、
∂^2x^i*/∂x^s∂x^t ∂x^s/∂x^k* ∂x^t/∂x^l* = ∂/∂x^l* (∂x^i*/∂x^s) ∂x^s/∂x^k* = -∂/∂x^l* (∂x^i*/∂x^l*)^.. + ∂x^i*/∂x^s ∂^2x^s/∂x^k*∂x^l* = ∂x^i*/∂x^s ∂^2x^s/∂x^k*∂x^l* .....(3a)
我々は、そのような量を擬テンソルという。線形変換のもとではテンソルのように変換されるが、一方、非線型変換では、 変換前の式に含まれず、変換係数似だけ依存する項が追加される。
1. 下の添字を位置変えした量 Γ~^i_kl (≡Γ^i_lk) も、(3)に従って変換するから移動場と同様である。
2. 下の添字 k*, l* に関して式(3)の対称化と反対称化によって、次のふたつの式を得る。
Γ'^i_kl*= (1/2 (Γ^i_kl* + Γ^i_lk*))
= ∂x^i*/∂x^i ∂x^k/∂x^k* ∂x^l/∂x^l* Γ'^i_kl - ∂^2x^i*/∂x^s∂x^t ∂x^s/∂x^k* ∂x^t/∂x^l*
Γ"^i_kl*= (1/2 (Γ^i_kl* - Γ^i_lk*)) = ∂x^i*/∂x^i ∂x^k/∂x^k* ∂x^l/∂x^l* Γ"^i_kl
このゆえに、ふたつの(対称と反対称性の) Γ^i_kl の構成要素は、互いに独立に変換される。すなわち、混合なしに。このようにそれらは、 変換法則の視点からは独立な量として現れる。2 番目の式は、Γ"^i_kl がテンソルとして変換されることを示す。変換群の視点から、これら ふたつの構成要素を単一の量に加算的に結合することは、最初、不自然にみえる。
3. 他方、Γの下の添字は、式(2)を定義するにおいては、下の添字に関して対称性の条件によってΓを制限することを強制する理由がないように、 全く違った役割を果たしている。それにも関わらず、もしそれがそうであれば、それは純粋な重力場の理論を導く。もし、しかしながら、 Γを対称性に制限する条件の下に置かなかなければ、重力の法則の一般化に到達し、それが私には自然なことに思える。
x0^t を固定点の座標とし、x^t を周囲の他の点たちとする。そのとき、ξ^t= x^t - x0^t は、全ての周囲の点において小さく、大きさのオーダー の定義の基礎に使うことができる。
積分 §δA^i は、そのとき計算すべき、より明示的な記述では、
-§Γ^i_st A^s dx^t または、 -§Γ^i_st A^s dξ^t
被積分のなかの下線を付けた量は、それらが円周の遂次点に (そして、初期点ξ^i=0 ではなく) 取られるべきことを示す。
我々は、円周の任意点ξ^t における A^i の最低の近似によって最初に計算する。最低の近似は、積分のなかの、開区間に広げられた Γ^i_stとA^sを積分の初期点(ξ^t= 0)のΓ^i_stとA^sに置き換えることである。積分は、そのとき、次を与える。
A^i= A^i - Γ^i_st A^s ∫dξ^t = A^i - Γ^i_st A^s ξ^t
ここで無視されたものは、ξのなかの2次以上の項である。同じ近似ですぐさま、次が得られる。
Γ^i_st= Γ^i_st + Γ^i_st,r ξ^r
これらの表式を上述の積分にいれて、適切な総和の添字の選択をして、最初に次を得る。
-§ (Γ^i_st + Γ^i_st,q ξ^q) (A^s - Γ^s_pq A^p ξ^q) dξ^t
ここで、全ての量は、ξを例外として除き、積分初期点のそれをとらねばならない。我々はそのとき、次を見出す。
-Γ^i_st A^s§dξ^t - Γ^i_st,q A^s §ξ^q dξ^t + Γ^i_st Γ^s_pq A^p §ξ^q dξ^t
ここで、積分は閉じた円周に渡るように拡張されている。(最初の項は、その積分の消滅により消滅する。) (ξ)^2 に比例する項は、高次であるから 省略される。他のふたつの項は、複合され、次になる。
[-Γ^i_pt,q + Γ^i_st Γ^s_pq] A^p §ξ^q dξ^t
これは、円周に沿う移動後のベクトル A^i の変化 ΔA^i である。我々は次をもつ。
§ξ^q dξ^t = §d(ξ^q ξ^t) - §ξ^t dξ^q = -§ξ^t dξ^q
R^i_klm = Γ^i_kl,m - Γ^i_km,l - Γ^i_sl Γ^s_km + Γ^i_sm Γ^s_kl ......(4)
の全ての添字の位置は、これ以降、固定される。i, m に関して縮約して、縮約曲率テンソルを得る。
R_ik = Γ^s_ik,s - Γ^s_is,k - Γ^s_it Γ^t_sk + Γ^s_ik Γ^t_st .........(4a)
Γ^l_ik*= Γ^l_ik + δ^l_i λ_,k .......(5)
ここで、λは座標の任意の関数であり、δ^l_i は、クロネッカー(Kronecker) テンソルである("λ-変換")。 もし、Γ* を(5)の右辺に置き換えて R^i_klm (Γ*) を形成するなら、λは打ち消され次を得る。
R^i_klm(Γ*)= R^i_klm(Γ)
R_ik(Γ*)= R_ik(Γ).................(6)
曲率は、λ-変換のもとに不変である("λ-不変性")。 結果的に、曲率テンソルに Γ だけを含む理論は、Γ場を完全には決定できず、λの 関数までだけであり、それは任意に残される。そのような理論では、Γ と Γ* は、同じ場の再現とみなすべきで、まるで、Γ* は、Γ から 単に座標変換によって得られるかのように。
ここでいう価値のあることとして、座標変換と違って、λ-変換は、i, k に対称な Γ から非対称な Γ* を作りだすことである。 Γの対称性の条件は、そのような理論では、その客観的重要性を失う。
主要なλ-不変性の重要性は、場の方程式系の"強さ"に影響をもつことである。我々が後に見るように。
対称場の理論では、次のテンソル、
(W_ikl≡) g_ik,l - g_sk Γ^s_il - g_is Γ^s_lk
が重要な役割を果たす。もし、それをゼロに等しくすると、Γを g によって表すことを許す式を得る。すなわち、Γを消すためである。 まず、先に証明したように (1) A^i_t≡ A^i_,t + A^sΓ^i_st がテンソルである事実から開始する。そして、(2)任意の反変テンソルが Σ_t A^i_(t) B^k_(t) の形式で表すことができる。場 g と Γ がもはや対称でなくても上の表式がテンソル性をもつことは、困難なく 証明できる。
しかし、後者の場合、もし、例えば最後の項のΓ^s_lk が交換され、すなわち、Γ^s_klに置き換っても、テンソル性は、失われない。 (これは、g_ik(Γ^s_kl - Γ^s_lk) がテンソルである事実からくる。) 他の形成法があり、全く単純とはいえないが、それはテンソル 性を保存し、上の表式の非対称の場合への拡張とみなされる。結果的に、もし g と Γ の関係の非対称場への拡張を望むなら、 任意選択を含むと思われる上の表式を 0 に等しく設定することで得られる。
しかし、上の形成は他の可能な形成から区別する特性をもつ。もし、同時に g_ik を g~_ik に、Γ^l_ik をΓ~^l_ik にそして、添字 i, k を交換すれば、それは、それ自身に変換される; それは、添字 i, k に関しての "交換対称性" である。この表式を 0 と置く ことによって得られる式は、"交換不変" である。もし、g と Γ が対称なら、この条件は、もちろん、また満足される; それは、 場の量が対称であることの条件の一般化である。
我々は、非対称場の方程式に、それらが交換不変性であることを仮定する。私は、この仮定は、物理的にいって、正と負の電気性が 対称に物理法則に入ることの要請に対応する。
(4a) を眺めれば、R_ik が完全には交換対称でないことを示す。交換による変換は、次になるから。
R_ik*= Γ^s_ik,s - Γ^s_sk,i - Γ^s_it Γ^t_sk + Γ^s_ik Γ^t_ts ....... (4b)
この状況が、交換不変の場の方程式を打ち立てようとする努力のなかで遭遇する困難の基礎をなしている。
U^l_ik≡ Γ^l_ik - Γ^t_it δ^l_k .........(7)
一方、
U^t_it= -3Γ^t_it
(7) から k, l に関する縮約によって、U による Γ についての次の表式を得る。
Γ^l_ik= U^l_ik - 1/3 U^t_it δ^l_k .........(7a)
これらを (4a) に代入して、
S_ik≡ U^s_ik,s - U^s_it U^t_sk + 1/3 U^s_is U^t_tk .........(8)
が縮約した曲率テンソルの U による表式であることを見出す。この式は、しかしながら、交換対称である。 擬テンソル U が非対称場の理論において、非常に価値があるのは、この事実のためである。
U のλ-変換 もし、(5)で Γ を U に置き換えると、簡単な計算で次を得る。
U^l_ik*= U^l_ik + (δ^l_i λ_,k - δ^l_k λ_,i) .........(9)
この式が U のλ-変換を定義する。(8) は、この変換において、不変である (S_ik(U*)= S_ik(U))。
U の変換法則 もし、(3) と (3a) で Γ を U に置き換えると、(7) の助けによって我々は、次を得る。
U^l_ik*= ∂x^l*/∂x^l ∂x^i/∂x^i* ∂x^k/∂x^k* U^l_ik + ∂x^l*/∂x^s ∂^2x^s/∂x^i*∂x^k* - δ^l*_k* ∂x^t*/∂x^s ∂^2x^s/∂x^i*∂x^t* .........(10)
- 1/2 [δ^l*_k* ∂x^t*/∂x^s ∂^2x^s/∂x^i*∂x^t* + δ^l*_i* ∂x^t*/∂x^s ∂^2x^s/∂x^k*∂x^t*]
+ 1/2 [δ^l*_i* ∂x^t*/∂x^s ∂^2x^s/∂x^k*∂x^t* - δ^l*_k* ∂x^t*/∂x^s ∂^2x^s/∂x^i*∂x^t*] ........ (10a)
これらふたつの式の最初は、交換対称である。(10)の右辺の最初の2項を結合して K^l_ik* で表す。次のとき、どうなるかをいま考えよう。 もし、次の変換が、
U^l_ik*= K^i_ik*
次のλ-変換に後続されていたら、
U^l_ik**= U^l_ik* + (δ^l*_i* λ_,k* - δ^l*_k* λ_,i*)
結合は、次をもたらす。
U^l_ik**= K^l_ik* + (δ^l*_i* λ_,k* - δ^l*_k* λ_,i*)
これは、(10a)の第2項が δ^l*_i* λ_,k* - δ^l*_k* λ_,i* の式に持ち込まれるなら、(10)が、そのような結合とみなすことができること を意味する。そのためには、λが次のように存在することを示せば十分である。
1/2 ∂x^t*/∂x^s ∂^2x^s/∂x^k*∂x^t* = λ_,k* ............ (11)
(and 1/2 ∂x^t*/∂x^s ∂^2x^s/∂x^i*∂x^t* = λ_,i* )
他方、
∂x^p/∂x^t* V^s_t*= ∂x^p/∂x^t* ∂D/∂(∂x^s/∂x^t)= Dδ^p_s
ここで、V^s_t* は、∂x^s/∂x^t* の共通因数を示し、逆に、行列式 D= |∂x^a/∂x^b*| の ∂x^s/∂x^t* に関する微分として表される。 それゆえ、我々はまた、次をもつ。
∂x^p/∂x^t* ∂logD/∂(∂x^s/∂x^t*)= δ^p_s ..........(b)
(a) と (b) から次が出る。
∂x^t*/∂x^s = ∂logD/∂(∂x^s/∂x^t*)
この関係を理由にして、(11)の左辺は、次のように書ける。
1/2 ∂logD/∂(∂x^s/∂x^t*) (∂x^s/∂x^t*)_,k* = 1/2 ∂logD/∂x^k*
これは、(11)が確かに次の式によって満足されることを意味する。
λ= 1/2 log D
これは、変換 (10) が次の交換対称変換
U^l_ik*= ∂x^l*/∂x^l ∂x^i/∂x^i* ∂x^k/∂x^k* U^l_ik + ∂x^l*/∂x^s ∂^2x^s/∂x^i*∂x^k* - 1/2 [ δ^l*_k* ∂x^t*/∂x^s ∂^2x^s/∂x^i*∂x^t* + δ^l*_i* ∂x^t*/∂x^s ∂^2x^s/∂x^k*∂x^t* ] .........(10b)
とλ-変換の結合とみなせることを証明する。(10b) は、こうして U の変換式として (10)の代わりをする。 表現の形式を変化するだけのどのような U 場の変換も (10b) に従う座標変換とλ-変換との結合として表される。
変化を受ける積分は、被積分関数hスカラー密度を必要とする。我々は、そのような密度を R_ik 又は S_ik から構成する。最も単純な過程は、 Γ 又は U それぞれに加えて重み 1 の共変テンソル密度g^ikを導入することである。次を設定して、
h=g^ik R_ik (= g^ik S_ik) ........... (12)
g^ik への変換法則は、次でなければならない。
g^ik*= ∂x^i*/∂x^i ∂x^k*/∂x^k g^ik |∂x^t/∂x^t*| ............ (13)
ここで、再び、異なる座標系を参照する添字は、たとえ同じ文字を使っても、互いに独立に扱われる。我々は、確かに次を得る。
∫h* dτ*= ∫ ∂x^i*/∂x^i ∂x^k*/∂x^k g^ik |∂x^t/∂x^t*|・∂x^s/∂x^i* ∂x^t/∂x^k* S_st |∂x^r*/∂x^r|dτ
= ∫hdτ
すなわち、積分は、変換不変量である。さらには、積分は、λ-変換 (5) 又は (9) に関しても不変量である。なぜなら、R_ik は、Γ 又は U で表現されるから。そして、このゆえ、h もまた、λ-変換に関して不変量である。このことから、∫hdτの変分によって導かれる場の方程式 もまた、座標系とλ-変換に関して共変である。
しかし、我々はまた、場の方程式がふたつの場 g, Γ 又は g, U に関して交換不変であることを仮定する。これは、もし、h が交換不変 であるなら保証される。我々は、R_ik がもし、U で表されたとき交換対称であり、Γで表されたときそうでないことを見た。 このゆえ、h は、もし我々が場を g と U (Γでなく、) を場の変数として表すなら、そのときだけ交換不変である。 その場合、我々は、∫hdτから場の変数の変分によって導かれる場の方程式が交換不変であることが最初から保証されるのである。
h(式(12)と(8))の g と U に関する変分によって、我々は次を見出す、
δh= S_ik δg^ik - R^ik_l δU^l_ik + (g^ik δU^s_ik)_,s
ここで、S_ik= U^s_ik,s - U^s_it U^t_sk + 1/3 U^s_is U^t_tk, .................. (14)
R^ik_l= g^ik_,l + g^sk (U^i_sl - 1/3 U^t_st δ^i_l)
+ g^is (U^k_ls - 1/3 U^t_ts δ^k_l)
δ(∫hdτ)= 0 ............ (15)
g^ik と U^l_ik とは、独立に変化されるとし、それらの変数は、積分の領域の境界では消滅するとする。変分法は、最初に次を与える。
∫δhdτ= 0
もし、(14)に与えられた式がここに代入されるなら、δhの表式の最後の項は、δU^l_ik が境界で消滅するから、何も貢献しない。 このゆえに、我々は、場の方程式を得る。
S_ik= 0 ............ (16a)
R^ik_l= 0 ..........(16b)
それらは、ーすでに変分原理の選択から明らかであるようにー 座標系とλ-変換に不変である。そして交換不変である。
これらの恒等式は、∫hdτ が座標系とλ-変換とに関して不変である事実からよく知られた方法で得られる。
なぜなら、 ∫hdτ の不変性から、もしδh に、無限小の座標変換又は、無限小のλ-変換によって生起する δg と δU を挿入するなら、 その変分が恒等的に消滅するからである。
無限小座標変換は、次によって記述され、
x^i*- x^i + ξ^i .......... (17)
ここで、ξ^i は、任意の無限小ベクトルである。我々はいま、δg^ik と δU^l_ik とを、ξ^i によって式(13)と(10b)によって 表さなければならない。(17)のために、次を置き換えなければばらない。
∂x^a*/∂x^b を δ^a_b + ξ^a_,b によって、
∂x^a/∂x^b* を δ^a_b - ξ^a_,b によって、
そして、ξの 1 次より高次の項を全て除外しなければならない。
こうして、次を得る。
δg^ik (= g^ik* - g^ik) = g^sk ξ^i_,s + g^is ξ^k_,s - g^ik ξ^s_,s + [- g^ik_,s ξ^s ] .......... (13a)
δU^l_ik(= U^l_ik*- U^l_ik)= U^s_ik ξ^l_,s - U^l_sk ξ^s_,i - U^l_is ξ^s_,k + ξ^l_,ik + [- U^l_ik,s ξ^s ] .... (10c)
(14)にこれらの"変換変分" δg, δU を代入すれば、積分、∫hdτ の変分は、恒等的に消滅する。もしさらに、ξ^i を積分領域の境界で それらの1次微分とともに消滅するように選択すれば、(14)の最後の項は、貢献しなくなり、次の積分、
∫(S_ik δg^ik - R^ik_l δU^l_ik) dτ
は、もし、δg^ik と δU^l_ik を (13a) と (10c) によって置き換えるなら、それゆえ、恒等的に消滅する。一方、この積分は線形に一様に ξ^i とその1次微分に依存するから、それは、次の形式に持ち込める。
∫M_i ξ^i dτ
部分の積分を繰り返すことによって。ここで、M_i は、よく知られた表式(S_ik の1次のオーダーで、R^ik_lの2次)である。これから、次の 恒等式がくる。
M_i ≡0 ........... (18)
場の方程式の S_ik と R^ik_l の左辺には4つの恒等式があり、それらは、ビアンキの恒等式に対応している。以前に導入された用語に従って これらの恒等式は3次のオーダーである。
δg^ik = 0, δU^l_ik= δ^l_i λ_,k - δ^l_k λ_,i
ここで、λは無限小で、積分領域の境界で消滅する。最初に次を得る。
∫R^ik_l (δ^l_i λ_,k - δ^l_k λ_,i ) dτ= 0
または、積分後に部分的に、
2 ∫R^(is)_s,i λ dτ= 0
(ここで、一般的に R^(ik)_l = 1/2 (R^ik_l - R^ki_l)。)
これは、欲した恒等式を得る。
R^(is)_s,i≡ 0 ............... (19)
我々の用語ではこれは2次のオーダーの恒等式である。R^(is)_s に関して我々は、(14) から真直な計算によって次を得る。
R^(is)_s≡ g^(is)_,s ........(19a)
もし、場の方程式 (16b) が満たされるならば、我々は次を得る。
g^(is)_,s= 0 ................ (16c)
g^ik = g^ik √-|g^st| ......... (20)
ここで共変テンソル g^ik は、次の式によって反変のそれと関係している。
g^is g^ks = δ^k_i ..............(21)
これらふたつの式から、我々は、次を得る。
g^ik= g^ik (-|g^st|)^-1/2
そして、そのとき、g_ik を (21) 式から得る。我々は次を仮定してよい。
(a_ikl)= g_(ik),l + g_(kl),i + g_(li),k ......(22)
又は、
a^m = 1/6 η^iklm a_ikl ....................(22a)
が電流密度を表すことを。ここで、η^iklm は、全ての添字に反対称な (±1の成分をもつ) レビ・チビタ(Levi-Cività)のテンソル密度である。 この量の発散は、恒等的に消滅する。
z= [16(4, n) + 64(4, n-1) - 4(4,n+1) - (4,n)] - [16(4, n-2) + 64(4, n-1)] + [4(4,n-3) + (4, n-2)] .......... (23)
最初の括弧は、g-場を特徴付ける n 次オーダー係数に関係する全体個数を表し、次のは、場の方程式の存在によってこの数を削減する個数、 3番目の括弧は、恒等式 (18), (19) のためのこの削減数の訂正である。大きな n における近似値として我々は次を見出す。
z〜 (4, n) z_1/n ....................(23a)
ここで、
z_1= 42
非対称場の場の方程式は、このように、純粋な重力場 (z_1= 12) のそれよりもかなり弱い。
h= 1/2 (g^ik R_ik + g~^ik R~_ik)
(U を場の変数として導入する代わりに)。もちろん、結果する理論は、上で述べたものと異なるものとなるであろう。このhには、λ-不変性が 存在しないことを示すことができる。ここに、また、我々は (16a), (16b) 型の場の方程式を得る。それらは、交換不変である(gとΓに関して)。 それらの間には、しかしながら、4つしか、"ビアンキの恒等式" がない。もし、この系に数え上げの方法を適用すると、そのとき、(23)に対応 する式のなかで、最初の括弧のなかの4番目の項と、3番目の括弧のなかの2番目の項とは消滅する。次を得る。
z_1 = 48
方程式系は、このように、我々が選んだものよりも弱くなり、そして、それゆえ、拒絶されるべきである。
Γ^s_(is)= 0, R_(ik)= 0 g_ik,l + g_sk Γ^s_il + g_is Γ^s_lk= 0, R_(ik),l + R_(kl),i + R_(li),k = 0
ここで、R_ik は、Γの関数として (4a) によって定義される(そしてここで、R_ik= 1/2(R_ik + R_ki), R_(ik)= 1/2 (R_ik - R_ki))。
この系は、同じ積分から変分によって導かれたから、新しい(16a), (16b) 系と全く同等である。それは、g_ik と Γ^l_ik に関して交換不変 である。しかしながら、差異は、次にある。変化させられる積分自身は、最初にその変分によって得られた方程式系と同じく、交換不変でない; しかし、それは、λ-変換 (5) に関して不変である。ここで、交換不変性を得るために、ある技巧を使用しなくてはならない。4つの場の変数 λ_i を形式的に導入する。それらは、変分の後に方程式 Γ^s_(is)= 0 が満たされるように選択される(*)。こうして、Γに関する変分によっ て得られる方程式系は、交換不変形式を示すようになる。しかし、R_ik 方程式は、まだ、補助的な変数λ_i を含んでいる。しかしながら、 それらを除去することができ、それは、上に述べた仕方のこれら方程式の分解を導く。得られた方程式は、交換不変である(gとΓに関して)。
方程式 Γ^s_(is)= 0 を仮定することは、Γ-場の正規化を含んでいる。それは、方程式系のλ-不変性を除去する。結果として、Γの全ての 等価な再現がこの系の解として現れるのではない。ここで実行されることは、純粋な重力の場の方程式に、任意の付加的方程式を組合わせて、 座標系の選択を制限させる過程に似たようなものである。我々の場合は、さらに、方程式系が不必要に複雑になる。これらの困難は、新しい 表現、全体を通してgと U を場の変数として使って、gと U に関する交換不変性をもつ変分原理から開始することによって、避けられる。
(*) Γ^l_ik*= Γ^l_ik + δ^l_i λ_k とすることによって。
(g^ik δU^s_ik)_,s = 0
ここで、δU^s_ik は、(10c) で与えられたものである。この発散方程式は、ベクトル ξ^i のどの選択にも成立する。最も単純な特別な選択 として、例えば、ξ^i が x に独立は、次の4つの方程式を導く。
J^s_t,s ≡ (g^ik U^s_ik,t)_,s = 0
これらは、運動量とエネルギー保存の方程式であるとと解釈、適用できる。そのような保存の方程式が、場の方程式系から決して一意に決定 されるものではないことは、注意されるべきである。面白いことに、次の方程式に従って、
J^s_t ≡ g^ik U^s_ik,t
エネルギー密度 J^4_4 と同様に、エネルギーの流れ密度 (J^1_4, J^2_4, J^3_4) も x_4 に独立な場において消滅することである。 これから、結論できることは、この理論に従えば、特異性から解放された定常な場は、決して 0 と異なる質量を再現しないことである。
場の方程式の以前の定式化が使われるなら、保存則の形成だけでなくその導出は、さらにより複雑になる。
より複雑な場の理論は、しばしば提案されてきた。それらは、次の特徴に従って分類できる。
(a) 連続体の次元数の増加。この場合、なぜ連続体が外見上4次元に制限されるかを説明しなければならない。
(b) 移動場とその関係するテンソル場 g_ik (又は g^ik)に加えて、異なる種類の場 (例えば、ベクトル場) の導入。
(c) 高次のオーダーの(微分の)場の方程式の導入。
私の視点では、そのようなより複雑な系とそれらの組合せは、そうするための物理的-実証的な理由が存在するときに限られる。
B. 場の方程式は、場の方程式系によって、まだ、完全には決定されていない。人は特異性が現れることを許容すべきか?人は境界条件を仮定 すべきだろうか? 最初の質問について、私の意見は、特異性が排除されるべきであるというものである。私には、連続体理論のなかに、そこ に場の方程式の成立しない点 (又は線等) を導入するのは、合理的であるように思えない。さらに、特異点の導入は、特異点を閉じて取り囲む "表面"において、(それは、場の方程式の視点からは任意である) 境界条件を仮定するのと等価である。そのような仮定なしには、理論はずっと、 余りに愛昧になる。私の意見では2番目の質問に対する答えは、境界条件の仮定は不可欠であるということである。 私は、これを初等的例を使って示す。人は、Φ= Σ m/r の形式のポテンシャルの仮定を、質点の外側の(3次元的)方程式 ΔΦ= 0 が満たされる という言明に比較することができる。しかし、もし、人が境界条件を、無限遠でΦが消滅する(又は有限に残る)と、付加しないならば、そのとき、 全ての x の関数、(例えば、x_1^2 - 1/2 (x_2^2 + x_3^2)) が存在して、無限遠を無限にする。空間が "開いた" ものであるとき、 そのような場は、境界条件を仮定することによってだけ、排除することができる。
D. 連続的な場によって、なぜ現実が決して再現され得ないかに、人はよい理由を与えることができる。量子現象から確かさをもって現れるのは、 有限のエネルギーの有限の系は、有限の数のセット(量子数)によって完全記述できることである。これは、連続的な理論と調和するようには見え ず、現実を記述するのに純粋に代数的理論を見出す試みに導かざるを得ない。しかし、そのような理論の基礎をどうやって得るか、誰も知らない。
(1) ページ48、上10行、(48)式の最後のΦ_ναは、Φ_νβが正しい。
(2) ページ48、下1行、p_zx は、p_xz が正しい。
(3) ページ51、下3行、σ_0 は、σ が正しい。
(4) ページ62、下10行、(54)の2つ前の式は、最初の + は = が正しい。
(5) ページ66、式(59)の前の1行、orthognal linear substitution は、(60) の前の1行の linear orthgonal transformation に合わせた。
(6) ページ69、下3行 (A_μ) は (A^μ) が正しい。
(7) ページ70、式(67)の前1行 A^ν は A^μ が正しい。
(8) ページ73、式(75)の右辺の A_α は、B_α が正しい。
(9) ページ80、式(91a)と(92)の間の式のδ_νμは、δ_μνが正しい。
(10) ページ81、下5行のΓ^μ_βαは、Γ^μ_αβが正しい。
(11) ページ88、式(103a)の√(-1 dl)は、√-1 dl が正しい怪しい訳者の誤り==>戻す。
(12) ページ97、式(114)の右辺第1項の∂Φ_μ/∂x_μは、∂Φ_μ/∂x_νが正しい。
(13) ページ101、下2行のΓ^αβ_μは、Γ^μ _αβが正しい。
(14) ページ115,117、式(2d),(2)の各次行 r= x_1^2 + x_2^2 + x_3^2 は、 r^2= x_1^2 + x_2^2 + x_3^2 が正しい。
(15) ページ116、上8行 x'_I = a_i は、 x'_i = a_i が正しい。
(16) ページ120、上13行 therefor は、 therefore が正しい。
(17) ページ120、式(6)の上2行 (5c) は、(5b) が正しい。
(18) ページ123、図(2)のなか G=0 は、ρ= 0が正しい。
(19) ページ126、式 (8)の最初の式の第3項 G^2 は、G'^2 が正しい。
(20) ページ151、式(10) 右辺第3項、δの上添字の活字の上半欠けしているが、l* が正しい。
(21) ページ152、上3,4 行の式に番号がないが、本文から、(10a) である必要がある。
"相対論の意味" には、矢野健太郎氏の名訳(岩波書店、1958年4月第1刷発行)があるが、手持ちの1967年第9刷発行のチェックでは、
次の誤りが見付かっている。
(1) 英文ページ60、岩波ページ63、 U/D≠π は、英文の U/D>π が正しい。
誤りではないが、矢野氏による式の改変(添字のαβをikに換えるなど)が多いことに注意が必要である。
(1) 式、(2)〜(5)等、多くの式に 3次元のΣに範囲1〜3の指定を入れている。
(2) 英文ページ8、岩波ページ9、式、s_μν^2 = (x_1(μ) - x_1(ν))^2 + (x_2(μ) - x_2(ν))^2 + ...
は、s_μν^2 = (x_1(μ) - x_1(ν))^2 + (x_2(μ) - x_2(ν))^2 + (x_3(μ) - x_3(ν))^2
になっているが、添字μとνが 3次元空間内部の n 点の指標であることを明確化するための改変と推察できる。
(3) 英文ページ 11の変換後の直線、x'_β - A'_β = λ B'_β を補足する式、 B'_β= Σ_ν b_βν B_ν ; A'_β= Σ_ν b_βν A_ν は、岩波ページ 12 では、 A'_β= α_β + Σ_ν b_βν A_ν、 B'_β= Σ_ν b_βν B_ν と改変されているが、 斉次であるべき変換がそうでなく、しかも点によって違う変換にする改変は、意味を成さない。
(4) αβγδμνで表される添字をi,j,k,l,... に変更することは誤りやすいので私は元のままにした。 とくに式(61)の下の式。