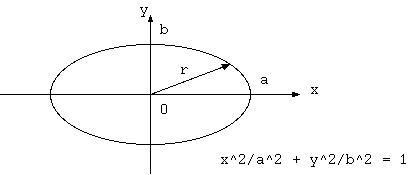
図 4. 計量(不変量への係数)と(楕円の半径)^2とは反比例
目次
はじめに
1. 暗黒星: 脱出速度>光速
2. 関連するニュートン力学
2.1 ブラックホールの議論
2.2 ブラックホールのSF
2.3 計量とローレンツ変換
3. 一般相対論の物差しと時計
3.1 ブラックホールの計量
3.2 不変の時空間隔 ds^2
3.3 計量は、中心までの累積距離を変える
3.4 地平面の発生
4. 三視点からみる落下物体
4.1 遠方(1)からは凍結星
4.2 近傍(2)からはブラックホールの中のよう
4.3 落下物体(3)からは単なる暗黒星への突入
5. 地平面の一方通行
5.1 一方通行とは
5.2 落下時間
5.3 内部の光速
5.4 質量の喪失
6. 地平面の内部
6.1 計量の符号変化は時空交換か
6.2 時空交換の落下時間
6.3 時空交換の累積距離
6.4 時空の虚数化
6.5 虚数化の落下時間
6.6 虚数化の累積距離
6.7 この宇宙は地平面内部か?
6.75 過去からの光経路長(宇宙の奥行き)
6.8 測地線方程式の示す運動
あとがき
ブラックホールは、特殊相対論のローレンツ短縮や時計の遅れのような程度の不思議な現象ではない。事態はもっと異様である。 一般向けの解説が少ないのは十分に理解したと自負する学者が少ないためで、学者がその理解の範囲で使用すべき"パラドックス" と思われている。天文学には一般相対論に関わる誤認識が多い。チャンドラセカールによる恒星レベルのブラックホール の記述があるが、銀河中心にある太陽質量の数百万倍のそれは、その生成過程が不明なまま観測が報告されてきた。 ここでは、ブラックホールへの物体落下などを考察し、末尾に膨張宇宙論について批評した。
ニュートン重力F/mをrで積分した重力ポテンシャル、 \[ Φ= -{GM \over r} \] は、半径rが0に近づくと -∞ に下がり、運動として抽出できるエネルギーは、無制限だったが、それに対して相対論は、無限遠の静止質量を限界にした。 そして、質量Mの周囲に半径(光速c=1とし)、r=2GM に、"事象の地平面" ができるとする。時間計量、 \[ g_{44}= -(1-{2GM\over r}) \] は、 \[ Φ = \sqrt{-g_{44}} \] として、その勾配(各成分が各方向の変化分であるベクトル) \[ F/m= -grad Φ= -(dΦ/dx, dΦ/dy, dΦ/dz) \] がニュートン重力Fを再現するが、r=2GMにおいてg_44は0になり時間停止し、空間計量g_rr=1/(1-2GM/r)(g_rrの添字r= 1〜3) が∞ になり、 物体は、半径方向が厚み0となって地平面に張り付く。しかし、チャンドラセカールによって、重い星の最期にブラックホールが形成されるというから、 物体落下の停止は、一時的であろう。地平面は、物質や情報の外から内への "一方通行"で、その内部は、知り得ないとされる。それらを少し確かめよう。
2) エネルギー保存:
外力F[N]を与え物体がD[m]だけ移動するとき、F方向の変位Dは、外力が物体にエネルギー(仕事)W= F・D[j=Nm]を与え、F,Dが反対方向では物体が仕事をする。
外力と変位が垂直なら仕事に関係しない。仕事Wは、力Fと変位Dの内積 W= F・D= Fx Dx + Fy Dy + Fz Dz である。運動の速さによる 仕事/秒をパワー(仕事率)
という。力は、テコ、滑車、歯車等によって拡大できるが、同時に移動量(又は速度)が小さくなり、逆に移動量(速度)を拡大すると力が小さくなる。
つまり、道具によってエネルギーは増大できず、逆に道具の摩擦によってエネルギーは減少する。
1)と2)は、重力のない平坦な時空間で成立し、重力があるとき以下の 3)〜6)がある。
3) 落体運動(ガリレオの斜面実験):
落下は、重力が物体に仕事を与え、運動を起こす。
逆に物体の上昇には仕事を要し、水平移動は仕事に関係しない。
電磁気のローレンツ力 F= q(E + v× B) (× はベクトル外積) において、電場Eは、電荷qを加減速して仕事に関与するが、
磁場Bは、電荷と速度vとの両方に垂直な力q(v× B)を与え、仕事に関与せず、速度vの方向を変えるが速さ|v|を変えない。
地上の静止物体mは重力mg (重力加速度 g= 9.8[m/s^2]) を受け、速度v[m/s]の2乗が落下の高低差h[m]に比例する。 落下前の高さh[m]にある質量m[kg]の位置エネルギー(Potential Energy) mgh、が落下後、運動エネルギー(Kinetic Energy) 1/2 mv^2 に変化する mgh= 1/2 mv^2。 速度の2乗がエネルギーに関係する理由は、力学についてを参照。物体の運動エネルギーと位置エネルギーの和は、 KE + PE = const 一定である(エネルギー保存)。物体は重力によって下方に加速され、時刻0〜tに速度は v= gt、変位hは、速度の時間積分(下の面積)である。 h= 1/2 gt^2 = 1/2 v^2/g, ∴ mgh= 1/2 mv^2.
4) 万有引力:
地上の落体では重力一定として PEが高低差hに比例するが、重力は、地球を天体としてみる高所では次第に弱くなり、天体Mからの距離rの2乗に反比例する
F= GMm/r^2 (G:重力定数)。重力は、距離rだけ離れた所に働く遠隔作用である。これをrで積分した重力ポテンシャル(PE) -GMm/r + c(c:積分定数)は、
その差だけが現実に影響し、無限遠で0 (c=0) とすると、天体の近くでは負である。
万有引力 F= GMm/r^2 による物体の質量mによらない重力加速度 g= GM/r^2 は、下向きのベクトルであり、空間にある重力ポテンシャル (スカラー) Φ= -GM/r の勾配である。g(x,y,z)= -grad(Φ)= -(dΦ/dx, dΦ/dy, dΦ/dz), 1/2 v^2 - GM/r = 0. 但し、このような重力の 1/r^2 比例を説明する 1/r 比例のエネルギー関数は、オルバースのパラドックスをさらに容易に引き起こす。
5) 遠心力:
遠心力は、F= mv^2/r = mrw^2 (半径r, 速度v, 角速度w=v/r)。天体の重力 GM/r^2 と遠心力 v^2/r が釣り合う位置と速度の (GM/r^2 = v^2/r) 物体は、
r一定の円運動をし、無限遠(r= ∞ )からのPE低下分 GM/r のちょうど半分の運動エネルギーをもつ。
6) 天体近くの物体運動 :
軌道が平面(x,y)上にあるとき、一方の速度成分v_xが大きいとき他方v_yが小さく、運動量は、x, y を交替するが、中心天体の運動によって補われ、
全体でエネルギー保存と運動量保存が成立する。物体が強い楕円軌道の場合、天体から遠方でKE= 1/2 v^2が小さく近くで大きいが、PE= -GM/r が近くで
負で補完してエネルギー和 KE+PE を一定にする。KE+PEによって軌道の形が決まる。
\[
{1\over 2} v^2 - {GM\over r} = \{負, 0, 正\}
\]
軌道は、KE+PE が、負では天体に拘束された(円を含む)楕円をとり、正では無拘束の双曲線、0ではつねにその場所rの脱出速度 v= √(2GM/r) をもち、
無限遠に達する放物線軌道 1/2 v^2 = GM/r をとる。 本論ではこれを落体の代表として使用する。
相対論では慣性運動は、測地線運動となり、重力は、時空の性質である計量 g_ik の微分方向差等によって働く加速度となった。 位置エネルギー、仕事と運動に変化する重力ポテンシャルは、時間計量 -g_44 =(時間経過速度)^2 となった。 運動量は、計量 g_4i、空間計量 g_rr (r= 1-3)は、(r方向の物差しの逆数)^2となる。
以降、BH には、ジョン・ホイーラーなど多くの研究者が、電荷をもつBH、回転するカーBH、クセナクス座標を研究した。 銀河系の中心にその周囲の恒星の軌道速度から、太陽質量の約400万倍の巨大なBHの存在が推定され、近傍のときの赤方偏移の増加、 遠日点の移動も観測された。また、2019年4月、M87銀河の電波干渉計の合成による高分解能のBH直接像が周囲の明るい降着円板の中心の黒い領域を示した。 (但し、最近これには反論があった。) 2020年ノーベル物理学賞がロジャー・ペンローズと銀河中心BH(射手座A*)の研究者2人に与えられた。 BH の存在は、殆ど確認されたと考える。
(b) BH の事象の地平面は、非常に大きな重力で、飛び込むとスパゲッティのように引き伸ばされる?
いや。多くの誤解がある。BHの近傍には自由物体を引き伸ばす潮汐力があるが、遠方からみると逆に天体方向に圧縮されている。地平面は、
物体に力を及ぼすバリヤではなく、その先が見えない面である。
地平面は、質量M/半径rによるポテンシャル(1-2GM/r=0)が決定し、その勾配が質点に加速度を与える重力も、
さらに重力を空間微分した潮汐力も、地平面を決定しない。地平面の半径rは天体の質量Mに比例し、地平面上の重力はMに反比例し、
潮汐力はさらに M^-2 に比例し、小BHで大きく大BHで小さい。とはいえ、値は極端で、
太陽質量(半径3km)では重力は、27.9G x (23.18x10^4)^2= 1.5x10^12 G。地平面重力が1Gになるのは1.5兆太陽質量である。
銀河中心の100万太陽質量では地平面の重力は1200Gだが、潮汐力は1[G/m]程度である。質量や半径が太陽(3km)の65億倍のM87銀河のBHの重力は、
太陽質量のBHの65億分の1で230Gだが、潮汐力はほとんどない。
(c) BHの周辺では空間が伸び、時間が伸びる?
いや、空間は縮み、時間は伸びる。そもそも一般相対論では、物差しの長さや時計の速さが、場所と時刻による時空の関数とする。
天体の半径r方向の空間計量 g_rr>1は、r方向を√ g_rr倍に拡大して標準の長さになる物差しの短縮を意味し、
時間計量の|g_44|<1は、√-g_44倍に短縮して標準の速さになる時計の緩慢を意味する。つまり、 BHの周辺では r方向の空間が縮み、時間が伸びている。
空間計量 g_rr (r=1〜3)の大は、そこからみて宇宙が縦に伸びているが、遠方からはその場所の高さ(厚み)の物差しの短縮である。
時間計量 g_44 の絶対値小は、そこからみると宇宙の全現象が忙しく時間短縮しているが、遠方からはそこの時間の伸長(時計の緩慢)である。
BH周辺の空間計量大、時間計量の絶対値小を"BHの周辺では空間が伸び、時間が伸びる" と表現しては、時空で主客が逆で、混乱させるだけである。
(d) 地平面のそばでは、無限の距離と無限の時間停滞があり、宇宙の終焉まで永遠に凍結し待たされるが、落ちた本人には一瞬である。
いや、"落ちた本人には一瞬"はほぼ正しいが、遠方から見ても無限の距離や無限の時間停滞はなく、むしろ短時間である。
(e) BH は真空中では増大しないが物質を取り込み、地球にBHが飛び込むと、地球は壊され吸収される。
太陽質量 (2x10^30 [kg]) のBHで半径 3km、地球質量(6x10^24[kg])で半径 8.87mm、月質量(7x10^22[kg])で半径 0.1mm。それらは、天体のサイズに
比べて遥かに小さく、接近すれば引力で大災害を起こし、接触すれば周囲の物質を吸収燃焼し、地球の反対側にまで達する穴を開ける。
BHへの物体の落下速度は光速に近づき、地平面の外側で質量をエネルギーに変換し、地球は崩壊を始め、そのうち完全に飲み込まれる。
地球形成後、46億年間平穏だったとすれば、小BHは宇宙に殆どないだろうが、BHに物質が吸収されるとBHの質量は増加し、地熱の原因になる。 空洞が拡大し軌道が安定すれば、激しい発熱は止まる。火星の調査で発見した異星人の作った施設がマイクロBHに電荷を与え、電場で支持していた。 その電源を過失で遮断してBHを落下させてしまい、"我々はもう火星を壊した" と恐怖するSFがあった。
BHは、太陽に接触すれば、効率的に質量をエネルギーに変換するだろう。太陽の熱源は、核融合でなく、BHかもしれない。これは奇論ではなく、 宇宙初期の Quasi-star がそういわれる。 太陽の中の質量分布の調査から複数の核が見つかり、それらがBHではないかというSF "サンダイバー" があった。BHを探すには宇宙よりも、収集、 検出能力がある太陽や地球がよいが、その取り扱いには、真空の宇宙で接触せずに支持し移動させる。これを探す理由は、これが究極のエネルギー 源だからである。その質量とサイズとは比例し、広範囲の可能性がある。ナノBH(10^-9m)で 10^15[t]、原子サイズで10^14[t]、原子核サイズで10^9[t]。
地熱は、自然の放射性元素、例えばウラニウムUの天然原子炉で説明可能だろうか。しかし、太陽熱源をBHとすると、水素核融合による主系列から 巨星のHe核融合への変化や、星の進化の過程全てに再考が必要となる。BHは、半径(∝ 質量)の2乗に比例する表面積で物質を流入させ、発熱するが、 ホーキング輻射との関係で、周囲の密度に反比例し、その質量以下で蒸発する消滅 BH 限界質量がある。例えば、太陽や地球ではナノBHも質量増加するが、 銀河内空間ではある小BHしか蒸発せず、銀河内真空より 10^-5 ほど密度が低い銀河間真空では、その10^5倍まで蒸発する。 この点でもBHを探すには宇宙よりも太陽や地球がよい。
(f) 地球に地球質量(半径1cm)のBHが接触し、表面に光速で物質が落ち込んでも、地球が全て飲み込まれるのに、90億年かかるという、
物質の流量によって説明する Youtube動画があった。それなら地球は過去にBHに遭遇した可能性がある。但し、私の計算では2桁違って 9100万年であった。
結果は逆に、最近の約1億年を除き、約45億年間、BH接触はなかったことになる。
毎秒の流量は、4 x 3.1416 x 10^-10 [km^2] x 3 x 10^5 [km/s]= 37.70 x 10^-5 [km^3/s]= 37.70 x 10^4[m^3/s]
地球体積 1.08 x 10^12 [km^3] / 流量 37.70 x 10^-5 [km^3/s] / (秒/年) 3.1536 x 10^7 [s/y]= 9.084 x 10^7[y]
(g) BH を時間反転したホワイトホール(WH)は、外に光や物質を一方通行に吐き出す
地平面の"一方通行" は、過去から未来への時間反転を許さない相対論の"時間の矢"だろう。量子力学の時間の矢は観測だが、時間の矢があれば BH があっても
WH はないことになる。BHは正の質量を吸い込む正の質量、WHは負の質量で正の質量を吐くことは、現実の現象とは思えない。時間軸逆転現象か。
ニュートン万有引力F= GMm/r^2が質量M,mの積の正負によって引力/斥力になる話は聞くが、負質量の存在は通常物質としては確認されていない。 宇宙が宇宙定数をもち、ある値以上の密度で引力、それ未満で斥力とすると便利だが、宇宙項は任意ではありえないと思う。それは、密度の任意 放棄だからである。 アインシュタインは、定常原理のために宇宙項を導入し、後に誤りとした。その点、現代天文学は、初期宇宙に強い斥力を仮定し、エネルギーを得て、 ビッグバンを経て平坦な減速膨張し、数10億年前に再び加速に転じたとするが、インフレーション時とその後の宇宙項なしのフリードマン宇宙の減速膨張は、 同一の原理によるものではない。インフレーション時の宇宙項は現在より$10^{120}$倍も大きい。減速膨張に小さい宇宙項が伴い空間拡大し、数十億年前に 宇宙項が発現して加速膨張に変じたという物語は可能だが、晴れ上がり時点の10^-5の平坦性からの早期の構造形成のために、宇宙物理学は1980年代から 30〜40年間もダークマターを探したが、まだ物質を特定できない。さらに重力方程式と計量に関係するダークエネルギー(宇宙項)は、その質量の正負さえ 不明である。宇宙論への宇宙項の適用は安易にすべきでないと思う。
質点力学を深化した特殊相対論の光速一定の原理が電磁気にはすでに満たされていた。電磁気は特殊相対論を待っていた。さらに質量がもたらす場の理論である 一般相対論は、電磁気よりも基本的な理論である。その勾配が重力を与え 1/rに比例するポテンシャル場は、遠方が近所より優位な理論であり、古くからの オルバースのパラドックスをさらに先鋭化するが、それによって宇宙を論じ、宇宙の時空を定式化できた。質量によって光さえ曲がり、電磁気の電流にはなかった、 近傍の速度が引きつり効果(水星の近日点移動)をもつ理論である。これらを宇宙論には考慮するべきである。
(h) ブラックホールにまつわる画期的な新説が登場!解説します: BHに物質が入り込むよりも先にホーキング放射で蒸発し地平面が縮小して逃げるというこの"宇宙やばいch"の話は、全く定量的でない。 BHへの物体落下とホーキング放射と蒸発との相反から新BH概念を作ろうとしても、蒸発は小BHで高速で最期は爆発的だが、普通のBHは殆ど蒸発しない。 殆ど光速で物体が落ち込む時間内のBHの蒸発による縮小はなきに等しい。ホーキング放射でのBHの寿命の長大さ(太陽質量BHで宇宙年齢を超える10^64年)と、 太陽地球間でニュートン力学で27日程度の物体の自由落下時間+地平面近傍の短時間とを同等に扱う無理な論理である。
BH の蒸発には幾つかの微分方程式が考えられる。
1. 蒸発が質量の2乗に比例: -dm/dt= a m^2 (質量と半径は比例し、蒸発は地平面の面積に比例)
変数分離し -dm/m^2= a dt 両辺を積分し 初期 t=0 の m を m0 とし、1/m = at + 1/m0, 解: m = 1/(at + 1/m0) 質量低減。半減期 t= 1/(am0)。
2. 蒸発が質量に比例: -dm/dt= am (放射性元素の崩壊と同じ指数減少。半減期一定) -dm/m= a dt, -log(m)= at - log(m0), 解: m= m0 exp(-at).
3. 蒸発が質量の2/3乗に比例: -dm/dt= a m^(2/3) (質量は体積に、蒸発は面積に比例)
-dm m^(-2/3)= a dt, -1/3 m^(1/3)= at - 1/3 m0(1/3) , m^(1/3)= m0^(1/3) - 3at, 解: m= (m0^(1/3) - 3at)^3
質量の1/3乗が直線低減で質量はその3乗、質量は急速低減し爆発的最期をもつ。ホーキング放射は、これか?
Wikipedia が第1式とするのは、 dE= {κ /8π} dA + Ω dJ + Φ dQ, (E:エネルギー、κ:表面重力、A:地平面積、Ω:角速度、J:角運動量、Φ:静電ポテンシャル、Q:電荷) 第1項のdAは、A でないか?そうでなければ、 これは微分方程式でない。κ 表面重力は、 mの-1乗、面積は2乗で、指数的減少解を導くか。太陽質量のBHでは寿命 10^64年で宇宙年齢を超える。 T_BH= κ /2π で温度は質量に反比例。エントロピーは表面積 S_BH = A/4。 ホーキング放射
(i) 超光速(1)〜(5)は、存在するか?
よく言われる超光速は、安易に認めたくない。場に速度はなく速度加算は、成立しない。
物体速度に光速を加えても、光速である。それが可能なら、祖父殺しのパラドックスが起きる。
(1) 宇宙の膨張の速度: 相対論ではj方向の光速は時空の関数で、√ (-g_44/g_jj) である。基準とする観測点の光速を超えることはできるが、
物体はその場所の局所光速を超えない。相対論の計量場 g_ik に速さの概念はなく、局所慣性系の速度(空間の速度)に物質が乗る速度を加算する
誤解が多い(*)。
膨張宇宙論では、ビッグバン前に宇宙が指数的膨張(インフレーション)をしたとして、超光速の膨張が等方性を満たすための根拠とするが、
インフレーション時の宇宙項が現在の宇宙項の120桁ほども大きいという物理的な不整合をもつ。更に、その宇宙項の変化に原因や証拠がない。
(2) 量子のもつれ?: EPR パラドックスは、ヒューエベレットIIIの多世界解釈で解決した。観測によって世界は分岐する。量子のもつれが超光速という
理解は不要である。それぞれの個別世界に光速限界がある。
(3) 群速度?: 波の群速度は光速以内で、光速を超える位相速度は、物体や波動の速度ではない。
(4) チュレンコフ放射する粒子: 粒子は "真空中の" 光速を超えない。水やガラスでは光速は真空中の(1/屈折率)で、それより速い粒子が存在する。
(5) 超光速ニュートリノ: 1987年2月23日午前7時35分、16.4万光年先の大マゼラン雲の中の超新星1987Aの光(23日10時30分)より約3時間先に神岡鉱山中の
カミオカンデは、11個のニュートリノに検出器が反応した。超新星爆発の中心から光が出るよりも先にニュートリノが抜け出たと当時私も理解したが、
ニュートリノの超光速を疑う人もいた。16.4万光年の距離で1時間は、1.64 x 10^5 x 365.25 x 24 = 1.4376 x 10^9、約9桁精度。3時間は、4.3 x 10^-9である。
光速の 10^-9 は、30 cm/s。地上でのニュートリノ速度計測に必要な精度は発生受信間300kmで1msで、1ms x 10^-9 = 10^-12 sec ピコ秒計測が必要。
(*) 物質が光速を超えるには無限のエネルギーが必要であり、それが起きたら宇宙のどこも存在できない。計量 g_ik は、物質から計算され、物質とエネルギー には無限大がない。物質の超光速は、宇宙の問題以上に因果関係を壊す祖父殺しのパラドックスが生じる。1/r^2 比例の重力や光の強さは無限遠がオルバースの パラドックスを起こすが、計量 g_ik は、1/r 比例で、より容易にこれを起こす。例えば太陽地球間の2000億倍は、隣のアンドロメダ銀河の距離だが、 その恒星数を2000億とすると、地球に対する太陽とアンドロメダ銀河の質量の計量への影響がほぼ等しい。宇宙の果てはさらに1万倍ほど遠いが有限である。 一般相対論は、その微分がそのまま測定できる物理量となる計量の2階のテンソル$g_{ik}$に基づく重力理論であり、物差しと時計の理論である。 それによって、宇宙膨張によって宇宙の果ての砂粒ひとつが光速を超えて飛び出す時の無限のエネルギーがなぜここに影響しないのか。 遠方は関係しないという別の宇宙原理を設定するのか。
宇宙項は、物質密度のもつ引力を打ち消す斥力である。初期宇宙で一定時間毎に倍々になる指数関数的な膨張、インフレーションから現在の宇宙に 変化したというが、数学的には任意な宇宙項を観測に合わせて臨時に設定するのは宇宙論のルール違反である。宇宙論は、原理だけから定式化し 説明されるべきで、基本物理だけで宇宙の概略を説明できる必要がある。つまり、宇宙項を使うならば、なぜ宇宙項があって、なぜ、そのとき変化したか を説明することが求められる。数学的に任意で他の物理量に依らない、"入力なき出力のみ"の宇宙項は、根拠薄弱である。 例えば、速度が距離に比例するハッブルの法則は、まずここで何かの疫病が蔓延し、特別に宇宙に嫌われ、他の銀河がここから一目散に逃げていると、 解釈できるが、一様等方の宇宙原理を優先して、これを宇宙膨張と解釈する。それによって、ここが他の場所と同等な均一性を得、ここが宇宙の中心 のように空想できる。この疫病論では、ハッブルの法則 "距離に比例する速度" でなく、一定加速で逃走するから時間(=√ 距離)に比例する速度になるが、 その場合も逃走加速度の変化には、物理的な理由が必要である。
ハッブルは、宇宙膨張と始まりの時刻 (ハッブル時刻)に対して否定的だった(*)。ハッブル定数(速度/距離)は、宇宙年齢を決める天文学の最重要な "定数"とされたが、天文学の数十年の歴史のなかで激しく値を縮小した(**)。あるとき一点から様々な速度で粒子が飛び散ったとするニュートン力学的な 膨張宇宙も、粒子の後退速度が粒子の距離に比例するハッブル法則を満たすが、超光速で逃げる粒子が存在しても、こちらに向かう光をこちらに進ませないから、 見えないだろう。つまり、膨張宇宙は、宇宙に光速で逃げる面の先のように、遠ざかるにつれて消えていき近づけば逃げる観測できない領域の存在を仮定する。 膨張による、(それをそういうのは一般的でないが)、地平面の先に、存在していても見えない領域を仮定している。光によって見える遠方は、 光が直進をはじめた晴れ上がり時点のとき、光速に近い速度で後退する物質からの可視光線は、現在、マイクロ波として観測され、 それより先の空間は、あるだろうが全く関係しない領域とする。
特殊相対論では光速粒子には無限のエネルギーが要るので存在しえない。宇宙論では光速以上で逃げる領域は、存在しているが見えないとする。 しかし逆に、向かって来る超光速粒子からの光は、見えない理由はない。地球に降り注ぐ宇宙線から地上に到達するシャワーまでの時間を調べ、超光速粒子を 検出する研究もあった。その結果を否定的とし、超光速粒子自体が存在しないのであれば、超光速粒子の逃げる領域を想定する膨張宇宙論も根拠を失うだろう。
超光速の逃げる粒子が存在するというのは、超光速で逃げる領域は無関係という別の原理を設定している。それが時間逆転か、周期宇宙の後期にあたれば、 超光速の粒子はいずれここに向かって降り注ぐのだろうか。膨張論は、膨張を利用して、光が時間を進む片方性を考えさせない。 特殊相対論をいれ、粒子速度が光速未満としても、膨張の初期点は特異点として時空連続体の物理を破綻させる無限大のエネルギーがある。
一様な密度を宇宙原理として一般相対論の計量に基づいて解くのが、空間計量の増大するフリードマン宇宙である。それは、本論のブラックホール解、 質量の側の計量とは仮定も結果も違う解だが、空間計量の時間的変化は、エーテル宇宙論のように時空のなかで光が曲り光速が変化する。しかし 空間計量には認識上の問題がある。本論のブラックホールのように、地平面から観測点が遠ざかり上昇するなら、空間計量は無限大から1に変化し、 時間計量は-0から-1に変化し、地平面の近くからの光が赤方偏移する。それは、交差点から離れる測地線を時間軸として、物質の密集時と疎ら時に 時間計量が異なることを認めることで説明でき、フリードマン宇宙の空間計量の矛盾の影響を受けない。膨張に伴うポテンシャル上昇でもハッブル の法則が成立するだろう。この自明な高度と密度によるポテンシャル変化の膨張宇宙論があり得る。
(*) エドウィン・ハッブル 1889-1953 (Allan.Sandage 1989)ハッブルの後継の天文学者、アラン・サンディジは、 ハッブルの業績を述べるなかで次のようにいう。
ハッブルは、彼の観測した log N(m) 分布が、赤方変移の効果が見掛けの等級に与える影響が赤方変移が現実の膨張によるとき、 ユークリッド幾何から大きく離れていることを結論づけた。もし、動きのないとき、赤方変移が未知の原因による場合、異なる校正が要求される。 ハッブルは、赤方変移の校正が "後退無し" を仮定する場合に、彼の計数データが空間曲率に関してより合理的な結果を与えると信じた。 彼の書き物の最後まで、彼は彼の位置を保持し、真の拡大が存在しないモデルを好み (または、ごく少なくともオープンであることを保持し)、 そして、それゆえ赤方変移は、"これまで認識できない自然の原理を表現している" とした。この視点は、(a)星雲の領土, (b) Eddington と McVittie による 1936年の論文の批判への彼の返事の中 (Hubble 1937a) (c)彼の 1937年のロードス講演("The Observational Approach to Cosmology" (Hubble 1937b)として出版) において強調される。 彼のダーウィン講演 (Hubble 1953)に入れられる彼の最後の科学的論文においてもそれは保持された。
(**) H0: 1925-1975 信じられないほど縮小する定数 (Verginia Trimble 1996) 1996年にハッブル定数について天文学者 3人の議論が行われ、その中でバージニア・トリンブルは、 500-550 km/s/Mpcから、50〜75 になった ハッブル定数の変化の歴史を述べ、私的に最小のハッブル定数 33 を主張した。H= 100を上回ると宇宙の年齢が球状星団の年齢より小さくなる。
概要: ハッブル定数の話は、論理的にカーティス(Curtis)とシャプレー(Shapley) の宇宙の距離スケールの議論が終わった所で、ハッブルの セファイド変光星の 幾つかの星雲のなかでの発見とともに始まった。それらの星雲を我々は現在、局所群の中の銀河と認識する。 この発見は、外部銀河の存在の事象を確定した。 ハッブル自身のHの値は500-550km/s/Mpcの範囲にあった。"ベストバイ"の値段は、1952 年に始まる幾つかの大きな段階のなかで縮小した。それぞれは以前の 距離スケールの較正のなかのある基本的な誤りを認識したことを示している。しかし、それは幾らかの人達には他よりさらに縮小し、1975年までに"長"と"短" の距離スケールには明白な偏在があった。 理論面で重要な出来事は、一般相対論が許す実際殆ど要求するものが膨張宇宙であるという認識、 赤方偏移と距離の関係の代替的な説明の漸次的な消滅、遅れてきた定常宇宙論の形式の襲撃への反発である。その枠組のなかでは、H0はよく定義され、 決して変わらない、 中程度の重要性の数である。
カールセーガンのSF "コンタクト"では、ブラックホールを穴の中に落ちるように描く。過去の父に出会って会話し、正確に落下時刻に戻るから、 誰にも信用されない。ブラックホールは、行為の本質、過去の修正、不可能事を実現する物語性を与えるが、 それ以前に、ブラックホールの近くで世界がどう見え、長さと時間がどうなっているかが重要と批判したい。 このSFのいうものよりもブラックホールは、現実的と思うからである。
まず、ブラックホールは、極彩色の模様の穴ではない。一般相対論の重力の説明に格子状の碁盤目の線を引いた平面の一箇所を押し下げるイメージが多用され、 物体運動を模擬すると思うのは比喩的にも誤りで、格子が伸びるのではなく縮む(ゴム膜の空間)のだが、物体落下、位置エネルギーの 運動エネルギーへの変化の相対論的理解が求められる。穴のような縦長の空間は地平面の外側近傍の静止点からみる光景であり、遠方からは落下物体は 一瞬、停止して消えていき、落下物体からは普通に地平面に到達し内部に入り外部世界が消えるだけである。
多くのSFでブラックホールは、物語の主題でなく大道具である。SFは、小説と違って非現実な状況、奇抜な世界の物語で、未来の科学、技術の予測だけでなく、 しばしば、それよりも根幹な作品の方向性や本質を誤る。それが科学でなく幻想でしかないなら、読者はそれに真実を見ず、含意さえ汲まないだろう。 しかし、いかに奇想天外と批判しても、科学自体が類似行為だから SFへの一般的批判には意味がない。そこにはSF作品の本質である科学への驚き、 パラドックスが伴う。
例えば、特殊相対論は、重力のない平坦時空を扱う。ロケットが速度を上げれば空間は速度方向に短縮し時間が遅れる。そこでの疑問は、ロケットからみて、 地球や目的地が逆向きの等速度をもつから、地球から目的地までの距離も対等に短縮する、つまり、速度をもつ座標系同士、互いに相手を短縮させるが、 それでいいのか? 時間の経過も、地球からみてロケットの時間が遅いとき、ロケットからみても地球や目的地の時間の経過が遅い必要がある。 このパラドックスは、相対論の同時刻=空間を理解すれば解決する。ロケットが地球から速度を得るには目的地への加速が必要だが、その加速中に 目的地の同時刻は未来に進み、到達直前の時刻になる。"空間"の意味が"同時刻"に変わって速度に依存するのである。
そして、"双子のパラドックス" では兄がロケットで遠方まで往復して再会すると兄の時計が弟の時計より遅れる。これも、兄のロケットからみると、 弟のいる地球が逆向きの速度をもつから、両者は一見、位置と速度の両方で対称のようだが、そうではない。ロケットは、出発の加速を除外しても、 地球に戻る時、地球に向かって加速するが、地球は加速されていない。遠方を往復した兄の時計の遅れは、ロケットが地球に向かって帰るための加速中に、 ロケットにとっての同時刻の地球の時刻が未来に進むことによる。ロケットの同時刻と地球の同時刻は違う。速度による時間の遅れのパラドックスは、 加速が行先の時刻を距離に比例して未来に飛ばすことによって起きる。加速と往復が生む時間差は、兄の時空図と弟の時空図を別々に書き、両者の対応で 明確化できる。それに対してブラックホールは、天体への単純な落下である。重力によって落下物体が光速の近くに加速され、地平面に接近するとき、 速度による特殊相対論のローレンツ短縮も起こす。重要なことは、一般は特殊を含み、特殊では一般を説明できないが、一般からは特殊を説明できることである。
計量 $g_{ik}$ を $dx^i dx^k$ に掛けて平坦時空に戻して後、特殊相対論のローレンツ変換を行う。時空の不変量の式、 \[ ds^2= g_{ik} dx^i dx^k ....(1) \] は、空間軸を選び直し、次式にできる。 \[ ds^2= g_{jj}(dx^j)^2 + g_{44} dt^2 ....(2) \] 平坦時空でx方向に速度vをもつK'系へのローレンツ変換は、係数 $γ =1/ \sqrt{1-v^2}$をもつ 1次変換類似の時空対称の式であり、 \[ dx' = γ (dx - v dt) .......(3)\\ dt' = γ (dt - v dx) .......(4) \] 観測系空間 $dt'= 0$ を(4)にいれ $dt= v dx$ これを(3)にいれ $dx'= 1/γ dx.$つまりdxは速度x方向に $1/γ$に短縮する。 観測先の一点 $dx= 0$ の時計は、(4)より $dt'= γ dt$ つまりdtはγ倍に伸長する。 速度系からみた物差し時計は$(dx, dt)$にローレンツ短縮$1/γ$倍と時計の遅れ$γ$倍の $(1/γ, γ)$倍が掛かる。 これらを不変量の式(2)に戻し、速度系からみる計量は、平坦局所空間でのローレンツ変換比率の逆数の2乗$(γ^2, 1/γ^2)$を計量に掛け、 \[ g_{jj}'= γ^2 g_{jj}, g_{44}'= (1/γ)^2 g_{44}......(5) \] つまり、速度によるローレンツ変換によって、空間計量に$γ^2$、時間計量に $1/γ^2$が掛かる。 地平面が天体の質量と距離により決まり、速度系からみても天体との相対位置により、球形物体の短縮と同じく、v方向に短縮した回転楕円体となる。
ブラックホールの中心に向かう直線の道に 1里塚をおく。その間隔は地平面まで限りなく密になり、√g_rrは、限りなく増加する。 しかし、天体まである距離rから地平面までの1里塚の数、局所の見る累積距離 D は、√ g_rr の定積分で D>r だが、無限ではない (→ 4.1章)。
物体落下ではPE低下分からのKEが静止質量に等しい地平面では脱出速度=光速だが、物体速度は光速を越えないだろう。 地平面近くの静止点からみると、静止質量と運動エネルギーの和(動質量) m= γm0 = m0/√(1-v^2) は増加するが、遠方からみると違う。 地平面へ近づくと質量(=エネルギー)は、時間の速さの2乗 g_44 に比例し、その低下に伴う。地平面で落下物体は、質量の増加分を失い、 地平面から出る全エネルギーは0となる。これには、物体の質量が衆合によって変化しないという原理を仮定した。 (→ 5.4章 )
さて、一般相対論は、物差し時計が場所と時刻、方向によって異なり、棒を立てたときと倒したときで長さが異なる時空を扱うために、上式の係数 $1,1,1,-1$ を計量 $g_{ik}$ (4x4の係数)に代え、物差し時計の微分の積項 $dx^i dx^k$に $g_{ik}$ を掛けて$i,k=1〜4$ に渉る総和を不変量 $ds^2$ とする。 \[ ds^2= g_{ik} dx^i dx^k .........(8) \] この式は、一般の時空から平坦の時空への微分の変換であり、物体が静止する系 $g_{4i}=0$ (i=1〜3)とし、$g_{ik}=0$ (i≠ k) にする空間軸を選べば、 \[ ds^2= g_{ii}(dx^i)^2 + g_{44} (dx^4)^2 (i=1〜3) ..........(9) \] となる。空間i方向の物差しの2乗 $(dx^i)^2$に計量$g_{ii}$を掛けて、平坦時空の物差しの2乗$(dx^j)^2$になる。つまり、物差し時計 $dx^i$ に計量の平方根 $\sqrt{g_{ii}}$を掛けて平坦時空の物差し時計 $dx^i$ になる。このとき $g_{ii}, g_{44}$ は、標準値 $1,1,1,-1$ から変化する。
一般相対論では $ds^2$一定なので、計量は、各所の物差し時計の逆数の2乗の係数である。物差しは空間間隔の代表で、 その場所の通常の固体の物差しや、太陽地球間の距離などを一定とみる観測側の物差しである。
一般相対論には計量$g_{ik}$の微分の方向差と速度の2乗によって、質点の加速度を与える運動方程式となる測地線方程式があり、一方、計量$g_{ik}$は、 質量の配置や分布によって重力方程式が与える。計量の微分は局所現象に影響するが、計量自体は影響しない。局所の観測者が計量を知り得ないのは 慣性系が自系の速度を知り得ないのと同じである。時空点は、その周辺との関連で自らの計量を知るというが、計量の時空間的微分を使って知るのである。
一般の時空では、空間ピタゴラスの定理が成立せず、所謂、"剛体の回転はない"といわれ、一様でない計量では平行移動もない。この一般相対論による 変形は、特殊の変形と同じく質点間の結合強度によらず、物体と空の空間を区別しない。強度と力とは、その質点の変形からの偏移に関係する。
一般相対論の不変量$ds^2$の微分形式は、累積の為ではなく、微分時空間隔の不変量である。正は空間(負は時間)の間隔、光で 0 という点は特殊と同じく、 宇宙のどこから見ても不変量という意味で剛体である。 また、時空間の和(9)式が不変量なので、空間短縮 ($g_{ik}\gt 1$) の起きる場合、必ず時間伸長 ($-g_{44} \lt 1$) が伴うだろう。これらの物差し時計の基準とするのは無限遠や測地線の物差し時計であり、$1/\sqrt{g_{ii}}$ (i=1-3) が局所の物差し、 $\sqrt{-g_{44}}$が局所の時計である。一般に、質量天体の近くで物差しの縦(r)方向が短く($g_{rr} \gt 1$)、時間経過が遅い ($-1 \lt g_{44} \lt 0$)。
半径rは、物差しを中心方向に延長した距離など任意のr'= f(r)変換が可能である。接線方向の物差しは伸縮せず周囲は 2πr である。 計量は球対称で、中心からの軸は直線で、目盛りは均等でなく地平面に近づくほど密で、さらに中心までの累積距離は、半径rに一致しない。
(*) 式の導出は、アインシュタインの一般相対論の基礎 E. 22にある("Principle of Relativity" に収録)。 物理と現実にも言及がある。W. パウリの"相対性理論"では厳密解(421a),(421b)の後に(p.282)、 ランダウ・リフシッツの"場の古典論"では§ 97 "中心対称な重力場" の式(97.13)にある(p.337)。

不変量と計量の関係を楕円の2方向の半径を使って説明する。x方向の半径a、y方向の半径b (a>b とする) の楕円 $x^2/a^2 + y^2/b^2 = 1$では $x^2$の係数である $1/a^2$ は、$y^2$の係数より小さい。 つまり、計量 $g_{ik}$ を積項 $dx^i dx^k$ に掛けikに渉る総和一定は、計量 $g_{ik}$の大がik方向の積項の小を表す。
A点〜B点の局所物差しdxに局所距離 $\sqrt{g_{xx}}$ を掛けた積分は、その場所の局所の物差しで測るAB間の距離であり、 観測点の物差しで測る距離 $\int_A^B dx$ ではない。 \[ \int_A^B \sqrt{g_{xx}} dx \] 計量と物差しの積和が不変量 $ds^2$ だから、局所距離 $\sqrt{g_{xx}}$ の増大は、局所物差し $dx$ の短縮を意味する。 \[ ds^2= g_{xx} dx^2 + ... \] 天体の近く(地平面の外)では半径方向の空間計量 $g_{rr}$は1より大きく、時間計量 $g_{44}$ が負の-1から絶対値が縮小する。 \[ ds^2= g_{rr} dr^2 + r^2... + g_{44} dt^2 \] では、例えば、$g_{rr}= 4 $とは、r方向の物差しdrが基準と比べて1/2に短縮していて、$g_{44}$ が-1/4になって絶対値が1/4とは、 その場所の時計dtが基準と比べ2倍に伸びて、遅いことを意味する。
ブラックホールの時空は、半径rの関数として計量 g_rr, g_44 が決まり、dr, dt がその場所のr方向の物差しの大きさと時計の速さを表す。計量g_rrを掛けた 距離の2乗とg_44を掛けた時間の2乗の和が不変量だから、計量は(物差し時計)^-2の指標である。ブラックホールの地平面外部の計量√ g_rr の増大は、 局所物差しdrの短縮である。その位置から中心天体に近い内側の空間計量 g_rr が大きいと、中心への累積距離は半径rを超えるだろう。
そこで、どの r'= f(r) 変換も可能だが、これを半径と計量との連動式とみても、半径rを累積距離で置換すると計量が変わり、それを繰り返しても 収束する保証はない。外部から地平面までの累積距離に無限大はないが、そうであれば困る。さらに地平面から中心までの半径が純虚数で半径に置換 できない。一般に計量場の変化は、波動として伝搬し、地平面をも抜け出せそうだが、計量場自体が時空構造に関わるから先与として、累積距離伝播は考えない。
空間計量の大(g_rr>1)は、その場所の物差しdrに乗算し拡大して基準の物差しになるから、物差しの短縮を表す。物体は半径方向に平坦化する。
時間計量の絶対値小(-1<g_44<0)は、その場所の時間dtを縮小し高速化して基準の時計になるから、そこからの全エネルギーは衰退し、光も赤方偏移する
時計の緩慢を表す。
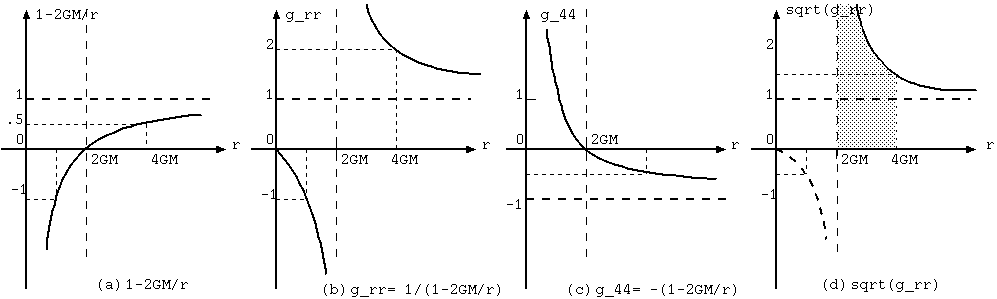
空間計量 g_rr= 1/(1-2GM/r) は、無限遠の 1から増大し、地平面で+∞を越え -∞ に飛ぶ (図1.(b))。
時間計量 g_44= -(1-2GM/r) は、無限遠の -1から絶対値を縮小し地平面で 0。これを越え正になる(図1.(c))。
そこで、r= 2GM を"事象の地平面"という。そこでは空間計量が無限大であり、物体の厚みが0になり、時間計量が0になり、時計が停止する。 地平面の内部では計量の符号が変化し、g_rr が負に、g_44 が正になる。時間と半径の役割が交代したかにみえるが、そこは、まだ特異点ではなく、 計量とその微分が存在し、物体はその面を通過して内部に入るだろう。
特殊相対論の速度によるローレンツ短縮は、相対的で、自らの短縮は知らず、そこからみる相対速度をもつ相手側の慣性系を短縮させる。 それに対し、(2)の重力による空間短縮と時間遅延は絶対的である。長さが短縮し、時間が遅延した(2)からみれば、遠方の宇宙は、伸長し高速化している。
地平面の外側の √g_rr は、地平面に近づくにつれて無限に上昇するが、地平面までの累積距離 (地平面のa倍から1倍までの
√g_rrの定積分 $D= ∫_1^a \sqrt{g_{rr}} dr$) は、区間端に無限があるが有限である(図1.(d)参照)ゆえに落下速度>0なら、
地平面までの落下時間も有限である(⇒ 5.2)。
\[
D = \int_1^a {1\over \sqrt{1-{1\over x}}} dx = \int_1^a \sqrt{x \over x-1} dx
= \int_0^{a-1} \sqrt{1 + {1\over x}} dx = \int_0^{a-1} t dx, \\
x= {1\over t^2-1} = {1\over 2} \{{1\over t-1} - {1\over t+1}\}, dx= {1\over 2} \{ {-1\over (t-1)^2} + {1\over (t+1)^2} \} dt \\
D = {1\over 2} \int_∞^\sqrt{a/(a-1)} \{ {t \over (t+1)^2} - {t \over (t-1)^2} \} dt
= {1 \over 2} \int_∞^\sqrt{a/(a-1)} \{{1\over t+1} - {1\over t-1} - {1\over (t+1)^2} - {1\over (t-1)^2} \} dt\\
= {1 \over 2} {[\log{t+1 \over t-1} + {1\over t+1} + {1\over t-1}]}_∞^\sqrt{a/(a-1)}
= {1 \over 2} \log{{\sqrt{a} + \sqrt{a-1} \over \sqrt{a} - \sqrt{a-1}}} + \sqrt{a(a-1)}
= \log(\sqrt{a} + \sqrt{a-1}) + \sqrt{a(a-1)}
\]
例: 地平面の2倍(a=2)から地平面(a=1)までの累積距離は、D= log(√2+1)+√2 = 2.2956、約2.3倍に、
a=3からa=1までは D= log(√3+√2)+√6 = 3.38228。約1.7倍に伸びている。
外光は、重力で曲げられ回りこみ、上方の狭い角度から射す。地平面の少し上に自分と同じ高さの地面があれば、そこからの光は、湾曲し、 星の外側の地上風景が上空の穴の周りに逆転し裏返してみえる。それ以外の方向は暗黒で、まだ、ここは地平面の外側(2)なのに、 上からのスポットライトを浴びる黒い穴の中のようだ。もちろん、細長い縦長空間と思うのは自身の平坦化が原因である。 そして、自分が地平面に近づき接触すると、上の穴は一点に収縮するだろう。
ブラックホール外側の静止点(2)のそばを落下物体(3)が通過するとき、(1), (2), (3)は、互いをどうみるか。
(2)と(3)は、(1)からみると共に重力短縮していて、その中で(3)からみると(2)が、(2)からみると(3)が、互いにローレンツ短縮している。
(1)からみる(2)は 1/γ に重力短縮し、 (1)からみる(3)はローレンツ短縮と重力短縮が二重になり 1/γ^2 に短縮する。
(2)からみる(1)は重力伸長し γ 、(3)からみる(1)はローレンツ短縮と重力伸長で 1 の比率である。
(但し、(1)からみる(3)は、重力短縮のために速度低下し、ローレンツ短縮しないなら、短縮 1/γ のみ、(3)からみる(1)は、γ伸長だけになる。(*))
この論理は、地平面から出られない説明に、地平面近傍の局所距離が∞と、局所時間0を使う。この片方の仮定が崩れ、§ 4.1のように地平面の半径の a(>1)倍から1倍までの累積距離Dが有限なら、一方通行が崩れるのではないか? と考え、(局所距離/局所時間)の積分を求める。 √(g_rr/-g_44)= 1/(1-2GM/r) x(=r/2GM)の1/(1-1/x) = x/(x-1) の1..aの積分は、(x+1)/x =1+1/x の 0..a-1 の積分が1/xを含み発散する。一方通行は崩れない。 \[ T= \int_{2GM}^{2aGM} \sqrt{g_{rr}\over -g_{44}} dr= \int_{2GM}^{2aGM} {1\over 1-2GM/r} dr, T/2GM = \int_1^a {x\over x-1} dx = \int_0^{a-1} {x+1 \over x} dx = \int_0^{a-1} (1 + {1\over x}) dx ⇒ ∞ \]
地平面では遠方(1)からみて、半径方向の空間計量が無限大、物体は面になり、時間計量は0で時間は止まる。しかし、地平面は、 物体が力を受けることのない真空の空間であり、物体が受ける潮汐力も、質点には無視できる。地平面は、地球上で船が水平線の向こうに消えるように、 または物体が地面の穴に姿を消すように、遠方から見えなくなるだけであろう。
地平面で光速 √(-g_44/g_rr) = 0 光が停止するからといって、それが一方通行の理由ではない。光が外に行かないとは、 地平面内側から外に向かう光が地平面で反射するのだろうか? いや、地平面内部では外に向かう光はないのである。
一方通行の理由がエネルギーだけなら、中心からの光は地平面の外に出ないが、地平面のすぐ内側からの光のエネルギーの低下は 小さいから外に出られるのではないか? それは地平面の一方通行の否定だから疑わしい。
さらに、地平面は、遠方(1)からみてそうであるだけで、近くの(2)からみると、もっと小さい半径の面でないか? という考えも、 地平面内部から途中の(2)を中継して(1)に光を送れ、一方通行の否定になるから疑わしい。
一方通行とは、過去から未来への時間のように、因果律の成立要件、時間の矢であり、容易には崩れないだろう。 空間的な地平面は実は、時間的未来であり、そこから外へ(つまり過去)への影響が全くないのだろう。
ブラックホールの物理を説明するある Youtube 動画で、地平面では、落下物体に付着した小さな光円錐が45度以上傾き、光が中心に即時到達し、 さらに内部からは中心近くの過去に到達しそうな図をもつ動画があったが、光円錐がまともな円錐とみるのは落下者(3)だけで、遠方(1)からや、 地平面の近く(2)からは、地平面で光円錐自体が平坦に押しつぶされているから、光が中心に即時到達することはないだろう。
地平面内部の計量を外部と同じ g_rr= 1/(1-2GM/r), g_44= -(1-2GM/r) で与え、落下運動を示すと考えると、計量の符号が変り、 局所距離√ g_rr と時間速さ√-g_44 がともに虚数になる。内部の質点を使う座標系では時空交換し、光速は√(-g_rr/g_44) か。 時空交換の根拠は、計量の正負の符号(だけ)である。計量の標準値 1,1,1,-1 からみて、rと4が交換しても ds^2 が不変量だから、物体は問題なく存在できそうだ。 測地線方程式は、計量の微分方向差と速度の2乗が加速度を与えるが、地平面でg_rrが∞ から-∞ になる不連続は、無限の加速度を与えないか?与えない。 計量は微分の連続性と2階微分可能が前提である。計量の不連続はそれに反するか? 反しない。 √g_rr=√ 1/(1-2GM/r) を√ x/(1-x) で表し、xで微分、 {(x/(1-x))^1/2}' = 1/2 {1/(1-x)^2}^-1/2 = 1/2 (1-x) 2階微分は (1/2 (1-x))'= -1/2. 微分も2階微分も x=1 で連続する。
遠方(1)からみて、落下物体は、重力ポテンシャル分を運動エネルギーに変換してもエネルギー全体は変わらず、地平面においても質量と慣性をそのまま持つ。 それに対し、地平面の外側で何かを支えにして静止する(2)は、重力ポテンシャルから変換した運動エネルギーをどこかに捨てて来ているから、 地平面では時間が止まり質量を失い、ブラックホールに質量を追加しない。GM/r= 1/2 c^2 は、2GM/r = c^2 であり、無限遠で質量 m だった物体は、 (2)の場所ではエネルギー mc^2 を失う。
そのとき静止物体(2)は、地平面での質量の喪失を知るだろうか。 一般に、加速度= (計量の微分の方向差) x(速度)^2 なる測地線方程式があり、 物体の運動の加速度は、計量でなくその微分だけに関係する。また、加速度は質量に依らず、(2)は質量の増減だけでなく質量の喪失さえ、自覚しないだろう。
物体の地平面通過でブラックホールの質量は増加するか? 外からみて質量が増加しなければ、宇宙の質量の減少を招くから、増加するだろうが、それなら、 何がそれを外に伝えるのだろうか。重力波が地平面を外に通過するのだろうか。正解そうな、"地平面が膨張する" は、一方通行のゴールポストを外に 動かすような話であるが、計量は、物質でも波動でもないから伝播せず、地平面を遠隔形成するのだろうか。計量の変動は地平面内部を伝播し、ぎりぎり 地平面に到達して動かすのだろうか。光速制限から無理だろうか。光でも外に出ないのに、質量増加を伝える重力波だけが外に出るということはない。
(*) 物体の慣性は、そのエネルギー内容に依存するかを参照。 質量喪失は、ネーターの定理(エネルギー保存は時間並進性、運動量保存は空間並進性に対応、角運動量保存は等方性に対応する)に反するが、 それは、相対論以前の古典物理の平坦時空の物理法則であり、一般相対論では局所の認識以外はそれを超えるため、一般時空へ適用はできない。 相対論は、場所と時間によってエネルギーも運動量も非保存だが、質量喪失なしには、落下物体のエネルギーが地平面で質量の2倍になる。
この、"半径方向は取り返せず、時間は行き来できる"、というのは理解が難しい。時間を往来できるとタイムパラドックスが起きる。 光は中心方向から来ないのは正しそうだ。中心からの方向は見えなくなり未来の時間になり、元の時間は半径方向になる。 全ての質点が特異点から始まる放射状の測地線をなす膨張宇宙では中心の特異点は過去だったが、中心の特異点までの測地線が未来の全てとなる。 内側世界はある時刻(現在)からスタートし、後から後から星が降るだろう。このなかで大きさのある物体は存在できるか。いや、 大きなブラックホールでは物体だけでなく地球や太陽系も地平面を通過できないといけないだろう。特殊の慣性系の対等に対し、 一般は局所対等であり、地平面内部も局所的には通常の時空として理解できなければならない。
g_44= -(1-2GM/r) は0を越え正となり、どこまでも大きくなる。(これが空間計量に変わるなら、地平面内部では物体は徐々に薄くなり、宇宙膨張をみる(6.7参照)。)
g_rr= 1/(1-2GM/r) は∞ から符号が変わり、-∞ から0にまで戻る。(これが時間計量に変わるなら、最初急速に時間が経過し、徐々に停止していく。)
虚数化の操作としては、g_rr の代わりに -g_rr= -1/(1-2GM/r)、g_44 の代わりに -g_44= (1-2GM/r) を使う。つまり、4とrの時空計量の符号を変える。 そのとき、-g_rr= -1/(1-2GM/r) と g_44= -(1-2GM/r) とは、0<r<1 で左右反転であり、その区間の局所距離の定積分である、累積距離は、 √g_44と (時空交換) √-g_rr (虚数化) で等しい。距離を速度vで割る累積時間(落下時間)は、左右反転でも速度が違うので違ってくる。
√ g_rr は地平面で不連続だが、微分は連続する。これを時空交換によって√ g_44 にすると元の値や微分は連続せず、地平面越境で全く違う値になるが、 これを虚数化によって√ -g_rr にすると値は無限大を含めて連続する。しかし、微分は地平面で符号反転する。その意味は、何だろうか。 測地線方程式の加速度の符号を変えるのではないか。
地平面内部の物差し時計の虚数化は、外からみて虚数自体が不可視又は非存在を表し、速度の逆数化や加速度の逆転がないことが時空交換よりも優れる。 時間の逆転は、いずれの方法でも発生しないようだ。微分の符号反転は、重力等の加速度が逆に働くことを表わすかもしれない。
問題: 赤方偏移をドップラー効果とし、時間計量一定で空間計量の増大をいうフリードマンの膨張宇宙論は、空間計量の時間関数部分G^2のGを"宇宙のサイズ"とした。
フリードマン宇宙論は、計量を時間関数にした。これは宇宙原理の"定常"を捨てた法則の普遍化であり、正しければ重要な進展であった。 それまでのアインシュタイン宇宙とド・ジッター宇宙とが使用した、数学的に任意な宇宙項を使わない単純さで優れていたが、それゆえ、 両者を包括する解ではなく、異なる解であった。宇宙項は、数学的に任意であるが、それを使う正当性が要求される。アインシュタインは、 宇宙項を使用する理由を"定常"に求めた。その次元を1つ増加させただけのド・ジッター宇宙は、宇宙項の反発によって存在する殻宇宙であった。 アインシュタインは、ド・ジッター宇宙が、宇宙項を "定常" 以外のために使用したと批判した。
フリードマン宇宙が空間計量を"宇宙のサイズG"の2乗とした問題は、それまでの宇宙論の、一定の密度と釣り合って定常になる宇宙項が存在するとして、 4次元空間内の球の3次元への射影であるアインシュタイン宇宙と、密度0の宇宙に宇宙項が存在する5次元空間内の球の4次元への射影である ド・ジッター宇宙との両宇宙解が、有限球から接平面への射影であり、宇宙の果てには銀河が縮小密集する。逆に、フリードマン宇宙は、 次のように空間計量の増大がそのまま空間の拡大とされている。
"相対論の意味" には、「G は、どの場合も、時間の関数であるふたつの物質粒子の計量距離の相対的尺度。 G'/G は、ハッブル膨張を表す。」とある。"計量距離" とは、ここでいう√空間計量を掛けた距離である。その増大を局所のみる主観的な 宇宙サイズの増大、宇宙膨張とするのは、一見正しそうだが、元々、一般相対論は、局所で違う物差し時計に√計量を掛けて特殊相対論の 平坦時空の物差し時計になるとする。物差しに√空間計量を掛けて標準的長さ、時計には√時間計量を掛けて標準的な時間経過になる。 計量と(物差し時計)^2との積が不変量とは、両者の反比例で、空間計量の増大する膨張宇宙は、物差し(=空間)の縮小する宇宙である。 これを膨張宇宙というのは、縮小する物差しを一定と錯覚し、一般相対論の原則を無視する人が主観的にみる宇宙でしかない。
ブラックホールの地平面外側近傍(2)からは、他の部分の宇宙の縦方向の伸長を見るが、膨張宇宙論の空間計量の増大=物差しの収縮は、現在の宇宙に 対応する部分がない。我々は現在から過去の宇宙をみるだけである。宇宙原理の一様等方から、"物差し"は、場所によらない空間間隔の任意代表であり、 遠方の銀河間距離さえそれに含まれると考える。空間計量の増大とは、均一な空間間隔の収縮であり、これは、膨張宇宙でなく、逆に収縮宇宙である。 ここで空間とは、同時刻の空間を俯瞰する概念で観測不能である。
強いていえば、膨張宇宙とは、現在の収縮した物差しから、一定の遠方過去の空間の物差しを光で観測し、相対的に膨張してみることである。なお、 遠方の現在の物差しは、観測点と同サイズと想定するが、観測不能である。一般相対論の宇宙論では密度は一様等方だが、計量は一様等方ではなく、 フリードマン宇宙は空間計量の時間変化を分析し、空間計量の空間変化については議論しない。
膨張宇宙論は、光の伝播について "何もない空間の膨張"による波長拡大の赤方偏移というが、物差し収縮の観点からは、元々長波長の過去の光の波長が 伝播中、物差しに比例して縮小するなら赤方偏移は起きないが、光は観測されて初めてエネルギーを知ることから、元の光の波長が伝播によって変化せず、 収縮した物差しによって観測されるときに赤方偏移を示すと考えられる。
また、膨張宇宙論では別に光の発生源の後退速度によるドップラー効果をいうが、それは近傍の物差し一定の錯覚が生む速度であり、物差し収縮の観点 からは、空間間隔物差しが同時刻に比例的に短縮するから同時刻の質点間に速度はない。そして、膨張宇宙の(現在の物差しを基準にした)過去tからの 光経路長は、$\int 1/G(t) dt$ であり、これが短縮中ならドップラー効果による青方偏移、伸長中なら赤方偏移があると考える。
一般相対論での光速は、場所時間方向によって異なる$g_{ik}$による。 \[ dx/dt= \sqrt{-g_{44}\over{g_{rr}}} \] 局所の物差しに $G(t)= \sqrt{g_{rr}}$ を掛けた、局所が見る"距離" ではなく、各時空点の"物差し"に光は時間を必要とする。 そのとき、膨張宇宙の奥行き = 光経路長は、光の過去から現在までの物差しの時間積分である。 \[ L= \int_0^1 {1\over G(t)} dt \]
単純な直線膨張の $G(t)= t$ では、この距離は、発散し、0から1までの時間に無限遠から光が来る不都合があるが、 直線膨張は、フリードマン解にないので一応、問題ないとする。このとき、増分 $1/t$ は時間反比例の赤方偏移である。 \[ L= \int_0^1 {1\over t} dt = [log(t)]_0^1 = ∞ \] フリードマン解の減速膨張、 $ G(t)= t^{2/3} $ では、 \[ \int_0^1 t^{-2/3} dt = [3 t^{1/3}]_0^1 = 3. \] となって光は、有限時間に有限距離からくる。このとき、増分は、$3t^{1/3}= 3\sqrt G$ の赤方偏移をもつ。
これに対して、物差しと光速とを一定とみる局所の誤解 $G(t)= 1$では、宇宙膨張を空間の膨張とし、 遠方は、距離にほぼ比例した後退速度のドップラー効果による赤方偏移をもつと考える。 \[ D= \int_0^1 dt = [t]_0^1 = 1 \] 物差し縮小による光の経路長は、物差しに相対した光の波長の伸長の効果となる。物差し縮小と空間拡大の両見解は両立せず、 遠方からの光の経路長が異なり、後退のドップラー効果では光速に近い周辺物体に殻を生み、物差し縮小の認識では逆に宇宙の周辺が伸びる伸長効果をもつ。 宇宙論で問題である(計量による宇宙論を破綻させる)宇宙の始まりの特異点を前提とせず、ビッグバンよりも優先的に、 一般相対論だけから宇宙の見え方を考える。
初期宇宙のインフレーションは、宇宙原理の等方性(光は現在初めて違った方向から合流するのに方向に依らない)と、平坦性 (この宇宙は曲率がほとんど0である)を説明する為に導入された。これは、宇宙が特異点から始まることを前提とする修正である。 さらに現在が加速膨張に転じた等の宇宙の全てのアドホック(臨時的)な異変の導入を排除したい。それらは、観測との整合を満たす為に不正に 基本物理に導入された疑いがあるからである。
膨張宇宙論は、局所局時の空間間隔である物差しを一定とみる局所の誤解である。それは、局所の物差しと時計とが$g_{ik}$によって変化する 一般相対論の原理を無視し、局所の物差しと時計とを主観的に一定とみる。そのため不変量の式、 \[ ds^2 = g_{ik} dx^i dx^k \] は、任意の時空点で、空間計量$g_{ik}$と物差し$dx^i dx^k$の積和$ds^2$が不変量で、空間計量$g_{ik}$の増大は、物差しの短縮を伴う。 物差しを一定とみる局所の誤解は、空間計量の増大が不変量である筈の $ds^2$ を増大させ、この一般相対論の計量の原理に反する。 不変量の一定は、一般相対論の計量場$g_{ik}$が従う重力方程式に依らない、計量場の最も基本的な性質である。
膨張宇宙に適用される一般相対論の質点間の変形は、空間計量の増大がそのまま、物差しの短縮である。 同様の誤解が、ブラックホールの地平面外側の近傍にあり、よく"空間伸長、時間伸長"といわれるが、 そこからみる主観は、"空間伸長、時間短縮" だが、計量$g_{ik}$ を使う客観は、"空間短縮、時間伸長"である。
さらに、膨張宇宙論ではよく、「膨張は、何もない銀河間空間だけに現れ、重力結合した天体系や電磁気力結合した物体には表れない」というが、 銀河間にも重力による結合がある。空間計量の増大は、動質点に加速度を与えるが、それには、次のような力学的説明が必要である。 "銀河間を含め重力結合した天体間は、加速度が与えられた質点間のバネは加速度が招く慣性力に対抗するバネ係数の逆数の柔軟さ(compliance) に比例して平衡位置が広がる、空間計量の増加は、動質点の速度に加速度を与え、太陽系の惑星衛星も、膨張の加速度を受け続けると軌道が広がるが、 太陽系の結合は銀河間より遥かに硬い"。
しかし、一般相対論の剛体概念は、計量と(物差し)^2との積和一定が質点運動を決めるもので、力と強度による変形ではない。一般相対論の測地線方程式は、 速度積 $dx^i/ds dx^k/ds$ と時空の歪(計量の方向差) Γ とが質点に力でなく加速度を与える。特殊相対論のローレンツ変換が、相対速度による時空の座標変換 であり、力による短縮ではないのと同じく、一般相対論も、局所間の微分時空の座標変換であり、力による短縮ではない。
膨張宇宙論ではよく「固体の物差しは、重力でなく電気的結合、いや量子力学の電子軌道や不確定性による」とし、「一般相対論は、天体間の重力を説明する マクロの法則だが、固体の原子の大きさを決定するミクロの法則は別」という。さらに特殊相対論のローレンツ短縮が固体に及ばないという誤解は、 速度の座標系間のローレンツ変換を認めない誤りさえ生むことがある。量子力学の位置と運動量の積の不確定性は、物差し時計の計量の基礎の上にあって、 物差しと時計の再定義を要求しない。計量は、原子サイズや核力の到達距離を決定し、不確定性とは矛盾しない。膨張宇宙は、力による変形ではなく、 固体から銀河間空間までの比例的膨張を要求する。ゆえに、陽子の大きさを初期宇宙の遡りの限界とする一部の膨張宇宙論者は、相対論を放棄している。
但し、重力関係全てが比例的ではない。地面は、重力に対抗する抗力を発生し質点の加速度を止める。周回軌道上の人間を天体方向に引き伸ばす 潮汐力も頭と足の間の重力差であり、人体はバネとなって平衡位置を変える。これは膨張宇宙論では変化しない時間計量の勾配による重力である。 宇宙膨張の空間計量の増大は、速度をもつ質点に加速度を与え、周回軌道を(拡大でなく)縮小させるが、静止質点には加速度を与えず変化させない。
現在の物差しからみると、遠方過去の物差しの増大だけがある。空間計量増大をそのまま物差し縮小と理解するなら、赤方偏移のためにはその逆の 空間計量縮小か、又は時間計量のポテンシャル上昇が必要である。しかし、膨張宇宙論は一般相対論から宇宙の変化、時間逆転の宇宙膨張を導き、 現時点が密度が臨界を超えるサイクロイド周期解のビッグクランチ前ならば、宇宙膨張とフリードマン解を許容できるかもしれない。 物差し縮小は、物差しを一定とみる局所誤解によって、宇宙膨張と解釈されるが、過去から現在までの物差し縮小の根拠を失う。なぜにここまで物差しは 短縮したのかを説明しない。
そして、その膨張宇宙の雛形が地平面内部にある。ブラックホール内部で我々が中心特異点に向かう測地線は、我々が中心特異点から始まる測地線とする 膨張宇宙と時間軸の向きが逆であり、地平面内部の計量の "時空交換" 解釈によれば、中心に近づくにつれて空間計量が増大する。時間計量も変化するため、 時間計量一定の膨張宇宙の計量とは違うが、それは膨張宇宙というより、少なくとも外部からみると一定半径のブラックホール内部での収縮宇宙である。 中心特異点に向かう地平面内部の空間計量 $g_{44}$ の際限なき増大は、質点間隔や物体の薄膜化、時間計量の絶対値 $|g_{rr}|$ の0への縮小は、 時計の際限なき遅延である。これは、地平面外部の計量 $g_{rr}$ と $g_{44}$ と同様である。それは膨張宇宙に期待される赤方偏移の逆であるから、 収縮宇宙のドップラー効果とポテンシャル低下による青方偏移を生むと推測する。但し、地平面内の小速度差の落下質点間の物理現象は、 膨張宇宙と区別が難しいだろう。これが章題 "この宇宙は地平面内部か?" の意味である。
但し、この話は、地平面内部の"虚数化"解釈では違う。半径rの縮小に伴い、空間計量の無限大から0へ縮小は物差しの膨張、時間計量の0から負無限大へ 増大は、高速化である。計量の微分の符号逆転によって仮に時間が逆進するなら、特異点からの半径rの増大に伴い、空間計量の0から無限大へ増大は 物差しの縮小、時間計量の負無限大から0への縮小は低速化である。
アインシュタインは、時間計量一定で空間計量の増大をいうフリードマンの膨張宇宙論を、彼の "相対論の意味" の第2版への付録、"宇宙論的問題について" にフリードマン説をそのまま採録し、彼は、定常宇宙論を捨て膨張宇宙を認めたとされるが、 その本意の理解は難しい。彼は、空間計量を宇宙のサイズとするフリードマンの誤り(局所誤解)を最初から知っていたと推測されるからである。
または、彼の"相対論の意味" では赤方変移の解釈がドップラー効果だけに限定している点から、宇宙膨張には必ず物差し縮小が伴うという計量の 基本原理を忘れていたのではないか。彼は、物差しの縮小について明確に記述しない。"相対論の意味”の膨張宇宙は、物差しの縮小を考慮していない。 ならば、ビッグバン理論は、基本から再考すべきだろう。
これは、現在までの宇宙の時間発展に、重大な相違を生むだろう。彼の当時の宇宙膨張には、多くの間違いがあった。”相対論の意味”は、 19億年という地質年代よりも短期の宇宙生成を主張した。1929年のハッブル定数は、現在の10倍も大きかった。つまり、ハッブルの膨張速度(km/s/MPC)は、 9割も間違いであり、その縮小の歴史は、天文学の観測の誤りの歴史である。1996年のハッブル定数の3人の議論では、 バージニア・トリンブルは、私的にハッブル定数に33を望んでいた。距離と速度の関係を示す、ハッブル定数は、距離の推定に使われる様々な梯子が、 その時々の科学的発見によって、セファイド変光星の周期と絶対光度の関係に2種あったこと、キップ・ソーンが批判したSNIa型超新星の光度一定など、彼らが見出し、 宇宙論の距離の推定に用いられた距離梯子によって改定された。そして、現在、多くの天文学者はハッブル定数 60〜70程度の値に妥協し収束しているが、未だに問題とされている。 そして、背景輻射が10万分の1の精度で一様なのに、現実の銀河の大規模構造を実現するには、 ΛCDMの理屈によれば、宇宙のバリオン物質は、5%であり、残りのダークマターが20数%、ダークエネルギーが70%であり、それらは、全く未知のものであるという矛盾を生む。 今後どうなるかは、彼らの望む膨張宇宙次第である。つまりは、膨張宇宙論は、宇宙論に導かれた天文学ではなく、観測に依る宇宙論であった。 アインシュタインは、観測に頼る宇宙論には、ステップマザー(継母)のような態度で臨むとした。宇宙項のような基本的変数の変動の導入が本質を歪める。 極力排除すべきその最たるものが、ビッグバンの初期宇宙に必要であったインフレーションの導入である宇宙項の導入である。
この "局所誤解" は、どのような誤りを生み、どう解決されるべきだろうか。 赤方変移の原因を宇宙膨張とするのは、片方のg_ik の増大だけを捉えて、近傍の物差しの縮小を把握しないのは宇宙を膨張させる操作であろう。 初期宇宙から現在までの物差しの縮小は、宇宙のどこに表れているのか。現在と初期の物差しのサイズの比が、宇宙膨張の比に一致し、 宇宙背景輻射の初期の温度(数千度)と現在の温度(2.7度)の比約1000倍がそのまま膨張縮小比なのか。現在の物差しのサイズには、 どのような理由があり得るのか。仮に、初期宇宙というものを認めるなら、初期宇宙と現在の宇宙の物差しの比は、宇宙膨張の比を 表しているのではないか。また、無限の過去からの膨張は、無限の物差しの収縮となる。
また、"ブラックホールの中心には特異点がある"という一般的な理解は推測でしかない。例えば、一時的に半径r内に質量Mが一定以上存在だけで 暗黒星の条件は満たすから、地平面内部が通常の宇宙である可能性がある。フリードマン宇宙で仮定しなかった宇宙項も存在すれば崩壊を防げるだろう。 地平面内部は、光でさえ中心に向かうとして、中心特異点しかあり得ないと外部からする推測も証拠はない。 このことに関連するのは、臨界以上の密度の球状宇宙と外部真空は、間に地平面をもつことである。 また、中心に質量があるブラックホールは内部地平面と宇宙項Λ があれば外向き一方通行の外部地平面をもつ 宇宙定数について。膨張宇宙論についての全般的問題は、宇宙論的問題を参考。
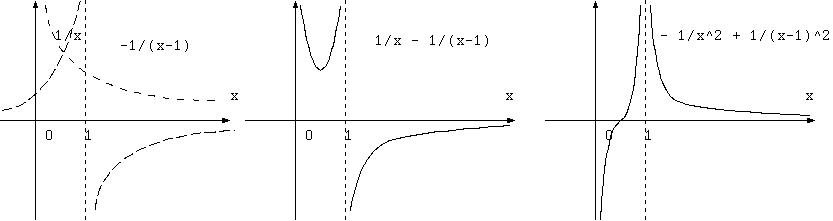
加速度は中心へのg_44の勾配と地平面へのg_rrの勾配との和。x=1/2 で加速度0になる。 1/2 ∂_i g_{44} は 1,1,1,-1 ならgrad山登り、 -1,-1,-1,1なら -grad 坂下り。 1/2 ∂_i g_{rr} (v^r)^2 が速度質点への加速度を増すには g_rrの勾配符号は+であるが、逆である。
以上は、速度の2乗 (v^r)^2 を掛けた後の微分であり、速度の2乗を微分の後に掛けるべきとしても大差なく、地平面への接近における 速度の2乗と空間計量との積は減速になる。質点が無限のポテンシャル壁を超えられない? 速度が光速度未満から、ポテンシャル壁は無限ではない。 これが質点の凍結の説明をする可能性がある。 \[ 1/2 ∂_r(2GM/r) - 1/2 ∂_r (1/(1-2GM/r)) (v^r)^2 \\ = 1/2 (2GM/r)' - 1/2 (1/(1-2GM/r))' (2GM/r) \\ = 1/2 {(1/x)' - (x/(x-1))' 1/x} = 1/2 (-1/x^2 - ((x-1)-x)/(x-1)^2 1/x)) \\ = 1/2 (-1/x^2 + 1/x(x-1)^2) \]
以下、現代の科学常識への疑問:なぜ、光速に近い速度をもって逃げる銀河にローレンツ短縮を適用しないのか? 赤方偏移をドップラー効果としながら、 それは速度でないのか? 空間の膨張であって自分で稼いだ速度でない? それは一体、どういう速度か。宇宙論には"局所慣性系の速度"という名のエーテル 的観念が入っている。"座標系"とは、物体の座標を表わすためにあるが、系の速度に系内の物体の速度は、相対論では加算できない。また、"空間の膨張" とか "空間の速度" とかいう概念は、相対論にない。アインシュタインは、"エーテルと相対論"(1920)において、計量場には速さの概念がないといった。
要約すれば、一般相対論によれば、空間は物理量を付与されていて、この意味でそれゆえエーテルは存在する。 一般相対論によれば、エーテルなしの空間は 考えることもできない。; そのような空間では、光の伝播もないだけでなく、 時空の標準(物差しと時計)の存在の可能性もない。 それゆえ、物理的な意味でのいかなる時空の間隔もない。 しかしこのエーテルは、時間のなかを追跡できる部分からなる、重さのある媒体の性質を備えると、 考えることはできない。 動きのアイデアは、それに適用できない。一般相対論は離れた所の速度をいわないか? いや、その測地線方程式が離れた所の速度と加速度の関係を扱う。特殊相対論は、物体が光速を超える ことがないが、一般相対論では超えることができる? これには、ブラックホールの地平面での物体速度の例のように、 全宇宙の崩壊を招く可能性がある物理量の無限大は、注意深く避けられるべきである。
宇宙論は一般相対論の領域であり、特殊相対論は無限小の平坦空間にしか適用すべきでない? 一般相対論は、無限小の微分幾何学であり、 計量で重力のある宇宙を扱い、特殊相対論を平坦な無限小領域に閉じ込めたとされる。それに対して、特殊相対論は元々、有限サイズを扱う時空幾何学である。 宇宙の果てを準光速で逃げる物体には宇宙がほぼ平坦と仮定して、まず、ローレンツ短縮を適用すべきでないか。
そのとき、紙のように薄くなって重なる銀河の間の光速が疑問となるだろうが、一枚奥の銀河と手前の銀河との間には大きな時間差がある。 特殊相対論でロケットが目指した星の時刻が、加速によって到着の直前の未来に進むように、逆に後退系からは、奥の銀河は手前の銀河より ずっと過去が同時刻になる。それら銀河間の光速が遅いのではない。特殊相対論の光速は一定である。
こう考えれば普通の科学常識で使う、円形俯瞰図の周辺の初期宇宙の部分が逆に引き伸ばされていて、これは物差し縮小概念の正しい図示かもしれないが、 物差し一定の局所の誤解からは、ローレンツ短縮の逆の伸長である。ともあれ、膨張宇宙の果てにローレンツ短縮を考慮すれば、宇宙の大きさ、宇宙年齢などに再考が必要だろう。
そもそも宇宙は、膨張しているのか? まず、物差しと計量と不変量の関係、 (物差し)× (計量) = (不変量) は、物差しと計量との積和一定である。 正確には計量は、その時空点の物差し時計の-2乗表示である。物差し時計の変化を知らない局所は、縮小する近傍の物差しを一定と誤解し、 空間計量の増大を宇宙膨張とみて間隔の増大とみる。それは、膨張する累積距離を伝播する光がドップラー後退する意味で正しいが、 空間計量の増大は、物差しを含めた空間間隔、銀河間隔の縮小を伴う。それは、宇宙の膨張でなく縮小である。それでもドップラー後退するだろうか? ドップラー後退とは逆の青方偏移を招くかと思うが、それでも過去からの光は、縮小による後退によって赤方偏移するだろう。
元々、物差しは空間の代表、時計は時間の代表で、共に特別な選好なく、どの空間間隔も物差し、どの時間間隔も時計でありえるが、 物差しが何かは重要であり、膨張宇宙論は、質点運動として塵の漂う宇宙解を求めたものであり、物差しは質点の空間間隔以外ない。 積和一定からくる空間計量の増大=物差しの短縮の認識では、銀河間隔でさえ、物差し側でないか。
ゆえに、空間間隔と物差しを別物として、物差しが縮小すれば、天体の慣性によって間隔は変化せず、何もない空間が相対的に膨張するとして、 物差し縮小を空間膨張に整合させるよくある考え方は、物差しを空間間隔から分離し不当に特別扱いする。同じく、物差しは固体の原子、 空間はその間隔とする同様な考え方は、相対論の物差し時計の計量の原理よりも量子力学の不確定性を優先する誤りである。不確定性は、物差し時計の基礎の上にあると思う。
特殊相対論に物体と空間とに均一なローレンツ変換を認め、一般相対論には何もない空間だけを伸縮させる事には根拠がない。 相対論にいわゆる"空間の膨張"はない。特殊は座標変換だから力によらず、一般は重力による変形だからと何もない空間を伸縮させる。 相対論は、原理的に計量による質点系の変形や膨張を扱う物理概念であり、計量による新たな剛体概念だから、特殊も一般もともに、 変形は力による圧縮ではなく座標変換であり、物体と空の空間とは等しい比例的伸縮を基本にする。
このように相対論は、常識的な理解を排除し、頻繁に手近な誤解による俗論を生み、現在、正しく理解されていないと思う。 そのなか、膨張宇宙を信ずる化学に強いだけのSF作家アシモフでも、膨張宇宙の宇宙の果てのローレンツ短縮を明確にイメージしていた。 それは、宇宙の果てに速度なしに重力短縮した多くの銀河の重なりを想像するアインシュタインの定常宇宙解に類似する。 これには本編で述べたブラックホール地平面の外側の重力短縮とそこからみる伸長の関係が理解の助けになる。 但し、アシモフの宇宙膨張によるローレンツ短縮、奥行きの短縮よりも正しい膨張宇宙の認識は、3方向の空間縮小である。
SF 作家達の物理感覚が正しかった例: A. C. クラークは "宇宙のランデブー" のどれかの巻(2?)で、異星の船が太陽表面のスイングバイによって、 低い重力ポテンシャルの場所で加速して方向転換するとき、宇宙が回転するという驚異を表現した。一般相対論の測地線は、平坦な時空と同じ時空の 計量をもつことからみて、自身は回転せずに宇宙が回転するというのは、正しい認識である。力学でそれまで受容されなかった遠隔作用である万有引力 を導入して成功したニュートンの重力は、そこで絶対座標系を回転させたのである。
ブラックホールには、"2001年宇宙の旅"の最期の10分間のような別世界への抜け道のような、アインシュタイン・ローゼン橋がある (物理と現実)。彼は、これを素粒子論における中性粒子の存在と考えていた。 同様な重力と電気的特性の複合方程式の解は、最も単純には質量のない電気的粒子を導くという。