目次
A. 相対性の仮説への基本的考察
1. 特殊相対論への見解
2. 相対性の仮説の拡張の必要
3. 時空連続体、自然の一般法則を表現する方程式への一般共変性の要求
4. 時空の測定と4座標との関係
B. 一般共変方程式の定式化のための数学的準備
5. 反変と共変の4元ベクトル
6. 2階と高階のテンソル
7. テンソルの乗算
8. 基本テンソルのいくらかの側面
9. 測地線の方程式、粒子の運動
10. テンソルの微分による形成
11. 特に重要な幾つかの場合
12. Riemann-Christoffel テンソル
C. 重力場の理論
13. 重力場のなかの質点の運動方程式、重力の場-成分の表式
14. 物質のないときの重力の場の方程式
15. 重力場のハミルトン関数、運動量とエネルギーの法則
16. 重力の場の方程式の一般型
17. 一般の場合の保存の法則
18. 場の方程式の帰結としての物質の運動量とエネルギーの法則
D. 物質の現象
19. 摩擦なし断熱流体への Euler 方程式
20. 自由空間への Maxwell の電磁場方程式
E.
21. 1次近似としての Newton 理論
22. 静止重力場における棒と時計の振舞い、光線の曲り、惑星運動の近日点の移動
特殊相対論は、Galileo と Newton の力学によっても満足される次の仮説を基礎にしている。
もし、座標系 K がそれに相対して物理法則がその最も単純な形で成立するように選択されているならば、その同じ法則が K に相対的に均一な平行移動をする他のどの座標系 K' 系に関しても、また成立する。この仮説を "特殊相対性の原理" という。 "特殊" の言葉は、この原理が K' が K に相対的に均一な平行移動をする場合に限定され、K'と K の同等性は、K に対して不均一 運動する K' の場合には拡張しないことを暗黙に意味する。
このように、特殊相対論は、相対性の仮説を通しては、古典力学から離れない。しかし、真空中の光の速度の一定の仮説を 通しては、そこから、特殊相対性の原理と結合して、よく知られた方法で、同時刻の相対性、Lorentz 変換、運動物体と時計の行動 について関係する法則を導く。
特殊相対論が空間と時間の理論にもたらした修正は、実に広範に渡るが、ひとつの重要な点が影響を受けず残った。幾何学の法則は、 特殊相対論に従ってさえも、静止した固体の可能な相対的位置に関する法則であると直接に解釈されるべきである;そして より一般的な方法で、運動学の法則は、測定体と時計の関係を記述する法則と解釈されるべきである。静止した剛体のふたつの選択 した質点には、全く確定的な長さの距離が対応してつねに存在し、それは、その物体の場所と方向に独立であり、時間にも独立である。 ひとつの特権的な参照系に静止した時計の針のふたつの選択した位置には、確定的な長さの時間間隔が対応してつねに存在し、 場所と時間に独立である。我々はすぐに、一般相対性理論が時空のこの単純な物理的解釈に固執できないことを見るだろう。
古典力学のなかには、特殊相対論にも軽減なくある、生来の認識論的な欠陥が存在し、それは、多分最初に Ernst Mach によって明確に 指摘された。我々は、次の例によってそれを解明する:ー 同じ大きさと性質のふたつの流動体が空間に浮動して存在し、互いと他の質量 からの距離が大きくて、同じ物体の異なる部分の相互作用に起因するそれらの重力しか計算する必要がないほどとする。 ふたつの物体間の距離は不変とし、その物体のいずれのなかにもその部分の互いにいかなる相対運動もないとする。しかし、それぞれの 質量は、他方の質量に静止した観測者から判定して、両質量を結ぶ線の周りに一定の角速度で回転をしているとする。 これは、検証可能な 2 物体の相対運動である。 いま、各物体がそれ自身に対して静止した測定機器によって測定されたと想像し、S_1 の表面が球であり、S_2 は、回転楕円体であると証明された。 そこで我々は、問う。ふたつの物体のこの違いの理由は何か? 経験の観測可能な事実 の与える理由でない限り、認識論的に満足を 許され得る答えはない(*)。原因結果の法則は、観測事実が最終的に原因と結果として現れない限り、経験世界への言明の意味をもたない。
Newton 力学は、この問いに満足する答えを与えない。それは、次のようにいう:ー 力学諸法則は、物体 S_1 がそれに対して静止している 空間 R_1 には適用されるが、物体 S_2 がそれに対して静止している空間 R_2 には適用されない。しかし、このように導入された Galileo の特権的な空間 R_1 は、単に 人工的な 原因であり、観測され得ることではない。それゆえ、Newton の力学は、考察中の場合において、 原因結果の要求を現実に満足するのではなく、単に外見的にそうしていることが明らかである。なぜなら、物体 S_1 と S_2 との観測可能な 違いの原因として人工的な原因 R_1 を作りだすからである。
唯一の満足できる答えは、S_1 と S_2 とを含む物理的な系は、S_1 と S_2 との異なる行動が、それ自身のなかに、理由付けできる想像上 でない原因を明らかにするものでなければならない。原因は、それゆえ、この系の外になければならない。 我々は、それを、運動の一般法則にとり込まなくてはならない。特に S_1 と S_2 の形態を決定する運動法則は、S_1 と S_2 の力学的行動が 考慮の系に含まれていない遠方の質量によって、全く本質的な点において、部分的に条件づけられる、というようなものでなければならない。 これらの遠方の質量とその S_1 と S_2 に対する運動は、ふたつの物体 S_1 と S_2 との異なる行動の原因 (それらは観測によって検出できな ければならないが) のあり場所と考えなければならない。それらは、人工的な原因 R_1 の役割を引き継ぐ。それぞれに相対的ないかなる種類の 運動をする、全ての想像可能な空間 R_1, R_2 等々には、前述の認識論的な反論を生き返らすことなく、我々が特権的に 先験的 と みなしてよいものは存在しない。 物理諸法則は、それらがいかなる種類の参照系にも適用できるような、ある性質を持たなければならない。 この道にそって、我々は相対性の仮説の拡張に到達する。
この重要な議論に加え、知識の理論から、よく知られた物理的事実が存在して、相対性の理論の拡張を支持する。K を Galileo 参照系、 すなわち、その系に対して、(少なくとも考慮する 4 次元の領域において) 他の質量から十分離れた質量が、直線上を均一な運動をする系とする。 2 番目の系 K' を K に相対的に均一な加速の平行移動運動する系とする。そのとき、K' に対しては、他の質量から十分に離れた質量は、 その加速と加速の方向が物質の構成と質量の物理的状態とに依らないような加速運動をもつであろう。
このことは、K' に相対的に静止した観測者が、彼が "現実の" 加速参照系にいると推論することを許すだろうか? 答えは、否定的である; なぜなら、K' に対して自由に運動できる質量の前述の関係は、等しくよい、次の解釈ができるためである。K' は、加速されているのではなく、 その問題の時空領域が重力場の影響のもとにある。それが、K' に相対して物体の加速運動を発生する。
この見方は、全ての物体に同じ加速を与えるという、注目すべき特性をもつ(*) 力の場、すなわち重力場の存在についての経験を教えることによって 我々に可能になっている。K' に対する物体の力学的行動は、我々が "静止" 又は "特権的" とみなすことに慣れた系の場合の経験と全く同様に表れる。 それゆえ、物理的観点から K 系と K' 系とが両方とも "静止" と見られてよい等しい権利をもつ仮説を示唆し、それはいわば、それらが現象の 物理的記述のための参照系として等しい肩書をもつのである。
これらの熟考から、相対性の一般理論の追求によって、我々は、重力の理論へ導かれるのを見るだろう。なぜなら、我々は座標系を変更するだけで、 重力場を "造る" ことができるからである。また、"真空中の" 光速一定の原理も変更を受けなくてはならないことも、明らかである。なぜなら、 もし、K 系に関して光が確定的な一定の速度をもって直線的に伝播するならば、K' 系に関する光線の経路が一般に曲線でなければならないことを 我々は、容易に知るからである。
古典力学において、また、特殊相対論においても、空間座標と時間とは、直接の物理的意味をもっていた。 点事象が X_1 座標値 x_1 をもつというとき、それは、点事象の X_1 軸への投影が、剛体棒によって決定され、Euclid 幾何に従って、 座標の原点から X_1 軸に沿って、与えられた (単位長の) 棒の x_1 倍として測定されることを意味している。 点事象が X_4 座標 x_4 = t をもつということは、確定的な単位周期をもつ時間を測定するために作られた標準時計が、その点事象と空間的に 実際的に一致した位置に座標系に静止して存在し、その点事象(*)の発生が、x_4 = t 周期であると測定されることを意味している。
時空のこの見方は、物理学者が概して意識しなくとも、彼らの心中につねにある。このことは、これらの概念が物理測定に果たす役割から明らかである; それはまた、前章(§2)の読者の思考の下にも存在するに違いない。彼がそこで読んだものに何らかの意味を繋げるために。しかし、我々は、 それを脇に置き、もし、特殊相対論が重力場のないときに適用されるならば、一般相対性の仮説を実行するために、より一般的な見方に換えねば ならないことをいま示すだろう。
重力場のない空間のなかに、Galileo 参照系 K(x,y,z,t) とまた、K に相対して均一に回転する系 K'(x',y',z',t') を導入する。両系の原点だけでなく、 それらの Z 軸を永久に一致させる。我々は、K' 系のなかの時空の測定において、長さと時間の物理的意味の前述の定義が保持できないことを示そう。 対称性の理由から、明らかに、K の X, Y 平面のなかの原点を囲む円は、同時に、K' の X', Y' 平面の円ともみなせる。我々は、この円の円周と直径が 半径と比べて無限に小さい単位物差しによって測定され、ふたつの結果の商を得ていると仮定する。もしこの実験が、Galileo 系 K に相対的に静止した 測定棒によって実行されたならば、商は、πであろう。K'に相対的に静止した測定棒をもってすれば、商は、πよりも大きいであろう。 このことはもし、我々が "静止系" K から測定の全過程を描写し、周囲に適用される測定棒が Lorentz 短縮を被ること、そして半径に沿って適用される 棒にはそれがないことを考慮にいれるならすぐさま理解できるであろう。 こうして、Euclid 幾何学は、K' 系には適用されない。上で定義された座標値の注意、Euclid 幾何学の有効性の前もっての推測は、K' 系に関係しては 壊れている。同様にまた、K' に相対的に静止した時計によって示される K' 内の物理的要求に対応する時間の導入を行うことができない。 この不可能性を、我々自身が確信するために、同一構成のふたつの時計を想像し、ひとつを座標原点におき、もうひとつを円の円周に置く。そして、両者 を "静止系" K から心に描くことにしよう。特殊相対論の親しい結果によって、円周にある時計は、ーK から判定してー 他方よりもゆっくりと進む。 なぜなら、前者は運動し、後者は止っているからである。共通の原点にいる観測者は、光の手段によって円周の時計を観測することができるから、それが 彼の側にある時計よりも、遅れていくのをみるだろう。 彼は、問題の経路に沿った光の速度が時間に明示的に依存することに決心できず、彼は、彼の観測が円周の時計が "現実に" 原点の時計よりもゆっくり進む ことを示していると解釈するであろう。それで、彼は時間を定義するのに、時計の速度が時計ある場所に依存するような方法で定義せざるを得ないだろう。 我々はこの結果に到達する:ー 一般相対論の時空は、空間座標の差が直接に単位測定棒によって測定され、又は時間座標の差が標準時計によって測定され るようには定義できない。
時空連続体に確定した仕方で座標値を置く、これまで採用した方法は、このように崩壊した。そして、その適用から自然法則の特に単純な定式化を我々が 期待できるような、座標系を 4 次元宇宙に適用させる他の方法もないようである。そのため、全ての想像できる座標系は、原理的に、自然の記述のために 等しく適していると考える以外の方法はない。これは、次を要求するようになる:ー
自然の一般法則は、全ての座標系でよく成立する方程式、すなわち、いかなる置換に関しても共変的な方程式で表現されるべきである。(一般共変性)
この仮説を満たす物理理論は、又、一般相対性の仮説に適するだろうことは明らかである。なぜなら、"全ての" 置き換えの総和は、どの場合も 3 次元 座標系の全ての相対運動に対応するものを含んでいるからである。この一般共変性への要求は、物理的な客観的実在性の最後の残り火を時空から取り去り、 次の熟考から自然なものと見られるであろう。我々の全ての時空の検証は、常に結局は、時空の一致の決定によっている。もし例えば、単に質点運動だけ からなる事象であれば、究極的にはふたつ又はそれ以上の質点の会合以外に観測可能なものはないであろう。さらには、我々の測定の結果は、我々の測定 機器のそれら質点の他の質点との会合、時計の針と時計の目盛の点との、観測される点事象の同場所、同時刻の発生との一致の検証に外ならない。
参照系の導入は、そのような一致の全体性の記述を容易にする以外の何の目的をも助けない。我々は、全ての点事象に対応する変数 x_1 .. x_4 の値の系 があるような方法によって、宇宙に 4 時空変数、x_1, x_2, x_3, x_4 を割り当てる。ふたつの一致する点事象には、ひとつの変数 x_1 .. x_4 の値の系 が対応して存在する。すなわち、一致は、座標値の同一に特徴づけられる。もし、変数 x_1 .. x_4 の代わりに、新しい座標系として、それらの関数 x'_1 .. x'_4 を導入して、値の系がひとつひとつ、あいまいさなく対応をなして、新しい系の全ての 4 座標の等しさが、また、ふたつの点事象の時空一致の 表現として役立つであろうようにするのである。全ての我々の物理的表現は、究極的には、そのような一致に還元でき、ある座標系を他よりも特別にする 直接の理由はないから、それはいわば、我々は、一般共変性の要求に到達したのである。
この議論のなかでは、一般相対論を最小数の公理をもつ、可能なかぎり単純で論理的な系として示すことが目的ではない;私の主要な目的は、読者が我々 の入り込む道筋を心理的に自然であって、下に横たわる仮定は、可能なかぎり高い安全性をもつように見えると感じるような方法で、この理論の開発を行 うことである。見方にこの目的をもって、いま、次のことが認められる:ー
無限に小さな 4 次元領域において、もし、座標系が適切に選ばれるならば、制限された意味の相対性の理論が適切である、
この目的のために我々は、重力場が発生しないように、無限小の("局所")座標系の加速を選択せねばならない;これは、無限小の領域では可能である。 X_1, X_2, X_3 を空間座標、X_4 を適切な単位で測定される(*) 時間に属する座標とする。もし、剛体が単位尺度として与えられると想像すれば、 与えられた座標系の原点とともに座標値は、特殊相対論の意味で直接の物理的意味をもつ。特殊相対論によって、表式、
ds^2 = - dX_1^2 - dX_2^2 - dX_3^2 + dX_4^2 .............................(1)
は、局所座標系の原点に依らない値をもち、空間と時間の測定によって確認できる。無限近傍の 4 次元連続体の点に属する線形要素の大きさを我々は、 ds と呼ぶ。もし、dX_1, .. dX_4 に属する ds^2 (**)が正なら、我々は、Minkowski に習って時間性(time-like)と呼び;もしそれが負なら、それを空間性 (space-like)と呼ぶ。
問題の"線形要素"、又は無限近傍のふたつの点事象には、任意に選択した参照系の 4 次元座標の確定した微分 dx_1 ... dx_4 がまた対応する。もし、 この系だけでなく "局所" 系を考慮する領域に与えるなら、dX_ν は、ここで確定した線形斉次の dx_σ の表式によって表わすことができる:ー
dX_ν = Σ_σ α_νσ dx_σ ...................................(2)
これらの表式を(1)に挿入して、我々は、次を得る。
ds^2 = Σ_τσ g_στ dx_σ dx_τ ..................................(3)
ここで、g_στは、x_σの関数であろう。これらは、もはや、"局所" 座標系の原点と運動状態とに依らない。なぜなら、ds^2 は、時空の無限近傍の 点事象の棒時計測定によって確認できる量であり、どの特定の座標系の選択にも独立であると定義されるからである。g_στ は、ここで g_στ = g_τσ であるように選択されている; 総和は、全てのσとτに渡る 4×4 の項からなり、その内の 12 個が対で等しい。
有限の領域の g_στ の特定の関係を理由として、g_στ に次の一定値を仮定するような方法で、有限領域の参照系を選択することが可能ならば、 通常の相対論の場合がここで考慮する場合から出て来る。
-1 0 0 0
0 -1 0 0 ..............................................(4)
0 0 -1 0
0 0 0 1
我々は今後、そのような座標系の選択が一般に有限領域に可能でないことを見出す。
§2 と§3 の考察から、量 g_στ は、物理的観点から、座標系選択と関係して、重力場を記述する量とみなすべきことが出てくる。なぜなら、我々がいま、 もし、ある 4 次元領域に座標の適切な選択を伴って特殊相対論が適用することを仮定するなら、そのとき g_στ は、(4) に与える値をもつからである。 そのとき、自由質点は、この系に対して、直線上を均一な運動をする。そのときもし、我々が新しい時空座標値、x_1, x_2, x_3, x_4 を我々が選ぶ任意の 置き換えによって導入するならば、新しい系のなかの g_στ は、もはや定数でなく、時空の関数となる。同時に自由質点の運動は、新しい座標系のなかで 曲線の不均一運動として表れるだろうし、そして、この運動の法則は、動く粒子の性質に依らないであろう。それゆえ、我々は、この運動を重力場の影響の 下の運動として解釈するに違いない。我々は、こうして、g_στの時空変数と結合した重力場の発生を見出すのである。それゆえまた、一般の場合、有限の 領域に特殊相対論の適用をための適切な座標系の選択がもはやできないとき、g_στ が重力場を記述するという見方をまずもつのである。
こうして、一般相対論に従う重力は、他の諸力、特に電磁気的な力から比較して例外的な位置を占める。なぜなら、重力場を表す 10 の関数が同時に測定 された空間の計量的な特性を定義するからである。
前述の、一般相対性の仮説が、物理の方程式が座標 x_1 .. x_4 のどのような置き換えにも関わらず共変でなければならないという要求に導く ことを見て、我々は、どのようにして、そのような一般に共変な方程式を見出せるか、を考察しなければならない。我々はいま、この純粋に 数学的な仕事に方向を変え、その解のなかに式(3) によって与えられた不変量 ds によって果たされる基本的な役割を見出す。それは、Gauss の表面の理論から借りてきたもので、我々が "線形要素" と呼んだものである。
この共変性の一般理論の基本的な概念は、次のようなものである:ー任意の座標系に関して、テンソルの "成分" と呼ばれる座標値の幾つかの 関数によって、あるもの("テンソル")を定義しよう。そのとき、もし、それらが元の座標系で既知であり、ふたつの系の間の変換の関係が知ら れていれば、ある規則が存在し、それによってこれら成分が新しい座標系のために計算できる。以降、テンソルと呼ばれる、そのものは、その 成分の変換の方程式が線形で斉次である事実によってさらに特徴付けられる。従って、もし、元の系でそれらが消滅していれば(0 ならば)、 新しい系においても全ての成分が消滅する(0である)。それゆえもし、自然法則がテンソルの全成分が 0 に等しいことによって表されるならば、 それは、一般に共変である。テンソルの変形の法則を検証することによって、我々は、一般共変法則を定式化する意味を獲得する。
反変 4 元ベクトルー 線形要素を定義する 4 成分 dx_ν の変換法則は、次式で表される。
dx'_σ = Σ_ν ∂x'_σ/∂x_ν dx_ν ...............................(5)
dx'_σ は、dx_ν の線形斉次関数として表される。それゆえ、これらの座標微分は、反変 4 元ベクトルという特定の種類の "テンソル" の成分 とみてよい。4 つの量によって座標系に相対的に定義される A^ν であって、同じ法則で変換されるものは、いずれも反変 4 元ベクトルという。
A'^σ = Σ_ν ∂x'_σ/∂x_ν A^ν ...............................(5a)
(5a) からすぐに次がいえる。A^σとB^σがそうなら、和 A^σ±B^σ もまた 4 元ベクトルの成分である。対応する関係は、全ての "テンソル" に成立する。(テンソルの和差の規則)
共変 4 元ベクトルー任意に選ぶ反変 4 元ベクトル B^ν に対し次が成立する、4 つの量 A_νを共変 4 元ベクトルの成分という。
Σ_ν A_ν B^ν = Invariant ......................................(6)
この定義から、共変 4 元ベクトルの変換法則がもたらされる。なぜなら、もし、我々が次式の右辺の B^ν を
Σ_σ A'_σ B'^σ = Σ_ν A_ν B^ν
(5a) の逆転によって得る次式によって置き換えるなら、
Σ_σ ∂x_ν/∂x'_σ B'^σ
我々は、次式を得る。
Σ_σ B'^σ Σ_ν ∂x_ν/∂x'_σ A_ν = Σ_σ B'^σ A'_σ
一方、この式は、B'^σ の任意の値について真であるから、次の変換法則がいえる。
A'_σ = Σ_ν ∂x_ν/∂x'_σ A_ν ...............................(7)
表式の書き方の単純化された方法についての注意
この章の式を一見すると、総和の記号の下に 2 度現れる添字について総和がいつもあることが分かる。(例、式(5)の添字ν) そして、それは、 2 度現れる添字についてだけである。そのため、明快さを失うことなく、総和の記号の省略が可能である。そこに我々は慣習を導入する:ー 表式の一項に同じ添字が 2 度現れるとき、例外を明示しない限り、それは、つねに総和がとられる。
共変と反変の 4 元ベクトルの違いは、変換の法則にある(それぞれ (7) と (5))。両方の形式は、前述の一般的な見解の意味において、テンソルである。 そのなかにそれらの重要性がある。 Ricci と Levi-Civita に従って、我々は、反変の性質を添字を上に置いて示し、共変はそれを下に置いて表示する。
反変テンソルーもし、我々が、ふたつの反変 4 元ベクトルの成分 A^μ, B^νの 全ての 16 の積、A^μν を形成するとき、
A^μν = A^μ B^ν ..............................(8)
そのとき、(8) と (5a) によって、A^μν は、次の変換法則を満たす。
A'^στ = ∂x'_σ/∂x_μ ∂x'_τ/∂x_ν A^μν .......................(9)
我々は、どの座標系に対しても 16 の量によって記述され、変換法則 (9) を満たすものを2階の反変テンソルという。そのようなテンソル全てが ふたつの 4 元ベクトルから (8) によって、形成されたとするわけではない。しかし、任意に与える 16 の A^μνが 4 つの適切に選ばれた 4 元 ベクトル対の成分の A^μ B^ν の総和として表されることは容易に示すことができる。それゆえ、我々は (9) で定義される2階のテンソルに適用 されるほとんど全ての法則を、(8) の型の特別なテンソルのためにそれらを明示することによって、最も単純な仕方で証明することができる。
任意階数の反変テンソルー(8) と (9) の線に沿って、3階とそれ以上の階数の反変テンソルもまた、4^3 成分をもって、など定義される。 同じ方法で (8), (9) から、反変 4 元ベクトルは、この意味で1階のテンソルとすることができることが出てくる。
共変テンソルー 一方もし我々が、ふたつの共変 4 元ベクトル A_μ と B_ν の 16 の積 A_μν を、
A_μν = A_μ B_ν ..............................(10)
これらの変換の法則は、
A'_στ = ∂x_μ/∂x'_σ ∂x_ν/∂x'_τ A_μν .......................(11)
この変換の法則は、2階の共変テンソルを定義する。我々が以前に反変テンソルのためにの全ての注意は、共変テンソルにも等しく適用される。
注意、ー スカラー(不変量) を0階の反変又は共変テンソルとして扱うことは便利である。
混合テンソルー 我々は、次の型の2階のテンソルを定義してよい。
A^ν_μ = A_μ B^ν ..............................(12)
これは、添字μについては共変で、添字νについては反変である。その変換則は、
A'^τ_σ = ∂'x_τ/∂x_ν ∂x_μ/∂x'_σ A^ν_μ .......................(13)
当然、任意数の共変性質の添字をもち、任意数の反変性質の添字をもつ混合テンソルが存在する。 共変と反変のテンソルは、混合テンソルの特別な場合と見なすことができる。
対称テンソルー 反変又は共変の2階以上のテンソルで、ふたつの添字の交換によって、一方から他方が得られて等しい場合に対称という。 テンソル A^μν 又は A_μνは、μ,νのどの組合せにも次であるとき、対称である。
A^μν = A^νμ ..............................(14)
又は対応して、
A_μν = A_νμ ..............................(14a)
このように定義された対称性が参照系に独立であることは、証明する必要がある。実際、(9)から、(14)を考慮するとき、次がでる。
A'^στ = ∂x'_σ/∂x_μ ∂x'_τ/∂x_ν A^μν = ∂x'_σ/∂x_μ ∂x'_τ/∂x_ν A^νμ = ∂x'_σ/∂x_ν ∂x'_τ/∂x_μ A^μν = A'^τσ
最後のひとつ前の等式は、総和の添字μとνの入れ換えによる、すなわち、記号の変化だけである。
反対称テンソルー 反変又は共変の2,3,4階のテンソルで、ふたつの添字の交換によって、一方から他方が得られて反対符号で等しい場合 に反対称という。それゆえ、テンソル A^μν 又は A_μνは、次のとき反対称である。
A^μν = - A^νμ ..............................(15)
又は対応して、
A_μν = - A_νμ ..............................(15a)
16 の成分 A^μν のうち、4 成分 A^μμ は消え;残りは対をなし、反対符号で等しく、6 成分だけが数学的に異なる(6 元ベクトル)。 同様に、3階の反対称テンソル A^μνσ は、4 つだけの数学的に異なる成分をもち、A^μνστ は、唯一つである。 4 次元連続体には 4 階を超える階数の反対称テンソルはない。
テンソルの直積 ー我々は、階数 n のテンソルと階数 m のテンソルの成分から、階数 n+m のテンソルの成分を得る。ひとつの テンソルの各成分と他の各成分を乗算することによって。このように、例えば、異なる種類のテンソル A, B からテンソル T が生起する。
T_μνσ = A_μν B_σ,
T^μνστ = A^μν B^στ,
T_μν^στ = A_μν B^στ.
T のテンソル性質の証明は、(8), (10), (12) の表現によって、又は、(9), (11), (13) の変換の法則によって、直接に与えられる。 (8), (10), (12) の式は、それら自身、1階のテンソルの直積の例である。
混合テンソルの縮約 ーどの混合テンソルからも、我々は、その階数が 2 だけ少ないテンソルを作ることができる。共変の添字 を反変の添字に等しくして、この添字に関して総和をとることによって("縮約")。こうして、例えば、4階の混合テンソル A^στ_μν から、我々は、次の2階の混合テンソルを得て、
A^τ_ν = A^μν_μτ (= Σ_μ A^μν_μτ)
そして、これから、2 番目の縮約により、次の0階のテンソルを得る。
A = A^μ_μ = A^μν_μν
縮約の結果が現実にテンソルの性質をもつことの証明は、(6)と関連して (12)の一般化によるテンソルの表現によって、又は、(13)の一般化 によって与えられる。
テンソルの内積と混合積 ーこれらは、直積と縮約の結合にある。
例 ー2階の共変テンソル A_μν と1階の反変テンソル B^σ から、我々は直積によって次の混合テンソルを形成する。
D^σ_μν = A_μν B^σ
添字νとσに関する縮約によって、我々は、次の共変 4 元ベクトルを得る。
D_μ = D^ν_μν = A_μν B^ν
これを我々は、テンソル A_μνと B^σ の内積という。同様に、テンソル A_μνと B^στ から、外積と2回の縮約によって A_μν B^μν を形成する。直積と1回の縮約によって我々は、A_μν と B^στ から2階の混合テンソル D^τ_μ = A_μν B^ντ を得る。この操作は、 混合であると適切に特徴づけ得る。添字μとτに関しては "外的" であり、添字νとσに関しては "内的" である。
我々は、いま、テンソル特性の証拠としてしばしば役に立つ定理を証明する。先ほど説明したことから、A_μν と B^στ がテンソルならば、 A_μν B^μν は、スカラーである。しかし、我々はまた次の仮定を立ててよい: どう テンソル B^μν を選んでも、 A_μν B^μν がスカラーであるなら、そのとき、A_μνは、テンソルの性質をもつ。なぜなら、仮定によって、どの置き換えにおいても、
A'_στ B'^στ= A_μν B^ν
しかし、(9)の逆転によって、
B^μν = ∂x_μ/∂x'_σ ∂x_ν/∂x'_τ B'^στ
これを上の式に代入して、次を得る。
(A'_στ - ∂x_μ/∂x'_σ ∂x_ν/∂x'_τ A_μν) B'^στ = 0
これが任意の B'^στ において成立するのは、括弧内が消滅する(0 になる)ときだけである。結果は、そのとき、式(11)を導く。 この規則は、どの階数どの性質のテンソルにも適用でき、その証明は全ての場合、同様である。
その規則はまた、次の形式において力を示すことができる: B^μと C^ν がどのベクトルであっても、これらの全ての値において、 内積 A_μν B^μ C^ν がスカラーであるなら、A_μν は共変テンソルである。後者の定理は、また、さらに特別な次の仮定が正 しいときでさえ、よく成立する。どの 4 元ベクトル B^μ においても内積 A_μν B^μ B^ν がスカラーであって、もしさらに、 A_μνが対称の条件 A_μν=A_νμ をみたすと知られているなら。 なぜなら、上に与えられた方法によって、我々は (A_μν + A_νμ) のテンソル特性を証明し、そして、これから、A_μν のテンソル特性が対称性を引き継ぐからである。これもまた、容易に一般化でき、共変と反変のテンソルのどの階数にも適用できる。
最終的に、すでに証明されたことから、どのテンソルにも一般化できる次の法則が出る:もし、任意に選択された 4 元ベクトル B^μ において、量 A_μν B^ν が1階のテンソルをなすならば、そのとき、A_μν は2階のテンソルである。なぜなら、もし、C^μが 任意の 4 元ベクトルならば、そのとき、A_μν B^ν のテンソル特性のために、ふたつの 4 元ベクトル B^ν と C^μ の選択に依らず、 内積 A_μν B^ν C^μ がスカラーであるからである。それから、定理は出る。
共変基本テンソル ー 線形要素の 2 乗の不変式、
ds^2= g_μν dx_μ dx_ν
のなかで dx_μ は、任意に選べる反変ベクトルの役割を果たす。一方、さらに、g_μν = g_νμ であり、前章の考察から、g_μνが 2階の共変テンソルとわかる。我々は、それを "基本テンソル" という。以下に、我々はこのテンソルのいくらかの性質を導くが、 それは、実際、どの2階テンソルにも適用できる。しかしこれは、基本テンソルとして、我々の理論のなかで特別な役割を果たし、 重力に固有な性質の物理的な基礎をもつので、開発される関係式が我々に重要なのは、基本テンソルの場合だけのようなことが起きる。
反変基本テンソル ー 我々は、行列要素 g_μνによって行列式を作り、各 g_μνの小行列を行列式 g = | g_μν |で割ってある量、g^μν(= g^νμ) を得る。 我々が示すように、それは反変テンソルをなす。
行列式の知られた性質から、
g_μν g^μν = δ^ν_μ ...............................(16)
ここで、δ^ν_μ は、ν=μ 又は、ν≠μ に従って、1 又は 0 。
ds^2 の上の式の代わりに、次のように書くことができ、
g_μσ δ^σ_μ dx_μ dx_ν
又は、(16) によって、
g_μσ g_ντ g^στ dx_μ dx_ν
しかし、前章の乗算則から、次の量は、
dξ_σ = g_μσ dx_μ
共変の 4 元ベクトルを形成し、そして実際、任意のベクトルである。なぜなら、dx_μが任意であるから。 これを我々の式に代入して、次を得る。
ds^2= g^στ dξ_σ dξ_τ
一方、これは、ベクトル dξ_σの任意の選択においてもスカラーであり、そして、 g^στ はその定義からσとτに対称であるから、 前章の結果に従って、 g^στ は、反変テンソルである。
さらに、(16)から、δ^ν_μ は、またテンソルであり、我々は、混合基本テンソルと呼ぶ。
基本テンソルの行列式 ー 行列式の乗算への規則から、
|g_μα g^αν| = |g_μα|×| g^αν|
一方、
|g_μα g^αν| = |δ^ν_μ| = 1
それゆえ、
|g_μν|×|g^μν| = 1 ..........................(17)
体積スカラー ー 我々はまず、行列式 g= |g_μν| の変換法則を求める。(11)によって、
g' = |∂x_μ/∂x'_σ ∂x_ν/∂x'_τ g_μν|
このゆえ、行列式の乗算の規則を2回応用して、次が出る。
g' = |∂x_μ/∂x'_σ|・| ∂x_ν/∂x'_τ|・| g_μν| = |∂x_μ/∂x'_σ|^2 g
又は、
√g' = |∂x_μ/∂x'_σ| √g
一方、体積要素の変換法則、
dτ= ∫ dx_1 dx_2 dx_3 dx_4
は、Jacobi の定理に従って、
dτ'= |∂x'_σ/∂x_μ| dτ
最後の 2 式を乗算すると、次を得る。
√g' dτ'= √g dτ ...........................(18)
√g の代わりに、我々は、これ以降、√-g という量を導入する。それは、時空連続体の双曲線的な特性のためにつねに実数である。 不変量である √-g dτ は、"局所" 参照系において、特殊相対論の意味の剛体棒と時計をもって測定された、体積(間隔?)の 4 次元 要素の大きさに等しい。
時空連続体の性質についての注意 ー 特殊相対論がつねに無限小領域において適用できる、という我々の仮定は、ds^2 が実数 の量 dX_1, dX_2, dX_3, dX_4 による式 (1) に従って表現できる、ということを意味する。もし、我々が dτ_0 を体積 dX_1, dX_2, dX_3, dX_4 の "自然な" 要素とするとき、そのときは、
dτ_0 = √-g dτ ............................(18a)
もし、√-g が4次元連続体のある点で 0 に消滅するなら、それは、無限小の "自然な" 体積が座標値のなかで有限の体積に対応する だろうということを意味する。我々は、これが決して起きないことを仮定しよう。そのとき、g は符号を変えることができない。 我々は、次を仮定するだろう。特殊相対論の意味において、g はつねに有限の負の値をもつことを。これは、考慮中の連続体の物理的 性質についての仮説であり、同時に座標系の選択についての約束である。
しかしもし、-g がつねに有限な正値であるなら、この量がつねに1に等しいという、後験的 な座標系選択を設置するのが自然である。 我々は後に、そのような座標選択の制限によって、自然法則の重要な単純化を達成することが可能であることを見る。
(18)の代わりに、我々は、そのとき単純に dτ' = dτ とし、それから、Jacobi の定理の見方のなかで、次のことがでる。
|∂x'_σ/∂x_μ| = 1 .........................(19)
このように、座標の選択において、行列式を 1 にする置き換えだけにするのは、許容される。
しかし、このステップが一般相対性の仮説の部分的な放棄を示すと信じるのは、誤りであろう。我々は、 "全ての置き換えがあるにも関わらず、 共変的なものを行列式を 1 にする自然法則は何か?" とは尋ねない。そうではなく、我々の問は、 "一般共変的な自然法則は何か?" である。 特定の座標系の選択によって、これらの表式を単純化するのは、我々がこれらを定式化してからにする。
基本テンソルによる新しいテンソルの形成 ー 外的、内的、そして混合のテンソルの基本テンソルによる乗算は、異なる性質と階数のテンソルを与える。例として、
A^μ = g^μσ A_σ,
A = g_μν A^μν
次の式は、特別に注意してよい:ー
A^μν = g^μα g^νβ A_αβ,
A_μν = g_μα g_νβ A^αβ
(共変、反変テンソルそれぞれににおいて、"共役的"である。) そして、
B_μν = g_μν g^αβ A_αβ
我々は、B_μνを、A_μνに付随する還元テンソルという。同様に、
B^μν = g^μν g_αβ A^αβ
g^μνは、g_μνの共役に外ならないことは、注意してよいだろう。なぜなら、
g^μα g^νβ g_αβ = g^μα δ^ν_α = g^μν
線形要素 ds は、座標系に独立に定義されたので、4次元連続体のふたつの点 P と P' の間に∫ds が停留に引かれた線ー測地線ー も座標の選択に独立であるという意味をもつ。その方程式は、
δ∫_P^P'ds= 0 ...............................(20)
通常の方法で変分を実行して、我々はこの方程式から、測地線を定義する 4 つの微分方程式を得る; 完全さのためにこの操作を ここで挿入しよう。λを座標 x_ν の関数とし、これが求める測地線だけでなく、点 P と P' を通して描かれた全ての直近接する 線に交差する表面の属を定義するとする。そのような線のどれもその座標 x_ν をλの関数として表現することによって与えられる と仮定することができる。記号δを求める測地線の点から隣接する線上の同じλに対応する点への移動を示すとする。そのとき、 我々は、(20) を次式で置き換えることができ、
∫_λ_1^λ_2 δw dλ = 0
w^2 = g_μν dx_μ/dλ dx_ν/dλ ........................(20a)
しかし、一方、
δw = 1/w { 1/2 ∂g_μν/∂x_σ dx_μ/dλ dx_ν/dλ δx_σ + g_μν dx_μ/dλ δ(dx_ν/dλ) }
と
δ(dx_ν/dλ)= d/dλ (δx_ν)
(20a) から部分積分によって次を得る。
∫_λ_1^λ_2 κ_σ δx_σ dλ = 0
ここで、
κ_σ = d/dλ { g_μν/w dx_μ/dλ } - 1/2w ∂g_μν/∂x_σ dx_μ/dλ dx_ν/dλ ..................(20b)
δx_σ の値は任意であるから、次が測地線の式である。
κ_σ = 0 .................................(20c)
もし、ds が測地線に沿って 0 でないなら、パラメタλには測地線に沿って測定される "弧の長さ" として s を選ぶことができる。 そのとき、w = 1 であり、(20c) の代わりに我々は次を得る。
g_μν d^2x_μ/ds^2 + ∂g_μν/∂x_σ dx_σ/ds dx_μ/ds -1/2 ∂g_μν/∂x_σ dx_μ/ds dx_ν/ds = 0
又は、単に記述法を変え、
g_ασ d^2x_α/ds^2 + [μν, σ] dx_μ/ds dx_ν/ds = 0 ...........................(20d)
ここで、Christoffel に従って我々は、次のように書いた。
[μν, σ]= 1/2 (∂g_μσ/∂x_ν + ∂g_νσ/∂x_μ - ∂g_νμ/∂x_σ) ........................(21)
最後に、(20d)に g^στ を乗算し(τに関し直積、σに関し内的)、次の形式の測地線方程式を得る。
d^2x_τ/ds^2 + {μν, τ} dx_μ/ds dx_ν/ds = 0 ...........................(22)
ここで、Christoffel に従って我々は、次のようにした。
{μν, τ} = g^τα [μν, α] ........................(23)
測地線の方程式の助けをもって、我々はいま容易に、微分によって新しいテンソルを古いものから形成する法則を導くことができる。 この手段によって我々は初めて共変微分方程式を一般的に定式化できる。我々は、次の単純な法則を繰返し適用することで、この目標に到達する:ー
もし、我々の連続体に曲線が与えられ、その上の点が曲線上の固定点から測定された弧の距離 s によって指定できるなら、そしてもしさらに、 φを空間に不変な関数とするなら、dφ/ds もまた不変量である。この証明は、dφだけでなく ds も不変量であることにある。
dφ/ds= ∂φ/∂x_μ dx_μ/ds
とするなら、
ψ= ∂φ/∂x_μ dx_μ/ds
も不変量である。連続体のある点から始まる全ての曲線に不変量であることは、つまり、任意のベクトル dx_μ についてである。 これからすぐにでる、
A_μ = ∂φ/∂x_μ ............................(24)
は、共変 4 元ベクトル、φの "勾配" である。
我々の規則に従って、曲線上にとった微分の商、
χ= dψ/ds
は、やはり不変量である。ψの値を代入し、我々は第1段階として次を得る。
χ= ∂^2φ/∂x_μ∂x_ν dx_μ/ds dx_ν/ds + ∂φ/∂x_μ d^2x_μ/ds^2
これから、すぐさま、テンソルの存在が導けるわけではない。しかしもし我々が、それに沿って微分をされた曲線を測地線としてよいなら、 我々は、(22)から d^2x_ν/ds^2 を置き換えて、次を得る。
χ= (∂^2φ/∂x_μ∂x_ν - {μν, τ} ∂φ/∂x_τ) dx_μ/ds dx_ν/ds
一方、我々は微分の順序を変更してよく、そして (23), (21) によって、{μν, τ}は、μとνに対称だから、括弧の中の式は、μとνに対称である。 一方、連続体の点から全ての方向に測地線が引け、そのため、dx_μ/ds がその成分比が任意な4元ベクトルであるから、§ 7 の結果から、
A_μν= ∂^2φ/∂x_μ∂x_ν - {μν, τ} ∂φ/∂x_τ .............................(25)
は、2階の共変テンソルである。我々は、それゆえ、この結果に来た:1階の共変テンソルから、
A_μ = ∂φ/∂x_μ
微分によって2階の共変テンソルを形成することができる。
A_μν= ∂A_μ/∂x_ν - {μν, τ} A_τ .............................(26)
テンソル A_μν は、テンソル A_μ の "拡張" (共変微分) という。 第1段階として、ベクトル A_μ が勾配として表せない場合でさえ、操作がテンソルを導くことをすぐに示すことができる。 これを見るには、まず、もし、ψとφがスカラーなら、次が共変ベクトルであることを観る。
ψ ∂φ/∂x_μ
もし、ψ^(1), φ^(1).. ψ^(4), φ^(4) がスカラーなら、次の 4 項の和は、また共変ベクトルである。
S_μ= ψ^(1) ∂φ^(1)/∂x_μ +..+ ψ^(4) ∂φ^(4)/∂x_μ,
しかし、どの共変ベクトルも S_μ の形に表現できることは明らかである。なぜなら、もし、A_μ がベクトルでその成分が x_ν の 任意に与える関数なら、S_μ が A_μ に等しいことを確認するには、次のように置くだけでよいから (選択した座標系の観点から)。
ψ^(1) = A_1, φ^(1)= x_1,
ψ^(2) = A_2, φ^(2)= x_2,
ψ^(3) = A_3, φ^(3)= x_3,
ψ^(4) = A_4, φ^(4)= x_4,
それゆえ、A_μの右辺にどの共変ベクトルが代入されても A_μν がテンソルを示すには、ベクトル S_μでそうなることを示す必要 があるだけである。しかし、この後者の目的には、次の場合に (26) の右辺が証明をもつことを我々に教えることを一瞥するだけで 十分である。
A_μ= ψ ∂φ/∂x_μ
いま、(25)の右辺にψを乗算した、
ψ ∂^2φ/∂x_μ∂x_ν - {μν, τ}ψ ∂φ/∂x_τ
は、テンソルである。同様に、
∂ψ/∂x_μ ∂φ/∂x_ν
は、ふたつのベクトルの直積であるから、テンソル。両者の加算によって、次のテンソル性がでる。
∂/∂x_μ(ψ ∂φ/∂x_ν) - {μν, τ}(ψ ∂φ/∂x_τ)
(26)の一瞥は、これが次のベクトルについての証明を完了させることを示すだろう。
ψ ∂φ/∂x_μ
そして、それゆえ、すでに証明したことから、任意のベクトル A_μ についても。
ベクトルの拡張の手段によって、どの階数の共変テンソルの "拡張" も容易に定義できる。この操作は、ベクトルの拡張の一般化である。 我々は、2階のテンソルの場合に自ら制限する。なぜなら、これが形成の法則の明確なアイデアを与えるのに十分だからである。
すでに見たように、どの2階の共変テンソルも A_μB_ν の型のテンソルの和として表現できる(*)。それゆえ、この特別な型のテンソルの拡張 について表現するだけで十分である。(26) によって次の 2 式、
∂A_μ/∂x_σ - {σμ, τ} A_τ
∂B_ν/∂x_σ - {σν, τ} B_τ
は、テンソルである。第1式に B_νを、第2式に A_μを直積して、我々はそれぞれに3階のテンソルを得る。これらを加算して3階のテンソル、
A_μνσ= ∂A_μν/∂x_σ - {σμ, τ} A_τν - {σν, τ} A_μτ .............................(27)
ここで、我々は、A_μν= A_μB_ν と置く。(27) の右辺は、A_μν とその1次微分のなかで線形斉次であるから、このテンソルを導く形成の 法則は、A_μB_ν という型の場合においてだけでなく、それらのテンソルの総和の場合もまた成立し、すなわち、どの2階の共変テンソルにも 成立する。我々は、A_μνσ をテンソル A_μν の拡張と呼ぶ。
(26) と (24) が拡張の特別な場合(それぞれ1階と0階)の拡張に関係することは、明らかである。
一般に、テンソルの形成の全ての特別な法則は、テンソルの乗算と関連して、(27) に包含されている。
A_11, A_12, A_13, A_14,
0, 0, 0, 0,
0, 0, 0, 0,
0, 0, 0, 0,
基本テンソル ー 我々は、今後、役立つであろう幾つかの系を最初に証明しよう。行列式の微分への規則によって、
dg= g^μν g dg_μν= - g_μν g dg^μν ..........................(28)
最後の項は、最後の前の項から、g_μν g^μ'ν= δ_μ^μ' ゆえに、g_μν g^μν= 4 そして、それゆえ、
g_μν dg^μν + g^μν dg_μν = 0
を心に抱けば、得られる。
(28) から、次を得る。
1/√-g ∂√-g/∂x_σ= 1/2 ∂log(-g)/∂x_σ= 1/2 g^μν ∂g_μν/∂x_σ= - 1/2 g_μν ∂g^μν/∂x_σ ...(29)
(訳注) 元の(29)最右辺には負号がなかったが誤植と解釈し訂正した。
さらに、g_μσ g^νσ = δ_μ^ν から、微分の次の式がでる。
g_μσ dg^νσ= -g^νσ dg_μσ
g_μσ ∂g^νσ/∂x_λ= -g^νσ ∂g_μσ/∂x_λ ..........................(30)
これらから、それぞれ g^στ と g_νλ の混合乗算と添字の記述を変えて、次を得る。
dg^μν= - g^μα g^νβ dg_αβ
∂g^μν/∂x_σ= - g^μα g^νβ ∂g_αβ/∂x_σ ..........................(31)
と
dg_μν= - g_μα g_νβ dg^αβ
∂g_μν/∂x_σ= - g_μα g_νβ ∂g^αβ/∂x_σ ..........................(32)
(31)の関係式は、変換を許し、我々はそれを頻繁に使う。(21)から、
∂g_αβ/∂x_σ= [ασ, β] + [βσ, α] ..........................(33)
これを (31) の第2式に挿入して、(23) の視点を使えば、
∂g^μν/∂x_σ= - g^μτ{τσ, ν} - g^ντ {τσ, μ} ..........................(34)
(34) の右辺を (29) に代入して、次を得る。
1/√-g ∂√-g/∂x_σ= {μσ, μ} ................................(29a)
反変ベクトルの発散 ー (26) と反変基本テンソル g^μν との内積を取れば、右辺は、初項を変換後、次の式になり、
∂/∂x_ν(g^μν A_μ) - A_μ ∂g^μν/∂x_ν -1/2 g^τα ( ∂g^μα/∂x_ν + ∂g^να/∂x_μ - ∂g^μν/∂x_α) g^μν A_τ
(31),(29) に従って式の最終項は次のように書ける。
1/2 ∂g^τν/∂x_ν A_τ + 1/2 ∂g^τμ/∂x_μ A_τ + 1/√-g ∂√-g/∂x_α g^μν A_τ
総和の添字の記号は実体のないものであるから、この式の最初の2項は、上の式の第2項とキャンセルする。 そのとき、もし我々が g^μν A_μ = A^ν と書き、A^ν を A_μに似て任意のベクトルであるとすると、最終的に次を得る。
Φ= 1/√-g ∂/∂x_ν (√-g A^ν) .................................(35)
このスカラーは、反変ベクトル A^ν の発散である。
反変ベクトルの回転 ー (26) の第2項は、μとνの添字に対称。ゆえに、A_μν - A_νμ は、特に単純に構成される 反対称テンソルである。次を得る。
B_μν = ∂A_μ/∂x_ν - ∂A_ν/∂x_μ ..............................(36)
6ベクトルの反対称拡張 ー (27) に2階の反対称テンソル A_μν を適用して、それに付け加えて、添字の周期的な転置 を通してできるふたつの方程式を形成し、これら3つの方程式の加算によって3階のテンソルを得る。
B_μνσ = ∂A_μνσ + ∂A_νσμ + ∂A_σμν = ∂A_μν/∂x_σ + ∂A_νσ/∂x_μ + ∂A_σμ/∂x_ν ..........(37)
それが容易に証明できるのは、反対称であるからである。
6ベクトルの発散 ー (27) の g^μα g^νβ による混合積をとり、我々はまたテンソルを得る。(27)の右辺の第1項は、 次の式に書ける。
∂/x_σ (g^μα g^νβ A_μν) - g^μα ∂g^νβ/x_σ A_μν - g^νβ ∂g^μα/x_σ A_μν
もし我々が、g^μα g^νβ A_μνσ を A^αβ_σ と、g^μα g^νβ A_μν を A^αβ と書き、最初の項を変換するのに、
∂g^νβ/∂x_σと∂g^μα/∂x_σ
を(34)でそれらに与えられた値に置き換え、(27) の右辺から結果は、7つの項でできる式になり、そのうち4つはうち消され次が残る。
A^αβ_σ= ∂A^αβ/∂x_σ + {σγ, α} A^γβ + {σγ, β} A^αγ ......................(38)
これは、2階の反変テンソルの拡張の表式である。より高階と低階の反変テンソルの拡張に対応する表式も形成できる。
類似の方法によって、混合テンソルの拡張もまた、形成できることを注意する:ー
A^α_μσ= ∂A^α_μ/∂x_σ - {σμ, τ} A^α_τ + {στ, α} A^τ_μ ....................(39)
(38)を添字βとσとによって縮約(δ^σ_βによる内積)して、次のベクトルを得る。
A^α= ∂A^αβ/∂x_β + {βγ, β} A^αγ + {βγ, α} A^γβ
もし、A^αβを反対称テンソルと仮定するとき、βとγの添字に関する {βγ, α} の対称性のため、右辺の第3項が消える。 第2項は、(29a) に従って変換され得て、次を得る。
A^α= 1/√-g ∂(√-g A^αβ)/∂x_β ............................(40)
これは、反変6ベクトルの発散の表式である。
2階の混合テンソルの発散 ー (39) の添字αとσに関する縮約をして、(29a) を考慮すれば、次を得る。
√-g A_μ= ∂(√-g A^σ_μ)/∂x_σ - {σμ, τ}√-g A^σ_τ ....................(41)
もし、我々が最後の項に反変テンソル A^ρσ = g^ρτ A^σ_τ を導入するなら、次の式が仮定され、
- [σμ, ρ] √-g A^ρσ
もし、さらに A^ρσ が対称であるなら、これは、次に還元される。
-1/2 √-g ∂g_ρσ/∂x_μ A^ρσ
もし、我々が A^ρσの代わりに、やはり対称の共変テンソル A_ρσ= g_ρα g_σβ A^αβ を導入していれば、次の式になる。
1/2 √-g ∂g^ρσ/∂x_μ A_ρσ
問題の対称の場合、(41)は、それゆえ、次の2式に置き換えられる。
√-g A_μ= ∂(√-g A^σ_μ)/∂x_σ - 1/2 ∂g_ρσ/∂x_μ √-g A^ρσ ....................(41a)
√-g A_μ= ∂(√-g A^σ_μ)/∂x_σ + 1/2 ∂g^ρσ/∂x_μ √-g A_ρσ ....................(41b)
それらは、後に使用しなければならないものである。
我々はいま、基本テンソル だけ から微分によって得られるテンソルを探す。一見では、それは明らかに見える。 我々は、(27)で、任意のテンソル A_μνの代わりに基本テンソル g_μνを入れて、新しいテンソル、つまり、基本テンソルの 拡張をもった。しかし、この拡張が全く同一に消滅することを容易に確信することができる。我々は目的に、しかしながら、 次の方法で到達する。(27)に次を置く。
A_μν= ∂A_μ/∂x_ν - {μν, ρ} A_ρ
すなわち、4 元ベクトル A_μ の拡張である。そのとき、(添字を命名を変え)3階のテンソルを得る。
A_μστ= ∂^2A_μ/∂x_σ∂x_τ - {μσ, ρ} ∂A_ρ/∂x_τ - {τμ, ρ} ∂A_ρ/∂x_σ - {τσ, ρ} ∂A_μ/∂x_ρ (-∂{μσ, ρ}/∂x_τ + {μτ, α} {ασ, ρ} + {στ, α} {αμ, ρ} ) A_ρ (*)
この表式は、テンソル A_μστ - A_μτσ の形成を示唆する。なぜなら、もし我々がそうすれば、A_μστの表式の第1、第4、 2重括弧の最後の項に対応する要素が A_μτσ の表式のそれらと打ち消すから; これらの項はσとτに対称であるから。 同じことが第2と第3の和について成立して、次を得る。
A_μστ - A_μτσ = B^ρ_μστ A_ρ ............................(42)
B^ρ_μστ= -∂/∂x_τ {μσ, ρ} + ∂/∂x_σ {τμ, ρ} - {μσ, α} {ατ, ρ} + {μτ, α} {ασ, ρ} ............(43)
この結果の本質的な特徴は、(42) の右辺に A_ρ だけがそれらの微分を伴わずあることである。 A_μστ - A_μτσ がテンソル特性 であり、A_ρ が任意のベクトルである事実と関連し§7 の理由から、B^ρ_μστ がテンソル (Riemann-Christoffel テンソル)である。
このテンソルの数学的重要性は、次にある:もし連続体に、それに参照して g_μνが一定であるような座標系が存在するような性質 ならば、全ての B^ρ_μστ が消滅する。もし我々が元の座標系の代わりにどの新しいものを選択しても、それに参照される g_μνは 一定でないが、テンソルの性質の帰結として、変換された B^ρ_μστ の成分は、新しい系のなかでまだ消滅しているだろう。 このように、Riemann テンソルの消滅は、適切な座標系を選ぶことによって、g_μνが定数になり得る必要条件である(*)。 我々の問題のなかで、これは、適切な座標系の選択を伴えば、連続体の 有限 領域に特殊相対論が成立するという場合に対応する。
τとρに関して、(43)を縮約すれば、次の2階の共変テンソルを得る。
G_μν= B^ρ_μσρ= R_μν + S_μν
ここで、
R_μν= -∂/∂x_α {μσ, α} + {μα, β} {νβ, α} ......................(44)
S_μν= ∂^2log√-g/∂x_μ∂x_ν - {μν, α} ∂log√-g/∂x_α
座標の選択についての注意 ー §8 において、式 (18a) との関連で見たように、√-g= 1 であるような利点をもつ座標系を選択する ことができる。前2章に得られた式をみれば、そのようなテンソルの形成の法則の選択が重要な単純化を実行することを示している。これは特 にいま作られ、理論のなかで述べられるべき基本的な役割を果たす G_μν に適用できる。なぜなら、座標系選択のこの特殊化は、S_μνの 消滅をもたらし、G_μνを R_μνに還元するからである。
この理由から以降、座標の選択のこの特殊化がもたらす単純化された式のなかの全ての関係を与えるであろう。そのときは、もしこれが特定の 場合に望ましいと見えるなら、その一般な共変方程式から元へ戻すことが容易なことになるだろう。
(*) 数学者は、これが 十分条件でもあることを証明した。
外部的な力の影響の下にない自由運動物体は、特殊相対論に従えば、直線上を均一に運動する。このことはまた、一般相対論においても、 (4)に与えられた特殊な定数値をもつように選ばれた、であろう、そしてそうである、座標系 K_0 のなかの 4 次元空間の部分においても 成立する。
もし、我々が、任意に選択された座標系 K_1 からこの運動を正確に考察するならば、その物体は、K_1 から観測すると§2の考察に従えば、 重力場のなかで運動する。K_1 に関する運動法則は、次の考察から困難さなくもたらされる。K_0 に関しては運動法則は、4 次元的な直線に 対応する。すなわち、測地線である。いま、測地線は、参照する座標に独立に定義されるから、その方程式は、K_1 に関しての質点の運動 方程式でもあろう。もし、我々が次を設定するなら、
Γ^τ_μν = - {μν, τ} ........................(45)
d^2 x_τ/ds^2 = Γ^τ_μν dx_μ/ds dx_ν/ds ............................(46)
我々はいま、仮定をする。すぐに心に浮かぶが、この方程式の共変系は、それに参照して有限領域に特殊相対論の成立する参照系 K_0 がない 場合の、重力場のなかの質点の運動を定義すると。この仮定をなおさら正当化するのは、(46) が g_μν の1階の微分しか含まず、 K_0 の存在する特殊の場合にさえ、それらの間に関係がないことである。
もし、Γ^τ_μν が消滅するとき、点は直線上を均一に運動する。それゆえ、これらの量が運動の均一性から離脱を条件付ける。それらは、 重力場の成分である。
我々はこれ以降、"重力場" と "物質" との間を次の方法で区別をする。重力場以外のもの全てを "物質" と記述することによって。 我々の言葉の使用は、それゆえ、普通の意味の物質だけでなく、電磁場も含むのである。
我々の次の仕事は、物質のないときの重力場の方程式を見出すことである。ここで、我々は再度、先行する章で質点の運動方程式を定式化 したとき採用した方法を適用する。ある特別な場合に必要とされる方程式がどの場合にも満足されなくてはならない。それは、その g_μνがある一定の値をもつ特殊相対論の場合である。これを確定した座標系 K_0 に関して、ある有限の空間における場合としよう。 この系に相対して、(43) で定義した Riemann テンソル B^ρ_μστの全ての成分が消滅する。そのとき、その考察の空間については、 他のどの座標系においても、それらが消滅する。
このように、物質のない重力場に要求する方程式は、どの場合も、全ての B^ρ_μστ が消滅することを満足しなければならない。 しかし、この条件は、余りに行き過ぎている。なぜなら、例えば、質点によってその環境に発生された重力場は、確かに、座標系の どういう選択によっても、"変換して無くす" ことができないことは、明らかであるからである。すなわち、それは、一定の g_μνの 場合へと変換することができない。
このことは、我々に、物質のない重力場に対して B^ρ_μστ から導かれた対称テンソル G_μνが消滅しなければならないことを 要求することを促す。このように我々は、10個の g_μνに対する10個の方程式を得る。それらは、全ての B^ρ_μστ の消滅の 特別な場合に満足させられる。座標系の選択を行い、(44)を考慮すれば、物質のない場の方程式は、次である。
∂Γ^α_μν/∂x_α + Γ^α_μβ Γ^β_να= 0, ................(47)
√-g = 1
これらの方程式の選択においては、最小限の任意性しかないことを指摘しなければならない。なぜなら、G_μν 以外には、g_μν とその微分だけから形成され、2 次を超える微分を含まず、それらの微分に線形である、2階のテンソルはないからである(*)。
これらの方程式は、一般相対性の理論の要求から、純粋に数学的な方法によって、生起したものであるが、運動方程式(46)と結合して、 1次近似までで、Newton の引力法則、2次の近似までで、Leverrier によって (摂動の較正がなされた後の残りとして) 発見された 惑星の水星の近日点の運動の説明を我々に与える。これらの事実は、私の意見では、この理論の正しさの納得させる証明ととられ なければならない。
(*) 適切に言えば、これは、次のテンソルによってだけ肯定され得る。
G_μν + λ g_μν g^αβ G_αβ
ここで、λは定数である。 しかしながら、もし、我々がこのテンソルを = 0 とおけば、我々は再び、方程式、G_μν= 0 に戻ってくる。
場の方程式が運動量とエネルギーの法則に対応することを示すのに、最も便利なのは、それらを次のハミルトン形式で書くことである:ー
δ∫H dr= 0
H= g^μν Γ^α_μβ Γ^β_να ...............................(47a)
√-g = 1
ここで、我々が視野に持つ積分の有限の4次元領域の境界では、変分は消滅する。
我々がまず示さなければならないのは、式(47a) が (47) と同等であることである。この目的に我々は、H を g^μν と g^μν_σ
(= ∂g^μν/∂x_σ) の関数とみる。
そのとき、第1段階として、[(47a) の第2式の微分を作り]
δH = Γ^α_μβ Γ^β_να δg^μν + 2 g^μν Γ^α_μβ δΓ^β_να
= -Γ^α_μβ Γ^β_να δg^μν + 2 Γ^α_μβ δ(g^μνΓ^β_να)
しかし、[(21),(23),(45) から]
δ(g^μνΓ^β_να)= -1/2 δ[ g^μν g^βλ (∂g_νλ/∂x_α + ∂g_αλ/∂x_ν - ∂g_αν/∂x_λ) ]
丸括弧のなかの最後のふたつの項から起きる項は、異なる符号をもって、添字μとβの交換を通した互いから結果する (総和を記述する添字は実体がないから)。それらはδH の式の中で添字μとβに関して対称なΓ^α_μβ と乗算され、 互いに打ち消す。こうして、丸括弧のなかは、最初の項だけが考慮される必要が残る。(31)を考慮して次を得る。
δH = - Γ^α_μβ Γ^β_να δg^μν + Γ^α_μβ δg^μβ_α
こうして、
∂H/∂g^μν= - Γ^α_μβ Γ^β_να ........................................(48)
∂H/∂g^μβ_σ= Γ^σ_μβ
(47a) の変分を実行するのに、我々は、最初に次を得て、
∂/∂x_α (∂H/∂g^μν_α) - ∂H/∂g^μν = 0 ...........................(47b)
これは、(48) のために、証明されるべき (47) に一致する。
もし、我々が (47b) に g^μν_σ を乗算するなら、そのとき、
∂g^μν_σ/∂x_α = ∂g^μν_α/∂x_σ
のためそして、結果的に、
g^μν_σ ∂/∂x_α (∂H/∂g^μν_α) = ∂/∂x_α (g^μν_σ ∂H/∂g^μν_α) - ∂H/∂g^μν_α ∂g^μν_α/∂x_σ
次の式を得る。
∂/∂x_α (g^μν_σ ∂H/∂g^μν_α) - ∂H/∂x_σ = 0
または(*)、
∂t^α_σ/∂x_α = 0,
-2κ t^α_σ = g^μν_σ ∂H/∂g^μν_α) - δ^α_σ H .....................(49)
ここで、(48)、(47)の第2式、及び (34)のために、
-2κ t^α_σ= 1/2 δ^α_σ g^μν Γ^λ_μβ Γ^β_νλ - g^μν Γ^α_μβ Γ^β_να ............(50)
t^α_σ がテンソルでないことは、注意すべきである; 一方、(49) は、√-g = 1 である全ての座標系に適用できる。 この方程式は、重力場の運動量とエネルギーの保存の法則を表す。実際に、3次元空間 V に渡る、この方程式の積分は、 次の 4 元方程式をもたらす。
d/dx_4 ∫ t^4_σ dV = ∫ (lt^1_σ + mt^2_σ + nt^3_σ) dS ..................................(49a)
ここで、l, m, n は、(Euclid 幾何学の意味の) 境界表面の要素 dS に内側に引いた法線の方向の方向-余弦である。 我々はこのなかに、通常の形式の保存則を認識する。量 t^α_σ を重力場の "エネルギー成分"と呼ぶ。
私はいま、(47) 式を第 3 の形式で与える。それは、我々の主題を鮮明に把むために役に立つ。場の方程式 (47) に g^νσ の乗算によって、これらは、"混合"形式になって得られる。次を注意して、
g^νσ ∂Γ^α_μν/∂x_α= ∂/∂x_α (g^νσΓ^α_μν) - ∂g^νσ/∂x_α Γ^α_μν
この量は、(34)の理由によって次に等しい。
∂/∂x_α (g^νσΓ^α_μν) - g^νβ Γ^σ_αβ Γ^α_μν - g^σβ Γ^ν_βα Γ^α_μν
または (総和の添字を変更して)、
∂/∂x_α (g^σβΓ^α_μβ) - g^γδ Γ^σ_γβ Γ^β_δμ - g^νσ Γ^α_μβ Γ^β_να
この式の3番目の項は、場の方程式 (47) の第2項と打ち消す;(50)の関係を使って、第2項を次に書くと、
κ(t^σ_μ - 1/2 δ^σ_μ t)
ここで、t= t^α_α である。こうして (47) の代わりに、
∂/∂x_α (g^σβΓ^α_μβ) = -κ(t^σ_μ - 1/2 δ^σ_μ t) .............................(51)
√-g = 1
(*) 係数 - 2κ の導入の理由は、後に明らかになる。
§15 によって定式化された物質のない空間の場の方程式は、Newton 理論の次の場の方程式と比較される(*訳注)。
∇^2 φ = 0
我々は、次の Poisson 方程式に対応するものを必要とする。
∇^2 φ = 4πκρ
ここで、ρは、物質の密度を示す。
特殊相対論は、慣性質量は、エネルギー以上又は以下の何者でもないと結論した。それは、完全な数学的な表式、2階の対称テンソル を見出した。そのように、一般相対論において我々は、対応する物質のエネルギーテンソル T^α_σ を導入しなければならない。 それは、重力場のエネルギー成分 t^α_σ (式(49) と (50))と似て、混合の性質をもつだろうが、対称の共変テンソルに属するだろう。
式系(51)は、どうのようにこのエネルギーテンソルが(Poisson 方程式の密度ρに対応して)重力の場の方程式に導入されるべきかを示す。 なぜなら、もし我々が完全な系(例:太陽系)を考察するならば、系の全体質量は、それゆえ、全体の重力作用もまた、系の全体エネルギー に依存するであろうし、それゆえ、重力エネルギーと一緒になった重さのある物質のエネルギーに依るだろうから。これは、(51)式に 重力場だけのエネルギー成分の代わりに、重力場と物質のエネルギー成分の和、t^σ_μ + T^σ_μ を導入することで、それ自身を表現 することができるであろう。こうして。(51)の代わりに、我々は、次のテンソル方程式を得る。
∂/∂x_α (g^σβΓ^α_μβ) = -κ(( t^σ_μ + T^σ_μ) - 1/2 δ^σ_μ (t+T)) ....................(52)
√-g = 1
ここで、T= T^μ_μ (Laue のスカラー)と置いた。これらは、要求された一般の重力の場の方程式で、混合テンソル形式である。 これから遡って、(47) 式の代わりに、次の式をもつ。
∂/∂x_α (Γ^α_μν + Γ^α_μβ Γ^β_να = -κ(T_μν - 1/2 g_μν T) ...........................(53)
√-g = 1
この物質のエネルギーテンソルの導入は、相対性の仮説によって正当化されるだけではないことを認めなければならない。なぜなら、 ここで我々がそれを導いたのは、重力場のエネルギーが、重力として他のどの種類のエネルギーとも同様に同じ方法で作用しなければ ならないという要求からであったからである。しかし、この方程式を選んだ最強の理由は、その結論にある。運動量とエネルギーの 保存が、それぞれ正確に式(49)と(49a)に対応して、全体エネルギーの成分において成立すること。これを、§17 において示すだろう。
方程式 (52) は、右辺の第2項が消滅するように変換することができる。(52)を添字μとσに関して縮約し、結果の式に 1/2δ^σ_μ を乗算して後、それを式(52)から引く。これが次を与える。
∂/∂x_α (g^σβ Γ^α_μβ - 1/2 δ^σ_μ g^λβ Γ^α_λβ) = - κ(t^σ_μ + T^σ_μ) ..........(52a)
この式に我々は、∂/∂x_σ の演算を実行し、次を得る。
∂^2/∂x_α∂x_σ(g^σβΓ^α_μβ)= -1/2 ∂^2/∂x_α∂x_σ[g^σβ g^αλ (∂g_μλ/∂x_β+∂g_βλ/∂x_μ-∂g_μβ/∂x_λ)]
丸括弧の第1と3項は、互いに打ち消す働きをする。第3項の働きは、一方で総和の添字αとσ、他方ではβとλの交換によって見ることができる。 第2項は、再度、(31)によって整え、次になる。
∂^2/∂x_α∂x_σ(g^σβΓ^α_μβ)= 1/2 ∂^3g^αβ/∂x_α∂x_β∂x_μ ......................(54)
(52a) の左辺の第2項は、第1段階で次になり、
- 1/2 ∂^2/∂x_α∂x_μ (g^λβ Γ^α_λβ)
または、
1/4 ∂^2/∂x_α∂x_μ [g^λβ g^αδ (∂g_δλ/∂x_β + ∂g_δβ/∂x_λ - ∂g_λβ/∂x_δ)]
前述した座標系の選択をすれば、丸括弧の最後の項から導く項が(29)の理由で消える。他のふたつは結合して、(31)によって次を与える。
- 1/2 ∂^3 g^αβ/∂x_α∂x_β∂x_μ
そして、(54)を考慮して、我々は次の恒等式をもつ。
∂^2/∂x_α∂x_σ( g^σβ Γ^α_μβ - 1/2 δ^σ_μ g^λβ Γ^α_λβ) ≡ 0 ..................(55)
(55) と (52a) から、次を得る。
∂(t^σ_μ + T^σ_μ)/∂x_σ = 0 ..................................................(56)
このように、我々の重力場の方程式から、運動量とエネルギーの保存の法則が満足された。このことは、最も容易に (49a) を導く考察からも 得られる; ただここで違いは、重力場のエネルギー成分 t^σ_μ の代わりに、物質と重力場のエネルギー成分の全体を導入しなければならない ことである。
(53)に ∂g^μν/∂x_σ を乗算し、 次が消滅することをみると、
g_μν ∂g^μν/∂x_σ
§15 で採用した方法によって、次を得る。
∂t^α_σ/∂x_α + 1/2 ∂g^μν/∂x_σ T_μν = 0
または、(56)を見れば、
∂T^α_σ/∂x_α + 1/2 ∂g^μν/∂x_σ T_μν = 0 .......................(57)
(41b)と比較することによって、前述の座標系の選択をすれば、この方程式の述べるところは、物質のエネルギーテンソルの発散の消滅以外の 何者でもないとこが分かる。物理的に左辺の第2項の生起は、運動量とエネルギーの保存則が厳密な意味で物質だけには適用できないこと、 または、そうでなければ、g_μνが定数、すなわち、重力の強さが消滅するときに適用できることを示す。第2項は、運動量、エネルギーの 単位体積、時間あたりの重力場から物質への転送を表す。このことは、さらに明確に(57)を (41)の意味に書き直し、次になる。
∂T^α_σ/∂x_α = - Γ^β_ασ T^α_β ......................................(57a)
右辺は、重力場の物質へのエネルギー的な効果を表す。
このように、重力の場の方程式は、物質現象の軌道を支配する4つの条件を含んでいる。それらは物質の現象の方程式を完全に与える。 後者を、互いに独立な4つの微分方程式によって特徴づけることができるならば(*)。
B の部で開発された数学的な助けは、我々に物質の物理法則(流体力学、Maxwell の電磁力学)を、それらは、特殊相対論のなかで 定式化されたため、それらを一般相対論に適合するよう一般化することを可能にする。これがなされたとき、一般相対性の原理は、 我々に可能性の制限をさらに与えず; それは、いかなる新しい仮説の導入も我々がもつことなく、全過程での重力場の影響に我々 を精通させる。
こうして、(狭い意味の) 物質の物理的な性質について確定的な仮定を導入する必要がなくなることがやって来ている。 特に、電磁場の理論は、重力場のそれとの関連で、物質の理論への十分な基礎を備えるかどうか、を未解決な問いに残すことができる。 相対性の一般仮説は、これについて原理的に我々に何も教えない。理論の働きの経過によって、電磁力学と重力の理論とが共同して、 前者だけではできなかったことを、実行することが可能かどうかは、観察すべきこととして残されているに違いない。
p, ρ をふたつのスカラーとし、流体の前者を"圧力"と呼び、後者を"密度"と呼ぶ; それらの間には方程式が存在するとする。 反変対称テンソルを、次にとり、
T^αβ = -g^αβ p + ρ dx_α/ds dx_β/ds ........................................(58)
を流体の反変エネルギーテンソルとする。それに属する共変テンソル、
T_μν = -g_μν p + g_μα g_νβ dx_α/ds dx_β/ds ρ.......................(58a)
さらに、混合テンソル(*)がある。
T^α_σ = -δα_σ p + g_σβ dx_β/ds dx_α/ds ρ..............................(58b)
(58b) の右辺を (57a) にいれ、我々は一般相対論の Euler の流体力学方程式を得る。それらは、理論上運動の問題の完全な解を与える。 (57a) の4つの方程式と、p と ρ の間の与式と一緒に、さらに次の式、
g_αβ dx_α/ds dx_β/ds = 1
は、十分である。g_αβ が与えられるとき、次の 6 つの未知数を与えるために。
p, ρ, dx_1/ds, dx_2/ds, dx_3/ds, dx_4/ds
もし、g_μνも未知なときは、式 (53) を持ち込む。そこには、11 個の方程式が 10 個の関数 g_μνを決めるために存在し、 これらの関数は、過剰に定義された状態となっている。しかしながら、我々は、式 (57a) がすでに 式 (53) に含まれ、(53)は7つの 独立な方程式を示すだけであることを思い出さねばならない。定義の不足にはよき理由があり、そのなかの座標系の選択の自由度が 残された数学的未定義の原因であり、空間の関数の3つが自由に選べる程度のものである(*)。
φ_ν を共変ベクトルー電磁ポテンシャルベクトルの成分とする。それらから我々は、(36) に従って、電磁場の共変6ベクトルの成分 F_ρσ を次の式系に従って形成する。
F_ρσ = ∂φ_ρ/∂x_σ - ∂φ_σ/∂x_ρ .........................(59)
(59)から次の式系がでる。
∂F_ρσ/∂x_τ + ∂F_στ/∂x_ρ + ∂F_τρ/∂x_σ = 0 ....................(60)
が満足される。式の左辺は、(37) によって、3階の反対称テンソルである。式系(60)は、本質的に次に書く下す 4 つの方程式を含む:ー
∂F_23/∂x_4 + ∂F_34/∂x_2 + ∂F_42/∂x_3 = 0,
∂F_34/∂x_1 + ∂F_41/∂x_3 + ∂F_13/∂x_4 = 0, .........................(60a)
∂F_41/∂x_2 + ∂F_12/∂x_4 + ∂F_24/∂x_1 = 0,
∂F_12/∂x_3 + ∂F_23/∂x_1 + ∂F_31/∂x_2 = 0,
この式系は、Maxwell の方程式系の第2番目に対応する。これは、次の設定ですぐに理解できる。
F_23= H_x, F_14= E_x,
F_31= H_y, F_24= E_y, ............................(61)
F_12= H_z, F_34= E_z,
そのとき、(60a) の代わりに、通常の3次元ベクトル解析の記述法で書く。
- ∂H/∂t = curl E, ........................(60b)
div H = 0
我々は、Minkowski によって与えられた一般化形式によって、Maxwell の最初の方程式系を得る。F_αβに付随する反変6ベクトル を導入する。
F^μν= g^μα g^νβ F_αβ ...........................(62)
そして、電流密度の反変ベクトル J^μ をも導入する。そのとき、(40)を考慮すれば、次の方程式は、 (座標系の選択に合意した) 不変量が 1 であるどの置き換えに対しても不変である:ー
∂F^μν/∂x_ν= J^μ ...............................(63)
F^23= H'_x, F^14= -E'_x,
F^31= H'_y, F^24= -E'_y, ............................(64)
F^12= H'_z, F^34= -E'_z,
これらの量は、特殊な制限された相対論の場合に H_x,...,E_z に一致する。さらに、
J^1= j_x, J^2= j_y, J^3= j_z, J^4= ρ
とすれば、(63) の代わりに、
∂E'/∂t + j = curl H' .............................(63a)
div E' = ρ
(60),(62), そして (63) は、座標系選択に関して我々が確立した習慣を伴い、自由空間の Maxwell の場の方程式の一般化を形成する。
電磁場のエネルギー成分 ー 我々は次の内積を形成する。
κ_σ = F_σμ J^μ ................................(65)
(61)によってその成分を3次元的作法で書けば、
κ_1 = ρE_x + [j. H]_x .............................(65a)
.....
κ_4 = - jE
κ_σ は、その成分がそれぞれ負の、電荷から電磁場に、単位時間体積あたりに移る、運動量とエネルギーに等しい共変ベクトルである。 もし、電気的質量が自由である、すなわち、電磁場だけの影響の下にあれば、共変ベクトル κ_σ は、消滅するだろう。
電磁場のエネルギー成分 T^ν_σ を得るには、式 (57) を κ_σ = 0 の式に与えるだけでよい。(63)と(65)から、最初に、
κ_σ= F_σμ ∂F^μν/∂x_ν = ∂/∂x_ν(F_σμ F^μν) - F^μν ∂F_σμ/∂x_ν
右辺の第2項は (60) の理由から、次の変換を許す。
F^μν ∂F_σμ/∂x_ν = - 1/2 F^μν ∂F_μν/∂x_σ = - 1/2 g^μα g^νβ F_αβ ∂F_μν/∂x_σ
後者の表式は、対称性の理由から次のようにも書ける。
- 1/4 [g^μα g^νβ F_αβ ∂F_μν/∂x_σ + g^μα g^νβ ∂F_αβ/∂x_σ F_μν ]
しかし、このため、こうも書ける。
- 1/4 ∂/∂x_σ (g^μα g^νβ F_αβ F_μν) + 1/4 F_αβ F_μν ∂/∂x_σ (g^μα g^νβ) ]
この最初の項は、
- 1/4 ∂/∂x_σ (F^μν F_μν)
第2項は、微分を実行後、いくらかの整理の後、結果は、
- 1/2 F^μτ F_μν g^νρ ∂g_στ/∂x_σ
全ての3項を合わせて言えば、我々は、次の関係を得る。
κ_σ= ∂T^ν_σ/∂x_ν - 1/2 g^τμ ∂g_μν/∂x_σ T^ν_τ ........................(66)
ここで、
T^ν_σ = - F_σα F^να + 1/4 δ^ν_σ F_αβ F^αβ
(66) は、もし、κ_σ が消滅するとき、(30)のために、(57) 又は (57a) と各々同等である。それゆえ、T^ν_σは、 電磁場のエネルギー成分である。(61) と (64) の助けによって、特殊相対論の場合に、これらの電磁場のエネルギー 成分が、よく知られた Maxwell-Poynting 表現を与えることは、容易に示すことができる。
我々はいま、√-g = 1 である座標系を整合的に使うことによって、重力場と物質によって満足される一般法則を引き出した。 我々は、それによって、かなりの式と計算の単純化を、一般共変性の要求への合致を失敗することなく達成した;なぜなら、 我々は一般共変方程式から、座標系の特殊化によって我々の方程式を描いたからである。
まだ、問題は形式的興味なしにではない。重力場と物質のエネルギー成分の一般化された定義に関連して、座標系の特定化 なしにさえも、式 (56) の形式での保存則、(52) 又は (52a) と同様な性質の重力場の方程式、の定式化が可能である。 左辺には(通常の意味での)発散をもち、右には物質と重力のエネルギー成分の和がくるような仕方によって。両方の場合とも、 これは実際にそうであることを私は見出している。しかし、この主題への私の何かの拡張的な熟考の通信に価値があるとは 私は考えない。なぜなら、結局それらは、実質的に新しい何物も我々に与えないからである。
何度も言及したように、一般理論の特殊な場合としての特殊相対論は、g_μν が一定値 (4) をもつことで特徴付けられる。 既に言ったことから、これは、重力の効果の完全な無視を意味する。我々は、g_μν が (4) の値から 1 と比べて小さな量 だけ異り、2 次以上のオーダーの小さな量を無視する場合を考慮することによって、現実へのより近い近似に到達する。 (近似の第1の視点)
さらに、g_μνを考察する時空の領域は、座標の適切な選択によって、空間的な無限において、(4) の値に漸近するとする; すなわち、有限領域内の物質だけによって排他的に発生した重力場を考察する。
これらの近似は、我々を Newton 理論に導くと考えられる。しかし、その目的に向かって、基本方程式をさらに第 2 の視点 から近似しなければならない。我々は、方程式 (46) に従う質点の運動に注意を向ける。特殊相対論の場合、成分、
dx_1/ds, dx_2/ds, dx_3/ds
は、どの値も取ることもできる。これは、どの速度も、
v= √((dx_1/dx_4)^2 + (dx_2/dx_4)^2 + (dx_3/dx_4)^2)
起きることができるが、それは、真空中の 光の速度より小さい。もし我々が、我々の経験にほとんど排他的に提供されている、 その v が光の速度と比べて小さい場合に自らを制限するならば、これは、次の成分が、
dx_1/ds, dx_2/ds, dx_3/ds,
小さい値として扱われるべきことを示す。一方、dx_4/ds は、小さい量の 2 次のオーダーまでは、1 に等しい。(近似の第2の視点)
いま、我々は、近似の第1の視点から、Γ^τ_μν の大きさは、全て小さく、少なくとも1次のオーダーである。(46) を見れば、 この方程式に、近似の第2の視点から、我々がその μ= ν= 4 の項だけを考慮しなくてはならないことが分かる。我々は自身を最低 のオーダーの項に制限して、(46) の代わりに我々は最初に次を得る。
d^2x_τ/dt^2 = Γ^τ_44
ここで、我々は、ds = dx_4 = dt とした; 又は、近似の第1の視点から、1次の項に制限して:ー
d^2x_τ/dt^2 = [44,τ] (τ= 1,2,3),
d^2x_4/dt^2 = -[44, 4].
もし、さらに我々は、我々が自らを、重力場が発生する物質の速度が (光の伝播速度に比べて) 緩慢である場合に制限することによって、 重力場が疑似静止であることを仮定するならば、我々は右辺の、空間座標に関する微分に比較して、時間に関する微分を無視することができ、 次の式をもつ。
d^2x_τ/dt^2 = - 1/2 ∂g_44/∂x_τ (τ= 1,2,3) ......................(67)
これは、Newton の理論に従う質点の運動方程式である。そのなかで 1/2 g_44 が重力ポテンシャルの役割を果たしている。 この結果の注目すべきことは、基本テンソルの g_44 成分だけが、1次近似までは、質点の運動を定義しているということである。
我々はいま、場の方程式 (53) に目を転じる。ここで我々が考慮しなければならないのは、"物質" のエネルギーテンソルがほとんど 排他的に、狭い意味の物質の密度、すなわち (58) [又は各 (58a)又は(58b)]の右辺の第 2 項、だけによって定義されることである。 もし、我々が問題の近似をするなら、ひとつの例外 T_44 = ρ = T 以外の全ての成分を消滅する。(53)の左辺の第 2 項は、2次のオーダー である; 最初の項は、問題の近似について、次の式をもたらす。
∂/∂x_1 [μν, 1] + ∂/∂x_2 [μν, 2] + ∂/∂x_3 [μν, 3] - ∂/∂x_4 [μν, 4]
μ= ν= 4 について、これは、次の時間に関する微分の省略を与える。
- 1/2 ( ∂^2 g_44/∂x_1^2 + ∂^2 g_44/∂x_2^2 + ∂^2 g_44/∂x_3^2) = - 1/2 ∇^2 g_44
方程式 (53) の最後の項は、こうして、次をもたらす。
∇^2 g_44 = κρ ..........................................(68)
(67) と (68) は、一緒になって Newton の重力法則と同等である。
(67) と (68) によって、重力ポテンシャルの式は次になる。
-κ/8π∫ρdτ/r .........................................(68a)
一方、Newton 理論では、時間の単位を選べば、次になる。
-K/c^2 ∫ρdτ/r
ここで、K は、定数 6.7 x 10^-8 であり、通常、重力定数と呼ばれる。この比較から、我々は次を得る。
κ= 8πK/c^2 = 1.87 x 10^-27 ............................(69)
1次近似として Newton の理論に到達するために、我々は、重力場の 10 個の g_μν のひとつの成分 g_44 だけを計算しなければ ならなかった。なぜなら、この成分だけが、重力場のなかの質点の運動の方程式である 1 次の近似 (67) に入ってくるからである。 このことから、しかしながら、g_μν の他の成分は、(4) に与えられた値から 1次のオーダーの少量だけ異なっていなければなら ないことは、すでに明らかである。これは、g = -1 という条件によって要求される。
なぜなら、場を作りだす座標原点にある質点は、我々が得る、1次近似までは、点対称な解、
g_ρσ = - δ_ρσ - α x_ρ x_σ/r^3 (ρ,σ= 1,2,3) ,
g_ρ4 = g_4ρ = 0 (ρ= 1,2,3) , .........................(70)
g_44 = 1 - α/r
ここで、δ_ρσ は、ρ=σ 又は、ρ≠σ によってそれぞれ、1 又は 0 をとる。そして、r は、量 √(x_1^2 + x_2^2 + x_3^2) である。(68a) のために、
α= κM/4π ...............................(70a)
もし、M が場を作る質量を示すなら。場の方程式(質量の外部)が小さな量の1次のオーダーを満たすことを検証することは易しい。
我々はいま、空間の計量の特性の上に質量 M の場によって働かされる影響を検証する。"局所的に"(§4) 計測される長さと時間 ds を一方とし、座標の差 dx_ν を他方とする、両者の間に次式の関係がつねに成立する。
ds^2 = g_μν dx_μ dx_ν
長さの単位物差しは、x 軸に平行に置かれ、ds^2 = -1 にしないといけない; dx_2 = dx_3 = dx_4 = 0 である。それゆえ、 -1 = g_11 dx_1^2 である。もしさらに、単位物差しが x 軸に置かれているなら、(70)の 1 次近似は次を与える。
g_11 = -(1 + α/r)
これらのふたつの関係から、1次の少量への較正は、次になる。
dx= 1 - α/2r ............................(71)
このように、単位の測定棒は、座標系との関係では重力の存在によってすこし短くされる。もし、棒が半径に沿って置かれるならば。
類似の仕方で、接線方向の座標の長さを得ると、例えば、次のようにして、ds^2= -1; dx_1= dx_3= dx_4= 0; x_1= r, x_2= x_3= 0 結果は、
-1 = g_22 dx_2^2 = - dx_2^2 .........................(71a)
接線方向の位置では、それゆえ、質量の点の重力の場は、棒の長さへの影響はない。
このように、重力場のなかの1次近似においてさえ、Euclid 幾何学が成立しない。もし、我々が同じ間隔の実現として、その場所と 方向に依らない、どれも同じ棒をとることを望むなら; 確かに、(70a) と (69) を眺めれば、期待される逸脱は、地球の表面の測定 において検知できるには余りに軽微であるが。
さらに、単位時計の速度を検証してみよう。それは、静止重力場のなかに静止して配置している。ここで、我々は、時計の周期として、 ds= 1; dx_1= dx_2= dx_3= 0 をもち、それゆえ、
1 = g_44 dx_4^2;
dx_4= 1/√g_44 = 1/√(1 + (g_44 - 1)) = 1 - 1/2 (g_44 - 1)
又は、
dx_4 = 1 + κ/8π ∫ρdτ/r ............................(72)
このように、時計は、もし、重さのある質量の側に設置されたなら、よりゆっくり進む。このことから、次のことが導かれる。 大きな恒星の表面から我々に届く光のスペクトル線は、スペクトルの赤い端に向けて偏移する(*)。
我々はいま、静止重力場のなかの光線の経路を検証する。特殊相対論では、光の速度は、次の式で与えられる。
- dx_1^2 - dx_2^2 - dx_3^2 + dx_4^2 = 0
そして、それゆえ、一般相対論では次の式である。
ds^2 = g_μν dx_μ dx_ν = 0 ............................(73)
もし、方向、すなわち、dx_1 : dx_2 : dx_3 が与えられれば、(73) は、次の量を与える。
dx_1/dx_4, dx_2/dx_4, dx_3/dx_4
そして、従って、次の速度、
√( (dx_1/dx_4)^2 + (dx_2/dx_4)^2 + (dx_3/dx_4)^2 ) = γ
が、Euclid 幾何学の意味で定義される。我々は、g_μν が定数でない場合、光線の経路が座標系に関して、曲らなければな らないことを容易に認識できる。もし、n を光の伝播に垂直な方向とするなら、Huyghence の原理は、平面 (γ, n) に描かれ る光線は、曲率 -∂γ/∂n をもつ。
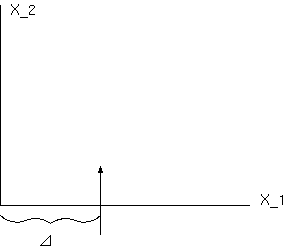
我々は、質量 M の側を距離 △ で通過する光の線によって実行される曲りを検証する。もし、我々が座標系を付録の図に合う ように選択すれば、線の全体の曲り(原点に向かって凹を正と計算して)は、次によって十分な近似で与えられる。
B= ∫_-∞^+∞ ∂γ/∂x_1 dx_2
一方、(73) と (70) は、次を与え、
γ= √(- g_44/g_22) = 1 - α/2r (1 + x_2^2/r^2)
計算を行って、これが次を与える。
B= 2α/△ = κM/2π△ ................................(74)

これによれば、太陽のそばを通過する光の線は、1.7" の屈折を実行する; 惑星木星のそばを通過する光線は、0.02" である。
もし、我々がより高い近似の程度まで重力場を計算するならば、そして、同様に対応する精度をもって、相対的に無限に小さな 質量の質点の軌道運動を計算すれば、我々は、惑星運動の Kepler-Newton 法則からの次の種類の逸脱を見出す。惑星の軌道楕円 は、次の量だけのゆっくりした回転を運動の方向に実行している。
ε= 24π^3 a^2/(T^2 c^2 (1-e^2)) ...........................(75)
回転毎に。この式のなかで a は長軸、c は通常の測定における光速、e は離心率である。T は回転の秒の時間である(**)。
計算は、惑星、水星には、世紀あたり、43" の軌道の回転を与えた。それは、天文学の観測 (Leverrier) に正確に対応する。 なぜなら、天文学者は、この惑星に近日点の移動を発見し、他の惑星による摂動を許した後も、説明できない残差としてこの 大きさがあった。