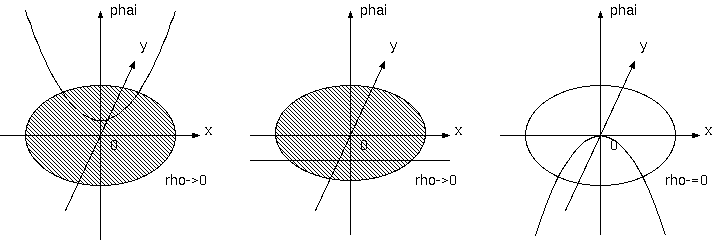
fig 1. Λの効果は、下に凸の2次超曲面を打ち消し、一様なρに一様なΦを用意する。
目次
はじめに
1. ニュートン重力への宇宙定数の影響
2. シュワルツシルト計量への宇宙定数の影響
3. 銀河回転曲線とパイオニア異常
4. 宇宙項の影響の論文1
5. 宇宙項の影響の論文2
その 100 年後のいま、膨張宇宙論は宇宙項を必要としている。宇宙項なしのフリードマン宇宙ではなく、膨張に宇宙項が支配的である、 物質を含むド・ジッター宇宙である。インフレーションは、空間曲率を0を導き、輝く物質の 10 倍程度の通常物質バリオン、その 5 倍 程度のエキゾチックなダークマター、そしてその 3 倍の宇宙定数の存在を必要とする。しかし、宇宙定数が宇宙平坦の要求だけに由来し、 他に証拠がなければ、その根拠は薄弱である。そして、宇宙項の存在は銀河団内の運動に影響する可能性がある。最初のそして最も確か なダークマターの証拠であった銀河回転曲線を、宇宙のサイズ(数Gpc) から5桁も小さい数10kpcのサイズの現象を宇宙項で説明しようと するものが現れる。この文では、宇宙項の基本的性質を考察し、それがどのように宇宙の力学に影響するかを解説したい。
ΔΦ = 4πρ ....................(1)
で規定されるニュートンポテンシャルΦは、空間的に一様なρ>0 があるとき、Φの空間的2階微分の成分の和(ラプラシアンΔ=∇^2)は 正であり、下に凸の2次超曲面となって無限遠で発散する。それゆえ、ニュートン重力の宇宙は、無限遠のΦは無限に大きく、遠方からの 光が無限に青方偏移し、現実と逆の性質である。これは、物質が互いに収縮する万有引力という基本的性質をもつニュートン宇宙の破綻 と理解される。ところが、宇宙項Λがあれば、ポアソン方程式には宇宙定数に対応する項ができ、
ΔΦ - ΛΦ = 4πρ ...........(2)
一様なρ (ΔΦ=0である) の無限宇宙にも物質密度ρの働きをちょうど打ち消すΛΦによって、一様なポテンシャルΦ= -4πρ/Λという 解が存在できる(fig 1.)。もちろん、そのようなΛの大きさで、ちょうど打ち消しがある理由の理解は難しい。ニュートン宇宙は、 空間が有限なら有限時間内に崩壊し、無限ではΦの無限大が発生するが、宇宙項は、それに対抗する。

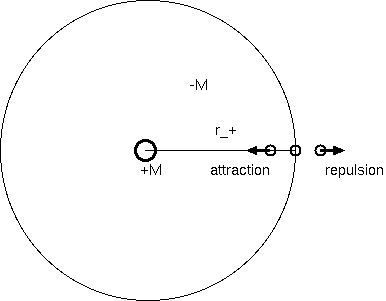
F= -GM/r^2 + Λr/3 ..............(3)
となり、引力と斥力がちょうどつり合う(F=0)距離は、
r_+ = (3GM/Λ)^1/3 ..............(4)
F を勾配とする (F= -dΦ/dr) ポテンシャルΦ(r) は、
Φ= -GM/r - Λr^2/6 .............(5)
宇宙項Λは、ニュートンポテンシャルΦ= -GM/r を、遠方では中心からの距離rの2乗に比例する上に凸の2次超曲面を与え、無限遠で下に発散させる。 この第2項は、回転系の遠心力と似た2次の超曲面であるが、回転系のように軸対称ではなく、3次元の全方向の遠方でポテンシャルを低下させる。 このΦの超曲面は中心質量 M によらないから、これをΦの宇宙解とみなせば、遠方からの光が距離の2乗に比例する赤方偏移をもつ宇宙になる。 球対称でなく物質密度ρが一様に分布する宇宙では、距離rに比例する引力を任意の点から受けるが、ΛΦ はそれに対抗して打ち消すことができる。 任意のρの分布にも、Λを対抗すれば、ΔΦへの効果を消すことができるだろう。
ds^2 = A(r) c^2 dt^2 - dr^2/A(r) - r^2(dΘ^2 + sin^2 ΘdΦ^2) ...........1.4
A(r) = 1 - 2GM/c^2r - Λr^2/3
質点の周囲から平坦でなくΛに対応した曲率に漸近する空間を記述する。弱い場の極限で計量に対応する一般化ニュートンポテンシャルΦから、
g_00= A(r)= 1 + 2Φ/c^2 ..............1.5
Φ= -GM/r - Λc^2r^2/6 ...............1.6 (論文では右辺の符号が逆)
ニュートン近似の結論は、前章と同じくポテンシャルΦへの遠方で低下する 2次超曲面の追加し、遠方の物体の距離に比例する斥力である。
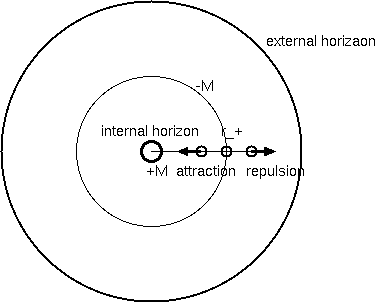
式 (1.4) の時空間の計量を作る A(r) は、その√が時間経過に比例するのは、非負の範囲に制限される。 r→0 で A(r)→-∞ に発散し、 A(r)= 0 になる特異面は、r の小さい側に r= 2GM/c^2 という質量に比例する半径をもつ内向き一方通行のブラックホールの事象の地平面 がある。
宇宙定数Λがあるとき、r→∞ で A(r)→-∞ に発散するから、r の大きな側に、中心質量に依らない r= √(3/Λ) に外向き一方通行の 散逸壁、吸い込み(シンク)の外部地平面ができる。その外側では A(r) の符号が反転し、時間と空間計量の役割が入れ替わることは、 ブラックホール内部と同様である。外部の地平面 A(r)= 0 までの距離は、r= √(3/Λ) であり、平坦を実現するΛ〜 10^-52 [/m^2] であれば、〜 2 x 10^26 m (〜 6Gpc)であり、宇宙の半径とほぼ一致する。 Lars Begstrom and Ulf Danielson, "Dynamical effects of a cosmological constant"、によると、Ω_Λ= 1 のド・ジッター宇宙は、 指数的膨張をし、ハッブル定数 H= √(Λ/3) は、定数である。この逆数の宇宙年齢は、この空間的外部地平面の大きさと一致する。
Marek Nowakowski, "The Consistent Newtonian Limit of Einstein's Gravity with a Cosmological Constant" gr-qc/0004037 によれば、 1+Φ= 1 - GM/r - Λc^2 r^2/6 = 0、 GM= r - Λc^2 r^3 /6、d(r)= r - Λ/6 r^3, d'(r)= 0 から、r = √2/Λ という大きさがある。
銀河サイズの重力の異常な現象である銀河回転曲線は、ダークマター存在を最初に明確に示す観測であった。斜めにみる渦巻銀河では、 銀河回転による中心軸の両側に逆方向の速度が光学スペクトルや21cm中性水素HI線の電波によって検出でき、中心軸からの距離に対する 銀河回転の速度をグラフにすることができた。中心窩(バルジ)では速度は半径に比例する剛体回転をし、それを過ぎると速度がある大き さに達し、そこから外部にあまり低下せずほぼ一定を保っていた。ある半径の外に質量がないなら、銀河回転速度の曲線は、半径の -1/2 乗で低下するはずである。ニュートンポテンシャル Φ= -GM/r の勾配を(球対称性から r で微分して)符号反転して重力 g は起き、
g(r)= -dΦ/dr= -GM/r^2
g= rw^2 から、w^2r^3= GM というケプラー法則がでるが、g= v^2/r から v= √GM/r である。
この現象は、見える物質の外側にダークマターが銀河を取り巻くハーローとなっていると考えられた。半径 r に比例する質量 M(r)∝ r によって速度一定の回転曲線になる。これによるダークマターの量は輝く物質の約 10 倍程度、これがダークマターの全体の存在の証拠 というには、宇宙平坦を実現するのに必要な量の 2 %程度である。この現象を、ダークマターによるものでなく、ニュートン物理からの 逸脱として宇宙項の負の斥力で説明しようとする Lars Begstrom and Ulf Danielson,"Dynamical effects of a cosmological constant"、 astro-ph/0002152"> astro-ph/0002152 がある。
銀河回転曲線が必要とするのは、引力の追加である。宇宙定数の斥力は符号が逆である。また銀河回転に影響するには、4桁程度不足する。 重力の修正でこれを説明する、v 一定の回転速度になるには、 g= v^2/r から、ある距離 r> GM/a (〜数10kpc) において 1/r に比例する 重力 (-dΦ/dr) と log(r) に比例するポテンシャルであればよい。
Φ= -GM/r + a log r
g= -GM/r^2 - a/r
太陽系サイズの重力の精密な測定で問題になっているものがある。 パイオニア異常 は、1972年と 1973年に それぞれ打ち上げられたパイオニア10号と11号が太陽系の外縁部に達し、中心に引かれる余分な加速度 (8.74+-1.33)x10^-8 cm/s^2 が説明 ができず残されている問題である。距離 20〜70AU で発見された。遠方ほど線形に上がるポテンシャルを考えると、ある距離 r> √(p/GM) (〜数10 AU)で一定加速に移行する引力の追加となる。
Φ= -GM/r + pr
g= -GM/r^2 - p
宇宙サイズ、銀河回転曲線、パイオニア異常の3者は、スケールの大きな違いがあり、宇宙のスケールが〜4Gpcに対して、銀河スケールは、 数kpc〜数10kpc であり、5,6 桁の比をもつ。さらに、銀河スケールの〜数10kpcは、太陽系外縁部〜100 AU と比べ 7桁の比をもつ。加速膨 張を説明する正の宇宙項は斥力であり、銀河回転曲線とパイオニア異常に必要なものは引力の追加であるから、宇宙定数で説明できるもので はないと考えられる。
概要: 宇宙論的定数の存在の観測的証拠が強くなってきた。それゆえ、銀河、銀河団、より大きな構造の力学への最終的影響を調べること はタイムリーである。我々は、最近のある主張とは反対に、宇宙定数の銀河の力学 (例、銀河回転曲線) への影響は無視できることを見出 した。大きな銀河団から始まるより大きな構造では、宇宙定数によるニュートン重力への斥力の効果が観測できる潜在的可能性がある。
内容の抄訳: ダークマターは、バリオン物質の存在最大量の5倍はあり、それらは exotic であると考えられている。さらに、十分結論的ではないが アインシュタインが導入し彼の一般相対論に拒絶した宇宙定数のダークエネルギーの存在の兆候がある。この可能性は Type Ia 超新星 の観測の結果によって注目を集めている。
宇宙定数の宇宙の計量への影響と光度距離関係の赤方偏移依存性以外に、銀河の力学に影響を与えるという主張がある。(S.B. Whitehouse and G.V. Kraniotis(1999) の astro-ph/9911485 ) 我々は宇宙定数が強く銀河 回転曲線に影響するというこの主張に合致しないことを見出した。しかしながら、いくらかの銀河団力学への小さな影響は排除されないと思われる。
アインシュタイン方程式は、次に読める。 [重力方程式の右辺に物質の係数 8πG_N (G_N はニュートン重力定数) を書くのは、 □Φ= 4πρ と同様にニュートン重力にπが出ないようにする。Λ g_μνが宇宙定数の働きを表す宇宙項である。]
R^μν - 1/2 g^μν R - Λ g^μν = 8πG_N T^μν ..........(1) [論文にはスカラー曲率 R が欠けていたので追加した。]
宇宙定数Λの形式のエネルギー密度は臨界密度にスケールして表わすことができ、
Ω_Λ= ρ_Λ/ρ_crit............(2)
ここで、
ρ_Λ= Λ/8πG_N ...............(3)
そして、G_N= 1/m_Pl^2(プランク質量の数値は、m_Pl= 1.2 x 10^19 Gev)。臨界密度の現在の値は、
ρ_crit= 3H_0^2/ 8πG_N ........(4)
こうして、
Ω_Λ= Λ/(3H_0^2) .............(5)
H_0= 100h kms^-1 Mpc^-1 (観測から h= 0.6 +- 0.1)。臨界密度の現在値は、
ρ_crit 〜 8 x 10^-47 h^2 GeV^4 ..........(6)
これは粒子物理単位 (c= h^- = 1) を使用して導かれた。cgs 単位では、現在観測の選ぶ値は、Ω_Λ〜 0.7 +- 0.2 であり、次に翻訳される。
Λ_obs 〜 10^-56 cm^-2 ..........(7)
最近のプレプリント S.B. Whitehouse and G.V. Kraniotis は、"伝統的" なダークマターによる解釈の代わりに宇宙定数を平坦な銀河回転曲線の 説明にする。しかし、これには、3-4桁大きさが不足する。これは観測に対し極端な不一致を示すものである。事実さらに、さらなる間違いがある ように思える、符号のエラーである。観測によって選ばれた正の宇宙定数は、宇宙膨張を加速する傾向があり、何にせよ、銀河の外部領域の物質 の結合を少なくし、多くするものではない。
一方、このように宇宙定数の影響は、銀河サイズでは無視できる量であるが、銀河団では観測結果を期待してよいかもしれない。 そのような効果をみる最初の試みとして、平坦な宇宙定数ありの膨張宇宙における円軌道の運命を考察する。これをするのに、 追加的な重力ポテンシャルをもつ膨張宇宙のなかの粒子の次の運動方程式をもって開始する。
x''+ 2a'/a x = -g/a
ここで x は、共動座標、a は、スケールファクタである。物理距離として R= ax として、次を見出す。
R'' - R a''/a = -g
例として、de Sitter 宇宙で Ω_Λ= 1 では、宇宙は宇宙定数が主要であり、
a(t)= e^Ht
H= √(Λ/3) は、定数。
v^2/R = G_N m/ R^2 - Λ/3 R ..........(8)
De Sitter metric では、
ds^2= (1 - 2Gm/r - Λ/6 r^2) dt^2 - dr^2/(1 - 2Gm/r - Λ/6 r^2) - r^2 dΩ^2 [Λ/3 は Λ/6 に直した]
(8) は、 R > (3 G_N m/Λ)^1/3 では、もはや束縛する軌道がないことを示す。このことは、観測できる結果をもつであろうか? 不幸にも、効果は、その周期が宇宙年齢になるような軌道だけにおいて重要になることが容易にみてとれる。さらに、宇宙定数の 効果はより小さい軌道では急速に減少する。それゆえ、回転曲線の考えは、その意味を失い、宇宙定数の可能な効果に接近するに は、他に探したほうがよい。ひとつの可能性は、銀河が構成する銀河団、超銀河団の方向である。
最初の段階として、線形の摂動の理論が有効な領域のなかでの銀河団への物質の降下を考察することができる。これは事実、Peebles 等が扱った。Ω_M + Ω_Λ= 1 (すなわち、零曲率) それは、インフレーションの視点からは自然な場合である。そして、それは偶然、 宇宙背景輻射の最近の気球測定で兆候を示す。Peebles は、不幸にも、固有半径 R の銀河団への特定降下速度がΩ_Λ の密度過剰δ への依存が全く弱く、次式でパラメタ化されることを示した。
v= 0.3 H_0 R δ Ω_M^0.6 ...................(9)
0.03 < Ω_M < 0.3 かつ 1 < δ < 3 において本質的に Ω_M に依存しない。この式は、任意の Ω_M + Ω_Λ に一般化される。 非線型の崩壊過程において、宇宙定数の存在のときの状況で、単純な一定密度と球状崩壊モデルを適用することによってΛの影響の 推定を得ることができる。我々はそうして、過剰密度の領域が最大半径 R_max に拡がるときと、ビリアル半径 R_vir に短縮するとき を見る。
この状況を分析するとき、固定の質量を含む固有半径 R(t) の質量の塊の単位質量のエネルギーへの方程式(cf. [6]の(20)又は(8)) を使う。
E= R'^2/2 - G_N m/R - ΛR^2/6 .....................(10)
ここで、3 つの項は、運動エネルギー、ニュートン重力エネルギー、真空のエネルギーにそれぞれ対応する。標準的分析のように、 運動エネルギー T の平均値とポテンシャルエネルギー V との関係のビリアルの定理を採用して、
<2T>= <r・∂V/∂r> .......................(11)
エネルギー方程式を一定密度の球全体に平均をとって(運動エネルギーゼロの半径 R_max を巡回する)
E= T_vir + V_vir^G + V_vir^Λ= V_max^G + V_max^Λ.............(12)
次を使って、
<Λr^2>= 3Λ/R^3 ∫_0^R r^4 dr = 3ΛR^2/5 .................(13) [Λが欠けていた]
と
<G_N M(r)r^-1>= 3G_N M /R^6 ∫_0^R r^4 dr = 3G_N M /5R ..........(14)
Λ= 0 のときは、よく知る結果に戻る。
3G_N M/5R_max= 3G_N M/10R_vir ...................(15)
すなわち、R_vir= R_max/2。Λが0でないとき、対応する式は、
3G_N M/5R_max + Λ/10 R_max^2= 3G_N M/10R_vir + 2Λ/5 R_vir^2 ..................(16) [右辺第2項は、Λ/5 R_virでなく 2Λ/5 R_vir]
宇宙論的平均質量密度と比較して質量の過剰密度コントラストが最大半径(周回)でω(= 5.6 標準の場合) を仮定し、Ω_M + Ω_Λ= 1 を仮定する。 そのとき、我々は M= 4πR_max^3ωρ_M/3 と書くことができ、これを(16)に入れて(3)を使えば、
1+κ= 1/2μ + 2κμ^2 .....................(17)
ここで、我々は、μ= R_vir/R_max (= 0.5 標準の場合)と、
κ= Ω_Λ/ ω(1-Ω_Λ)(1+z)^3
を導入した。この結果は、[8]の式(26)とすこし違った形式であるが一致する。もし、我々がΛ= 0 の場合の ω= 5.6 を1次近似とするなら、 そして、Ω_Λ= 0.7 について、(17)を数値的に z=0 について解くことによってμ= 0.5 から約 0.39 に減少することを見出す。
このことは、ビリアル半径が小さくなることを意味する。それは、不合理ではなく、与えられた質量について、よりコンパクトな質量だけが 正の宇宙定数の斥力を"生き残れる"からである。
我々は、ωもΛに依存することを考慮にいれることによって、この分析をいくらか改良できる。これが中間的な赤方偏移でωを増加させる効果 をもつことが見られる。この増加は、μを増加し、上のΛの効果を過大に評価したことを意味する。しかしながら、その効果は小さい。 また、銀河団の最終密度コントラストはいくらになるか、について推定することができ、これをするには、今日の宇宙の最大に膨張したときの 密度と比べた表式を得ている必要がある。これは、次で与える。
ω= 9π^2/16 1/f(a)^2 1/(1-Ω_Λ) ...................(18)
と、
f(a)= 3/2 ∫_0^a da/√((1-Ω_Λ)/a +Ω_Λ a^2) ................(19)
結果は、μによって与えられる上記のものよりも、さらに、正味の相対的な銀河団の圧縮を宇宙定数によってもたらす。
我々は宇宙定数のない"標準的" なシナリオとΛ!=0 であるものとの間の想像的な状況を扱ってきたから、銀河団スケールで小さいな効果であると しても、それが難しくても、観測的な不確かさを考慮すべき現実の宇宙のΩ_Λの値についての結論を描くためには、多分排除できないからである。 探された効果は、正のΛによって、ビリアル的な銀河団が小さくなること、そしてさらに過剰密度になることである。
しかしながら、回転曲線への銀河スケールの効果は極端に小さく無視できることは、明確であるように見える。
(謝辞、文献は、省略した)
概要:宇宙膨張の加速を説明する宇宙項の存在は、銀河回転曲線を説明することはできないが、天の川銀河とアンドロメダ銀河が共動座標系で初速 0で137億年の間に重力だけで運動するとする説に従って宇宙項の影響を計算すると、局所銀河群の質量の推定を 35 % 増加しないといけなくなる。 それより大きな構造、銀河団、超銀河団の運動ではより大きな影響があり、観測される可能性は排除されない。
ニュートン重力を修正し、距離に比例する弱い斥力の効果 SnIa から Λ〜 10^-52 m^-2 の宇宙定数を仮定して これがもたらす様々な天体のスケールにおいての効果を検討した結果、銀河以下の天体のスケールでは小さい。 銀河スケール(10kpc以下)では無視できる。 1Mpc以上のスケールでは重大に運動に影響を与える。例えば 局所銀河団の速度データは、真空のエネルギーの存在下では銀河質量の35%増加に対応する。その効果は、 より大きな低密度の系、銀河団、超銀河団ではより重要になる。
ほとんど2年前、ふたつのグループ、超新星宇宙論プロジェクト、と High-Z 超新星チームは、宇宙の膨張が 減速でなく加速している証拠を提示した。Ia 型超新星の内在的光度が、一定ではないが、独立に測定できる 最大輝度からの減衰率に強く相関する事実を使って宇宙論的な超新星の距離を測定した。これらの測定は、 超新星の赤方偏移のデータと結合して、加速の宇宙を予測する。非零の正の宇宙定数Λ、と
Λ= 10^-52 m^-2 .............(1.1) (= 10^-56 [cm^-2])
が加速宇宙現象を説明するに必要な斥力を作りだすことができる。分離したタの宇宙論観測もまた、宇宙が物質 のエネルギー密度と同じオーダーの真空のエネルギーに対応する零でない宇宙定数をもつことを主張するように示唆する。
R_μν -1/2 g_μν R = 8π G T_μν - Λ g_μν ...........(1.2)
R'^2= 8πG/3 R^2 ρ_M -kc^2 + ΛR^2 /3 == 8πG/3 R^2(ρ_M+ρ_Λ) - kc^2 ..........(1.3)
(ρ_Λ= Λ/8πG) 真空のエネルギーが赤方偏移に大きさを影響されないので、1.3 は宇宙膨張の加速 (R''>0)をもたらし得る。 しかし、1.1 の意味する 10^-10 erg/cm^3 は、粒子物理からの予測から多くの桁数、小さ過ぎる。そして、真空のエネルギー ρ_Λと物質のエネルギーρ_M が異なる速度 ρ_M /ρ_Λ 〜 R^-3 で変化する。いま、それらが同じオーダーにあることは、 全くありそうもないことである。スカラー場(クインテッセンス第5元素)の進化を導入することによって又は人間原理に基づく 確率の議論がこれらを正当化する面白い試みがここ数年になされた。
宇宙定数の、重力相互作用に対する影響
(1.2) の球対称真空解が、
ds^2 = A(r) c^2 dt^2 -dr^2/A(r) -r^2(dΘ^2 + sin^2 ΘdΦ^2) ...........(1.4)
A(r)= 1- 2GM/c^2r - Λr^2/3
この計量は、シュワルトシルト・ド・ジッター計量として知られる。漸近的平坦でなく、Λに対応した真空エネルギーによって 誘導された曲率に漸近的な空間を記述する。弱い場の極限ではシュワルトシルト・ド・ジッター計量に対応するニュートンポテンシャルΦ
g_00 = A(r) = 1 + 2Φ/c^2 ..............(1.5)
に対応して、次の一般化ニュートンポテンシャルΦを導く。
Φ= -GM/r - Λc^2r^2/6 ...............(1.6) (論文では両方の符号が逆)
この一般化されたニュートンポテンシャルが重力相互加速を導く。
g= -GM/r^2 + Λc^2 r/3 ...............(1.7)
この一般化された力は、次の斥力を含み。
g_r= Λc^2 r/3 ...............(1.8)
次の距離より大きな領域では支配的と期待される。
r_c = (3GM/Λc^2)^1/3 〜 10^2 (M_1/Λ_52)^1/3 pc 〜 2 x 10^7 (M_1/Λ_52)^1/3 AU .............(1.9)
ここで、M_1 は半径 r_c の球内の質量(単位は太陽[M= 2x 10^30 kg])そして、Λ_52 は(10^-52m^-2 を単位にする宇宙定数。 (太陽中心には 100pc= 2000万 AU (300光年) 銀河では M_1= (2x10^11〜)10^12 では、r= 1Mpc)
太陽系の近日点運動から見出されるには、10^14 小さいという[文献13]。 (Λは、r の3乗に関係するので 2x10^7 で地球軌道半径、その1/200である 10^5でΛは 10^15 大きくないといけない。) [文献11] では銀河回転曲線に適用し、M33 では、Λ〜10^-48 m^-2 がこれを満たすという。4桁大きくないといけない。 数10kpc の銀河スケールでは、0.1% 以下無視できる量 (かつ符号が逆)である。銀河団では無視できない。 銀河系とM31 を含む局所銀河群(1Mpc)の質量は、この斥力を補償するには 35% 増加しなければならない。
比、
q= Λc^2r^3/3GM 〜 0.5 x 10^-5 Λ_52 r_1^3/M_1 ...............(2.1)
r_1 は、[pc] 太陽系では r_1〜 10^-5, M_1= 1, q_ss〜10^-20 銀河系では、r_1= 10^4, M_1〜 10^10, q_g〜 5 x 10^-4 クラスタでは、r_1〜10^7, M_1〜 10^14, q_c〜 O(1) (1 以上になる)
太陽系では、ΔΦ_Λ= 6πq rad/orbit .................(2.2)
感度は最も高い。水星では r_1= 10^-6, q_mc= 10^-23, ΔΦ_Λ= 10^-22 rad/orbit 不確かさ 0.1''/century、ΔΦ_unc= 10^-9 rad/orbit であり 13 桁大きい preseccion/century は r_1^(3/2)、 r_1(Pluto)= 10^2 r_1(mercury) なので、3桁向上する。それでも10桁不足。 銀河では、中性水素の 21cm 線は、光りより拡がっている。
v_c^2= GM/r - Λc^2r^2/3 ..............(2.3)
v_100, r_10, M_10
v_c=100 v_100 km/sec ............(2.4)
r= 10 r_10 kpc, M= 10^10 M_10 M_1
v_100^2= 1/2M_10/r_10 - 3 x 10^-5 Λ_52 r_10^2 ..............(2.5)
p= (M(Λ_52= 1) - M (Λ_52= 0))/M(Λ_52= 0) = 3 x 10^-5 r_10^2/v_100^2 ...............(2.6)
22 の銀河についての比 p を表1に示す。 p〜10^-4 なので少なくとも3桁不足する。 [文献 11]では拡張大数仮説に基づいて整合するというが整合しないと思う。局所銀河群 銀河とアンドロメダは、
r_0= r(t= t_0) = 800 kpc ................(2.7)
離れている。その距離の変化比は、
dr/dt(t= t_0)〜 -123 kms^-1 ...............(2.8)
M31と銀河の重力によって接近運動していると仮定されている。 角運動量は無視でき、共動座標では初期速度は0として、距離r(t)の運動方程式は、
d^2r/dt^2= -GM/r^2 + Λc^2/3 r ..............(2.9)
M はふたつの銀河の質量和。[文献 20] ではΛなしの同様な運動方程式を使い、数値的検討 [21]ではこの近似が 合理的とし、銀河質量の相対的な小さな(約25%の)過推定がなされた。その補正は、無視した矮小銀河によるとした。 精密な推定を目的とせず宇宙定数のこれらへの影響を知りたい我々は"孤立2体近似"を使用する。
r(t= t_0)= 800 kpc .................(2.10)
dr/dt(t= t_0) = -123 km/sec ..............(2.11)
dr/dt(t= 0)= 0 ................(2.12)
t_0= 15 Gyr
(dr_100/dt_15)^2= M(1/r_100 - 1/8) + Λ(r_100^2 -64)+420- f(r_100) .........(2.13)
r= 100 r_100 kpc ................(2.14)
t= 1.5 x 10^10 t_15 yrs ..........(2.15)
M= 4 x 10^8 M Msun .................(2.16)
Λ= 1.3 Λ_52 ......................(2.17)
いま、条件(2.10)と(2.12) を使い、我々は、種々のΛの銀河質量への影響を評価するために解く ことのできる方程式を得る。
1= t_15(t= t_0) = - ∫^r_100(t=t_0) _r_100(t=0) dr/√f(r_100) ...........(2.18)
積分(2.18) の下限は、r への条件(2.12)から得られ((2.13)を使って)、一方上限は、式(2.10)に よって、その再スケーリングした式から、得られる。 この方程式は、種々の宇宙定数Λについて、銀河の総質量Mを計算するためにMについて数値的に 解くことができる。結果的にMのΛへの依存は図2(連続する線)に示される。
図2 局所群(実線)と銀河スケール(M33、破線)の速度データを使って、種々の宇宙定数Λについて 計算された、相対的な銀河の総質量 M(Λ)/M(Λ=0)。複数の点線は、SnIa データの意味するΛの 値と、真空エネルギーだけで宇宙を閉じさせる値Λ_clとに対応する。
明らかに、最近の SnIa 観測と整合するΛの値(Λ= 0.7 x 10^-52 m^-2)に対して、局所群を使って 計算された銀河質量は、Λ= 0 で計算された対応する値のより 35% 大きい。図2には、我々は、また 銀河M33の銀河力学(回転速度)を使って計算されたΛへの M(Λ)/M(Λ=0) の依存をプロットする(破線)。 明らかに、局所群に対比して銀河系は、宇宙定数の感度の高い検知器としては、あまりに小さく、 密度が高すぎる。
III. 結論
我々は、局所銀河群が、宇宙論的に期待される値と最近の SnIa 観測に整合する値をもつ宇宙定数の 重力効果の感度の高い検出器であるための、十分大きく十分低い質量密度をもつ系であることを結論 する。より小さなそして密度の高い系は、この特性をもたない。一方、Λの重力効果は、より大きな 宇宙論的な系において、より明確に示されるに違いない。
ここで議論された特定のクラスタ力学の効果は、宇宙定数が、銀河の"ダークマター"ハーローへの貢 献を、独立に決定する方法を提供する。これは、我々の天の河銀河のような銀河の銀河質量が、非力 学的な(例、重力レンズ)方法を使う方法だけからでなく、我々の局所群のようなクラスタ力学からも 導出され得る事実と整合する。
"クインテッセンス"[22]のような真空のエネルギーの異なる形式が支配的であれば、宇宙論的な定数の検 出できる作用が、小から大きなスケールにわたるかどうかは、継続的に驚きであることは正当である。 このタイプの効果的なスカラー物質は、状態方程式、p= wρ (-1<w<0) をもち、宇宙定数(w= -1) に関係するものに比べてずっとソフトである。そのため、それは通常のダークマター(w>=0)と後者 の間を内挿する。それだけでなく、我々は、それがずっと小さな斥力効果を起こし、wの増加によって 純粋なダークマターにスムースに引きわたすことを期待すべきである。我々の分析の結果として、 そのような"削減された"タイプの反重力は、最もそれらしく、局所群から導出された相対的な銀河総 質量へのクインテッセンスの質量貢献と銀河速度データとの不一致をwの増加(-1<w<0)によって首尾 よく小さくするかもしれない。平坦な銀河回転曲線へのクインテッセンスの力学的な影響の最近の分析 [23]は、事実、この視点を確証するものである。
もし、局所群のような系の銀河の質量が非力学的な方法(例、重力レンズ)を使って独立に測定される ならば、ここで議論した重力効果だけが、宇宙定数の独立の確認方法として使えるものである。 その場合、Λは、図2に示したようなプロットで示すことができるだろう。このタイプの研究が現在、 進行中である。
(図、謝辞、文献を省略)