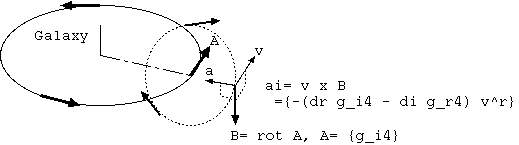
図1. 銀河回転による重力磁場 B の v x B の加速度
一般相対論の測地線方程式の示す重力は、ポテンシャル勾配以外にベクトルポテンシャルの時間微分と、質点速度と重力磁場の外積に比例する コリオリ加速度をもつことを解析し、そのなかで空間計量の項が速度又は速度積に比例し、静止物体に加速度を与えないことを見出した。
目次
概要
1. 一般座標と計量 $g_{ik}$
1.1 速度と計量
1.2 テンソル
2. 測地線と質点運動
3. 測地線方程式
4. 測地線方程式の解析
(1) 速度に関係しない項
(2) 速度に比例する項
(3) 速度積に比例する項
5. 電磁気のような重力場
5.1 アインシュタインの電磁気的重力(引用)
5.2 重力の電磁気との類似性
5.3 電磁気を再現する線形2階微分のR_ik近似式
5.4 重力加速の符号
5.5 天体近傍の質量
5.6 質量の衆合
6. 測地線方程式からみたLIGOの重力波検出
7. LIGOの重力波検出を受けて
8. 重力波のレンズ
9. 銀河回転曲線の説明
10. 銀河の渦巻きの説明
あとがき
ニュートン重力は遠隔力であったが、一般相対論は、物質の種類によらず質量に比例する重力を、加速系の慣性力や回転系の遠心力とコリオリ力のような、 系が原因の「みかけの力」として説明する。重力場の中で自由落下する測地系は、計量が標準値でみかけの力がなく、他の系にみかけの力が現れる。 系によって、各点の「計量」が決まり、計量の微分方向差と速度積から「質点の加速度」を与える測地線方程式は、4次元の一般座標系の性質であり、 アインシュタイン以前に見出され、彼は工夫の余地なく受け入れ、測地線方程式の解析を行なった。小論は、それを補完する。
測地線方程式が示す重力のニュートン重力を再現するポテンシャル勾配の項は必然的に見出されたが、電磁気との類似は、予想外だっただろう。しかし、 それは重力が遠隔力でなく伝播するために必要なのだろう。測地線方程式の重力は電磁気に似て、第1種クリストッフェル記号[rs,i]のr,sのパラメータ によって、質点速度によらない(1)、速度比例の(2)、速度積比例の(3)、に分類される。
(1) rs共に時間では、ポテンシャル勾配$1/2 \ ∂_i g_{44}$以外にベクトルポテンシャルの時間微分$-∂_4 g_{i4}$ をもち、静止物体にも加速度を与える。
(2) rsの片方が空間では速度比例のコリオリ力 $ -(∂_j g_{i4} - ∂_i g_{4j}) v^j = {\bf V}\times rot {\bf A}$ の項と、空間計量の時間微分の項
$-∂_4 g_{ij} v^j$ がある。
(3) rs共に空間では、空間計量の勾配に比例する ${1 \over 2} ∂_i g_{ii} (v^i)^2$をもつ。
空間計量の項は、(2)の $-∂_4 g_{ij} v^j$ と(3)の ${1 \over 2} ∂_i g_{ii} (v^i)^2$ にあり、速度又は速度積に比例し、静止物体に加速度を与えない。 これは、重力波測定への測地線方程式からの視点を与える。重力波が空間計量の変動なら、LIGOの光干渉計のような静止した鏡を揺らさない。
一般相対論の重力を知ることは、相対論的な世界認識に重要である。計量の生む加速度は、項数の多さから繁雑だが、測地線方程式だけで考察でき、 考え方はむしろ単純である。これによって我々は、重力波の検出方法の是非を考察でき、渦巻銀河の生成の謎、巻き付きの謎さえ解明できるかもしれない。
となる。$g_{ik}$は、系に依存し各点に違う値をもつ場であり、積項 $dx^i dx^k$に掛かり、$ds^2$を導く係数であり、 局所慣性系(及び慣性系)への元の座標微分$dx,dy,..$の変換係数$(a,b,c,,...)$からくる2次同次式で表される(*)。2添字の2階テンソル(実数配列の成分)である。 時空の性質を表す基本テンソルで、物差しの長さと時計の速さを決める計量(メトリック)という。 i,k(=1-4)について対称($g_{ik}= g_{ki}$)で、独立10成分をもつ。その微分方向差が力場となるポテンシャル場であり、密度と運動量に対応するとき、 その値と微分は積和まで2階微分は1次まで考慮する滑らかな場である。$g_{ii}$のi=1-3を空間計量、i=4を時間計量という。$g_{ik}$(i!=k,i,k=1-3)は空間軸を選択して0にできる。 重力のない時空を慣性系からみた標準値はミンコフスキー時空で式(2)から(1,1,1,-1)である。重力のある場合、有限領域の$g_{ik}$を標準値にはできない。 $g_{i4}$は時空の混合計量で、近傍の質量が速度をもつとき0でない値をもつ。
(*)局所慣性系への変換を $dx'^j = a^j_i dx^i$ として計量は、$g_{ij}= a^1_i a^1_j + a^2_i a^2_j + a^3_i a^3_j - a^4_i a^4_j$ と表せる。
となり、$g'_{xt}= 4vηγ^2$ が現れ、$g_{xx}, g_{tt}$の偏差$η$ は拡大され、その拡大率 $(1+v^2)/(1-v^2)$は、速度合成則でvを2倍した $u= 2v/(1+v^2)$ の $γ(u)=1/\sqrt{1-u^2}$ である。 \[ \begin{align} g'_{xx}&= 1 + ηγ(u),\\ g'_{xt}&= 2u ηγ(u), \\ g'_{tt}&= -1 + ηγ(u). \end{align} \tag{5-1} \] 速度vの方向xが天体方向に垂直なら、 $g_{xx}= 1, g_{tt}= -1+η, g_{xt}= 0 (0<η<1)$を式(4-1)に入れ、 \[ \begin{align} g'_{xx}&= 1 + ηγ^2 v^2,\\ g'_{xt}&= 2vηγ^2\\ g'_{tt}&= -1 + ηγ^2. \end{align} \tag{5-2} \] $g'_{xt}= 2vγ^2$が発生し、$g_{xx}$ には $η(γ v)^2$ 項が加わる。$g_{tt}$ の拡大率は$γ^2$である。 なお、我々が不変量の式(3)の速度の方向xとtの $g_{xx}, g_{xt}, g_{tt}$ だけをみたのは、 ローレンツ変換がポテンシャル場の速度方向の成分だけを変化させるからである。
基本テンソル $g_{ik}$ の(行列式gで、$g_{ik}$ の余因子を割った成分をもつ)逆行列が反変テンソル $g^{ik}$ である。$g^{ik} g_{jk}= δ^i_j= 1(i=j),= 0(i≠j)$ $dξ_j= g_{ik} dx^k, dx^i= g^{ij} dξ_j$として、反変ベクトルと共変ベクトルのテンソル添字の上下を移動できる。
計量$g_{ik}$は、基準(座標)系によるが、物理的意味をもつ物理量であり、人間の都合による単位の違いなどの単なるスケール変換を表すものではなく、 (宇宙項以外は)時空間にある質量の分布だけによって決定される。局所慣性系への微分の変換係数からくる計量は、一般座標系の時空点の性質を一意に表す。 その例として質点の運動方程式、空間の弯曲ともいう測地線がある。
ある速度ベクトルを移動するとき、時空の湾曲による変化量は、元の速度ベクトルと移動量の積に比例する。速度の変化量の$ds$による微分は加速度、 移動量の$ds$による微分は速度になり、元のベクトルとこれの両方が速度のため、両速度の積に時空の湾曲(計量の微分の方向差)$Γ$を乗算して加速度になる。 ある速度を別の速度だけ移動したとき$Γ$によって加速度を生むと読むこともできる。 dsが局所慣性系の時間なら、移動体の系に対する加速度は、移動体の質量の全てに掛かる重力なので、人体は感じない。
左辺の2階微分にこの偏微分記号を使うのは歴史的な理由である。$x^i$のsによる2階微分の微分記号は、$ds= dx^j とし、dx^i_{,,j}$とも書けるが、 $ds$を時間、$dx^i$を空間に限定して、$ds$の4元表示を避けている。観測点の時間$dt$とせずに、不変量の意味がある$ds$とするのは測地線の固有時を意味する。 時間は伸縮するが、測地線上の時間は固有時であって変換によらない。
\[ {∂^2 x^i \over ∂s^2 } + Γ^i_{rs} {dx^r \over ds} {dx^s \over ds} = 0 \tag{10} \] 測地線方程式(10)は、測地成分$-Γ^i_{rs}$に、r方向とs方向との速度積を掛け、i方向の加速度(重力) を与える。 $Γ^i_{rs} $は、第2種クリストッフェル記号{rs, i} であり、$g^{ik}$と第1種クリストッフェル記号 [rs, k] との積である。 計量の微分方向差 [rs, i] は、$g_{ir}$ のs方向微分と$g_{is}$のr方向微分の和から$g_{rs}$のi方向微分を引いた差の${1 \over 2}$でありr,sに対称である。 これは測地系(自由落下、局所慣性系)で0で、他の系で0でない。ゆえにこれはテンソルでない。テンソルは1次同次式の変換しか受けないから、 テンソルは、ある系で0なら全系で0である。 \[ \begin{align*} Γ_{i,rs}&= [rs, i]= g_{ik}\{rs, k\} (第1種クリストッフェル記号)\\ Γ^i_{rs}&= \{rs, i\}= g^{ik}[rs, k] (第2種クリストッフェル記号) \end{align*} \tag{11} \] \[ [rs, i]= {1\over 2} ({∂g_{ir} \over ∂x^s} + {∂g_{is} \over ∂x^r} - {∂g_{rs} \over ∂x^i}) \tag{12} \] 偏微分 ${∂ \over ∂x^i}$ は$∂i$ と略記し、 \[ [rs, i]= {1\over 2} (∂_s g_{ir} + ∂_r g_{is} - ∂_i g_{rs}) \tag{13} \] [rs, i]から$Γ^i_{rs}$にする $g^{ik}$は i,k=1-3 なので1に近似でき [rs,i] を考察すればよい。 質量に対する静的な$g_{ik} (g_{i4}=0)$で、$g_{ii}= 1, g_{44} != -1$ だが、$-1$の近くという条件では(10)は、 \[ {∂^2 x^i \over ∂s^2 } = -Γ^i_{44} = -[44,i] = {1\over 2} ∂^ig_{44} = -grad φ, (φ=\sqrt{-g_{44}}) \tag{14} \] として、ニュートン重力のポテンシャル勾配(6)を再現し、時間計量$g_44$の勾配ベクトルがニュートン重力を与える。 (空間の各点にスカラーのポテンシャル$φ$が空間の関数としてあり、その下り勾配ベクトル$-grad$が重力。$φ$が天体からの距離に反比例なら 距離の2乗に反比例の重力となる。これが$g_{44}$の1/2乗に比例。$g_{44}<0$から-を付け$φ=√-g_{44}$。$0<φ<1$であり無限遠で$φ= 1$である。) 一般に計量自体は質点に影響を与えず、計量の時空間微分の方向差 $-Γ^i_{rs}$ (Γはガンマとよみ、曲りを意味する) が質点に加速度を与える。 このニュートン重力は測地線方程式の第1近似であり、式が示す重力(i=1-3はベクトルの成分。rs=1-4,1-4によって16項)の一項にすぎない。
次章では測地線方程式が示す質点に与える加速度は、式(14)のニュートン重力の再現 $-grad φ$だけではなく、天体の側を通過する光の屈曲の例のように、 空間計量は速度2乗比例項まで考察すれば時間計量と同程度に働き、重力が 2倍まで増加することを示す。 さらに5章では電荷の受けるローレンツ力のような速度比例項があって、近傍の大質量天体が運動する座標系において電磁気のベクトル・ポテンシャルに相当する A={$g_{4i}$}が存在し、その時間微分 -dA/dt が静止質点に加速度を与え、その回転である重力磁場B=rotA が運動質点の速度との外積 v x Bの項をもつことを示す。
加速度(i) = -測地成分{rs,i} 速度(r) 速度(s)
近似条件として空間計量{$g_{ii}$}を時間計量$g_{44}$と同程度に緩め、$g_{ii} 〜1$(の近く)とする。物質に対する静止条件を緩め、運動を許し、 時空間の混在計量 $g_{4j}!=0$とし、静的計量条件を緩め計量の時間微分!=0とするが、空間計量には座標系を選択し $g_{ij}=0 $(i≠j)とする。 測地成分 $Γ^i_{rs} = \{rs, i\} = g^{ik}[rs, k]$ の$ik$はともに空間であり、空間対角要素〜1、他は=0 とし、$g^{ik}$を1で近似し、 $g^{ik}$を掛けた総和は素通しで $[rs, i]$ に近似し、それだけを考察すればよいとする。 \[ Γ^i_{rs} = \{rs, i\}= g^{ik} [rs, k] 〜 [rs, i] = 1/2 (∂_s g_{ir} + ∂_r g_{is} - ∂_i g_{rs}) \]
rsの両方がr=s=4(時間)のとき、$g_{44}$と$g_{i4}$(i=1-3)が関係する。速度積は時間比率の2乗$(dx^4/ds)^2$である。静止物体にも働く加速度である。
\[ -[44, i]= -{1\over 2} (∂_4 g_{i4} + ∂_4 g_{i4} - ∂_i g_{44})= - ∂_4 g_{i4} + {1\over 2} ∂_i g_{44} = - d{\bf A}/dt - grad φ \tag{16} \]
加速度(i) = -測地成分{44,i} (dx^4/ds)^2
運動質量がなければ$g_{i4}=0$、定常計量では$∂_4=0$、式(16)は第3項の$g_{44}$の勾配、$-grad φ (φ= \sqrt{-g_{44}}) $ ニュートン重力だけになる。 第1,2項の和 $-∂_4g_{i4}$は、運動質量が発生する${\bf A}= \{g_{i4}\}$ の時間微分${-d{\bf A}/dt}$ であり、両者は、電磁気の電場 ${\bf E}= -d{\bf A}/dt -grad φ$を再現する。このAの回転 rot A は、重力磁場 B として次の(2)に現れる。
rsの一方がr=4(時間)で他方がs=1-3(空間)なら、sをjと書き、速度積は時間比率$dx^4/ds$と速度$v^j$との積である。質点速度に比例する加速度を与える。
\[ -[4j, i] v^j = -{1\over 2} (∂_j g_{i4} + ∂_4 g_{ij} - ∂_i g_{4j}) v^j= - {1\over 2} (∂_4 g_{ij} v^j + \{{\bf V}\times rot {\bf A}\}_i) \tag{17} \]
加速度(i) = -測地成分{4j,i} (dx^4/ds) 速度(j)
i=1-3は加速度の3成分、j=1-3は質点速度の3成分である。rsの両方が時間となるから係数1/2は消える。全体48種のなか18種である。 これには第1,3項の(a)重力磁場の項と第2項の(b)空間計量の時間変化の項とがある。運動質量がなければ(a)の$g_{i4}$は0、定常計量では(b)の$∂_4$で0になる。
(a)重力磁場の項
式(17)の第1,3項の交代的な$ -(∂_j g_{i4} - ∂_i g_{4j}) v^j$ は、${\bf A}=\{g_{i4}\}$、$rot {\bf A}= {\bf B} =∂_j g_{i4} - ∂_i g_{4j}$ のとき、${\bf v} \times {\bf B}$ のi成分であり、重力磁場${\bf B}$のなか速度${\bf v}$の質点にコリオリ加速度を与える。 j!=iの非0値の6項を、j,i=1-3をx,y,zと書き、ベクトル表示し、 \[ \begin{align} -(∂_r g_{i4} - ∂_i g_{r4}) v^r= - ( &(∂_z g_{x4} - ∂_x g_{z4}) v^z + (∂_y g_{x4} - ∂_x g_{y4}) v^y , \\ &(∂_x g_{y4} - ∂_y g_{x4}) v^x + (∂_z g_{y4} - ∂_y g_{z4}) v^z , \\ &(∂_y g_{z4} - ∂_z g_{y4}) v^y + (∂_x g_{z4} - ∂_z g_{x4}) v^x) \end{align} \tag{26} \] は、${\bf B}= \{∂_y g_{z4} - ∂_z g_{y4},\ ∂_z g_{x4} - ∂_x g_{z4},\ ∂_x g_{y4} - ∂_y g_{x4}\}$ とすれば、 \[ = -( (B_y v^z - B_z v^y) , (B_z v^x - B_x v^z) , (B_x v^y - B_y v^x) ) = -\{{\bf B} \times {\bf v}\}_i = \{{\bf v} \times {\bf B}\}_i \] $B_k= (∂_j g_{i4} - ∂_i g_{j4})$ (kはi!=jの残りの空間成分)は、i,j面${\bf A}$の回転を表すベクトル成分。 $-(∂_j g_{i4} - ∂_i g_{j4}) v^j= \{{\bf v} \times {\bf B}\}_i$は、速度と重力磁場の外積が質点に与える加速度のi成分であり、 電磁気の磁場中で速度をもつ電荷へのローレンツ力 ${\bf F} = q({\bf v} \times {\bf B}), {\bf B} = rot {\bf A}$ と同形式である。 質量と電荷が別のため電磁気では電荷比例の力、重力では質量によらないコリオリ加速度と表れる。
(b)空間計量の時間変化の項
式(17)の第2項、 $-1/2 ∂_4 g_{ij} v^j$は、空間計量の時間微分と速度の積が加速度を与える。空間計量が距離及び速度の係数だから、 加速度に空間計量の時間微分が表れる。運動方向jと関係してi方向に作用する抵抗/反抵抗で、電磁気にはない項である。空間計量 $g_{ij}$ の増加時に抵抗、減少時に反抵抗である。空間計量$g_{ij}$の減少する膨張宇宙で速度$v^j$をもった質点がi方向に加速される現象を意味する。 i=jでも作用するから、$g_{ii}$の増減を考慮すればよい。
rs共に空間(r,s=1-3)ではrsをjkと書き、$[jk, i]$の3項は全て空間計量の空間微分に $v^j v^k$ の速度積が掛かる。3x3x3=27 (=48-3-18) 種の項がある。 速度積は、$g_{jk}=0 (j!=k)$とし、$g_{jj}$をみるとき質点速度の2乗になる。
\[ -[jk, i] v^j v^k = -{1\over 2} (∂_k g_{ij} + ∂_j g_{ik} - ∂_i g_{jk}) v^j v^k \tag{18} \]
加速度(i) = -測地成分{jk,i} 速度(j) 速度(k)
第1,2項は $g_{jk}= 0 (j!= k)$から、j,kの何れかがiに一致するとき非0プラス項が各iに6項あり、一致の他方をlと書いて $∂_l g_{ii} v^i v^l $と表せ、 第3項は j=kのとき非0マイナス項が各iに3項あり、一致したj,kをlと書いて $- 1/2 ∂_i g_{ll} (v^l)^2$ と表せる。(両者は元のi=j=kで重なる)。すなわち、 \[ -[jk, i] v^j v^k = -∂_l g_{ii} v^i v^l +{1\over 2} ∂_i g_{ll} (v^l)^2 \tag{19} \] 以上、(1)〜(3)に分類して説明したが、 共通に i= 1-3, r,s= 1-4 の $-Γ^i_{rs}= -g^{ik} [rs, k] $の$g^{ik}$のikは空間であり $g_{ij}= 0(i!= j)$から、$g^{ik}$ を対角要素は1、他は0で近似でき $g^{ik}$ を掛けた総和は素通しである。 \[ -Γ^i_{rs}= -g^{ik} [rs, k]= -[rs, i] \tag{20} \] 空間計量$g_{jk}=0$ (j!=k)では、ニュートン重力の項と、空間計量の勾配に後方の速度積を乗算した項とをもつ。 \[ {∂^2x^i \over ∂s^2}= {1 \over 2} ∂_i g_{44} - ∂_j g_{ii} v^i v^j + {1\over 2} ∂_i g_{jj} (v^j)^2 \tag{21} \] 速度$v^j$がi方向と一致するとき$-∂_j g_{ii} (v^i)^2 + 1/2 ∂_i g_{jj} (v^j)^2 $ は、$ -1/2 ∂_i g_{ii} (v^i)^2 $で、 空間計量$g_{ii}$(i= 1-3)は速度の2乗を伴って、時間計量$g_{44}$と同程度にともに勾配として現れる。 静的計量には時間計量と同様に空間計量の勾配が現れ、それが質点速度の2乗に比例する。 \[ {∂^2x^i \over ∂s^2}= {1\over 2} ∂_i g_{44} - {1\over 2} ∂_i g_{ii} (v^i)^2 \tag{22} \] 天体の側で半径方向の計量$g_{ii}$の標準値1からの偏差ηが時間計量$g_{44}$の標準値-1からの偏差ηと等しい(空間計量が1+ηで時間計量は-1+η) とき、時間計量の勾配に空間計量の勾配が質点速度の2乗に比例して追加され重力が増大する。重力による質点運動の折曲は、(22)から速度が光速に 近いとき2倍まで増加することは、太陽の側を通過する光線の折曲がポテンシャル理論の2倍であることと整合する。 空間計量の項は、速度又は速度積に比例し、静止質点には加速度を及ぼさない。
式(19)から
\[
-[jk,i] v^j v^k = -∂_l g_{ii} v^i v^l + 1/2∂i g_{ll} (v^l)^2
=-(∂_x g_{ii} v_i v_x + ∂_y g_{ii} v_i v_y + ∂_z g_{ii} v_i v_z) + 1/2 (∂_i g_{xx} v_x^2 + ∂_i g_{yy} v_y^2 + ∂_i g_{zz} v_z^2)
\]
天体方向をx, それに垂直な2方向をy,z として、$g_{xx}=1+η, g_{yy}= g_{zz}= 1(const)$とする。
質点位置は、(D,0,0)
(a) 質点速度vをx方向とする ${\bf v}= (v_0, 0, 0)$ のとき、
加速度のx成分i=1は、$ = -∂_x g_{xx} v_x^2 + 1/2 ∂_x g_{xx} v_x^2 = - 1/2 ∂_x g_{xx} v_0^2$
加速度のy成分i=2は、$ = 1/2 ∂_y g_{xx} v_x^2 = 0 (∵ ∂_y g_{xx} = 0)$
加速度のz成分i=3は、$ = 1/2 ∂_z g_{xx} v_x^2 = 0 (∵ ∂_z g_{xx} = 0)$
$g_{xx}= 1+η (η= κM/4πr) $は天体の近くで大きく $∂_x g_{xx}>0$であるが、$- 1/2 ∂_x g_{xx} v0^2$は、測地線方程式で同符号になり、
天体の方向 x に向かう。その大きさはニュートン重力に対して$v_0^2/c^2$ に比例する。
(b) 質点速度vをy方向とする ${\bf v}= (0, v_0, 0)$ のとき、
加速度のx成分は後半のみで、$ 1/2 ∂_x g_{yy} v_y^2 = 0 (∵ ∂_x g_{yy} =0)$
y成分は、 $= -∂_y g_{yy} v_y^2 + 1/2 ∂_y g_{yy} v_y^2 = 1/2 ∂_y g_{yy} v0^2 = 0(∵ ∂_y g_{yy} =0)$
z成分は、 $= 1/2 ∂_z g_{yy} v_y^2 = 0 (∵ ∂_z g_{yy} = 0)$
全て、0となる。天体の側を真横に通過する質点への重力がニュートン重力から増加しない。しかし、屈折の経路の前半で天体に接近し
後半は離れる経過を考えれば屈折も(a)が使用できる。加速には速度の2乗が働くので、天体に接近中も離反中も天体方向の引力増加である。
x方向にDだけ離れ、y方向にy離れた位置の$v_y$は、天体方向成分$v_y sinθ $をもち、その方向のx成分は$v_y sinθ cosθ$である。
$∂_x g_{xx}= κM/4πr^2 , r= D/cosθ $加速は$ a_x= (v_y sinθ)^2(∂_x g_{xx}) cosθ = v_y^2 sin^2θ(κM/4π cos^2θ/D^2) cosθ$
の$θ$の$π/2〜-π/2$の積分として計算できるだろう。
天体の側の時間計量(-1+η)と空間計量(1+η)はともに同程度の偏差をもち、ニュートン重力(時間計量の勾配(-grad))だけでなく、高速粒子には より強い重力が働き、そして、"一般相対論の基礎"において、光の重力による屈曲もこの空間計量の偏差 が同じく使用されたのは、それが質量のある粒子であれ光であれ時空間のなかの測地線という経路が質量によって用意されているからである。 時計と物差しという計量がともに変形して長さを変えることがこのような事態を生じる。
成分がほとんど0になる(a),(b)以外、(c)質点速度が天体の方向から45度のとき、質点速度をxy方向とする v= (v, v, 0) のとき、
Ax= [-1/2 ∂_x (g_xx-g_yy) - ∂_y g_xx ] v^2
Ay= [-∂_x g_yy - 1/2 ∂_y (g_yy-g_xx) ] v^2
Az= 1/2 ∂_z (g_xx + g_yy) v^2
∂_x g_xx だけ非0から Ax= - 1/2 ∂_x g_xx v^2 だけ。(a)と同じ方向、1/2の大きさである。
電磁気のMaxwell方程式の4つの式の重力への再現において、次の1. 2.は成立する。
1. 磁場の時間変化は電場の回転 (dB/dt= -rotE): $(d{\bf A}/dt)_i= ∂_4 g_{i4}$ がニュートン重力grad $φ$に加算され、 ${\bf B}= rot {\bf A}= ∂_j g_{i4} - ∂_i g_{j4}$。 -[44,i]である ${\bf E}$のなかの -rot grad $φ = {1\over 2} (-∂_{ji} g_{44} +∂_{ij} g_{44} )= 0$から、 -rot ${\bf E}= ∂_{4j} g_{i4} - ∂_{4i} g_{j4} = d{\bf B}/dt.$ は自明である。
2. 磁場の発散は0 (divB= 0): rotのdivが0という必要もなく、計量の成分を記述すれば=0であることが分かる。 \[ ∂_ xB_x +∂_ yB_y +∂_ zB_z= (∂_{xy} g_{z4} -∂_{zx} g_{y4}) +(∂_{yz} g_{x4} -∂_{xy} g_{z4}) +(∂_{zx} g_{y4} -∂_{yz} g_{x4}) = 0 \]
($∂_{xy}$ は、$∂_x∂_y$の意。)
次の3. 4.は、電磁気と一致しないだろう。$Γ^i_rs$の積を含む非線形の 「重力方程式」に関係するから、その線形近似式が電磁気と一致するだろう。
3. 電場の発散は物質密度 (divE= ρ):
$-[44,i]= -∂_4 g_{i4} +{1\over 2} ∂_i g_{44}$は電磁気の電場
${\bf E}= -d{\bf A}/dt -$grad $φ$ に対応し、$div{\bf E}$は、$-∂_{i4} g_{i4} +{1\over 2} ∂_{ii} g_{44}$ である。
4. 磁場の回転は電流と電場の時間変化 (rotB= dE/dt+i):
\[
\begin{align}
rot {\bf B}= & \{ (∂_y B_z - ∂_z B_y), (∂_z B_x - ∂_x B_z), (∂_x B_y - ∂_y B_x) \}=\{\\
&(∂_{xy} g_{y4} - ∂_{yy} g_{x4} - ∂_{zz} g_{x4} + ∂_{zx} g_{z4}),\\
&(∂_{yz} g_{z4} - ∂_{zz} g_{y4} - ∂_{xx} g_{y4} + ∂_{xy} g_{x4}),\\
&(∂_{zx} g_{x4} - ∂_{xx} g_{z4} - ∂_{yy} g_{z4} + ∂_{yz} g_{y4}) \}= ∂_{ki} g_{i4} -∂_{ii} g_{k4} (k,i=1-3)
\end{align}
\tag{30}
\]
例えばx成分に$ +∂xx g_x4 -∂xx g_x4 (=0)$の2項を加算すれば、
+の項の加算は、空間成分の方向微分和(div)の勾配のx成分$(grad(divA))_x$ を与え、
-の項の加算は、$A_x$ の空間2階微分の和を与える。y成分、z成分も同様である。
式(30)の右辺2項は、ベクトル公式$ rot(rot {\bf A})= grad(div {\bf A})- Δ{\bf A} $ に対応していて、k成分を与える。
\[
\begin{align}
(rot {\bf B})_k&= ∂_{ki} g_{i4} -∂_{ii} g_{k4} \\
(-d{\bf E}/dt)_k&= ∂_{44} g_{k4} -{1\over 2} ∂_{4k} g_{44}\\
div{\bf E} &= -∂_{i4} g_{i4} +{1\over 2} ∂_{ii} g_{44}
\end{align}
\tag{30-1}
\]
計量が電磁気法則を満たす左辺は、rot ${\bf B} - {d{\bf E} \over dt}$とdiv ${\bf E}$とが4元ベクトルをなし、右辺は電磁気では電流密度の(k成分の)ベクトルiと電荷密度ρだが、 $v^i v^k$に比例し、i,kについて対称か交代でi,k=1-3が運動量、i,k=4がdiv${\bf E}$で密度であるべきである。 i=1-4, k=1-3 において、 \[ (rot{\bf B} -{d{\bf E} \over dt})_k= ∂_{ki} g_{i4} -∂_{ii} g_{k4} + ∂_{44} g_{k4} - {1\over 2} ∂_{4k} g_{44} \tag{30-2} \]
はk=4で、$(rot{\bf B} -{d{\bf E} \over dt})_4= div{\bf E}$ を満たすか。 質量が質点を引く符号は-で $divE= -ρ$、(30-2)式が $-ρ$と$-{\bf i}$ の4成分をもてば電磁気類似となる。
(引用開始)
最初に我々は、$γ_{44}$ を1次のオーダーの小ささと考える。重力の影響のもとに運動する質量の速度の 2 乗は、エネルギーの式に従って、 同じオーダーである。それゆえ、我々の考慮する物質粒子の速度だけでなく、場を発生する質量の速度も同様に、オーダー 1/2 の小ささと みなすのは論理的である。我々はいま、場の方程式 (101) と運動方程式 (90)、その考慮する項については、(90) の第2項のなかの速度に 線形なものに限り、起きる式のなかの近似を実行する。 さらに我々は、ds を dl に互いに等しいとは置かず、より高次の近似に対応して、次のように置く。 \[ ds= \sqrt{g_{44}} dl = (1 - {γ_{44} \over 2}) dl. \] (90)から最初に我々は次を得て、 \[ \tag{116} {d \over dl} [(1 + {γ_{44} \over 2}){dx_μ \over dl}]= - Γ^μ_{αβ} {dx_α \over dl}{ dx_β \over dl} (1 + {γ_{44}\over 2}). \](引用終わり)(101)から、我々は、探した近似までに次を得る。 \[ \tag{117} \begin{align} -γ_{11}= -γ_{22}&= -γ_{33}= γ_{44}= {κ\over 4π} ∫{σdV_0\over r}\\ γ_{4α}&= -{iκ\over 2π}∫{σ{dx_α \over ds} dV_0\over r}\\ γ_{αβ}&= 0 \end{align} \] ここで、(117)では、$α$と$β$は、空間添字だけを示す。
(116)の右辺で我々は、$1+{γ_{44}\over 2}$ を 1 に、$-Γ^μ_{αβ}$ を $[αβ, μ]$に、置き換えることができ、それに加え、この近似の程度には、 我々が次を置かなければならないことを容易にみる。 \[ \begin{align} [44, μ]&= -{1\over 2}{∂γ_{44}\over∂x_μ} + {∂γ_{4μ} \over ∂x_4}\\ [α4, μ]&= {1\over 2}({∂γ_{4μ}\over ∂x_α} - {∂γ_{4α}\over ∂x_μ})\\ [αβ ,μ]&= 0 \end{align} \] ここで、$α$, $β$, $μ$は、空間添字を示す。我々は、それゆえ、(116)から、通常のベクトル記述で、次を得る。 \[ \tag{118} \begin{align} {d \over dl} [(1 + ~σ)v] &= grad ~σ + {∂{\bf A}\over∂l} +[curl{\bf A}, {\bf v}]\\ ~σ&={κ \over 8π}∫{σ dV_0 \over r} \\ {\bf A}&= {κ \over 2π} ∫{σ {dx_α\over dl} dV_0 \over r} \end{align} \]
ここで我々の考察を纏め、質点に働く加速度は、 \[ {∂^2 x^i \over ∂s^2} = r2\{ -∂_4 g_{i4} + {1\over 2} ∂_i g_{44} - (∂_r g_{i4} - ∂_i g_{r4} +∂_4 g_{ir}) v^r - (∂_j g_{ii} v^i v^j - {1\over 2} ∂_i g_{jj} (v^j)^2)\} \tag{32} \]
または、ベクトル表記を使えば、 \[ {∂^2 x^i\over∂s^2} = r2\{ (-d{\bf A}/dt - gradφ)_i + (\{{\bf v}\times rot{\bf A}\}_i - ∂_4 g_{ir} v^r) - (∂_j g_{ii} v^i v^j - {1\over 2} ∂_i g_{jj} (v^j)^2)\} \tag{33} \] 第1項はベクトルポテンシャルAの時間微分、第2項はスカラーポテンシャル$φ= \sqrt{-g_{44}}$の勾配。第3項は速度に比例するローレンツ力、 第4項は速度と空間計量の時間微分に比例する抵抗/反抵抗、第5,6項は速度積に比例する空間計量$g_{ii}$の勾配和及び、空間計量$g_{jj}$の勾配にあたる。 引用の式(118)は第3項まで記述し、式(32)とは符号が逆である。式(118)では慣性としてポテンシャルに関係する$1+~σ$が取られたが、質点の固有時を$ds$とし、 時間$dx^4$との比の2乗$1/r2=(ds/dx^4)^2$が慣性(3,4項もr2が掛かる)となる。大質量の側で慣性は大きく、時間比率は速度によるものも包含する。
(*) $ds$を観測系の時間$dx^4$とすれば、左辺は加速度で、(1)のrs両方が時間では速度積は正確に1。(2)のrsの片方が時間では速度積の片方は1で他方は速度。 rs両方が空間では速度積は正確に$(速度)^2$になり、速度積と測地成分の積が加速度を決める式となるが、慣性を表示しない。dsを測地線の固有時とすれば、 物体の慣性の大きさを示す。時間比率 $r1= dx^4/ds$は、観測系時間/測地系時間である。速度によらないとした(1)にも質点速度の2次の影響 $r2=(時間比率)^2 = (dx^4/ds)^2 = γ^2 = 1/(1-v^2)$ の"時計の遅れ"がある。式(32),(33)は、測地線時間$ds$に対する加速度が観測加速度の$γ^2$倍であるをいう。 質点の速度$v$は、一般に慣性係数$γ>1$をもたらし、観測される加速度をその$1/γ^2$ に小さくするのである。
重力の電磁気との類似は、類似で収まらず、電磁気が電荷の測地線方程式に基づくのではないか。電磁気の法則は、和で作用する3種類の力 -grad φ、 -dA/dt 、 vxBからなる。電荷(+)の受ける力が質量の受ける加速度になっている。Maxwell方程式は、 4元電磁ポテンシャル (A, φ)が存在すれば自動的に成立するだろう。測地線方程式には他の項の要素もあり、電磁気法則の成立は、近似的である。
以前、光さえ曲がるとき電磁気法則は違う、電磁気法則は慣性系にしか成立しない法則であり、回転系や重力場の中では別の法則が成立するという 考えは、まだ浅薄だった。$rot, div$を用いる微分型の電磁場法則の半分($rot {\bf E}= -d{\bf B}/dt, div{\bf B}= 0$)は、 電磁ポテンシャルを認めるとき数学的恒等式とされるが、もしも電磁気が一般座標系の重力法則、測地線方程式から来ていて、重力が電磁気と同じ法則をもつなら、 重力波伝播が、進行方向に垂直な2方向の空間計量の伸縮という理解は必ずしも必要でない。電場と磁場の両ベクトルが互いに関係して伝播する電磁波的理解 もでき、4元ポテンシャル$\{g_{i4}\}$または、計量それぞれが波動方程式をもつという理解も可能である。複雑な電磁場のベクトル法則は、電磁気独特の法則 ではなく、より根底的な計量テンソルの測地線方程式から導出でき、それによって、より単純に理解できる。
可能な "重力の電磁気との類似性" の意味は、重力と電磁気とが同じ測地線方程式をもち、これが重力と電磁気を別々に扱う結果であろう。そのとき、 電磁気の計量は電荷が作り電荷に働く計量である。電磁気も重力も、場から物質へは近接的に局所に成立する測地線方程式をもち、物質から場へは微分方程式を 大局的に解いてポテンシャル場(背後場)を、それに影響を受ける質量/電荷から求める。そこにいう背後場は、重力では時空の計量$g_{ik}$ であり、電磁気では電磁4元ポテンシャルで、それに4元回転(空間間に$rot$, 時間から空間には$grad$、空間から時間には$div$)して2階反対称テンソル$F_{ik}$として 表せば成分に電場と磁場が現れる。しかし、電磁気にそれ以外の計量成分を考えれば、電磁気の時空法則による理解が可能になる。
一般的な理解、「電磁気は、線形であり時空に乗るだけで質点の時空に関係しない。」は、「時空の法則とは無関係で線形」の意味なら、電磁気力の測地線方程式由来に よって誤りだが、後半の「質点の時空に関係しない」は正しいだろう。電磁気の線形性については、測地線方程式は、時空の曲りの測地成分に関係し、 この測地成分に速度積を掛けて加速度になる。これは電磁気力が速度積と湾曲に双線形を表す。ローレンツ力は質量と速度に比例し、加速度はそれらに比例する。 このように電磁気と重力は作動要素の「測地線方程式」が線形だが、物質が計量を生成する「重力方程式」が非線形のため、重力は非線形、電磁気は線形とされる。
電荷は質点の計量に関係しないだろう。電荷と質量とは、同じ測地線方程式と異なる計量をもち、質量のみる計量は質量が、電荷のみる計量は電荷が決定する。 電荷が計量を作る式は、重力方程式と同一かも知れず、電磁気法則 Maxwell方程式の残りの半分 ($div{\bf E} = ρ , rot{\bf B} = d{\bf E}/dt + {\bf i}$)は、 その近似かもしれない。電荷と質点とが同じ時空計量を共有し電荷計量が時空計量の付属物という意味ではない。 さらに、リーマン曲率を縮約したリッチーテンソル$R_{ik}$は、2階の共変微分を模型としたのではないか。 確かな時空の法則で最も単純で必要を満たすものとしてアインシュタインはそれを選び、 ビアンキの恒等式によって $G_{ik}= R_{ik} -{1\over 2} g_{ik} R $に修正したとき、他の候補はなかったのだろうか。 電磁気を必要最小限に、最も単純に再現する「重力方程式」は何か? を次に考える。
"相対論の意味"では、96aの次にある線形2階微分(i,k=1-3)、 \[ R_{ik}= -{1\over 2} (∂_{44} g_{ik} +∂_{ik} g_{44} -∂_{4k} g_{i4} -∂_{4i} g_{k4}) \tag{34} \] から(96b),(101)を導き、電磁気的な重力が説明された。(34)の第1,2項は44とikは波動方程式に必要な時空の2階微分。第3,4項の運動量はrotの時間微分なら交代的だが 共に負で対称的である。これは計量の微小変化が波動方程式を満たす真空 R_ik= 0に対応した近似である。和が勾配の-2倍は、式(24)の要求を満たす。式(23)から","を 微分記号とし、$[ik,4],4= {1\over 2}(∂_{k4} g_{4i} + ∂_{i4} g_{4k} - ∂_{44} g_{ik}) $ の各項が式(34)の第3,4,1項だから単純に、 $R_ik= [ik,4],4 -{1\over 2} ∂_{ik} g_{44} $ と表される。 しかし(34)はi,kともに空間であり、i,k何れか4なら恒に0であり、密度や運動量に対応する$T_{44}, T_{4k}$を考慮せず、物質との関係が明らかでない。
エネルギー運動量テンソルを$T^{ik}= ρ dx^i/ds dx^k/ds$ とし、密度が$g_{44}$に、その速度が $g_{4i}$ になる$R_{ik}= T_{ik}$の近似$R_{ik}$ を考えるとき、 3. 4.の再現を要する。発散 $∂_i T^{ik}= 0$エネルギー運動量保存も欲しい。但し、重力へ電磁気法則の符号再現はできないだろう。 電磁気は同極が斥力、重力は引力である。電磁気では $rot{\bf B}-d{\bf E}/dt= {\bf i}, div{\bf E}= ρ .$だが重力では左右辺の符号反転、 k=1-3では $rot{\bf B}-d{\bf E}/dt= -ρ{\bf v} $、k=4で$div{\bf E}= -ρ$を再現する(30-2)から、$R_{ik}$の近似(i,k=1-4)、 \[ R'_{ik}= (∂_{ki} g_{i4} -∂_{ii} g_{k4}) +{1\over 2} ∂_{4k} g_{44} \tag{35} \] は、符号反転した電磁気法則を満たすだろう。測地線方程式には電磁気との符号の問題は現れず、近似$R_{ik}$で符号の問題が顕著になり単純化に寄与した。 2階回転、$(∂_{ki} g_{i4} -∂_{ii} g_{k4})$ だけでは、ニュートン重力に関する$g_{44}$の$R_{ik}$への影響が2倍であり、 ニュートン重力とその他のコリオリ力等との大小関係が違ってくる。 重力方程式は未知数10個の連立方程式だが、近似$R_{ik}$は計量全て10未知数を決める必要はなく、電磁気の背後関数4成分だけを導けばよい。(35)は、i,k対称でない。
アインシュタインは重力の測地線方程式の符号を電磁気から反転して解釈し、$R_{ik}$を電磁気と独立に与えたが、我々は測地線方程式は電磁気を模型として解釈し、 $R_{ik}$の電荷符号を電磁気から反転し、電磁気の4元ポテンシャルに対応する計量の自動的な符号反転を図ったが正しいのか。 $g_{ii}$は1の近辺で$g_{44}$は-1の近辺としたのは、アインシュタインと逆なので、測地線方程式の理解が違ってきてしまう。 計量微分が質点に加速度を与える測地線方程式を電磁気から符号反転とみると、質量が計量を生む重力方程式の$R_{ik}$の符号にも反映する。
ニュートン力学では回転系のみかけの力として遠心力とコリオリ力が説明され、"相対論の意味"では、円筒状の大質量が回転するなかで静止系に遠心力とコリオリ力が 表れると説明された。それらみかけの力は回転系の測地線方程式にある筈であり、コリオリ力は重力磁場だが、遠心力は静止質点にも働く(1)にだけ関係し、そのなかでも $grad$は空間微分なので回転系によらず、場の運動量$g_{i4}$の時間微分だけが回転系に関係する。本当の時間微分がない定常な物体の回転又は系の回転のとき、 運動量のみかけの時間微分を加速度にみる。時間微分は、本当の時間微分と系のみかけの時間微分の和である。
ベクトルポテンシャルを$A= \{g_{i4}\}$とし、天体の運動 ($-{\bf v}$) の方向に定義し、ベクトルポテンシャル(そして磁場)の時間変化を防ぐ方向に加速度は働く。 アインシュタインは「相対論の意味」で、天体の側の質点は天体の加速度と同じ方向を受けると書いた。 先の引用部分の少し前 を参照。
電磁気と符号一致する式(32),(33)は、引用式(118)の3項ともに符号反転だが、まずニュートン重力は共に引力である。式(118)はポテンシャルが質量近傍で増大する ~σ= GM/rでありその重力は grad であり、-grad ではない。 ds^2= g_ik dx^i dx^k に対応する慣性系の不変量の式を彼は時間を正、空間を負(ds^2= dt^2 -dx^2-dy^2-dz^2) としたが、私は空間を正、時間を負(ds^2= dx^2+dy^2+dz^2-dt^2)としたから、考察中の全計量は符号反転である。空間計量$g_{ii}$(i=1-3)は1近辺、 時間計量 $g_{44}$は -1 近辺である。ポテンシャルは $φ= √-g_{44}$、$0<φ<1$ 無限遠で1の $φ= 1 - GM/r$ のように、重力はその$-grad φ $になる。 彼の式は慣性(時間遅れ)を$1+~δ$とする。
(118)ではベクトルポテンシャル A が近傍の天体運動の方向に一致するが私は逆である。Aの時間微分が加速度になる点は、式(118)では加速度は空間のもつ 運動量の時間微分 dA/dt であるが、私は A の時間微分の符号反転 -dA/dt である。また、重力磁場 rotA の速度との外積で加速度になるとき [curl A, v] 私は v x rot A であり符号が逆である。全ての計量の符号が逆、A={g_i4}の符号が逆なので打ち消され、両者とも彼と同符号になる。つまり、式は3項とも式の符号は反転だが、 全て物理量は同符号である。
式(5),(5-1)のように、質量に速度vのK'系からみた A'= {g'_4i} は、v 方向、K'系からみた天体運動(-v)と逆方向で、Aは場の運動量である。 天体衝突によってK'系からみた天体運動が0から-vに変化する前後のAの時間変化の負、-dA/dt は、-v 方向である。乗物は、天体の加速度方向の加速を受け、 後ろに弾かれる。これは、電磁気のベクトルポテンシャルAの減少-dA/dtの方向に電荷を加速することと同じである。 重力磁場の働きも電磁気と同じである。(ゆえに、9章と10章は、逆符号になる。)
この問題は、重力の工学で引き続き考察される。
コイルにエネルギーを蓄える電流(または磁場)の変化を打ち消す方向に巻線比例の起電力が発生する。電源投入時に逆電圧を発生し電流を防ぎ、 遮断時に順方向の大電圧を起こし接点に火花を飛ばし電流を保つ。この磁場の時間変化を防ぐ向きに起電力が起きる現象は、磁場の即時的原因(rotA=B)である 電磁気のベクトルポテンシャルAの変化を防ぐ向きに電荷を加速しているのである。電流遮断時には大電場-dA/dtを発生する。 電流と同様に運動する電荷も磁場とAを発生し、磁場を介し電荷に力を与え、Aは、正電荷に運動量を与えるものとされる。 そして、電流に近づく電荷にはAと逆向き、遠ざかる電荷にはAの向きの力を与え、電荷のみるAを保存しようとする。
保存は、磁場のエネルギー保存による rotE = -dB/dt というより、A が電荷に与える運動量の保存の E= - dA/dt - grad φ である。 スカラーポテンシャル φ は電荷の1/Rの空間積分であり、 -grad φ が向くのはマイナス電荷の方向であるが重力ではマイナスを付加する。 ベクトルポテンシャル A は、電流又は電荷速度の1/Rの空間積分である。重力では g_4i が質量運動の逆方向のため、 重力加速 -∂4 g_4i は、-dA/dtに対応するが、符号が逆である。同様に、速度に比例するローレンツ(コリオリ)力も符号が逆になる。 これの理由は、物体が天体への接近によって運動エネルギーを放出し、質量をその分減少しているのである。失った位置エネルギーの代償として 局所には質量と時間経過の低下が存在する。その慣性の削減分が-dA/dtで加速度となる。
次に、電流同士の作用を考える。電流は、動く電荷のローレンツ短縮を含めて電荷を中和しているとすると、電流同士は同方向は吸引、逆方向は反発する。 (これは静電荷の関係とは逆である。) 電磁気の正電荷同士の反発(重力では引力)は、速度v系からみると電場は磁場となり、クーロン力がローレンツ力 で削減されるが符号を変えない。この電磁気力の側面の作用は重力にも適用でき、反発は反発のまま重力の引力は引力のまま速度に従って低下し0に近づく。 並進2質量間の引力は、速度系からみて重力磁場によって弱まる。銀河の腕中質量が腕方向に速度をもつと仮定すれば、腕内の質量は同方向の速度を持ち、 互いの引力が重力磁場によって減少し、反対側の腕の間では引力は弱いながら、逆速度を持つから重力磁場によって増加する。 しかし、我々の銀河系の太陽系近辺の速度の程度(光速の千分の1)では小さく、重力磁場の効果の確認は難しいだろう。 より大速度に達する2つの中性子星やBHの合体過程では確認できる可能性がある。
質量の衆合によるエネルギー抽出が元の静止エネルギーに制限されることは、どのような素粒子の新知見が出ても不変だろう。粒子がさらに素粒子に分離されても、 元の質量を超えるエネルギーを取り出すことはできない。原子核の陽子と中性子の数で核力の結合性が鉄で最大であることから核分裂と核融合があるが、 素粒子研究のエネルギー獲得の目標は、反粒子との結合で質量の100%がエネルギーに変わることで、失っている。
また、ブラックホールに物質が落ち込む現象に、質量の減少は重要である。物質がブラックホールに落下するとき、ブラックホールを凍結星というように、 ブラックホールの地平面近くの外側は無限に平坦化し、物質は地平面にへばりつく薄い膜となって(g_rr⇒ ∞)、時間経過はどこまでも遅くなっていく(g_44⇒ 0)が、 地平面に近づく質量は位置エネルギーを運動エネルギーに変え、互いに接触してエネルギー放出して質量減少する。地平面の時間経過が0から、通過するとき質量 は0ではないか。完全に0ならブラックホール全体の質量は増大できない。こうして落ち込む質量が永遠に落ち込めない疑問と、ブラックホールの質量増加が ありえない疑問があったが、外側点から地平面までの距離は有限である(参照)。無限の値を含む区間の定積分は無限とは限らない。 永遠ではない。質量増加もないとはいえない。
(1) $[44,i]= 1/2 (∂_4 g_{i4} + ∂_4 g_{i4} - ∂_i g_{44})= ∂_4 g_{i4} - 1/2 ∂_i g_{44}$
rsが共に時間の[44,i]、$∂_4 g_{i4}$ は、${\bf A}=\{g_{i4}\}$ とするとき$d{\bf A}/dt$である。
-1/2$∂_i g_{44}$ は、ニュートン重力ポテンシャル勾配$grad φ、φ= \sqrt{-g_{44}}$である。
(1)の項だけが静止質点に加速度を与える。
(2) $[r4,i]v^r= 1/2 (∂_r g_{i4} + ∂_4 g_{ir} - ∂_i g_{r4})v^r$ = 1/2 $(∂_r g_{i4} - ∂_i g_{r4})v^r + ∂_4 g_{ir} v^r$= -1/2 $v×rotA +$ 1/2 $∂_4 g_{ir} v^r$
rsの片方(sとする)が時間である[r4,i]には、$v^r$ r方向の速度が掛かる。1/2 $(∂_r g_{i4} - ∂_i g_{r4})v^r$ = -1/2${\bf v}×rot{\bf A}$ は、
速度比例の重力磁場である。項$∂_4 g_{ir} v^r$はi方向の計量付速度の時間微分。 (2)の項は、質点速度 $v^r$が掛かるため、静止質点には加速度を与えない。
(3) $[jk,i]v^j v^k= 1/2 (∂_j g_{ik} + ∂_k g_{ij} - ∂_i g_{jk}) v^j v^k $
rs両方とも空間の[jk,i]は、j,k 2方向の質点速度$v^j v^k$が掛かるため、静止質点には加速度を与えない。
重力波が仮に、時間計量$g_{44}$の変動や$g_{i4}$の変動なら、静止質点に加速度を与え検出できるが、空間計量$g_{ii}$(i=1-3)の変動なら検出できない。 運動質点には加速度を与えるが、LIGOの静止した鏡には力を与えない。もとより、間隔は力(加速度)なしに伸縮する空間と物体を区別しない物差しを含めた 局所の全ての間隔に空間計量 $g_{ii}$ が掛かる座標変換であるから、局所の間隔を局所の光の波長で測ることは意味をなさない。
私は重力波を空間計量の変動と誤解し悲観的な意見を述べてきた。誰も誤解していない? いや、その点で、全ての人が誤 解していたのだ、波の進行方向に垂直な平面内の2方向に伸縮する空間計量と多くの教科書にあるし、LIGOは、垂直に交差するふたつの腕をもち、両者の 差である光の位相差をみた。計量の他の成分を考えるなら、どうして、ふたつの腕を垂直に交差させたのか。誰もが空間計量の変動が2腕の距離の差として表われ、 それが光の変わらない物差しで測定できると素朴に誤解していたのではないか。 空間計量の変動は、実は物差しの変動であって、光の波長が間隔と同じだけ伸縮すると空想できたなら、LIGOは決して、このような特殊相対論以前のエーテル論者の マイケルソン・モーリー装置を模した不吉な構造の設計をしなかっただろう。この形態を不吉にする理由は、それがもつ相対論の歴史である。
マイケルソン・モーリー実験は、地球の絶対速度、エーテルに対する速度 30km/sを測定できるはずだったが、いつまでも望みの結果を得ず、そのため実験は、 マイケルソン実験、マイケルソン・モーリー実験、モーリー・ミラー実験と続いた。当時の学者の頭を疑ってはいけない。科学者は常に一寸先が見えないものである。 実験者は、その原因を突き止められず、その精度を向上するために、多重反射で短い腕の中を何度も反射させ、実効的な長さを何百倍にもした。 得られるはずの実験結果がいつまでも得られない "ヌル検出" であることは、実験者の悪夢である。最悪さは、それだけではない。最終的に考え方の誤りとなる。 測定できる筈の絶対速度が、元もと存在しないでは測定できるわけがない。考え方の前堤のミスは気が付くことが難しい。 これは論理的思考を訓練した筈の科学者にも著しい。これが当時の彼らを相対論に対して頑迷にした。古典的物理学者は、エーテルに「実体性」を求めた。 "量子と実在"、ニック・ハーバート著、はやし・はじめ訳、白揚社 p.23からの引用。
イギリスの指導的物理学者、かの高名なウイリアム・トムソンのちのケルビン卿が、マイケルソン・モーリーの実験の数年後に語った次の言葉は、 物理学者の一般的な態度を示すものであった。 "私たちにとって確実なことが一つある。それは、光エーテルの実在性と物質性(substantiality)である。"
それほど相対論は基本的な時空概念に変更を要求した。ローレンツとフィッツジェラルドによるエーテル圧縮によるローレンツ短縮を仮定して一部理解でき、 それがさらに、アインシュタインによる、時空の座標変換 "ローレンツ変換" という古典的な時空間概念の否定によって正しく把握できた。時間も空間も 絶対的でなく両者は一部入れ替わる。人々は、最初、存在する筈として測定し、測定できないのには理由があると考え、最後に「エーテルは存在しない」となった。 相対論は物理学の依って立つ基本的概念である時間と空間の根本的な変更であった。そこには大きな抵抗があって当然である。 物理法則は慣性系間のローレンツ変換に耐え得る "ローレンツ共変" な記述をすべきとした。しかし、それはまだ特殊相対論である。
それに対して、重力を扱う一般相対論は、より理解を困難にした。慣性系だけでなく全ての一般座標変換において共変な法則記述を求めた。座標系が曲線になり、 特殊相対論の不変量の式を微分の線形の2次同次式で表し、特殊相対論を局所の微分に適用する。そのなかで基準である局所慣性系の不変量への微分2次項の 係数 $g_{ik}$ を "計量" という。計量は時空点によって違う値をもち、重力以外の外力をなくした局所慣性系に常に移行でき、計量は時空点の性質を示す。 局所の物理法則を表す数学は難解となり、ユークリッド空間を放棄し、当時完成したリーマン空間を使わざるを得ず、ベクトルは大きさ又は方向を変えずに 平行移動さえできない。速度ベクトルを移動してベクトルの違い(共変微分)を0にして導かれる「測地線方程式」は、計量場の微分の方向差と質点の速度積が 質点に加速度を与える、一般座標系の重力を示す方程式であり、「重力方程式」の名は測地線方程式に相応しい。逆に一般的にいわれる「重力方程式」は、 計量場の2階微分にあたるアインシュタインテンソルと質量との関係であり、ラプラス、ポアソンの方程式、ダランベールの「波動方程式」と同様に、 グローバルに周囲の物質分布から計量場を与える微分方程式である。重力方程式という名に相応しくない。多くの学者が正しく理解しなかった証拠である。
遠隔力のニュートン重力を否定し、近接作用の場の物理によって重力を説明するには、計量変動は伝搬する必要があった。電磁気力も遠隔作用を避けるために 必要であった電磁波がマックスウエルによって定式化され、それが光の速度をもち、光もその一種であるとされ、それがヘルツによって実際に発見され、送受信、 反射屈折、速度が測定され、20世紀の通信の時代に大きく利用された。電磁波と同様に計量変動の伝播は「原理的な要請」であった。しかし、我々は一般相対論の 計量をエーテルとみるエーテル論者の道具を引き出してきた。彼らにとって、系のもつ絶対速度「エーテルの風」は測定できなかったが、 真空を通して遠方から物質を揺動させる「エーテルの波」が測定されれば、真空を嫌い空間を充填するエーテルの実在性の証明と受け取られる。
マイケルソン・モーリー実験は、今でも当時の測定データを整理して、特殊相対論を否定する論文が作られる、前相対論的、絶対時空の証明実験である (相対論 19 あとがき)。それがなぜ、一般相対論の重力波に関係するのだろうか、計量は(宇宙項を例外とし) 質量だけから 存在し、真空を充たす非物質的存在で、真空に特性を与え、場の背後にあって、その微分が物質に作用するエーテルとみなせるからである。重力波という一般相対論 の重力変動を伝播する波動は、計量変動として非線型な時空に微小なさざ波として線形の波動方程式をもち、電磁波のように正のエネルギーをもつ波動として伝播する(*)。 真空は、そのとき光だけでなく重力波の媒体でもある。それは我々に、エーテル論に逆戻りするのか、と問う。
そのとき、アインシュタインは、一般相対論の真空は、速度をもったエーテルではない、計量という存在が速さの概念に似合わない、時空のなかの軌跡を追跡できる 存在ではないことを "エーテルと相対論"(1920)の末尾で注意した。これを彼は、「このエーテルは、 時間のなかを追跡できる部分からなる、重さのある媒体の性質を備えると、考えることはできない。 動きのアイデアは、それに適用できない。 」といった。 これは膨張論に関係する。重力波に関しては、時空点の計量変動がどう力学に結び付くか、空間計量の変動は殆ど測定できず素通りであることを知る必要があり、 これを明確に示すのが、計量が質点に加速度を与えるみかけの力(=重力)を記述する、測地線方程式である。
測地線方程式はいう。空間計量 g_ii (i=1-3)は局所の物差しである。その値の違いは局所に知り得ない。g_ik 自体である物差しの長さと時計の速さとは、 局所の測定に掛からない。そして、物差しの時間的変動は、静止質点に加速度を与えない。それは速度をもった質点には加速度を与える。静止質点に 加速度を与えるのは、ベクトルポテンシャル時間微分の負(-dA/dt= -∂4 g_i4)と、時間計量の勾配(-gradφ= 1/2 ∂i g_44)とだけである(**)。 速度に比例する加速度は、重力磁場のような項とひきずり項がある。速度の2乗に比例する項もある。重力波が空間計量の変動なら、静止質点に加速度を 与えない。さらに空間計量g_ii自体は、局所の光の波長では測定できない。ゆえに、2重の意味で、LIGOの光干渉測定に掛かることはない。
重力波がそれでも検出されたということは、重力波が空間計量の変動でなかった証拠であろう、空間計量の変動は静止質点を決して動かさないのだから。 それは、各々が確定値をもち差分0が誤差で測定された(2腕差より、各々に明確に出ていた)のかもしれない。それは、g_44 時間計量、ポテンシャルの波 だったかもしれない。距離は√ g_ii (i=1-3) に比例し、光速が√(-g_44/g_ii)に比例するから、光で測定した時間には 1/√(-g_44)が掛かり、 波長でなく周波数に関係し両腕の差で消えるが、誤差又はデータの操作によって測定に出る可能性がある。
(*) 計量変動の全成分は独立にダランベールの波動方程式をもち光速伝播する。 又は"相対論の意味"
(**) その勾配が加速度を与えるφ=√-g_44は、ニュートン由来で時計の速さを与える。その時間微分が加速度を与えるベクトルポテンシャル項 A= {g_i4}が存在し、電磁気に類した重力を与える。時間計量の時間微分∂4 g_44は加速度を与えない。
重力波の音、ハンフォードH1のほうは、よく聞き取れる。リビングストンL1は、ノイズが大きくて確かでない。2重BHや2重中性子星の結合でこのような音 になると数年前から放送されて知る典型的な上昇チャープである。これは以前の疑似信号でないのか、さすがにそれはないだろう、用意周到の発表だから。 PRLには 10^-21 までの振幅の波形である。これなら、advanced LIGO でなくても、LIGOでも、GEO600でも、検出できた 筈である。GEO600は休止中だったという。検出は、非常に稀な宇宙的に大規模な事件への偶然の遭遇によるだろう。
しかし、とにかく、一件落着、おめでとう、Congratulations! である。 1989年からのLIGOの苦闘は、終わった。
発見は高く評価され、検出前よりも関心が薄れるだろう、LIGOの重力波検出の構造的問題:
(1) 重力波を空間計量の波動と考え、(これは誰の研究が元か詳しくないが、パウリの「相対性理論」(p.288)にもある。)
(2) それに基づいて直角の2方向にファブリ・ペロー型共鳴を使ったこと、(これは原理的にマイケルソン・モーリー型干渉計と同じ)
(3) 空間計量が局所検出できないこと、 (慣性系と比べて分かることは時間計量と同じだが、より困難な空間計量という計量考察)
(4) 空間計量の時間微分も空間微分も静止質点には加速度を与えない。(動質点に与える。これは測地線方程式を解析して分かる。)
(5) 空間計量に依存する光の波長を物差しとして物体間隔を測定したこと。(光も物体も間隔と同じく伸縮することの理解の欠如。)
LIGOの重力波研究が基礎的知見なしに原理的な問題に全く触れずに、重力波を検出しようとした。相対論の専門家と思わせる何百人もの著者 の集団論文は10年以上続いたが、内容はそれである。LIGOの道具立ては、測地線方程式と相対論自体に反する思考の道筋を自ら示している。 その肯定的結果は、相対論を解する人がいれば中止可能な数10年だったとは、永く認識させないだろう。
空間計量は観測できない、重力波が検出された、故に重力波が空間計量でない、という論理は、正しくないかもしれない。重力波の大半のエネルギーを 空間計量が持っていて、少しあるその他の成分が静止質点を振動させた可能性もある。いずれにしても観測装置の、2方向の位相差検出は疑うべき道具 である。L字型の2本の腕の間の反射光の位相差でなく1本毎に投入光と反射光の位相差をみれば、空間計量以外が働いて両腕が同じ伸縮するとき、差で 消されることがない。時間計量の変動は、両腕に同位相で表れる。片腕の装置も、2方向の位相差検出と同じく、空間計量とその変動は観測できない。
重力波検出にはどういう方式がよいか?
ポテンシャル変動検出である。空間計量は基本的に検出が難しい。時間計量g_44の変動を検出すべきである。 時間計量の変動検出は、空間計量の変動検出よりも遥かに容易である。γ線と結晶の鋭い共鳴を使って数10mの高低差による時間経過の違いを検出器を動かして ドップラー効果で調べたメスバウワー効果(1958)のように、g_44変動は時間経過の変動で、そのまま光などの周波数変動になり、変動は遠方に伝播する波になる。 それが伝播しなければ全てのニュートン重力の変動はないから重力波に含まれない筈はない。全ての計量の微小変動は、ほぼ独立に波動方程式をもつ。g_44変動は、 横波ではなく縦波である。なぜなら、x方向に平面波が伝わるとき、空間計量全体が時間計量に対応することはあっても、またx方向だけは違うことはあっても、 進行方向に垂直な面内のy,z方向の間に違いがないからである。マイケルソン・モーリー型光干渉計は、片腕で十分であり、両腕差はg_44信号を消すだけである。 空間計量全体の和は体積変動であるが、計量と不変量の基本的関係式 ds^2= g_ik dx^i dx^k が示すように時間計量に対抗して変動する。
それは周波数の一定のレーザー光線の離れた所での反射光との周波数差の検出でよい。反射鏡は、一定時間ずらした過去の光を得るためにあって、光の遅延線の働き である。例えば月面にはアポロが50年前に置いてきた3面鏡の反射鏡がある。鏡はある程度離せるなら月でなくてもよいが、 LIGOの片腕4km(26μ sec)程度はまだ局所局時 である。本当の光遅延線でも数100kmが可能である。鏡との空間的なポテンシャル差は、往復で打ち消される。反射鏡との距離は、重力波によって光の波長で測定する 距離が変動すると考えていたLIGO等の光干渉とは逆に、測定点と鏡の距離は変わらないとする。(前述のように、重力波による空間計量の変動は鏡の距離を変えない。) 一定距離からの反射によって、往復時間だけ遅れた反射光と現在の送信光との光干渉を使った周波数の差は、送信受信時刻のポテンシャル(時間計量)の差を与える。 周波数差は、干渉計の位相の時間微分で、周波数差によって位相は徐々に進み/遅れて大きな差になっていく。この場合、差分の位相が停止することは期待せず、 干渉の明暗の周期を計測する。LIGO等の光干渉は完全な位相停止を利用した強力な光出力(20Wレーザーは半鏡入力時700W,共鳴によって100kWに増強)の暗点近くの 微小変動の測定であった。それよりも、ずっと緩やかな測定になる。しかし、鏡との距離が一定でないとき、鏡の速度によって、送受信の光干渉は一定の位相でなく 一定の周波数差として表れる。大気のゆれ、地震や月の軌道の問題を避けるには、測定器と鏡、両者を宇宙に上げ、地球の陸海の重力異常の影響を避けるために、 軌道は地球からできるだけ離した方がよい。
LIGOで開発された精密測定技術は利用できるなら利用すべきだが、ファブリペロー型共鳴は使えないと思う。10^-21 の変動なら、月との往復76万km(約10^9 m)に対して 10^-12 m (10^-3 nm)では測定不可能だろう。時間計量の 10^-21 は、300nm の青色光で、30万km/300nm= 10^15 Hz からビート周期は 10^6 sec必要だがこれも無理だ。 実際は、時間計量は10^-15も変動するかもしれない。その場合 1Hz のビート。月の距離は1月に38万kmの1割、4x10^7m/(15x86400)= 30 m/secも変動する。
ポテンシャル変動は局所独立に測定できない。必ず少し離れた時刻との差分の計測である。光の往復時間を例えば2秒とすると、2秒前の光と現在の光との干渉(等しい強 さの光の和)は、時刻tのポテンシャルと2秒前のポテンシャルとの差 P(t)-P(t-2) による周波数の差のビートをもつ。ビートが変動するとき、これが2秒前のポテンシャル 変動か、現在のポテンシャル変動か区別するには、2秒前の観測 P(t-2)-P(t-4) と加算すれば 2秒前の変動を打ち消し、現在と4秒前とのポテンシャル差になる。ポテンシ ャルの計測は、こうした過去の計測との和によって多少とも独立に抽出できる。さらに、和をとるのが2秒前の既に和によってそれ以前の影響を無くした処理後信号なら、 現在の信号だけを取り出せる。周波数差を取り過去との和を取るのは可能な限り連続的にでき、しかも、2秒より長い変動をも抽出できる。そのため、短めの反射鏡までの 距離の設定も意味がある。変動が音響帯域なら、2秒前の計測ではなく、それより短い時刻差の観測を考えればよい。むしろ、反射鏡の距離は、自由にできる。
ここで注意すべきは、g_44変動は、エネルギー保存の破れである。エネルギー保存を利用した測定結果の処理はできない。これには、場所の移動なくg_44が時間変化する ことを理解する必要がある。エネルギー保存は近似的にだけ成立する。g_44の変動は、局所の時計の存在の否定だろうか? 局所からみた時計は存在するが他所からみた 時計は存在しないだろう。局所局時ごとに違う時間計量g_44は、空間計量の物差しの長さと同じく、局所に知り得ない時の流れの速さであるが、その勾配は局所の力学に 表れる重力であり、その変動なしにニュートン重力が伝播できない重力波の必須の要素であり、時空的に離れた点からは他の計量より遥かに容易にスペクトル偏移として 測定できる成分である。
しかし、重力波の存在が確認された後の追加実験の重要度は低い。次段階の実験としては、ポテンシャル変動による重力波の像形成である。次章の太陽レンズによる重力波 の像形成は、太陽系内を自在に移動する測定器の必要がある。ある程度、距離の離れた反射鏡を伴った、直接光と反射光のスペクトル偏移の測定装置を上げることになる。 但し、重力波にg_44の変動が伴うことを地上で検証する方が先であろう。
重力波にはレンズがある。現在の重力波検出は、2箇所の光干渉計を使って角度を600平方°に絞れるというが、方向を殆ど絞れないに等しい。 銀河の巨大質量が、さらに遠方の銀河の光を凸レンズのように弧状やリング状の姿を見せるアインシュタインリングと呼ばれる現象がある。 光と同じく重力波も重力によって屈折する。恒星もマイクロレンズ効果をもつ。太陽では表面近くを通過する光の偏角が 1.7秒角である。これは、 どれだけ離れればリングに見えるか、70/15000/1.7pc= 566AU = 3.27光日程度、これは海王星(30AU)の19倍、この距離に行けば重力波測定の感度は 一気に向上するだろう。
そんな遠くに行かなくてもよいかもしれない。太陽も月も地球も使えるかもしれない。というのは、重力波は、太陽内部もほとんど素通しだから、 太陽内部がレンズになる。重力レンズは半径rのM/rに比例して屈折する。中心からrまでの質量M(r)がr^3乗比例する均一密度では偏角Δθ∝ M(r)/r= r^3/r= r^2。欲しいのはΔθ∝ rである。なぜなら焦点を結ぶ普通の凸レンズはΔθ∝ rである。そのためには M(r)∝r^2が必要。 密度ρ(r)∝ 1/r なら M(r)= ∫ρ(r)4πr^2 dr ∝ 2πr^2 で目的に合う。圧力勾配が重力による dP/dr= -M/r^2 圧縮性の気体ρ∝ P/T が それを導くだろうか。太陽内部はきっと(?)、かなりの部分そうなのではないか。そうすると、太陽辺縁のアインシュタインリングから、 面的な凸レンズになり、感度は極端に上がる。焦点距離は、辺縁がリングを見せる距離と同じだろうか。いや、地上観測でも程度は違うが 太陽方向が大感度だろう。今回の検出にこれが働いたかもしれない。全天の50倍の振幅の観測は、稀なBH合体現象の大エネルギーによると思うが、 恒星、太陽、月の配置が関係したかもしれない。地球は真下が感度最大だろう。
今回は、2015年9月15日UTC9:50:45.ルイジアナ州UTC-6= 3:50 ワシントン州UTC-8= 1:50 真夜中ではない。L1からH1に10msの距離に6.9ms遅延で、 地面の下からというが、太陽方向ではなさそうだ。それならもっと遅延は小さい。レンズ効果は重力波の定常的観測を前堤にした話であり、 発生の方向が予測できない偶発に依存した観測は、全天観測になる。
太陽全体の密度1.4は、水素原子(1.1A)分子が密集した非圧縮性の複数段階をもつだろう。液体水素の密度は、水素ガス2g/22.4Lの800倍、 70.8g/L= 0.071g/cm^3だが、密度1.4はその20倍。原子が密集状態の密度は、水素原子1個の重さ1.674x10^-24g 1A立方体が1cm^3に*10^24 で1.6。 太陽はその大半が水素原子の密集状態か。太陽内部の温度、圧力、密度の推定は、太陽に類似する恒星の質量、温度(色)、光度等の関係を満たすか で判断される大変に難しい問題である。太陽内部に全面凸レンズは期待しないが、リングに幅をもたせるだろうか。
まず簡単には、理科年表(天20(94頁))の標準太陽内部のr,ρ(r),M(r)(下表)から、偏角を与えるM(r)/rは、r=0.3〜0.4に表面の約2倍の丘があり、 その内側でM/rがほぼ半径rに比例し、表面偏角の焦点距離の1/2の面的凸レンズが想定できる。
+----+----------+--------++------+ | r | ρ[g/cm^3]| M(r) || M/r | +----+----------+--------++------+ | 0 | 156 | 0.0 || | |0.1 | 88 | 0.08 || 0.8 | |0.2 | 35 | 0.35 || 1.75 | |0.3 | 12.0 | 0.61 || 2.03 | |0.4 | 3.9 | 0.79 || 1.98 | |0.6 | 0.50 | 0.94 || 1.57 | |0.8 | 0.09 | 0.99 || 1.24 | |1.0 | 2.7x10^-7| 1.0 || 1.0 | +----+----------+--------++------+
ArXiv には、 http://arxiv.org/abs/0711.4811 Bijunath Patla, Robert J. Nemiroff, "Gravitational Lensing Characteristics of the Transparent Sun" という論文があった。 拙訳 最小焦点長は、23.5 AU 天王星の先にある。
重力レンズ効果は、重力波だけでなく、重力自体にも影響を与えるだろう。モーリス・アレによる「アレ効果」という、日蝕のときの重力変動が 存在するかもしれないことを私は最近知ったが、これは重力レンズ効果によって肯定的に理解できる。月も重力レンズの働きをもつから、 日蝕のときの太陽の重力は、太陽と月それぞれの重力よりも強い重力を及ぼす。そのとき、これが地球の軌道に影響を与えるだけでなく、 地球の重力も慣性も少し大きくする。
但し、人工衛星のような浮動系で地球上の重力異常を測定するときは自らの軌道の測定をするのであり、局所現象となるのはよほどの大きな変動である。 昔からの精密重力計でも設置場所の数10cmの高低を検出するが、この効果は検出可能だろうか。日蝕のとき潮汐と温度変化によって地面の高低が起きる。 日蝕が起きるときその地域の周辺から地球はすでに重力変動しているから、その地域の日蝕の瞬間にでる重力変動は、半分は既に変動している中での その場所の質量変動だけである。時間計量の変動は、時間経過の変動だから局所測定できず、太陽からの光のスペクトルの偏移によって測定すべきか。
一般相対論の重力は遠隔的ではなく変動が伝播しなくてはならない。重力が伝播するとき波の形をもつ。それゆえ重力波だけでなく重力にもレンズは働く。 一般相対論は「非等方」な時空を表現する計量場の力学であり、特殊相対論以前のエーテル論ではないが、計量場は、具体的な10次元特性をもつ媒体である。 このことが重要なのは、重力レンズによって、重力が、ある方向に集中できることである。(以上3段落 2017/1/21-27)
定性的説明:
中心から半径r0の周囲に、速度v0で回転する質量がある。それは点質量でなく円環質量と考えたほうが考察が容易で実際の銀河にも一致するだろう。
その少し外側rには、電流の流れるコイルの外側のような重力磁場Bがあって、速度 v をもった質点に v x B の加速度を与える。vがv0と同じ方向
のとき、同方向電流が互いに引力をもつように、この加速度は中心に向かい、中心からの重力を増加させる。速度 v^2 > GM/r となり、v〜 v0となる。
逆に r0 より内側では磁場の働きは外側を向き重力を削減するから、速度 v^2 < GM/r となり、両者は、速度曲線を平坦化する。

重力磁場は、ニュートン重力 (1/r^2) から、速度一定 v= const から M(r)∝ r の質量で説明された重力 (1/r) への増加分 1/r - 1/r^2 を与え なくてはならない。ある半径の内側電流をまとめてループ電流にする。ループ電流内の磁束Φ(r) = r から、そのすぐ外側rの磁場はその面積 (r^2) での商から B(r) = 1/r。ならば、ローレンツ力 v(r) x B(r)= 1/r - 1/r^2 とすると、速度は v(r)= 1 - 1/r で一定に近い。
反論:磁場は速度の方向だけを変え大きさを変えない。速度の2乗であるポテンシャルを変更しないから、速度一定は導けないのではないか。
いや:磁場はポテンシャルを変更しないが、磁場のある空間ではポテンシャルは速度を規定しないから、速度一定は導けるだろう。
反論:速度比例の重力ローレンツ力は、例えば銀河系の中心から太陽系の位置 8kpcの速度 220km/s では、ニュートン重力の0.073%までの影響である。
しかも、重力磁場も速度比例であり、影響は速度の2乗比例ではないか。
台風やハリケーンの渦巻きにはコリオリ力が関係する。地球自転によるコリオリ力は北半球で速度をもつ質点を進行方向の右に曲げる。南半球の渦は北半球とは逆回転 だから吐き出し(ドレイン)渦の説明に地球自転からのコリオリ力は必要だろう。しかし、台風の渦は左巻きで、風は進行方向の左に曲がりコリオリ力の反対方向である。 気象学では「地衡風」といい、圧力勾配とコリオリ力とが釣り合う方向に風が速度をもつと説明し、風の原因の圧力勾配に対して風の結果のコリオリ力の対抗をいうが、 不十分な説明である。力が釣り合うとき風はその場所で直進する。実際の風は、渦の方向に一致しその大半で曲がっている。その風を曲げるのは不平衡である。「地衡風」 はコリオリ力に圧力勾配が勝って左に曲がる事を説明せず、むしろ直進を原理にする。地衡風は風が実際にどちらに曲がるのかさえいわない。そして平衡(力=0)を使う から質量に関係しない。また、質量をもつ風は近傍と関係するから局所独立に与えるのは無謀で、局所で直線風を繋ぎ合わせて大局的に曲った風を描くのは矛盾である。 現実の気象学は実際の風の速度を与えられた初期値として、質量をもつ風が力を受けて曲がることを流体力学の全要素でもって数値的に解くのであり、風を曲げる圧力勾配 とコリオリ力は加算されるが、両者が釣り合う理由はない。それより単純に、台風の風は周囲より低気圧で低密度であり、負質量の運動として進行方向の左にコリオリ力を 受けると考えると渦の方向に合致し、高気圧の吐き出し渦が右に曲がることも同時に説明できる。
銀河団のなかの多くの銀河はあらゆる方向を向いて円盤を成し渦を描く。銀河の規模では慣性系であり、回転系によるコリオリ力はなく、そして圧力勾配もないと考えら れる。球状に分布した恒星が、最初もっていたランダムな運動を互いに衝突やニアミスの相互作用を繰り返し、相対速度を削減して重力収縮するとき、角運動量を保存し、 物質はひとつの面上に降着し、円盤状に分布してほぼ同方向に回転する円運動をし、さらに相互作用して、相対速度を削減し重力収縮し、中心からの距離を縮めるとき、 流体のような中心に吸い込まれる渦が形成されるだろうか? 慣性系のニュートン重力で渦形成は可能だろうか? コリオリ力のある地上の渦のようにニュートン力学で銀河 の渦は説明できるのだろうか?
ニュートン重力場は、静止した電荷が起こす静電場のような「渦なし場」である。ニュートン重力は中心質量による質点運動は、位置エネルギー(PE) -GM/r と運動 エネルギー(KE) 1/2 v^2 との和(PE+KE)が一定である。質点移動は、速さを変えるが、その差は始点と終点(のポテンシャル差)だけによって決まり、経路によらない。 質点の一巡閉路は速さを変えず、軌道は完全に元に戻り、楕円軌道の長軸の回転、水星の近日点移動は、他惑星の摂動以外なく、これが一般相対論の検証に用いられた。 ニュートン重力場に回転なくその勾配が重力を与えるポテンシャル場をもつ。これが銀河の渦の説明を難しくする。いや、それは力場であり、速度場もそうといえるか? 重力場の「渦なし場」は空間微分特性であり、重力場が回転なしなら、その時間積分、速度場も回転がないだろう。速度場の初期値に渦があれば残るが、それに余り理由 はない。質点が複数でも分布して存在しても同じである。渦なし場は、位置を変えて重ね合わせても渦なし場である。つまり、ニュートン重力では、渦自体が謎なのである。
(但し、例えば連星のように天体が互いに重力で結合して回転する場合も渦なしか? 他惑星の摂動による水星の近日点移動と同じくニュートン重力でも回転を生むだろう。 太陽系のように質量の殆どが中心にあるのではない、銀河の分布した質量のニュートン重力は、大きな摂動をもつだろう。すでに銀河シミュレーションを行う研究の結果は、 渦巻きや、棒渦状構造さえ示している。それらはダークマターは利用しているだろうが、一般相対論の(測地線方程式の)重力磁場を考慮していないだろう。)
「半径の縮小は半径対速度の関係によって速度を変化させる。"剛体回転" なら速度は半径に比例して下がり模様が変化しないが、"一定速度" や "ケプラー回転" では 内外の角速度の違いによって模様が変化する。銀河形成からの回転数は半径によって違い、既に多く巻き付く筈なのに、巻き付き回数は少なく数回でしかない」として、 「銀河巻き付きの謎」がいわれる。しかし、渦巻銀河を、構成する恒星のニュートン重力のなかの質点運動と考え、一般的な流体の渦の性質を考えないから、謎になる。 一般的な渦では物質は重心の周りを回転をするのではなく渦方向に移動し、渦は全体として回転しないか、または物質よりもゆっくり回転をする。ボークルールが銀河 回転を「巻を解く方向」でなく「巻き込む方向」と決定したとき、渦状分枝を物質に対応させたが、その速度は渦方向でないと考えたのだろう。スペクトル偏移は、そ の視線方向成分だけを教え、正確な物質の速度を教えない。もしも、速度が渦方向なら「巻き付きの謎」はなくなるのではないか。
測地線方程式には、質量の速度場に対応するベクトルポテンシャル場 A={g_4i}があり、その時間微分がポテンシャル勾配以外に質点に加速度を与え、その回転が重力 磁場になる。重力磁場は、速度に比例する加速度を与え、一巡経路で速度を増減する。重力磁場は、回転系のコリオリ力のように働き、物質対応の渦状分枝によって 銀河の渦巻きを説明するだろう。例えば、環状質量の回転による重力磁場Bは、左回り電流のコイル外側磁場と同じく下向きで、渦巻きに沿って中心に向かう、前向き速度 v をもった恒星に v x B は、内(左)側に力を与え、銀河回転を基準にして、銀河回転とは逆回転のコリオリ場を、その近辺の慣性系に与える。 これは台風の右側の風が進行方向の左に力を受けるのに類似する。
回転系のコリオリ力なしにニュートン重力が渦なしなら、銀河渦の存在は、一般相対論の測地線方程式の重力磁場の働きではないか。我々は、アンドロメダ銀河 M31(NGC224)やM81(NGC3031)、 糸巻き銀河 M101(NGC5457) の壮大でこれ以外ないほど自然な姿をみて、渦巻きの存在と生成に疑いを抱かないが、 ニュートン重力では台風と比較して説明 は難しいのである。ニュートン重力の「渦なし場が渦をもつ」謎は、一般相対論の重力、測地線方程式のベクトルポテンシャルの回転が重力磁場を与え、速度場にある回転(渦) によって、説明されるだろう。我々は前からの風に反応しない風車を用意し、流体の一点の回転を表す。風車を渦巻銀河の中に置けば回転をするだろう。
v(r)= r^(-1/2) の速度場は回転をもつか?天の河銀河の回転方向に向かい銀河中心を左にみて、中心に近い左側の星は速く回転し我々を追い越し、右側の星は遅く回転し 我々より遅れる。そのため、斜め左と後ろ斜め右方向の近傍の恒星は遠ざかり、斜め右と後ろ斜め左は我々に近づく正方形を菱形にする変形運動があるが、 そこには遠方銀河に対する局所回転はないか。銀河回転の軌道上の前後の恒星は、銀河回転の軌道と等しい回転をもつ。左右の隣接軌道の恒星は、左は追い越し右は 後ろに遅れる。これは我々を中心にした逆回転である。右をx,前をyとして dVx/dy<0, dVy/dx<0。両者が等しいなら、 速度場の回転は (rotV)z = dVx/dy - dVy/dx = 0 かもしれない。v(r)= const も質量が分布した場合、渦なしかもしれない。
dVx/dy = (dVx/dθ dθ/dt) dt/dy, ここで()= w d(rwsinθ)/dθ = w [-rw cosθ]_0= -rw^2 = -GM/r^2, dy/dt= Vy = √(GM/r), ∴ dVx/dy = -√ GM r^-3/2.
dVy/dx = d√(GM/r)/dr = -1/2 √ GM r^-3/2 で、(rotV)z は0でない?
渦銀河の v(r)= const の速度場に回転があるか? それは、角速度 W(r)= 1/r の局所回転をもつか。重力磁場は、ある半径の外側で 1/r に比例する重力の増強になる。 重力磁場 B(r)= 1/r は、渦の各部の回転による角速度 W(r)= 1/r のコリオリ力に対応し、これが速度場の回転を起こし、渦の各部での速度一定 v(r)= const を導くだろう。 また、重力磁場は速度をもった質量を収束させ、渦状分枝を明確にするだろう。
LIGO-Virgo GW170814 Skymap2017/9/28 APOD.
アインシュタインの"相対論の意味"(1921年5月のプリンストン大学スタッフォード小講演に基づく初版1922年、第2版は補追、第5版は補追IIの全面修正1956年)は、 [rs,i] からポテンシャル、ベクトルポテンシャル、重力磁場が出ることを示していた。我々の多くはその理解に到達しなかった。パウリやディラックの相対論の本は、 もちろん測地線方程式に対して説明したが、その内容を詳しく分析しなかった。パウリは、(P.77)§ 15 "測地線"で詳述したが、dsを空間パラメータのように説明し、 (P.244)§ 51で初めて運動方程式と関連付けた。
パウリの"相対性理論"(内山龍雄訳、講談社) P.249§ 53 "等価原理からの簡単な結論"の"α) 弱い重力場における小さな速度をもった質点の運動方程式"のなかで、 「質点の運動方程式、(80)は、その速さ$v$が光の速さに比べて非常に小さいときは、つまり、$(v/c)^2$ を無視できる場合には、方程式の形が非常に簡単になる。」 から始まる節で、$g_{ik}$の時間微分を無視するとき、$g_{i4}$の存在とそれに伴う速度 $v/c$ に比例する項を誤って無視し、ニュートン重力だけを導き、 式(389),(390),(391)を誤導出して、「この結果をみるとはなはだ興味あることに気づくであろう。すなわち、ここに述べた近似ではすべての$g_{ik}$の標準値からのズレは、 いずれも$g_{44}$のズレ$Φ$と同じ程度の量であるにもかかわらず、運動方程式にはただ $g_{44}$だけが顔をだしているということである。」と誤った結論を述べている。
また、P.282 § 60でも「場の中の粒子の運動とニュートン力学からの結論との違いは、実験からも予想されるように、$(v/c)^2$の程度の量である。」としたのは 速度比例の項が存在しないとする 重大な誤りであり、彼が測地線方程式の内容に疎かったことを表す。それではThirringによる円環質量の回転する中での遠心力とコリオリの力の発生を説明できない。 また、ディラックの本(1975)は、測地線方程式を運動方程式であるといい、測地線の偏移を考察するが、"相対論の意味"から数10年後にこの重要事に言及しない。
まさしく相対論は創始者の本が頼りである。"相対論の意味"はこの点において、他の量子論のパウリやディラックの理解を超えていた。パウリの"相対論" (1921)は、 "特殊と一般の相対論"(1916)の後、"相対論の意味"の初版の1年前に出版された。その序で量子論側に立ったアインシュタインへの対立を示す彼は、当時の学者が 理解する範囲の百科事典的な相対論の解説であり、その学問の創始者を十分に尊重しなかった嫌いがある。創始者に聞けば§ 53,§ 60 の誤りを訂正できただろう。 R.L.フォワードの「SFはどこまで実現するか」(講談社ブルーバックス)は、一般向けの本でありながら、重力の電磁気的性格を説明していた(**)。
要するに、難解な測地線方程式(10)が鍵である。計量の微分の方向差[rs,i]に速度積を掛けて加速度ということを受け入れれば、その解読を開始できる。 みかけの力=重力は、全てこの中に示される。 (1)rsともに時間の分は、静止質点にも働く加速度で、重力ポテンシャルの勾配 (ニュートン重力) の項と重力ベクトルポテンシャルの時間微分の項がある。 (2)rsの一方が時間で他方が空間のとき、磁場のように速度に比例した加速度を与える項がある。 空間計量の時間微分の項もある。(3)のrsともに空間のとき、空間計量の空間微分と速度積に比例する項がある。 測地線方程式は、計量の微分方向差が加速度を与える式であり、計量が既に求まっている必要がある。 通常の物理であると理解することが難しいのは、微分同士の式であるからである。
さらに、計量を求めるためにある重力方程式を運動方程式とする考えは、計量場に運動を求める誤りである。フリードマン宇宙論のように、 計量が物質を包含することを前提にする宇宙論では、その方法論は可能だが、一般に、重力方程式は、物質の運動を表さない。 座標系の運動に光速制限がないというよりも、物質ではない計量場の運動に意味がないことが重要である。
測地線方程式は、計量下の質点の運動方程式であり、質点運動を与え、計量が物質を支配する。両者は対等ではなく、計量が物質に先行する。そこでは 計量から物質へ影響し、逆向きの物質から計量は意識されない、そのことが顕著なのは宇宙論である。宇宙論では計量自身が変化し、その中にある物質は、 計量の変化に包まれて変化する。物質が計量を導く側面は殆どなく、宇宙が無限に開いた膨張か、臨界的か、有限時空でリバウンドするかが先に与えた 空間的に一様と仮定した物質密度によって決まる。宇宙の計量と物質の運命はそれに従うだけである。
重力波検出実験が肯定的結果を得た後に、それが原理的に不可能という主張は人に不可解な感じを与えるだろう。原理的理解が実験に優先するという信念は、実験結果 を疑うことまで可能にする。但し、アインシュタインのいうように、実験家に対しては"継母のような態度で接すること"が必要である。静止質点に加速度を与える(1)には時間 計量(ポテンシャル)$g_{44}$の勾配だけでなく、$-dA/dt$の項がある。電磁場のベクトルポテンシャルに対応して計量には$A= \{g_{4i}\}$(i=1-3)が存在し、その時間微分が 静止質点を動かす。それはマイケルソン・モーリー型のL字型の光干渉計に検出されても不思議ではない。重力波は、空間計量$g_{ii}$の変動だけではない。(2)の質点の 速度比例項、電磁気のローレンツ力$v \times rot A$に対応するコリオリ力も同じく存在する。空間計量 $g_{ii}$(i=1-3) の時間微分項は、速度比例で微小すぎ重力波に 関係しないだろう。(3)の速度積比例項はさらに関係しないだろう。計量の全成分は、非線形ながら波動方程式様の式をもち、伝搬できなければ、重力の存在自体が理解 できない。重力波が空間計量の変動として、何もない空間だけが伸縮するような理解は、物差しである光も伸縮することを忘れているため十分でない。物差しと時計の 変動の、何が局所で検出可能かは測地線方程式が示していて、その理解は一般相対論の発展に繋がると信ずる。
相対論は、デカルトの座標に対する返礼であったかもしれない。もし時空の座標系を優先すれば、理解が難しい特殊相対論は、慣性系の法則の一致(特殊相対性原理) と時空間隔(と光速)の不変性を用いて、速度による時空の座標系の相対性を示した。一般相対論は重力の解明のために、系の意味を慣性系の速度から各点で異なる 計量にまで深化させ、局所の物理法則の一致(一般相対性原理)に基づき、時空微分の不変性を用いて、計量の微分による「測地線方程式」と、 計量の2階テンソルが物質による、いわゆる「重力方程式」とを導いた。それらが示す重力の電磁気的特性の解明のために我々はさらに思考を要するだろう。
電磁気法則の理解に測地線方程式を用いることができる。マックスウェル方程式や、電磁ポテンシャル(Aとφ)が存在し、Aの時間微分とφの勾配の電場 E= -dA/dt-gradφ 、 Aの回転を磁場 B= rotA とし、ローレンツ力の式 F= q(E + v x B)。それらがなぜそうなのかの解答は電磁気になく、重力は吸引だが電磁気は同極に対して反発という 極性を除き、測地線方程式にある。
(*) 速度積が加速度を生む: $Γ^i_rs$が分子側の2方向$dx$積から1方向を生み、分母側の2つの微分時間$ds$が加速度の2階微分に対応している。速度がL/Tなら、(速度)^2 が加速度になるにはLがひとつ多すぎる。ここでは距離と時間とを同じ次元とするから、速度はL,Tを区別せず、しかも速度は光速を1とする比率である。物理的な次元解析は 使えないともいえ、時空の湾曲を示す$Γ^i_rs$ がL(またはT)を一つ減らす次元をもつともいえる。下添字r,sが入力、上添字のiが出力で、r,sからiにする(ベクトルの 変化がベクトルとベクトルとの積に比例する)から次元が合わないのである。i= 1-3で、$dx^i/ds$が速度なら、$0<dx^i/ds<1$だが、それが時間比率なら制限がない。
(**) この本は驚くことに現在も批判が多い。一般向けの姿をして、学者も知らないことを書くからか。重力の電磁気的側面は、正式に一般相対論を習った人も知らない。 そういう人には、この本は楽観的な空想に思えるのであろう。"相対論の意味"(矢野健太郎訳)は、学生時代池田市石橋のガード下の古書店で見つけ入手したが、 当時の私には殆ど読めなかったが、学部時代、ファインマン物理でさえ購入できなかった反動で、相対論を表題にする本は全て入手していた。1990年代、ディラックで 相対論を学んだ友人との議論で、パウリで学んだ私は電磁気や相対論の知識を確実にした。(勿論、パウリに導いてくれた先人がいた。大学には議論のなかで相対論の 重要性を教えてくれ、この本を示してこれを真剣に学ぶことがどれだけ自身の世界観を開いたかと教える先輩がいた。) しかし、重力をMaxwell方程式で記述するという 清家新一を一度信用したという彼は、重力と電磁気との関連付けを否定し、フォワードの上記本を信用しなかった。電磁気は重力方程式右辺の運動量エネルギーに加わる だけで、一般相対論は最終的に重力方程式だけで、測地線方程式が速度によって加速度を与えると考えず、一般相対論には離れた所の速度の概念がないとさえいう。 それはすでに物理でないと思う。測地線方程式は離れた所の質点の速度から加速度を生む式である。大質量物体を回転させるとき、その内部空間に遠心力とコリオリの力 が慣性系に発生するサーリングの話から、"相対論の意味"の本を開き式(118)を私は彼に示した。その後、私は2008年に原文を翻訳し詳しく読んだため、重力波がそう であるとされる空間計量の重力への役割を知るために、測地線方程式の解読を始めて暫くした2016年、"相対論の意味"の式(118)を想起し、アインシュタインが重力の特性 の解読を既に大半成し遂げていたことを知った。電磁気的重力は、測地線方程式にある。