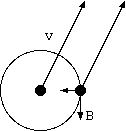
図2. 動く質量の重力磁場のローレンツ加速度 v x B は、引力の増加
目次
1. 重力場の工学利用
2. 恒星のニアミス
3. 生起した確率
4. 二重星の利用
5. 恒星の交差
6. 重力工学の初歩(並進する二質点)
7. 重力工学の初歩(一般相対論の重力とポテンシャル理論)
8. 円環質量の垂直回転
9. 円環質量の水平回転
10. 浮遊と位置エネルギーの蓄積
11. 電磁気力と重力の釣り合い
12. 重力場のローレンツ変換
13. 円環質量の逆回転
ロケットは、規模の小ささが利点だが、エネルギー効率が低い。静止軌道エレベータ による上昇は、位置エネルギーだけを支払えばよいため効率的である。 人ひとりの重量102kgw(1kN)を地上から宇宙に脱出させるエネルギー1kN x 6500km= 6500 MJ= 1800 kWh (1kWh= 3.6MJ) (なぜ6500kmか? gh= GM/R, g= GM/R^2, ∴ h= R) は電気代 (1kWh=20円として)36000円である。1kgの費用は18kWh= 360円。ロケットでは1kg費用は200万円、1人数億円かかる。しかし、軌道エレベータの静止軌道までの 距離3万6000kmは、這い上がりに通常の摩擦による懸架と車輪駆動の限界を時速200kmとして1週間かかる。半径1000km程度の小規模な ロータベータ は、静止軌道 エレベータの1000倍の比率で10分毎に我々を宇宙に放り上げることができる。 ロータベータの力学
地球の自転に同期した衛星が静止衛星であり、その衛星は赤道上のある地点の真上にいつもいる。だから、軽くて強い紐を下ろし地上に結びつけ 軌道エレベータ を動かすことができる。国際宇宙ステーション(ISS)の軌道は高さ数100km、それに対し静止軌道の高さ3万6000kmは、100倍である。なぜこれほど静止軌道が遠いのか? 原因は、自転が音速の1.5倍程度で遅いことで、それが2倍なら静止軌道半径が1/4になる。マッハ3の航空機で紐に乗り換えれば、自転と加算した速度は3倍になり、 静止軌道半径は1/9の4000kmになる。そして例えば、マッハ15の航空機なら、10倍の速度、1/100の軌道で、ISSから下ろした紐に捉まり飛び移ることができる。 紐は重力で常に地球の方向に垂れ、遠心力が大きい問題があるが、紐の先端を振り子のように揺らして、速度0のときに乗降する。 さらに ロータベータ は振り子を大回転をさせ、軌道速度を打ち消す回転の速度で紐の対気速度を0にする。
地球の重力圏を脱して後、利用できるのは惑星の自転と公転である。一般に自転速度は小さく公転速度は大きい。地球の自転速度は赤道で463m/sに対して公転速度は、 30km/s光速の1万分の1だが、それでも恒星間の数光年の距離の旅行のためには小さすぎる。太陽系を出るのに利用できる天体は太陽と惑星だけである。地球の自公転 速度は初速でしかない。天体とのスイングバイには相対速度が必要である。太陽や惑星とそれを行うには相対速度が小さい。 内惑星(水金)は公転速度が大きいが脱出速度が小さい。外惑星(火木土天海)は脱出速度が大きいが公転速度が小さい。さらに困ったことに全惑星の公転は同じ方向で、 相対速度は公転速度の差でしかない。 これらを克服し、どうにかして1000km/sまで加速したとしても、地球の公転速度30km/sでは1パーセク(3.3光年)先の近隣の恒星に行くのに3.3万年かかるが、1000km/s ではその1/33になって1000年で到達できる。その意味は明白である。数10年以上かかる宇宙航行は、調査であっても実行されないだろう。つまり我々は、隣の星までの 距離の深淵(1パーセク=太陽地球間の20万倍)によって閉ざされ(*)、太陽系を脱出できないのである。
(*) まだ差し迫ってないが人類の戦争、環境の急変、他の生命体の太陽系への攻撃のとき、太陽系からの脱出は、人類の運命を左右するだろう。太陽の変光星へ変化による 「太陽系最後の日」(A.C.クラーク 1946)がある。不安定化した太陽から逃走に、我々はどのような手段/方法をもつのだろうか。70年前も現在も、確かな方法はロケット 推進しかない。
外惑星や太陽系外に行くのに重要な方法に太陽面加速がある。太陽面近くでの少しの加速が太陽重力圏外での大きな速度に変わる。太陽面の脱出速度Vは618km/sもある。 太陽面に落下し速度Vに近い速度を得てロケット推進でvを追加すると、太陽系脱出後に残る速度を大きくできる。1/2 (V+v)^2 - 1/2 V^2= Vv + 1/2 v^2、エネルギーの利得は Vvである。太陽面落下に地球の公転速度の打ち消しが加速と同様に費用がかかる、太陽面に近付く危険を考えても、このエネルギー利得は大きい。 力学について
しかし、それらはニュートン力学、すでに誰もが知るだろう技術である。まだ誰も気付いていない方法は、きっと重力の電磁気的な性質の利用にあり、それを考える。
重力井戸の底にいるという意味、速度を出して飛び出しても、太陽重力によって引き戻され、運動エネルギーから位置エネルギーが引き算される。太陽系を脱出するに は地球軌道からは45km/sec以上の速度が必要である。これは地球の公転速度30km/secに15km/secを加算してもよい。恒星間の深淵を越える速度を得る方法を知らないと いう意味で、例えば光速の半分を出すには静止質量エネルギーE= mc^2の1/8である(1/2 mv^2 に v= 1/2 cをいれる)。我々は、これほどの比率でエネルギーを取り出す方法を 知らない。そのため太陽系からの脱出が難しい。質量からエネルギーへの変換効率は、核融合で0.7%。これでは乗り物の100倍の燃料がいる。ブラックホール合体では29%。 物質の反物質への変換では200%だが、実現性がない。我々はただ不可能を直視するのである。
太陽程度の恒星が太陽系内部を掠めたら、放射が倍加し、地球上の水は沸騰する。どれぐらいの速度で?何年間?例えば 300km/s だったら、3億kmの地球軌道の直径を 100万秒= 11.6日で通過する。微妙な所である。30km/s なら 116日、これなら絶滅だろう。3000km/s なら1.16日で大丈夫。星の平均速度100km/sぐらいなら1ヶ月の灼熱である。太陽系が 銀河系を周回する速度が210km/sで、腕の中の質量分布のばらつきで、恒星間速度を100km/s とするなら、最も近い恒星の1.3pc=(1.3x3.3= 4.3光年)を4000年程である。4000年前 の3等星が、最近とても輝くなら危険である。
はるかな昔、太陽系の形成に恒星のニアミスがあったとするジーンズの説を私は子供のとき読んだ。この頃は、まだ科学者が一般向けの本を本気で書いていた。太陽を掠 める恒星によって惑星が弾き出されたとする考え方で、昔からある太陽系の同時形成とは異質な考え方であるが、この説は、角運動量のほとんどが惑星にあって、質量のほとんど が太陽にあることを説明できるという。そして、それがいかに確率的に稀であるか、を理由に捨てられたと聞く。
地球軌道を恒星が掠める確率は、1パーセク(pc)の距離が地球軌道半径(1AU)からみた恒星角度1秒角だから、(180度)^2= 32400 と比べて、(1/3600度)^2 = 1/1296万は、1/4000億 である。銀河系の星数の数倍である。この確率は、不可能ではないが銀河系が数10回回転する50億年前に起きたというのには無理がある。4000年かかる試行は、50億年では125万回。 恒星は100万回打ち出されても足りない。4000億回あれば当たる確率が0.5になるが、50億年はその32万分の1、生起確率は30万分の1程度である。又は、50億年前の太陽系の開始は 間に合わない。又は、説の確率が30万分の1である。しかし、その30万倍の時間があれば、この説の太陽系生成は、その確率によって否定できないことになる。
しかし、ジーンズ自身、太陽系形成がいかに稀かを強調していた。その点も私には異質であった。例えばヘリウムの3個の合体で窒素ができる確率の低さや、 DNAや生命発生の起こり得ない低確率、この世界が単なる偶然では決して成立しないと強調するのは、神の手の介在または存在証明として昔から欧米人の思想的 傾向又は霊感で、その強調は科学から遠ざかる作業仮説である。そして、彼らは次の説を組み上げる。我々にそれが証明されることもなく、動機は理解できず、 次の仮説に対処を迫られる。月の生成仮説、ジャイアントインパクト説(**)が出てきた大学生の時、ジーンズ説を思い返し、いつの時代もこのような説 をいう人がいると思った。その意味に共感できない。
衝撃説に反対する理由は、証拠(evidence)がないことである。地球に衝突したという火星大の惑星は何処から来て、何処に行ったのか? 状況証拠は、少し考えれば ありえないと分かる。天王星や海王星と冥王星は、自転軸の横倒し、軌道交差など天体力学的な様相が激しい衝突事象を表わすが、月地球と惑星の関係は、地球軌道面、 地球軌道の離心率、地軸の傾斜、月の軌道面の傾き、月の軌道の離心率、月の自転軸の軌道面からの傾斜が全て静穏を表わす。地球への他の惑星の衝突がこれらのいく つかに激しい痕跡を残さない筈はない。説の蓋然性は、衝突の明白な低確率と、衝突して痕跡がない低確率との積である。唯一、地軸の傾斜の23.5度が長期の外的トルク で説明できれば、この説は捨ててよいだろう。(いや、火星(25.19度)と同程度の地軸の傾斜は、衝突に関係付ける必要はない。)
(*) 連星系は25%の頻度で存在し、その10%は3重以上である。(連星は人工物でないとして) 星は形成時に半数以上は連星といわれる。独立形成され、自由運動していた 2天体は重心中心に束縛運動を始めない。恒星間ガスや塵の抵抗程度でない何か特別な減速がない限り。しかし、3体以上では可能かもしれない。
(**)最近のこの説の評価:宇宙2017 - 最新版 地球誕生の謎 本当に46億年前? - ドキュメンタリー テレビ NHKのBS放送 "コズミックフロントnext"。リンクを貼っても、2回もリンクが消え検索し直す。著作権移行か、すぐ消えるYoutube動画。 nhkスペシャル 宇宙 地球大進化~46億年 第1集 大衝突からの始まり 衝突が特別な事件でなく、太陽系形成直後でもなく、複数の衝突の最後で、"大衝突からの始まり"では、太陽系形成過程に含まれ、説の意味を失う。
ロケットという質点にとって天体の運動は、所与の条件である。天体の速度は、質点の加減速に利用できるだろう。惑星の自転に沿う質点は その方向に加速されるか? 自転の重力磁場は、単純なコイルの磁場に形が似る。その側で電荷は加速されただろうか。電磁気にそれはなかった。 一定電流は隣接電線に電流を生まず、電流の変化があるときだけ、並行電線のなかに逆起電力を生み、電荷の加速を起こした。
磁場の時間変化が電場の回転(rot E= -dB/dt)を生む。それは元の電流の変化を打ち消す方向に働き、天体が減速するとき、近傍のロケットは加速されるだろう。 例えばコイルを流れる電流のスイッチを切って瞬間的に遮断するとき、コイルのなかの電流にはまるで慣性Lがあるかのようにその方向に流れ続けようとして、 電荷を加速する大電圧を発生する。電流遮断のそばの電線にも起電力を発生し、電流遮断した電線の代わりに同じ向きに電流を流させようとする電圧が発生する。 インダクタンスLと電流の時間変化-dI/dtの積、磁束の時間変化がコイル一巡の電圧を生み、コイル巻数を掛けた電圧を発生する。その重力版にはコイルの巻数の 対応物はないのだろうか?
この交流の変圧器の原理的説明は、大質量が減速するとき、そばの質点にどのような加速を生むかを説明するだろう。もし、大質量の加速度の逆方向の加速度を 側の質点に与えるなら変圧器が成り立つが、もし、加速度と同じ方向の加速度を受けるなら、変圧器はないのではないか。符号が違うだけであると仮定すると、 磁束の一定を保つ向きという原理を逆にして、磁束が不安定になるから、ありえないように思う。電磁気と同様に、質量の移動にも重力磁場が存在するなら、 それは安定でないはずはない。その時間微分の負が重力のrotを生み出すだろう。
惑星の衝突で、2惑星の運動が停止する。それまで一方の惑星を周回した乗物は、惑星の衝突時には、慣性によって以前の速度を保持するだけではなく、外から みて前に投げ出される衝撃的な加速を受けるだろう。ただ、2惑星の重力が急になくならないから、ハンマー投げでハンマーを離すことは実現しないが、重力加 速されるだろう。いや、ハンマーを離す働きをするのかもしれない。それはロケットと乗客を等しく加速するから、瞬間的な大加速があっても乗客には感じさせ ない "無衝撃加速" だろう。これは、スラスタ(推進剤)走法でなく、"重力走法" に属すが、勿論、光速を超えないから、ワープ走法ではない。 惑星を周回する乗物の軌道は螺旋のように惑星衝突の方向に垂直でよいが、衝突線を含む面内軌道なら衝突前の周回軌道速度も利用できる。
電磁気で直線電流の停止が近傍の電荷を加速することは、電場の回転が負の磁場の時間変化の式(rotE= -dB/dt)ではなく、ベクトルポテンシャルの時間変化が 電場になる式(E= -dA/dt -grad φ)である。さて、重力加速の符号を決めないといけない。∂4 g_i4 が質点の加速度になることは測地線方程式から確かとして、 重要なことは、g_i4 が何か知ることである。ある天体の側の計量が g_xx= 1+η, g_tt= -1+η, g_xt= 0 (0<η<1) のとき、 速度vをもったK'系へのローレンツ変換、 x'= γ(x-vt), t'= γ(t-vx)から、
g'_xx= 1+ γ^2η(1+v^2),
g'_xt= 4γ^2vη,
g'_tt= -1+γ^2η(1+v^2)。
つまり、g'_i4= 4γ^2vηである。速度vの天体に沿う乗物かみて、天体衝突は天体の0から-vの速度への変化である。g_i4 は0から4γ^2vηに増加する。 測地線方程式の加速度、∂4 g_i4 は元の天体の速度vの方向である。きっと、乗物は前に弾かれる。ベクトルポテンシャルを A= {g_i4}とすれば、 重力場の性質は、電磁気の幾つかの方程式に一致する。
E= -dA/dt -grad φ, B= rot A, rot E = -dB/dt, そして F= q (E + v x B)
ベクトルポテンシャルを天体の運動-vの方向に定義し、ベクトルポテンシャル(そして磁場)の時間変化を防ぐ方向に加速度は働く、これならありそうだ。 但し、アインシュタインは「相対論の意味」で、天体の側の質点は天体の加速度と同じ方向を受けるという。恐らく私の誤りか。符号の考察は難しい。 先の引用部分の少し前 を参照。これは、円環質量の内部空間での話であるから、問題でないかもしれない。
測地線方程式の電磁気的な重力場を利用しても、これが起こす速度が、4γ^2vηまでなら残念ながら効果は小さい。ニュートン重力のスイングバイと比べ 利点は何か。重力加速が乗客に加速を感じさせないことは、スイングバイも備えている。スイッチを切った瞬間の大電圧の発生に対応する大加速はある。 コイルの巻数の効果はなく、むしろ多重スイングバイがもつ。大小質量の物体が衝突し、運動量を保存し小質量の物体に大きな速度が与えられる、 普通の衝突力学も、スイングバイやこれにはない。これらは、重力加速において、どうすれば可能かと考える。
また、高速な自転をもつ白色矮星、中性子星、パルサーは、周回によって加減速できる。近傍を自転方向に周回通過し速度を減速し、その逆向きで加速 する。星の近傍での加減速は遠方での大きな加減速になる。恒星への接近時に恒星自転による加減速を使うことができるだろう。

同符号の電荷q q'を横に並べ静止系ではクーロン斥力 qE しかないが、それらに垂直な速度-vをもつ慣性系からみると、相手の電荷の速度によって発生した磁場Bの中に速度 をもつローレンツ力 v x B 引力を受ける。それでは、両者の和の力 F= q(E + v x B) は、ある速度を超えると斥力から引力に変わり、時間が経つと間隔がみる系によって 増加/減少するのかという疑問(異符号電荷間ではクーロン引力とローレンツ斥力)が起き、それがありえないことから、速度をもつ系がみる横方向の電場Eが増加することを 知るのである。
重力が電磁気と同じ特性なら、ニュートン重力も電荷間のクーロン力と同様に速度系からみると増加するだろう。重力は同極で引力だが、コリオリ力もニュートン重力と 同じく引力なら引力を増しても、速度-v系からみた動質量は増加するから問題はない、つまり、同極電荷のように斥力が引力に変化するのかという疑問を提出しないが、 そのこと自身、疑問が残る。重力の仕組みが電磁気と同じなら、電磁気と重力がある系で釣り合えば、他の系でみても釣り合うだろう。ローレンツ力がクーロン斥力の反 対符号の引力で、電場が速度系で増加することに合わせると、コリオリ力は斥力で、引力は弱まり、ある速度以上でみると引力が斥力に変わるのかという疑問提示形でな いのか。符号の考察は難しい。11章にこの考えを引き継ぐ。それまでは、速度に比例するローレンツ力は、同方向に速度をもつ質量が引力、逆方向に速度をもつ質量が 斥力をもつとする。
ポテンシャル理論の光線の偏移は、天体の側の時間計量(ポテンシャル)の空間的微分(勾配)による項であり、質点速度に依らない。場所によって 光速の異なる媒体であるとき波面が偏移する ホイヘンスの原理 が適用できる。偏移の程度を倍にしたのは、 天体の側の空間計量の増大(=物差しの半径方向の短縮)であり、短縮の程度が天体からの距離によって変化する。 天体の側の時間計量の縮小と空間計量の増大は、同じく光速の低下を起こし、やはりホイテンス原理が 適用できる。光がニュートン重力からのポテンシャル理論(時間計量だけの理論)の倍の偏移をするように、 質点の場合も、ニュートン力学のポテンシャル理論よりも引力が増大すると考えられる。
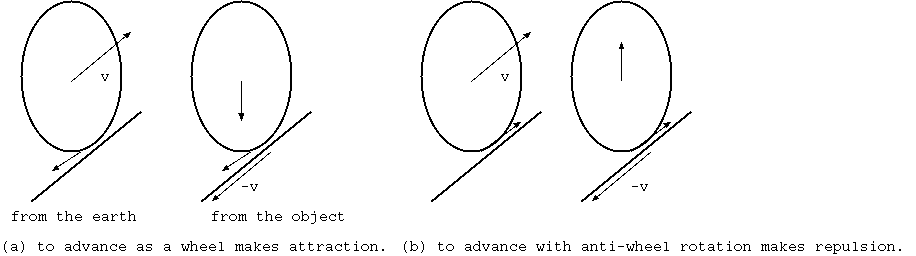
円環質量の回転では、その内側には円環回転と同じ方向のコリオリ場を慣性系に与え、その外側には逆方向のコリオリ場を外部の慣性系に与える。 重力磁場は、コリオリ場と同型であるだけでなく同一で、速度に比例するみかけの力を生む。円環物体中心の慣性系からみて地面は速度をもちコリオリ力を受ける。 こうして重力を斥力として働かせることはできそうだが、コリオリ力の性質から、反発力が並進速度に比例するから、その操縦は難しいのではないか。
円環物体の重力磁場の力の大きさはどの程度だろうか。円環物体の生む重力程度で、地球が円環に与える重力と比べて遥かに小さいだろうか? 小質量が大質量に与える力は、 大質量が小質量に与える力と大きさが等しい。円環の生む重力磁束の下半分1/2が地球全体に反発の加速度を与えるわけではなく磁場の強い部分である近傍の地表に与える 作用だから、物体の受ける重力に比べてそれは小さいだろう。しかも、与えるのは力でなく加速度である。この測地線方程式のときに、ニュートン力学の"作用反作用の原理" は異なった原理であり、利用すべきでない。円環からみて、地表の局所的な地面に加速度を与えることで十分であり、自分が地面から受ける反作用をいう必要はない。
磁場Bの向きは、質量の移動を電流(電磁気と同じく正電荷の移動)と考え、電磁気の磁場を当てはめ、速度vの質点の受ける加速度を v x B とする。反作用を原理にいれ ないとき、円環内外で磁場の方向が逆なので、円環内部質量に逆方向の加速度が働くには地面と同速度をもつ必要があるが、円環系では地面は速度をもつが円環は速度が ないので斥力がないがそれでよく、地面の系で円環内部質量に斥力が働けばよい。
円環質量を回転させ、磁場を下向きにして、地面には磁場が浸透する。全磁力線は円環(コイル)の境界を越えて内部から外に横に広がる。速度は回転が用意し、 地面が円環と逆に速度vをもって回転するとき、v x B は下を向く。これが円環質量よりゆっくりした回転系からなら、速度も磁場も存在する(図4)。しかし静止した地面に、 回転系からみて下向きにローレンツ力を働かせて、実際に浮遊可能だろうか。地面は回転系からみなければ静止しているから、疑がわしい。回転系からみるコリオリ力は、 その回転系からみて逆回転するための求心力を与えるだけだろうか。いや、求心力は水平面内で、ここでいう下向きではないから違うようだ。可能性は消えていない。
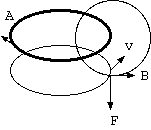
質量浮遊自体にはパワーはいらない。同じ高さにいること自体は、毎秒のエネルギーを要しない。それはまず、重力に対する抗力を提供する紐や棒の支持であり、次には その代わりの"動的支持"でもよい。鉄球のような質量のある物体を地面との間に往復させれば、毎秒の質量の方向転換による (放出の2倍の) 運動量変化(力積)を与える。 飛ぶ間に重力加速が働き上下端で速度の違いがあり、上端での小さい速度変化だけが支持力になる。これが原理的には可能だがとても現実的に思えない理由は、大気との 圧縮や摩擦が容易に邪魔をし、さらに両側の反発係数が限りなく1に近くないといけないからである。R. L. フォワードの本には電磁レールガンで鉄板を往復させる動的 支持の"スペースファウンテン"の説明があった。
質量を往復させず、質量放出だけを考えるのがロケットである。同じ運動量を出すのに必要なエネルギーが低いのは低速な大質量の放出であるが、毎秒の運動量変化(力) をもたらすのに放出体の速度が高いほど質量あたりの運動量が大きい。ロケットは燃料を運ぶから、毎秒の質量損失が重要である。気体分子の速度は √(温度/分子量) に比例する。水素ガスは分子量2で、同じ温度で酸水素炎(水は分子量18)の3倍の速度をもつ。1万度か100万度かによって速度は10倍違う。これによって、小質量の高速度 のほうが放出体の質量あたりの1G滞空時間(比推力)が長い。可能な限り高温のガスを噴射するにしても、機体を溶融しない技術的に可能な温度がそれを制限する。
そのような時空の高度な原理による方法でなく、上空から地上近くに降りてくるとき、大気圧縮と摩擦によって外殻を高温にして減速するとき失っているエネルギーを 蓄えるだけでよい。それは再び上昇するのに必要である。それは、脱出速度程度のエネルギーであり、化学エネルギーの数倍で大した大きさではない。しかし、降下時 に位置エネルギーを何の支えもなく蓄えることが難しい。自然は、位置エネルギーを運動エネルギーに容易に変換し速度にする。我々は、位置エネルギーを工学的な箱 に閉じ込める貯蔵ができない。それは、ニュートン力学でそれを容易に行う大規模な機械、軌道エレベータ、ロータベータなどを使えばできるが、そのような大規模機 械を作るのは大変だから、コンパクトな飛翔体に収納したい。電磁エネルギーや電磁運動量 (E x B) を空間に蓄えることは可能だし、重力的なそれも可能であろう。 重力に対抗して質量を支える仕組みは、力を出す方向(上)と移動の方向(下)が逆だから、エネルギーを得る。それを移動体に収納することは可能と思う、未来には。 さらに下降時に位置エネルギーを蓄え上昇時にそれを使う機械で上昇は可能になっても、運動量を蓄えないと同方向の速度に戻るのに何かの支えを必要とする。
以前の考察: 力のローレンツ変換から重力への考察 (数式表示)
電磁気力は、力を与えるMも受けるmも電荷で、速度による電荷の増加(2)を考えないから、加速度は1/γ^2倍に減少する。さらに電磁気にはローレンツ引力が クーロン斥力を削減するが、クーロン斥力の増加がローレンツ引力の1/2程度を引き受けていた(速度に比例する力が、γ や v^2に一致するはずがないと考え るのは間違い。磁場が速度に比例するから速度と磁場の積は、速度の2乗に関係する)。 測地線の物理 から、重力磁場のローレンツ加速度は、同極性である質量は、引力を増加させると考えたのは間違いだった。 符号を考えるのが難しいとき、類似から推定する。同じ方向に流れる電流の電線は互いに収束する力を受ける。という電磁気の現象からの類似である。 それならば、質量が並進するとき、それらの間の引力は、増強するか。これはこれを肯定/否定するよく知られた事実が確認されていない。しかし、 これには反論があった。それは、電磁気力と重力が釣り合うとき、速度をもつ系からみても両者は釣り合う、という原理的な要請である。
この要請から重力にもローレンツ力と同種の速度比例のコリオリ加速度が必要といえることは(測地線方程式を知った後知恵であるが)素晴らしいが、 電磁気のクーロン斥力が速度比例のローレンツ引力によって斥力を削減するとき、重力の引力も速度に比例して削減しないといけない。これは以前の考えの 反対である。質量の速度比例のコリオリ力は、ニュートン引力を削減する斥力であるべきで、重力磁場の働きは電磁気とは逆に -v x B か(その必要はなかった)。 同方向電流は引力をもつが、質量の同方向の流れは、コリオリの斥力が必要だった。
"相対論の意味"の符号が逆の式(118)、加速度= grad φ + dA/dt - v x B は、φとAだけではなく、v x B の符号も逆であるが、φとAの定義が違うために、 ニュートン重力とコリオリ力の符号が違うのではない。つまり、ニュートン重力が引力で、コリオリ力が斥力である。
式(118)はAの符号が逆なら磁場Bの符号も逆になるから、(118)は-vxBと書くだけである。(118)は同方向電流と同じく同方向質量流のコリオリ力が 引力を意味するかどうか。コリオリ力はニュートン引力と同符号でない。物体系Kに対して速度-vのK'系からみた電磁場をE', B'とし、電場EからE'への 変換は(γはvに垂直成分は1/√1-v^2、平行成分は1)、
E'= γ(E - v x B) , B'= γ(B + v x E)
Kで磁場B=0である。(仮にK'系で磁場なしB'=0なら、逆変換 E= γ(E' + v x B'), B= γ(B'- v x E') から、電場の削減 E'=1/γ E。) K'系の電場は E'= γEであるが K'系には磁場 B'= γ(v x E) が存在し、ローレンツ力全体では1/γに削減している。
F'/q= E'+ v x B'= γ(E + vx(vxE))= γE(1-v^2)= E/γ
それに質点の質量増加を考慮すれば、加速度は1/γ^2に削減する。まだ(2)を考慮しない電磁気の変換でしかない。 (2)を考慮すれば、 E'はさらに増加するが、受ける質点の質量増加によってF'/qが減少し、両者は打ち消され、釣り合いの原理を満たす。 質量が同方向に並進するとき、引力が重力磁場によって増大するかは怪しい。
電磁気のローレンツ力類似の測地線方程式は、加速度を与えるから、考えを修正する。 ローレンツ変換は力を1/γにし、質量のγ倍増によって加速度は1/γ^2になる。電場はγ倍するが、磁場の影響で力と加速度を削減する。 重力 F'/m は、重力源Mの増加により、速度によって加速度は変化しない。これは釣り合いの原理を崩す。釣り合いを原理とすると、 ニュートン重力は、Mの増加γ、速度による増加がγ、両者でγ^2に増加するが、ローレンツ変換で加速度が1/γ^2になる必要がある。
速度vの系からみた質点の側の時間計量 g'_tt= -1+γ^2η(1+v^2)の標準からの偏差は、ηからγ^2 (1+v^2)に増倍。 ベクトルポテンシャルAは0から変化し、4γ^2vηであり、その時間微分あれば発生する。速度vの変化がないからAに時間変化なしとして0。 このAに rotA が存在して重力磁場を与えるか?Aが0でなくても時間変化がなく、rotAもないとできるか。
rotA は存在して、電磁場のローレンツ変換に類似の重力場のローレンツ変換が行われ、重力磁場がある。それがないとvxBの項がない。E+vxBがあって、 それがγ^2倍される。これが電磁場のローレンツ変換と違うように思うがそうではない。加速度としてはγ^2倍され、γ^2(E+vxB)でγ^-2に なることが必要であるが、質点がγ倍しているから変換で力がγ^-1 されるとき加速度はγ^-2される必要がある。
(1)は横に並ぶ2物体が互いにみる重力と加速度は(0)と同じである。ニュートン重力(0)を速度-vを持った系からみると(1)になる。電磁気のローレンツ力によって (0)が(1)になると斥力が引力に変わることがないように、重力もローレンツ加速度によって、引力が増加することはない。速度によって横方向の動きが緩慢になる 減少は、1/γの力、1/γ^2 の加速度は電磁気と同じである。(1)は(0)のγ^-2 倍の加速度。 A0= A1 γ^2 、A0>A1
(a)と(b)とは、(0)や(1)とは状況が異なる。aは静止(固定)していて、bは(レール上を一定の)速度vをもつ。bの受ける重力はそれに対抗した固定やレールの抗力から でしか知りえず、bの加速度は相手の慣性系でしか存在しないが、bの運動をレールが拘束してはbに横加速度はない。丁度横に並んだ瞬間、bの拘束を解けば、加速度 が現れ、bはa方向に速度を増加する。最初からa,b に固定や拘束がなければ横幅が変化する。2物体を自由に運動させ、ある一瞬の位置と速度が垂直のときの重力と 加速度である。2物体が重心のまわりを円運動しているどの瞬間でもよい。
さらに位置と速度が垂直の交差瞬間の前後のどの瞬間も、片方が静止し相手が速度をもつ系では、電磁気では片方のaは静止し磁場の影響を受けず、磁場を出さない から互いに電場の影響しか受けない。a,bは交換対称性をもつ。図示は、aが静止したa系であり、b系でa,bのみる重力/加速度は、a系でb,aのみる重力/加速度と等しい。
そのとき速度をもつ相手の質量は、自分の質量よりも大きく、自分の受ける重力と加速度は、相手の受けるものより大きい。そこで力と加速度のローレンツ変換で、 自分の受けるものを相手の系からみれば、重力は1/γ、加速度は1/γ^2 に減する。a,b は互いに電場だけをみる、対称で、Aa= γ^2 Ab。 b系でaの受けるものを変換でa系に移した Aa はなぜ大きいか。a系のAaはb系のbの受けるものと等しいから。力を受けた自身の系に戻すと力や加速度は大きくなる。 a系ではaが受けるものは大きくなり、bの受けるものは小さくなって、大小比率が逆転する。
問題は、a,b と0,1 の関係である。a,b の何れかが、0,1の何れかと関係が分かれば、4つの関係が分かる。静止質量aのそばを通過する質点bも静止質点0と加速度は 同じとすると、Ab= A0 である。 Ab= A0= A1 γ^2、Aa= γ^2 Ab
この議論は一見、単純化しすぎた即時的な重力/電磁気のようにみえるが、そうではない。電磁気も重力も作用の伝播の現象だが即時を装う。力/加速度は、 等速直線運動をする電荷からの電場のように、距離に相当する相手の過去(t-r/c)の位置ではなく、現在tの相手の位置の方向を向く。B= rotA の磁場Bに 速度vの、ローレンツ加速度も電場と同じく2物体を結ぶ線上にあって現在の相手の方向を向く。それゆえこの議論は、真面目な思考を要する構成を与えている。
電磁気では電荷は質量を衣として纏う。電荷が受けるものは物体への力となる。電磁気のローレンツ変換γ(E+vxB)は、速度をもった電荷は増加せず質量はγ倍の増加、 力から加速度 a= F/m になる時に質量増加が反映され、1/γ倍になる。(つまり電荷間の力は、γ^2ではないか。) 速度をもった電荷のローレンツ力 E+vxB はγの0乗は 正確だろうか? 速度をもった質量間の重力(1)は、与える質量と受ける質量がともに増加、力はγの2乗に関係し、加速度は1乗である。 力2乗、加速度1乗。力のローレンツ変換は-1乗で1乗になり、加速度のローレンツ変換は-2乗で-1乗になる。
これの v を -v にして EとE'を入れ替え、逆変換して元に戻ることを要請すれば、正確なローレンツ変換が得られる。 x'= γ(x - vt), t'= γ(t - vx) が得られたように、4元ポテンシャルの変換、A'= γ(A - vφ), φ'= γ(φ- v・A) のように。 また、次のように得られる電磁場のローレンツ変換のように、重力場のローレンツ変換も得られるはずである。
A'= γ(A - vΦ), Φ'= γ(Φ- v・A)(γは、方向係数で、 vに垂直成分 (⊥v)にだけ1/√(1-v^2) が掛かる意味で使う。) A'= γ(A - vΦ)の両辺の rot を取り、rot A'= γ(rot A - rot(vΦ))
公式 rot(Φv)= gradΦ × v + Φ rot v を使い、v は一様 rot v= 0で、また、Aは一定 dA/dt= 0 として、
rot A'= γ(rot A - gradΦ × v) ∴ B' = γ(B - v x E)
Φ'= γ(Φ- v・A) の両辺の -grad を取れば、 -grad Φ'= γ(-grad Φ + grad(v・A))
公式 grad (v・A)= (A・∇)v + (v・∇)A + v×(rot A) + A×(rot v) の右辺は、第3項だけ残り、
Aの一定 dA/dt= 0 を仮定して E= -grad Φ。∴ E' = γ(E + v x B)
電磁気での速度をもつ電荷がみる電場は、正負の電荷の存在を元にする、電流が存在するとき電荷が移動しその反対電荷が静止して、両者の速度差による ローレンツ短縮の違いが飛ぶ電荷のみる電場を生むという説明は、負質量の存在しない重力には適合しない。速度をもつ質点1,bがみる重力は、静止した相手 aの質量が増加し、共に動く相手の質量1は増加しない事だけしかない。そこにその説明に利用する道具、負の質量がない。(電磁気のその説明が正しく、 重力のローレンツ加速度が電磁気と同じなら、負質量の可能性が残る。) (2017/7/3)
磁力浮遊:磁石は周辺に小磁石を置くと力を受ける。磁石が受ける力は磁場自体ではなく磁場勾配である。少磁石の方向を変えるモーメントを受けるが、 上手にそれをバランスをとりひっくり返らないよう浮遊する。少磁石はできるだけ長い磁石を使うと磁場の勾配への感度が大きい。電磁石を利用して制御すれば、 小磁石の強さと方向を変える。地球の弱い磁場だが、受ける側の磁石を強くすれば受ける力は大きくなる。これが重力に比べ磁場が便利な所である。 静止するには、磁場の勾配がどうなっているかに合わせて、小磁石の方向を制御して、重力と反対の真上の方向に力が向かうようにすればよい。(2018/2/22)
平行電流が互いに引き合うのは、同極電荷の反発を弱めたことではなく、電線のなかの電荷は中和されていて存在しないとみなせる。真空中の電荷の並進流れが 集束する現象をみると、質量の並進の流れでも集束すると考えられるか?それは同極電荷が反発を弱めて集束したのと同じく、集束を弱めるのではないか。 並進質量の重力磁場の働きは、発散ではないか。
電磁気では、電流は実際は、電子の流れから来ているが、その逆方向のプラスの電荷の流れと考える。それを包み込むベクトルポテンシャルは、プラスの電荷の 流れと同じ方向の引き連れの場を用意することである。電磁気のベクトルポテンシャルAはそう定義されていて、磁場Bはその回転B= rotAとして表現される。 そのなかで、v x Bの方向の力を受けるのは、正のテスト電荷である。重力において、全く同様の、E= -dA/dt -grad φで表すみかけの力(ニュートン重力と コリオリの場 E'= -dA/dt -gradφ + v x B)をもつことを、測地線方程式は示す。このことから、重力において電磁気と同様の力学が存在することを知ったが、 その符号の問題は混乱を生む。電磁気では異符号の電荷同士がクーロン引力であるが、重力では同符号の質量が静止時にニュートン引力である。これは電磁気の 電流とベクトルポテンシャルの定義からみると、正の質量が速度をもつことでベクトルポテンシャルが生まれることと対応すべきである。その点では私の符号の 付け方は逆、式(118)のもつAの定義は電磁気に一致するものだろうとして、その点を検証する。両者ともに、A={g_4i}であるが、慣性系の計量を111-1とした (アインシュタインは-1,-1,-1,1) g_ik全てが逆符号だから、Aの符号は逆で、
(118) d/dl [(1+~σ)v] = grad ~σ + ∂A/∂l +[curl A, v]
が全て逆符号だから、その表現する現実の加速度は私と変わらない。それでなぜ、天体の側の質点が天体の加速度と同じ方向にコリオリ力を受けるというのか。 それは、彼が A を場の運動量と考えているからと推量でき、私もAを場の運動量とするからである。反対符号のものを同じ運動量とするからである。それでは、 2つの質量は並進系からみて、引力を増大するのか、の点では私に分はない。質量が速度をもつとき、その側のg_4iはどちらの向きをもつかそれを再検証しよう。 速度vをもって天体の側の計量をみたとき、
g'_xt= 4vη/(1-v^2), ....(5)
は、速度v方向のベクトルで、それは天体の速度の逆の方向である。つまり、私の間違いであった。Aは電磁気とは逆に運動量場を定義し実際はその逆である。 それゆえ、磁場の働きも逆で、2質量が並進するとき引力を増大し収束すると勘違いしたが、引力は磁場に相当するコリオリ力によって緩まると理解すべきである。 では、電磁気の同方向電流の収束は説明できるだろうか。重力ではその磁場の向きが逆なのか。6章で前に弾かれると書いたがそれが間違いなら、 なぜ電磁気で電荷が前に弾かれ、インダクタンスが遮断する接点に高電圧を出すのだろうか。ところが、"測地線の物理"5章の最後 で"-dA/dt は、-v 方向である" は間違いだが、-dA/dt が v 方向なら前に弾かれることになる。