
図 1. 静止した2電荷と動く2電荷の相互に及ぼす力
1. はじめに
2. クーロン力とローレンツ力
3. 電磁場のローレンツ変換
4. すれ違う電荷の場
5. 重力における同様の議論
6. 重力場と重力の間
7. 質量から重力場への関係
8.おわりに
重力の特殊相対論的扱いは、Nordstormと、Mie によってなされた試みがあり、 一般相対論は、これらの試みの不備を解消する理論とされる。 この文章は、それらにどのような限界があって、 一般相対論がなぜ必要かを知るために役立つのかもしれない。

電荷間の力は、他の系から見ると、斥力から引力に変わるのだろうか?
これは、そのようなことはなく、どの系から見ても斥力であろう。そうでないと、 慣性系によって、速度と垂直な方向の電荷間の距離に意見が分かれてしまう。 $q (v \times B')$ という磁場による引力は、なにが打ち消しているのか?
これは、電場が増加していることによる。 電磁場のローレンツ変換によって、$K'$ 系での電場 $E'$ は、速度 $v$ と平行な成分は変わらないが、 速度と垂直な成分は $E'= γ(E - v\times B)$ となる。 $B= 0$ であり、$E$ と $v$ は垂直であるから、 $K'$ 系では、$E'= γE$ である。この $γ= {1\over \sqrt{1-v^2}}$ による増大が埋め合わせるのである。
ただし埋め合わせは、そのちょうどの大きさではなく半分ていどである。 電場の増加分を入れても、別の系から見て、この力は小さくなる必要がある。 後述するように、横方向の力は一般に別の系から見るとき $1/γ$ に小さくなる。 (磁場の効果 $v \times B'$は、速度 $v$ と磁場$B'$に比例し、$B'$ も $v$ に比例するから、$v^2$に比例し、 $γ$ による電場の増加比の、2倍の減少比 $(1-v^2)$となって、全体は$1/γ$倍になる。)
最初のパラドックス的な混乱は、クーロン力が正しい表式でないために起こる。 クーロン力は、静止した電荷間では成立しているが、式に速度の項を含んでいないのに、 別の系から見ると電気的力だけでなく磁場の力もある。 それに対して、最初から磁場の効果を入れたローレンツ力は、系による電磁場の変換に耐える。 これで求めた力は力の変換によって別の系に移せるのである。 同様に、ニュートンの万有引力もクーロン力のような表式であり、ローレンツ変換に乗らない。 これをローレンツ力のような形式にすることが希まれる。
前章の状況で、$K$ 系の磁場 $B=0$ から、$K'$ 系では $E'= γ E, B'= γ(v \times E) $ となるが、 $K'$ から $K$ へ電磁場を逆変換すると、$v \times (v \times A)= -v^2 A $から、電場 $E$ が再現できる。 \[ γ(E'+ v \times B') = γ(γ E + v \times γ(v \times E)) = γ^2 (E+ v \times (v \times E)) = γ^2 (1 - v^2)E= E \] $K'$ 系のローレンツ力は、$F'= q (E'+ v \times B')= q E/γ$
つまりローレンツ力は、電荷の見る電場 $E$ の力 $F= q E$ を変換して、$1/γ$ に弱めたものである。 一般に $K$ 系の横方向の力 $F$ は、それと $-v$ の系 $K'$ からみると $F' = F/γ$ に弱められる。 ローレンツ変換で、電場は $E'= γ E$ で強まっているのに、その増強を打ち消し、さらに $1/γ$ に弱める働きを磁場がしているのである。

前章の状況と関連して考えると、$a$ が受ける電場は $b$ が受ける電場とは大きさが違う。 $a$ が受ける電場は、$b$ が受ける電場 $E$ を速度 $v$ でローレンツ変換したものである。 それは $a$ が見る電場 ($a$ が受ける電場) と $b$ が見る電場 ( $b$ の静止系 $K'$ 系で $b$ の受ける電場)が等しいという対称性からくる。
静止した電荷 $a$ から $r$ の距離の電場を $E$ とすると、$a$ が受ける電場は、$E'= γ E$ であり、 $b$ が受ける電場 $E$ より大きい。この瞬間の $a, b$ 間の力はつり合わず、左に片寄っている。 これは、パラドックスだろうか。
電磁気では離れた物体間の作用反作用は考えない。作用反作用は、場を含めてはじめて成立する。 クーロン力を電場の中の電荷が受ける力に置き換えたとき、 場は、物体への力の原因を遠隔力なしに説明するために仮想的に作られた。 そのとき、場は力を与えるが力を受ける対象ではなかった。 相対論ではあらゆる相互作用が光速に制限されるため、作用と反作用は接触的である。 場は実在的であり、場に働く力も存在し、場の運動量もある。 場の硬さ(マックスウエル張力テンソル)さえ考える必要がある。(*1)
この反作用として、右の方向に出る電磁波を考えるのは間違いである。 $b$ は等速直線運動をし、$a$ は静止しているため、$a, b$ ともに電磁波を出さない。 電磁場は線形で加算される。$a, b$ の電磁場は、$a$ による電磁場と $b$ による電磁場の加算である。 だから $a, b$ はすれ違いの全過程を通じて電磁波を出さない。
さらによくないことに、$B$ の静止する $K'$ 系からみると場の運動量変化は、逆方向(左)になる。 同じ場の運動量変化がそれと垂直に運動する系から見るだけで方向が逆になるのだろうか。(*4)
2 つの電荷は遠方まで届く電磁波は出さないが、局所的な電磁場の時間変動はあり、 それに伴う場の運動量変化がある。奇妙に感ずるのは、場の運動量を考えないからであろう。 この問題は、電流の側に電荷を接近させる問題と同じく、場の運動量であると思う。
電荷が速度を持つとき、電荷の全ての方向の電場が増加するわけではない。 電場の速度方向の成分は、逆に減少する。 等速直線運動をする電荷の作る電場は、次のような式になる。 \[ {\bf E}= q {{\bf R} \over R^3} {1-v^2 \over \sqrt{1-v^2sin^2\theta}^3} \] ここで、$\theta$ は電荷から測定点までの位置ベクトル ${\bf R}$ の速度${\bf v}$からの角度である。 $\theta$ が 90 度のとき、$γ$倍に強まるが、0 度のときは、$1/γ^2$ に弱まる。
別の方法で考えると、全ての方向の電場の総量は電荷であり一定である。(電荷を覆 う閉曲面$s$の法線 $r$ と電場 E の内積の面積分が、電荷である。) そのため、電荷から ある方向に電場が増えるとき、他の方向では減るのである。 \[ ∫_s{\bf E}・d{\bf r} = q \] 円盤の電荷は、他方の円盤上の全ての電荷の影響をうける。 回転によって近傍の電荷の影響は増加するが、遠方の電荷は速度の方向に近く電場は弱まるだろう。 回転する円盤の回転面に垂直な方向の遠方への電場は、ポテンシャルの計算の方が楽であるが、 結果的にこれも変化しない。すれ違いの瞬間には左右のバランスは崩れているが、 その前後では逆にバランスが崩れているのであれば、無反動推進はできないだろう。
電場が即時的にみえる方向をもつということに関連して、ニュートン重力も遅延を与えると正しくなくなる。 即時的な働きがあるとしないと誤差が大きく出るのである。電磁気も遠隔作用を装っている。 重力もそうである。リエナール・ウィーヘルトの遅延ポテンシャルは、 重力にも同様に適用できるのではないだろうか。
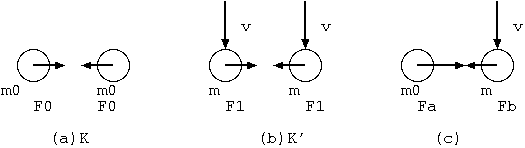
図 2 のよう、通過する質量について重力も同様に、 静止した $a$ が受ける側が強くなるのだろうか。 通過する $b$ はすでに横方向に、$γ$ だけ質量が大きくなっている。 それとの関係はどうなのか。動質量は、重力を受けるときには有効で、 重力を発生するときには有効でないのか。
すなわち、電磁気では電荷一定から考慮する必要がなかったことが重力では問題になる。 それは、(i)重力を受けるとき動質量が有効かということと、 (ii)重力の源として動質量が有効かということである。 (i)は重力を時空の歪みとしてとらえる一般相対論で認めるし、 非常にありそうなことである。そして(ii)は、どうだろう。 これらを、力の特殊相対論的な関係だけで考察する。
まず、現象の対称性を利用して説明できることがある。 図 3 (c)の $a$ と $b$ のそれぞれの見る重力は $a, b$ 両者において対称で等しい。 それが一方から見ると、相手側の受ける力は小さく、自分の方が受ける力は大きくみえる。 これは相手側の時間の経過が遅くなっていることと、つじつまが合う つまり、相手側の変化が、ゆっくりであるためにはその分だけ、 相手側の受ける力は $1/γ$倍に減ってないといけない。 相手側の質量は増加しているため、相手側の加速度は $1/γ^2$ 倍に小さくなる。 相手側の速度は、$1/γ$ だけ小さく、変位はこちら側と同じになる。 これが、特殊相対論における力と加速度、速度、変位のローレンツ変換である。 \[ \tag{3-1} F_b= F_a/γ \\ A_b= A_a/γ^2, V_b= V_a/γ, X_b= X_a \] もうひとつ利用できる原理として、1 点でつりあっている 2 種の力は、 別の系からみてもつりあうということである。 もし重力の引力と電磁気力の斥力がつりあって $F_0= 0$ であるときには、 $F_1= 0$ とならなくてはならない。 そのためには、電磁気力も重力も同じローレンツ変換を受ける必要がある。 重力も電磁気力と同じく、別の系から見ると $1/γ$ に変換され、 それによる加速度は $1/γ^2$ に変換されると結論してよい。(*2)
図.3 (a),(b) で、$K$ 系で静止した 2 個の質点が及ぼし合う力を $F_0$ とすると、 速度 $v$ で動く 2 個の質点の互いに及ぼす力 $F_1$ との間には、 \[ \tag{3-2} F_1= {F_0 \over γ} \] という関係があり、$K'$系から見た加速度 $a_1$ は $K$ 系での加速度 $a_0$ と \[ a_1= {a_0 \over γ^2} \] の関係がある。
両者は、共通する静止物体から発する重力場の中で、$F_0$ は静止した物体が、 $F_b$ は動物体が受ける重力を表している。電磁気では、この静止物体がつくる場は、 電場しかないので、動物体も静止物体も等しい力を受ける。 (付言すれば、このとき動物体の系ではより大きい電場を見ていて大きな力を受けているが、 それをローレンツ変換して静止物体と等しい力を受けるのである。)
重力場では、受ける側の質量に差がある。図 3 (c) の $b$ は質量が増している。 その影響をどう判断するかである。重力においては場の大きさは、そのまま力に直結するとは限らない。 そこで、重力場から重力による加速度の間に、重力という力を置き、2 段階に分解して考える。
後半の力と加速度との間には、逆数係数である質量がある。 力は $1/γ$、加速度は $1/γ^2$ に減るという特殊相対論の要請から、 比例係数 $m$ は動質量でないといけないことがわかる。
前半の場と力の間の関係については、電磁気では電荷がどのような運動をしても、 $F = q E$ として、場から力への関係は運動に依らなかったが、重力ではそれが問題になる。 重力は、場の強さと(1)静止質量と、(2)動質量に比例する 2つの場合の考察を試みる。
このような変換は、電磁場では、ローレンツ変換を 2 回繰り返したときに起きるものであり、 その理由を理解するのは難しい。
側を通過する質量の重力の変化を測定することで、どちらが正しいか実証されるかもしれない。 (1) なら単純な3 次元ベクトル場によって重力の表示が可能である。 (2) の動質量に比例するとするとき、今までは単純さのために、運動と横方向だけを考えたが、 縦方向のときも考え、重力が縦方向の動質量に比例するなら、 重力による加速は光速の限界を持たないことになる。 これが特殊相対論の禁止事項を犯すことは注意する必要がある。 それを避けるため、方向による質量によらずに横質量によるとすると、 重力がすべての物体に同じ加速度を与えるという要請は満たされない。二者択一である。
(2)のときニュートン加速度場 $e$ と、コリオリの場 $b$ は、 座標系の加速と回転によって局所的に完全に見えなくなることに注意されたい。 それゆえ、$e$ と $b$ は、一般相対論における局所慣性系と同じ特性を持ち、 その加速度と、回転を特殊相対論的に示すものである。
また多少状況が違うが、 地球上のように一様な垂直重力場の中に静止物体 $m_0$ と水平方向に動く動物体 $m$ があるとき、 静止物体には、重力 $m_0 g$ が働き、動物体には、重力 $m g$ が働くとするとき、 動物体の系では、自分の質量は $m_0$、加速度場 $e$ は $γ^2$ 倍に増加して、 重力は$γ^2 m_0 g = γ m g$ を受ける。それが元の系では、$1/γ$ になって $m g$ となっている。 この話からは $e$ 場は、(2) のように $γ^2$ に変換される必要がある。
(*) 本文のように、"さらに質量の比を考えると、$F_1$ のかかる場 $(e + v \times b)$ は、$F_a$ の場の$1/γ^4$倍になる"というとき、 $F_1$ の受質量は $m$ 、$F_a$ の受質量は $m_0$ であるから、場は加速度場を意味している。 この$(e + v \times b)$ 場が、動質量に由来し、力でなく加速度を与える場と考えるなら、 ローレンツ変換から考えられる2式は、$A_0 = γ^2 A_1, A_a = γ^2 A_b$ であり、(1)のように、$A_b= A_0$ とできる。 そのとき、$A_a = γ^2 A_b = γ^2 A_0 = γ^4 A_1$ である。物体aと物体1の違いは2回のローレンツ変換に相当する。 (1)のように、単純なベクトル場によって、重力の加速度場の変換が可能になる。縦質量を考えるときは問題が残る。(2017/6/12)
(1)の場合、電場と同様に、$e$ の総量は保存され、 \[ m_0 = ∫_s e・dr \] または、$div e = m_0$ であることが示されよう。(2)の場合は、 \[ m = ∫_s e・ dr \] となるかどうかさえ確かでない。 $m$ の方向による変換は、$e$ の方向による変換と一致しない。
電磁気のローレンツ変換を、ニュートン重力に適用することには抵抗がある。 既存の一般相対論を否定する必要はあるのかという意見である。 しかし一般相対論は、それまでの特殊相対論を重力の存在しない平坦な時空に限定することで、 重力の特別扱いを要求し、特殊からの連続性を諦めた理論である。 数学的扱いは一変して高度な数学が使われるため、両者の対応の付けは難しい。 図 2 のように、通過する質量のもたらす重力について、一般相対論ではなにかいうことは難しい。 重力を扱う3 次元ベクトル理論があれば、どれほど便利か想像も付かない。 初学者には電磁気の磁場にあたる、 コリオリ場の存在さえ一般相対論に存在することを認めることが難しいのである。
これらの 3 次元ベクトル場で重力を説明しようとする場合、問題となるだろうことを挙げておく。
(a) (2)の場合、加速度系がでてくるが、これはすでに特殊相対論で扱わない系である。 それは、系の中の座標によって時間の進みかたが異なり、光速が系の座標によって異なる系である。 そこで、重力理論を立てる場合、 "一様な重力場が、重力のない場合の加速度系と原理的に区別できないという要請は、 満たしているのだろうか"という問をつねに投げかけることができる。 上の(2)の場合これを満たしている事を示すのはたやすいだろう。 e は加速度を与える場であることに関連している。
(b)また、光の重力による屈折はどうだろうか。問題はまだまだ解決されていない。
電場の y, z方向成分は、γ倍に拡大する。 \[ E_x = E'_x, E_y = γE'_y, E_z = γE'_z \] これらから、 \[ \begin{align} E_x = E'_x &= qγx'/R'^3,\\ E_y = γE'_y &= qγy'/R'^3,\\ E_z = γE'_z &= qγz'/R'^3 \end{align} \] $x$ 方向は、距離が$γ$倍に、$y, z$ 方向は、電場が$γ$になり、 結局全ての方向で同じ式になって、等速直線運動をする電荷の電場の式が導かれる。 \[ {\bf E}= q {{\bf R}\over R^3} {1-v^2 \over \sqrt{1-v^2sin^2\theta}^3} \] 別の定性的な説明としては、$b$ の系では $b$ を中心とする球状の等電場面がある。 移動するその球は、$a$ の同時刻で切断すると、$x$ 方向にパンケーキ状にローレンツ短縮をする。 その短軸上の位置($1/γ$の距離)で $b$ 系の球状のそれと等しい力を受けるためには、 $x$ 方向の電場は$1/γ^2$倍に減っていなくてはならない。 $y, z $方向では、$a$ 系の静止電荷が受ける力を、$b$ 系からみると $1/γ$ に減って球状の等しい力 になるから、$a$ 系ではその$γ$倍を見ているのである。
(*5) すれ違う電荷の現象を重心系からみると、両電荷は、電場以外に同じ大きさの反発力をローレンツ力で受け、 対称性から場の運動量を考える必要がないと思われる。 場にエネルギーがあるなら、それを片側の電荷静止系で見るとき運動量があって当然である。
私がこの2物体間の電磁気力の非対称についての思考の端緒を得たのは、 R.セクル, H.シュミット, 広瀬立成訳、"相対性理論講義"(東京図書) P.192, 図14.8 だろうか。 また、M.ボルン, 林一訳、"アインシュタインの相対性理論"(東京図書)にも、補説2(P.304-305)に 図138-141を使った議論がある。 最近手に取らず書庫に埋れて引用できないが、電磁気の教科書のなかにも、図を示してこの非対称性を解説する本があったと記憶する。
電磁気のローレンツ変換は、電磁気学のローレンツ力 F=q(E+vxB)の相対論的説明であり、特殊相対論の重要な結果である。速度をもつ電荷から出た 電場ベクトルの先を結んだ立体(方向による電場の強さ)は球対称ではなく進行方向に潰れた回転楕円体である。その潰れ方は、ローレンツ短縮よりも強く、 電場は速度に垂直方向はγ倍、平行方向は1/γ^2倍である。動く電荷からの電気力線は、側面に集中しているが、本数は変わらない。
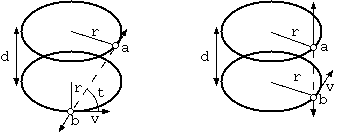
物体a,b のすれ違う時の対称的な2物体が受ける非対称な力は、電磁気と相対論の基本的思考の訓練である。一見して無反動推進を可能に思わせる。 同極に帯電させた円周をもつ2円盤を上下に接近、中心を連結し、上下円盤の下側を回転させると、上側は下側より強い反発を受け、上下円盤全体は上に力を得るか。 基本的な思考は誤りやすい。地味で困難な数式的な理解によって不可能とすることは、正しいとき辛いが必要な認識であるが、その理解の方が誤りで、 長い論理のなかのミス、間違った前提、例えば、無反動推進はあり得ないという、余計な専用原理の導入の誘惑が原因かもしれない。永久運動は関係せず、 物体だけの運動量保存=作用反作用は、場に運動量をもつ電磁気、同時性(=空間=場)が系による相対論では使えない。
静止電荷と動電荷は、互いに電場の力だけをやりとりする。両者の与える電場と力は、つねに相手の現在位置を指し、両者を結ぶ線分上にあるが、 その大きさが等しくなく、作用反作用の関係にない。両者は静止と等速直線運動なので電磁波は発生しない。(ここまで正しい。) 動電荷の速度に垂直な電場成分は、動電荷が与える方が、γ倍であることは、すれ違いのどの位置(角度)でも起きる。(間違い。) つまり、動電荷の位置の角度θが0度(速度に平行)に近いと、動電荷の受ける電場(球対称)に比べ、与える電場は平坦化し小さい。その垂直成分はγ倍に大きいとはいえない。
しかし、電荷が全方向にもつ電場の、電荷を包む閉曲面の法線成分の面積分は、内部電荷に等しいから、上下円盤は同じ大きさの反発力を得るという説明は、 どこまで近づけたら全方向か?という疑いがあり、十分近づけないと全方角を含まない。少し離せば、下側の接線速度vに対して下側の電荷の位置abには最小角度がある。 例えば円盤の半径rに距離dが同程度なら下側電荷の角度θは30度程度までである。さらに距離を大きくしてもよい。 そのとき、連結した上下の円盤は上に力を得るか。下側の電荷の速度に対して、真下の電荷の位置は垂直だが、下側円周の他の位置の電荷の速度と位置は考えにくいが、 厳密にいえることである。しかし、距離を無限にすれば当然、非対称な力は0になる。こうして単純で美しい問いは、難しいだけの詰まらない演習問題になる。
(2017/7/8)