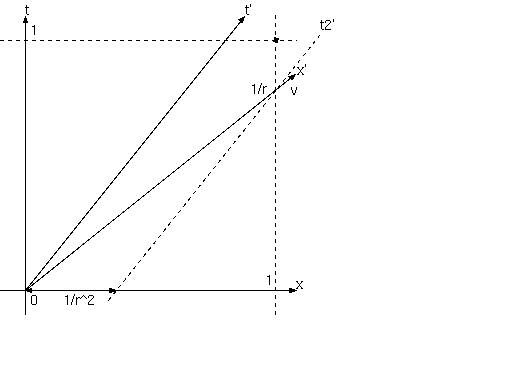
図 2. マイケルソン・モーリー実験
1. はじめに
2. 慣性系
3. マイケルソン・モーリー実験
4. 同時刻の定義と時空図
5. 時間と空間のローレンツ変換
6. ローレンツ短縮と時計の遅れ
7. 双子のパラドックス
8. ローレンツ変換と、短縮と時計の遅れの関係
9. パラドックス
10. 速度の合成則
11. 相対論と、決定論
12. ローレンツ変換と加速度
13. 双子のパラドックス(続き)
14. 時計の公準
15. 相対論における不変量
16. 円筒時空と双子のパラドックス
17. 円筒宇宙の絶対静止座標系
18. 重力と双子のパラドックス
19. あとがき
高度な数学的表現は、すばらしく思考の節約になる。しかし数式には必ずその思想なり言葉がある。 それを意識して数学的結果を鵜のみにしないことも重要である。 数式は理解を助けるための方法であるのに、高度な数学が逆に物事を見えなくさせることもありえる。 記述が難しくなると、素人が近付けなくなる。なにか混乱があるとき、見通しをよくするには、 すっきりした初等的な説明が一番必要なものである。数式のもとの考え方のほうが重要である。
一般的に思考は間違うものである。定式化よりも概念を、量的な議論より定性的な性質、 誤差の議論の前に、まず正負の符号をとらえる必要がある。 整合性よりも、基本特性が現実の検証に耐えるかどうかを考えるべきである。
この文章を起こしてみようという気になった発端は、数年前の次の経験がもとであった。 ローレンツ短縮と時計の遅れは、非常にポピュラーで、 相対論の入門書には真っ先に出てくるものであるが、両者は性質が逆であり、 片方は短縮、もう一方は伸長である。
数日間の混乱のあと、見る条件が違うことに気が付くのであるが、 そのとき、自らの誤りに驚いたのである。勘違いは伝染する。 手持ちの本を調べてみると、相対論の入門書のひとつが本当に間違っていた。 意識的に理解しないとき間違いは入り込む。 自ら考えることを助けることが書物の働きであるはずが、 天下り的な思考方法の押しつけや初歩的誤りが多いことを嘆く。
相対論は、経験を超えた思索が真実の領域に関わるという基本的面白みだけでなく、 電磁気の理解のために欠くことのできない方法である。 相対論なしには、 どうやって飛んでいる電荷が磁場の中で受ける力を電場とみることを説明することができるだろう。
電磁場中を動く電荷は、ローレンツ力 F= q(E + v x B) を受けるが、 電荷に並進する系からみると電荷は静止しているから、力の原因はその系のローレンツ力の内、 電場でしかありえない。磁場は速度をもった系では、 系の速度に比例する電場に変わる。速度 v に垂直な成分は、ローレンツ力と非常に似た式になる。
E'= γ(E + v x B)
磁場自体も動く電荷の相対論的効果ではないかと思わせる。 電流の流れる電線に沿って飛んでいる電荷が磁場の力を受けるのは、 電荷にとっては、電線の中の正負の電荷のもつ速度差、 これは通常の電線と電流の大きさでは、毎秒 0.1 mm 程度の驚く程わずかな速度であるが、 そのわずかな速度差の、 なんとローレンツ短縮の違いで電荷には電線が帯電して見えることが原因である。 これはまさに相対論的現象である。この電線の帯電を別に説明する、 電流の電荷密度へのローレンツ変換も、同時刻が前方では未来にあたることだけから、 容易に説明できる。行き来する定期航路の密度である。
磁場の速度に比例する力とは、不思議なものである。速度は相対的であり、 上限は光速まで存在するからである。そこまでの力を出す真空とは、 いかに硬いものかと驚くべきだろう。 また、電荷の受ける磁場による力は、まるで力学のコリオリの力のような形をとっている。 回転系の角速度にあたる磁場がどうして、電流からもたらされるのだろう。 電磁気には、昔から議論となった単極誘導の議論がある。これの理解のしかた、 回転系と電磁気の関係をうまく説明できれば、この文章は成功である。 それ以外に静止場の運動量という、困った話を付け加えたい。
ニュートン力学では、慣性系間に位置と速度について意見の不一致が存在する。速度 v で移動する点 a から見ると、 自身は止まっていて、止まっている b が速度 -v で動く。それは、常識的なものであるが、相対論では その座標系の物差し(スケール)の目盛、時計の刻(間隔)に意見の不一致が出て来るのである。
慣性系は対等である。静止した慣性系と、動いている慣性系の中で成り立つ法則は、同じとする(相対性原理)。 物理での原理とは、数学における公理のように、誰もが前提として、認めることができ、それを満たさない物理法則は 法則に値しないとする、"原理的要請"である。特殊相対論は、ふたつの原理をもつ。相対性原理と光速度の不変である。
ふたつの慣性座標系 K系(x,y,z,t)とK'系(x',y',z',t')があり、K'の空間軸がKの空間軸と各平行で、 K' の原点が空間軸 x 方向に速度 v を持つとき、K 系の事象点を K' 系に座標変換する。
x' = x - vt
t' = t
これをガリレイ変換といい、ニュートン力学での速度をもつ系への変換公式である。 ニュートンの力学法則 F = ma が、座標系の位置と時刻、 速度が違っても成立するのは、a が加速度であるからである。それら(位置と速度)をずらしても、 力と加速度の関係は不変であり、どの系からみても F = ma が成立する。 ニュートン力学のガリレイ変換は、慣性系の対等を満たしている。
電磁場E,Bが系によって姿を変える、電磁場のローレンツ変換がこれの帰結であるが、 恐らく誰もが最初にローレンツ力の式に接したとき、基本公式に速度 v が出て来ることに気味の悪さを感じたことだろう。 これは一体、なにが起こるのだろうか、という感じがあったはずである。 電荷の測定系に対する速度 v は、本当は何に対する速度だろうか、 電磁気はエーテルを要求しそのエーテル(絶対静止系)に対する速度なのか、 磁場又は磁力線に対する速度なのか、磁場源との相対速度なのか、と考えてしまう。
相対論は、電磁気を手がかりにした。相対論によってニュートン力学は修正を受けたが、電磁気は無傷であった。 電磁気はもともと相対論的であった。マックスウエル (Maxwell(1831-1879)) によって電磁場が定式化され、 波動となって空間を一定の速度で伝播することがわかる。その速度が光速に等しいことから、光も電磁波の一種とされる。 ヘルツ(Heinrich Hertz 1857-1894)によって、リングアンテナに火花を飛ばす原始的な方法で、 電波が実際に発生され受信される(1886)。この時代は、19 世紀の終りである。 アインシュタインの若い頃には、電波や電話、電灯(1879)すらまだなかっただろう。
音が空気中を粗密波として伝搬するように、また海の波が水の重力による波であるように、波は媒質に対して速度をもつ。 光速を媒質に対して一定とすると、地球の絶対速度が測定できるはずだった。絶対運動が測定できないのは、 後世の哲学者が言うようには、決して自明ではない。
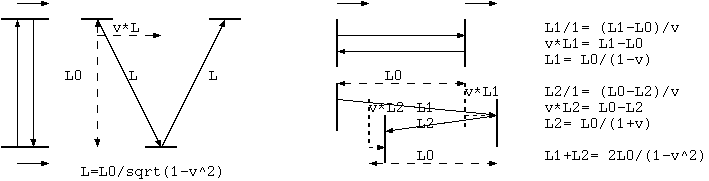
マイケルソン(1852-1931)とモーリーは、光の干渉計を使って、エーテルの風の速度を測定した。 中央に半透明の鏡をおき、地球進行に対し垂直に往復した光と並行に往復した光とを干渉させる。 精密なこの装置自体を石盤の上の水銀だめに載せて 90 度回転させることで干渉の変化をみる。 歴史的な実験の日には町中がこの実験に協力しすべての交通機関を止めたという(1881)。
図 2. は静止座標からみている。地球の運動と垂直に光が距離 L0 を往復する場合、光が斜めの距離 L を行く間 t に、鏡は v*t だけ進む。光速を 1 とすると、t= L とすることができ、 L^2 = L0^2 + (L*v)^2 から、L = L0/√(1- v^2) となる(左図)。
それに対して、地球の絶対運動に平行な光の往復は、左の壁から光がでて右の壁に到着する(L1 の距離を進む)までに、 壁が v*L1 だけ先に(逃げる方向に)進む。行きは L1= L0/(1-v) であり、帰りは v が符号を変え L2= L0/(1+v)、 往復の時間(又は距離)は、L1+L2 = 2L0/(1-v^2)である(右図)。

地球が空間の中を進む速度、(太陽の周りを 1 年で回る公転軌道速度は、太陽地球間が 1 億 5000 万kmだから、 1.5 * 10^8 km * 6.28 /365/24/3600 から、) 毎秒 30 km は、v=10^-4 つまり光速の 1 万分の 1 にもなり、√と 1 - v^2 があるので、0.5*10^-8 の精度がいる測定だが、光の干渉を使えば、当時の技術で十分に測定できるはずであった。 ところがこれは、種々の条件で測定に失敗した。地球の速度と垂直と平行で差がでないのである。
これを説明するために、エーテルが地球に随伴して、引きずられるという考えも出てくる。 また、媒質を必要としない粒子のように、光速には光源の速度が加算されるとする W. Ritz 等のエミッション理論(1908)もマイケルソン・モーリー実験の説明には成功する。
光速に光源の速度が加算されるのであれば、 進行方向に垂直な光は、斜めの L の距離を光は同じ時間で行き、往復で 2 L0 である。 進行方向に並行な光は、行きに、1+v 帰りに 1-v の速度をもち、往復は L1+L2 = 2L0、 両者の往復の時間差はない。しかし、この理論は、反射光との干渉が起こり得なかったり、 媒質だけを運動させた場合のドップラー効果をみるフィゾーの実験の説明も技巧的にした。 また、連星の円運動が楕円運動になることなどで、否定された。(章末の注*1)
ローレンツは、両者の時間差が無くなるようにエーテル中を速度をもって動く物体は、 エーテルによる力学的圧縮を受け、進行方向に短縮すると考えた(ローレンツ短縮)。 光と運動が並行の場合に、L0 が進行方向に √(1 - v^2) 倍に短縮すれば、 往復時間は進行方向に垂直な場合と一致するのである。
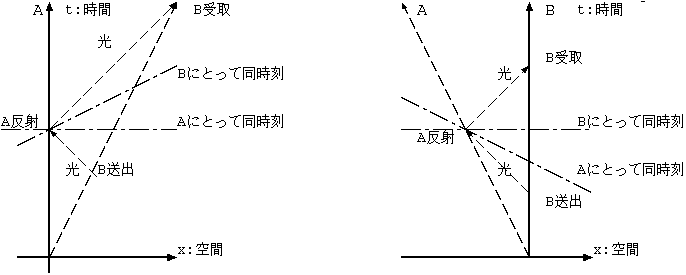
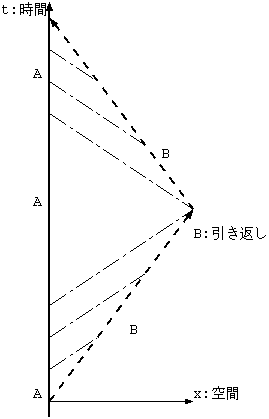
離れた場所の同時刻を次のように決める。B は A から見て速度 v で x 方向に移動している(図 1.)。 B 点から A 点へ光を送り、A は即座にその光を B に返すとする。 B は送ってから受けるまでの、ちょうど真中の時刻を A が受けて返した時刻と同時刻とするのである。
光はつねに傾き 1 の直線である。A の返した時空点への光の行き帰りの距離は、A からみたこの左図では ひどく違っているが、B にとって等しい距離であり (B のみるものを右図に示す。)、光速を一定とするから、 この定義は理屈にあっているのである。このように B にとっての同時刻を決めると、 A からみた B の動きを示す左図に B にとっての同時刻線が書ける。これは A の同時刻(左図の水平)とは違っている。
B の同時刻線は、B の進行方向、前方では A の未来になっている。
A にとって未来(水平より上)で、B の同時刻線より下の時空点は、B にとって過去である。 このように、時空は慣性系によって違ってとらえられる。A から見た B の同時刻が傾いているのは、 B の空間の時間との混在を表わす。相対論では、時空は相互に関連した存在となった。
この B の軌跡は B の時間軸であり、B の同時刻線は B の空間軸(x 軸)である。これらは、B の時空を A の時空上に写している。 ニュートン力学では Aの時空図上のBの軌跡をBの時間軸とせず、Bの存在する時空点を示すだけとしたが、 特殊相対論では、運動物体Bの時間軸と、同時刻(空間軸) とをAの時空図上に示すことができるのである。
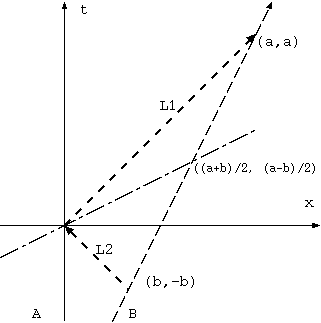
同時刻の定義どうりに、A の送受の時空点を原点にとり、それを通る +/-1 の傾きの光 L1, L2 を引き、 B 点の受信点として L1 上の 1 点 (a,a) と、B の送信点として L2 上の 1 点 (b,-b) を結ぶ線分の中点、 これが原点と同時刻である。((a+b)/2,(a-b)/2)と原点とを結ぶと、その傾きは、(a-b)/(a+b) である。 これは、もとの L1, L2 上の 2 点を結んだ線分、B の軌跡 (これがx= vt+cである) の傾き、 (a+b)/(a-b) の逆数である。つまり同時刻線は、t= vx である。
x= vt は、時間軸 (x'=0) であり、t= vx は、空間軸 (t'=0) であるから、d, e を仮に定数として、
x' = d (x - vt),
t' = e (t - vx)
とする。これの逆変換を ' を入れ換え v, -v を入れ換えた式とし、 順逆の変換を掛けると元に戻ることを要請して、つぎのローレンツ変換の式を得る。
x' = γ(x - vt),
t' = γ(t - vx) 但し、γ= 1/√(1-v^2)
この式は、A の座標系 K(x, t)から、速度 v をもつ B の座標系 K'(x', t') への変換を示している。 速度 v の方向 x と時間 t の 2 次元の座標変換であり、v に垂直な、y, z は変換に関与せず、 y'= y, z'= z である。
この変換は、速度だけによって決まり、加速度を含まない。ローレンツ変換は、虚数角の回転として 表すこともされるように、x と t について線形変換であるため、大きな値も許される。一般相対論の 座標変換は、微小な dx, dt についての式であり、大きな x, t について直接言及できない。
ローレンツ変換は、ガリレオ変換の x'= x - vt、 t'= t の"速度による位置の変化" x'= x - vt については類似するが、それと対称な (1) "速度による時刻の変化" があること、t'= t - vx と、(2) x', t' のγ倍拡大があることが違っている(*)。位置 x の変換と時刻 t の変換は、 同じ式を使用している。ローレンツ変換は時間と空間において対称なのである。
(*) それによって、x', t' は速度に線形でない。ガンマ(γ)は速度の2乗の関数なので、速度vが光速(1)よりはるかに小さい、v≪ 1 のとき表れないが、vが1(光速)に近づくと、x' と t' の係数のふりをしていたガンマはどこまでも大きくなる。
図 2. の左の図のように、光が一定距離 L0 を往復する仕掛を時計として使う。光は延びた斜めの距離 L を往復する。距離 L を光が行く間 t に、鏡は v*t だけ進む。静止系からみると光は延びた距離 L を往復しないといけないから、速度 v の時計は、γ= 1/√(1-v^2) 倍にゆっくり時を刻むのが当然と思える。 高速に移動すると、"忙しくて時の経つ暇もない"、ということだろうか。
ローレンツ短縮とは、エーテル中の運動物体が、進行方向にだけ√(1 - v^2) 倍に短縮する現象である。 ローレンツ短縮は、マイケルソン・モーリー実験が測定できるはずの絶対運動が、決して測定できないこと を説明した。これがローレンツの考えたように分子間の力学現象ではなく、物差しと時計自体が変化する、 時空の座標変換であったと判るのは、相対論による。しかし、時空図だけで何とか説明するのは難しい。 B のみる時間の目盛、空間の目盛はこの図には、表れていないからである。*(付録 2)
相対論には光速の制限があり、光の速度には物体はどのようなエネルギーを費しても到達できない。 しかしそういう負の側面ばかりではない。地球から遠方の恒星を目指して旅行する場合、時計の遅れのために、 乗った者の時間の経過が緩慢になり、10 光年先の恒星系に行くのに、搭乗した人にとって 1 年もかからず 到着できるという現象がある。 静止寿命が 2.2 マイクロ秒のミューオンは、大気上層から地上までの約10km(光速で30マイクロ秒かかる)を通過して、 地上に到達することが観測されるという。
複数のロケットがある距離をもって存在し、その列の方向に同時に一瞬で加速したとき、速度をもったロケット列の全体の長さが縮むなら 先頭と末尾のロケットで移動量が違うのか? 同時に同じ速度を獲得するというのなら、それぞれの間の間隔は確保され短縮を受けず、 物体であるロケットだけが短縮されるのか?逆に、空の空間は短縮を受け、物体であるロケットは短縮されないのか? ロケットの間の空間は短縮できるとして、物体であるロケットは、何の力で短縮するのか? 物体が力なしに短縮するのは力学ではありえない。 両方の疑問は、共に間違いである。速度の方向に、先頭から末尾のロケットまでが一体として短縮するのである。
静止状態で同時の加速は、速度を得たロケットの同時の加速ではないから先頭と末尾に移動量が違ってよい。 ローレンツ短縮は、見る系と見られる系との速度による座標変換であり、力学的な力による物体の圧縮ではないから、 物体と空の空間は、区別なく元の比率を保ち "比例的に" 短縮する。物体に対して大きな速度をもつ系からみて短縮する座標変換は、 光による見え方や幻想ではなく、実際に短縮している。速度をもった系間では特殊相対論が成立する。系内の長さを固有長といい、 速度をもつ系の間でみる長さは、固有長よりも短い。
物体は、原子からできている。原子には縮退圧があり、どこまでも圧縮できるわけではない。ローレンツ短縮には限界があるのか? これも間違いである。速度が光速にどこまでも近づけば、ロケット列は、限界なく短縮され薄膜はどこまでも薄くなり、 量子力学が決める原子の大きさや核力による原子核の大きさよりも薄くなれるのである。
これがパラドックスとされる理由は、B からみても A が離れていって帰って来ていることである。 刻々の相対速度は、A から B を見たものと B から A を見たものとは大きさが等しい。 これはどう解決するのだろうか。
B はもう一度 A と会うために、引き返している。B の引き返しのときに B はロケットをふかし逆向きに推進している。 つまり B は慣性系ではない。行きと帰りそれぞれについては、B の慣性系からも時空図を書くことができるが、 B の引き返しの加速時には慣性系の時空図は書くことができない。特殊相対論は、慣性系から見る限り、 等速直線運動以外の加速運動さえも含めて、全ての運動を説明するが、見る系が慣性系であることを前提にしている。
慣性系 A から見た B の動きと B の同時刻線 図 3. を使って説明する。 B が離れていく間と B が帰って来る間の B の同時刻を A の世界線上に記録する。 それらを見ると密集した同時刻線がならぶ。これは、B から地球の時間の経ち方が緩慢だと見ることを表す。 帰路も、やはり B の同時刻は密集している。ところが、B が引き返すための逆推進している間、A の場所の B の同時刻線は大きく未来に飛んでいる。そのため、B の時計は、A と比べて遅れるのである。
ローレンツ変換は、ある慣性系 K からみた(x, t)から、 (光速 を 1とした) 速度 v をもつ別の慣性系 K' からみる(x',t')を与える。
x' = γ(x-vt)
t' = γ(t-vx) γ = 1/√(1-v^2)
これの逆変換、速度 v をもった K' 系からもとの K 系への変換式で考えよう。 速度をもった物体が元の系からどのように見えるかを表す式である。
x = γ(x'+vt')
t = γ(t'+vx') γ = 1/√(1-v^2)
このローレンツ変換は、次のように短縮にも伸長にもなることができる式である。 この式に見られる側の空間(同時刻)である t' = 0 をいれると、
x= γx'
となりγ= 1/√(1-v^2)が 1 以上であるから、空間を拡大する式になる。
x= γ (x'- v(vx')) = √(1-v^2) x' = x'/γ
それに対して、"時計の遅れ" は、見られる側の K' 系上の時計の経ち方をみるため、x'= 0 を代入する。 これは、t' = 0 をいれた空間の拡大と同じ操作であり、伸長の式である。
t= t'/√(1-v^2)= γ t'
つまり、ローレンツ変換自体は、どこを切って見るかで短縮であったり拡大であったりする。 "ローレンツ短縮" はこちら K の空間(同時刻)で切って見るのに、 "時計の遅れ" は向こう K' の 1 点の時間(空間=0)で切って見る。 両者は切り方が全く違う操作なのに、それが感覚的に自然に理解されるのは、不思議に思う。
"ローレンツ短縮"と"時計の遅れ"とを、空間と時間において対称な現象とみるのは間違いである。 向こうの物差を含めて物体の長さが短縮し、その構造が詰まるローレンツ短縮と同等なのは、 向こう側の時計の刻を含めて、時間方向の構造が短縮すること、つまり変化の高速化現象である。 時計の遅れは全く逆の低速化現象である。
また、回転の成分のように、一方が伸びれば他方が縮むのは当たり前とするのも間違いである。 ローレンツ変換は、ピタゴラスの定理の平方の和が一定の話ではなくて、平方の差 s^2= t^2 - x^2 を不変にし、 一方が伸びれば、他方も伸びる変換であるからである。
A から見て B が縮むというなら、B から見ると A が延びているのではないだろうか。 ところが、B から見ても A は相対運動の相手であり、同じく短縮しなければならない。 A から見て B の時計がゆっくり時を刻むなら、B からは A の時計は速く動くべきではなかろうか。 しかし、相対運動の大きさは、B から見ても同じである。 相対速度の大きさだけで決まる相対論的現象は、一方が他方を見るとき起こることは、 すべて逆の方向にも起こらなくてはならないために起こるパラドックスである。
ローレンツ短縮は、見る側の空間(同時刻)によって切断した時空の断面で相手が縮んでいるのであった。 感覚的には見る側から光らしたストロボ写真のように同時刻の描像が見られるとしたときの話である。 (もちろんこれは喩えであり、光で照らすのは、相対論的現象の議論では、同時刻とは程遠いものであるが。) 見られる側の空間(同時刻)で切った写真、ロケットの中央からのストロボで照らした猫像は、 逆に延びているだろう。船の先端と末端に付いたライトを電気的に同時に光らすとき、 地上からみたライトの間隔は延びているだろう。
このようにこの基本的なパラドックスは、矛盾ではない。ローレンツ短縮と時計の遅れは A から見ても B から見ても、 速度をもった相手側に、同じく起こるものである。相対論のパラドックスの混乱させる性質は、驚くべきものである。 しかも混乱は、それだけでは済まない。
地球から見てロケットに乗った者の経つ時間がゆっくりなのは理解したとする。 それなら逆に、ロケットに乗った人にとっては地球や、遠方の恒星系の方が速度を持っているため、 そちらの方が時間の経過が遅いはずだという疑問がすぐにでる。これは、前前章の図 3 でも説明したが、 ロケットに乗った人には地上の時間の経ち方が遅くないといけない。それをどう説明するのだろう。
また、乗った者の時間があまり経たないのに、遠方には光速でしか行けないということは、 彼はどこかで時間を失っている。かれは、世界の時間とのずれができているが、 それはどこで発生したのだろう、どこで彼は時間を失ったのだろう、という疑問がでる。
これは相対速度自体ではなくてその前後の加速に関係している。 ロケットが地球の慣性系から離れて、前方の恒星をめざして加速し、速度を獲得するまでの間に、 前方の恒星の(ロケットとの同時刻の)時刻は急激に進み、到着の直前の時刻になってしまう。 彼がロケットの中で経過する時間は、到達直前の時刻になった前方の恒星の経過する時間より、十分に長いのである。 彼は、この加速時に、世界と対応する時間を失っている。加速は前方が未来に進み、後方は過去に遡るが、加速で得た速度は、 未来に向かう。彼は時間を失って未来に行けるが、逆に時間を得て過去に行くことはない。
(*)このような特殊相対論のパラドックスは、一般相対論では存在しない。一般相対論では、 その場所の微分的な物差しの大きさと微分的な時計の経過の速度を決めるg_ikという計量が 時空の各点に付属していると考え、見られる側は、その場所の一点であるから。
ローレンツ変換の視点から双子のパラドックスを疑ってみよう。刻々の相対速度の大きさは、A から B を見たものと B から A を見たものとは等しい。相対速度だけでローレンツ変換はできていて、加速度の項をもたないから刻々のローレンツ変換は、 A, B について完全に対称である。B だけ時間の経ち方がゆっくりになるのはやはり不合理かと思われる。 これはどう解決するのだろう。
刻々というものが違うために対称的でなくなっているのであろうか。B からみてもそのことは同じだから、それは正しくない。 じつは、ローレンツ変換は、慣性系での変換法則である。ローレンツ変換は、加速物体の運動を扱うことはできるが、 加速系で、ローレンツ変換を使うことは正しくない。加速系ではローレンツ変換に不変な電磁波である光も曲がり、 マックスウェル方程式も成立しない。ローレンツ変換自体は A, B について対称的だが、加速物体の B からみた系で、 それを使うことが、間違っていたのである。
ローレンツ変換、K 系から、速度 v で動いている系 K'への変換は、
x'= γ(x-vt)
t'= γ(t-vx)
であるが、K' 系から元の K 系への変換は、v の代わりに -v をいれ、' を入れ換えた式になる。
x= γ(x'+vt')
t= γ(t'+vx')
速度 v2 は、K' 系の dx'/dt' であり、速度 v1 は v である。上下の x,t の式を dx, dt で書いて辺辺割算すると、γは消え、
dx/dt= (dx' + v1 dt')/(dt' + v1 dx')
右辺の分母子を dt' で割ると、次の式になる。
dx/dt= (v2 + v1)/(1 + v1 v2)
速度の合成式は v1, v2 に対称であり、v1, v2 が 1 に近くても、その合成速度は 1 (光速)を超えない。
速度の合成を、v2 の分がローレンツ短縮分 1/γ倍に小さくなり、時計の遅れでさらに 1/γ倍に小さくなると考えると、 v1 + v2(1-v1^2) = v1 + v2 - v1^2*v2 になるが、間違いである。v1, v2 について対称でもなくなる。
決定論の観念自体の妥当性は疑ってよい。価値を論じるのはすでに科学の領域ではないが、 通常人は行動で価値判断されるのに対して、それが行動の前にすべて用意されているという観念は、 自由意志と行動の価値を否定するものでしかない。
しかしながら、一方では、相対論は因果関係の起こる範囲を明確に限定した。 全ての物質の移動と通信を光速が制限し、 ある時空点は、その点からの光の円錐以内への影響を許し、 光円錐の中を時間的未来領域としている。
s^2= x^2 + y^2 + z^2 - t^2 <= 0
光円錐とは、空間を 2 次元に制限した(x,y,t) の猫像である。 3 次元と時間では、光の 3 次元的広がり、光球の爆発のイメージである。 逆に、その反対側の時間的過去の光円錐、収縮する光球の内側領域だけからその時空点は、影響を受ける。
s^2= x^2 + y^2 + z^2 - t^2 > 0
空間領域とは、ニュートン力学では厚さのない隔膜だったものが大きな領域、光円錐の外部領域になったものである。 この空間領域と原点の時空点とは、光速を超える物体や情報の速度がないために、因果関係にはなりえないので、 座標系によって過去、未来のいずれに見えても、差し支えない。 そのように相対論は、因果関係の許す限りの自由度を時間と空間とに与えている。
遠方の空間の未来が現在の空間にみえる系があってもよい。原因とそれがもたらす結果からみれば、 その未来はすでにあるという観念はその程度の希薄なものである。
宇宙の果てには、この宇宙の終末がすでにある。1000 億年後の未来に、そこに行くのにひとの一生も 必要としないかもしれない。だから、すでにそれは用意されていなければならないというのである。 しかし地球の 1 年後からは、その時空点に影響することはできない。 つまり、現在変更可能な遠方の未来は、1 年後の便では、すでに変更可能でないものになる。 そのように、相対論の時空概念は、因果関係を壊さない。因果関係を壊さないということは、 決定論は、一種の誤解の産物かもしれないことを示している。
決定論者が、未来がすでにあるというのは、空間領域であり、もともと影響の与えられない領域のことである。 時間的未来はこの時空点から変更可能な領域であり、そこでの出来事は何事も決定されていない。 高速な船に乗って行けば変更できるのである。
ニュートン力学の決定論は、自分の位置の未来の出来事すら決定できないとするのである。 何事も変更できないなら、自由意志も決定も全て剥奪されているようなものであり、 人権意識のある社会で、このような考え方が受け入れられるはずがないようなものである。 自由意志の剥奪は、人を奴隷にする。それでありながらこの決定論の風潮は、一体どうしたことかと考えさせる。
ひとは、自由を与えられても十全な自由は与えられたことがないと訴えているのであろうか。 或は、なにか神の意志を感じているのだろうか。独裁者の任意さは許容できないで、 神の自由気ままを許すのは、公平ではない。 宇宙の法則には、存在しない神さえも自由気ままは許されない、 ということを考える方がまだ救いがある。
なお、光円錐は、リエナール・ウィーヘルトの遅延ポテンシャルが示すように、 電磁的相互作用の唯一の場所である。光円錐の中が影響できるわけではなく、光円錐でしか影響できない。 電荷は、光の速度が出せないため、過去の自分の光円錐の内側にしか存在しない。 そのため自分の出した電場の影響を受けないで済んでいるとも考えられる。 電荷が過去の自分の電場の影響を受けると、自分で自分をどこまでも加速していくだろうからである(*)。
(*) 反射があれば光円錐の内部も影響を受けると、この段落には否定的反応があった。 但し、遅延ポテンシャルが反射できるとはいわないから、荷電粒子の運動への疑問として意味があるかもしれない。 なぜ、電荷は自分の発生する電場に影響を受けないのか。自分の出した電場をどう判別し無視するのだろうか。
その瞬間、物体に並進する慣性系との間のローレンツ変換は可能であるが、 並進慣性系の見る時空は、加速物体のみる時空と同一ではないはずである。 固有時というのは、小物体に付着した小さな時計の経過であり、 それには、加速系の理解が必要ではないだろうか。 一般相対論では、重力井戸の底で時間の経過が緩慢になる。 加速系でも時間の経過が緩慢になるのではないだろうか。
双子のパラドックスの弟 B の引き返しの時点で、B が慣性系を乗り換えるとき、 B の時計の時間が飛ばないという保証はなぜあるのか。A の方の時間が飛ぶのなら、 B の慣性系の乗換に B 自身の時間がかかってもいいではないか。これではパラドックスが消えない。
ところがよく考えると、加速系で時間の経過が緩慢になることは、B 自身の時間がかかるのではない。 パラドックスが消えない方向とは、符号が違い、逆方向である。B の固有時が小さいことを打ち消さない。 同じことの別の説明でありうるのである。
一般相対論の重力の存在する場合に、時空 a 点から時空 b 点までの全ての経路の中で、 測地線は固有時の停留経路、極大の固有時を与える経路である。
時空点には必ず測地線がある。測地線は、重力(時空)以外の力無しに経路を辿るものであるから、 一般に多数ある。高速な測地線、低速な測地線、それから空間の方向によっても多数(∞^3)ある。 重力がないときの特殊相対論の双子のパラドックスでは、地球にいる兄の経路を非常に遅い速度 の測地線運動と見ることができる。
そこで、双子のパラドックスの時計の違いは、時空点 a から b に至る経路の中で、加速をする系は、 加速をしない系(測地線)より、時間の経ち方がつねに少ないと考えることができる。
それでは、地球上のような一様な重力場で、地上に置いて静止した兄のボールと放り上げた弟のボールとは、 どちらが時間の経ち方が速いのだろう。これは放り投げるときの加速がないとすると、つまり最初から速度 を持ったボールなら、測地線運動である放り上げた弟のボールの方が時間の経ち方が大きいとわかる。 これは、双子のパラドックスの逆の結果となることに注意すべきである。
これはそうではない。地球上の時空の時計の遅れは、平坦な時空と比べてさほど大きく違わない (太陽表面でも1/100万の差しかでない)。 それに比べて、1 g での減速と加速の放物運動では十分遠方にまで出かけると時計の遅れは明確にでる。 同じ 1 gの加速系と重力でありながら時間の経ち方は違うのである。 等価原理からいえばこれは同じでよさそうだが、違うのである。
一般相対論は、ある時期のアインシュタインがそうしたように、一様な重力場は、加速系と原理的に区別できない とするわけではないのだろうか。いや、固有時が経路によって異なることは、この等価原理に矛盾することではない。 重力が原因で、ある時空点から別の時空点まで複数の測地線があるときにおいてさえ、一般に所要時間は違うと考える。
また、時計の遅れは、重力加速度 GM/r^2 には依らず、重力ポテンシャル -GM/r に依る。 4 倍の質量と 2 倍の半径 をもつ大きな惑星は、表面で同じ重力加速度であるが、重力ポテンシャルは、2 倍低く、そのため、時計の遅れは大きい。 電磁気もそうだが重力も、ポテンシャルの方が重力場自体より実在的なのである。
その前提を受け入れるなら、速度を変える物体の固有時も平気で扱うことができる。 (x,y,z,t) において s^2 = x^2 + y^2 + z^2 - t^2の固有時 s は不変である。 そのとき、ds^2 = dx^2 + dy^2 + dz^2 - dt^2 という微分固有時 ds を考える。 固有時の経過とは、微分固有時 ds の経路による線積分∫_a^b dsである。 時空点 a から b までの複数の経路において、兄の A と 弟の B とでは、 経路が違うためその値が違うのであると思ったが、これは間違いである。
経路で線積分すると、経路は平方の和の分長くなっており、固有時が平方の差の分 短くなるのを、ほぼ打ち消してしまう。∫(1/γ)dt だけに止めるべきである。 時空図では空間的に移動した B の経路はピタゴラス的に(√(1+v^2))斜辺がのびるが、 ほぼその分だけ(1/γ = √(1-v^2))、固有時が減少する。長い経路には、短い固有時である。
B が一定速度 v で距離 L の恒星まで往復するときの A の経過時間は、単純に 2L/v である。 B の固有時の経過は、その 1/γで 2L/v/γである。その固有時の差は、(2L/v)(1-√(1-v^2)) = 2Lv/(1+√(1-v^2))となる。v≪1 では分母は約 2 で速度 v と距離 L に比例する。
相対論の否定論者にとって双子のパラドックスの最も深い本質は、時空の経路による固有時の 違いを認めるかどうかである。物体がその歴史によって時間のずれを得るというのは、 常識を外れていて認めにくい。しかしこれが相対論の要求する驚くべき結論である。 これで相対論が実証性を失う事はなかった。
似たようなことが、アインシュタイン自身にもあった。ワイルの理論が出たとき、彼は、 物体がその歴史によって、時間の経過が異なることを理由に否定したのであるが、それは、 本当に正しかったのだろうか。原子のスペクトルの均一さを証拠にしたのである。
双子のパラドックスには、まだ相対論の否定論者の付け込むすきがあるだろうか。 一般的な当時のニュートン力学的世界観の慣性系の対等と電磁気学からの光速一定を原理として、 相対論は、時間空間の理解の変更を強いた。もし慣性系の対等を否定し、空間と時間との絶対性 を原理におくと、困難は、マイケルソン・モーリー実験の結果の理解にくる。また、相対性原理 を認め光速一定を否定すると実験事実に合わないだろう。高校生でも理解できる相対論だが、 原理的な部分の理解は、決して容易とは思わない。
s^2 = x^2 + y^2 + z^2 - t^2
光速は s = 0。 s^2 > 0 の場合を固有長、 s^2 < 0 の場合を固有時という。 固有とは、どの慣性系でみるかによらないからいう。系によらずこの量は保存され、 ローレンツ変換によって変化を受けない。
s'^2 = x'^2 - t'^2 = γ^2 ((x - vt)^2- (t - vx)^2 ) = x^2 - t^2 = s^2
不変量は、この変換のもつ性質を最も端的に表す。その物体に伴う時計による時間の測定、 その物体に沿う物差しでの長さの測定、そういう局所的事実は、 みる系によって変わらないという原理的要請である。
重力場、回転系、加速度系などの座標系間の一般座標変換を扱うことができる一般相対論の 一般座標変換における不変量は、ローレンツ変換における不変量 s^2 の式を一般化し、 局所化、微分化したものである。
ds^2= Σ{j,k= 1,1}^{4,4} g_{j,k} dx^j dx^k
円筒時空とは、空間的には等方的で時間的には静的な宇宙である。 これは宇宙項をいれたアインシュタインの定常宇宙でも近似的に同じだろうが、 平坦なミンコフスキー時空(不変量がs^2= x^2-t^2である時空)が、 トポロジー的に閉じている場合であり、このような宇宙が生成するかどうかは別としても、 一般相対論からは、宇宙項がない場合に存在が許される解である。 また、平面を曲げるだけで伸縮無しに作ることができることからわかるように、 円筒の表面には曲率がない。それと同じく、円筒時空も重力のない平坦な時空であるから、 特殊相対論が成立する宇宙である。
この円筒宇宙では、双子はどちらも引き返すことなしに再会する。 A も B も慣性系であり、互いに速度を持っている。 このとき相手の固有時が自分のより経過が少ないことを、互いに主張することは、 困難を引き起こす。 つまり、円筒時空では、双子のパラドックスは実際のパラドックスになってしまう。 A, Bは、通常の双子のパラドックスでは B は、加速してまた戻って来るため、 慣性系とは言えないが、 この円筒宇宙では A も B も慣性系という点では区別する方法がないのである。
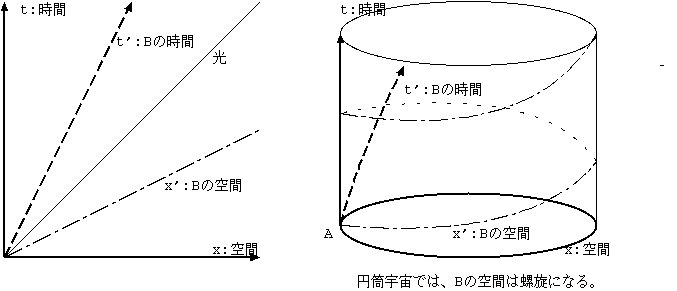
円筒宇宙で、A 点から前後に光を出すと両方の光はもう一度 A 点に同時に戻る。 ところがそれと相対的に動いている B では、受けるまでに B 点が移動するから同時でなくなる。 前方に出した光は、後方から追い付こうとして遅れるし、後方に出した光は、 前方からくるから早い目に到着する。
この前後に出した光が同時に到着する系が絶対静止座標系である。
A と相対的に動く物体 B は、光を前後に出し、 待つだけで自分が動いているかどうかがわかるのである。 相対論によって完全に無用とされた絶対静止系は、円筒宇宙では存在する、 または少なくとも区別できる座標系である。
A の乗る宇宙を取り巻く帯と、B を含む動く帯を考えると、A の帯の長さと、 B の帯の長さは、どちらが長いのだろうか。 B の帯はローレンツ短縮し、宇宙の直径は、静止系で最大というのは間違いである。 短縮した物差しで計測するBにとって宇宙は長く、宇宙の直径は静止系で最小である。 B の帯は短縮してはじめてAの帯と同じ長さだから、B にとって B の帯は長いのである。
では、B からみて A は短縮していないのだろうか。 もしそうなら、Bからみても先の議論は成り立ち、帯の長さは確定できないことになる。
この宇宙に絶対静止系が存在するなら、 A にとって宇宙は静止していて B にとってはそうでない。 B からみて A が同様に動いているとかは、無視するしかない。 動いているのは Bであって、Aではないからである。
特殊相対論を発見した二つの原理である、 光速度が慣性系によらず一定ということ(光速度一定)と、相対性原理(慣性系の対等)の内、 少なくとも後者の方を捨てるのである。慣性系の対等性はない。 相対性原理はない。しかし、局所的には慣性系は対等でないと特殊相対論は成立しないので、 局所的には対等だろうか。短縮は局所現象である。
(また、Bは、後方に出した光が前方に出した光より、先に届くので、宇宙の大きさが 前後で違うか、光速が方向によって違うというだろう。)
時計の遅れについても、A は円筒の軸(時間)方向に並行に移動し、B は螺旋を描くので、 B の固有時に時計の遅れを生じ、A にはそれがない。 B における同時刻(または、空間軸)が傾いていて、一周すると違う時刻の同じ場所に戻ることは、 同時刻という言葉が意味を失っている。時空の図の中で傾いたものを B の見る空間だと、 Aはいうが、これは B の帯の中で大勢の人が手をつないだものとは別のものであろうか。
以上の議論で納得できないのは、局所的には対等と言いながら、 大局的には対等でないことを前提にしていることである。 B からみて自分が静止しているとみて、A が運動して来る螺旋の世界線をみるのを、 何が禁止するのだろう。上の議論では、パラドックス自体が禁止するみたいである。
現実の宇宙空間では、双子のパラドックスはどうなるだろう。 A と B が、同じ軌道を描く人工衛星同士ですれ違っている場合、 相対速度はあっても両者に時間の経過の違いがあってはならないと、 普通考えるだろう。なぜなら、両者は、完全に対称的であるからである。 しかし、それは対称性に頼って結果を導いただけである。
人工衛星の軌道上の時空は、重力を遠心力が大半を打ち消して、一見無重力だが、 潮汐力のある平坦でない時空である。これがその原因だろうか。 これは、そうではないのである。
まず、これは、どこまでも拡張できることに注意して欲しい。 30 km/secで太陽を公転する地球から、 60 km/sec のロケットを公転軌道上を反対方向に公転させるときも、 ロケットと地球で時間の経過(時計の遅れ)は同じであろう。 銀河系の中心を、220 km/secで周回する太陽系から打ち上げた、 440 km/secのロケットも、方向によっては引き返しなしに再会する。 さらには、どんな速度をもつロケットも、 宇宙の不規則さによってどこかを中心とした周回軌道をとり、それらはいつかは再会するだろう。
宇宙にこのようなエルゴード仮説をおくなら、離れて行った慣性系は必ずいつか再会する。 そのとき、双子のパラドックスは、どうなるだろうか。
局所的に、引き返せばそれが成立することは確かであり、引き返しなく再会するとは、 ぐるりとまわって来るという位相幾何学的な部分が効いているのである。 双子の固有時の差は、幾何学的な経路によるものだからである。
再会するのに局所的引返しが必要な、開いた空間では、A から見て、B の時空経路が曲がっていて、 空間的移動がある分、固有時が小さいと考えられるが、ある時空点から別の時空点への、 複数の経路がともに直線、測地線であるとき相手の時間の経ち方、固有時を正しく推定する方法は、 (特殊相対論には、) もはやないと考えるべきなのかもしれない。
相対性の原理は、どうだろうか。すべての慣性系は対等でありその中の物理法則は一致するということ、 そして光の伝播に必要と考えられていた、絶対静止系というものが必要でなくなるということ、 それが最も核心をついた相対論の本質なのだろうか。 しかし、当時は、それほどいま必要でない、エーテルという仮想の真空充填物質を考えなければならなかったこと自体が、 理解しにくいことであろう。
時間の空間化、時間を系に附属したものとして扱うこと、空間もそうだがとくに時間が、系によって違ってみえるということ、 これは、時間の相対化であり、空間の相対化である。それが相対論の本質だろうか。これは帰結であり、本質ではない。
相対論という表題がとられたのは、当時の風潮に従ったもので、実は相対論とは、時空の絶対化であるという人がいる。 ある時空の性質は、どこから眺めてみても変わらない性質であり、それが重力の説明になっている。 g_ik は、系によって 異なるが系によって消しさることのできない部分を問題にしているのである。時間は相対的で、空間も相対的である、 しかし、時空は絶対的であるというのが相対論の基本的姿勢ではなかろうか。
一般相対論で、周囲のすべての物体を回したとき、回転系と全く同じ遠心力とコリオリの力が発生することを、示すのは難しい。 一般相対論は非線形の微分方程式である。無限遠の境界条件の困難を避けるために、弱い近似での解だけ示されていて、そこでは、 静止系に弱い遠心力とコリオリの力があることは示されたが、回転する周囲の物体を増やして行けば、そのうち回転系が静止系と 入れ替わることを示しているわけではない。アインシュタインの目指すマッハの原理からいえばこれはまだ、不十分な到達地点であった。
最後に、相対論を学んで最終的に絶対静止空間を信じるようなことになってしまった人達に対して、何をいうべきか、 ああ地球平坦論者たちよ、"世の中に確かなことがひとつだけある。それはエーテルの存在だ。" 1902 年にケルビン卿(W.トムソン1824-1907)がいってる。君達も頑迷な学者の類である。 疑いは解明の母、大いに疑うことはよい。それらが十分に理解され常識となり、 その上に立って全ての考えが形成されるほどの重要な考え方の変化には、 抵抗があって当然であるからである。
パウリの"相対性理論"(内山龍雄訳)PP25-PP30 にはこの理論の事情説明がなされている。それによると、 特殊相対論は相対性原理と光速度不変の原理を用いることで時間の新しい概念を与えたわけであり、 エミッション理論は、相対性原理だけを用いて光速度不変の要請を外し、時間の概念に影響を与えずに、 実験結果を説明できるものを探すものである。光の光源に対する速度一定として光速に光源の速度が 加算されるとする理論を一般にエミッションセオリーと呼び W.Ritz, C.Tolman, J.Kunz によるものがある。 これらはすべてマイケルソン・モーリー実験を説明できた。
この理論では、ドップラー効果に対して光速が変化し、振動数は変化するが波長は変化しない。 Tolmanは、プリズムでなく回折格子ではドップラー効果が出ないと考え、Stewart はそれに反対した。 運動する鏡によるドップラー効果では、J.J.Thomson と Stewart は、反射光に鏡の光源像の速度を用い、 ドップラー効果は出ない。Tolman は反射光を鏡の面上の光源にして 1/2 の効果しかでない。W.Ritz は、 入射光の光源速度を保つとするので普通の光学理論と同じ結果を導き、生き残った。閉じた光の経路では、 この理論と普通の光学、相対論との v/c の 1 次の効果には差がでないことが証明できる。2 次の効果に 差がでる可能性があり、La Rosa と Tolman は、地球上の光源でなく太陽光源ならマイケルソン・モーリー 実験で回転によって干渉縞の移動が起きることを指摘した。
開いた経路では、v/c の 1 次の効果の範囲で Ritz の理論の是非を検証する現象が存在する。 Comstock は連星を用いてこの効果を観測できることを指摘した。De Sitter は、分光連星で、 円軌道が楕円軌道と観測されることを定量的に示した。 (以上、パウリの相対性理論から要約引用。)
また、太陽光の光源は、約 6000 度の熱運動による速度をもつ。皆既日蝕が終わって最初に光がくる ダイヤモンドリング現象時に月までの距離 38 万 km からの光速が6000 度の熱運動の分広がり分布するなら、 最初青い光りが見え、その後赤い光りが届くだろうか。全ての遠方の光の遮りの現象で、これが起こらなくてはならないが、 そういう現象はあるのだろうか。日没時の"グリーンフラッシュ"は、逆ではないか。
深部宇宙のドプラー効果の赤方変移を受けた光は、実はずっと古い光ということになる。 宇宙がプラズマ状態から原子を形成し、電磁波と相互作用を失った宇宙の晴れ上がりの時期、 宇宙のサイズが 1/1000 の時代の数千度の黒体放射の名残と言われる 2.7 度の宇宙の背景放射は、 今言われる 150 億年の千倍の過去の事件になる。背景放射のマイクロ波が、他のマイクロ波とは違って、 光速の 1/1000 の速度ということは、あり得るだろうか。すこしでも速度の違う光があれば、 測定できないはずはないように思える。速度の違う光は、局所において分離可能である。
それを通せば過去の光景がみえる A. C. クラークの SF "スローグラス"がある。速度が遅いと遅延線になりメモリーになる。 低速な光は、存在すれば貴重である。そして光よりも高速な光は、さらにもっと貴重である。 それが存在しない特殊相対論では決して達成できない(因果律を壊す) 超光速通信である。
しかし、Michelson-Morley の実験以降も、Morley-Miller の実験など多くの実験がなされて、その測定結果は、再解釈されている。 "From classical to modern ether-drift experiments: the narrow window for a preferred frame" M. Consoli and E. Costanzo (arXiv:physics/0410245 v1 25 Oct 2004) によると、当初の結果も測定のセッション間を単純に平均しなければ、 8.5 km/sec +- 1.5km/sec の絶対運動を検出していた。これは、予想した 30km/sec の 1/4 である。そして空気より、ヘリウム、真空 の結果がより小さな値をだすことから、v_air = c/N_air 光の屈折率 (N_air= 1.00029, N_helium= 1.000036, N_vacuum= 1.0) の真空 との差がこれを導いているとして、
v_earth = 204 +- 36 km/sec
と地球の絶対運動が出たかにみえる結果には背筋が寒くなる。この数字自体もありそうな数字だし、+-36 km という誤差は、地球の公転 による季節変化のようにみえる。実験は恐いものである。未だに決着しないマイケルソン・モーリー実験では、話にならないのであるが、 実験データが残っているから再検証はすべきである。
2005 年で、特殊相対論から 100 年になる。いまだにエーテルについて研究している人などいないだろうと思ったのだが、 一般相対論の時空には、エーテルに類似する解釈が可能で、特殊相対論が絶対静止空間を明確に否定したようには、一般相対論は、 明確に否定しないから、一般相対論の多くのエーテルの理論間の検証の議論がある。 "Empty space-time, general relativity principle and covariant ether theories", (Alexander L. Kholmetskii) (arXiv:physics/0501060) この arXiv の physics で "ether"という言葉を abstract に使う論文は 58 あり、本文に使う論文は、200 もある。
付録 1:速度 v と γの逆数との関係
γ= 1/√(1-v^2) の式からその簡便な暗算法を探す。
v= 1/2 のとき、γ= 1/√(3/4) = 2/√3 = 1.1547
v= 2/3 のとき、γ= 1/√(5/9) = 3/√5 = 1.3416
v= 3/4 のとき、γ= 1/√(7/16)= 4/√7 = 1.5119
v= 4/5 のとき、γ= 1/√(9/25)= 5/√9 = 1.6667
v= (n-1)/n のとき γ= 1/√((n^2-(n-1)^1)/n^2) = n/√(2n-1)
v= 63/64 のとき、γ= 64/√127 = 5.6791
v= 99/100 のとき、γ= 100/√199 = 7.0888
v= 999/1000 のとき、γ= 1000/√1999 = 22.366
v= 9999/10000 のとき、γ= 10000/√19999 = 70.712
グラフは、速度 v が小さい間、γは 1 からゆっくり離れるが、v が 1 に近づくと発散する。 しかしこれではあまり、関係が明確に見えない。 1= γ^2*(1 - v^2) から、(1/γ)^2 + v^2 = 1。 γの逆数、つまり、ローレンツ短縮率 1/γ と v との関係は、斜辺の長さ 1 の直角三角形の ピタゴラスの法則、長さ 1 の物差しの回転である。素晴しい。しかし、これをγの式の物理的意味と、 簡単に言わないほうがようさそうである。数学的関係が同じでも同等な物理的意味をもつとは限らないのであるから。
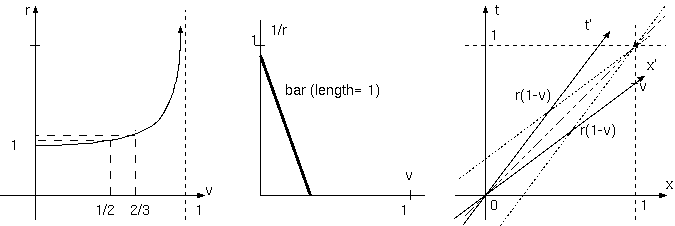
時空図とは、ある慣性系(K)の時空に別の慣性系(K')の時空を示す図である。 K 系に対して速度 v をもつ K' 系の時空を K 系上に示す図である。 特殊相対論の本質、速度をもった系間に成り立つローレンツ変換は、式で考えるのが正確だが、 図は、式より雄弁である。重要な定性的性質 (例えばローレンツ短縮) を、時空図で示せたらと思う。 光速は、1 にとる。光速を c にすると、ローレンツ変換の時空対称性が見えなくなるから。
まず、K 系の時空図での K'系の座標軸 x'軸, t' 軸は、(原点を通る)直線である。座標軸は、他の座標値が 0 を表す。 x'軸は、t'= γ(t - vx)= 0 を表し、t'軸は、x'=γ(x - vt)= 0 を表す。 x'軸は、t= vx であって、v は 0 以上 1 未満であるから、光経路の 45 度の傾きの線 t= x より下に、 t'軸は、K' 系の軌跡 x= vt であって t= x より上にある。両者は、光経路に対称である。
x' 軸: t= vx
t' 軸: x= vt
x', t' 軸を書くときに v だけを使ってでき、x', t'軸には拡大率γを表せないからγの効果が見えない。時空図は、 もしγを変えても同じ図になる。実際はγは v から決まるので、表示されているのだが、γが時空図にどう表れているのか、 よく見えない。それは、軸に目盛がないことが原因である。そこで軸に目盛を振ることを考える。
時空図では、t' 軸は、K' 系の原点の軌跡、そのものである。これは、とくに奇妙なことではなく、 ニュートン力学のガリレオ変換においても同様なのである。
x'= x - vt
t'= t
K 系の点 (1,1) が K' 系でどうみられるかは、ローレンツ変換式、
x'= γ(x - vt)
t'= γ(t - vx)
に、x= t= 1 をいれ、x'= t'= γ(1 - v) を得るから、K' 系はそれを (γ(1 - v), γ(1 - v)) 点とみるのである。
K'(γ(1 - v),γ(1 - v)) = K(1, 1)
ローレンツ変換は線形変換であるから、その座標軸に平行に座標値を軸に降ろし、x'軸に x'= γ(1 - v)、t'軸に t'= γ(1 - v) の目盛を振ることができる。しかし、この γ(1 - v) がどういう値であるかについては、あまり、明確なイメージを持つことができない。 図 6.に示したのは v= 0.8 のとき、γ(1-v)= 1.666*(0.2)= 0.333 であるが。
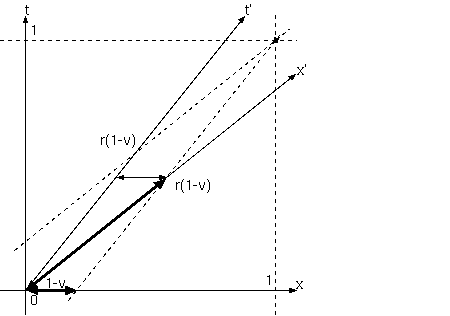
式に x= 1, t= 0 をいれると、x'= γ, t'= -γv になる。 K'(γ, -γv) = K(1,0)
K 系の空間(同時刻)間隔は、K' 系からは、γ倍に伸びている。逆にこの K' 系の座標値を K 系から同時刻でみると、 見られる側 K' のγが 1 に 1/γ倍に短縮するローレンツ短縮である。 (本文のように逆変換式に x= 1, t= 0 をいれても同じ結果になる。)
K'(1/γ, 0) = K(1, v)
そうして、x' 軸に目盛 x'= 1/γ を書くと、この図は、K 系からみて、K' 系の物差し 1/γ が 1 に、γ倍に伸びることを表している。 見られる側の同時刻で切ると、伸びる。面倒なことを止めて、K'(1,0) を K 系にローレンツの逆変換、
x= γ(x' + vt')
t= γ(t' + vx')
に、x'= 1, t'= 0 をいれると、x= γ、t= γv である。K'(1,0) は K(γ,γv) である。
K(γ,γv) = K'(1,0)
これによって x' 軸上の(γ,γv)に 1' の目盛を打つことができる。 その間隔は、かなり広い。見られる側の同時刻で切る伸張である。
K' での空間距離 1/γは、K 系での距離(t'と t2' の水平方向距離)では、1/γ 倍に短縮している。 K' 系の空間距離は、ロケットの先頭(直線 t2')と尻尾 (直線 t')の距離であるが x' 上の目盛で読むしかなく、 それが水平距離よりは長いだろうとは、考えられるが、この図の x' 軸の斜線の長さには対応していない。
K 系の間隔は、t'軸 と 直線 t2'に挟まれる帯の水平距離であり、それは、K' 系のロケットの長さ 1/γ の 1/γ 倍の 1/γ^2 である。x 軸上の短い距離は、t= 0 のとき、ロケットが先頭と尻尾を同時に加速するなら、 その間隔はすでに短くなければならないことを示している。それは、加速したロケットにとって同時ではない。 ロケットにとって同時なのは、x' 軸である。