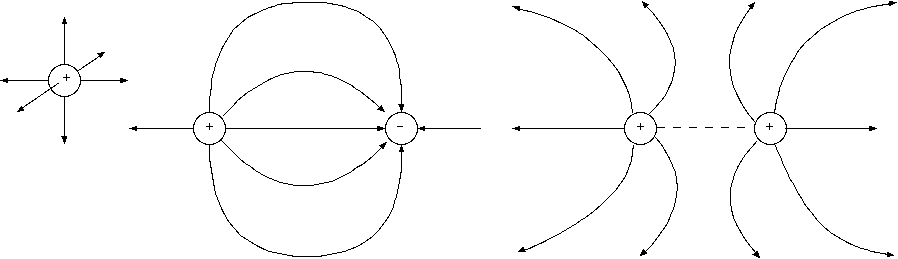
図 1. 力線の表現
はじめに
1. 力線の表現
1.1 磁力線を横切るときに電場をみる
1.2 磁力線の速度?
2. クーロン力から電場へ
2.1 ローレンツ力の式
3. ベクトル場の発散と回転、スカラーの勾配
3.1 電場の発散
3.2 電場の回転
3.3 ポテンシャルの勾配
3.4 アンペールの法則とファラデーの法則
4. Maxwell 方程式とポテンシャル
4.1 電磁ポテンシャルは4元ベクトル
4.2 波動方程式
4.3 異なるポテンシャルが同じ電磁場を与える
4.4 クーロンゲージとローレンツゲージ
4.5 ポテンシャルから Maxwell 方程式を導く
5. ローレンツ力と座標変換
5.1 磁場のローレンツ変換
5.2 速度に平行な成分と垂直な成分
6. 電線の側の電荷
6.1 電線の帯電
7. 飛んで来る電流ループ
8. 馬蹄形磁石のそば
8.1 一様な磁場を動かしても磁場の時間変化はない
8.2 "磁場の時間変化が電場になる"は、不正確
8.3 rot E = -dB/dt は E を規定しない
9. 電場をみるために
10. rot E = 0
11. 場の概念と相対運動
12. 電流ループの飛行
13. 行き帰りする定期航路
14. 飛んでくる電線
15. 単極誘導
15.1 単極の発電機
15.2 単極のモータ
15.3 戻り線がトルクを受ける
15.4 戻り線にも起電力が発生する
15.5 磁石だけを回転させても起電力差はない
15.6 戻り線の存在
16. 三要素の回転
16.1 磁力線が生えている場合と、根がない空間固定とで結果は変わらない
16.2 磁石だけの回転で電場があるか
17. 回転磁石の近辺の電荷は力を受けるか
18. どう解釈するのか?
18.1 回転相対は Wへの1次性か
19. *注
20. 磁場の源の速度が電場の効果をもたらすシナリオ
21. 電磁場に回転相対がない証拠
22. 回転系の電磁場
23. 回転系の電磁場の発散
24. 回転系の電磁場の回転
25. 地球の磁場の原因
26. 公転軌道上の電場
27. ファラデー板の磁場
28. 訂正とまとめ
旧版
磁場中を飛んでいる電荷は、電場を見なくては力を受けることができないから、 電荷に並進する系では、磁場を電場とみるという説明は、非常に基本的で明確である。 その系では、電荷は静止しているから、電場以外に力をうける理由がない。 これには相対論の力の変換が係わり、力の大きさは変化するが、力の存在の有無は明確である。 だから電荷に並進する系において、磁場は電場に変換されなくてはならない。
F = q (E + v x B)
というローレンツ力の式は、非常に基本的、汎用的な式である。 電磁場のローレンツ変換は、それを壊さずに、それを満たすように作られたといってもよい。
このローレンツ力の式は、回転系のコリオリ場の中を飛んでいる質量が、 速度に比例して力を受けるという形と、全く同じ形態を取る。 重力加速度 g、回転系の角速度Wの中の質量 m の受ける力は、
F = m (g + v× W)
と書ける。そう、磁場とは電荷にとっての系の回転である。ところがその場合、そのような説明をしただろうか。 コリオリ場と遠心力の場は同じものの別の側面であり、それらがローレンツ変換されるとは言わない(*)。なぜだろうか。 片方はニュートン力学、もう一方は電磁気である。それらは、形式が似ているだけで本質的に関係のないものだろうか(**)。
(*) 全く性質が違うようにみえる "遠心力とコリオリの力"は、同じものの別の側面ではないか。 遠心力は、回転系の静止点の速度 v と角速度 w との外積 v x w、コリオリ力は、物体の回転系内速度 V と角速度 w との外積 2V x w、 両者の和は、速度和と角速度wとの外積 (v+2V) x w である。(v+V) は、慣性系に対する物体の速度で自由質点では一定である。 回転系の原点の採り方は任意で、物体の位置にとれば物体の受ける力全てがコリオリ力、系内速度Vを回転系の原点に加算すると遠心力になる。
(**) 電場E、磁場B等の3次元ベクトルを太字(bold)にする改修は、未完了(2023/1/30)。旧版 (2020/3/23) 。
このように回転と磁場との間には、疑問が渦巻く。これこそ電磁気の醍醐味である。もやもやした疑問は、明らかにする値打ちがある。
もうひとつの大きな疑問は、ローレンツ変換である。ローレンツ変換は、慣性系に限定した系の間に成立して、その他の系では、 並進速度 v だけを使っても間違いかもしれない。なぜなら、慣性系間でしか確認されてないものを、拡張して用いるのだから。 ローレンツ変換の式に速度以外の項をもたないからといって加速度や、回転が関係がない訳ではない。それは、慣性系間の法則であり、 加速度や回転の無い場合の式である。ローレンツ変換に加速度や、系の回転が出てないのは、それがない場合に成り立つ式だからである。 そういう恐ろしく基本的なことを考えないといけない。これは単極誘導に関係する。
加速度系、回転系では、Maxwell 方程式が成り立たず、その他の不思議な現象が起きるだろうという。回転系での電磁気の方程式は、 電磁気の教科書であまり見かけない。さらに、回転系のような非慣性系では電磁場が静止系のように定義できないのではないかというが、 これは間違いだと思う。電場は、系に静止した電荷が受ける力を電荷で割ったものであり、磁場は系に速度vを持った電荷が速度vに比例する力を 速度と磁場の外積方向 v x B に受ける、力を電荷でわる局所の通常の場である。回転系では、それがどうして定義できないのだろうか。 回転系で電磁気の方程式が違うというなら、回転系での電磁気の式を示すべきである。そうすれば、慣性系は回転系のひとつとして扱え、 電磁気の回転相対の有無が議論できる。そして、単極誘導の電位が角速度に比例し、遠心力のような角速度の2乗の項がないから、 静止系の存在がいえず、誘導は相対回転による可能性がある。
電磁気の分かりにくさ、疑わしさは、そういう基本的な疑問に答えないからである。論争は、そういう基本的疑問からくる。 回転と磁場の説明から単極誘導など難しい問題を明確にしたい。これらの基本問題を解くことがこの章の目的である。
電気は、電圧と電流でその大きさをいう。電圧の単位は、[V](ボルト)で、例えば、乾電池で約1.5V、リチュウムイオン電池で約3.5Vである。 しかし、電圧は片方で計測できない。テスターの測定電極2点間の差である。それを空間の一点の性質とした電場Eは、電位の下がる方向の 空間微分ベクトルであり、スカラーである電位 Vの勾配 E= -grad(V)であり、単位電荷に与える力[N]を表し、[V/m] の単位をもつ。
電流は、電荷の流量であり、回路の電流を測るには回路を一時的に切り離しテスターの電流測定を入れないといけない。 電流の基本単位は[A](アンペア)で、1[A]は、1秒間に電荷1[C](クーロン)を運ぶ([As]=[C])。 電子の電荷は、1.602176634 x 10^−19 [C] (電気素量)、アボガドロ数 6.02214076 x 10^23[/mol]の電子の電気量は 96,485.33212[C] (ファラデー定数) である。9万6485秒の1Aで1グラム当量(1価なら1mol)を電気分解できる。電圧は圧であり、電流は毎秒の流量で抵抗が両者を決める。抵抗R[Ω]、電圧E[V]、 電流I[A]のとき I= E/R, E= IR, R= E/I (オームの法則)[Ω]=[V/A]。電圧と電流の積が電力[W=VA](ワット)で、毎秒の仕事("仕事率")[J/s]である。 仕事は、[Ws]=[Nm]=[CV]=[J] (ジュール) である。 地表(重力加速度 9.8m/sec^2)の高さ1mから1kgの質量を下ろすとき、なされる仕事は、1kg重m= 9.8Nm= 9.8Jである。
電源には一定電圧の直流(DC)と、関東50Hz、関西60Hzの正弦波の交流(AC)の100Vがある。発電機の外側の界磁と回転する回転子が方向の切替(転流)なしの ブラシを通して正弦波になる。交流100Vは、同じ抵抗に直流100Vと同じ電力を送るために、ピーク電圧+-約141Vまで振れる。交流は変圧でき、発電所から 高圧電線(数万V〜)で送り、変電所で数千Vに下げ、電柱の変圧器から100V(又は200Vの中点アースの3本(2組の100V電力線に相当))を家庭配電し、工場には 120度毎に位相がずれた3本の正弦波の三相交流が配電される。
送電はエネルギー問題に関係する。電圧を上げて送電するのは、送電線の抵抗による電力の損失を避けるためだが、それでもなお、送電は電力の数10%を失うという。 低い電圧では導体の抵抗損失(銅損)、高い電圧では空中放電を招く(1万Vの電圧で約1cmの放電)。変圧器(トランス)には銅損以外に鉄心にも交流1周期毎に ヒステリシス(履歴)面積の損失(鉄損)がある。送電の短い太陽光発電には電力貯蔵が必要で、リチウムイオン充電電池や、発光効率の高いLED照明には 電力節減の功績がある。
見えない電気を最も信頼性の高い道具にした近代の電気工学、交流理論、電気回路、電子回路、電気通信技術は、その基礎である電磁気の理解によって、 さらに高度な応用を可能にするだろう。電線の中では微小な電場が電流を作るが、我々は、晴天の空気中にある数100V/mの電場も感じられない。 静電場では導電体はほぼ等電位で導体表面には電場の平行成分がない。電荷[C]が発する4πr^2の表面積の電場が1/4πε0= 8.98755 x 10^9 (=c^2/10^7) の係数を掛けて電場[V/m=N/C]になる。数値にπを出さないMKS有理化単位系が使われる。1[C]の電荷同士が1[m]の距離で 1/4πε0[V/m]の電場と力[N]を授受する。
磁場は電流から起き、N回のコイルは電流の磁気の効果をN倍にし、鉄心の透磁率μは、磁場(磁束密度B)を数100倍に増大するが、鉄心の磁場は飽和し、 最強の磁場は空心コイルで得る。磁場の単位にはテスラ[T] とガウス(gauss)がある(1[T]=10^4[gauss])。直線電流(1A)から1mの距離の磁場は正確に 2[m gauss]である。電線を取り巻く円周2πrの磁場Bは、円内を貫いて流れる電流iに等しい(rotB= i)。
磁場中に速度をもつ導体が電池になる現象(ファラデー円板、単極誘導)では、その磁石だけを回転させても誘導が測定されない。ファラデー円板の起電力、数mV は 測定可能でも、rot E のない電場は回路に電流を発生せず、数mVの電位は浮遊電荷を動かさない。電位VをコンデンサーC[F](ファラッド)に貯めた後の測定もできない。 コンデンサーは空隙を挟む狭い極板間に電荷Q[C]=CV[FV]を蓄えるが、電場は空隙でなく導線上に電荷の偏移として表れるからである。

電気力線は、正電荷から放射状に広がり負電荷で消滅する、方向をもつ曲線である。正電荷が単独のときは、力線は周囲に発散する。 力線の本数は、任意の単位の電荷(ε_0[C])に 1 本を与える。力線は、ゴム線のように張力をもち、力線同士が互いに反発して間隔を保つ。 力線は、電場ベクトルの方向を繋いだもので、力線の方向が電場の方向を表し、力線の面密度が電場の大きさを表すから、 その張力は、異種電荷のクーロン引力を上手に表現する。力線は、途中の空間で発生や消失をせず、枝分かれや合流をしない。 磁力線は、磁石の場合、N 極から出て S 極に向かうが、磁石の内部を補間するとコイルの磁場と同じく一巡する輪になる。 力線は、かなり正確に電場、磁場の性質を表現するが、同種電荷の斥力を力線間の反発力で説明するのは、苦しい。 また、場の大きさが0の場所に力線を書くことはできない。 (例えば、図 1. の正電荷の間の点線の場所)
例えば、磁石の上に紙をおいて砂鉄を撒くと砂鉄が線を描き互いに広がる。砂鉄が一時的に磁化して小型の磁石となって線をなして並ぶのを、 磁場のベクトルは十分に説明しない。砂鉄の線は、磁力線に沿って、互いに反発しながら弾力をもつ、とするほうが、現象を定性的、直感的、 具体的に説明する。また、小さい矢印を空間に多数並べるよりも、力線の曲線は、場が滑らかに連続的に変化することを上手に表わす。 力線が途中の空間で発生消滅、枝分かれ合流がないのは、電場の発散の源が電荷であること、磁力線が一巡するのは、磁場に発散源がないことを表す。 また、力線は、任意の閉曲面を横切る力線の総数が、内部の電荷を表すというガウスの定理を自然に説明できて、 電場よりも概念の有効性がある。しかし、電磁場は、ベクトル解析によって数学的に正確に扱われる。
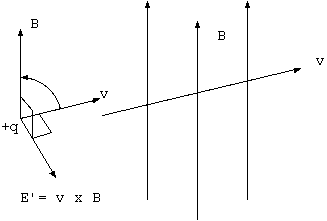
外積×は、クロスと読み、線に交差する、線を横切るという言葉が適切である。速度をもって磁場を横切ることが意味をもつのは 場の概念では不可解である。ローレンツ力の v× B は、vとB の外積 (ベクトル積) であり両方のベクトルに垂直で、 vとBを始点を合わせて(要を合わせた扇を広げるように)、vの矢印からBの矢印へ右ネジを回すときの進行方向をもつ。 その大きさは、vからBへの角度をθとして、平行四辺形の面積|v||B|sinθ をもつ。両者が垂直のとき|v||B|である。 外積のベクトル表示は一意的だが、成分表示は右手系と左手系で異なる。(x,y,zを右手の親指から順にあてる)右手系の成分表示を次に示す。 vがx方向Bがy方向を向くとき v× B は、|v||B|の大きさのz方向のベクトルである。
v× B= ( v_y B_z - v_z B_y, v_z B_x - v_x B_z, v_x B_y - v_y B_x )
ファラデーは、 "磁力線を横切るときに電場をみる" といったが、それと対称な "電気力線を横切るときに磁場をみる" という必要は なかったのだろうか。そこまで電磁場に対称の予想はなかっただろうし、これは、電荷の運動が磁場を発生することを示したローランド の実験まで待たされるのであろう。しかも、力を受ける主体が存在しない磁荷であるから、なおさらである。しかし、磁力線を切ること と電気力線を切ることは対称である。もし、磁荷 m があれば、電磁場でうける力は、 F = m (B - v x E) で、m がみる磁場は、 B' = γ (B - v x E) である (電磁場のローレンツ変換)。なお、小磁石は磁気双極子であり、磁場の空間微分によって力を受ける。
力線は、場の発散を表し(前章)、場との交差(vxB)をベクトルよりも表現する。力線なしの磁場との交差は仮想のようだ。例えば、 一定の磁場のなか速度をもつ電荷点で何が起きえるか? ところがその点は電場をみる。磁場の概念が交差を表すのに不得意な証拠に、 磁力線を切る(交差する)は、磁場の時間変化とは違うのに、よく混同される。磁力線は、面を通過する磁束密度を代表する線で、 その線と交差する瞬間だけ電荷が電場をみる訳ではない。ずっと同じ磁束密度の中で速度をもつ。一様な磁場中を運動する点は、 磁場に時間変化はない。磁場の時間変化には磁石の配置変化や、周囲の電流の変化などが必要である。
但し、磁力線と交差するとき速度vの点がみるのは電場 E' = v x B だが、元の系で交差したのはその E'でなく(電場自体がない) 磁場Bである。このように、磁力線と電気力線との関係は直感的でない。さらに力線は、 静電場、静磁場のような渦なし場(rotが0の場)を表すが、渦や、場の時間変化、さらに系による変換を表すのは難しそうである。
ファインマンは次のようにいう。「力線による場の図示化は有効だが、実在的にとらえすぎる危険がある。ある系で力線が止まっていて、 別の系ではその線を横切るかどうかは確かでない。その系ではその力線はないかもしれない。」
電場と磁場が共存し直交するとき、別のある速度の慣性系では磁場だけになる。 その系に静止した電荷は力を受けない。その系の速度を "磁力線の速度" という。 その導出は容易で、ローレンツ力= 0 の式の両辺に B を外積して求まる。 その系で力を受けない電荷は、この系でも力を受けないからである。
E + v x B = 0
B x (v x B) = B x (-E)
これに A x (B x C) = (A・C) B - (A・B) C と v・B = 0 を用いて、
v = ExB / B^2
この式は、場の運動量 g= ε_0 ExB を、磁場のエネルギーε_0 c^2 B^2/2 の 2 倍で割ったものとなり、速度の概念ではある。 (場の運動量を場のエネルギー (E^2 + B^2)/2 で割った速度は、方向は同じでも大きさが違う。)
その速度では電場が0で電荷は場から力を受けない。それより速度が小さいと電場の影響が残り、それより速度が大きいと逆の電場が見え、 電荷がその速度まで加速されるなら、電場とは、磁力線の速度と電荷との速度の差によるひきずり現象のように思わせるが、 磁場中に速度をもつ電荷の受ける力が速度に垂直だから、加速されない。(流れる磁力線のイメージは、ときに成功するが、ときに失敗する。)
磁力線の速度は、電場を大きくすれば大きくなるが、速度は光速限界を持ち、E = B となると純磁気的系をもたなくなる。 純磁気的系をもつのは、E < B のときで、この速度は、c E / B となり、B < E のときは純電気的な系を速度 c B / E にもつことが、ランダウ・リフシッツの”場の古典論”にある。
この話は、電場Eを磁力線と交差で、磁場Bを電気力線との交差で説明する。B - vxE= 0 から始めて、 v= ExB / E^2。これも前のvとは方向は同じで大きさが違う。この速度の系では磁場はない。 v<1のためには、B<Eである必要がある。「磁力線と交差する電荷は電場をみる」を電荷の立場からみて、 「交差する磁力線は電場に、交差する電気力線は磁場になる」は、正しいのだろうか?
F_1= 1/(4πε_0) q_1 q_2 e_{12}/ r_{12}^2 = -F_2
1/(4πε_0) = 10^{-7} * c^2 = 8.98755 * 10^9
(e_{12}は2から1の方向の単位ベクトル。r_{1,2}は1から2への距離[m]。qは電荷[C=As]。力は[N]。 1/(4πε_0) は、力線の面密度からくる係数で光速c^2を含む。)
いまもし第三番目の電荷 3 があっても、2 と 3 からの力は、2 からの力に 3 からの力を加算したものであるという事実がある。 この力の重ね合わせは、クーロン力が相手の電荷量に比例しなければありえない。 2, 3 が同じ位置にある場合に電荷量を加算して一つの電荷とすることができるためである。
F_{1,23}= F_{1,2} + F_{1,3}
その反作用もその大きさであるためには、クーロン力は、受ける側の電荷量にも比例する必要がある。 それは実際正しく、この事実が場の概念を生みだすのである。
クーロン力を受ける電荷量で割って電場とし、場(空間の一点)の性質とする。 電場は、その位置に単位電荷を置けば受けるであろうクーロン力である。 電場は、相手側の電荷による。クーロン力に加算が成り立つことから、電場も線形であり加算ができる存在になる。 クーロン力から電場へという概念の変化によって、不可解な遠隔力は、場との間の近接力となった。 それは、空間の物体化の始まりでもあった。
F_1 = q_1 E
E = 1/(4πε_0) q_2 e_{12} / r_{12}^2
それに対して、速度をもった電荷qの受ける力、ローレンツ力は、静止電荷ではクーロン力からの電場の式 F = q E と 等しいが、電荷が速度 v をもって動くとき磁場 (これも動く電荷だけが生み出すものだが) から受ける力 q(v x B) の項が付け加わる。
F = q (E + v x B)
ローレンツ力の中の電場 E と磁場Bは、電磁場のローレンツ変換が定義され電磁場は相互に変換される。この式は速度を含み、 系の速度による変換に耐えるはずはないと思うかもしれないが、これが逆に電磁場のローレンツ変換の式を導くのである。ローレンツ力の式は、 電磁場が姿を変えることを使うと、どの系でも厳密に成立する。誰もがこの式に最初に出会ったときに、この速度をもった式を 不思議に思っただろう。この速度は、何に対する速度なのか、測定系に対する速度であろうが、本当は、何に対する速度だろうか、 そこに相対性は、あるのかと。
(*) 両方の電荷を結ぶ線分に対して垂直な速度をもった系からみるとき、クーロン力以外に磁場中を速度をもつことによる力が加わる。 それは、同種の電荷の反発だけでなく、速度に比例する吸引を伴う。ある速度を超えると、反発は吸引に変わるのだろうか? というパラドックスができる。見る系によって速度に垂直な距離という局所事象が変わることはない。
電磁気にはこのようなスカラー場、ベクトル場の数学が使用される。場の演算は加算が成立する線形の演算である。スカラー場には gradient (勾配)というベクトルを生む空間微分があり、ベクトル場には、div(発散)と rot(回転)という 2 種の空間的微分が大きな 役割をする。div(発散)はスカラー、rot(回転)はベクトルを生む。それらは全て線形演算である。
発散 div E はスカラーであり、ベクトル E の"各成分の成分方向の微分の和"である。正が流れの源(湧き出しsource)を、 負が出口(排出drain)を表す。電場の発散 div E は、その点の電荷密度ρ(SI 単位では、ρ/ε_0)である。任意の閉曲面 s を貫く電場 E の面の法線 n 方向成分の総量 (面積分)は、閉曲面に囲まれる体積 v 中の div E= ρの総量(体積分)であり、電荷量に一致する(ガウス(Gauss)の定理)。
∫_sE・n ds = ∫_v div E dv
発散の定義とガウスの定理とは、次のように密接に結合した概念である。 図 2. の左図の微小な立方体において、x,y 面でのベクトル A の z 成分 A_z をその面積 dxdy だけ積分する。 こちら側の面の分から dz だけ離れた裏面の分を引く。同様な、y,z 面、z,x 面の減算も加算すると、 次の式となるが、これは、体積 dxdydz と div A との積となる。
(A_x(x+dx,y,z)-A_x(x,y,z))dydz + (A_y(x,y+dy,z)-A_y(x,y,z))dzdx + (A_z(x,y,z+dz)-A_z(x,y,z))dxdy
= dxdydz ( dA_x/dx + dA_y/dy + dA_z/dz )
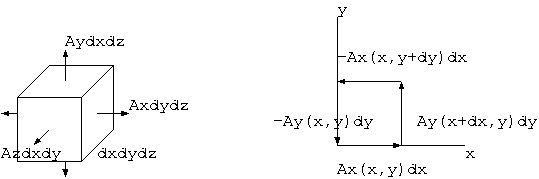
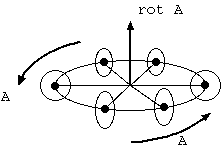
空気の渦を調べるために軸方向からの風の影響を受けない迎角 0 度の羽をもつ微小な風車を考える。風車の回転は、ある方向に向けたときが一番大きい。 回転 rot E (curl E) は、その方向と大きさを持つベクトルであり、その点の流れの循環、渦を表す。渦の向きに右ネジを回して進む方向と、 渦の大きさの長さをもつ。静電場のように渦のないベクトル場もある。
rot E = ( dE_z/dy - dE_y/dz, dE_x/dz - dE_z/dx, dE_y/dx - dE_x/dy )
任意の閉曲線 c の曲線に沿うベクトルの線積分は、c が囲む面 s 内のベクトルの回転の法線成分の面積分に等しい(ストークス(Stokes)の定理)。 rot E の面積分は、E の周上の線積分を表す。
∫_cE・dc = ∫_s rotE・dn
回転の定義とストークスの定理とは、密接に結合した概念である。図 2. の右図の微小な正方形で、 面内ベクトル A と 4 辺の矢印との内積の線積分を一巡すると、この式は、面積 dxdy と (rot A)_z の積となる。
∫_c A・dx= A_x(x,y) dx + A_y(x+dx,y) dy - A_x (x,y+dy) dx - A_y (x,y) dy
= (A_x(x,y)-A_x(x,y+dy))dx + (A_y(x+dx,y)-A_y(x,y))dy
= dxdy ( dA_y/dx - dA_x/dy )
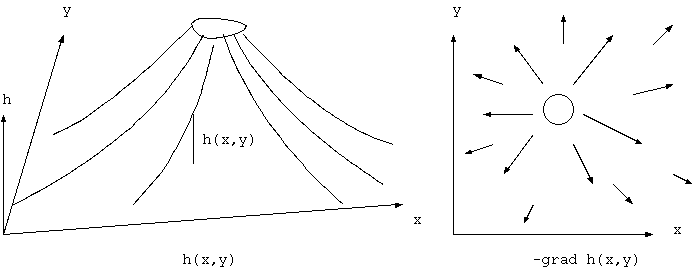
スカラー場の勾配 (gradient) は、その空間座標方向の微分を成分とするベクトルである。 時間的に変動しない場(静電場)では、電場はスカラーポテンシャル(電位)の下り勾配である。
E= -grad φ = -∇φ
grad φ= (dφ/dx, dφ/dy, dφ/dz)= ∇φ
∇は、デル又はナブラと読む。grad の記号の代わりに使う。∇= (d/dx, d/dy, d/dz) 微分オペレータ(演算子)をベクトルのように考え、 div は、∇との内積であり、∇・と書き、rot は∇との外積、∇x とも書く。
ρ= - ∇・∇φ
(∇・∇)は、∇^2 又はΔと書き、div(gradφ)、スカラーの勾配の発散でスカラーである。Δ= d^2/dx^2 + d^2/dy^2 + d^2/dz^2 は、 ラプラス (Laplace) の演算子、ラプラシアンという。電荷密度ρが存在するときのポテンシャルが従う式Δφ= -ρをポアソン (Poisson)の 方程式という。ポテンシャルφの空間的 2 階微分の負(上に凸)が、電荷密度ρと等しい。ρ= 0 の真空中では、Δφ= 0 これをラプラスの方程式 という。電荷密度のない空間に張るポテンシャルは極をもたず電荷を安定させない。なお、ポアソン方程式もさらに電荷を安定させない。 正電荷を安定させるにはそこに負の電荷密度が必要である。ポアソン方程式は静的な2階の微分方程式である。 動的な電荷密度やポテンシャルを記述するには、時間の2階微分を加えたダランベールの方程式□φ= -ρが必要である。 (□ = d^2/dx^2 + d^2/dy^2 + d^2/dz^2 - d^2/dt^2 ) また、Δφ= ρ と書くときはΔの定義が違う。
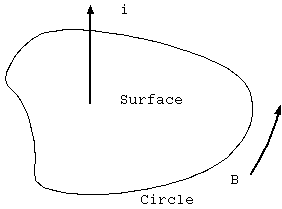
磁場には電場における電荷に相当する磁荷(磁気単極子、モノポール)がない。だから電荷のクーロンの法則に対応する式はなく、 電場と電荷の関係に相当する式もない。磁場は電流によって作られる。磁場Bの周c上の線積分は、s面内の電流密度の面積分である(アンペールの法則)。
∫_c B・dc = ∫_s i・dn
面 s 内の磁場の時間的変化が周 c 上の起電力を生むことも発見された(ファラデーの法則)。
∫_c E・dc = -∫_s dB/dt・dn
二式は、ストークスの定理を使って次の微分型の式になる。
rot B = i
rot E = -dB/dt
div B = 0, rot E = -dB/dt
そして、最初の組と電場と磁場に対称である次の第2組をもつ。
div E = ρ, rot B = dE/dt + i
電場の発散 div E は電荷密度 ρ に等しく、磁場の回転 rotB が電流密度iと電場の時間変化 dE/dt の和である。 rot B = i は、アンペールの発見だが、それに dE/dt を付け加えたのは Maxwell である。この電場の時間変化は、 通常小さいので発見しにくい。しかし、電流の経路の一部にコンデンサがある場合、空隙の電場の時間変化が電流と同じ働きをする必要がある。
両組の電場と磁場の対称性から、真空中の電磁場は対称であるが、電荷を含めた電磁場は対称ではなく、 第2組には電荷密度ρと電流密度iがある。両者に対応する第1組の "磁荷"と"磁流"の空席は、発見までその場所を空けた訳ではない。
B = rot A
なるベクトルポテンシャル A を考えれば、両辺の div をとると、ベクトルの rot の div は常に 0 だから div B = 0 であり、
E = -grad φ - 1/c dA/dt
なる電場Eと電磁ポテンシャル(φ,A)を考えれば、両辺の rot をとると、スカラーの grad の rot は常に 0 だから、rotE = -dB/dt である。 こうして、Maxwell方程式の第1組は、(φ, A)が実在すれば数学的な恒等式となって、磁荷の非存在を同時に表わす。 つまり磁荷とポテンシャルの実在とは排他的である。
電磁気と相対論とは、密接に関係し、電磁気なしには相対論は発見出来なかっただろうといわれる。相対論のできる前に、 Maxwell方程式はすでに相対論的であった。 E と B がそれぞれ波動方程式を満たし (φ もAも同様)、 光速度の波となることは、"任意の慣性系で光速が一定" という考えに一致している。
電磁ポテンシャルは、他の 4 元ベクトル(例:電荷密度ρと電流密度i) と同様に、x 方向に進む速度 v の系からみると、 時空間と同じ形式のローレンツ変換をうける。
φ' = γ(φ - v A_x)
A'_x = γ(A_x - v φ), A_y'= A_y, A_z'= A_z
電磁ポテンシャルは、4 元ベクトルである。φ_μ (φ_1,2,3= A_x,A_y,A_z, φ_4= φ)、電磁場は、4 元ベクトルではなく、 その4元回転である2階の反対称テンソル F_μν= ∂φ_μ/∂x_ν - ∂φ_ν/∂x_μ の 6 成分 (E_i= F_i4, H_1= F_23, H_2= F_31, H_3= F_12) のため、電磁場のローレンツ変換の形式は、これと異なる(後述)。
div E= 0, rot B= dE/dt
div B= 0, rot E= -dB/dt
rot B の式の両辺の rot をとり、公式 ∇x(∇xA)= ∇(∇・ A) - ∇^2 A と、div B= 0 とを使い、 磁場は、2階空間微分の和が 2 階時間微分となる。これを波動方程式という。
rot (rot B)= rot (dE/dt)
grad div B -∇^2B = d(rot E)/dt
-∇^2 B = d(-dB/dt)/dt
∇^2 B = d^2B/dt^2
□= ( d^2/dx^2 + d^2/dy^2 + d^2/dz^2 - d^2/dt^2 ) = ∇^2 - d^2/dt^2 をダランベールの演算子、ダランベリアンといい、 これを使い、□B= 0 と書く。同様に rotE の式の両辺の rot をとれば □ E= 0 となり、電場も同じ形の波動方程式になる。
□ B= 0,
□ E= 0
空間中のベクトルの波がこの "波動方程式" で表されるとき、任意の形をとった波が光速で 3 次元空間を任意の方向に移動する。 Maxwell 方程式は SI 単位系では、
div E= ρ/ε_0, rot B= μ_0 ε_0 dE/dt
div B= 0, rot E= -dB/dt
真空の透磁率と誘電率の積 μ_0 ε_0 (= 1/c^2) に光速が隠れている。
B= rot A, E= -dA/dt -grad φ .........(1)
ポテンシャルは、時空と同様にローレンツ変換する 4 元ベクトル (φ, A) である。 H. A. ローレンツは、ポテンシャルには余分な自由度があって、任意のスカラー関数 f(x,t) を使って、
A' = A + grad f, φ'= φ - df/dt (ゲージ変換)
のようにポテンシャルに変化を与えても、同じ電磁場 (B'= B、 E'= E) を与えることを示した。
B'= rot A' = B + rot grad f = B
E'= -dA'/dt - grad φ' = -d(A + grad f)/dt - grad (φ - df/dt) = -dA/dt -grad φ = E
例えば、(1) 式によって電場は、A の時間微分とスカラーポテンシャルφの勾配との和の符号反転であるが、 電場をφの勾配だけで表す、A= 0、φ= -z E0 とすると z 方向の E0 の電場になるが、 A の時間微分だけで E を表す、A_z= -t E0、φ= 0 としても同じ電場を与える。
余分な自由度を削るためにポテンシャルが従う制限を"ゲージ"と呼ぶ。クーロン・ゲージは、A の発散を 0 とする保存式であり(∇・A = 0)、 ローレンツ・ゲージは、ポテンシャルの 4 元発散を 0 とする連続の方程式である。(∇・A + dφ/dt= 0)
1960 年頃にアハラナス・ボーム(Aharonov-Bohm)によって、長いソレノイド外部を通過する電子の干渉縞がずれる現象が確認された。 これは、磁場を通した鉄のホイスカーを通す電子の回折実験であった。理想的に長いソレノイドの外部には磁場はなく(*)、 ベクトルポテンシャルしかない。このようにポテンシャルの実在は、量子の干渉現象によって確認されたが、それは、量子力学が ポテンシャル中の波動関数を記述するからである。古典電磁気にはポテンシャルの影響は全くない、とは言いきれない。
ゲージの制限、例えばローレンツ・ゲージは、数学的な容易さのためにするものではなく、実在するポテンシャルの物理特性であり、 保存則、連続の方程式であるという捉え方がある。電磁波の伝搬の方程式もクーロン・ゲージでは正しくでないという。 クーロン・ゲージ∇・A= 0 は、ローレンツ・ゲージの光速を∞にする近似であり、ローレンツ変換に対するガリレオ変換に相当し、 ゲージ変換は、古典電磁気にある本質的な対称性を表すのではなく、単なる制限不足の不定性であった可能性がある。 この説について、ジェルマン・ルソー (Germain Rousseaux)の "The gauge non-invariance of Classic Electromagnetism" (arXiv physics/0506203 v1 28 Jun 2005) を参照。
(*) 長いソレノイド(円筒状の一様なコイル)は、円筒内部空間に一様な磁場を作り、外部には磁場がないと近似できる。 外部には、両磁極からの距離 L の L^-2 に比例する磁場しかない。L が十分大きければ L^-3 比例であり 0 と見なせる。 単位長に n 回巻かれた円筒形コイルに電流 i を流す。円筒を横切る軸に平行な単位長の 2 辺と垂直な 2 辺をもつ長方形経路の 中に電流 ni が流れ、rot B = i から経路に沿う磁場の一順は、内部電流に比例する、ソレノイドには軸方向の電線 1 本分の電流 i があり、 外部の水平方向磁場は、B= i/2πr である。その軸対称性から磁場が軸と平行な成分だけとすると、内外の軸方向の磁場の差が B= ni。外部辺を無限遠に遠ざければ磁場は内部辺だけで B= ni。これは、ソレノイドの半径によらない。 rot A= B から、軸から r の点の外部の水平方向のベクトルポテンシャルの大きさは、ni/2πr。内部は、niπr^2/2πr= nir/2。
B= rot A, E= -dA/dt -grad φ .........(1)
Maxwell 方程式の1組は、次のように数学的な恒等式となる。
div B = div rot A = 0
rot E = -d/dt rot A - rot grad φ = -dB/dt
Maxwell 方程式のもう1組、div E = ρ、 rotB = dE/dt + i を導出するには、 ポテンシャルの定義とポテンシャルが従うどのような式を与えればよいのだろうか、 それには、ローレンツ・ゲージ (Lorentz gauge)
div A + dφ/dt= 0 ............(2)
とポテンシャルの波動方程式
□φ= -ρ, □ A = -i ..............(3)
とがあればよい。
(1) から div E = div(-dA/dt -grad φ) = -d/dt div A - div grad φ
(2) から = d^2φ/dt^2 - div grad φ = d^2φ/dt^2 - Δφ = -□φ
(3)を使って、= ρ
rot B = rot rot A = grad div A - Δ A
(2)を使って、 = grad (-dφ/dt) - Δ A
(3)を使って、 = grad (-dφ/dt) - d^2/dt^2 A + i = d/dt(-grad φ - dA/dt) + i
(1)から、 = dE/dt + i
電磁場の中で、速度 v で動く電荷がローレンツ力 F = q(E + v x B) を受ける。 速度に依存しない部分を与えるのが電場、残りの速度に比例する部分を与えるのが磁場である。この式には、加速度は出て来ていない。
電場と磁場の定義とローレンツ力の法則とが慣性系が代わっても不変とすると、ローレンツ力の式が速度を含むということは、 系を移るに伴って電磁場は姿を変えなければならない。速度をもった電荷に並進する系では、その系に磁場はあっても電荷が静止している (v=0)から、電荷はその系の磁場の影響を受けない。元の系の電磁場のローレンツ力は、電荷静止系ではこの系の電場E'の力だけになる。 つまり、もとの系の E + v x B が、電荷のみる電場E'にほぼ含まれる必要がある。
ここで、速度による時間経過の変化によって、力のローレンツ変換がある。電荷の見る力は、F'⊥ = γF⊥, F'// = F// であり、速度に垂直成分だけがγ倍される。逆に、物体に静止した系では力は、それに対して速度をもつ系からみて、速度に垂直な方向が 1/γ に小さい。 γ= 1/√1-v^2。vは光速を1とする。
以上から、電荷の見る電場は、 E'⊥ = γ (E⊥ + vxB), E'// = E// である。 こうして、電磁場の一体的関係である電磁場のローレンツ変換は、ローレンツ力と力のローレンツ変換とによって導かれる。 電磁場は、速度によって姿を変えるのであり、空間に分布する電磁場の構造が速度 -v で動く訳ではない。 vで動く電荷の系では、元の磁力線が速度-vをもって横切るとはいえない。元の磁力線は存在しないかもしれない。
E' = γ(E + v x B)
B' = γ(B - v x E)
E' の式はすでに示したが、B'の式は、存在しない磁荷のローレンツ力に対応する磁場の変換式である。 これを導こう。E'の式の逆変換は、' を入れ換え、v と -v を入れ換え、
E = γ(E' - v x B')
式中の E'を順変換式で置き換え、 B'と B と E の式を得る。後はこれを整頓するだけである。
E = γ(γ(E + v x B) - v x B')
E(1-γ^2) = γ^2(v x B) - γ(v x B')
E(v^2/(1-v^2)) = (v x (B' - γB)
v x (v x A)= -v^2 A から、両辺に v x をかけ、
v x E/(1-v^2) = -γ(B' - γB)
v x E γ^2 = -γ(B' - γB)
-v x Eγ = B' - γB
B' = γ(B - v x E)
さらに、速度 v が x 方向なら、
E_x' = E_x, B_x' = B_x,
E_y' = γ(E_y - v B_z), B_y' = γ(B_y + v E_z),
E_z' = γ(E_z + v B_y), B_z' = γ(B_z - v E_y)
とも書ける。
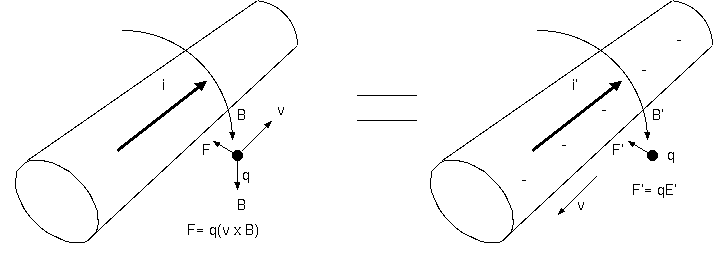
直線状の電線のなかを電流が流れて、近辺にはそれが原因の磁場が発生する。 磁場は、電流に比例し、電線の長さが無限のとき、電線からの距離に反比例する。 電線に平行に飛ぶ電荷を考えると、それに並進する系から見ると電荷は静止している。 どうして電荷は、力を受けるかというと、この系では電線が帯電しているのである。
電線の中には、格子の電荷+qと自由電子-qがある。その和は 0 とする。 +qは静止していて、-q は平均速度 u をもつ。これは、1 Aの電流、0.1 mol/m の電線のとき、 u= 約0.1mm/sec 程度の速度である。
電線の単位長の電荷を q [C/m]とし、電流 I= qv [A= C/m]から u を求めてみよう。 6.35 g/m の電線(銅 Cu の原子量= 63.5 から 0.1mol/m)では、 q= 0.1 [mol/m] x アボガドロ数 6.02x10^{23} [/mol] x 電子の電荷1.6x 10^{-19}[C]より、 q= 10^4 [C/m]であり、1[A= C/sec]を得るには 10^{-4} [m/sec]、つまり 0.1mm/secでよい。
どうして帯電するかであるが、速度 v の系からみた帯電の原因は、驚くべき事に、 格子電荷+qのvと自由電子の速度 v+u のローレンツ短縮の差によるとして説明するのである。 ここで、u,v≪cとする。比 v/c, u/c は小さい。速度 v によるローレンツ短縮は、 1/γ(v) = √(1-(v/c)^2) 〜 1 - 1/2 (v/c)^2 に近似する。
q_0^- = q/γ(u) 〜 q(1 - 1/2 (u/c)^2)
速度 v の系からみた、q^+ は、q を速度 v のローレンツ短縮したものであり、 (格子の密度)
q^+ = qγ(v) 〜 q(1 + 1/2 (v/c)^2)
q^- は q_0^-を v+u のローレンツ短縮したものだから、 (電子の密度)
q^- = qγ(u+v)/γ(u) 〜 q(1 + 1/2 (u+v)^2/c^2 -1/2 (u/c)^2) = q(1 + 1/2 (v/c)^2 + uv/c^2)
それらの差の電荷は、
q^+ - q^- = q(γ(v) - γ(u+v)/γ(u)) = -q uv/c^2
qu は1[A=C/sec], vが 1[m/sec]のとき、総電荷(q^+ -q^-)は1/c^2[C/m]となる。 1[C/m]の直線電荷から 1m の距離の電場は、2/(4 π ε_0) [V/m]であるし、 (4 π ε_0)*c^2 = 10^7 から 2*10^{-7} [V/m]の電場を電荷は見ることになり、 1[C]の電荷なら2*10^{-7} [N]の力を受ける。
磁場からの説明では、1A の電流から 1m の距離の磁場は、正確に2 [m Gauss]= 2*10 ^{-7} [T]であり、 1[C]の電荷が 1[m/sec]の速度をもつとき、2*10^{-7} [N] の 力を受け、結果は一致する。
驚くべき事は、電流の起こす磁場という非常に普遍的現象が、電子と格子とのわずかな速度差の、 さらにローレンツ短縮の差による帯電として電荷は見ているという説明がうまくいくことである(*)。 これほど説明がうまく行くのは、電流に並進する電荷の場合であり、電線に直交する方向に移動する電荷では こうは上手くいかないのであるが(**)。我々の電磁現象は、巨大な電気的力と微小な相対論的効果によってできている。
(*) なお、q^+ = qγ(v), q^- = qγ(u+v) とするだけでも u≪v という仮定を入れれば、
q^- = qγ(u+v) 〜 q(1 + 1/2 (u+v)^2/c^2) = q(1 + 1/2 (v/c)^2 + uv/c^2 + 1/2 (u/c)^2 )
q^+ = qγ(v) 〜 q(1 + 1/2 (v/c)^2)
u^2の項は、uv の項より小さいとして、
q^+ - q^- = q(γ(v) - γ(u+v)) 〜 -q uv/c^2 となる。
(**) 電荷の速度 v が電線に垂直の場合、電荷のみる電場の原因は、左右の両側の帯電の差が必要になる。前の例にならって、 遠ざかる電流をもつ近付いてくる電線が負に帯電し、向かってくる電流をもつ近付いてくる電線は、正に帯電するとして、 これも説明可能のはずと思ってもそうはいかない。12章の飛んで来る長いループ電流の話は、左右の 電線の帯電で説明するが、その帯電はループ内の磁場に対応し、この問題はループ外に対応し磁場はループ内磁場と逆の 向きである。この近付いてくる右向き電流の電線は、左向きの電場を与えないといけないのである。その逆なら説明容易 だが(下図参照)。
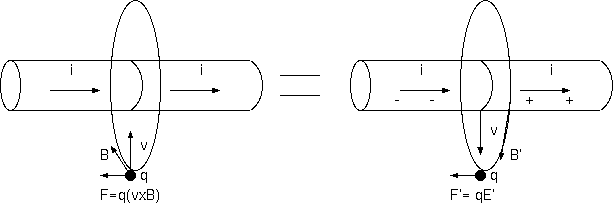
磁場中を速度 v で飛ぶ電荷と同じ速度を持つ座標系(電荷の並進系)から見ると電場をみる。 それでは一様な磁場の発生源に速度 -v を与えた場合に電場はでるか? 飛んでくる巨大な一様な磁場源、たとえば巨大な電流ループ、巨大な永久磁石が飛んで来るとき、 それは電場になって見えるだろうか。それ以外に関係する物体はないとする。
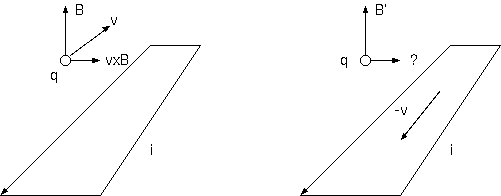
図 3. 飛んで来る電流ループ
「電場源でないから電場はない、飛来するのは "磁場源"だから」と笑う人は、「磁場中を飛ぶ電荷が電場を見る」ことを真面目に 考えるべきである。電荷が見る電場の説明は、言い訳ではない。磁場中を飛ぶ荷電粒子が電場をみるなら、人間だって見るだろう (勿論、電磁場は目に見えない)。 慣性系が対等なら、磁場源である磁石なり電流ループが速度をもつとき電場を出すのでないか。
もう一つのよくある答え「磁場の時間変化がないから電場はできない、電磁場は、Maxwell 方程式が全てだから、磁場の時間変化 がないと電場はできない」という答である。
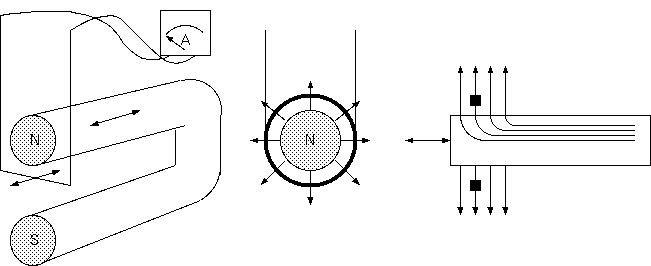
ブランコを振らせ、導線を馬蹄形磁石の内外方向に移動すれば、検流計の針は振れるがこれは、磁場の中を電線が速度を持っている から、磁場中を移動する導体に発生する電磁起電力 (ローレンツ起電力) と説明される。それでは逆に「磁場は軸方向に一様である。 磁石を前後に移動した場合、検流計の針は振れるだろうか?」と質問する。
磁石に対して移動する導体に起電力が発生するとき、磁石を移動させて導体を固定しても同じ現象がでるだろう、そのような相対性 の原理が基本的に成り立つと期待するのは自然である。ここで、「検流計の針は振れない」ということは信じがたい。慣性系を変える だけで局所現象が変わることはない。磁場源と相対運動する電線に電場が発生するのであり、一様な磁場源も速度を持てば電場源になる のではないか。
「磁石を移動する場合には、電流ループの中を貫く磁束の変化が電位を生むが、電流ループ上の任意の位置には磁場の時間的変動はない。 磁場の時間変動がないと電場はできない。場の基本的な考え方として、速度をもった磁場と速度をもたない磁場の区別は不可能である。 電場、磁場しかもたない一点が、一様な磁場源の移動を知る方法はない。磁場が全く変化せずに、電場ができるとは、Maxwell 方程式を 知らないのではないか」という意見である。
(*) アインシュタインの 1905 年の "運動物体の電磁力学について" の冒頭にこのことが記述されている。 電磁場の問題は、力学の問題とともに彼の特殊相対論の主要なテーマであったと思う。彼以前に Maxwell 方程式は、現在と同様に存在していた。 彼は、そこに特殊相対論とその 6 章にある電磁場のローレンツ変換を与えた。つまり、特殊相対論は、Maxwell 理論のもたらした時空と電磁場 の理解の仕方を変更した。私のこの文章 7 章以降最後までは、これを正確に把握することを目的としている。
状況は説明を要する。電線ループの各点において磁場の時間変化がないが、ループの内側のどこかに磁場の時間変化がある。それによって、 「電線の場所に磁場の時間変化がなくても電線に電場ができることがある」のである。
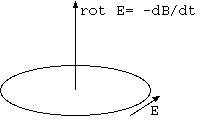
電線上を一巡する電場 E の成分は、ループの囲む面内の rot E による。「おい、そこに磁場の時間変化があるじゃないか」と怒りの反論がくる。 一様な磁場中に電線があるといい、ループ内部に磁場の時間変化があるというのは、設問の罠ではない。ループ内部を貫通する、 磁極の側面から磁力線が一様に出ている事自体、磁極の先の方では、磁力線が側面から出た分だけ、内部の磁束が減少することを表す。 磁極を前後に動かすと、電線ループ内部の磁極の磁束は当然、変化するのである。
それに対して、反論は、「これは問題の設定が奇妙なためであって、ループ内部にもうひとつの馬蹄形の磁石を対面させると 磁束の減少分は打ち消されゼロになる」という。しかしこれは錯誤である。一方の磁極で先に行くにつれて減少する磁束は、 対面させた他方の磁束の増加によって補われる訳ではない。逆方向磁束の増加(=磁束の減少) が付け加わるだけである。 それでなくて、外(磁極の側面)に磁力線が出ることはない。
そして反論、「普通の円板型永久磁石を上下において、電線を挟んだ場合、磁場が一様であるとき、電線を動かすと電場ができ、 上下の磁石を動かす場合には電場はできない。この磁石を前後に長い電流ループに置換え、それが飛んでくるとき、前後に長いので、 飛んでくることによってどこも磁場は変化しないとする。そのような場合には、電場はできないのではないか。」という。
これも間違いである。そこに電場がある。それを示すには、簡単にはそのループと交差する辺をもち、 飛んでくる長いループの外側まで長いループを考えればよい。 この新しい検出用のループの中の磁束は変化するので電流が検出できる。磁場の時間変化の無い場所にも電場はできるのである。
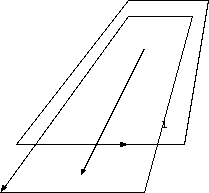
図 5. 電場を見るために 巨大電流ループの飛来
反論、「待ってくれ、細長いループの外側にまで広がったループを考えるのは、現象の局所性を無視している。その場合は、広がったループ面内の 磁束変化を認めることができるが、今議論している測定点では、誤差の範囲内の話になる。」という。
巨大な円盤形の磁石の間に発生した電場は、その電場中での小ループには電流を発生しないため、電場発生には実感がない。しかし、これは ファインマン物理の電磁気にある、地球磁場の中を飛ぶ飛行機の話と同じで、電場は発生しても電流計を使っては測定できないものである。 電流計までの電線で丁度キャンセルされるからである。馬蹄形の外を通る電線、元のコの字型の電線では電流は計れるわけである。 そのような経路が明白な場合は明確である。
rot E = (-1/c) dB/dt, rot B = (1/c) dE/dt + i
Stokes の定理より、rot E はループが囲む面内で面積分して、ループ一巡に発生する E を与える。ループ上で dB/dt = 0 だからといって ループの囲む面内は磁束変化を持ちえる。馬蹄形の磁石の話は、まさにその例である。Maxwell 方程式は電磁場の直接の値 E を与えない。 それは、空間の1点の微分方程式であり、磁場の時間変化は rot E という空間的微分しか与えない。その領域外の rot E の影響を説明しない。 全空間は関連していて、各点は互いに影響する。微分方程式には境界条件がある。 電線ループ上の E を説明するのは、ループの内部面内の rot E である。
「おい、どこか(ループ内部面)に磁場の時間変化があるではないか、(ループ)に磁場の時間変化はないといったではないか、」という反論について、 確かに、全世界に磁場の時間変化がなければ電場はできるといえない。 しかし、初期の状況設定は、電線近傍の磁場が一様で、運動しても磁場の時間変化がないことだった。 ある部屋の全ての点に、磁場の時間変化が無くても隣の部屋から電場がくる。隣りから来る電場は反則のように見えるかもしれない。 Maxwell 方程式は、もともと1点の物理である。しかし、rot E = - dB/dt の意味は、"その場所の磁場の時間変化なしに電場が発生しない" ではなく、"となり(閉曲面内)の磁場の時間変化が(周上に)電場を生む" である。
例えば、スピーカの円筒形ギャップに小部屋があって、磁石を軸方向に動かした場合、ボイスコイルの一部の小さい部屋のなかに電場はできる。 部屋の壁(又は天井)の向こうには鉄心があって、鉄心の中に磁場の時間変化はあるが、隣のことを持ち出すことはない。すでに、部屋の中に磁場の 時間変化なしに電場はできる例を示した。反論者は、rot E が dB/dt によるのを E 自体が dB/dt によると勘違いをしたのでないか。 E の変化は、 Maxwell 方程式 dE/dt = rot B - i から rot B と i の差である。
空間の各点に電場と磁場のベクトルを考えこれを使った Maxwell 方程式は正しい。しかし、"磁場の時間変化"という誤解に苦しめられた のはこの考え方である。相対運動では発生が明白である電場は、磁場の時間変化に置き換えることができない。磁場の時間変化は相対運動 を表現しないが、磁力線との交差は相対運動を表す。Maxwell方程式から電磁場のローレンツ変換を導くのは、可能なはずだが容易でなく、 交差を記述し電荷系のみる電場を示すローレンツ力からローレンツ変換は導けた。
磁石から磁力線が生える力線論なら、速度をもった電荷が磁力線と交差して電場をみる。そのとき逆に磁石を動かせば磁力線が動くという 見方が容易である。磁力線を磁場に換えると、飛来する一様な磁場は静止と変わるはずがなく、電場はできないという誤解を生む。 場はもと遠隔論をさけるための仮説であった。遠隔作用を避け、有限の伝播速度のために設定された電磁気の場は、物体と同様に実在的に 扱われ、場にも運動量、エネルギーがあるとされる。そしてそれは決して間違いではない。しかし場の概念は、現象が物体間の関係である ことを忘れさせる。力線が系に依存するのと同程度に場も系に依存しているのに、力線はそれとの交差を意識するが、場は交差を意識させない。 磁場中を飛ぶ電荷が電場をみることを認め、一様な磁場が飛来するとき磁場の変化がないとして電場はないと答える場実在論は、 磁場が電場に変化することを想像できず、電荷の並進系に移ることができなかった。 場実在論よりも力線実在論が電磁場のローレンツ変換に近かったのである。
場が速度をもつとか移動する場、力線の速度という概念は使う必要はない。場が移動するのでなく電磁場が変化する。しかし、磁場が時間的 に変動しないからといって、移動する磁極が作る電磁場は、静止した磁極が作る電磁場とは違うのである。 電場源(電荷)の速度が磁場に与える影響があるなら、磁場源の速度が電場に与える影響もある。 これを、「モノポールは実在しないから、その速度をいえない」と、これをモノポール非存在に結びつけるのは、正しくない。
相対運動は、系の間の電磁気のローレンツ変換に帰結する。さらに、同じ時空点の電磁場が慣性系によって異なるだけでなく、場とは、 相対論の同時刻の空間によるから、系によって場自体が異なることに注意すべきときがある。同時刻空間が即時にここの現在に影響する ことはないが、すこし待てば過去のその空間が見えて影響する。場が系によって異なるのは、同時刻の空間が違うことによることがある。
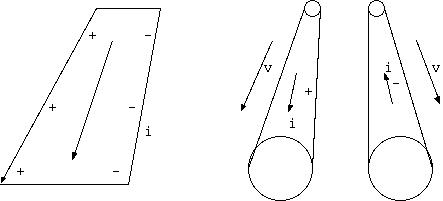
図 6. 電流ループの飛行(両側の電線が+-に帯電して見える)
また、右に y 前方に x 上方に z を取るとき、 2 つの面(y=0,y=1)に電流が逆方向(-x,x)に流れているとき、 y が 0 と 1 の間では磁場は z 方向に向く。電荷の速度が x 方向であるとき、電荷系からみた 2 つの面の間は 反対方向の帯電をした面に挟まれた電場をみる。
進行方向に多少細長い電流ループを前後に動かすとき、その近辺の磁場の時間変化はないが電場を生じる。 それを横切る電線に電場が生じるがそれをみる方法はないかというと、無いわけではない。 電流ループよりもさらに細長いループで電流ループの端を内側に含む面をもつループをつくり、 その電線を閉じると、そのループの囲む面には磁束の時間変化があるため電流が流れる。 この電流は、もとの近辺の電場が原因の電流であると言うことができるだろう。
検出用ループの長い 2 辺をレールにして、横切る電線を飛んでくる電流ループとともに移動する棒とすると、 この検出用ループは磁束の時間変化をもたない。このとき検出ループには電流が流れないだろう。 これは磁場中を速度 v で移動する導体に発生した起電力が、電場で打ち消されていると考えて初めて納得できる。
航路は地球やアルファケンタウリからみると 1 隻到着するたびに、1 隻が出発するため、行き帰りの密度が変化しないが、 これを太陽系を離れ、アルファケンタウリに向かって加速したばかりの光速に近いロケットは、違ってみる。太陽系や アルファケンタウリは、光で 4 年かかる距離をロケットは、半年も経たずに目的地に着くのである。 船の同時刻である空間は、地球は、2000 年だが、前方は未来であって、アルファケンタウリは、2004 年になっている。
だから、ここからの眺めは、次のようなものである。もちろん、この光景を描写する光は、このロケットには、まだ届いていないが ロケットにとっての空間は、こうなる。往路の船は、すでにすべて目的地に到着していて、行きの航路上にはこの船だけしかなく、 戻りの航路には 2004 年までにアルファケンタウリを出発した全ての船がまだ太陽系には到着せず、8 隻が並んでいるのである。(下図右)
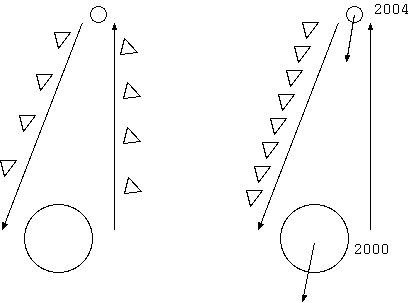
図 7. 行き帰りする定期航路 (速度系(右)からみると、前方が未来なので、行きはガラ空き、帰りは混雑)
地球とアルファケンタウリの間には時間差があるため、行きの船はまばらで、帰りの船は密集する。飛んでくる電流ループは、 電子の航路が向かってくる側が密集し、むこう向きがまばらになる。そのためむこう向きの電流方向をもつ電線の部分は、 マイナスに帯電し、こちらに向かう電流の部分はプラスに帯電している。そして、磁場のなかの速度をもった系が電場をみる。
これが電磁場が系の変換によって姿を変える理由である。場は、同時刻の空間からくるものである。系によって同時刻の空間が 異なることが基本的な原因である。速度をもった系では、同じ場所にいても同時刻空間が違うから、場が違って当然である。
一本の無限に長い電線の電流が、そばを電線に並行に飛んでいる電荷からみると、帯電してみえることは、多くの教科書で示されている。 この事の説明としては、プラス電荷とマイナス電荷のローレンツ短縮の違いで説明される。通常程度の電流では電子の平均速度は、 毎秒 0.1 mm 程度であるのに、電荷からみた相対速度のこの微小な違いがローレンツ短縮の違いとなって、電流の流れる電線が帯電して見えるのである。
電線に静止した座標系からは磁場は電線までの距離に反比例する。粒子から見て電線が帯電している場合も電場は電線までの距離に反比例する。 磁場の座標変換による電荷のみる電場は速度と磁場の両方に比例する。
磁場を電荷の相対速度の微小な違いから説明する以外の説明がある。4 元電流ベクトルである、電荷密度ρと電流密度 i は、 ちょうど時間と空間のようにローレンツ変換される。(速度 v の系の電荷密度、電流密度を ρ', i' とすると、ρ'= γ(ρ- v・i), i'= γ(i- vρ)) 速度をもった電荷から見て向かってくる電流はプラスの電荷密度に変換され、電流と速度との両方に比例する項 v・i これが電場の原因である。
電流が電荷密度に変換される理由としては、次のようなものである。電流はある断面から流出し、ある断面から流入する。 両者の断面に向かっている座標系では同時でないものを同時とみるからである。物体が向かってくる時、前方は物体の未来に対応する。 向かってくる電流は、前方断面からすでに流入した量が後方断面から流出する量より多くて当然である。 この時刻の差は、速度に比例する項であり、電流密度が電荷密度に変換される項である。
この説明は無限の長さの電線でなくとも成立する点で優れている。要するに、飛んでくる電流は帯電している。 2 本の電線は逆に帯電していてその近辺の空間には電場が発生するのである。
単極誘導は、場の概念を基本的とするか、相対運動を基本的とするか、によって解釈が異なる現象である。磁石を回転させたときの現象 を相対運動による現実の電場発生とすると、回転する磁石の近くの静止した導体円板に電場が発生する必要がある。それは Maxwell方程式 と矛盾するように見える。場の概念を基本にして、Maxwell 方程式を優先すると、電荷なしに電場の発散はなく、磁石の回転運動は何らの 電場をもたらさない特別な運動になる。いずれが正しいかの実験的検証は不可能ではない。しかしまずは、その種々の側面の説明に入ろう。
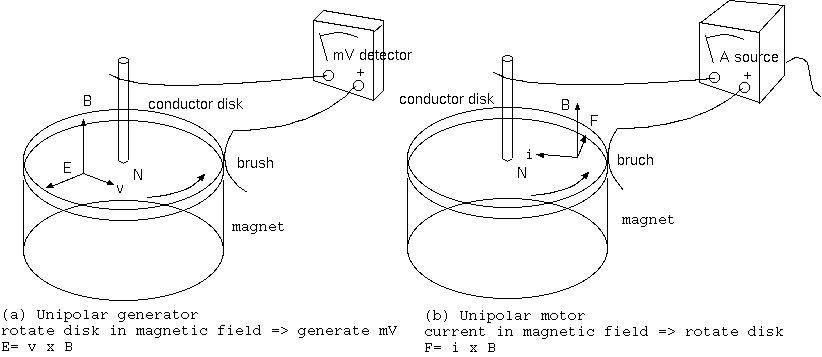
この回転円板上の各点で発生する起電力 E= v x B は、各点の接線速度をもった電荷が力をうけるローレンツ力 qv x B が原因ともいえる。 運動できる電荷は負であっても負電荷の受ける逆向きの力は、正電荷の受ける力と同じ働きで起電力を生む。 またこれは、回転する導体円板内の各点のみる電場、回転系に静止した電荷が力を受けるから、回転系にある電場といえる。 磁場中に運動する導体は、導体各部の電位が違い、軸から外向きに電場 E を積分した電位は、半径 r の 2 乗に比例する。
円板は外周が中心よりも電位が高くなり、外周と円板の軸にブラシ(摺動端子)をつけて、電位差 V を測定すると、 円板の半径を r、磁場を B 一様とし角速度を W とするとき、V= (1/2) B W r^2 となる。 (極端例で接線速度を音速、直径 10 cm円板、磁場が1[T](=10kgauss)のとき 340v/m * 5 cm/2= 8.5 voltである。) またブラシと軸の間から電流を取りだすと、円板中の電流は、磁場中での回転の反対方向の抵抗力 I x B を受ける。
単極誘導の原理的しくみは、軸対称磁石上での導体円板の回転であるが、注意してほしいのは、電流は円板上だけでなく、電流計と一巡する電線 の"戻り線"が存在することである。戻り線には、回転円板上の電流と逆方向の電流が流れ、磁場中に静止した電線に電流が流れている。
この装置がモーターのとき、発生する偶力(トルク)の反作用は磁石が受けるわけではない。定常的に円板上を電流が内から外に向かうなら、外か ら内へ向かう電流が同じだけ必ず存在し、それはその偶力の反作用を受け持つことである。磁石は磁場を提供するだけで作用と反作用からは独立 している。円板に電流を通しても磁石を回転させることはできない。
軸からブラシへいく円板と、ブラシ以降の戻り線を外から内に向かう電流がある。一巡する電線は閉じていて、戻り線は磁石から離れていて磁場 が弱くても、電線に交差した磁力線は、再度必ず交差して、一巡する電流がうけるトルクは、ブラシで分割された円板と電線の他の部分を合計で 0 である。両部分は逆方向のトルクを受けるが、戻り線は機器に固定され、円板だけが回転する。戻り線がトルクを受けるのである。
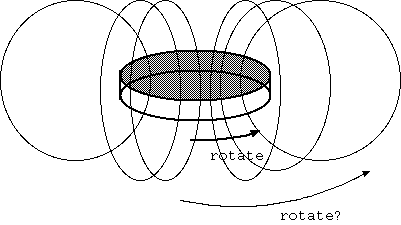
円筒状磁石から上に磁力線が出る。それを導体円板が速度をもって横切る。そのために起電力が起きるという力線的な見方では、磁石を回転して、 円板は固定しても同様な起電力が起きると考えることができる。磁石は電気的回路から離れているから、磁石を回転させるのは、磁石が円板より 重いという欠点はあるが、それよりも、円板が固定できれば大きな機械的抵抗を生むブラシが不要になるという実用的利点がある。
しかし、実験するとそれでは起電力を検出しない。やはり、磁力線は、磁石に固定されていないのか。いやそれなら、固定磁石の磁力線は、 なぜ静止できるのだろう。円板の回転に流されない理由がない。磁石は円板からは多少でも抵抗をうける。磁石の軸対称性が完全でないた めに回転円板にはうず電流が起き、磁石と円板との差の角速度に比例する機械的抵抗を生む。場は空間固定の概念だが、磁力線は空間に固定 される制限はないように思う。
磁力線を磁場として見ると、磁場の軸対称性から、回転してもどこも磁場が時間的に変動しない。磁場の時間変化がないから電場が起きない(*) のは当然である。単極誘導の電位は、ローレンツ起電力の電位であり電場ではない(*)と考えることができる。こうして、単極誘導現象では 場の概念が正しく、磁力線の概念が間違っていたことが証明されたのだろうか。場の実体論は、磁場の時間変化では捉えられないとして、 平行移動の運動では実体的な力線論に敗北した (8〜11の項参照) ものである。
(*) 電場が起きない、は誤り、電場の回転 (rot E) が起きないが正しい。電場ではない、は誤りで、ローレンツ起電力の電位は、 電荷のみる電場であり、系を跨いでローレンツ起電力となる。
磁石だけを回転するときは、磁石の上の面から出て広がった磁力線は磁石の下の面の S 極の対応位置に向かって空間を広がっている。 この広がった磁力線も空間を横切って回転をしている。電流測定のための線にも速度をもって磁力線は交差し起電力が発生する。 磁場(磁力線の密度)は、遠方ほど小さくなるが、磁力線の速度が距離に比例するから、遠方まで弱まらない。中心軸ブラシを通した線と 円板の周辺部ブラシを通した線は測定器に繋がる。測定器を含めてそれはひとつの閉じたループになっている。一本の磁力線にこの閉じた 電線の片側に交差したら、少なくとも1回転の間には、他の片側にも交差する。そうして、両方の電線が速度が等しいなら、等しい起電力を 生むから測定できるはずがない。磁石だけの回転の場合、磁力線が回転して走るイメージでも起電力差がないという現象を説明できる。
しかし、磁石の回転によって磁力線が空中を交差するなら、そこら中の導体に中心対称の電場を生むだろう。それが測定しにくい電場であるこ とは事実だが、それ自身問題である。仮に電場ができるとするとこの電場は、Maxwell 方程式を満たさない。軸対称電場は、一様な電荷密度ρ の存在なしには得られないはずだからである。
(0)は三要素全て静止である。(1)〜(7)は、要素のいずれかが回転するので 2 進法番号付した。(1)が通常の円板だけの回転、円板に電位が出て、 円板(b)-測定系(a)= (c)に差が検出される。(2)は測定系だけの回転、これも電流計までの電線が磁石の上を走るから逆の電流が検出される。 (4)は磁石だけの回転である。円板と測定系の両者に起電力がでて、差は検出されない。これが(1)の回転相対であると誤認されたが、正しくは (6)がそれである。また、(3)の円板と測定系の両者の回転では、電流計への電線と、円板とには等しい起電力があり電流は流れない。 (5)磁石と円板を回転させると、測定系には起電力がでる。(1)では、円板の起電力が原因だったが、(5)では測定系に逆の起電力が出て、 (1)と同じ結果になる。(5) は、(2)の回転相対である。(6) 測定系と磁石を回転させると、(2) と同様に電位が検出できる。(6)は(1)と 回転相対で、(1)と逆符号が検出される。
磁石 測定系 円板 測定系の電位(a) 円板の電位(b) 円板-測定系(c) (0) 0 0 0 0 0 0 (1) 0 0 1 0 1 1 (2) 0 1 0 1 0 −1 (3) 0 1 1 1 1 0 (4) 1 0 0 −1 −1 0 (5) 1 0 1 −1 0 1 (6) 1 1 0 0 −1 −1 (7) 1 1 1 0 0 0
そのことから、磁石の磁力線は根が生えていないと結論するべきだろうか。磁石の回転は、この宇宙から無視されると考えることも 可能かもしれない。磁石を中空のループ電流に置き換えてイメージし、空廻りをするという説明をする人がいる。しかし、この結果 から測定系の電線に発生する起電力を忘れて、磁力線は磁石から生えていないと結論づけるのは誤りであることが明らかである。 磁場の源との相対運動を起電力の原因として、磁力線との交差だけを考えた場合も、同じ結果を説明するからである。
磁力線に根がないとする考え方は、磁場源が速度を持っていることを無視し、磁石の回転は磁場の時間変化を生まないので、起電力が 発生しないという解釈である。しかし、磁場源が速度を持てば電場源となること、つまり、前章までの相対運動の成果と折り合わせる 方法がない。それでは、磁石が固定されている場合は、どうして磁力線は磁石に保持されていたのだろう。物体のない空間に保持され ていたのだろうか。これは磁力線でなく磁場であるとする見方をとるだけで、座標系に保持されるのだろうか。磁石は、現実には一様 でなく、磁場の凸凹によって時間変化がはっきりある場合から、それが無くなるまでのどこで磁力線は磁石から根が途切れるのかも 説明できない。
実体的な磁力線論が単極誘導を説明できないということはなく、その主張をする人の見落とした測定系の戻り線への誘導を考慮すれば 現象を十分に説明することを示した。また、この表の実体的磁力線の考え方が、 "相対的な角速度だけが現象を決定する"という、回転 相対性を許すことがわかる。すなわち、この結果だけからでは" 電磁気には回転相対性がない" ということはできない。
磁石を回転する場合も、速度をもった磁場源が電場源であるなら、局所的に円板の一部に立った人は回転する磁石の一部をそのように みるのではなかろうか?
併進系では電場を見て、回転する磁場源にはそれをみないのか。回転運動には加速度があるため併進運動とは違うが、加速度は ローレンツ変換には、関係しないとされている。しかし、回転系の上の点に並進する慣性系の物理と回転系の物理は違う。電磁気の Maxwell 方程式は、慣性系にしか適用できない。特殊相対論が双子のパラドックスを解釈できるように、慣性系から回転系を推測する ことはできるはずである。これのもたらすディレンマは、回転する磁石が、固定した円板に軸対称電場を生むなら、電場の発散が電荷 密度だけでないことになり、Maxwell 方程式に抵触することである。
磁石の回転は静止系に電場をもたらすのではなかろうか。慣性系にのみ磁場源の速度の効果をみとめ、回転する磁場源に認めない理由はない。 ただし、それに乗ったひとが電場を見ていない磁場源である必要があり、回転磁石に乗ったひとが電場を見ているなら話が違う。 磁場中の回転系は軸対称電場を見ているだろうか。磁石が止まって円板が回転しているときは、一様な磁場中を飛ぶ電荷の話と同じで その円板の部分は軸対称電場をみる。磁石と円板がともに回転しているなら、それに並進する慣性系は、電場を見ている訳ではない。 並進する系から電磁場のローレンツ変換をうけると、静止系がその部分に電場を見て、磁石には外から軸に向かう電場ができる。 電場の大きさは軸からの距離に比例し、ポテンシャルは半径の 2 乗に比例するものとなる。
この考え方は、Maxwell 法則を無視しているため、間違っているとみる人がある。 磁石の元を環状電流とすると環状電流以外は真空で有りえるのに、真空中に電荷なしに軸対称電場ができるからである。 このような軸対称電場は、一様な電荷密度のあるときと同じになる。しかしこれもあり得るかもしれない。 磁石を回転させることなど Maxwell方程式は、想定しているのだろうか。真空中に電荷なしに電場の発散があってもいいとすると、 Maxwell 方程式とぶつかる。だからといって、電磁場のローレンツ変換はどうするのかが明確でない。
そこにすでに電場はあるではないか、という考え方は間違っている。磁石が固定しているときの円板の回転で起こる電位は、 磁場中の速度をもった電荷のローレンツ力によるものである。電場は、静止した電荷に作用する力である。結果的には、 同じような形の電場とポテンシャルになるため混乱しがちであるが、状況が違う。(又は、回転系には電場があると認めるべきだろう。)
(いや、静止円板は回転系からみて回転している。ローレンツ力(E+vxB)のvが磁場源との相対速度なら、電場とローレンツ力は同一になる。)
固定磁石の上の回転円板によるローレンツ力による電荷の変移による電場は、磁石の同方向の回転による電場発生とは区別できる。 それは符号が逆であるからである。回転相対であるなら、ローレンツ力と同じく外側にむく電場を固定した円板に発生させるには、 磁石は逆向きに回転させないといけない。ところが、磁石と円板を同じ元の方向に回転させてできる電場を、磁石の回転が原因とはいえない。
(いや、磁石との相対回転が電場発生をするなら、方向も同じである。しかし、磁石と円板の結合回転の電位発生は相対回転とはいえない。)
ローレンツ力は、ローレンツ変換そのものである。ローレンツ力は、静止系の電磁場をローレンツ変換した、円板上の電磁場による力を、 元の系に戻すときに γ分が消えるだけである。つまり、ローレンツ力はほとんど、回転円板のその部分の系の見ている電場である。
これの解決は、絶対静止空間をとることである。ギョッとすることだが、静止系だけは磁石は電場を生まない、回転系では磁石自体が 電場を生むとするのである。回転した磁石の系が中心軸対称電場を見ていてくれると、静止系はそのお蔭で、ローレンツ変換による 磁場の電場への変換によって中心軸対称電場を見ることがない。そうすれば、Maxwell 方程式は安泰である。
基本的に、静止系と回転系では電磁気法則は異なる。静止系で成り立つ電磁場の法則、Maxwell 方程式は、回転系では成り立たない。 電磁気には回転相対はない。それだけでなく、自分の座標系が絶対静止系か回転系かが判断できるのである。磁石をおいてその上に 電荷を浮かべて力を受けるかどうかみてみればよい。力を受けないのが静止系で、力をうけるのが回転系である。軸対称電場の大きさで、 自分の系の回転を知ることができる。(そんなことがあるのか。自分の系が静止系という主張は、特殊相対論が並進について否定した。) 便利な御都合主義に聞こえるが、そうすれば一応、辻妻合わせはできる。
この考え方は磁場源の回転だけはまったくこの世界に効果をもたらさないとしているし、ローレンツ変換は守っているが、その代わり 原始的な相対運動の原則を無視している。回転において絶対静止系というものがあるとみている(*)。磁場というものを磁極の物体から 切り離して存在させている。磁場源の速度というものを忘れている訳ではないが、この系(静止系)には出て来ないように法則を細工している。 ゴミをカーペットの下に掃き込むという表現があるが、慣性系の不都合を回転系に負わせるのは、ゴミを隣の家に掃き込んでいるのではないか。 このように仮定すると確かに便利だがそれが本当かどうかは怪しい。整合性は高いと見るべきか、ローレンツの例を挙げるまでもなく、 辻妻合わせは意外に成功するものである。簡単な実験確認が必要と思う。確認はかなりの考慮を必要とするが。
(*) 電磁気の基本原理に絶対静止系はないだろう。△Φ= -ρ、又は□Φ= -ρは、電磁場は、電荷の存在だけによるのではないか。
しかし、無限に長い直線電流のそばを進む電荷の慣性系からみると、直線電流が帯電するということでローレンツ力の電場による説明がされた。 これが回転においては全く様相が異なるというのは、現象の局所性の成り立たない説明である。 環状電流の近辺では環状電流は、無限に長い直線電流とどこが違うのであろう。 帯電で説明できない場合、なにをもって環状電流のそばの磁場のローレンツ力を説明するのだろうか(*)。
この解釈は、回転の絶対性は遠心力の存在で確認できるとするニュートンの見解に近い。 バケツの水面のように、ポテンシャルが半径の 2 乗に比例する点はそれのようである。
ところが、よくみると、回転角速度との関係は明らかに違う。遠心力は回転の方向に依らずにつねに外向きであるが、単極誘導の電位は、 回転の方向に依存する。逆に回せば逆の電位がでる。それは、遠心力は角速度の 2 乗に比例するのに、この軸対称電位は角速度の 1 乗に 比例するからである。遠心力と同じように解釈することは間違いである。つまり、測定系の角速度との差だけが効果を持つという、 回転相対の可能性は、まだ残っている。単極誘導の現象をみると、回転はその相対回転速度だけしか効果をもたらさないように見える。
(*) 静止系で回転するコイルの電流と回転方向とが一致していれば正に、逆なら負に帯電し、軸対称電場を作るだろう。 磁石の外側の磁場は、磁石の系に対して回転する系からみると軸対称な電場になる。そういう回転相対は、ローレンツ力と整合する。 静止系で電荷がないコイル電流を回転系からみれば帯電しているが、静止時に電荷のないコイルを回転させれば帯電するというのは 電荷保存則から誤りである。中心から自らの系にアースを取れば、(相対回転の電位程度に)帯電するだろう。
単極誘導を単に説明するだけの本は、熊谷寛夫、荒川泰二の電磁気学 (朝倉書店 朝倉物理学講座 5 1960) がある。
岡村総吾の電磁気学 III (岩波書店 岩波講座 基礎工学 2 1971) では、磁場中の導体円板でなく、棒磁石を使っても電位が発生する ことを図示している。
砂川重信氏の電磁気学(岩波全書297 1977)では、測定系固定での磁石の回転は電流を生まないことを根拠に、磁力線が磁石に固定していないと結論する。 磁力線は、磁荷からブラッシの毛のように生えているのではなく、磁石をひとつのソレノイドに置換えて考えるとよいとし、磁力線は、 空間の各場所に固定している"エーテル"のゆがみなのであるという。さらに、"逆にいえば、磁石の回転が回路に電流を発生しない事実は、 磁荷が電荷のような実在ではないことを示唆しているともいえよう。"と述べる。
磁石に固定していない磁力線という概念は、空間に固定した磁場の概念である。それではローレンツ力と電磁場のローレンツ変換とが十分説明できない。 磁場源の速度は、単極誘導では議論が残るが、並行運動では意味があった。モノポールの非存在は、より直接的な実験で確認すべきことであり、 この実験で示されるものではない。古典電磁場は対称的だが、ポテンシャルの実在とモノポールが排他的である。特殊相対論が否定した ""エーテル"のゆがみ" という言葉を電磁気で使うと、相対論との関係を誤解させる。
霜田光一氏は、単極誘導を謎めいた現象としてとらえ、基本的には、"導体が磁力線を切るときに起電力が生ずる" というとらえかたで説明する。 その場合には導線に発生する起電力も意識することができ、磁力線が磁石に固定しているという仮定も、空間に固定しているという仮定も、 同じ結論が得られることを正しく指摘している。
(*) 訂正:ランダウ・リフシッツの電磁気学 I (東京図書)には、§49 磁場中の導体の運動 のなかで多少述べている。
かれは、単極誘導を"磁力線の速度" への反証としてとらえ、霜田光一氏の"磁力線が磁石に固定しているという仮定も、 空間に固定しているという仮定も、同じ結論が得られること" を使って、磁力線の運動が不要な廃棄すべき概念とする。
一般の並進運動では、"磁力線の運動"が有効であるが、"磁力線の運動"よりは、並進の座標変換、ローレンツ変換がその本質である。 単極誘導で否定されるべきは磁力線の運動でなく、並進のローレンツ変換である。単極誘導は回転であり、円板上の点の並進慣性系 への変換はローレンツ変換できるが、回転系への変換では使えないこと、回転系の電磁気法則は慣性系とは異なることが重要である。
かれの電磁気は、磁場中の運動する導体内のローレンツ力による電荷の変移による電場を強調する。それは電流= 0 としたときの E + v x B = 0 とおいた式を根拠にしているが、電流があろうとなかろうと、導体内の電荷はローレンツ力を受けており、 それが磁場中を運動する導体の電位のもとである。しかも、電荷と並進する系がみる電場はかれのいう電場とは極性が逆である。
相対論からみれば、真空中においても電磁場のローレンツ変換による電場がある。それがもとの系からみたときのローレンツ力の正体である。 導体内は、その系の電場の中に置かれた導体としてみる方が単純である。その系では導体内部には電場はなく等電位で、その外に電場がある。 元の系にもどってはじめて、かれのいう"電池" になる。私には、そういう説明が要するほど、かれの電磁気は独特にみえる。 通常の電磁気の論理を使ったほうが、ずっと見通しがよい。ただ、電磁気の基本的な疑問、静止場の運動量の問題をとりあげ、 その解決に取り組んでいることを、高く評価する。
ローランドの実験では、電荷の付着した円板を回転すると電流が存在し、それが定常的な rot Bを生み、定常的な磁場を生んだ。 それと同じく、磁石を磁気双極子の集まりとしてみると、円筒磁石の表面の円板には磁荷が付着していて、円板が回転して磁流を生み、 それが定常的な rot E を生む。この電場は上面と下面では逆方向であり、軸対称電場をもたらすのだろう。この説明は、 存在しない磁荷を持ち出した点で感心しないが、磁荷を持ち出さなくても、相対運動だけで考えても、電場はあるのではないだろうか。
数 V にも達する電位を、いまどき測定できないはずはない。そんなものは中学校の教育用機材でも十分だと考える人は、電場を理解していない。 この電場や電位は、空中電場や、ファインマンの地球磁場との相対速度を利用した速度計と同じで、ループ状に発生しないために測定が難しい。 ループ状電場なら数[μV]でも測定できるが、空中電場は通常、100 [V/m] もある中での話である。
この話には、磁石の回転で電場ができるなら、Maxwell 方程式に修正が必要かもしれない、という重要性がある。 つまり、そばで磁石が回転しようと、div E は変わらないというのが、Maxwell 方程式であり、電荷なしに div E が出て来ては困るのである。
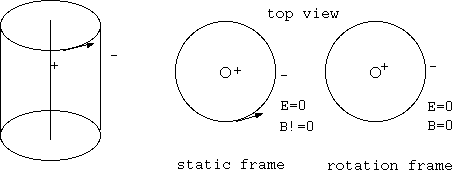
軸対称な系を考え、中心線に電荷があり、周囲にそれと等量の反対電荷が円筒状に分布し回転(角速度W)している。 (無限長のソレノイドは外部に磁場を出さないから、筒長は有限とし、短くして、さらには環でもよい。) 周囲の外側には、磁場がある。そのため速度をもった電荷にはローレンツ力が働く。 ところが回転と同じ角速度Wの回転系では、 全ての電荷が静止しているため電場も磁場もなく、どんな電荷にも力は働かない。これは矛盾である。それゆえ、電磁場には回転相対はない。
円筒が静止し静止系で磁場も電場もない場合、筒外部にはガウスの定理から電場がない。移動する電荷がないから、外部に磁場もない。 回転系では円筒表面の電荷の移動のため、磁場が発生するのではないか思うと、そうはいかずに、回転系でも電場も磁場も発生してはならない。 なぜなら、磁場や電場があっては、静止系からみても、電荷はその運動状態によって何らかの力を受けるはずであるから。
回転系には遠心力とコリオリの力という、みかけの力があり、回転系の電場と磁場は単独で0でなくみかけの力との合計で0ではないか。 力を受ける実体が質量と電荷との違いから合致することはあり得ない。回転系の力学的なみかけの力を除外しての話である。
回転系の電磁場法則が慣性系の法則と違うのだろうか? そうではなく、円筒との相対回転(角速度の差)の法則でないか? 磁場はそれに比例する。同期回転系で電場磁場共に0は基準ぎめで、静止系でなく同期回転系が、特別な系ではないか。
しかし、このような論証よりは、むしろ数式による摘出が必要である。 そうでないと、どのような違いがあるかを全く明確にできないからである。
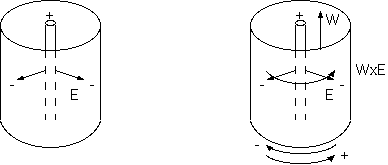
一様な磁場 B の中を飛ぶ電荷が円軌道を描くことは、回転系の電磁場を示す。初速vを与えられた電荷の系では、その速度と磁場の強さに比例した ローレンツ力 v x B を側面に受け、それを向心力にして円運動する。(v x B はvとBの両方に垂直で、vにB方向成分があればB方向に運動を残す螺旋運動をする。) この回転系では電荷は自ら静止していて、遠心力に対抗する力は電場 v x B であり、円内部に反対電荷の分布する電荷密度をみる。 又はそれを代表する電荷が円の中心にあるような運動する。 ローレンツ力 F= q(E + v x B) に対応した電磁気のローレンツ変換で電場 E'= γ(E + v x B) を見る。 (元の静止系に電場Eがあれば磁場も B'= γ(B - v x E)に変化する。)
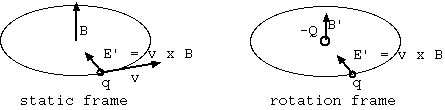
E'= γ( E + v x B )
B'= γ( B - v x E )
但し、γ=√(1-v^2) は、定数のように書くが、速度vの関数であるだけでなく方向に依存し、E' の式ではEの速度vとの並行成分 E//には働かず、垂直成分E⊥ にだけ働く。
E'//= E//, E'⊥= γ(E + v x B)⊥
B'//= B//, B'⊥= γ(B - v x E)⊥
E'= E'// + E'⊥
E'= E// + γ(E + v x B)⊥
E'= E// + γ(E⊥ + v x B)
E'= (1 - γ)E// + γ(E + v x B)
ローレンツ変換ではvは定数だったが、ここでvを空間に分布するベクトルとして扱う。分布する速度ベクトル v=定数は慣性系、 v= W x R は回転系である。後者の条件で、Maxwell 方程式をみる。とくに、div E' と rot E' とを明確にしたい。予期する式は、
div E'= ρ' + 2 W・B
rot E'= -dB'/dt + W×B
div B'= 0 + 2 W・E
rot B'= i + dE'/dt + W×E
である。とくに、div E' の式があれば、BとWが平行 (B//W) の単極誘導の回転系の電場の発散が慣性系と違って、 磁場のある空間に回転系がみかけの電荷密度をみることができる。
電流密度と電荷密度のローレンツ変換、速度 v の系の電荷密度ρ'、電流密度 i' として、 ρ'= γ(ρ- v・i), i'= γ(i- vρ) から、
div E'⊥= ρ' + 2 γ W・B - γv・dE/dt
EはE⊥なのでvとの内積は0として、回転系Wの電場の発散には電荷密度ρ'に 2 γ W・B が加わると考えられる。
div E'= div E// + div E⊥= ρ' + 2 γ W・B
電場の発散の 2γW・Bの項は、単極誘導の回転系のみる電場を説明する。これがあれば、慣性系には電場がなくてよい。
一様な磁場中に様々な初速をもって運動する電荷は、磁場に垂直な平面内で初速に応じた半径の円運動をする。電荷が受けるローレンツ力 qv×B が円運動の向心力 mv^2/r になり、qv×B=mv^2/r から rがvに比例 v/r= qB/m 一定。角速度は w= qB/m で一定である。または、 qv×B= mrw^2 の半径rが初速vに比例し、電荷は速度vによらずw一定の回転系 w 上にある。
ローレンツ力の存在、磁場の中を速度をもって進む電荷のみる電場の存在は、円軌道の内部に荷電密度と同じ働きをする電場の発散を回転系 が持つことが支えている。
もうひとつの B'= γ( B - v×E )も、v×E の符号が変り BとEとが入れ替わるだけで、
div B'= div B'// + div B'⊥
div B'⊥= γ(div B - div(v×E))
= 0 - γ(E・rot v - v・rot E)
= - 2 γ W・E + γv・rot E
= - 2 γ W・E - γv・dB/dt
第2項のBはB⊥なのでvとの内積は0として、回転系は慣性系にない磁場の発散をもつ。
div B' = - 2γW・E
rot E'= γ(rot E + rot(v x B))
= γ( -dB/dt + (B・∇)v - (v・∇)B + v div B -B div v )
慣性系の Maxwell 方程式から div B = 0、回転系の速度 v は、div v = 0 から、最後の2項とも0である。
rot E'= γ( -dB/dt + (B・∇)v - (v・∇)B )
右辺第1項と第3項は合わせて、速度 v 系の -dB/dt の全微分になる。第2項、速度 v のB方向微分は、
(B・∇)v = (B・∇)(W×R) = W×(B・∇)R + ((B・∇)W)×R
位置ベクトルRのB方向微分は (B・∇)R = B、 Wは一様だから第2項は0で、(B・∇)v = W×B.
rot E'= γ(-dB/dt - (v・∇)B + W×B)
同様に B'= γ(B - v x E) についても、両辺の rot をとり、
rot B' = γ( rot B - rot(v x E))
= γ( i + dE/dt - (E・∇)v + (v・∇)E - v div E + E div v)
= γ( i + dE/dt - (E・∇)v + (v・∇)E - v ρ)
= i'+ γ(dE/dt - (E・∇)v + (v・∇)E)
= i'+ γ(dE/dt + (v・∇)E - W×E)
dE/dt + (v・∇)E は、速度 v 系の -dE/dt の全微分である(*)。 これらの式はまだ、E' B' を使って表されてないため、回転系の電磁気でないが、ほぼ様子は分かる。 rot E' の式は、-dB/dtに W×B が加算され、内部に dB/dt なしに閉曲線に電場の一巡ができ、 rot B' の式は、i+dE/dtから W×E が減らされ、内部に i+dE/dt なしに閉曲線に磁場の一巡があることを示す。
(*)これは回転系の電場の微分 dE'/dt ではない。速度を持った系に電磁場をローレンツ変換するとき電磁場は大きく姿を変えること を我々は知る。電磁場の速度による変換は、3次元ベクトルを速度を持つ系からみるというものではない。静止した山々の風景が高速 に流れるということではない。動く電荷にとって磁場が電場になるように、電磁場が変化するのである。
電磁場のローレンツ変換は、動く系からみて速度に垂直な成分がγ倍になることは、少し奇妙にみえる。電場がポテンシャルの勾配なら、 電場は通常の山の傾斜のように速度と平行な成分E//がγ倍になるのではないか? ローレンツ短縮は、速度に平行な成分の短縮である。 時空間と同じ4元ベクトルの電磁ポテンシャルのローレンツ変換は、速度に垂直な成分は影響しない。これと電磁場のローレンツ変換は かなり違う。この理由は、電場がスカラーポテンシャルの勾配だけでなく、ベクトルポテンシャルの時間微分も加わるからと思う。
t' = γ(t - v・x), x'//= γ(x// - vt), x'⊥= x⊥
Φ'= γ(Φ - v・A), A'//= γ(A// - vΦ), A'⊥= A⊥
電磁場は、速度に平行な成分//は変化せず、速度に垂直な成分⊥だけが速度に外積された相方(電場には v×B、磁場には -v×E)が加わ ってγ倍される。ローレンツ力 F=q(E + v×B) 類似のローレンツ変換 E'⊥=γ(E⊥ + v×B) をみれば、それが同じ電磁ポテンシャル (Φ、A)から4元回転という微分演算によって作られた2階の反対称テンソル(16成分のうち、4対角成分は 0で、他の成分は対称成分と 符号反転で6種)の2つの3次元成分と考えることで、もとが4元ベクトルだから電場と磁場とが独立でないことが理解できる。
の第4項は、これを説明するかもしれない。γは相対論がらみでここでは無視する。電場Eは中心軸から外筒に向かい内部の空間を拡がる 方向で軸近くで強く遠くで弱い。ガウスの定理から電場の大きさは中心軸からの半径rに反比例する。-W×Eは、回転WとEの外積の回転系 の速度vと逆方向の電流の働きをする。外筒のマイナス電荷の逆回転方向の移動に対して、この電流項も同方向でともにWに比例するから、 両者は打ち消す可能性がある。どのように完全な打ち消しをするか不明だが、回転系でも筒内部に磁場(のrot)の不在を期待できる。 (Wは一様でEは半径に逆比例から、電流項も半径に逆比例である。ソレノイド内部の一様な磁場を打ち消すことは難しいかもしれない。)
少なくとも、回転相対が成立して回転系の rot B' に第4項がなく rot B'= i' + dE'/dt とするなら、筒表面のマイナス電荷の逆回転の 電荷移動が作るソレノイド電流は、筒内部に磁場を発生し、(ソレノイドが長くなければ外部にも磁場が存在して)矛盾するだろう。
筒内部の空間には静止系で電場があって、負電荷の粒子は、軸に向かう向心力を得るから、2種類の方向の円運動ができ、そのひとつの回転系 W系からみると、電場-1と遠心力1がつり合って電荷は静止している。静止しているから、このW系に磁場はあっても関係しない。 静止系に静止する無電荷粒子は W系からみると、-W の円運動をする。その向心力-1は、W系の遠心力とその-2倍のコリオリ力が与える。 逆方向に回転する荷電粒子は W系からみると、 -2W の円運動をする。W系の電磁場と遠心力とコリオリ力の和が、-2Wの円運動の向心力-4を与える。 W系の電場-1と遠心力1はつり合うから、その残りを与える磁場とコリオリ力があるが、コリオリ力は-4であるから、W系の磁場は0であるといえる。
(これは怪しい。なぜなら、電磁場のローレンツ変換 B'= γ(B - v x E) の -v x E は 0 でない。軸に平行で上向きの磁場を回転系は 筒内部にみてよい。その磁場は、筒のマイナス電荷の逆回転方向の移動(=回転速度方向のソレノイド電流)から発生するのではないか。)
dB'/dt = dB/dt + (v・∇)B - W×B
一般に慣性系のベクトルBの時間微分は、回転系のBの時間微分と W × B との加算である。
(dB_I/dt)_I = (dB_R/dt)_R + W×B
Bがガリレイ共変のとき、速度v系のベクトルBの時間微分は、Bの時間偏微分とBのv方向微分との和である。
dB/dt = ∂B/∂t + (v・∇)B
回転系に静止し、慣性系で速度vをもつとき、(v・∇)B は回転系で0だから、
(dB_I/dt)_I = (dB_R/dt)_R + (v・∇)B + W×B
以上、Bをガリレイ共変とする場合、回転系の電場の回転の式、 dB'/dt= -rot E' が導かれるとする。拙文の磁場の回転の式、 rot B' も同じく形式上、慣性系と同じ式になる。これでは回転系の電磁場が慣性系と同じようだが、発散については同じではない。
rot E'= -γdB'/dt
rot B'= i' + γdE'/dt
その他、http://arxiv.org/abs/1109.3624 "なぜ磁力はコリオリ力に類似するか"。 も回転系の電磁場を解説する。
地球には固体の内核と液体の外核があり、さらに外側に固体のマントルと地殻がある。固体の内核がその外側よりも高速な自転をもち、 その緯度の余弦の速度で液体である外核を回転させ、太陽や木星に見られるような、赤道と極の自転のズレが外核に生ずる。 (赤道と極の自転速度の違いは、内部の自転が赤道付近に現れること以外に説明可能だろうか。)
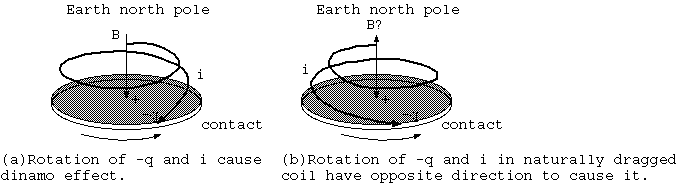
ところが、太陽のように赤道の回転が極の回転よりも高速な、一般的な導体の流体でできた球がダイナモになるのは、 コイルの向きと回転の向きが逆の場合であり、ブラシが赤道円盤に付き刺さる方向の場合であり、 自然な流体の流れからの引きつれによる構造、赤道円盤の動きにコイルが付き従う流れ構造ではダイナモにならないのである。
つまり、電磁気の教科書で地球磁場の原因とされているダイナモの説明は、自然な流体の構造とは逆の場合に動作するものであり、 間違っているかもしれない。そこで、導体のファラデー板だけで磁場を説明することを試みた。以下がその考察である。
地球は北極が S 極をもち、南極が N 極をもつ磁石となっている。 北極を上とすると上から下への地球内部の磁場 B がある。回転は左回りであるから、 赤道面のファラデー板では各点の荷電は中心からの距離 r に比例するローレンツ力を受ける。 移動できる荷電である電子は外向きに力を受ける。
ファラデー板から電流を取り出さないとき、電荷が静止するためには、 円盤中の任意の点で電場とローレンツ力は向きが反対で同じ大きさを持つ。 電場 E は電子を内側に引き寄せる、外向きの電場であり、その大きさは r に比例する。 このような電場をもたらす電荷分布は、一様なプラスの電荷分布である。 一部の自由電子が外にはり付き内部を一様なプラスの電荷分布にし、 マイナスは円板の端面に集まり、地球の赤道面に表れる。
地球の自転は 24 時間で一周である。地球の半径を 6.5 x 10^6 m とすると、 赤道上での接線速度は、472.7 m/sec である。地球磁場を 0.4 gauss= 0.4 x 10^-4 [T] とすると、E = v x B = 0.01891 v/m である。計算を簡単にするため、地球内部では、 磁場は一様とし、ローレンツ力に対抗する電場は半径に比例して中心から増大するとすると、 赤道の電位は、電場の積分であるから、 6.5 x 10^6 (m) * 0.01891 (v/m) /2 = 61450 (v) であり、 粗く地球の静電容量を C= 0.1 F とすると、 地球の表面に溜っている電荷は、 Q= CV= 6145 (Coulomn) である。これが赤道の接線速度 472.7 m/sec で動いていると、 その全体の電流は、QV= 2.9 x 10^6 A となる。 内側に同量のプラスの電荷が同じ方向に回っていることによる低下を無視すると、 この大きさは地球磁場を維持するのに十分な大きさであろうか。
電流 I [A] の流れる、半径 r [m] のコイルの中心の磁場 B は、 3.14 x 10^-7 x 2 x I / r [T] であるから、 I= 3 x 10^6, r= 6.5 x 10^6 から、(2 x I)/r = 1 程度である。 これから B = 3 x 10^-7 [T] = 3 x 10^-3 gauss である。 最初に示した 0.4 gauss と比較して、これはその 1/100 である。
必要な磁場の 1/100 にしかならないため、この考え方は、放棄するべきだろうか。 地球が空心の電磁石でなく、内部に鉄を含むなら透磁率が大きく、磁場を100倍位にすることはすぐにできるが、 地球のコアの鉄は熱と圧力で熔融して磁性体ではないだろうから、その場合、地殻とマントルの成分に期待するしかない。 それが地球磁場を説明するほどに透磁率が高いという期待は、少々無理がある。 しかし、ダイナモによる説明(図 12)は、正常な物質の流れ構造と電流の向きが交差するから、それよりも説得力があると言う訳でもない。
但し、ダイナモ効果には別形態が考えられ、内核自転が外核自転より大とし、外核内部での物質の引きによる流れと、 それに沿う逆向きの電流は、ダイナモ効果をもつ。この方が自然な物質の流れと電流の方向が交差しないから、 従来の赤道自転が極自転より大である条件下の球面上電流のダイナモ効果よりも有りそうである。
ダイナモは、流体の構造を電流のコイルとして磁場形成に利用し、内核の自転がその外側よりも高速という仮定をもつ。 赤道と極の自転の大小から説明しようとする従来のダイナモ(図12)は、表面の流れと電流で説明が定性的に失敗していて、 外核の内部流れと電流で説明する平面ダイナモ(図12.1) は、説明が定性的に成功している。 これらに対して、導体の電荷の内外偏りの回転で説明するファラデー板の磁場形成は、流体や電流という仮定なしに説明でき、可能性が残る。 内外核の自転差、流体と電流の磁場発生は、惑星内部の大きな摩擦熱と長期に渉る自転低減との整合が難しいのではないか。
よく、地球磁場が荷電粒子を巻き込んで、北極と南極の空にオーロラを形成する話は、 誰もが聞く話であるが、荷電粒子がみる地球の昼側と夜側への分離は、 あまり聞かない話である。これは少し考える値打ちがあるかも知れない。
磁場 B(r) と、電荷密度 ρ(r) が半径に依存するようにし、外部磁場 B_e は一様とし、
ファラデー板は十分に大きく系全体が軸対称、つまり軸からの距離 r だけに依存するとする。
速度が半径に比例する固体の場合を考える。半径 r の位置の荷電密度を ρ(r)とすると、
内部から円筒表面 r = R への移動した長さあたりの電荷量 Q は、 2 π で割ると、
Q = - ∫_0^R ρ(r) r dr
である。半径 r の位置の電荷密度 ρ(r)と、磁場の大きさ B(r)の関係は、次のようになる。
ρ(r) = - 2 w B(r)
∫_0^{r_0} ρ(r)r dr = -2 w r_0^2 B(r_0)
軸を含む平面内で、r_0 から R まで一順する経路を考えると、
軸から r_0 の位置の B(r_0) は、
その経路内の電流と外部磁場の和で求まり、
B(r_0) = w ∫_{r_0}^R ρ(r) r dr + w Q + B_e
= - w ∫_{0}^{r_0} ρ(r) r dr + B_e
この場合は、中心の最大磁場が、外部磁場に等しくなる。外周の Q を ρ(r)に含めれば、
B(r_0) = w ∫_{r_0}^R ρ(r) r dr + B_e
となり、 r_0 = R で、 B_e に等しくなる。これから、
ρ(r) の r についての微分方程式を得る。
ρ(r)'= -2 w^2 ρ(r) r
ρ(r)= -2 w B_e exp( w^2 (R^2 - r^2) )
B(r)= B_e exp( w^2 (R^2 - r^2) )
ただしこれは、 ∫_0^R ρ(r)r dr = 0 を満たしていないようだ。
E'// = E//、E'⊥= γ(E + vxB)⊥ = γ(E⊥+vxB) (B'も B'// = B//、B'⊥ = γ(B - vxB)⊥)
vxB= vx(B⊥)= (vxB)⊥ なので、
E' = E// + γ(E + vxB)⊥
E'= (1-γ)E// + γ(E + v x B)
力と加速度が系によらないニュートン力学と対照的に、速度vの粒子系(K')での力,加速度,質量は、元のK系の f, a, m とは違う f', a', m' とする。K'系の f'= m' a'と、K系の f=ma の両者が成立し、K系からみた質量mは、横方向に m⊥= γm'⊥で縦方向には m//=γ^3 m'//。そして、時間経過は、γである。静止質量 m0= m' とし、
横方向の質量がγ倍、横方向の力が1/γ倍に変換され、横方向の加速度は、1/γ^2 倍、横方向の速度は、1/γ 倍に、横方向変位 は1倍に変換される。このことを逆順に説明すると、まず、横方向の変位は1倍である。速度をもった座標系の横方向は独立である。 x方向の速度vをもつ座標系のローレンツ変換は、x'= γ(x - vt), t'= γ(t - vx), y'= y, z'= z である。y, z は変化しない。
そして時間経過がγ倍で、横方向の速度は、1/γ倍である。動きの速度の大きさが 1/γ と時間経過 γ は、垂直変位の同等 要請と同じ要請である。そしてさらに、時間経過がγ倍のとき、横方向速度1/γを満たす横方向加速度は、1/γ^2 倍である。 例えば、γ=2 のとき、粒子系で1秒で1m移動する速度 1m/sec は、元の系からみて 2秒で1m移動する速度 0.5m/sec に変換され、 粒子系で1秒で速度1m/secになる加速度1m/sec^2 は、元の系からみて 2秒で 0.5m/sec になる加速度 0.25m/sec^2 に変換される。
そして、横質量がγm'で、横加速度が1/γ^2で、横方向の力は1/γ倍に変換される。それゆえ、粒子系のみる横方向の力は、元の系のγ倍である。 同様に、縦方向の力の変換を導くと、縦質量γ^3 m0 と、時間経過の1/γを使う。縦方向加速度は、1/γ^3 に、縦質量がγ^3 に変換されるため、力の平行成分は恒等変換である。電場の平行成分は、ローレンツ変換によって変化しない。
粒子のみる力 F'= F// + γF⊥
ローレンツ力 F= F// + F⊥
粒子系(K'系)の電荷に力を与える電場となる元の系の電磁場(ローレンツ変換)は、K系のローレンツ力に整合する。(2013/05/01)
まとめ、
電荷qに力F= qEを与えるとき単位電荷が受ける力を電場 E=F/q という。電気力線は、+電荷から放射状に発し、一定の電荷から一定の本数で、 電荷の近傍で強く遠方で弱くなるが(E= q/R^2)どこまでも続き、-電荷に終わる。また、磁力線は、一定の極から一定の本数をもち、 磁石の外側ではN極から始まりS極に終わるが、磁石中も一巡し、終端となる"磁荷"はない。力線は張力をもち、横方向には互いに反発する。 線に沿う方向に同じ効果をもつ。力線は場の方向を示し、力線の面密度が場の強さを示す。力線は電磁気の性質を体現する。+電荷には必ず 同量の-電荷が対応し、力線の張力は電荷間のクーロン力であり、一定の閉曲面から出る力線の本数が内部の電荷量に対応するガウスの法則である。 力線はどこまでも伸び、場が距離の2乗に反比例して遠方にまで伸び、力線は空間で勝手に生成や消滅をしない。また磁力線と電荷は関係し、 電荷は速度vと磁場Bに比例して速度vの方向を変えるローレンツ力 F= q(E + v x B) を受ける。これは相対論の電場E、磁場Bのなか速度vの系が 電場 E'= γ(E + v x B) をみるという電磁場のローレンツ変換に対応する。(但し、γ=1/√(1-v^2) 拡大は、vの垂直成分にだけ効く。)
力線は、場の概念に衝突する。力線は、電場、磁場の矢の方向を連ねた線であり、線と垂直な方向に動きそうだが、動く場という考え方は、 系に依存する場という概念と矛盾している。ファインマン物理には "力線を実体的に捉えすぎないように。その系ではその力線は、 存在しないかもしれない" と注意があった。電線が磁力線を切る(磁場と交差する)系では、電荷が電場をみる。一様な磁場と交差するとき、 マックスウェル方程式から、磁場が時間的に変化しない(-dB/dt= 0)から、電場はない、という説明は誤りで、"電場の回転(rot E)がない" であり、むしろ、磁場中に速度をもつ電荷は、電磁気のローレンツ変換によって、磁場を自らの速度に比例した電場とみるのである。 "磁力線を交差する、横切る" は電荷が受けるローレンツ力の v x B の表現として、ベクトルの矢印を意識する電磁場の概念よりも適切である。
磁石の並進には電磁場のローレンツ変換を認め、回転磁石にはそれを無視:
磁力線と電線の交差による起電力は、磁場中に速度をもつ電荷のみる電場で説明する。磁石は、静止系では磁場、並進運動系では電場の発生源であり、
静止系で一様な磁場を与える巨大磁石が速度をもって飛来するとき、磁場から電場へのローレンツ変換によって電場を与える。
しかし、円筒磁石を回転させる単極誘導では、磁力線と交差する電線の軸内外に向かう電場は、電荷なく発散なし(divE= 0)だから、内外に電場はないとし、
回転磁石の磁力線には根がない、とする説明は、静止系では正しいが、根を任意に切断し、磁力線との交差、電磁場のローレンツ変換を無視している。
それなら(1) 磁場中の速度vの電線が起電力 v x B をもつなら、静止電線に磁力線が速度-vで交差するとき電場が発生しないのか?
さらに、(2) 磁場B中の電流iが力 i x B を受けるなら、静止電流に磁力線が速度-vで交差するとき力は受けないのか?
場の発散(divE= ρ)の概念が(1)を否定し、電場や力を生じないとするが、円板の近辺の局所の相対性は説明を求め、反論する。 力は他の系からみても無視できない。何かを生じないといけない。同現象を別系から違う説明をするのも良くないがまだしも、 現象がないのは不合理である。
最近の強力なNd(ネオジウム)磁石での単極誘導の実験は、接点を通して軸内外に流れる電流が磁石を回転させる。磁石とその被覆導体が 回転を始めるときのトルクに対抗する、接点外部の静止電流に回転磁石からの動く磁力線交差によるトルクの発生(2)がなければ、 より基本的な角運動量保存則を否定することになるが、よいのか(*)。(2)を認めるなら、(1)も認めないといけない。
電場測定は、されていない:
回転磁石が側面に電場を発生していて、静止閉回路に電流が測定できないのは閉回路で包まれる面に電場回転(rotE)がないからとすると、
電場の発散=電荷(div E=ρ)を崩さないためには軸方向の電場が違うと仮定しなければならない。静電場は、ポテンシャルの勾配場であり、
閉回路に電流を生じない非回転場(rotE= 0)に非等方性は可能か? 静止電荷の作る場は等方的だが、動く電荷の作る電場は、側面に強く
等方的ではない。円環状の電荷が円環方向に回転するとき、軸方向に弱く側面(円環面)方向に強い非等方電場を定常的に生むかもしれない。
(1),(2)を認めるならこれが本当である。
回転系の電磁気が原因か:
回転系で磁石は、磁場だけでなく回転の側面への電場源となる。回転系上の静止電荷は、静止系からは半径に比例する速度(v= w x r)をもつ。
電荷は速度と磁場に比例した電場をみるから、直線電流に平行に進む電荷に並進する系が電線を帯電したとみるのと同じく、回転系では
円環コイルの帯電をみる。円環の一部が帯電し、反対側は逆に帯電する。回転系Wでは磁石のW・Bが電荷密度ρと同等に働き(divE= 2W・B)、
内外電場を与え、静止系で回転する磁石は、磁場との交差が回転系のみる電場をちょうど打ち消し内外電場がないとする回転系の電磁場の
定式化は、辻褄合わせか(**)。
(1)の電場は発生するのではないか。磁場の時間変化なしに電場が発生しても閉回路を一巡する電流はないから、電場が見落とされがちである。 静止導体内部は常に等電位で、導体の外部に電場があれば、内部電場を打ち消すように導体の端面に電荷が集まり、導体中の電子は、変位して (電流を流し)内部を等電位にして停止するが、磁場源の速度v系の円板のようなブラシ速度のある閉回路によって、電流を取り出せる。 23章の div E'= div E// + div E⊥= ρ' + 2 γ W・Bにより、電場の発散にはW系の電荷密度に、元の系の磁場Bと回転Wの内積の2倍が加わる。 Wは、任意の基準系からの相対回転である。
(*) 単極誘導円板への内外電流による磁石回転には反動がないとする、角運動量保存を疑う 意見 がある。電場と磁場の交差ExBは場の運動量密度である。 電場は軸から外向きにあり、磁場が上から下で、場の運動量ExBは角運動量として単極誘導を取り巻いている。E,Bの何れかがOFFになると空間の角運動量は、 物体に移り回転を始める(ファインマン物理の3巻で紹介され、4巻で説明された)その回転は場からだが、単極誘導は、持続的回転であり、少し違う。 磁石の上の内外電流をもつ導体円板に回転トルクがあり、接点外部導体にトルクがないなら、そのトルクはどこから来たのか、場から来たのか。 持続回転の間、場の角運動量は変化しない。回転を持続するには接点の機械抵抗などに対抗する円板にトルクが要る。円板にトルクがあって、 接点外部導体にトルクがないのは不可解である。電流と磁場には(ixB)のトルクがある。外部導体とは、軸接点から電源を通し円板外接点までの電線である。
磁石の上で導体円板2枚を重ね円板外縁部で接し、軸に電池を置き上円板に外向き下円板は内向きに電流を流す。両円板は逆向きトルクをもつ。 今、上円板を手で抑えれば、下円板が回転する。それが単極誘導の状況である。逆に、下円板を抑えれば、上円板だけが逆方向に回転するだろう。 そして両方共抑えないなら、両円板は逆方向に半分の角速度で回転するだろう。回転円板には必ず、逆トルクを受ける導体がある。
これは電流と磁場の交差(ixB)からくるトルクであり、磁石は固定である。(磁石回転による動く磁力線の交差の話(2)ではない。) 外部導体は、磁場が弱いから関係しないというのは誤りで、接点を含む電流回路と磁力線とはともに閉じていて、2つの閉曲線は2度交わる。磁力線は一度、 電流と交差すれば、必ず再び電流と交差する。対称な断面に必ず2回のixBの交差があり、1つの交差にトルクがあり、他の交差にトルクがない理由がない。 電流の経度線が少しずれても、1回の回転内に過不足は収まり、外部交差が遠方で半径が長いと、力は小さいがトルクは等しい。 磁力線と電流の単位は任意だが、交差は一定のトルクである。面には磁束の一致、電流には磁力線との交差の一致がある。
すなわち単極誘導円板への内外電流による磁石回転を無反動とし角運動量保存を疑うだけの根拠ではない。接点外部の導体へのトルクの存在を認めれば 磁石回転による磁力線交差の電場の存在を認めることもできよう。それは単極誘導の磁石だけの回転が電場を発生する可能性の例示でもある。 円板の電位と測定系の両方に電場が発生して検出できないのである。
(**) 一様な磁場中に2枚の導体円板を重ね、それらが軸接点と外周接点を持つとき、各円板の回転系では電場を導体に吸収し、円板周囲の外接点で初めて 電位の違いを知る。各系は自らの内外電場を見ず導体上の等電位を主張し、他の回転系の角速度差に比例する電場をみる。静止系も含めて回転系は対等で、 自らを特別な静止系といえない。回転系の電磁気が静止系に0点をもつが力学の遠心力(***)のようなWの2次でなく、Wの1次の相対回転である。 慣性系の速度のような1次の関係が自系を静止系と示せないように、磁場中の回転系は自らを静止系と証明できない。
ファラデー円板の発電、又はローレンツ起電力自体が、磁石又は系の回転による電場発生である。一様な磁場中の電荷の円運動は、回転系の電磁場の証拠 と思ったが、その一様な磁場は、静止系と思う自系に磁石を置いて作られたもので、別の回転系に置いた磁石回転での電荷の運動を我々が知らないから、 電磁場の回転相対の可能性を排除する反証といえない。
こういう電磁気の単極誘導の解釈によって電磁気の基本の考え方の少しの違いがすぐに技術に影響するものではないが、物理の見方は、理解をはっきりとする ことを身上にし、それの僅かな違いはその後の科学技術に大きく影響してきた。歴史上正しい考え方が、アンペール、エルステッド、ファラデー、 マックスウェル、アインシュタインと受け継がれ、発展されてきたのである。
(***) 遠心力に類似する現象:
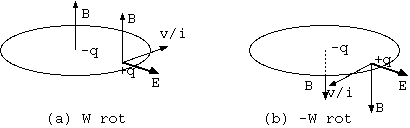
ファラデー円板の軸対称電場は、電荷の偏り(q)を生み、その円板の回転は電流(i)を生み、磁場(B)を生む。その現象は正帰還して磁場を増強する(図13(a) W rot)。 そのようなファラデー円板において、磁場一定の回転では回転対称を否定する現象はないが、その磁場を自ら生成する自己ファラデー円板の軸対称電場は、 逆回転(-W)において周辺の電荷が同じ電荷(q)なら、逆回転(-v)によって逆電流(-i)となり、磁場は逆(-B)である。ixB 又は vxB のBが電流iの関数であり iは2回掛けられて、(-i)x(-B)又は(-v)x(-B)は、それぞれ(ixB)又は(vxB)と等しい。電流の受ける力(ixB)は順回転と同符号、電荷のみる電場(E'= vxB) も同符号である (Fig(b)-W rot)。自己ファラデー円板現象は、逆回転でも順回転と同方向の電場をもち、電荷の偏りも等しい。これは遠心力のような 回転Wの二次の現象である。そもそも、電磁気と重力の類似("測地線の物理"参照)から、電磁気にも遠心力に類似する現象がなければならない。
逆回転では、図13の(a)と(b)は、同一現象をひっくり返して裏側からみるように、磁場が逆転し、軸対称電場は変わらない。軸から外側が正電荷(q)として話を 始めたが、それが負電荷(-q)とすると、電流iと磁場Bは順回転で(-i,-B)、逆回転で(i,B)、電流の受ける力(ixB)は図13(a)と同じく外側、電場(vxB)は片方が負で 内側を向き、負電荷(-q)は外側に力を受ける。
ファラデー円板の軸対称電場は半径に比例し、その半径方向の積分である電位が半径の2乗に比例する放物線を描くこともバケツの水面と同じである。 それは回転Wと磁場Bの内積が電荷密度に代わる役割をすることから始まり、自己ファラデー円板の電荷の受ける力は、回転方向や電荷の正負によらずに、 力は外に向かう遠心力と類似性をもち、ローレンツ力は回転系のコリオリ力と類似性をもつ。バケツの水面の遠心力はニュートンの絶対静止空間の根拠であり、 特殊相対論が慣性系の対等によって並進の絶対静止を排除したが、一般相対論の計量の満たす"重力方程式"の質量以外が計量を与えない"マッハの原理"が 回転における絶対静止を排除している。
我々は、遠心力の有り/無しによって、回転/静止系は判定できないことを知る。遠心力は近傍にある地球など周囲の質量との相対回転を原因とする "マッハの原理"がある。座標系は重力に支配され、乗物が天体の側を飛行(swing by)するとき座標系は重力によって自然に回転する。そのような重力と同様、 単極誘導でWの一次現象(角速度Wに比例する電場と円板外縁の電位の生成)は回転の相対性を示し、磁石だけの回転で円板に電流がないことは、 回転の絶対性を示すようだが、円板外接点の外側の電線を意識すべきで、磁石との相対回転が電場を発生しても(rotE= -dB/dt)から、一巡回路に電流を生じず、 電場の有無をいえない。慣性系の Maxwell方程式の、電荷なしに電場の発散なし(divE= ρ )は、慣性系でそうなるように回転系の磁石が軸対称電場をもつ 電磁気法則の構築は可能だが、電場0= 静止系 という主張にはMaxwell方程式以外の証拠はなく、絶対静止系の導入はマッハの原理以上の意味はない。 それゆえ、電場0= 磁場源系 を否定できない。自己ファラデー円板は、遠心力と同様に、絶対静止系仮定よりマッハの原理を優先すべきである。
重力と電磁気力とは測地線方程式という同じ仕組みからくるとした考えを支える、周囲の宇宙の質量が近傍の重力の仕組みを支えるマッハの原理は、 電磁気ではその双極性によってあまり有効でない、周囲の電荷は影響しない、どこにも静止系の存在を支える仕組みは難しい、回転系に遠心力のような 回転Wの2次の性質はない、という考えは、この電磁気における遠心力類似の現象によって否定されるのかもしれない。
確かに地球、木星、太陽、銀河系には磁場があるが、宇宙は電荷が移動できる真空の静電遮蔽のなかにあり、宇宙の電場は0と仮定でき、 周囲に電荷がないとする仮定は通用しそうで、重力において質量が遠方まで1/Rで影響するポテンシャルの存在とはかなり違う性質をもつ。
これに対する反論は、電磁気のベクトル解析は静止系を前提にしていて、Maxwell方程式は、慣性系にしか成立しないが、電磁気において 絶対静止系を特別扱いし優先する法則はない。ラプラス、ポアソン、ダランベールの方程式は、電荷のみによって決定される、 ポテンシャルが満たすべき電磁気法則である。それゆえ、マッハの原理は電磁気にも適用されるべきだろう。