運動方程式
運動方程式-物体の移動・回転-
運動方程式が的確にたてられていないと、選択したモータで負荷が動かないとか、応答性能が仕様に入らないとかのトラブルに巻き込まれます。このページでは、わかりやすく運動方程式のたてかたを解説することを目的とします。
さて、運動方程式とは、直線運動の場合には「力のつりあい」の方程式になります。また、回転運動の場合には、「トルクのつりあい」の方程式になります。基本的な式は以下のとおりです。
| F=M(d2x/dt2) | → 直線運動 : 力 [N] =質量 [Kg] x加速度 [m/s2] | 式A-1 |
| T=J(d2θ/dt2) | → 回転運動 : トルク [N m] =イナーシャ [Kg m2] x角加速度 [rad/s2] | 式A-2 |
ここで、物理学・数学を忘れてしまった方のために、基本的なことを追記します。
上の式の加速度は、「単位時間あたりの速度の変化量」ですから、速度 (dx/dt) [m/s] をさらに微分したものとなり、(d2x/dt2) [m/s2] となります。角加速度は、加速度における「距離x」[m] を「角度θ」[rad] に変えただけです。
また、トルクは単位の示すとおり、力x距離 [N m] です。たとえば、半径 0.05 [m] の糸巻きの糸を 10 [N] の力で引っ張ると、糸巻きには、0.05x10=0.5 [N m] のトルクが発生します。また、イナーシャJについては、別ページに詳しく解説しましたのでご参考ください。
ところが、私たちが設計する機構系には、ほとんどの場合「ダンパー」や「ばね」が存在します。「ダンパー」により生じる力は、速度に比例し、F = D (dx/dt) となります(ダンピング係数D)。 また、「ばね」により生じる力は距離(変位)に比例し、F = k x となります(ばね定数k)。実は式A-1では、物体に加速度が加わった時に生じる力のみを記述してあり、「ダンパー」や「ばね」により発生する力は記述してありません。式A-3には、物体に加速度が加わり生じる力+ダンパーの力+ばねによる力 を記述します。
| F=M(d2x/dt2) + D (dx/dt) + k x | → 直線運動 | 式A-3 |
ここで、ダンピング係数Dの単位は [N/(m/s)]、ばね定数kの単位は [N/m] です。
回転運動に関しても全く同様で、回転方向のダンピング係数をDr [N m/(rad/s)]、ねじりばね定数kr [N m/rad] とすると、式A-4のようになります。
| T=J(d2θ/dt2) + Dr (dθ/dt) + kr θ | → 回転運動 | 式A-4 |
運動方程式-モータ-
物体の制御をモータで行うには、モータの運動方程式も必要です。モータの場合は、電圧についての等式と、トルクについての等式の2つの方程式より構成されます。式A-5-1、式A-5-2にリニアモータ(まず、直線運動について説明するためリニアモータの例を示します)の運動方程式を示します。
| V=L(dI/dt) + R I + Ke (dx/dt) | → リニアモータ | 式A-5-1 |
式A-5にて、R は直流抵抗 [Ω]、Lはインダクタンス [H]、Keは誘起電圧定数 [V/(m/s)]、Kfは推力定数 [N/A]です。ただし、モータの製品カタログでは、各社呼び方が異なっていることが多いので単位を確認してから、値を使用してください。もちろん単位も各社ばらばらで、[rpm] や [Kgf] 等入り交じっていますので、すべてSI単位に直してから計算しましょう。
式A-5の意味を簡単に解説します。式A-5-1では、入力電圧Vが、L(dI/dt) と R IとKe (dθ/dt)に消費されます。これらは、インダクタンスx電流の単位時間当たりの変化量と、抵抗x電流と、誘起電圧定数x角速度 です。また、式A-5-2は、発生推力=推力定数x電流 ということです。
同様に、通常のDCモータ等の回転モータについては、式A-5において x [m]→θ[rad], Kf[N/A]→Kt[N m/A]、Ke[V/(m/s)]→Ke[V/(rad/s)]、 F[N]→T[N m]のように書き換えると式A-6のようになります。
| V=L(dI/dt) + R I + Ke (dθ/dt) | → 回転モータ | 式A-6-1 |
運動方程式の実例-リニアモータ編-
リニアモータ駆動で制御されるエアーステージの例を参照して、運動方程式をたててみます。まずは、一軸のみのステージに関して紹介したあと、実用的なXYの2軸ステージについて解説します。
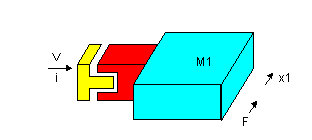
一軸エアーステージにおいて、エアーで浮いているステージの可動部質量を M1 [Kg] とします(可動部質量には、ステージの質量に加えてリニアモータの可動子の質量も含まれます)。可動部の移動距離を x1 [m] 、可動部に働く力を F [N] とします。またリニアモータへの入力電圧を V [V] とした時の簡単なモデルは下図のようになります。
モータに関わる電気的な運動方程式は、式A-5と全く同じとして良く、モータからステージへ加えられる力は F [N] ですので、この力 F が可動部 M1 の加速度としてすべて費やされます。発生する加速度は d2x1 / dt2です。これをまとめると以下のようになります。
|
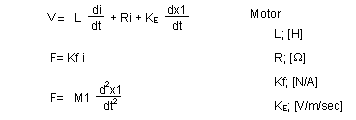
| 式A-7-1 式A-7-2 式A-7-3 |
さて、現実のステージ等のシステムはもっと複雑で、これに伴い運動方程式も複雑になります。次は、2軸のXYエアーステージにした場合の方程式を解説してみます。
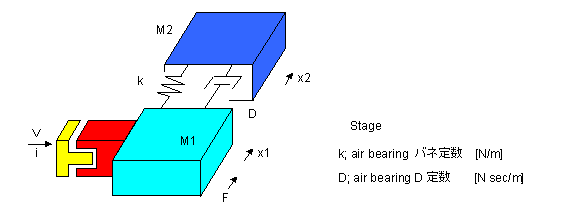
下図は、図A-aの可動部 M1 に、ばね k および ダンパー D を介して可動部 M2 を連結させたモデルです。M1 がXステージだとすると、M2はその上に搭載されたYステージということになります。XステージとYステージの間には、エアーパッドによる圧力空気層が存在しますので、このエアーパッドの(X方向の)剛性(ばね定数)が k ということになります。また、ここにはダンピングも生じますので、このダンピング係数を D としました。
このモデルでは M1 の移動距離 x1 に対して、M2 の移動距離は異なってきますので、あらたにこれを x2 とします。
この運動方程式を作成すると、式A-8に示す4つの式になります。モータに関する式は同様ですのでそのまま利用します。式A-8-3 は可動部 M1 に関する方程式で、モータから入力された力 F が右辺の、① M1 が加速度 d2x1 / dt2 を発生した時の力と、②速度 d(x1-x2) / dt によりダンパーで発生する反力と、③エアーパッドのばね k を (x1-x2) 縮めた反力 に変換されたことを表わしています。k や D には、M1 と M2 の移動距離の差が関連してくることに注意してください。
式A-8-4 は可動部 M2 に関する方程式で、①速度 d(x1-x2) / dt によりダンパーで発生する力と、②エアーパッドのばね k を (x1-x2) 縮めた力が、 M2 を加速度 d2x2 / dt2 で移動させた、ことを表わしています。
|
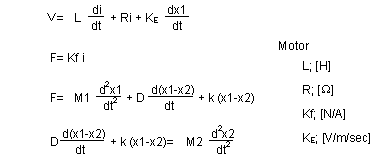
| 式A-8-1 式A-8-2 式A-8-3 式A-8-4 |
このように各等式について、入力と出力を整理して考えることにより、簡単に運動方程式を作成することができます。
Copyright 2000 Shinobu Tokushima. All Rights Researved