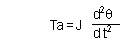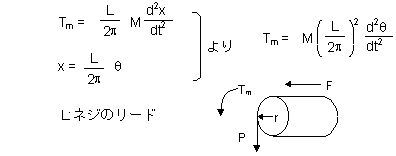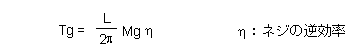トルクの計算
トルクの数式
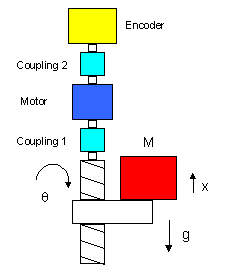
ここでは例題として、ネジを使って質量Mの負荷を上下に駆動させる機構を設計してみます。ネジには、モーターおよびエンコーダーが、それぞれカップリングを介して一直線上に連結されています。図B−aに簡単なモデルを描いてみます。図では表わしませんが、もちろん負荷Mはガイドレールに連結されていて上下方向に直線移動する機構です。また、ネジの回転量をθ、この時の負荷の移動量を x 、また、重力加速度をgとします。
さて、この図の場合のモーター軸にかかるトルクをすべて列記すると、
回転軸に直結されたイナーシャを回転させるためのトルク + 負荷Mを加速させるトルク + 負荷Mにかかる重力を支えるトルク となり下の式B−1となる。
ここで、Ta は 回転軸に直結されたイナーシャ x 最大角加速度 となるので、
また、軸上に直結されているイナーシャ J は、
モータ+エンコーダ+カップリングx2 +ネジ の各イナーシャで下の式B−3となる。
J = Jm + Je + Jc x2 + Js | 式B−3 |
つぎに、負荷Mを加速させるトルク Tm について解説します。ネジのリードをL、半径をr、ネジの接線方向に働く力をPとする時、トルク Tm は Tm = Pr です。また、ネジのスラスト方向の力 F と Pの関係は比で表わすと、2πr : L = F : P となります。スラスト方向の力 Fは、質量M x 最大加速度となり、また、xとθの関係は、下に示した通りになるので、これらを総合すると、トルク Tm は式B−4のようになります。
これと同様に、重力加速度による力 F=Mg をトルクに変換すると、トルク Tg は式B−4のようになります。ただし、このなかでは、ネジの逆効率を考慮して記入してあります。
トルクの実計算
これで、すべてのトルク式は書き出しましたので、現実の数値を代入して、モータの選択を行ってみます。まず、以下のようにモーター、エンコーダ、カップリング、ネジを選び、そのイナーシャをSI単位に換算してみます。また、負荷の質量Mは、1.6 [Kg] として計算します。イナーシャについての詳細は、別の章で詳しく解説してありますので、参考にして下さい。
| DCモータ | ミニモータ社/2842S012C | Jm = 1.18 x 10-6 [Kg m2] |
| エンコーダ | コパル/RE38-1000-211-1 | Je = 1.25 x 10-6 [Kg m2] |
| カップリング | 特殊精工/U2AC | Jc = 1.5 x 10-6 [Kg m2] |
| ネジ | Φ10mm、全長100mm リード0.5mm | Js = 1.25 x 10-6 [Kg m2] |
式B−3にこれらのイナーシャを代入して計算すると、J=6.23 x 10−6 [Kg m2] となります。
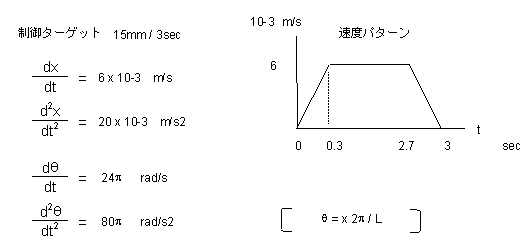
Ta, Tm を求めるには、最大加速度、最大角加速度を決める必要があります。目標として15mmのストロークを3秒で加減速駆動する場合について考えます。最高速度を 6 x 10-3 [m/s] とした時は、台形制御では、最高加速度は、20 x 10-3 [m/s2] で15mm移動できます。速度、加速度をそれぞれ角速度、角加速度に換算すると以下のようになります。(ただし、実際の制御では、加減速を台形制御で行うより、S字制御で行うことの方が多くなっています。ここでは、モータの選択のために簡易的に台形制御を例にとって説明しています。)
これで全て必要な数値が求められたので、トルクを計算します。ただし、ネジの逆効率は0.5としてみました。ボールネジの場合は、0.9あるいは1.0を入れて安全をみたほうがよいでしょう。
| Ta= | 6.23 x 10-6 x 80π | = 1.57 x 10-3 [N m] |
| Tm= | 1.6 x ( 0.5x10-3/2π)2 x 80π | = 2.55 x 10-6 [N m] |
| Tg= | 0.5 x (0.5x10-3/2π) x 1.6 x 9.8 x 0.5 | = 6.24 x 10-4 [N m] |
T = 2.28 x 10-3 [N m]
必要最大トルクTがこれで求められました。このモータの性能は、最大トルクが 0.05 [N m] であり、トルクの余裕は十分です。また、このモータの最大角速度もカタログ上では、167π [rad/s] であり問題ありません。
トルクや速度が不足していたり、モーターのパワーが多すぎる場合は、モーターの型番を変更して、計算し直して最適化をしていって下さい。
Copyright 2000 Shinobu Tokushima. All Rights Researved