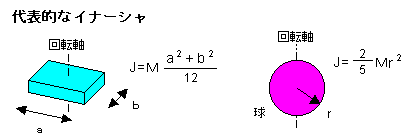イナーシャの計算

モータで何かを制御するユニットを設計するにあたって、モーターを選択しなくてはなりませんが、このためには、なにより最初に，制御される対象のイナーシャを計算しておく必要があります

ここでは、基本的なイナーシャの計算の方法を解説するとともに、少し複雑な回転体のイナーシャの計算、および代表的な回転体のイナーシャの式もご紹介します。

図にように、質量Mの質点が回転中心からRだけ離れているときに、この質点のイナーシャは、MR²となります。このとき、イナーシャの単位(SI単位系)は、[ Kg・m² ] です。このことを念頭において下図にある円板のイナーシャを計算してみます。

まず、円板の直径をD、厚さをt、比重をη、XYZ座標も図のように定義します。青の四角で表示された微少な面積の一辺の長さをdXととった時、もう一辺はXdθとなります。つまり、この質点のイナーシャdJはこうなります。

dJ＝Xdθ * dx * ｔ* η * X² → 面積ｘ厚さｘ比重ｘ距離²

この質点のイナーシャｄＪをすべて集めてくれば、円板全体のイナーシャになる訳ですから、ｄＪを積分してあげれば良いわけです。ここでは、xの範囲が： 0 < x < D /2、θの範囲は： 0 < θ < 2π ですので、dJをxおよびθで積分します。

この積分の結果を整理すると、図に示した式になります。また、この円板の質量Ｍを式にすると

M = D²tηπ/4

ですので、これらを整理すると、最終的に円板のイナーシャは、Ｊ＝ＭＤ²／８となります。

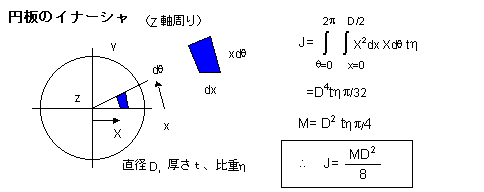
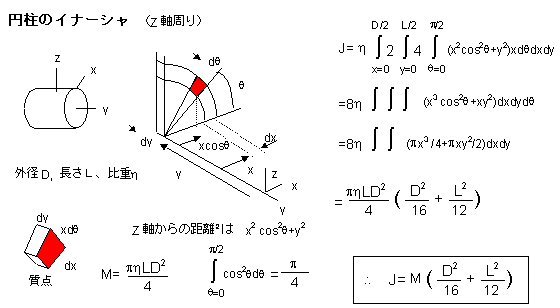
下図には、代表的な形状のイナーシャを紹介します。時間があれば、微少な部分のイナーシャを積分して確認してみてください。矩形の場合の厚さは一様なものとして計算されています。こちらの場合は、回転軸の取り方に注意してください。また、球体では、半径rの関数で示してあります。

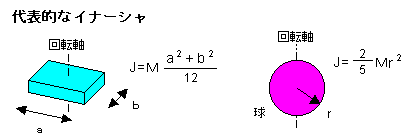
それでは、最後にむずかしい例題で締めくくります。下の図のように、円柱を横にして、上下方向に回転軸をとった場合です。ここでは、具体的な数値も求めてみます。

まず、ＸＹＺ座標、およびθの方向を下図のように定義します。円柱の直径はD、長さはLです。円柱の微少な一部を赤で示されたように取り出したとき、この質点の各辺の長さは、dx、dy、Xdθとなります。比重をηとしたときに、この質点の質量は、

dM ＝ dx * dy * Xdx * η

次はこの質点のＺ軸からの距離Ｒをもとめます。質点のＸ座標は X cosθ、Ｙ座標は Yとしていますので、単純な三角関数で計算します。（最終的には、R²を求めますので、ここでもR²であらわしておきます。）

R² = X²cos²θ+Y²

あとは、この結果をもとに、ｄＭ・Ｒ²を必要な範囲だけ積分してあげれば完成です。θの積分範囲は、0<θ<π/2 として結果を４倍にします。またＹの積分範囲は、0

今まで説明してきたように、イナーシャは質量Mの関数になりますので、ここでも円柱の質量を求めておきましょう。

M = πηLD²/4

これらの式から、この円柱の場合のイナーシャは、下図の□内のように表わされるとおり、J=M(D²/16 + L²/12) となります。（参考として、cos²θ の定積分の結果も、図中にしめしておきました。）

この円柱のイナーシャの具体的計算例を示します。

直径Φ25mm、長さ30mmのアルミの円柱を上図と同様に回転軸を定義してイナーシャを求めます。単位はすべてＳＩ単位系で計算しますので、代入値としては、D=25 x 10^-3 [m]、L=30x10^-3 [m]、また、アルミの比重ηは約2.7（比重は単位を合わせるため、2.7x10³を代入します。）として、M=(D/2)²Lπη に代入すると、M=3.98x10^-2 [Kg]となります。

このD，L，Mを上図の式 J=M(D²/16 + L²/12) に代入していくと、J=4.54x10^-6[Kg m^２] となります。

このイナーシャは、モータの選択や、応答性能等に基本的に関わってきますので、間違えのないように計算しましょう。

HomeTop