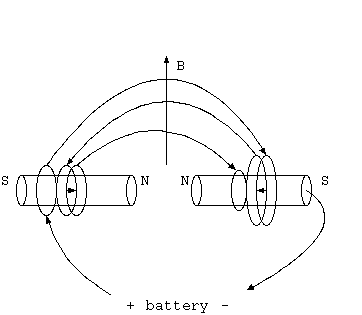
図1. 単極モータのコイル化
目次
1. 通常モータと比較
2. 単極モータの要素
....コイル化
3.単極モータの例
4.転がり往復運動はベアリングモーター
DCモータで回転子が電磁石のとき、回転子に回転位置によって電流を切り替えるブラシとそれに接触する近接した2つ(極数)の接点(整流子)をもつ。 液体金属ブラシは近接接点を短絡するが、2接点が軸両端のように離れた位置なら液体金属ブラシは使用可能で、接点抵抗が低く機械抵抗も少ない利点があるが、 銅等を溶解しアマルガムにする欠点があり、水銀は密閉しないと蒸発し、海に排出すれば極めて有害な有機水銀になって水俣病の原因となるから工業的製品に使えない。
2極モータではブラシ接点は、回転子が180度回転するとその電流を反転して以前と同じ磁極配置になり、磁極同士が吸引/反発を続ける。3,4極モータ等もある。 3極モータは回転子のひとつの電磁石(ステータ)が120度回転ごとに元の磁極配置になり、他の電磁石はそれと協調する。回転子/界磁の多極化は、回転速度低下 の代りにトルクを大きくする。また通常モータは、電気エネルギーと機械的エネルギーの間の双方向の変換器であり、機械的な回転を与えると、 その逆の電気を発生する発電機になる。それらは長い間に改良され多くの変種をもつ。
それに対して、単極モータは、磁場と回転軸が平行で、磁場の時間変化がない、同軸磁極に遠心又は求心の電流による。それは、磁場内の電流の作るローレンツ力 F=ixB (xは外積。ベクトルiをベクトルBに回転させて右ネジの進む方向のベクトルとなる)を原理的に示すだけに使われ、ファラデー板から始まる発動機/発電機の 実用化過程の最初の一歩である。電流をコイル化せず、磁場内の数cmの長さの電流に及ぼす力を1回しか利用しないため、極端な低インピーダンス(低電圧、大電流) で実用的でないが、磁極同士の吸引/反発を利用せず、接点の転流がないことは高速回転向きである。
以前、電磁気(15.単極誘導)又は 不可能な機械 を書いたとき、ネオジウム鉄磁石は高価だった。 その単極誘導は、外周ブラシの一点からくる電流によって、ファラデー板である銅円板を磁力で挟む2枚のドーナツ型フェライト磁石を一体化して回転させるものだった。 磁石を固定するファラデー板は、磁石が1枚なら容易だが、2枚使うには間に円板を挟む隙間を確保するために、磁石を強固に固定する必要があって難しい。 円板と共に回転させる磁石は重く、最初10A流し5Aでも10Hz程度の回転を確認した。当時は、円板だけでなく磁石も回転することが意外なデモとしてあった。
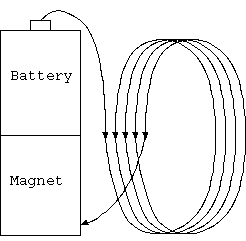
最近、磁石とモータの教育素材としてデモされる単極モータ(例、単極モーターの検証)は、 それに比べて驚くほど単純で、Niメッキされた小さな円盤型ネオジウム鉄磁石と電池を使う。電池の頂上(+極)から、電池底に磁力で結合した磁石周囲(-極)に接触させた 電線、(1本でも可能だが)2本のバランスした空中配線の下行電流を回転させる、誰でもすぐに手持ち素材で試せる容易で、効果が明確な優れたデモである。 コアレス(鉄心なしコイル)であることは、加速度が大きく出る点、磁石に吸引されない点、で有利であったのだろう。 しかし、単極モータの面白さは、あまり明示されないが、その理解しにくさである。 どうにかして、この無駄だらけの(電線が磁場の空間に占める割合が低い)モータが実用化できることを期待させるが、容易に解決しない。
2) 磁束の外側に外周点ブラシが必要で速度が大きい:
通常モータの回転子のブラシは、磁場と関係しないので任意に細くできるが、単極モータは両ブラシ間に磁束を通過させるため、あまり細くできない。
内周接点は回転だけで移動しないが、磁束筒の外周点のブラシ速度は、半径rと角速度 w=2πf の積wrで、これが機械的な抵抗になる。
3) 単極誘導が必要とするのは転流のブラシでなく、2つともに連続ブラシである。接点に液体金属が使用できる。
4) 外周ブラシの位置の首を細める:
全磁束を通す磁束路に細首の部分を設け、そこに外周接点を置き、外周接点速度 wr を小さくする。磁石の外部面がNiメッキされた小さな円筒磁石を細首とし
上下に半径の大きな太い円筒磁石を積層して、首に殆どの磁束を通過させる。首で磁束φ (φ= π r^2 B) 一定のとき、磁束密度は磁束/面積である。
首を細め、磁束密度を高めればその(√の)分、首半径に比例する接点速度uが小さくなる。
内外を結ぶ経度線の回転時に球にみえる膨らんだ弧(アーク)の電流経路の首の部分のブラシ接点で接点速度を低下する。一巡する磁束は、首の部分で磁束密度が 最大であり、首に単独の永久磁石をおくと、円形磁石に円形銅板を使う原型と違わないが、上下に半径の大きな磁石を積層すれば磁束は違うだろう。
5) 規模(サイズ)について:
外周接点速度uは、半径rに比例する。
磁束密度が磁石種類(例:Nd-Fe)だけに依存し、外周磁束密度B一定、磁束はr^2に比例。接点の uxB は、r比例。 電磁力F= vxBは、vがwr比例、Bは、r比例, Fは、r^2比例。Fr はr^3比例、
磁束密度が磁石種類(例:Nd-Fe)でなく外周磁束密度Bがr比例するとき、磁束はr^3比例。Bはr, 接点の uxB は、r^2比例。 電磁力F= vxBは、vがwr比例、Bは r^2。 Fは、r^3比例。Frはr^4比例、
のどちらが正しいのか。縦方向の長さは同じとする。
7) ファラデーの電磁誘導によって発生する逆起電力の電圧は、外部電圧に対抗し E=vxB で磁束密度Bと電線の速度vに比例する。電池電圧から逆起電力を 引いた差を回路抵抗で割って電流になる。そのため逆起電力も角速度の上限を決めるだろう。電線の位置の磁束密度Bは、軸からの半径rに反比例し(1/r)、 速度vは半径に比例し、E= vxB による角速度の上限は半径によらず、電線を横に張っても、狭く細くしても違わない。横に張ると、空気抵抗は大きくなるが。
しかし、同程度の速度で回転させた時の発生電圧を測定すれば、それが非常に小さいことから、実際はこれが制限でないだろう。逆起電力が電圧と電流を減らす 比率は小さく、機械的抵抗の方が大きいだろう。接点の機械的抵抗や電気的抵抗を減らして回転速度が向上すると、逆起電力が主要な対抗電圧になるだろう。
電流が1回しか磁場の中を通せないのは原理的な制限なのだろうか。接点を持てば回避可能であろう。 電流をコイル化して+から-にいくn本の電線が受けるトルクはn倍するが、逆向きの-から+へ行く電線が受ける逆トルクがn-1本ある。 上下行の線を力学的に分離し、上から下への電流と、下から上への電流とは逆のトルクを受ける。 そのためコイルの上下行の1本毎に逆回転させる接点がいる。その奇妙な構造は、不可能に近い(図1)。

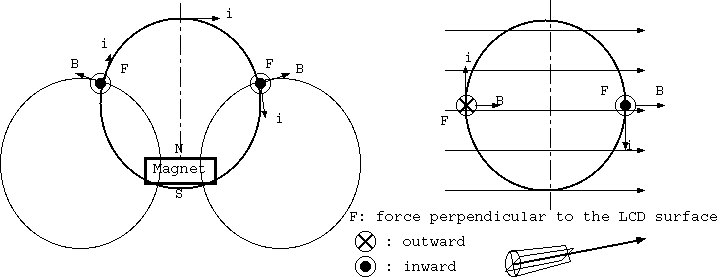
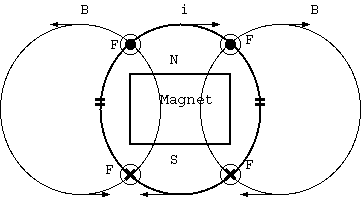
電流は一巡する。電池やコンデンサのなかに電池の-極から+極へ電流は流れていないが、電池は電気化学的で、-極から+極への電流があるのではない。 電流の代わりに同等な、電場の時間変化が力を受けるだろう。そばの電線を固定し、中心軸の磁石と電池を回転させるデモを見ることがあるが、それは、 導体磁石の回転によるのであって、中心を流れる電流が回転する訳ではないだろう。軸方向に磁化したトロイダル、ドーナツ型磁石に巻きつく電線の ドーナツの上側電線と下側の電線を水平に分離し、接点で接続すれば、上下の半ドーナツはドーナツの周方向に互いに逆回転するだろうか(図3)。
後者のとき、動電スピーカのコイルの軸方向ピストン運動のように、磁石と電池にゆるく巻いたコイルが上下振動するブザーになる、 Awesome Electromagnetic Tricks * Amazing Physics Experiments 。 コイルは磁石から放射状に広がる磁場に交差して電磁力で上に上がり、接点の電流が切れて、重力によって下に落ちて元に戻る。 接点はコイルの下端でも上端でも、両方でもよい。
コイル中を進むリニアモータ、 World's Simplest Electric Train も、後者の例である。 電池の前後に軸方向磁化磁石を前後逆方向に付けた、放射状の磁場があって、長いコイルの電池の前後の磁石の内側のコイル部分に電流が流れ、後方に力を与える。 その部分の外側のコイルには逆磁場があるが、電流がないので力は働かない。コイルへの力の反作用で磁石を付けた電池が進む。 別説明では部分コイルが電磁石となり、前磁石に反発、後磁石を吸引し、後に力を受け、リニアモータが前に進む(図6)。 2接点は共に外周である。
昔、阪大生物工学の研究科入試の問のなかに、カエルの足の先を水銀に漬け電池に接続する装置の説明要求があった。勿論、コイルと水銀だけの電気回路の ブザーの説明が必要であり、電流がコイルに流れ、同方向電流のコイルは収縮して、水銀接点が外れ電気を遮断する。コイルは自重で元の長さに戻り、 コイル端が水銀に入り電流が復活する。それら動作は一巡して、振動現象になる。
これを、コイルに電流が流れるとコイルが収縮し、接点は絶たれ電流が止まるから、前提とした前項に矛盾する、故にこれは起こり得ない(論理矛盾)と 理解してはならない。また振動は、当然に起きるのでなく、接点による電流遮断が離散的で比例的でないON/OFFを含む非線形系だから起きる。 上下位置から電流へが線形で、ある値との差に比例的なら、その値に収束する負帰還の制御系であり発振しない。論理素子での振動は、ヒステリシスと1次遅れ CRの負帰還で起きると習ったが、コンパレータと1次遅れの負帰還で起き(参照)、周期がCRで決まる。 線形系では丁度正帰還になる周波数があるとき発振が起きる。力学では加速度が力/質量に比例し(a=F/m)、位置の2階微分だから角周波数^2はバネ定数/質量に依る (x''= -k/m x, w^2= k/m)。振動の主要な要素は否定である。論理素子NOTを奇数段連ねたリング発振を連想してもよい。論理否定でなくバッファ(論理肯定)の正帰還は、 任意の値をとり、内部状態をもち、2状態のフリップフロップにさえなる。
論理が矛盾を導き、前項を制止するとき、現実には時間遅れを伴って、単なる順次動作(シーケンス)の振動になる。動作が適度の速度のときブザーになる。 そして、コイルよりもさらに電気に敏感な、カエルの足の筋肉の収縮をコイルの収縮に置き換えて振動現象を説明できる。生物機能の工学利用は無残だが、 ガルバー二のカエルの足による歴史的な電気の発見の実験によって、我々はボルタ電池を得た。我々が電池を知るより先に、カエルの足があった。
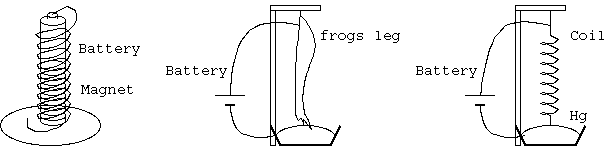
次に、 Roller Homopolar Motor は、電池の両端の磁石を中心から外れた銅線ブラシ又は鉄の針金で 短絡しただけの、転がる電池である。このなかの、銅線ブラシは何も問題がないが、針金での短絡は、全くブラシなしではないか? 針金は磁石に結合して、電池、 磁石と共に転がる。接点の両側にすべり移動やリニア運動が必要ではないことを示す。回転だけが作られる。電池と磁石と針金は、1つの物体として回転をしている。
These Hearts Are On Fire 後半のハート型の銅線では電池が少し逆回転するが、前半の磁石を両側から挟む銅線では、内部の(磁石と)電池が、外部の回転子と同方向に回転する。 これは、角運動量保存則に抵触しないだろうか。
ブラシ接点の両側の電流に逆向きのトルクが生じ、全体の角運動量が保存される、という予定調和を、これらの実験は否定するようにみえる。 単極誘導の接点外部の電線に働くトルクに対抗して、中心軸の電池と磁石の表面を流れる電流に逆トルクを考えるのは、角運動量保存則が、 このような教育素材ごときによって簡単に崩れる筈がないという信念であり、有り合せの概念による言い訳、辻褄合わせは、少なくとも、 有り合せの道具を組み合わせた証拠の提示に負けている。それは、余計な思い込みによる現実からの乖離かもしれない。 つまり、"電磁気には物体だけの角運動量保存はない"、のかもしれない。電磁気には物体だけの運動量保存もないのであるから。 しかしこれには、ファインマン物理の思考実験が関係するのである。
円筒形磁石の内外に電流が流れるとき、回転は起きる。それ単独のデモ。 CRAZY RPMs Fastest Homopolar Motor Magnet Experimt Most Fastest DIY Homopolar Motor? 円筒形という形によってトルクを受けないということはない。(電流だけがトルクを受け、渦になるのでスリットが必要、という考えは間違いと思える。 電流は十分物体と接着し、物体から離れて運動しない。これは、電磁誘導の渦電流の現象とは矛盾する。)
ネオジウム磁石とアルミ箔で 簡単モーターを作ってみました アルミホイルを筒にして被せるのは電線バランスの苦労がない。柔かく接触の確保が容易で、軽いので加速度が大きい。試すと、磁石12個積層にアルミホイル 2,3重巻筒(1重は加速度が大きいが壊れやすい)は激しくカサカサ音を立てて回転し、凸凹な筒が銀白色の筒にみえるデモの見栄えもよい。
0.3mm厚アルミ板で作った円筒(直径17mm長さ8cm)では、上接点は円筒上辺2箇所から軸に伸ばしたアルミ片を止める3mmネジの先を尖らし、 電池+極に作った凹みを中心に回転させる。外周接点は円筒の下端にアルミ箔を磁石底から接触させる。円筒の縦断面はヤジロベエ。 回転はアルミ箔だけより勿論遅いが、機械の回転を明確にデモする。しかし、円筒(や円板)は、磁場を覆うが電線の並列化であり、 電池から出し得る電流が効果を制限する。"コイル化"の望みは、その逆の直列化である。
そのような常識的信念は、磁極間の力で説明できる場面で便利に使われ、それを明確に否定する実験は少ない。しかし、この信念は、遠隔的な作用反作用であり、 場との近接的な作用反作用である電磁気では否定される。単極誘導では磁場は明確に周囲に広がり、その磁場中を電流が力を受け電線が軸の周りを回転する。 その電線を回転させたトルクには、てこの原理に従う対抗トルクが明確にみえない。電線が受けたトルクに直接に対抗するのは、場という硬さをもった空間であり、 離れた何かの物体、磁場中の円板にあたる磁石表面を流れる電流が受けるトルクは、対抗トルクではなく別の現象かもしれない。両者を結ぶのは電流と磁場だけである。
これは、"ファインマン物理"にあった、帯電したコイルの電流を切ると電流源を含め全てを載せた円板が回転する"場の運動量" の話に継がる。当時ファインマンが "これは実験しようとしてはならない" というほど検知不可能と思われていた。それが、これほど容易に目に見えるのだろうか。 帯電というほどの高電圧でなく電池ひとつの電圧が、場の運動量に関わるのか。電磁気学の常識は、単極誘導によって覆されるのだろうか。
単極モータの電線上の力 F= ixB 外をx、上をy、回転方向をz方向として、Fz= IxBy-IyBx (外向き電流Ixと上行磁場Byの積+下行電流-Iyと外向き磁場Bxの積) である。つまり、電流の下行と磁場の外向の積、電流の外向と磁場の上行の積の和が関係する。
私の追試:上側接点は、Ni-MH充電電池の+極に小凹みを作り20cm電線の両端をねじり1本を尖らせる。下部接点は、電線を1.5周の内側のエナメルを剥がし、 100円4枚の磁石12枚の積層した円盤磁石の側面に接触する。実際の接点は一部分でも揺れないように1.5周の円形にする。電線は太いと角加速度が小さいが、 細いと変形しやすく、最も重要な形のバランスを保つことが難しい。0.6mm径のエナメル線、0.9mm径の銅線で試した。接点に機械油は有効のようだ。 激しく回転する回転数は〜数10Hzだが、未計測。
その説明は、このデモの不可能性を証明しようとする。しかし、ここには既に現実にデモがあって、それを不思議に思うことは重要なことである。それがまだ 不明確なとき我々は考える。デモが正しいなら、不可能証明に誤りがあり、それを正せばデモが理解できるだろう。デモが正しくないなら、その理由を示さな くてはならない。意図的でない不正、不作為、別の要素があることもある。このようなことを、我々は繰り返してきたのである。一つの事実又は法則を明確化する、 反対論証とデモの対抗。
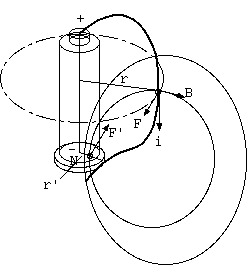
電流の経路は、接点によって力学的に内外に分けられ独立に回転できる。電流は一巡するから、内部の電流は、磁石表面をどう分布し流れても、 外部の電線上の電流と大きさが等しい。
磁場をイメージするのに磁力線を使う。磁力線は、磁場の矢の方向を連ねた曲線(流線)で任意の単位で磁束を代表する記述であり、その接線方向は磁場の方向であり、 磁力線の面密度が磁場の強さである。磁力線が広がるとき磁場B(磁束密度)は弱まる。磁力線は発生消滅なく一巡する。磁力線は張力をもち、互いに側面で反発する。 電荷のもつ速度の流線を電流という。電流は、電池の+極から発生し-極に消滅し、電池内部は電場の時間変化が電流を代行すれば、やはり一巡する。
電流が一巡し磁力線も一巡するから、平面上では2閉曲線が交差すれば再度交差するように磁力線と交差した電流は同じ磁力線と再交差する。 空間上では磁力線との交差は電線(経度線)の曲りで避けられるが、林檎の表面のような軸対称磁場では電線の曲りで横に外れても同等の磁場と交差する。 電流の磁力線交差は、T = rxF = rx(ixB) の、長さあたりトルクをもつ。これを電流経路で線積分∫Tdl してトルクになる。
これは、電流と磁力線との交差トルクでなく、電流iの、磁力線を平均した磁場Bとの外積、さらに半径rとの外積を、電流経路上の線積分がトルクをいう。 交差とはiとBのベクトル外積、交差角をθとして |i||B|sinθの大きさの力のベクトルを生む。sinθdlの線積分では電流の磁場との直交成分である。 半径rについては遠方で磁場は小さくなる分、経路は長くなる。軸対称では上からみて磁力線は放射状だから磁力線の密度Bは半径に反比例し、 経路は半径に比例し、|i||B|rsinθdlにおいてrの効果が打ち消し合い、電流経路での積分であるトルクは、電線が外に外れてもトルクは等しく、 横に外れても同等磁場と交差するから、電流経路に依らず、電流の交差する磁力線本数だけで数えられる。
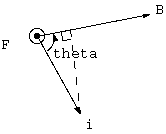
軸対称磁場では、磁力線は全て軸を含む断面の中にあり、外周接点の内部を通って上に向かいその後、外に下に向かい外周接点の平面では外周接点の外を下に向かう。 電流の一巡のなか、接点の外部で n本の磁力線と交差した電流は、接点の内部で再度n本の磁力線と交差する。こうして、 接点の内外部、電池+極から磁石の外周接点までの外路と、磁石外周の接点から磁石中心の電池-極までの内路とで、各総量としてトルクは常に一致対抗し和が0である。
磁場が軸対称でないとき、電流の磁場との交差に半径を掛けたトルクの経路による線積分は、経路中の電流一定から、経路と磁場の交差の半径を掛けた線積分になる。 磁石中心から外周への磁場の経路の磁力線との交差の積分は、磁場の面積分である内外で一致する磁束とは違うから、内外部分で一致するとはいえない。 しかし、回転の1周分を積分した磁場の線積分は面積分になり磁束となるから、磁場と交差する電流の回転の1周分は、磁束と電流との積となる。 こうして、内外部の1周トルクの和が0は、内外磁束の一致によって保証される。
しかし、鉄の針金によって側面を短絡した電池と磁石が転がる上のデモは、単極モータ全体の回転を示している。アルミホイルを敷いた床を電池と磁石が転がるデモは、 電流が床を蹴り床に外部トルクがあるが、短絡線を磁石に付着した電池と磁石は、導電体でない床を共に転がっている。もし単極モータを宙に浮かせれば、モータ全体が回転し、 真空無重力では電池が切れるか遠心力で構造が破壊するまで回転速度が上がるのか。電磁気では物体だけの角運動量保存はないことを、この単純な実験が示すのだろうか、 それとも、動画はフェイク(偽物)なのか、よく考えてみよう。(2017/4/5)
課題 8)と、角運動量保存とに関係して、下行電流を上にループさせ、再び下行させ、下行 n+1 回、上行n回のコイル化は、唯1本の下行と同じトルクだろうか。 トルクが経路に依らないなら、そうなる。電線がn倍に増える分、角加速度は1/nに低下する。もしも、経路に依るなら、上行と下行の経路によるトルクの差 (図8では上行が下行よりも軸から遠い)はn倍されトルクは増える。つまり、コイル化を達成する。ところがこれは、n本のコイルを永久磁石に置き換えれば、 1本の下行電流と磁石になる。磁石の側で磁石は回転を始めない。証明、終わり。つまり、フェイクである。(2017/4/19)
いや、デモは我々に再現を要求している。再現不能と推理しても、容易に可能かもしれない。物理は論理でなく現実の下僕である。現実は常に論理的でなく論理を裏切る ものである。それゆえ、理解不能だからと否定すべきでない。自らの論理ミスもあり得る。ループの磁石への置換可能は、1本の下行電流の全トルク0の理由にならない のではないか。一巡電流と磁力線の交差のトルク0の論理は疑わしい。 (2017/4/20)
軸対称磁場で回転のトルクが電流経路に依らないとするなら、経路が下行の途中で上行に変り、何回コイル化しようと、トルクが経路に依らない基本特性のバリエーション (変形)である。経路の一部であるコイルを別に考える必要もない統一的な理解ができることを示す。 また、経路が磁場の軸を軸にしてコイル化した図7のブザーは、上下の2接点を共に固定しない接点とすれば、上下に振動しながら一本の電線のときと同じ向きに回転をする。 上下振動によって接点は電流を導通/断絶するが、コイル電線が下に落ちて電流を導通したとき、電磁力に上下成分(上)が発生するが、水平成分が残り、それによるトルクが 経路に依らないことを表すと考えられる。 (2017/4/23)
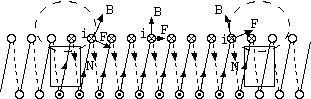
織り目模様の細かい凸凹をもつ台所のステンレス調理台(磁石が付かない)で転がすと、ゴロゴロと音を立てながら(暗くすると小さな火花がみえ)、推進力が起伏の傾斜と 湾曲に負けて元に戻る、転がり往復運動をいつまでも続ける。明確に自発運動である。(図9(a))。(2017/10/24)reciprocal.mpg(10秒1MB)
転がり往復運動の単三充電電池(Ni-MH)の両側のNd磁石を、磁石の向きと転がる方向の関係が明確でないので減らす。まず硬貨を電池に付着させる磁石を各側に1個だけ にしたが、問題なく動いた。車輪は、端にギザギザありの磁石に付くイタリア硬貨(L.100)。磁石に強く付きガリガリ音を立て元気に往復動作する。強い磁力は殆ど不要 なのだ。磁石を減らすと磁石表面の直列抵抗が減り電流は増えるが、磁力は大きく減る。両極の磁石が例えばN極内側なら、磁石の減少は車輪円筒側面から外に向かう 磁束に伴うローレンツ力を減らす。(図9参照。配置は磁石の外に硬貨。磁石が外では磁性体の硬貨が磁気遮蔽し電池に付着しにくい。)
ローレンツ力は、ひとつは、この転がり接点の外側の導体を通る電流と車輪円筒側面を外に向かう磁束密度の外積(ixB)によるローレンツ力Fがある。もうひとつは、接点内部の 車輪が磁場の中で電流が流れるファラディー円板になって、両車輪で電流は逆方向(一方は車軸から端、他方は端から車軸)である。そこで両車輪を横切る磁場が上の例の ようにN極を内側に向ける逆方向なら、両車輪は同方向に回転する力F'又はトルクを得て推進力を与える。これも、ローレンツ力である(図9(b))。それ以外の軸を流れる 電流の受ける力とかは軸対称を仮定すれば考える必要がない。両方の力を受ける物体は接点で分離し、両トルクは加算して0だろう。ところが、ローレンツ力は1方向に 推進力を与え加速し逆方向に進むとき減速のはずが、実際の現象は両方向とも加速している。ゆえにこれは、ベアリングモーター(ボールベアリングの内外輪に電流を流す と回転方向に加速する)の動作原理(図9(c))のようである。
硬貨も色々取り替えて試した。ギザあり非磁性100円硬貨でも動作した。+極の凸に安定させるワッシャ代用に、アルミ箔切れと5円玉を通し、−極は10円を通し磁石、 つまり磁石で外から硬貨を通して電池を挟む(硬貨の外に磁石)。付着力は下がるが問題なく動作する。つまり、車輪に磁性体の必要はなく銅や黄銅でもよい。(2017/11/1)
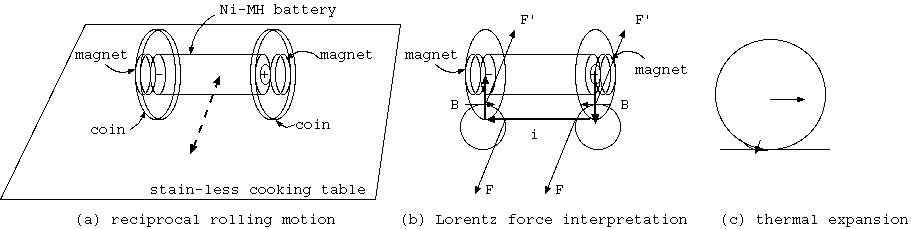
磁石を使わず、電池に5円と10円をグルーで硬貨と電池周囲とを付けると、あまり明確に動かない。両方ギザなし硬貨だからかもしれないが、グルー止めは導通確保も難しい。 11/1に磁石付着は動き、グルー止めは動かない。やはり磁石は必要か。ギザあり硬貨は、接点熱を他に広がらせないことで熱膨張を明確に動きに反映するだろう。 非磁性100円硬貨で動き、片方5円で他方にギザあり100円が、ギザなし10円より明確に動くのは、電磁気的説明より熱膨張説を有利にする(図9(b)と(c))。 次は、両極に非磁性ギザあり100円硬貨が、磁石なしのグルー付着で動作すれば、熱膨張説を明確にできる。 結果、小さいが揺れは起き、自然物体の振動とは思えない振動が数分以上続く。故に、転がり往復運動は、少なくとも熱膨張による寄与の存在を示す。(2017/11/3)