ちょっと考えると可能かと思うが、絶対にできない機械を考えてしまうこと。 昔、パリティに掲載されていた問題から始めよう。

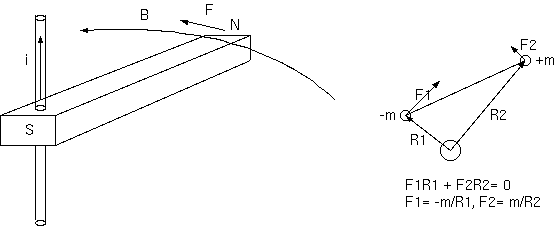
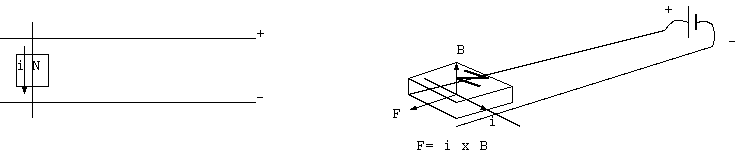
磁石の片方の極に穴をあけ、電線を通して強い電流を流す。 遠い方の極が電流を一巡する磁場によって力を受け回転する(予定の)モータ。 もし回転するなら、摩擦となってその回転速度を制限するブラシのない直流モータとなる。

磁石には距離の近い方の極も存在し、ともに電流から力を受ける。両磁極は、強さが等しく符号が逆で、 受ける力は、磁極と磁場の積に比例する。磁場(と受ける力)は、中心軸の電流からの距離の 1/r に比例する。 (F= +-m/r)。回転を加減速するには、両磁極の受けるモーメント F r の和が正か負である必要があるが、 それは常に丁度 0 である。そのため、このモータは、回転しない。このことは、両磁極がどこにあっても成立する。

ブラシレスモータは、すでに磁石とホール素子による非接触な位置検出によって実現されているから、 これは、すでに解決している。半導体による信号の電力増幅と制御によって電流の反転を行うことができるから、 電磁気による(不)可能性を追うことに技術的な意味はない。 しかしそれは、別の複雑な手段で達成しただけであり、最初の考えのもつ単純さと理想は実現されていない。 電子化したとしても、半回転ごとに電流の向きを変える直流モータは、技術の原始的な段階を示すのではないだろうか。

この問題の本質は何かという問を投げかければ、それは、単磁極モータであるといってよいだろう。 単磁極があれば、電流のそばで、それは磁場の向きに力を受けるだろう。その力は回転速度に依らないから、 軸の摩擦が均衡するまでどこまでも、速度を上げるだろう。単磁極が電流の軸から離れて行かないように 向心力を与える必要はあるが、それは、遠心力に耐える強度をもった回転子を作ることでしかない。 しかし、単磁極は存在せず、磁石を割っても単磁極は表れず、磁石の双極性が明らかになるばかりである。 この問題の美しさは、単磁極の非存在と不可能性なのである。

普通の直流モータは、ある角度ごとに磁極を反転する。それには回転子又は界磁(固定極)の電磁石の電流の反転(転流) で行う。 転流に伴って電磁石のインダクタンスが電流の遮断を拒んで高電圧を発生し、電流を流し続けようと切断点に火花を飛ばす。 インダクタンスは、電流の増加にも抵抗して逆電圧を発生する。電流の切断と通電には時間がかかり、それが高速な回転を妨げる。 転流器の機械的な摩擦も回転速度を制限する。転流器には摩擦の少ない接点が必要で銅面とカーボン(黒鉛)の組合せが永く成功 した組合せであった。カーボンは火花となって自ら擦り減り銅面との摩擦を減らすが、それには意外なことに湿度が必要という。 転流を電子化するには切断時の高電圧に耐える半導体が必要になるため、ブラシレスは小型機器にしか適用されないだろう。

家庭用の掃除機を分解してみると、古典的な直流モータが見える。エナメル線を巻いた回転子の複雑で美しい構造、 切れ目が入った銅滑面に接触する黒鉛棒。それがそのまま 100V AC で使われている。界磁と回転子が交流で同期的に反転するから 直流モータは、交流でも使えるのである。それを手で回すと転流器の摩擦の大きさがわかる。意外に大変に重いものである。

単磁極、モノポールは、マックスウエル方程式では、電磁気の電荷に対応する部分に存在を許されているかに見える。 マックスウエル方程式は、電場と磁場、電荷と単磁極に対称な理論である。それが電磁気の本質を明らかにしているなら、 単磁極は存在しても不思議ではない。マックスウエル方程式は、単磁極を否定しているのではなく、普通ならそれを 予言しているというべきところである。実際はまだ見付かっていないからそこに空席を残しているのではないか。 マックスウエル方程式は、2 組の式からできている。

div B = 0,　rot E = -dB/dt

div E = ρ,　rot B = dE/dt + i

符号の違いは、両式の 1 階微分を一巡して波動方程式となるために、一方の式で符号反転する必要があるだけである。 下の式の電荷密度ρ と電流密度 i にそれぞれ対応する上の式の磁荷密度が 0 であり、磁流密度の項がない。 これらは、磁荷と磁流の存在を否定しているのだろうか。数学的な対称性は、その存在を許すのではないだろうか。

ところが電磁ポテンシャルの理論は、単磁極の存在を否定する。単磁極の密度を表す磁場の発散 div B は、 ベクトルポテンシャル A (rot A= B) を存在させると恒等的に 0 である。また、電場 E = -grad φ - 1/c dA/dt の両辺の rot をとると rot E = -dB/dt も導ける。つまり、マックスウエル方程式の第1組 (div B = 0,　rot E = -dB/dt) は、 物理的意味をもつ式でなく、数学的な恒等式になる。物事は単純に説明できるほうが正しい理解であることが多い。 これは、ポテンシャルの実在の説得性を電磁場の対称性よりも高めている。電磁ポテンシャルφと A を場の背後に存在する 物理的実在とすると、磁荷と磁流の存在は自動的に消え去る。その意味で、単磁極は、電磁ポテンシャルの実在と排他的である。

現在、ポテンシャルには本質的に任意性があるから仮想の存在であるという見方は廃れ、ポテンシャルは、有効なだけでなく、 実在するという見方のほうが、優勢である。しかしそれは、単磁極が見つからないから、最初から存在しなかったという 言い訳かもしれない。もし、単磁極が発見されると、言い訳は、再度の言い訳を要するという、さらに困ったことになる。 SQUID を使ったモノポール検出の実験は、一度だけ検出されたという報告がされたが、その後の追試は、成功していない。

しかし、もしモノポールが再確認されるなら、電磁ポテンシャルを使った理論とそれに基づくすべての科学に恩恵があるだろう。 その存在がそれら全てが依って立つ考え方を否定するからである。単磁極は、色々と問題を引き起こすだろう。このモータ についても、すぐにそれを考えることができる。単磁極があれば、単磁極が受ける力の逆の運動量と角運動量をだれが引き 受けるのだろうか。場が受けることはできない。いま電場は 0 としている。そうすると電流がその角運動量を受けて電線 がそのために逆回転するのだろうか。そうでなければ、この機械全体が回転を開始してどこまでも加速する、という 不思議なことになる。単磁極がないとき +m と -m のモーメントの和が 0 となって、電流が回転から独立できるのである。

単磁極は、磁力線に沿って加速される。コイルや磁石から作られる磁力線は、空間を一巡して端を持たない。棒磁石を分割しても N 極部分と S 極部分とは、区別できない短く弱い磁石に変わるだけである。磁石は、コイルのような電流をもとにした存在と 考えられる。もしそうでなく、磁石の端に単磁極が存在するなら、磁力線は、磁荷と磁荷を結ぶものになり、磁石内部には 一巡する経路と同じ線だがそれとは逆向きの磁場が存在することになる。磁石の外部の磁場は、電流の存在しないとき静電場 と同じく渦なし発散なし場の同じ法則で記述される。(スカラーポテンシャル場φの勾配 B= -grad φまたは rot B= 0, div B= 0)。

恐らく磁石の中も磁力線は、一巡した閉曲線を描いているのであろう。単磁極は、外から磁石の片側の極に向って進み、 磁石の極にぶつかっても、それが素粒子なら素通りするかもしれない。また、電流による磁場では、一巡する磁力線が露わに 空間に出ているから全ての経路で加速をうけることが明確である。単磁極は、磁場からエネルギーをもらい、どこまでも加速 されるだろうか。いや磁力線は単磁極の加速の方向を結んだ線というだけであり、速度を得た単磁極の運動経路は磁力線を辿る わけではない。例えば単磁極モーターでは、この図のように電流との距離を保つものが必要だろう。その加速のエネルギーは、 他に単磁極のない場合、何が供給するのだろうか？ このように単磁極は余りにも縁遠いので、話が穴だらけになる。

それがモノポールの非存在の説明になるのなら、電荷と電場には決して一巡する電気力線はないのかいえば、そうではない。 磁場の時間変化は、電場の rot である。任意の閉曲面を横切る磁場の時間変化は、それをとり囲む周囲の閉曲線にそった 電場の一巡を伴う。トランス(変圧器)の 2 次巻線に交流電圧が発生すること、磁場とコイルの起電力発生の関係は、この 裏付けを持っている。一巡する電場は一時的であって、時間的に変動する磁場を同じ方向にいつまでも続けることはできない。 そのとき、電場を巻き線の経路で線積分したスカラーポテンシャルは、どうなっているのだろうか、巻き線の両端に電圧として 表れるのはポテンシャル差で明確な値をもつが、スカラーポテンシャル自体は、同じ場所に一巡して来ると違う値になる多値的 というべきではないだろうか。

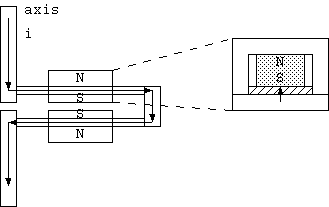
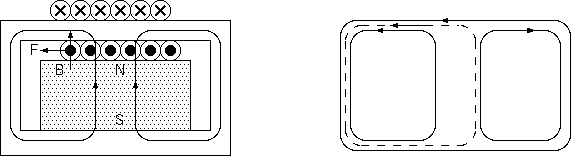
単磁極がないからといって、ここで簡単に思考は諦めない。 磁石の外に表れる磁極、それぞれのそばに逆向きの電流を流してみては、どうか。

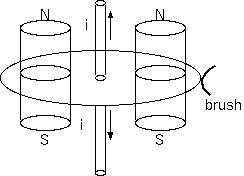
この図の場合、中央の赤道面の円板に電流を外から与えないといけないから、 ブラシが円板の外周に存在することになるが、このモータは、回転するだろうか。 この場合、磁石は上下に継っていて円板には磁石の通る穴が開いているとする。 これは回らない、という意見の方が多いと思うが、私は、少数派である。

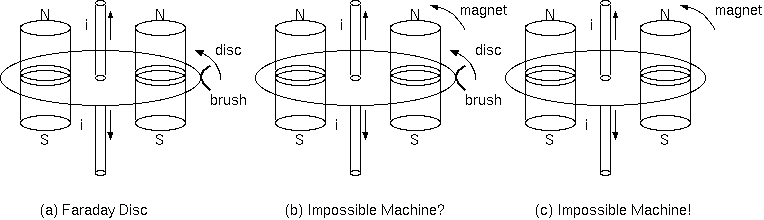
直流のモータでブラシ(*)が存在すれば、それは、もはやファラデー円板との違いは少ない。この図の形のままで、 磁石が円板に穴をもつのではなく、磁石が上下に分かれ上下の磁石は固定して、磁場が円板を通過して、 円板だけが回転できるようにしたら、それはファラデー円板そのものである(下図(a))。

さらに、磁石の吸引力が円板を上下から締めつけるモータもあり得る(下図(b))。ファラデー円板は磁石を離して設置するから 吸引力に対抗する必要があるが、これはないから、製作はファラデー円板よりも容易である。このモータは、回転するだろうか。 気になるファラデー円板との違いは、このモータは磁石と円板の相対速度がないことである。磁石と円板をともに回転させる。

(*)そのブラシ(摺動)は転流のためのブラシでなく、電流を接触して与えるだけのブラシである。 ブラシの接触部には切れ目がないが、ブラシの接触速度が高いのが問題である。

磁石から磁力線が生えているなら、円板は磁力線を横切らないから、円板は回転しないかも知れない。(磁力線を横切ろうと、 横切らなくとも、磁場の中で電流は、力を受ける F＝ixB。しかし、逆起電力E＝vxBはどうなるのだろう(*))。

逆に、磁力線が磁石から切り離された存在であるなら、(b)の場合も回転してもよい(**)。 磁石も円板も一体にすると、円板外周から導体を全体のカバーを通してブラシを速度の低い首の部分に移せるし、 よいことずくめである。ちょっと待て、これはモータ全体が回転してしまう構図ではないか。 それは、そんなに簡単にはあり得ない。ファインマン円板でしかあり得ないだろう。

それは、ファインマン物理の III で問題が提示され、IV で解説された。回転軸と同軸のコイル、コイルに流す電流源、 そのそばに電荷を集め、すべてを同じ円板の上において、電流を切ると周囲に回転電場ができ、電荷を回す、それによって 円板が回転する。これは原理的に可能な思考実験であった。このファインマン円板と同じく、モータ全体が回転することだけで 回転しないと判断してもよい。ファインマン円板には場の運動量による根拠があったが、これにはないからである。 またこれは、思考実験でしか扱えないほどの精妙な話ではない。ファラデー円板程度の容易な実験の話である。 問題は、ここまでの思考経路のどこが間違っていたのか、を明確にすることだけである。

円板と磁石との間が固定されているとき磁石と円板の相対速度がない。円板が回転するときブラシがいる。 そこで、磁石だけが上下に分かれたまま回転することができるしかけがあれば、円板は回転する必要もなく、 ブラシも要らない。この場合も、モータは回転するのだろうか (図 (c))。これは無理だろう。赤道面円板 で区切られた上下のそれぞれ半球の空間には両磁極があるから、すでに回転する理由が失われている。

図(a)のファラデー円板が回らないと考える人は、現代までの全ての電磁機械を止めてしまうことになる。図(b)が回転するとしても、 外側の導体カバーを通してブラシを首に移動すると回転しない。外周から首までの経路で回転力が打ち消されてしまう。 それが先程の間違いである。上の図ではすべて 2 本の磁石で構成したが、断面に極の出たバームクーヘン型の磁石で構成して軸対称にできる。

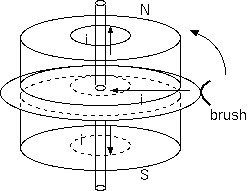
(*) 相対運動vは力には関係なく、起電力にだけ関係し、磁石を一緒に回転させるモーター(b)は、逆起電力なしに回転するのかという疑いが残る。

(**)逆起電力を生む vは磁石に対する相対速度でなく系に対する速度であり、逆起電力は、磁石との相対運動とは関係ない。磁石は、 円環電流(正負の電荷の回転の速度差)に置き換えられ、磁石の相対的な回転運動は関係しない。この考え方は、磁石の並進運動が電場 を生むことに殆ど矛盾する。局所を拡大すれば磁石との並進運動と殆ど違わない磁石の軸方向の相対回転は、この世界に無効な運動と するのかという疑問である。磁場のなかの速度をもった電荷が磁場から力を受ける説明に使われる、電流に沿って飛ぶ電荷に並進する 系が電線を帯電しているとみることと矛盾しないのか。円環電流の作る磁場のなかを飛ぶ電荷は何をみて力を得るのか。

この実験のよい結果を Web で見付けた (2002年ごろ東京工大のサイトだったが消え、その アーカイブ をリンクした。現在(2020/1/4)、九州大学のサイト。)

このサイトは、説明や理論の提示でなく実験を通した具体的な結果を示される。単極誘導モータで磁石を円板連動状態での回転 (上図(b))を実験で示し、また、移動部分の電流の流れる導体に磁石を載せた線形レールガンが磁石無しと比べて推進力が大きい ことも示された。レールガンの移動部分に磁石を載せることには、まるで boot strap、靴紐を引いて宙に浮かぶ不思議さがある。 こういう現象は、技術において極めて貴重で、そういうことに人類の生活は頼って生きてきた。我々は当り前のことに依存せず、 ほとんど奇跡に類することに依存した。歴史は、全面突破より、一点突破の事象に満ちている。爪の上の土である。

"boot-strap loader" コンピュータのプログラムをロードする初期プログラムは単純であるほどよい。それだけは、電源投入時に 毎回手入力する必要があったから。そのために単純化は、技巧を凝らした理解を超えるプログラムとなる。決してあり得ない ことを成し遂げる仕組を "boot strap" と呼んで靴紐を引いて宙に浮かぶあり得ないことに喩えるのはぴったりしている。 何の役に立つか分からない段階の力学や電磁気学を、他の何よりも信頼性の高い技術にまでするのには人類の不断の芸術的技術 を必要としたはずである。支点さえあれば地球をも動かす挺子の原理、どのようなものでも作る錬金術、滑車と斜面の永久運動。 電流を 1000 倍にも増加するコイル、すでに我々はこれらを不思議な技術と感じない。

ファインマンが驚く、一本の導体棒の電気振動に動画像を遠方に伝達する、ほとんどのひとに理解を諦めさせる魔術に近い技術。 2 次元を 1 次元信号にするのに平易な水平走査が使われペアノ曲線は使われなかった。標準にはモデルベース符号化でなく 波形符号化が使われた。全画面 DCT でなく、マクロブロック単位の符号化が使われた。DCT が使われ、ベクトル量子化は使われなかった。 画像間の動き補償フレーム間予測(MC) が使われ、3 次元 DCT は使われなかった。ポリフェーズ・フィルター・バンクが 使われ、MDCT は使われなかった(AAC では使われた)。そうである必要があったのか。大量の計算を使って画像と音響を符号化し、 やはり大量の計算を使ってそれらを復号する技術は、すでに人類の営為の一部、我々がそれによって糧を得る産業となった。 今後、人類の営為はさらに計算的に、通常人の知り得ないものになって行くだろう。そのような符号化技術と比べ、 計算と関係ない電磁気は、単純である。磁石を乗せて動くとは、まさに boot strap であるが、単極誘導や、レールガンは、 コイル化できない。それが、どうして不可能なのか、又は可能なのかが、難かしいと私は思うのだが。

力を受ける電流の流れる電線に磁石を乗せることは、以前の私の思考ではほとんど冗談であった。 それでは、磁石との相対運動ができないから、磁石を抱いた電流が力を受けても、その反作用を磁石が受けて全体は動くはずはないと 常識が反論した。事実は、驚くべきことにそうではなく、力を受ける電流に磁石を乗せて推進力が得られる。 これは、実物で示されて初めて納得する、いや目の前に示されても未だに納得できないような常識外れの現象である。

磁場は磁石から起きているが、磁石は、(回転運動でなくても並進運動でも) 作用反作用から切り離され独立している。 場から力を得る物体は、場とは作用反作用の関係にあっても、場を作った磁石と作用反作用の関係にあるのではないことを、 これほど明確に示すものはない。"反作用を受けるものがないときは、場を作った物体を疑え" という言葉は、基本的に間違いである。 騒ぎのもとである場を作った磁石は、作用反作用の騒ぎの当事者ではない。電流の動かない他の部分が反作用を受けると一般に解釈されている。

さらに、レール上に単極誘導を車輪にした車型の実験を示された。これならボールベアリングのボールを並べなくてもよいし、 ブラシは車輪とレールの転がりの接触になる。これは、うまく推進力を取り出すことができそうであるが、実験では期待した力と 逆方向の動きを示したという。筆者の言われるほどこれらの実験は、容易な実験ではなく、 その結果を明確に示すことが素晴しい。もちろん、その元には周到な計画、正しい思考が必要である。

"電磁気" に単極誘導について書いた。 モーターでなく、直流発電機としてこれをみたとき、砂川重信の"電磁気学"（岩波全書)P213-P215 では、磁石を回転させても 電線のループに電流が発生しないことを根拠に磁力線が磁石からブラシのように延びているものではないと結論し、磁荷の存在 もこれを使って否定する。最後には磁場を "エーテルのゆがみ" であるという。多くの人が電磁気をこれで勉強した本である。

この文章には、思考が欠落した部分がある。それは、磁石の上の回転するのは導体円板だけであり、その外のループを構成する 電線は固定していることである。磁石を回転させてもループに電流が流れないのは、当然で、円板を固定して磁石を回転させるなら、 普通は固定している電線と電流計も共に回転させる必要がある。そのとき電流は今と同様に流れるのである。

通常の磁石を固定した実験でも、円板と測定系全体を回転させては、電流は流れない。磁石からブラシのように磁力線が出ていても、 この単極誘導の現象はすべて説明できる。磁石と円板を回しても測定系が止まっているなら、測定系に磁力線が交差し、起電力は 測定系側に逆に出る。磁石を回して円板と測定系を固定しているなら、両方に発生する起電力は打ち消しあって電流は出ない。

その他、全ての場合で磁石から磁力線が生えている場合も、磁力線が磁石から外れている場合も同じく説明ができる。 それゆえ、この単極誘導の現象から磁石から磁力線が生えていないと結論するのは、余計な、間違った論理である。 さらに、これをもって磁荷の存在否定に言及し、磁場を "エーテルのゆがみ" という必要もない。この電磁気の先生は、 磁場をエーテルということに抵抗がないのだろうか。エーテルを否定しないのだろうか。ローレンツ・エーテルは、静止している 以外の全ての特性がなかった。歪みのあるエーテルとは一体なにを意味するのか。計量場のこととも思えない。電磁気をエーテル の力学的歪みで説明しようとする 19 世紀ではない。電磁気の本質は、特殊相対論と同じくエーテルの非存在ではないのか。 場の概念を使いたい、ということをこれほど説得力無く逆説的である (場の概念がこれなら私は捨てたくなる) 文章は珍しい。 以上、"砂川の電磁気学" 批判。

磁力線は磁場の方向を結んだ線でしかない。電磁場が系によって変換されるから、"別の系からみると、運動する磁力線は存在しない かもしれない" (ファインマン)。 磁力線を磁石に生えたように扱うのは、磁場が空間の特性であることを忘れさせる害がある。 磁力線との交差とは、物体の相対運動自体のようにみえる。E'= γ( E + v x B ) の E も B もある系からみたある場所の特性 であり、ある具体的物体である磁石との相対運動を言わないからである。逆に磁場が磁石から切り離されたものというのは、 その空間に磁場だけあるように思うという害がある。電場が無く磁場があるのはふつう磁石の並進系であり、磁石に対して動く系 には磁場以外に電場が見えるのである。しかしさらにそれが単極誘導では矛盾を導く。磁石が回転をすると、軸対称の電場がそこに できないといけないが、静止系の電磁場の法則では電場は電荷以外には発散源を持たない。回転系の電磁気の法則は、慣性系の電磁気 とは異なる。単極誘導の導体円板付近に電場はなく、回転系の導体円板に電場があるのである。

私の日曜工作。フェライト磁石(外径69mm穴径32mmx厚さ8mmx2)を使った単極誘導モーターは、ボールベアリング(外径 8mm 内径 4mm) を使って初めて回転した。 以前、銅板(厚み 1mm 直径 80mm)を銅棒(径 4mm)にハンダ付けして水平に設置し両側を支えるだけの仕掛けでは摩擦が大きいためか 回転しなかった。配線をハンダ付けし、薄い銅板(0.3 mm)を鋏で円形に切って使い、軸との接点の押える程度を緩め、最後に機械油 を注入したことが効いた。接点にも注油は有効だった。ブラシ接点は微妙で、指先で抑える力を変えるとすぐに回転速度が変化する。 回転速度は数回/秒〜10回転/秒。不安定な上側片支持では高速回転に耐えられないので、枠を作り直し上下 2 箇所のボール ベアリング支持に改造し、ブラシを固定した。

約 10 A ほども流さないと接点などの摩擦に勝てない単極誘導モーターは、その弱いトルクのために単なる実験であり、実用的な モーターには程遠い。いま磁石は、円板に固定されず、磁石の吸引力だけで付いている。高速回転時の安定性確保には軸と磁石を 固定するハブがあった方がよいと思うが未実行。銅板の円形の精度が悪く、作り直す。円形コンパスで銅板を切る道具が必要と 買い求めたオルファカッターのコンパスは銅板を切れず、結局やはり鋏で切った後、サンドペーパーで断面を滑らかにする。 これで約 5 A でも回転を持続し、10 回/秒以上の回転も可能になった。

逆起電力は、小さい。 v= 340m/sec, B = 1 [T]で 8.5 [v] と以前計算した。10Hz、8cm、3m/sec、B= 1000[G]では、その1/1000。 それは、小さくテスターでやっと存在を判別できる程度だった。単極誘導は、モーターの方が発電機よりも明確な実験なのだろう。 逆起電力への電力量は、力と速度との積、仕事(機械的エネルギー) に変化する。

円筒形磁石の遮蔽は難しい。工作可能な方法として鉄板で巻いて断面から銅板を出すことだろう(下図)。 磁気遮蔽した単極誘導モーターは回転できるのだろうか。

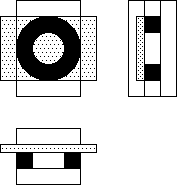
長方形型の遮蔽した磁石 4 個を使って、軸から外にでた電流を軸方向に返すことができるだろうか(下図)。 外部の電流に影響がない状態を作ることができそうではないか。

しかし疑いが残る。単極誘導の磁石を磁気遮蔽でき、軸から出た電流を軸方向に戻せるなら、上図のその部分の単体は、 無反動推進器ではないか。もし、電流を元の場所に戻せるなら、それは、コイルにすることができるではないか。 導体円板から外に出た電流を軸方向に戻すのに、逆向きの磁場がある磁石に軸方向に縦長の空洞を通して軸に戻す可能性もある。 磁気回路によって磁場を遮蔽した場合の電流の受ける作用と反作用は、どうなるのか。

(1) 磁石が受けるか、または磁気を通す目的の軟鉄のような磁気回路、遮蔽が受けるのではないか。単極誘導では磁石は作用反作用 から傍観者に抜け出ているが、通常の磁石の極、コイル同士の力は、作用反作用である。コイルが棒磁石に吸い込まれるとき、 棒磁石もコイルから引かれている。永久磁石は、永久電流が周りに流れる電磁石に置き換えることができ、作用を受けた電流が作る 磁場から、場を作る電流が反作用を受けるのではないか。なお、磁気回路が力を受けると考えることは難しいのではないかと思う。

(2) 戻りの電線が受けるのだろうか。単極誘導では戻り線に磁場の影響があると考えるのは自然である。単磁極モーターでも 遠方で弱まっていても磁場の中の電流は、力を受ける。この戻り線へのトルクは、円板のトルクとは逆向きで大きさが等しいのか。 これは、角運動量保存を優先して考えている。戻り線への磁場が磁気遮蔽できるなら成り立たない。

(3) 何も受けるものがなく、無反動推進を作るのは、実は容易であるのか。

(4) 磁場が遮蔽によって変化して磁場の中の電流が受ける力が減少するのか。遮蔽は外部に磁場を出さない。遮蔽によって磁場は 無駄なく目的の電線を通過でき、電線までの磁気回路の透磁率によって、磁場は逆に大きくなる。反作用がないからといって、 作用がその分減少して辻褄を合わせをするだろうか。これは、単極誘導モータは、遮蔽すると回らないという予想の、自らの 辻褄あわせではないか。

単純な構成として、コイルの内面では電流が磁場の強い磁気回路の中を通り、戻り線は外を通ってもとの場所に戻るコイルを考える。 コイルを使うと大きな力を発生でき、実験が容易である。この図のように、戻り線がコイルの外側の面であるとき (2)は、あたらない。

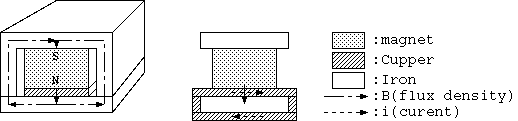
0.1 T程度のフェライト磁石の磁場に 24 回巻いた 2.5 cm の長さのコイルに 10 A 流す場合、コイルの受ける力は、 F[N]= N x I x B x d = 0.6[N]= 60 grw もの大きさであるのに表れない。磁場を遮蔽してコイルの内外面の磁場を違えて その受ける力の差は、磁気回路とコイルを一体化したとき表れない。結果は、説明がつかないまま (3) を否定する。

磁気回路に入ったコイルの電流の受ける力の反作用を、初等的に説明できるだろうか。下図において、コイルの電流が左に力 F を得るとき、もとの磁石の作る磁力線とコイルの作る磁力線とがある。図の左側で同じ方向である磁力線は増強し反発し、右側での 逆向きの磁力線は、互いを消しあい、点線のように変わる。結果的にコイルに電流を流さないときと比べて、左右のバランスの偏った 磁力線配置になる。これが磁気回路と磁石を右に動かす力 -F を与えると考えられないだろうか。

また、コイルを小さな磁石に置き換えれば、磁気回路の一部に磁石が埋まったとき、その小磁石の受ける力の反作用をその他の部分 が受けるのは当然といえる。もちろん、最初から磁石とコイルとを含めた系に作用反作用が成り立つと仮定するならば、つねに反作用 は存在し、それがどこにあるかという疑問をもつ必要もないが、磁石どうし、コイルどうし、磁石とコイルの系の三者に最初から作用 反作用を仮定するのは、磁場中の電流が受ける電磁気的力への力学の運動量保存則を天下り的に適用しただけであり、反作用の発生の 電磁気的な説明がほしいのである。 "よく分からないがどこかにある" というのは十分だろうか。説明できないとき不注意に 仮定が導入されるものである。

このサイトの筆者は、反作用の考察では単極誘導にはリード線が反作用を受けるという説、レールガンについては電源とレールが 反作用を受けるとういう説に対して、疑いをお持ちである。電源はどこまでも遠くできる。反作用を受けるのがレールかもしれないが、 磁場は任意に遮蔽できるから、それで説明するのはどうかと思われている。 そう、磁場が遮蔽可能ならレールガンは、無反動推進かもしれない。磁場は、磁石と電線の移動部分とをいれる透磁性の箱で 遮蔽できるのだろうか。その場合もレールガンの推進力が遮蔽した分だけ減ることはないのか。いや、磁気回路が外部に出る磁場を 遮蔽するに伴って透磁率で磁場が増強し推進力は増えると考えるべきだろう。しかし、より遮蔽しやすいように見える電荷は、 それを絶縁していれたアースしない導電性の箱では遮蔽できない。電荷保存則は、電荷を隠すことさえ許さないのである。

一般には永久磁石と電流回路とは、作用反作用の関係ではない。しかし、閉じた電流と磁石とは、永久磁石を永久電流に置換し、 両方とも閉じた電流回路とすることができ互いに作用反作用以外の力を受けないことが知られている。 A 点から B 点に定常電流が流れるとき B 点から A 点にも等しい電流の戻り経路がある。 電流の閉じた経路は、閉じた磁力線の経路と相俟って経路全体の受ける力の線積分が 0 を示すことが望まれる。 F= ∫_A^B di x B + ∫_B^A di x B = ∫_closed di x B ?= 0 そのような "電流と磁場" についての考察を次に示すが、多少回りくどく分かりやすくないことを了承されたい。

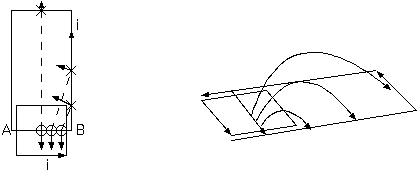
永久磁石の断面に直線電流を一本、交差させる(図(a))。その磁場の中の電流に生ずる F = i x B のローレンツ力によって 電線は場から横に(電流と磁場の両者に垂直に)力を受ける。その反作用は場を作った永久磁石が受けるのだろうか。 その永久磁石と直線電流との全体が多少でも力を受けることはないのだろうか。2 物体の相互作用は、間で運動量を やりとりする力だけで、全体が力を受けて動き出すのは見たことがない。(そもそも 2 物体しかないのに、どこから力を受けるのか。) しかし、それらの常識は確かだろうか。一般に電磁場の中の 2 者の相互作用は、場までを含めた 3 者の作用反作用である。 あとで説明するが、磁石と電線の関係が作用反作用であり両者が外から力を得ないことは、常識ほどには自明ではないのである。

磁石と直線電流は、N 回のコイルの電流と直線電流に置き換え、電流だけの系となる(図 (b))。電磁石のコイルから 電線を一本を移動し、電磁石の断面を交差させると、その磁場の中の電流に生ずる力によって、電線は横に力を受けるが、 電磁石全体としてつねにその力は打ち消されるかという問題になる。どのように電線を曲げても、任意の電流回路は、 自分の作り出す磁場で力を受けて動き出すことはないということか。それは予想されるが、容易に証明できないことである。 これは、普通むしろ証明もなしに受け入れるべき物理的な運動量保存の前提と思うのであるが、開いた電流では後述するように反例がある。

電流が抵抗のある電線に流れるためには電場が必要で、電場と磁場との両方があるとき場の運動量が存在する。しかし、 電線の抵抗を 0 に近づけると電場は任意に 0 に近づく。電場 0 を仮定することは現実的であり、場の運動量 E x B は、 関係しないと考える。

また、外部の磁場はないとする。外部磁場と自らの電流が発生する内部磁場とは、同じ電流に加算された力を発生する。 外部磁場は、外力になる。いま、内部磁場の力が内力かどうかを問題とするとき、外部磁場の存在は、夾雑物となる。

問題は、電流同士の相互作用は、作用反作用の関係だろうか、ということである。もちろん、もし、それら全体が力を受けるなら、 作用反作用の関係ではない。作用反作用の関係とは、全体の重心の運動量が保存され、重心は力を受けず加減速されないこと であるからである。

閉じた電流は、孤立物体になる

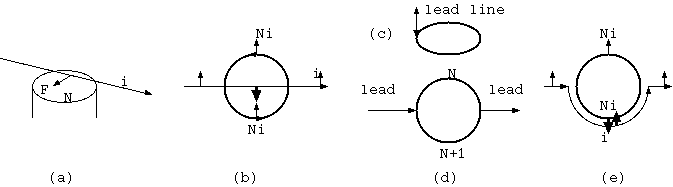
電流回路だけで力を受ける可能性があるとか、N 回のコイルと直線電流が作用反作用でないとかいうとすると、どういう構成が 力を受けないとするのか。リード線が回路の同じ場所から出ていて、電流源につながる回路(図(c)) が一番考えやすい。 閉じた電流回路がもっとも常識的で無害な回路である。しかし、閉じた回路が自らの磁場から力を得ないという証明も容易でない。

電流が往復するリード線は、電線の太さが十分小さければ、行き来の電流は打ち消され、磁場の影響を受けず磁場を発生しない。 電力供給による場の運動量は、電線全体の抵抗が 0 なら 0 である。しかも、送電線の場すら運動量をもつが力を与えるものではない。 リード線が往復線の場合、電流の回路は閉じ、回路は孤立物体になることができる。しかし、回路へのリード線が複線でなく、 両側の無限遠から電流が供給されるとき、それは開いた回路であり、そのとき回路は孤立物体ではない。

コイルと直線電流の話は、青野修氏の"いまさら電磁気学？"のコイル (円環電流) とそれに近付く電荷のパラドックスを想起させる。 コイルに近付く電荷を電流に置き換えることが可能なら、コイルに近付く電荷とコイルと直線電流との違いは、コイルの中を通る 電線の部分である。そのような一部を欠いた電流、部分的電流が可能なら、電流は、それだけで自らの磁場から力を受けることが 明らかである。そのためには、コイルの両側に電流のシンクとソースがいる。

コイルに流す電流のリード線が両側の遠くから来ていてそれらを直線電流の一部とみれば、コイル内部のコイルの磁場に交差する 部分が力を受けるのでその分だけが、"コイルに近付く電荷" と違うと思われるが、よくみると、コイルは両側からのリード線のとき 下側が N + 1 回、上側が N 回になっていて(図(d))、N 回のコイル + 直線電流とはすこし違って、コイルの中の磁場を交差する部分が 下に避けている。

電流素片間は、作用反作用の関係ではない

電流は磁場を発生し、磁場から電流は力を受ける。電線が磁場から受ける力 F は、電線上の電流素片 dl が磁場 B から受ける力 の電線全体の積分であり、磁場 B は、ビオ・サバールの式で電流 ds 全体がつくり出す。両電流素片間の角度をθとすると、 B= ∫cosθ/r^2 ds、F= ∫ B cosθ dl と書かれ、ベクトル記述では、B= ∫ds x r/|r|^3、F= ∫ dl x B と表される。

任意の電流素片(dl、ds)間に cosθ/r^2 を介して作用反作用の関係が成立して、電流経路全体で自らに与える力の合計が 0 ではないか、と考えるかもしれない。もし、どの電流素片間の力も常に作用反作用であるなら、部分で 0 ならその積分は、 0 になる。しかし、電流素片間に作用反作用が成立しないことを大抵の人が衝撃をもって知るのである。

平行電流は、同方向で互いに引き合い、反対向きの電流が反発するが、ともに作用反作用の関係にみえる。しかし反例がある。 十字交差する電流素片間のやりとりする力は、作用線上ですらない。交差前後の部分の電流は、交差角度を狭める方向に力を 及ぼしあう。力は、電流素片間で打ち消されず、同じ電線の交差の前後で打ち消されるだけである。

電流素片間は、作用反作用の関係ではない。

直線電流が自身に影響を及ぼすことはない

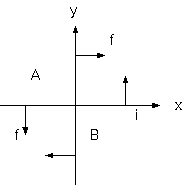
電流素片1, 電流素片2 があって、1 から 2 の位置の磁場が作られ (i1 ＝＞ B2)。2 から 1 の位置の磁場が作られる (B1 ＜＝ i2)。各電流がその位置の磁場と外積して力を受ける (F1= i1xB1, F2= i2xB2)。力の和は、0 でない(F1+F2= !=0)。 電流素片が他の電流素片の場所の磁場を決め、電流素片と磁場の外積が力をつくる。電流素片間には直接の関係はなく、 間に磁場を介在させて力をやりとりする間接の関係があって、磁場が電流とそれが力を受けることの間にある。

電流素片が距離 r の場所の磁場を生むビオ・サバールの式は、自分の場所 r= 0 については定義されない。磁場の大きさは 1/r^2 に比例し r= 0 で無限大になるが、それは、現実とかけ離れている。現実の電線は、ある程度の太さをもち、電流は、 電線の太さに広がって流れている。並行電流は互いに引力を及ぼすから、電流は自らを細めるピンチ効果をもつが、 電流が中心部に狭まると抵抗が高くなり、自然にそれを避ける性質がある。通常の大きさの電流でピンチ効果は小さく、 それ以外の効果もないので、電流素片が自分の場所に生む磁場を考える必要はない。そこの無限を外して計算してもよい かもしれないぐらいである。

電流素片は、その方向の直線を取り囲む円環状の磁場を発生する。素片からの距離の 2 乗に反比例し、直線との角度をθ とすると、sinθ に比例して直線に垂直な場所には強く、直線の方向で弱い。そのため、明らかにできることとして、 直線電流は、自身に影響を出すことはないことである。直線電流は、自ら発生する磁場から力を受けて進み出すことはない。 曲った電線以外、自身に影響を及ぼすことはないのである。それさえもあり得ないと考える方は、次を注意深くお読み下さい。

電線が自身に影響を及ぼす例がある

一般に、電流が自ら発生する磁場で力を受けて進み出すことはない、というのは間違いで、それには反例があることを示そう。 十字交差する電線の図において、交差する電流を中央で組み換える。電流が左から上へ x 方向から y 方向に曲り、右下角では、 y 方向から x 方向に電流が角を曲る。電流の組み換えによって電流と発生磁場は変わらないまま、物体としての電線が左上と 右下とに分離する。左上の電線の受ける力は、合計で右下を向き、右下の電線の受ける力は、左上を向く。これは、電線が 2 物体に再構成され、作用反作用になったということだけだろうか。そうではないのである。よく見て欲しい。ここには驚きがある。 左上と右下の電流それぞれが単独でも元の構成と同じ方向の力を受け、両方が十字構成をするときの半分の磁場を片方だけで発生し、 自分の磁場から力を受けるのである。

曲った電線は、それだけで自分の作る磁場から力を得て動き出す。これは、無限の長さの開いた電線だから起こり得る奇跡であって、 有限の物体の恐らくは閉じた電流では決して起こらないことだろうか、無限の電線は数学的に単純だから使うだけで、 遠方が距離の 2 乗に反比例して関係がなくなるなら、無限の長さは、十分長い有限の電線を近似しているだけかもしれない。 くの字型に折れ曲がった電線は、そのほとんどの力を折れ曲がりの近傍で得るのは確かである。また、有限の物体であっても、 電荷の移動なら開いた電流ができるから、まだ可能性が残る。しかしそれは、力学的な運動量保存に反するあり得ない物体である。 また、電流交差の力は無限大になるから、正しいことは何も言えないのかもしれない。直線 y=0 上の電流からの距離 y の点の磁場は、 1/y に比例する。∫_b^a dy/y = log |a/b| である。b→0 で ∞に発散する。

2 つの電流素片が平行のときの影響が作用反作用であるように、電流素片間のなす角度θの cosθ に比例する力は作用反作用成分 であり、sinθ 成分が残余を作ると考えられる。

閉じた電流は、作用反作用以外の力を受けない

電流は、電流密度の面積分であるが、電流素片の線積分である。電流 di_1 が点 1 から 2 への距離 r_12 によって遠隔に 磁場を作成する。di_1 と r_12 の外積に |r_12|^-3 を掛けた電流素片 di_1 の影響を電流経路 c1 について線積分したものが、 点 2 の磁場である。

B_2 = ∫_c1 di_1 x r_12/|r_12|^3

磁場中の電流が力を受ける。場から電流が力を受ける力 di_2 x B_2 を電流経路 c2 で線積分して電線の受ける力になる。

F_2 = ∫_c2 di_2 x B_2
F_2 = ∫_c2 di_2 x ∫_c1 di_1 x r_12 /|r_12|^3
F_2 = ∫_c2 ∫_c1 di_2 x(di_1 x r_12)/|r_12|^3

ベクトルの公式、A x (B x C)= (A・C)B -(A・B)C を使い、

F_2 = ∫_c2∫_c1 (di_2・r_12)di_1/|r_12|^3 - (di_2・di_1)r_12/|r_12|^3

この式の第 2 項は、di_1 と di_2 の内積に比例する電流素片間の作用反作用の成分である。第 1 項が作用反作用でない 電流間の力であり、c2 が閉路のとき次のように 0 になる。c1 の各点の di_1 に乗算するスカラー (di_2・r_12)/|r_12|^3 を 1 を動かさず 2 を経路 c2 で一巡させた値は、

∫_c2 (di_2・r_12)/|r_12|^3

di_2= dr_2 (2 の座標の微分)であるから、

=∫_c2 dr_2・grad (1/r_12)

これは、例えば電荷を中心とする電場のように 2 を中心とするポテンシャル場の閉路の線積分で 0 となる。r_s1 と r_e1 とを c2 の経路の一致する始点と終点として、

= [1/r_s1 - 1/r_e1] = 0

1 の位置によらず、2 の一巡で倍率が 0 になる、1 で動かす必要はなく、1 のどこからの影響も 2 の経路全体で 0 となるから F_2 の第 1 項は、0 となる。力を受ける側の 2 が閉路のとき作用反作用以外の力が経路で合計して 0 となる。 例えば 1 が直線電流、2 が円環電流のとき円環が受ける力は、作用反作用の力だけであるが、直線電流については同様とはいえない。 c1 c2 の両方が閉路のとき作用反作用である。

円形電流が直線電流の磁場から受ける力

(1)直線電流 (x軸 y= 0) の作る磁場は、直線からの距離 y によって決まる。(0,y) 点から直線上の点 (x,0) への 長さ r=√(x^2+y^2)の線分の直線電流の法線との角度をθとすると、r cosθ= y である。(0,y) 点の磁場は、

B(y)= 2∫0〜∞ cosθ/r^2 dx
= 2 ∫0〜∞ y/r^3 dx
= 2 [x/(yr)]^∞_0
= 2 (1/y-0) = 2/y

(2)この磁場を原点を中心にした単位半円形の電流が受ける力は、円上の(x,y) 点の x= sinθ、y= cosθ、B(y)= 2/y から、

F= 2∫(-1〜1) cosθdx/y= 2∫dx = 2[x]^1_-1 = 4

この値は、直線電流から 1 の距離 (距離によって大きく変化する) のコの字型の電流の受ける力と等しい。ただ、 y= ax という斜線電流の [0,b] (0＜b)の電流の受ける力は、無限大になる。直線電流の近傍部分の影響が大きく、 直線電流に交差する傾き a が垂直以外であれば、無限大になる。

F= ∫^b_0 a dx/x = 1/a [log x]^b_0 = ∞

(3)円形電流の受ける力は、直線電流の両側の半円 (2)の 2 倍、8 になる。

磁場とは、電荷の視線速度の角度積分

ある点と電線との距離を y とし、その点と電線上の点との線分長さを r、線分の電線の法線との角度をθとすると、ビオ・サバールの式 B(y) = ∫ cosθ/r^2 dx は、次のように、 r cosθ= y, r sinθ= x から B(y)= ∫dθ/r と表せる。 'をθによる微分として式の変形で、 dx/dθ = (r sinθ)' = rcosθ + r'sinθ = y + (y/cosθ)' sinθ = y(1 + sin^2 θ/cos^2 θ) = y(1 + tan^2 θ) = y/cos^2 θ または、もっと簡単に下図から、cosθ dx = r dθ から dx/dθ= r/cosθ= y/cos^2θ をビオ・サバールの B(y) の式に代入すると、

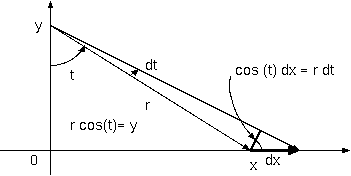
B(y) = ∫ cosθ/r^2 dx
= ∫ cosθ/r^2 (y/cos^2 θ dθ)
= ∫ y/(r^2cosθ) dθ
= ∫ dθ/r

つまり、電線上の線素 dx の線積分が、dθ/r を使うときは、電流の距離 r に反比例する電荷の視線速度の角度積分になる。 この見方は、電流がもたらす磁場において遠方がどう関係するかという問題に有効である。電流の原因は、電荷の速度である。 ある距離 r から電流素片を見たとき電荷の視線速度の角度積分が磁場を作るという見方は、もとのビオ・サバールの式よりも 基本的な理解かもしれない。

x 軸の直線電流が y 軸上の点に作る磁場がなぜ、1/y に比例するのだろう。それは、無限に長い電線だけのことで、有限の電線には そういう1/y に比例する性質はないのだろうか。ビオ・サバールの式は、なぜ cosθ がついた距離の 2 乗に反比例の 1/r^2 という 式であるのか、それでいてなぜ 1/y 比例なのか。そのような疑問を融くことができる。それは、y が大きくなれば、それだけ広範囲 の電線が視野に入るからである。電流素片の効果は、視野に入る部分が y に比例して拡大するから 1/r^2 から 1/y になる。

∫dθ/r = 1/y ∫cosθdθ =1/y [sinθ]^θ1_θ2

磁場が、電荷の視線速度の角積分なら、ある一定の高さ y から有限の電流を見た場合、磁場は、[θ1,θ2] の範囲の cosθ の積分であり、 無限の地平線の水平限界 [-90度,90度] をもつ。電線長が無限から有限に変わっても違いは小さい。±45度の視野では、 1/√2= 69%、±60度の視野では、√3/2= 86% である。電線が有限であっても y に比べて長いときほぼ 1/y に比例する。

磁場が電荷の視線速度の角度積分という磁場の理解は、実際に有効であるだけでなく、その式 ∫dθ/r の単純さも基本的な証拠である。 それに比較して、ベクトルポテンシャルに明確な意味づけがもし見出せないなら、存在の根拠の薄弱な概念ということになろう。

空間上に同符号の電荷が 2 個存在し、その電荷の大きさが Q1, Q2 とする。それらの速度を v1、v2 とすると、任意の場所からみた 2 電荷 の距離を r1, r2 としてスカラーポテンシャルは、φ= Q1/r1 + Q2/r2 と表せる。スカラーポテンシャルの勾配の符号反転 E= -grad φが、 電荷を結ぶ線分上で考えると、2 個の電荷の電場は距離の2 乗に反比例するから、両方の力がつり合う E= 0 となる場所では、 r1/r2= √(Q2/Q1) であるが、これは、重心ではない。重心は、1 次モーメントの和が 0 になる r1/r2 = Q2/Q1 であり、 ニュートン重力も同様である。重力の無いポテンシャルの勾配 0 の場所は、一般に重心とは異なる場所である。

(これは、一種異様な結果である。重心に質量を置くと、力を受けるだろう。置く質量は大きくても重心の位置を変更はしない。 全体系つまり、2個の電荷又は質量は、それと反対の力を受けるのだろうか。重心においた質量から受ける力は、その質量が受ける力を 丁度うち消すのだろうか、という疑問が出る。)

ベクトルポテンシャルは、A= Σq_iv_i/|r_i| とされる。A の回転が B= rot A であるが、B= Σ q_i r_i x v_i/|r_1|^3 が導けるか。 電荷が連続分布する、ρと i の式、φ= ∫ ρ/r dv, A= ∫ i/r dv から B= ∫ i x r/|r|^3 dv を導いてもよい。

電流素片 i を原点に x 軸方向に置き (x,y,z)での A を成分表示すると、A = i/r= (i_x/r,0,0)であり、rot (i/r)= (0, d/dz(i_x/r), 0), d/dz(i_x/r) = dr/dz d(i_x/r)/dr = z/r (-i_x)/r^2 = -i_x z/r^3 ゆえに B= rot (i/r)= (i x r)/|r|^3 これから体積分する前の式で 一致すると思われる。

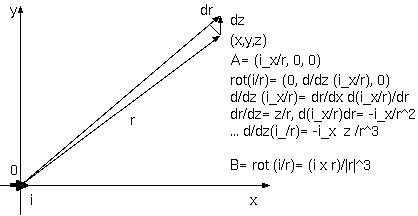
閉じた電流回路が任意の磁場から受ける力は、磁場の発生源の電流回路を考慮しなくても 0 である。 "箱の中の運動量"の 9. 磁場中の電荷の移動における力積 において、電荷が磁場のなかの 移動で受ける力の時間積分 (力積) を考えた。

電荷の速度と磁場の外積 qv x B の始点から終点までの移動の時間積分、 q∫v x B dt が力積である。 それは、磁場が一様でなくても始点から終点までの q ∫ dl x B という経路によらない値である。 線素の発散は 1 で (div dl) = d であり、A は、div A= 0 となるようとると、

B x dl = rot A x dl = A (div dl) - (div A) dl = dA

ゆえに、∫ dl x B = A これは、電流回路についても電流素片を dl とすると、任意の磁場中で回路の受ける力は、 終点のベクトルポテンシャル A の始点との差であるから閉じた電流回路では 0 である。