図1. 箱の中の運動量
目次 戻る∧
1. 箱の中の運動量は不可能か
2. ファインマン円板から、並進運動量へ
3. 電気双極子と磁気双極子の交差配置
4. コイルの両側の電荷
5. 円環電流とそれに近付く電荷
6. 一様な磁場の中の静止した電荷
7. 送電線の場の運動量
8. 直線電流の側の電荷
9. 磁場中の電荷の移動における力積
10. 磁場の発生源
11. 直線電流の側の電荷の運動量計算
12. 円環電流の側の電荷の運動量計算
13. 考察
14. 運動量の箱の中への閉じ込め
15. 浮揚装置ができてしまう?
16. 補足

Maxwell 方程式を満たす電磁場では、どのような静的な電荷と電流の配置でも、全体の場の運動量が 0、という仮説を立て、 証明すべきかもしれない。箱の中に運動量はあっても外にも電磁場があって、それが常に逆方向の運動量を持ち、 全空間の場ではつねに運動量はない、という予想である。この予想も証明は難しい。逆の予想では、一般に規制する法則のない場合、 任意というものである。私の結論も逆であった。
2 物体 a, b があり、a が b に 力 F_ab を及ぼすとき b が a に F_ba を及ぼす。 F_ab と F_ba は 向きが反対で、同じ大きさである F_ab = - F_ba (作用反作用の法則)。 力は、物体の質量mと加速度aの積 F= ma、加速度aは、物体の運動量pの時間変化(時間微分) a= dp/dtであるから、 物体間の作用反作用とは、a, b 間の運動量のやり取りが閉じていることである(F_ab + F_ba = 0)。 a が b に与える運動量変化 P_ab は b が a に与える運動量変化 P_ba と同じ大きさで逆方向である(dP_ab/dt= - dP_ba/dt)。 すなわち、物体間の作用反作用の法則は、a, b 全体の運動量Pの保存則である(dP/dt= 0)。 この法則は、衝突などの力学では成立するが、電磁気では成立しない。
運動する電荷には、ローレンツ力 q(v x B) がある
静止した電荷間のクーロン力は、つねに作用反作用の関係を満たす(図2(1))が、運動する電荷間には、磁場と速度による力がある。 速度 v をもつ運動電荷は、電流と同様に(右手親指方向の電流には四指方向に巻きつく)磁場を発生し、相手の発生した磁場 B からの力 q(v x B) が加算され、作用反作用を満たさない。
ファインマン物理の 2 電荷が直線交差する例で、電荷 a が x 方向に、電荷 b が y 方向に進むとき、 a が b に与える磁場 B は、 前半、紙面に向かう方向で、vはy方向だから、v x Bは、-x 方向。後半は逆に x 方向(図2の(2))。つまり、F_ab は 前半では -x方向、 後半では x方向、逆に F_ba は 前半 -y 方向、後半で y 方向である(図2(3))。作用反作用の関係は、どの瞬間も、作用線が一致し、 力の大きさが等しく方向が逆であるべきなのに、運動電荷の互いの磁場から受ける力はそれを満たさない。つまり、2電荷の運動量保存は崩れている。
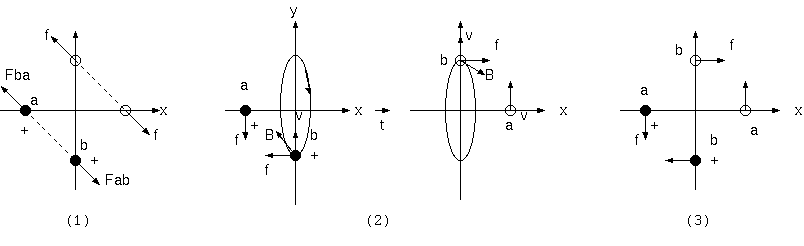
ファインマン物理の例は、x, y 方向に交差する2電荷を交差点に静止する座標系でみた例だが、同じ現象を片方の電荷静止系からみると、 相手が接近、接触し、遠ざかるだけの運動である。運動電荷の発する磁場に静止電荷は影響されず、静止電荷は磁場を発しない。つまり、 互いに電場だけの影響である。また、電荷の速度v方向の電場は、vによらない。a,bの対称性からも、作用反作用は成立する。
距離をもってすれ違う 2電荷を片方の電荷静止系からみると、上の例と同様、相手は磁場を発するが、自らの静止電荷は磁場の影響を受けず、 静止電荷は磁場を発しないから、速度をもつ相手に磁場の影響を与えない。つまり、互いに磁場の影響がなく電場の影響だけである。しかし この場合も、速度をもつ電荷の横方向に発する電場は、静止電荷の与える電場よりγ倍大きいという電場と力の非対称が2電荷間の運動量保存を崩す。 (力のローレンツ変換から重力へ参照)。
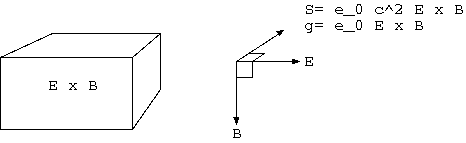
S= ε_0 c^2 E x B, g= ε_0 E x B
空間の一点には運動量密度 g が存在する。運動量は、エネルギー(質量)の移動を表す。 Poynting ベクトル S は、単位面積当たりのエネルギーの流れを表す。 これは、体積あたりの運動量、運動量密度 g に比例する。 その時間微分 dg/dt は、場が受ける圧力、その発散 div g は、場のエネルギーの発散、 その全空間での積分∫ g dvが場の運動量である。
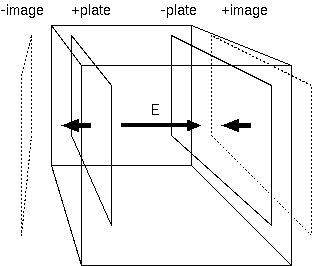
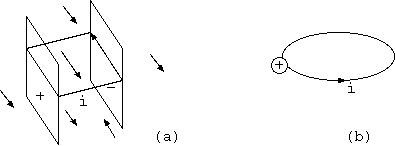
(反論者) (1) 箱の中の運動量を疑う。極板間に望みの電場を与えても、極板と箱の間にすきまの空間があり、そこには極板間と逆方向の 電場が存在する。導体の箱の内部の壁には+極板の反射像として逆の電荷ーの極板像がみえるから、すきまには極板間と逆の電場が存在する。 すきまは小さくて無視できるという訳ではない。すきまの間隔が小さいなら電場は間隔の逆数で大きい。電場と間隔の積は電位であり、 箱の中の和は一定0である。極板から箱の内壁までは像までの半分の間隔で、各極板と箱とのすきまは、極板間の電場と距離の積の丁度半分を打ち消す。 任意の電場の設定が可能どころではない。一様な磁場を外部から与える導電性箱の内部の運動量は0である。
(反論者) (2) さらに遮蔽を疑う。電荷を含む箱は導体によって包んでも遮蔽できない。導体によって電場遮蔽できるのは、外部から内部へだけである。 内部から外部への電場は遮蔽できない。箱の電場の発散はガウスの法則によって箱の中の電荷の総量であり、不変である。
(1) なるほど、一様な磁場中の導電性の箱ではそうなる。私は先程確かに、一様な磁場といったが、箱の外から与える磁場は一様である必要はなく、 極板の間に大きさを合わせたコイルで与えてもよいから、電場が一定の方向と大きさをもつ極板間だけに磁場を与えることができる。 磁場が一様なとき完全に打ち消されるなら、非一様のとき完全な打ち消しはできないということである。そして一般に箱の中の E x B の総量は、 0でない値を取り得る。例えば、極板の外側に内側とは逆向きの磁場を与えることも、長方形コイルを極板位置に合わせて設置すればできる。そのとき、 極板間の外側では電場と磁場ともに内側とは逆で運動量密度 E x B は箱の中全てで同じ方向を向き、総和は0でない値を取り得る。
(2) 箱の内部から外部への遮蔽は、単に包んだ導電体を接地すればよい。内部の電荷とその変動を打ち消す電荷と時間的空間的変動は、 アースを経由して導電体に現れ、導体表面が等ポテンシャル面になって、内部電荷は外部から見えなくなり、外部に洩れる電場を0にできる。 内から外への電気的遮蔽も、多くの機器で実際に使われている。
(3) さらに、これは、導体で覆われた箱に限定する必要はない。外部に磁場がない長いソレノイドを曲げ円環にしたトーラス(ドーナツ)型がよい。 このとき、磁場はトーラス内部に限定され、トーラスにギャップを設けてそこに電場を掛けて、空間全体で0でない運動量をもつことができそうだ。
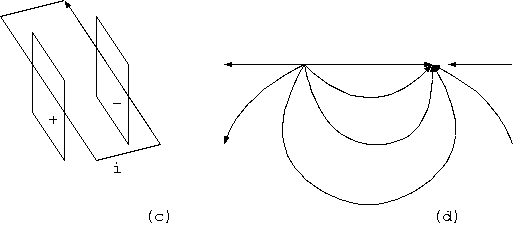
(反論者) 次々に不明な条件を出して幻惑してはいけない。電磁場は空間に任意に実現できるものではなく、Maxwell 方程式に従って電磁場はできる。 それによって、1) 結局、ある空間領域に運動量があって、それ以外の領域は運動量 0 は原理的に不可能ではないか。 さらに予想すれば、2) 基本的に、空間全体で電場と磁場との外積の空間積分が0でない電荷と電流の配置は存在しないのではないか。
1)の予想はすでに否定したのだが、論理が否定の否定、背理法だから説得性が薄いか。2)の単純な予想は、反論者の理想の表現だろうが、 この予想の証明は難しい。これには既に 送電線の電磁場の反例 (後述) があるのだから。
(反論者) (しばらく、送電線の電磁場の電場と磁場の方向を確認して、押し黙り、) これは、無限長の送電線の断面の2次元であり、 長さが限定された現実の物体、送電線を絶ち切った部分では、これは成立しない。
この反論の誤りは後に分かる。送電線型の電磁場は、無限長でなくても、十分長くなく短くても、帯電した電流だけで運動量をもつのである。
(反論者) 電場と磁場の外積 ExB ベクトルの空間積分を、数値計算してみればよい。どのような場合も計算すれば0に近く、近似精度を上げれば 上げるほど 0に近付くことを見出すだろう。
電流と電荷で構成する電磁場の運動量密度 E x B を空間全体で積分する 12章の数値計算は、 それが0でないことを確認できる。最も単純な運動量の存在する例として円環電流の側の電荷のなす場は、実際に 0 でないある単純な有限値になる。
(反論者) 反論者の原理的な疑いは、それでは解けない。これには理由がある。静止した箱に運動量が保持でき、場は物体でないからと 重心移動が必要ないなら、重心の静止した運動量が存在することになる。それは普通の世界ではない。逆にもし、箱が静止して重心が移動するのなら、 場の重さが箱という場の位置する場所に属さないことになり、場の概念を壊す。時間がたてば箱の重心は箱から離れて宇宙の果てまで行ってしまう、 これはさらに理解不能である。いずれも正常な物理ではないようにみえる。重心は場を生成した物体から離れてはならないだろう。 電磁場のエネルギー (E^2+B^2)/2 は場の特性であり、箱の場所に属することは明らかである。そのとき重心はエネルギーに依存して、 運動量には関係しないのか。これは何かが根本的に間違っていることを表すと考える(*)。
反論者の「原理的な疑い」は、その結果が反論者が期待する原理に合致しないだけであり、疑うべきはその「原理」だろう。 物体の静止系で場の運動量が存在するとき、それが物体静止系に付随して移動するのではなく、運動量が存在しなくなる速度 v<c の系の存在をいう。 (v/c)/(1-(v/c)^2)= (ExB)/(E^2+B^2)の式の値、場の運動量を場のエネルギーの2倍で割る非相対論的な速度は v/c である。
(反論者) この箱をのせたロケットは物体の運動量を箱に移せば空間で任意に静止でき、箱の電場または磁場を切って箱の運動量をなくすと、 その運動量は物体に戻し、また同じ方向に進行する、その様子はまるで UFO である。この箱の方向は任意に変更できるだろうか? 任意なら、 停止したロケットが向きを変え元の方向に戻る運動量を得られ、運動量保存則が崩れる。方向変更に運動量が必要か。 この変わった挙動を示す箱は存在するか? 妄想ではないか? ジャイロを入れた箱は、方向を変えるトルクに抵抗して歳差運動をするが、 質量は運動量をもつとき重心移動するものだ。運動量をもつ静止した箱は見たことがない。
しかし、実在とは法則の正しい適用でしかない。反論者は、運動量保存が、場と物体の両方の和の保存であることを認めた上に、 力学的な運動量保存を主張する。それは、場の運動量は局所にあって全体空間にないとすることである。Maxwell方程式や作用反作用の物理法則は 一般に微分と接触の法則である。そんな遠方の場の規制があり得るのだろうか。これは明確にする値打ちのある問題のようだ。
例えば、室内の扇風機の風は、循環しているが運動量を持つだろうか。室内でどれほど強く風を送って壁に圧力を与えても、部屋は動かない。 壁の受ける力は扇風機の受ける力と打ち消される。しかし、開放空間中のプロペラは空気に速度を与え、その流れは運動量をもち飛行機を推進する。 箱の中の風は循環するが、開放空間の風は、プロペラの力で起こされた運動量をもち、箱の中の運動量は、前後の壁をなくせば壁への圧力は推進力になる。 風は空気質量の流れ、これは電磁場のエネルギーの流れである。電荷に力を与える電場の時間積分、ベクトルポテンシャルが電荷に運動量を与える。 もしも、このベクトルの流線が電場と磁場の力線のように等方だったり開放空間でも循環するのなら、それは、運動量を持たないだろう。 粘性のない "乾いた水の流体力学" のように、流れのせき止めが圧力も与えないだろう。そうでなければ、運動量をもつのではないか。
(*) 両者気が付かなかった間違いは、運動量の場(=エネルギーの流れ)に重心移動があると思っていたことである。反論者がファインマンの 円板の周りには運動量がビュンビュン回っているだろうというと、私は質問した。ファインマンのコマは立つか? 反論者は電流をOFFするまで コマは立たないだろうという。それは場の運動量は力学的には見えないということか、ならば、運動量を閉じ込めた箱も、これと同じく不思議 な動作をしないだろう。"そのとき重心はエネルギーに依存して、運動量には関係しない" ことが正しそうだ。現実に力学的運動量があっても、 川の流れに重心移動はない。それは水という質量が流れているが、流れの位置は移動しない。
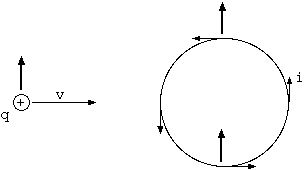
それは、ファインマン物理 III で提示され、IV で説明された。コイルの電流を切る前、電場は、円板上の電荷から放射状に広がり、 磁場は、コイルの外側では上下に回転軸にほぼ平行に存在する。場の運動量 E x B は、これらの物体を取り囲み回転する方向をもつ。 コイルの電流を切ると場の運動量が消える。磁場の時間変化 -dB/dt が電場の rot だから、一時的に回転電場ができ、 電荷が場から回転の力を受ける。こうして場の運動量は物体に移され、物体が回転する。もちろん、場の運動量は非常に小さい。 "これは思考実験であり、実験しようとしてはならない"、とファインマンは書く。しかし、現実に角運動量が場に蓄えられるのである。 物理や電磁気は、難しく悩ましい数学は本質ではない。現実の配置の微妙な解を得るために数学は必要だが、それは物理ではない。 物理学の問や解は、実にシンプルな美しいものである。
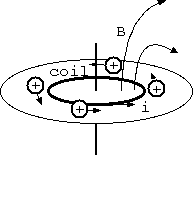
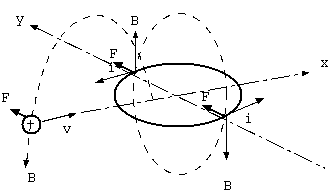
(反論者) そう、これは不思議ではない。ここに電荷を集めるとき、仮にまっすぐなレールを軸から放射状に用意する。 磁場の中を無限遠から引っ張りこまれる電荷はレールに垂直な力を与え、そのとき円板は回転をしようとした。 静止した物体はそれを止めた後の状態であるから、磁場を切ると、場から物体へと角運動量が解放されると説明できる。
磁場は下向きとして、放射状のレールに正電荷が左から近付くとき、力は v x B で紙面に向かう奥行き方向である。右から近付くとき、 速度vが逆で力は紙面から出る方向である。両方の力は偶力 (作用線に距離をもつ2力) を成して、回転を引き起こす。
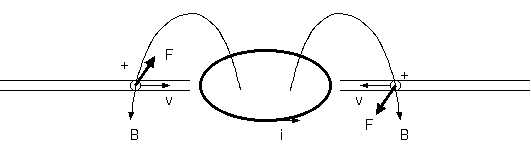
ところが、コイルのまわりに集める電荷をプラスとマイナスにして対極位置に持って来ると、これは並進の運動量を蓄えることができるのではないか、 という疑問がすぐに出てくる。右から近付く電荷を負にすると、それが受ける力は先程の逆で、紙面に向かう方向になる。両方の力は同じ方向を向き、 並進の運動を生む。
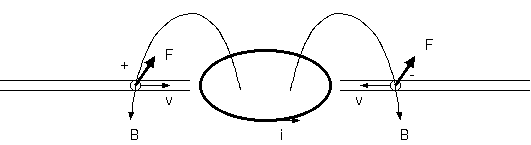
電荷を無限遠から軸に近付けるとき力を受けていたという、場に運動量、角運動量があることの反論者の明快な説明において、 両方正の電荷を正負の電荷に変更してまずいものは何もないのである。しかし、ファインマン円板では角運動量だから、 局所空間にあってもよいが、さすがに並進の運動量は、存在できないのではないかと、常識が否定しようとする。 この思考への抵抗は激しい。
(反論者) それを一言で言えば、"並進の運動量が場に蓄えられるなら、その重心はどこへ行ってしまうのか" ということである。 場といっても物質と特に区別するものではない。エネルギーも質量をもち、慣性も重力も持つ。運動量とエネルギーとがあれば、 重心はある速度で移動している。それが静止しているとは、どういうことだろう、ということである。
電場Eと磁場Bとの両者から、運動量がみえない座標系の速度(場の速度といえば誤解を招くかもしれない)v(<c)を導くと、(v/c)/(1-(v/c)^2)= (ExB)/(E^2+B^2)。場の運動量を場のエネルギーの2倍で割ると、光速を超える4元速度のような表現になるが一種の速度である。 これは、場の重心の移動速度であり得るではないか。それが静止し持続的に蓄積できるとは、どういうことだろう、ということである。
それに対して、電場Eや磁場Bの値は、座標系を決めれば変わる必要のない、一定不変のベクトルの値を取り得るし、そして、運動量に関する量 E x B も不変なベクトル値をもつことができる。そのような静止した電場と磁場で構成された運動量をもつ空間とは、一体、何を導くのだろうか。 冒頭のパスカルの言葉 "静止している運動量"のような、矛盾の集中ではないか。
そのような静止した運動量の箱は、まだ知られない禁止則によって、なぜか実現できないようにできているかもしれない。そのような理解の例は、 "環状電流のリングに電荷が近付くと静電誘導によって反対符号の電荷が集まって近くが帯電するから、常にリングと電荷のもたらす場の運動量は0である" と予想し、計算する論文はこの方向である。但し、環状電流リングの素材は、導電性とは限らない。環状電流は良導体だが、フェライト磁石は不導体である。 不導体と良導体とで静電誘導は異なるから、それだけで、この論文の場の運動量の否定は、成立しないと、私は判断した。 この論文の存在を教えると、反論者は残念なことに論文に即座に賛成した。
また、5章で述べる"いまさら電磁気学?"(青野修)の "変位電流が反作用を受ける" というのも場の運動量を否定するかにみえる。作用反作用が (電荷と変位電流との)物体間で成立して場に運動量はないように解釈できるが、これを変位電流(=電場の時間変化)を場と理解すれば、 場に運動量を貯める過程と解釈できる。
(反論者) それより、これは、UFO研究ではないか。
ファインマン円板を知っていて、並進に考えが及ばない人は、驚き、反発し、考えたくないと拒否する。そう、大抵の人は、このような考えの人とは、 つき合わないほうが安全と考えるかもしれない。「もしかすると、あなたは UFO 研究者ですか」と、慇懃に聞かれることを我慢できるだろうか。 ファインマンが並進に言及しないように、「李下に冠を正さず」、危険を察知してここで考察を止めるのも、当り前の態度である。
UFO研究は科学からの逸脱(=似非科学)で、恐らく99%ではなく100%嘘の雑多な目撃談を信じ、未知の運動力学を考案し、未来技術を期待し予見する。 その萠芽を目指すのならよいが、不可能な機械を作り出す目的が、最初の目撃談を裏付けるためと、話が一巡するのは無意味である。 現実にない未来科学を使用するSFは、現実性欠如であり、超現実的なSFを書く作家は、科学者からも尊敬される。SFは未来科学を使用するが、 未来にも実現しない虚偽科学がある。SF は未来を創作性に科学を現実性、実証性に使うから、物語性や面白さの為に、虚偽科学を入れてはいけない。 但し、虚偽科学かどうかは、作家の判断である。逆に作品によって作家が判断されるものだが。今までの UFO研究は恐らく実証性や蓋然性も無視して平気な、 "最低のSF" より悪い。UFOの推進原理とされるものが物理常識から唾棄すべき屑と分かるからである。当たり前に知ってほしいことは、 相対論や電磁気に真面目に取り組んで、相対論否定論者や、トンデモ学者、UFO研究者になることは決してないことである。 そこまで忘れることはあり得ない。いや、忘却ではなく、その人達は最初からそういう態度なのである。 学問の基本姿勢は、現実から学ぶことで、どこかで科学を捨て、空想に遊ぶことではない。そのため「UFO研究者ですか」は侮辱的である。
(反論者) 止めたほうがいい。エネルギー保存、運動量保存という巨大な原理を認めたなら、十分ではないか。電磁気や物理では素直に解けるものと、 そうでないものがある。いや、単純化して解ける問題は、現実の複雑な問題の、ほんの一部である。そして、原理的な問いは難しい(=この問題は君には無理)。 私もよく言われた「考えるな計算しろ」、量子力学の観測問題のような難しい問題に一生を棒に振るのは単なるバカである。 そのような基本問題に不用意に足を突っ込むのは大抵素人で、常に大きな誤解がある(=素人は口を挟むな)。 電磁気は、演習ばかりで面白くないものだ(=長い歴史をもち、多くの人が踏み固めた古い電磁気に謎が残るはずがない)。議論をする私の名前は出すな。
これは、電磁気学のなかの、少なくとも挑戦する値打ちがある、難問かもしれない。なぜなら、反論者(博士)はこの問題の存在自体を知らず、 未考察を露呈している。反論者も物体と場の全体の運動量保存を認めた上での議論である。箱の中の運動量を認めることは、中原中也の 「朝霧を煮釜に填めて跳起きられればよい!」のように、持ち運びできる箱に運動量を詰め込み移動することであり、 宇宙船に運動量保存を無視した動き、力学的な運動量非保存を望む。それに対し、力学的運動量保存を望めば、箱の中の運動量を認めず、 静止場の全体空間での積分が0という法則を仮想して整合性を計る。しかし、基本的に電荷の運動は物体だけの運動量保存がないのだから、 電磁場と力をやりとりするロケットは、力学的運動量保存を示さず、奇妙な運動をすると考えるのが自然である。
又は、可能なことも通常の生活から掛け離れた条件でしか発現しない物理であって、正しい結論も測定に掛からないことは十分に考えられる。 測定は無意味ではないが、重要なのは存在するかどうか、正しいかどうかである。その段階の方法論は、常に誤りやすい思考実験である。 ファインマン自身が "実験しようとしてはならない" というファインマン円板は、現在すでに測定可能と思うし、同じくその並進運動もと思うが、 電磁波で20年、重力波で100年のように、確認が難しいものは存在が疑われ、発生できないものは役には立たない。例えば、質量や重さを大きく 変化させる装置や反応は、聞いたことがないが、仮に1kgの質量の重さを1g減しても (測りで測定できるが) 物体が浮き上がることはない。 しかし、その効果を1000倍にできれば、その存在を "誰も議論しない" だろう。それは相対論で議論可能になった質量で、これは運動量だが、 普通に扱える電磁場の範囲では極端に小さく、存在が不明である。質量増減装置は現在全く手がかりがない、無いものねだりで、物体縮小や時間停止も 同じだろう。そういう装置を安易に望むことはSFでさえ批判されるが、手がかりは物理法則自体にあるだろう。
(反論者) 磁場中を電荷を引き込むときに回転を生む2個の正電荷と、正負の電荷とではエネルギー的な違いがある。正電荷2個を引き込むのには 仕事が必要だが、正負の電荷では仕事が要らず逆に仕事をさせることができ、自然にその状態に入ることができる。つまり、正負の電荷の接近は、 負のエネルギーをもつ。これは、場が運動量をもつ事と矛盾しないか。負のエネルギーが運動量をもつのか。
これは、場のエネルギーや運動量が、物体のエネルギー変化から生まれていると考えれば説明がつく。正負の電荷の接近では仕事をさせることができ、 電荷は運動をすることができるが、それは質量が万有引力のもとで接近するときに速度をもち、運動エネルギーを得ることと同種である。そのときも、 物体が負のポテンシャルにくることで、物体が運動し、運動エネルギーと運動量を得るのである。正負の電荷の接近では電荷は速度をもつ。この速度は 運動エネルギーであるし、電荷と場のエネルギーの総和は負であるが、正負の接近でも、電磁場のエネルギー(E^2+B^2)/2は正であり運動量も持てるだろう。
(*)コイルに左右から正負の電荷を近づけるとき受けた並進の力積は、装置経由で地球に止められ静止しているが、空間の運動量は力積の反対の値を持って 重心は移動せず、電流を切って磁場を無くすと運動量が装置に返され、装置が力積を受ける。単に技術的に遠いためこれを常識が不可能にする。本論は 可能かどうかの原理的な議論である。実際的な装置にするには多くの問題を克服する必要がある。ExBの値には透磁率の高い絶縁層をもつ積層コンデンサ が必要だし、上空からの降下には重力に反発しながら位置エネルギーから力積を運動量に徐々に変える方法が必要だろう。(2022/3/12)
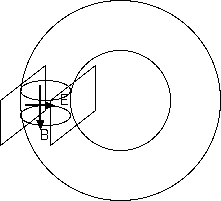
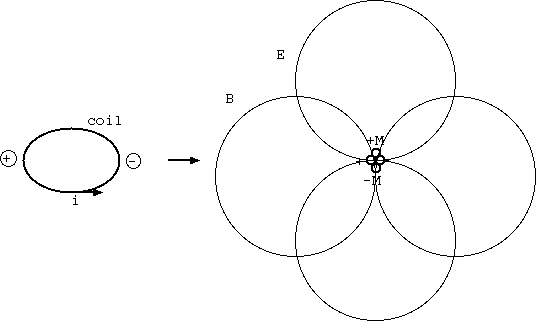
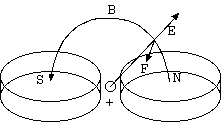
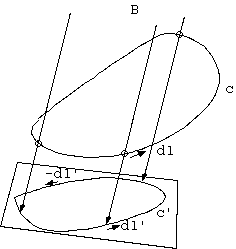
現実のコイルとそのそばの対極に置いたプラスとマイナスの電荷の配置の場の模型として、 磁気双極子と電気双極子を 90 度ずらした配置の全体場の運動量を計算すると無限大になる(16.4参照)。 ある半径より外では常に同じ方向の有限の値を持つ。 ある半径より内側が外側を打ち消すことはないので、 これは電子のエネルギーが無限大になるのと全く同じ困難さでしかない。 運動量は 0 ではないと予想される。
(反論者) 物理量に無限大を導く解は、解でないし、予想に意味はない。磁気双極子と電気双極子とは点電荷ほどには現実性がない。 現実のコイルと電荷の配置の遠方の場を表すかも知れないが、その内側の場が考慮されてないから無意味である。
このような場合、運動量が全空間でどのような値を持つかは、 数値的にでも解かない限りプラスともマイナスとも 0 とも言えない。 ただ前後の空間の運動量は、大したものではなくコイルの左右領域と同程度であろうか(図 7.(a))。
コイル形状が任意の場合、コイルの堀の内側に属する 3 次元領域では磁場が上向き成分があり、 外側では下向きを保つと単純化して仮定し、 異符号電荷の作る電場の水平成分が右向きである領域だけを囲むようにコイルを置くことができるとすれば、 そのコイルの内側領域全ての点で、E x Bの運動量はこちらに向かう成分を持つ。 しかもコイルの内側は、次のように任意にどこまでも広げることができる(図 8.(d))。
+ と - の電荷を x 軸上に配置し、xy 平面上の電場を見る。 電場の x 成分が正の領域だけを含むように xy 平面上にコイルがある。 コイルの磁場の z 方向成分は、コイルの磁場を単純化してコイルの内側に属する全ての z において正、外側で負であるとする。 コイルの内部領域で、E_x > 0 かつ B_z > 0から、運動量の y 成分、M_y= E_x B_z は正である。
コイルの外側領域の、電場の x 成分が負の領域は、つねに運動量の y 成分 E_x B_z は正であるが、 コイルの外側領域であって、電場の x 成分が正の領域が運動量の y 成分が負になる。 しかしこの領域の効果は、コイルを規則に従って拡張すればどこまでも減らせるのである。
(反論者) コイルの磁場の単純化があるため、これは、異符号電荷とコイルの磁場のもつ運動量が 0 でない証明ではなく、定性的説明である。 実際のコイルの磁場は、z が xy 平面から離れるに従って、内側領域( B_z > 0 )が広がるものである。また、1 対の電荷の作る電場は軸対称だが、 これも E_x >0 の領域は、z が xy 平面から離れるに従って広がるものである。そういう3次元で全領域の運動量が同方向ならよいが、 逆方向領域がどこまでも減らせるというのは説明としてよいのか、論理的なのか。逆領域は減っても運動量が減らない可能性はないのか。
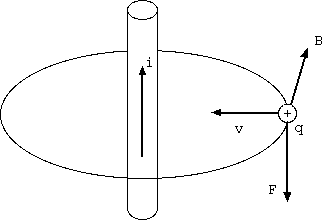
"いまさら電磁気学?" (青野修、丸善) の円環電流と直線運動をする電荷の話。右方に環状電流(電流は反時計回り)があり、 左から接近する電荷(+)がある。右方に環状電流があり、左から接近する電荷がある。電荷がコイルに近付くとき、 コイルの磁場が電荷に与える力と、電荷の移動がコイルに与える力とがともに上方、同方向である(図 9.1)。 環状電流から移動する電荷に作用する力と移動する電荷から環状電流に作用する力とは同方向を向く。 それらは、作用反作用の関係にはないとの説明だった。また、これらの力の反作用を電磁波とすることはできない。 電荷は直線上を進むので電磁波を発生しない。
この本は、電荷の移動によって、周囲には電場の時間変化(変位電流)が発生し、これが逆向きの力を受けると説明する。 しかし、電場の時間変化は、物質ではなく場であり、場が力を受け、運動量を蓄積する過程の説明である。 電荷がコイルの近傍にある事自体が、場の運動量をもつ配置なら、それに至る力の説明となりえるが、 静的電磁場の運動量への疑義に対し、電場の時間変化でどう理解できるか(*)。
電荷移動は電流に置換できる。運動する電荷は、遠方から環状電流の外で止まるコイルを挟む位置に電極をもつコンデンサを 充電する部分電流に置換できる。もし、変位電流が電流の一種ならコイルの内部を通過し逆向きのコイル内磁場による力を受け、 この静止場の運動量の謎は発生しないが、反作用を受けるという電場の時間変化(変位電流)は場であり、物体ではないのである。
(*) コイルの(少し内側)両側に極板をもつコンデンサの空間の電場の時間変化(変位電流=場)は、コイル外電流と逆向きの力を受ける。 電場の時間変化に等価な電流がコンデンサに充電されてコンデンサ電圧とコイル内の電場は上昇し、E x B は運動量をもつ。 コイル内磁束は外部磁束と逆で、コイル内の磁力線は全てコイル外を通るため、コイルを横切る部分の電線は、 コイル外の両側に延長した電流の受ける磁力線を逆向きに受ける。コイルを横切る直線電流が受ける力が全体で0なら、 コイル内変位電流の受ける力は、コイル外電線の受ける力の反作用であり、場に与えられる。図9.3 は動作原理図であり、 コイルはN回巻くことでN倍に増強できるが、こんな大きな空間のコンデンサは容量が少なく、一瞬で高圧になり、 逆に設定電圧までの電流の持続時間は短いから、運動量測定実験は容易ではないだろう。 また、導電性の箱の運動量(図3)と同じく、電極とコイルとの隙間にある逆向き電場の問題がある。
コイルの両側の電荷の作る電場は、それぞれの電荷の作る電場の和であり、運動量密度は E x B に比例するから電磁場の積に比例するが、 電場単独には線形加算でき、運動量密度はそれぞれの運動量密度の加算になる。そのためコイルの片側の電荷の運動量を考慮すれば十分 である(図 7.(b))。片側の電荷の作る運動量と、他方の電荷の作る運動量は独立に計算でき、両側の電荷の運動量は、それらの和である。
同符号電荷では、逆側電荷のもたらす運動量と打ち消し、並進運動量はなくなり、角運動量だけが残る、異符号電荷を置くなら、 両方の運動量は同方向を取り、並進運動量が姿を表し、角運動量はなくなる。片側で軸から外れた運動量がなければ、どうして同符号点対称において 角運動量が出来よう。その場合、異符号点対称において角運動量は消え、並進運動量が現れるのである。
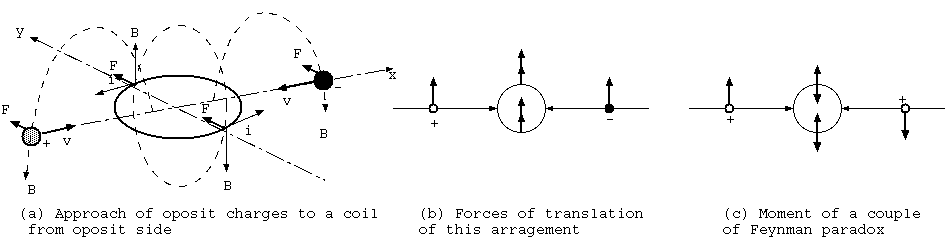
"いまさら電磁気学?"の円環電流に電荷を近付ける話は、図9.2の片側の形をしている。無限遠から電荷をそこに持って来る途中に、 電荷もコイルもずっと同じ方向の力を受けることは、片側電荷配置の静止場全体に運動量が存在することを示しているのではないだろうか。
(反論者) そんな無責任な疑問を読者に投げて平気なのか。コイルの磁場が共通で、片側の電荷の作る電場とコイルの磁場の作り出す E x B の空間積分の「運動量」が仮にあったとしても、左右両方から同符号で角運動量だけになって、異符号で並進運動量だけになるとは、なんと 都合のよい論理かと驚く。片側電荷が中心から外れた力を生み、両側同符号が丁度、偶力になり、左右異符号が、並進になるとは、逆なら よかったのではないか。運動量密度の空間分布が奇関数と偶関数でできている。左右同符号の和は、奇関数だけを残し、左右異符号の和が、 偶関数だけを残すという意味か。しかし、異符号が偶関数を残すという所は、君の都合のよい予想であり、私は残された偶関数は0だけと、 予想しよう。空間に角運動量は存在するが、運動量は存在しないと思う。
無限遠からの片側電荷配置への移動がコイル中心から外れた作用点をもつ運動量を与えるなら、同符号電荷で偶力、異符号電荷で並進になること が可能な証拠は、"いまさら電磁気学?"で指摘された、片側からの電荷接近がコイルに与える力と、コイルの磁場が接近する電荷に与える力の "同方向"の事実である。これが仮に逆方向の同じ大きさの力なら、片側の電荷の接近は(作用線が離れているため打ち消されず)偶力だけを与え、 両側の電荷が正負になっても偶力しかないが、そうでなく、同方向の力だから並進成分があるのである。
図5のようにコイルとそれへ接近する電荷という離れた場所への同方向の力は、和は0でない並進をもつ。下図9.2で左からの正電荷への力と、 右からの負電荷への力とは、コイルからの磁場Bが等しく、電荷qと速度vが共に反対だから、ローレンツ力 q(v x B)は、共に上方向である。 そして、左右の電荷からコイルへの力は、正電荷の速度方向を右手の親指にして他の指が包む方向の磁場を生み、左右の電荷は電荷qと速度vが 共に逆で発生磁場は加算され倍になり、コイルの上下の辺の電流iに上向きの力を与える(図9.2(b))。4ヶ所の並進の力は、全て同方向で打ち消せず、 合計は、0でない。 それが、異符号電荷の接近における0でない残された(偶関数)である。なお、同符号電荷の接近では左右電荷からコイルへの力は、速度vが逆で打ち消され、 コイルから左右の電荷に与える力は偶力であり、反論者の予想に一致する(図9.2(c))。こうした説明によって、反論者もその予想の誤りを理解されるだろう。
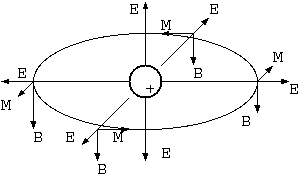
一様な磁場の中に静止した電荷は、対称性から考えて運動量を持たない。ある点には必ず電荷を中心にした点対称の位置があり、 そこでは電場が反対である。磁場が一様で、そこでも同じなら、運動量は反対になる。そのため、全空間の積分では運動量は 0 になる(*注 13. 考察を参照)。図10 にその様子を示すが、角運動量は、明らかに存在するだろう。
それなら、一様でない静磁場に置かれた電荷の作る場は運動量があるだろう。磁場が一様で、ちょうど打ち消されるのなら、 一様でない磁場に置けばよい。例えば、図10 の電荷の右側に磁場がなければ、バランスは崩れて、場の運動量が存在するのではないか。
(反論者) 電磁場は、任意に作成できるものではない。マックスウェル方程式を満たす電磁場でなければならない。 ここで、静止場とは、静電場と静磁場をいう。電流と静止した電荷で作成できる電磁場である。 また無限が介在してはいけない。例えば、どこまでも一様な磁場というのは実在しない。
しかし、コイルのそばの電荷は、まさにその可能な例であり、電荷の左右の磁場が対称でないだけではないだろうか。 コイルに左にある電荷は、その左側にはコイルからの磁場が徐々に弱まってあり、その右側には大きな逆向きの磁場のマンホールが 口を開けている。磁場が一様な場合に左右対称だから運動量が0なら、非対称なら運動量が0であるはずがない。
(反論者)そんな馬鹿な。言語道断。そんな無茶な論理はない。少しは論理立てて証明しろ。一様なら運動量がないは、 一様でなければ運動量があるを意味しない。一様でなくても運動量はないかもしれない。
コイルを電場に影響しないフェライトにして、左右にNS反対向きにした2個の磁石の間に +電荷を置く。電場は放射状で、 磁場は大半が(左右の磁石の外側を反対方向に流れる磁場もあるが、寄与は少ないとすれば)、右は上向き、左は下向きで、 左右で反対称である。それは、2個の磁石間を一巡する楕円のような周回を描く。このとき F = E x B は、右で前後成分 があれば、左の対称位置にも同じ向きの前後成分がある。上下は回転対称である。この配置は、運動量が0でないベクトルをもつ。
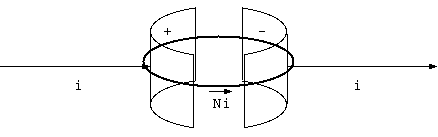
磁場はコイル電線の電流に巻き付いてあり、電場は電荷から放射状にある。電流の側の電荷について、8〜12章で考察した。 コイルのそばの電荷は、コイルと位置が一致した電荷(=帯電した電流)とあまり違わない。一致したそれは、次章の送電線の場だが、 電磁気の12章 のように、迫り来る電線の向かう電流は+に (逆に、逃げる電流は-に) 帯電してみえる。静止していても、+に帯電した電流は、電流方向の運動量が存在する。
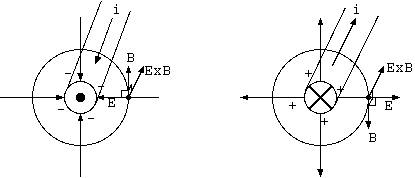
電力消費の現場に向かう電線を電線の軸に向かって見ると、2 本の電線には逆方向に電流が流れ、 進行方向の電流はプラスに、戻りの電流はマイナスに帯電している(図 11)。 この断面でのポインティングベクトルは進行電流には時計回りの磁場があり、 また、電場もその電線から軸対称、放射状に広がる電場がある。 そのため、近辺には電流に添った同じ方向のエネルギーの流れがある。 戻りの電線には、逆向きの電流による磁場は反時計回りであり、 マイナス帯電による電場の向きも反対であるので、 やはり行きの電線と同じ向きのポインティングベクトルがあることになる。 これは送電線で電力を遠方に送っていることを説明している。
つまり、電流が電位をもつと、運動量を持つ場をもつ。 断面での放射上の電場と電線を周回する磁場とは常に直交して電線方向の運動量をもつ。 戻りの電線も、電場磁場ともに逆だから、運動量は同じ方向、電力を送る方向に場の運動量が存在する。 戻りの電線と遠端点を結合したものを考えると、この長い長方形の電流は、 ポインティングベクトルが一方向を向いた空間を用意する。
ファインマン物理にあったように、抵抗を持った電線に電流が流れ、電流の方向の電場があるとき、 単位面積あたりのエネルギーの流れであるポインティングベクトルは、外から内に向き電線に向かう。 抵抗での発熱は空間から内側に向かうエネルギーの流れで補充されている。 このように、エネルギーの移動を場から説明する。エネルギーは、電線の中を流れるのではなく、 電線の周りを流れているのである。
電圧と電流との積で電力となるという通常の説明よりも、電線の局所に電位は見えないので、 この変わった E x B で説明する方がうまくいくことに驚いてしまうものである。 今までの交流理論とか、電気回路理論、過渡現象論、電気工学、電子工学、電気通信理論などすべては、何だったのかと。
(反論者) まだ、送電エネルギーを計算していない。符号が合致して大きさまで一致しても、違うことがある。 全てを信じてはいけない。似て非なるものがある。送電線の場では全体が無限に長いから運動量があっても不思議ではない。 そのような場の2次元的な輪切りでは、運動量が現実に存在しても当然である。有限長の物体の作る静止場が運動量をもつかどうかである。 問題は、箱の中の運動量であり筒の中の運動量ではない。(得意げに)どうだね。
無限長でなければ運動量が存在しないのではない。有限長の送電線でも、場の運動量は0でない。 発電所から電力消費地までの間に運動量が存在し、その先になく、その手前にもない。 それ以外のどこの空間領域が、発電所から消費地までの運動量を打ち消す運動量をもつのか。
直線電流に近付いて磁場が大きくなるにつれて、電流の方向を向いたベクトルポテンシャルA(*)も大きくなる。Aの中に電荷qがあれば運動量qAが存在し、 電荷qは、無限遠からその場所に近付くまでにその反作用の力を受ける。
(*) Aは、磁場BがAの回転(B= rotA)である4元ベクトル(A, Φ)の空間成分。伝達時間だけ以前の電流iからの距離Rに反比例するi方向のベクトル。 伝達時間だけ以前の電荷qからの距離Rに反比例するスカラーはΦ。 A= i/R_(t-R/c), Φ= q/R_(t-R/c)。Aには任意のスカラー関数fの勾配を加算した A + grad f = A' も同じBを生む任意性がある。緩い変化ではクーロンゲージ div A= 0 で任意性をなくせる。 スカラーポテンシャル Φ は電場 E と E= -grad Φ -dA/dtの関係がある。 Φへの任意の一定値(gradが0)の加算は同じEを生む。Aの時間微分の符号反転が電場を生む。
電荷がプラスで、直線上の接近のとき、電荷の受ける力はつねに電流と逆の方向である。 これの反作用は、場の運動量と考えられる。逆に電荷を無限遠に遠ざける場合に、その運動量は取り出される。 電流を切る場合、電線を取り囲む周上の磁場が減少する間、もとの電流の方向に電場ができる(rotE= -dB/dt)。 ベクトルポテンシャル A と電場 E の関係を使うとより単純に理解できる。
E= -grad Φ -dA/dt
の第2項 -dA/dt で、電荷は元の位置の A (電流の方向)に力を受ける。電流遮断の間の力の時間積分=力積は、運動量 qA である。
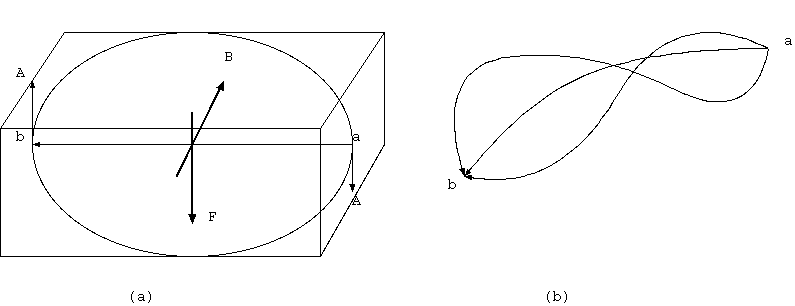
一様な磁場Bで電場0での電荷移動(図13.(a))は、電荷は、a点〜b点まで力 F = q(v x B) を受ける。この電荷移動の力積は、速度と時間の積dlで、 Bと位置a,b点により、vによらない。任意の磁場中(図13.(b))も同じく一定経路なら、力積(dl x B のa〜bの経路の線積分)は、速度によらない。
∫ dl/dt x B dt= ∫ dl x B
ローレンツ力の磁場の分 v x B の時間積分、dl x B と移動 dl はつねに垂直で、磁場は電荷移動の仕事Wに関係しない。仕事Wは電場の線積分であり、 静磁場(dB/dt=0)では b と a の位置のポテンシャル (電気的位置エネルギー) の差であり、a〜bの経路によらない。
W= ∫_l E・dl = Φ(b) - Φ(a)
なぜなら、rotE = -dB/dt より、閉曲線cを一巡する移動は仕事0である。
∫_c E・dl= ∫_s rotE・ds= ∫_s -dB/dt・ds= 0
c上に2点a,bをとり、cをa〜b移動の2経路l_1, l_2に分け(c= l_1 - l_2)、各経路の電荷移動の仕事は等しく、経路によらない。
力積、閉曲線 c 上で∫ dl x B = 0 を示そう。(1) c の力積は、その磁場 B (一様なら思考しやすいが、一様でなくて良い) の垂直面への Bによる射影経路 c' での B x dl' の力積を考え、経路の dl と、Bと直交する dl' とが対応し、dl x B = dl' x B 。 (2) そして、Bに垂直な平面(又は曲面)上の閉曲線 c' 上の dl' は、それを打ち消す対応する -dl' をもつから、c'上の線積分は0である。
∫_c dl x B = ∫_c' dl' x B = 0
ゆえに、仕事と同様に力積も、c= l_1 - l_2 と2点 a, b で c を分けた a〜b の2経路 l_1, l_2 は等しい。a〜bの電荷移動の力積は一定である。
∫_a^b dl x B = A(b) - A(a)
これは、電荷の移動に必要な運動量、電荷がその位置にあることの電気的運動量の場を示す。 ベクトルポテンシャルAは、rot A = B の関係で磁場Bの原関数で、qA が力学的な運動量である。
これは、力積(または運動量)であり、b〜aの逆方向移動では逆の運動量が与えられる。rot A= B という関係から、
B x dl = rot A x dl = A div dl - (div A) dl または別の表記をとれば、
= (∇ x A)x dl = A(∇ ・dl) - (∇ ・A) dl
第1項は A の dl 方向微分に dl を掛けた dA, 第2項は A の発散であり、クーロンゲージで div A = 0 とし、
-q∫_a^b B x dl = q∫_a^b dA = qA
ベクトルポテンシャル A の位置にある電荷 q は、運動量 qA をもつ。qA は、q による放射状の電場 E と、それを取り巻く A の渦 (rotA= B) によって E x B をもつ。電荷がそこへの移動で受ける力の反作用の力積が qA 又は E x B として場にある。 運動量は、位置だけにより、経路や速度によらない。静止場の運動量の存在は、E x B よりも、qA によって理解が容易である。 電荷 q は静止でき、Aも静止場であり得るからである。
一般にはないと考える。電荷が力を受けるとき、磁場の発生源が反作用の力を受けているなら、 それは、電荷と発生源の単なる2体の物体間の力学である。 電荷が逆方向に移動するときにバネを押し縮めた物体のように、電荷は行きと逆方向の力を受け、 磁場源もまた逆方向の力を受けるだけであり、2体の系全体の運動量は存在しないことになる。 それでは、場はバネでしかなく、場に運動量があるとか考える必要はない。
電磁気現象一般には、物体系の運動量と、場の運動量を加算して運動量が保存され、 物体と場の作用反作用の法則が成立する。
電磁気の運動量が、力学的に見えるかどうかも重要な争点である。 運動量が場に蓄えられているとき、電磁的運動量が力学的に見えるなら力学の用語で十分である。 重心移動が存在することを要求される。力学的に見えないなら、力学的法則は一部、破綻する。
電荷を通る面で電線と電荷を切ったx,y平面(z=0)で解析的に解ければ、 z 方向にずれた平面(z!=0)でも電場は放射状で、xy 平面に類似し、電場のz成分の効果は、 前後で打ち消されるだろう。これでも解析的に平面内を解くのは面倒である。
電線は (0,0) にあり、電荷が (1,0) とする。x 軸上だけを考えると、磁場は、
+-y 方向で、1/x に比例する。電場は、+-x 方向で、1/(1-x)^2 に比例するが x=1 で符号が反転する。
両者は直交するので、運動量の大きさは両者の積、
1 /(x (1-x)^2)
である。これの -∞から1 までの積分と 1 から+∞までの積分を比較すれば、 x 軸上の積分であるが運動量をもつかどうか決定できよう。
しかしよく考えてみると、これは帯電した電流の電荷が少し横にずれただけである。 遠方ではその差はないだろう。 一般に、少しずれただけで完全に様相が一変するということはない。 それなら、計算する必要もない。電線と電荷に大きさはない場合、 微小量のずれがどれほどの影響を与えるかは計算すべきだろうが、 現実の電線と電荷においてはもっと影響がないだろう。
数値的に解いた例は、 mom.c2 を参照。 ポインティングベクトルExBの面内積分は、 その面を通るエネルギー密度を表すが、数値積分では、ある値 6.28..を示す。 z 方向には磁場は変わらず、電場だけ 1/z^2 に比例で、運動量もその性質を持てば、 そのz方向の積分は有限かと誤認される。ところがx,y方向にも延びているため無限になる。 r 方向に延ばす場合、E は 1/r^2 に比例し、Bが 1/r に比例するが、体積が r^3 に比例し、 大きさを比例的に増加した殻も同じ運動量を持つ。 このような事情から、直線電流の側の電荷の持つ場の運動量は、無限大になる。
円環状のコイルが空間の各点に作る磁場と、電荷が各点に作る電場を単に外積すれば、 各点の運動量密度が求められ、これを全空間で積分すると、場のもつ運動量が計算できる。 コイルの作る磁場は、解析的にはかなり面倒な数学(第2種楕円関数)を必要とするので、 数値解によって求めるが、これが 0 ではないことを示す。
数値解は重要な確認にはなるが、その存在を示すのに、コイル形状のもたらす磁場の計算をして、 全空間の運動量を積分して見せる数値解がとくに説明において適切というわけではない。
コイルの作る磁場と、電荷の作る電場に従って、正確に数値的に解いた例は、 mom.c を参照。 円環電流の側の電荷の運動量の全空間積分の数値解は、次の方法で求めた。
原点(0,0,0)中心に半径 1.0 の円を、xz 平面上に置き、電荷の位置を、(1.5,0,0)におく。 ビオサバールの法則を適用して、(x,0,z) にある単位電流の流れる電流素片の点 Q から一点 P(x1,y1,z1)への磁場を円周一巡について計算する。
b+= dl x PQ /R^3
ただし、R は PQ の距離である。
電場は、単位電荷からの位置ベクトル x-xc を距離の 3 乗(R^3)で割ったものである。
e= (x-xc)/R^3
電場と磁場の y,z 成分の外積から運動量の z 成分を空間の連続点の代わりに、 メッシュ点で求める。それらにメッシュ体積を掛けながら、十分大きい体積まで加算する。 メッシュの間隔は、計算量削減のため、近傍では細かく (+- 10 までは0.1 )、 遠方では(+-10 を超え、+-100 までは 1 に)大きくとる。 また、対称性を利用し、x 軸方向には両方向、y,z 方向には片方向だけを計算し、 全空間はそれの 4 倍とする。
結果的に、運動量は存在した。コイルの側の電荷は静止場に運動量を与える。 静止電荷と定常電流で作られた静止場でも、場の運動量の全空間積分が常に 0 ということはない。 そのことが分かれば、円環電流に近付く電荷の作用反作用の力の問題も解ける。 それだけではなく、その場の構成を導くには物体にかかる力は、不釣合でなければできないのである。
これはまた、電荷点のベクトルポテンシャルと電荷量の積としても表現できる。 これも全く同じ値をもつべきである。これは、今井巧氏の著書”電磁気学を考える” (p383-384)に証明されていた。数値解では、4 π の比率がかかっている。
4 π q A = ∫ E x B dv
コイルと電荷が、ともに上に力を受けたのは、 場の運動量が下方に変化しているから物体には反作用が場から働いたのである。 場は物体の受けた力の反作用(下に向かう力)を受け、それが場に溜ったのである。
ドーナツ状の磁石の一部がギャップになって空間に磁場が出ているとき、 ドーナツ以外の部分に磁場がない理想状態において、 そのギャップの両側に磁場と垂直に電極を用意して電場を与えるとき、 このギャップの運動量はそれ以外のどこからも打ち消すことはできない。
一様な磁場の中の電荷が運動量を持たないように見えるのは、磁場だけを見るからである。 一様な磁場の異なる位置は、ベクトルポテンシャルが異なる。磁場だけを見てどこも 0 と いうのは理屈に合わない。電荷が磁場中を移動するとき、電荷はある力積を受ける。 電荷は変位によって異なる運動量をもつ。 このことは、一様な磁場中の静止電荷の運動量を言うことを不可能にする。 a 点で静止している電荷を移動させて b 点で静止させる。 移動の途中に電荷は場から力を受ける。b 点にある電荷はもとの a 点の電荷と、 周囲の場の運動量が違うのだろうか。一様な磁場という仮定では違いを言うことができないが、 途中で受ける力があり、違わなければならない。
(*) 電荷なしに場の運動量はない。電荷 q とベクトルポテンシャル A なしに、空間の運動量密度 E x B はない。 E x B の体積分を qA が与える。場の運動量が qA でもある、qAが E x B を起こしていること自体、 静止場に運動量を与える。なぜなら、q は静止でき、A は静止電流が起こせるからである。 エネルギーに重心はあっても、エネルギーの流れ、場の運動量に重心移動はない。ゆえに、場の運動量は、不可能でない。
長さ L の止まった客車が一両ありレールとの摩擦はないとする。 この客車の前方の壁から後方の壁に向かって鉄砲を打つ。 鉄砲の玉は後方の壁にぶつかって転がってもとの位置に戻る。 鉄砲の玉の質量を m、玉以外の客車の質量を M とする。
鉄砲は v の速度で打ち出され、 後方の壁に当るまでの時間 t だけ客車は速度 v' で動く。 その移動量を d とする。 運動量保存則から、mv= Mv'またはv'= mv/M、t= d/v' = (L-d)/v から、 d = Lm/(M+m)、移動量 d には v に関係する項がないので、 後方の壁にぶつかって転がってもとの位置に戻る時も全く同様に客車は d だけ逆方向に移動して、 元の位置に戻る。

箱の中の運動量は、重心の位置を変えることはできない、これは間違いである。 元の位置に戻るような鉄砲の玉に運動量はないのである。 玉に運動量があるのは飛んでいるときであり、もとの位置に戻るときには弱いが長時間、 逆向きの運動量があり、時間平均すると運動量はない。 また、ある瞬間をみて、飛んでいる玉の千倍も多くの戻っている玉があるから、 集合平均でも運動量がない。
だからこの例は、箱の中に運動量のある場合の例ではない。 箱の中の運動量がある例とは、鉄砲の玉が戻されない場合であり、 玉が後方の壁に止まるか、箱から落ちて消滅する例である。 このような場合、箱は d だけ変位する。 玉が次々と連続的に打ち出されるとき箱は連続的に移動する。 移動する箱の系から見ると、重心は後方に移動する。
ただ、鉄砲の玉のように物体の運動量の場合、移動の最大値は M=0 とした d= L である。 客車の長さしか移動できないのである。 最初、重心が先頭にあって、鉄砲を打ち終ると重心は客車の後尾に移動しているだけである。 鉄砲の玉が物体でなく光の場合、後方の壁に到着すると光は静止質量 0 のため、消え去るが、 エネルギーは後方の壁に移され、質量が後方の壁で消えるわけではない。 放熱すれば逃げて行くだろうが、エネルギー的に閉じた系としての箱なら、最大移動量は L である。
これを運動量に換算すると、c^2= 9*10^{16} [m^2/sec^2] で 8*10^{10} [VA/m^2]を割ると、 1 m^3あたり、0.88*10^{-6}[kgm/sec]= 0.88[milgm/sec]になり、無視できる程度の値になる。
電磁場のエネルギーの流れと運動量は、とても理解しがたい状態であるといわなければならない。 エネルギーの移動があって、エネルギーの発生と消滅が確認できないのであるから。
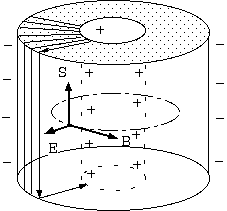
を考える。電磁場のエネルギー密度 u は時間において変化しない du/dt = 0。 電場Eと電流jの内積 E・j が配置(図 1)において2つの端面で存在する。 永久磁石は、磁石を取り巻く永久電流の存在と置き換えられる。 永久電流は円筒の上端面では中心から外に向かい、下端面では外から中心に向かう。 電場 Eは中心から外に向かっている。そのため下端面には E・j < 0 つまり、 場のエネルギーの発生があり、上端面には E・j > 0 で場のエネルギーの消滅がある。
つまり、客車の一方の壁にあたる下端面で鉄砲を打つためのエネルギーは、 電場の逆方向を向いた電流が発生させ供給し、場のエネルギーの流れ、 ポインティングベクトルを発生させ、後方の壁にあたる上端面では、 鉄砲の玉が当たったエネルギーは、 電場に向かった電流の発生するエネルギーに必要なエネルギーに使われているのである*。
このとき玉は消えているのだろうか。これは鉄砲の玉が帰って来る例だろうか。 鉄砲の玉は一方から他方に移動し続け、後方に溜るのだろうか。
しかし、電子が電圧の高いところに来るだけで質量を増すのだろうか(*)。 電子の質量は速度に依存するが、電位には依存しない。 電子のランダム運動を介在して質量が増えるかというと、 電子のランダム運動は与えられたエネルギーだけ増えているかというと、 調べてみるべきで、温度上昇がなければ増えてはいないだろう。 場の運動量を電流の運動量で打ち消す説は、このように成功しないように思える。
今井功氏の”電磁気学を考える”によると、 電荷がベクトルポテンシャルのあるところに存在するだけで運動量があるとする(*)。 これが場の運動量を打ち消しているかもしれない(**)。 ドーナツの穴の中には電流方向と同じ上に向かうベクトルポテンシャルがある。 そこにプラスの電荷を配置したわけだから、上を向いた運動量がある。 これは場の運動量を打ち消すことはできない同じ方向である。 場の運動量の別の説明かもしれないが、少なくとも打ち消す運動量ではない。
またその本によると、運動量をスカラーポテンシャル中の電流の体積分として表す。 これも場の運動量を打ち消すものではなく、同じ方向になる。 ドーナツの穴の中を上方に流れる電流は、コアの場の運動量と一致する。 これらは、この運動量という同じものの別名であろう。
(*) 帯電した電流は、E x B の場の衣を着ている。qA は、物質である電荷とベクトルポテンシャルの関係だから、
場の E x B と関係ない訳ではない。 qA が E x B の場の衣を着ているのである。
(**) 打ち消しではなくqAと、ExBの体積積分とは、同じ運動量を表している。
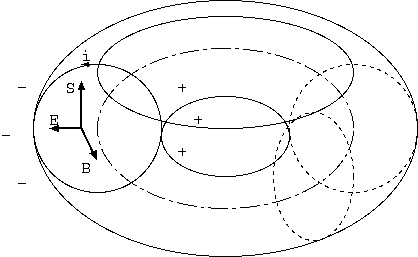
ある時刻に電荷と磁場がある。ここで、(1)電流の向きを変え磁場の時間変化を作る。 そのとき、コア内の磁場の時間変化により、コアを取り囲む周内に回転電場ができ、 コアの内側と外側は逆方向の電場をもつが、二つの電極の極性は反対なので同じ方向に力を受ける。

しかし、(1)のとき電極が受ける力の反作用を直接、物体としてのコアが受けるのであれば、 場の運動量変化はそもそも存在しない。コア内部の場の運動量は、電場と変化する磁場のために変化する。 それが電極の受ける力と逆方向であり、その大きさも電極の電荷と磁場の時間変化に比例する。 これは場が力を受けるのであり、コア内の場の運動量変化である。物体であるコアが力を受けては、 場が運動量変化をする必要はない。
電磁気の法則は、電場と磁場においてほぼ対称的で、電場中の磁場の時間変化は、 磁場中の電場の時間変化(変位電流)が力を受けるのと同様に力を受ける。 電場の時間変化は、電流と同じく力を受ける。磁場の時間変化は、存在しない磁流と同じく、 力を受ける。両者は、ともに場の受け取る力であり、場の運動量変化の言い替えである。 それにしても一定の運動量しか蓄えられないものに、 持続的浮遊力を期待するのは間違っているかもしれない。空間に運動量を蓄えられるとしても、 どこまでも磁場と電場の強さが強くなる仕組みがないから、これは無意味な夢想、靴ひもを引いて飛ぶ願望 かもしれない。コアの場の運動量が上下して下方向の力が持続的に出せるはずがないという疑いである。 (2)のとき物体に力が及ぶなら起こるのは振動であろう。
E= -1/c dA/dt -grad φ, B= rot A あるポテンシャル A とφが E, B をもたらすとき、 f を任意の関数として A'= A + grad f,φ'= φ - 1/c df/dtという A' φ' も同じ E, B をもたらす。 ベクトルポテンシャル A にはこのゲージ不変性という任意性が要請されている。 (2)の電荷移動のとき物体が力を受けないとするのは、この任意性の利用である。
(2)のときの磁場のない所での電荷移動は、その電荷は力を受けないが、 ドーナツコアの磁場を作っているドーナツ表面の電流に力を及ぼすかもしれない。 ドーナツの穴側の正電荷が外に出るとき、ドーナツの下側を通すなら、 ドーナツ断面のコイルの電流と同じ方向であり、近傍の電流を引き付けるし、 上側を通すなら、逆方向であり反発する。円環電流に与える力はともに下方向である。
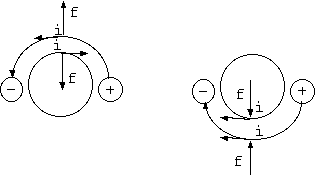
一般に、電流の部分どうしの受ける力は、作用線は一致しないため作用反作用の関係ではないが、 大きさが同じで反対方向の力を互いに及ぼす。そのため、電線全体では力をうけることはない。 それは、電線が自ら作る磁場で、内力で変形することはあるが、 自らの磁場で、電線自体が力を受けて自然に並進を開始することはないからである。
そうすると、ある部分電流が電流の他の部分に及ぼす力は、電流の他の部分がその部分に及ぼす 力を知れば十分である。その場所に磁場がないなら、その部分の電流は力を受けないし与えない。 ドーナツ表面電流全体が外部に磁場を作らないなら、 外部の電流がドーナツ表面電流全体に力を及ぼすこともないということである。
浮揚装置は、そのようなものがあればいい、という最たるもののひとつであるが、これはどの程度に不可能なのか。 一様な重力場内で静止するのは、それほど不可能には見えない。簡単にいえば、見えないつっかい棒のようなものですら、 浮揚装置でありうる。弱い場ではレーザー光往復でいいし、物体を往復させても圧力を作れる。動的斥力を作り出す方法は、 種々の方法がある。その逆の牽引ビームは、ずっと難しい。一様な重力場で静止浮揚する装置は、エネルギー供給すら要らないだろう。
浮揚装置をONにして上に持ち上げ、それをOFFにして下に下げる。下げるときに仕事をさせるなら永久機関である。 つっかい棒を使って登るときのように、上がるとき位置エネルギーを支払うならよいが、そうでないなら永久機関になる。 しかし、それを平坦な時空に持ってくると、とんでもないものになる。継続的に浮揚力をだす装置は、平坦場では持続的な加速装置である。 そしてそれにはふつう、この装置ではほとんど考慮されていない、エネルギーが必要である。エネルギーが考慮されないことは、疑わしい。
浮揚装置をONにして...について、
それが、ONで質量を消し、OFFで質量を戻すようなスイッチなら、それは大きくエネルギーが関係するだろう。
質量とエネルギーとは同じものの別名だからである。重力遮蔽板のようなものも、これに類似するとみるべきか。
上げるときエネルギーを吸い込み、下がるときエネルギーを吐き出し、静止浮揚でエネルギーは関係しないなら、
それは決して永久機関ではないだろう。不可能事の望みではなく、当たり前のことを当たり前に支払って、
その効果を得るのが科学である。場の運動量が存在することは、電磁気の基本的な知識である。それを否定すべきでない。
ある系でエネルギーが存在するとき、それを動く系からみれば、運動量が存在して当然である。
箱にエネルギーを認め、運動量を認めないのは、自然認識が間違っている。
箱の中の運動量が存在して不思議に思うのは、そのとき箱の重心は移動してどこにいってしまうのだろうか、と想像するからで、 場の運動量が存在して、その系で場の運動量が有効に働かない(消えたように見える、あるいは運動量による重心移動が無視できる(*)) なら、誰も原理的な疑問を抱かないだろう。
(*)運動量には重心移動はない。qA が場の運動量 E x B の元であるなら、q も A も静止できるので、箱の中の運動量は存在する。
B_y = B_0, B_x = B_z = 0
原点の荷電 +q が電場を形成する。
E_z = q/(4πe_0) z / r^3 ,
E_x = q/(4πe_0) x / r^3 ,
E_y = q/(4πe_0) y / r^3
これらより、ポインティングベクトルは、
S_x = -z/r^3 B_0, S_y = 0, S_z = x/r^3 B_0
となる。ポインティングベクトルの成分が座標の奇関数であるから、 全空間での積分した運動量は 0 になる。角運動量は存在する。
B_y = B_0, B_x = B_z = 0
電気双極子の作る電場は、
E_z = p /(4πe_0) (3 z^2/r^5 - 1/r^3),
E_x = p /(4πe_0) 3 zx / r^5,
E_y = p /(4πe_0) 3 zy / r^5
とすると、
S_x = - E_z B_0, S_y = 0, S_z = E_x B_0
これは y 成分はなく、 x 成分が電場の z 成分の逆方向、 z 成分が電場の x 成分の方向を向いている。 これは円筒状であり、ポインティングベクトルは y を軸として回転している。
空間での積分を考える場合、すでにある半径の球殻での積分で 0 となる。 全空間での積分も 0 となる。
2π∫_0^π S_x r^2 \sin \theta d\theta dr
= 2π∫_-1^1 1/r (3t^2-1) dt dr = 0
この電気双極子は 2 つの互いに反対符号の荷電が一様な磁場のなかにあると考えられ、 それらのポインティングベクトルも重ね合わせになると考えられる。
原点の荷電 +q が電場を形成する。
E_z = q / (4πe_0) z/r^3,
E_x = q / (4πe_0) x/r^3,
E_y = q / (4πe_0) y/r^3
磁気双極子(y 方向)が磁場を形成する。
B_y = u / (4πe_0 c^2)(3 y^2/ r^5 - 1/r^3),
B_x = u / (4πe_0 c^2)(3 xy / r^5 ),
B_z = u / (4πe_0 c^2)(3 zy / r^5 )
S_x= 3 zy^2/r^8- z/r^3(3y^2/r^5 - 1/r^3)= z/r^6
S_y= 3 xyz/r^8 - 3xyz/r^8= 0
S_z= x/r^3 (3y^2/r^5 -1/r^3)-3y^2x/r^8= -x/r^6
やはり奇関数であることから運動量の全空間積分は 0 であるが、 これはコイルとその近辺に荷電を置いたEinstein-Dehars効果実験の例と同じく、 角運動量が存在する。
電場は $1/r^2$ に、 磁場は$ 1/r^3$ に比例するので、 運動量は$1/r^5$ に比例する。ある半径 $ r_0 $ の外側の角運動量は有限の値になる だろう。$r_0$ が小さいほど角運動量は大きい。
E_z = p /(4πe_0) 3 z^2/r^5 - 1/r^3,
E_x = p /(4πe_0) 3 zx/r^5,
E_y = p /(4πe_0) 3 zy/r^5
磁気双極子の作る磁場は、電気双極子の作る電場の式と同じで、
B_y = u / (4πe_0 c^2) (3 y^2/r^5 - 1/r^3),
B_x = u / (4πe_0 c^2) 3 xy /r^5,
B_z = u / (4πe_0 c^2) 3 zy /r^5
両者から求められる、ポインティングベクトル(S = E x B)は
S_x= E_y B_z - E_z B_y =
(3zy/r^5)(3yz/r^5) -(3z^2/r^5-1/r^3)(3y^2/r^5-1/r^3)
= 3/r^8 (y^2+z^2) - 1/r^6
= 3/r^8 (r^2-x^2) - 1/r^6
= -3x^2/r^8 + 2/r^6
= 2/r^6 - 3x^2/r^8
S_y= E_z B_x - E_x B_z = (3z^2/r^5-1/r^3)3yx/r^5 - 3zx/r^5 3yz/r^5 = -3xy/r^8
S_z= E_x B_y - E_y B_x = 3zx/r^5 (3y^2/r^5-1/r^3) - 3zy/r^5 3yx/r^5 = -3xz/r^8
となり、 x=r のとき S_x= -1/r^6 であり、 x=0(yz 平面 ) では 2/r^6 である。 これの全空間での積分を行なう。ある半径 r_0 の外側空間での積分は、
2π∫_{r_0}^∞ ∫_0^{π} S_x r^2 \sin\theta d\theta dr
S_x= {1 \over r^6}(2-3\cos^2\theta )
∫ (2-3\cos^2\theta ) \sin \theta d\theta
= ∫_-1^1 (2-3t^2) dt = [ 2t - t^3 ]_-1^1 = 2
4π∫_r_0^∞ 1/r^4 dr = -4π/(5 r_0^5)
となり、r_0 の外側の空間での積分は、r_0 を 0 にすると無限大になる。 つまり、このような電気双極子と磁気双極子の交差配置では、 無限の運動量を持つことになる。 電気双極子と磁気双極子の交差配置は遠方からみたときの電場や磁場の近似であり、 実在しないからこの結論は無意味というわけではなく、 ある r_0 での有限の運動量は意味がありえる。 しかし、実在する物体配置では r_0 の内側がつねに外側を打ち消す可能性は残っている。