一般相対論の宇宙

目次

０. 一般相対論の考え方
　0.1 一般座標変換と計量 g_ik
　0.2 測地線と運動
　0.3 測地線の方程式
　0.4 重力方程式
１. アインシュタインの定常宇宙
　1.1 射影による g_ik
　1.2 その他の射影
２. ド・ジッター宇宙
　2.1 アインシュタイン宇宙とド・ジッター宇宙の成立
３. フリードマン宇宙
　3.1 フリードマン解
　3.2 空間曲率０の解
　3.3 空間曲率非０の解
４. 一般相対論の宇宙

０. 一般相対論の考え方

質量から座標系と計量g_ikが決まり、系のみかけの力(重力)が求まる。例えば1つの天体の重力場は、天体のそばを取り囲むタマネギの皮のように、 薄くなった物差しと遅い時計の層を与え、その時空の計量場は、静的な天体の質量から来るニュートン重力を説明するだけでなくそれ以上のことを 予言する。

一般相対論の宇宙論は、大きく3つに、一般相対論の成立とそれに伴うアインシュタインの定常宇宙、ド・ジッターの宇宙、フリードマンの膨張宇宙 に分けられる。最初の2つは、g_ikという計量の定常を仮定し、現時点からみた宇宙の全体像を示した。両者は、宇宙項を使用した。フリードマンは、 宇宙項を使わず、計量の定常性を放棄して宇宙の膨張を表現した。これが現実を説明するとして永く受け入られた。

相対論は、アインシュタイン自身の"相対論 特殊と一般の理論"がよい解説である。そこに彼の定常宇宙論が ある。パウリの"一般相対論"、ディラックの"相対論"もよく読まれ、それらによって理解した人も多い。しかし、最も深い "相対論の意味" はアインシュタイン自身が与えた。妥協なく難しい内容のなかに彼の定常宇宙論とフリードマン の宇宙論がそのまま入り、その「まとめとその他の注意」には宇宙論への深い思い入れが綴られる。受け入られなかった非対称場の理論も含まれる。 彼の一生の作業は、科学における時間と空間という基本通念を覆す相対性という概念をどこまで一般化した法則にできるかという戦いだったのだろう。 慣性系という範囲を超えた一般化座標系を扱うことで重力を捉え直し、その新たな深い視点は、物理学に多くの果実を生み出した。

0.1 一般座標変換と計量 g_ik

dx' = a dx + b dy + c dz + d dt
dy' = ...
...

そのとき変換先の局所慣性系は、特殊相対論のローレンツ変換が成立し、慣性系間には慣性系によらない不変量 ds^2 をもつ。

ds^2= dx'^2 + dy'^2 + dz'^2 - dt'^2

不変量 ds^2 を与える式は、微分の2次式だけでできた 2次同次式だから、元の一般座標系で表し、(dx, dy, dz, dt) を (dx^1, dx^2, dx^3, dx^4) と書き、i,k の各項の総和のΣを省略すれば、

ds^2= g_ik dx^i dx^k

と表される。元の dx, dy,... の積項からできた2次同次式の積項への係数 g_ik は、元の微分の変換式の係数 a,b,c,...の2次同次式で表される。 元は g_μν ジー、ミュー、ニューと呼ばれた g_ikは、i,k は次元を表し、1-3は空間で4を時間にする。時間に0を使い0-3とすることも多い。 時空間を扱う物理で1個の添字をもつベクトルの成分のように、i,k の2個添字をもつ2階のテンソルは実数配列の成分である。g_ikは、時空の性質 を表す基本テンソルで、計量(メトリック)という。i,k(=1-4)について対称(g_ik= g_ki)で、独立な10成分をもつ。g_ikは、系に依存して各時空点 に違う値をもつ場であり、系によらない不変量dsを導く係数である。g_ikは、局所慣性系への変換だけでなく、どこを基準にしてもよいから、任意 の微分線形変換に使われるが、まずは局所慣性系を基準にした、それへの微分の変換係数である。そして、同じ値で遠方の平坦時空の慣性系への 変換係数でもある。

慣性系間のローレンツ変換、x'= γ(x - vt), t'= γ(t - vx), y'= y, z'= z. γ= 1/√(1-v^2) によって、g_xx,xt,ttの点に速度vを持つ計量、 g'_xx, g'_xt, g'_ttは、

dx= γdx' + γv dt',
dt= γdt' + γv dx',

dx^2= γ^2 dx'^2 + γ^2v^2 dt'^2 + 2γv dx'dt',
dxdt= γv (dx'^2 + dt^2) + γ^2(1 + v^2)dx'dt',
dt^2= γ^2 dt'^2 + γ^2v^2 dx'^2 + 2γv dx'dt' 

g'_xx dx'^2 + g'_xt dx'dt' + g'_tt dt'^2=
g_xx dx^2 + g_xt dxdt + g_tt dt^2=
 g_xx(γ^2 dx'^2 + γ^2v^2 dt'^2 + 2γv dx'dt')
+g_xt(γv (dx'^2 + dt^2) + γ^2(1 + v^2)dx'dt')
+g_tt(γ^2 dt'^2 + γ^2v^2 dx'^2 + 2γv dx'dt')

g'_xx= γ^2(g_xx + v^2 g_tt) + γv g_xt,
g'_xt= 2γv g_xx + γ^2(1+v^2) g_xt + 2γv g_tt,
g'_tt= γ^2(g_tt + v^2 g_xx) + γv g_xt.

一般座標変換の変数、テンソルは、微分を扱う式で使われるから2種類の成分がある。dx^i や g^ik のように i,k が上添字のとき座標微分と同様 な変換 A'^i= ∂x'^i/∂x^k A^k を受け、「反変成分」と言う。 g_ik のように下添字を持つものは、i,kにおいて偏微分の分母側の添字の変換を受け B'_k= ∂x^i/∂x'^k B_i、「共変成分」という(例：スカラーのgradは共変ベクトル)。反変成分と共変成分は添字の上下で区別する。φ= B_i A^i のように上下の同じ添字は1-4にスカラー(内積)に縮約される。A^i_j のように添字を上下にもつ混合テンソルの成分もある。ベクトルは1階、g_ikは 2階のテンソルである。

基本テンソル g_ik の行列式gで、g_ikの余因子を割った成分をもつ逆行列が反変テンソルg^ikである。g^ik g_jk= δ^i_j= 1(i=j), = 0(i!=j) dξ_j= g_ik dx^k, dx^i= g^ij dξ_j 反変ベクトルから共変ベクトルを導出し、逆にも変化させるテンソル添字の上下移動に使うことができる。

この計量g_ikは、物理的意味をもつ物理量であり、人間の都合による単位の違いなどの単なるスケール変換を表すものではない。慣性系への微分 の変換係数とみれば、これが一般座標系を一意に表し、同時にそれに対応した時空の性質を表すことが理解できる。計量は、場所と時刻によって 値が変わる場であり、基準(座標系)によるが、時空間にある物質だけによって存在し、時空間にある質量の存在と分布だけによって値が定まる。 計量は、空間の弯曲を表現する。その例として測地線を挙げる。

0.2 測地線と運動

∂^2 r/∂t^2 = -grad φ

をどうローレンツ共変に書き直すかが問題だった。しかし問題はより深く、一般座標系が重力場を与えると考えるのである。放物のように重力以外の 外力がない質点の運動を「測地線」(geodesic line) といい、時空の一種の直線(最短距離、最大固有時をもつ経路)とした。固有時の停留経路(経路を 微小量だけ変化したときのds^2(時間又は距離)の変分が0の経路)である。測地線は時空点の周りに速度によって無数(∞＾3)にある。 そしてある経路が測地線かどうかは座標系によらない。

δ∫ds= 0

共変微分：ベクトルA^iをdx^kだけ平行移動し、A^i+dA^iに変わる、その差dA^iは、通常の微分∂A^i/∂x^k dx^kと時空の弯曲の分がある。後者は、A^j と dx^k の積に比例する。比例係数Γ^i_jk を測地成分という。

dA^i= (∂A^i/∂x^k + Γ^i_jk A^j) dx^k

()内を共変微分といい、下添字kの前の";"がkによる共変微分を表す。

A^i_;k= ∂A^i/∂x^k + Γ^i_jk A^j

ベクトル A^i を速度 ∂x^i/∂s とし、移動 dx^k によるベクトルの変移を dA^i= 0 とする。これは、速度を保存して平行移動する線を意味する。 これをdsで微分し、移動量dx^kを速度dx^k/dsにして、測地線の方程式になる。(この説明は、まだδ∫ds= 0 を表さない。)

0.3 測地線の方程式

測地線の方程式は、重力を記述する測地成分(アフィン接続) Γ^i_rs が、r方向とs方向とのdsに対する速度の積に掛けられ、i方向の加速度を与える。 測地成分Γ^i_rsは、第2種クリストッフェル記号{rs, i}といい、第1種クリストッフェル記号[rs, k]とg^ikとの積である。[rs, i]は、g_irのs方向 微分∂g_ir/∂x^sとg_isのr方向微分∂g_is/∂x^rの和からg_rsのi方向勾配∂g_rs/∂x^iを引いた差の1/2でありr,sに対称である。測地成分は、 計量の1階微分の方向差だから測地系(自由落下、局所慣性系)で0で、他の系で0でないのでテンソルでない。テンソルは、1つの系で0なら全系で0である。 なぜなら、テンソルは1次同次式の変換しか受けないからである。

Γ_i,rs= [rs, i]= g_ik{rs, k} (第1種クリストッフェル記号)
Γ^i_rs= {rs, i}= g^ik[rs, k] (第2種クリストッフェル記号)

[rs, i]= 1/2 (∂g_ir/∂x^s + ∂g_is/∂x^r - ∂g_rs/∂x^i)

静的な g_ik で、g_ii= 1 (i=1〜3)とし, g_44= -1 の近くでは、

∂^2x^i/∂s^2 = -Γ^i_44 = -[44,i] = 1/2 ∂g_44/∂x^i

として、第1近似でポテンシャル勾配の式に戻りニュートン力学を再現する。しかし、 ５. 測地線方程式の第2近似 から、 測地線の方程式は、時空間の計量和の勾配と速度積が加速度を生む形をしている。左辺が加速度になるようiを1〜3にし、座標系を選択して g_ij=0 (i!=j)とすると、Γ^i_rs= g^ik[rs, k] には空間計量 g_ii (i=1-3)の勾配が、時間計量の勾配と同程度に現れる。

∂^2x^i/∂s^2= - 1/2 ∂(g_11 + g_22 + g_33 + g_44)/∂x^i dx^j/ds dx^k/ds

0.4 重力方程式

c1 R_ik + c2 R g_ik + c3 g_ik = k T_ik

の形をとる。これの発散 div は、(1/2 c1 + c2)√-g ∂R/∂x^i であり、これを恒等的に0にする、c2＝-c1/2 から、G_ikは次式になる。

G_ik = R_ik - 1/2 R g_ik

重力方程式は、物質の全エネルギー運動量テンソル T_ik がそのまま、時空の曲率 G_ik を与えるという式である。

G_ik = -κ T_ik

テンソルG_ikを、g_ikの2階微分は1次式に、g_ikとg_ikの微分の2次式に限定するのは、テンソルによる能力拡大でニュートン力学を 最小限に再現しそれ以上の複雑さを避ける意味だろう。g_ikの2階微分までの使用は、g_ikの微分には連続を要求し、g_ikの2階微分と 右辺の物質には連続を要求しないという意味をもつ。

このg_ik場は、√g_44 が重力ポテンシャルに対応し、測地線の方程式は、g_ik場の中の質点運動を示すが、重力方程式は、スカラーであった ポテンシャルを10次元の計量g_ikに拡張した場が質量と関係する力学である、10元連立非線型偏微分方程式は、物質密度などからg_ik場を求める ことを可能にする。

１. アインシュタインの定常宇宙

G_ik = R_ik - 1/2 R g_ik

物質の全エネルギー運動量テンソル T_ik が時空の曲率 G_ik を与えるのが、一般相対論の重力方程式である。

G_ik = -κ T_ik

これは、次のようにも書かれる。

R_ik = -κ(T_ik - 1/2 g_ik T)

ここで数学的に導入が任意な定数c3のλ g_ik の宇宙項(斥力項)を導入し、物質密度μ_0とのバランスを要請する。

G_ik - λ g_ik = -κT_ik

R_ik + λ g_ik = -κ(T_ik - 1/2 g_ik T)

R + 4λ = κT

任意の物質密度に対してそれに対応するλを与えると、宇宙は平衡し静的になる。空間的に球状、時間的に静的な4次元円筒となる。 4次元ユークリッド空間のなかの3次元超球面を我々の宇宙の空間とする。その上では一様性がいえる。例えば、

g_ik= δ_ik + x^i x^k/( a^2 -(x^1)^2 -(x^2)^2 -(x^3)^2 ) 　(i,k= 1,2,3)

g_i4= 0, g_44= -1

とおけば、

R_ik= -2/a^2 g_ik,　R= -6/a^2,　G_ik= 1/a^2 g_ik　　(i,k= 1,2,3)

R_i4= R_44= 0

となる。これから、

T_44= μ_0 c^2　他の T_ik= 0,　T= -μ_0 c^2

λ= 1/a^2 = 1/2 κμ_0 c^2 = 4πk μ_0 c^2

物質密度μ_0によって、宇宙の半径aと宇宙項λが決まる。彼は定常を前提とし、0でない物質密度には宇宙項を必要とした。λ= 0を与えると μ_0= 0となり、宇宙の半径 a は無限になる。T_ik=0, R_ik= 0, R= 0, G_ik= 0 から、真空は、平坦なミンコフスキー時空に戻る。 これよりは、0 でない物質密度をとる有限宇宙の方を合理的と考えた。λをいれると物質密度0の重力方程式には g_ik が定数という一般解が なくなり、g_ik= 0 という特解だけになり、物質の存在しないとき場すら存在しないという "マッハの原理" に合う。その場合、光も真空中を 伝播できず、時計や物差しも存在しない。それがλの重要な意味と考えた。

(*)アインシュタイン(1917)では、G_ik はまだ R_ikの意味である。G_ik = -κ(T_ik -1/2 g_ik T). λ項を加え、G_ik + λ g_ik = -κ(T_ik -1/2 g_ik T). これらの式中の G_ik は、リッチテンソル R_ik を意味する。

１.１ 射影による g_ik

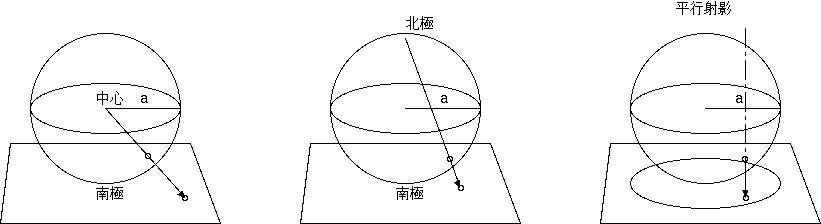
この方法の最初の宇宙解である、アインシュタインの宇宙解は、4次元ユークリッド空間中の 3次元超球面を赤道面の平坦な空間に射影する平行 射影であった。ド・ジッター宇宙は同様に、5次元ユークリッド空間中の4次元超球面を4次元虚数時間ミンコフスキー時空に平行射影した。

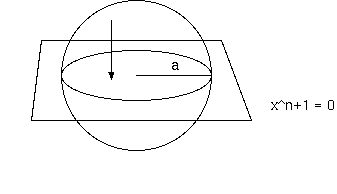
定曲率空間を表現するために n+1 次元ユークリッド空間中の n 次元超球面上の点を赤道面 x^(n+1)= 0 に平行射影する。ユークリッド空間、

ds^2= Σi= 1〜n (dx^i)^2 + (dx^(n+1))^2

の中に半径 a の n 次元超球面を考える。

Σi=1〜n (x^i)^2 + x^(n+1)^2 = a^2

これを使って、x^(n+1) を消去する。x^(n+1) = √((a^2 - Σ(x^i)^2 ) から、

dx^(n+1) = 1/2 ((a^2 - Σ(x^i)^2)^(-1/2) d(Σ(x^i)^2) = -Σ(x^i dx^i) / √(a^2 - r^2), r^2= Σi=1〜n (x^i)^2

ゆえに、

ds^2= Σi=1〜n (dx^i)^2 + (-Σ(x^i dx^i))^2 / (a^2 - r^2) , r^2= Σi=1〜n (x^i)^2

これから、

g_ik= δ_ik + (x^i x^k)/(a^2- r^2), r^2= Σi=1〜n (x^i)^2

4 次元ユークリッド空間中の 3 次元超球面への射影によって x^(n+1) を消去し、平行射影の結果を空間とし、時間は別に与え定常とする。 時間は空間と違って特別扱いで、局所の特殊相対論にシームレスに繋がらない。射影は半径a(赤道)で特異となる(g_ik→∞)が、超球面と射影 とは有限から有限への写像であり、無限空間を有限空間に閉じ込めるものではない。

１.２ その他の射影

x^i = r/r' x^i', r^2 = Σ(x^i)^2, r/r'= |x^(n+1)|/a = a/√(a^2+r'^2)

という変換で得られた座標系では、r' を r と書き直し、

ds^2= a^2/(a^2+r^2) Σ (dx^i)^2 - a^2/(a^2+r^2)^2 (Σ x^i dx^i)^2 となる。

また、北極 x^k= 0, x^(n+1)= a から南極の外接面への射影は、北極だけが特異となり、 Stereographic projectionという。 これも有限から無限への写像である。 ds^2= 1/(1+r^2/4a^2)^2 Σ(dx^i)^2 という g_ik を与え、形を変えない同形変換 (conforming transform)である。これは、アインシュタインが"幾何学と経験"のなかで言及した写像であるが、 彼の定常宇宙で使われたのは平行射影であり、周辺の計量は全く異なるものになる。 平行射影では赤道近辺の射影された剛体球は奥行きが短くなり平べったくなるが、 ステレオグラフィックでは逆に北極近辺の射影された剛体球が遠方において巨大化する。

２. ド・ジッター宇宙

g_ik= δ_ik + x^i x^k/(a^2 -(x^1)^2 -(x^2)^2 -(x^3)^2 -(x^4)^2), (i,k= 1,2,3,4; x^4= ict)

T_ik = μ_0 = 0, λ = 3/a^2

これは、4 次元 "擬球" 状世界である。アインシュタインは「 a^2= Σ(x^i)^2 で特異だから、これは物質のない宇宙のモデルではなく、 殻のある宇宙のモデルである」と批判した。しかし彼自身の定常モデルも空ではないが空間的果てで特異である。これらの宇宙解は、一様なのは 密度と曲率であり、計量 g_ik は一様等方でない。宇宙の中心の時空がミンコフスキー的で遠方はそうでない(**)。宇宙の中心部と周辺で g_ik が 異なり方向にもよる。どの点も対等という空間的一様等方性は g_ik にはない。g_ikのδ_ik との差が中心からの距離に斉次(x^i と x^k との積に 比例)である。このとき g_ik dx^i dx^k において等方性をもつと考えられる。任意点からみた遠方の時空の様子、宇宙の果てが計量 g_ik を使って 表現される。ここでは、誰もが中心から宇宙をみる。どの点も対等にこのような g_ik 構造をみるのである。

アインシュタイン宇宙は、定常かつ静的であり、膨張もないのに周辺短縮する。同様にド・ジッター宇宙にも周辺短縮がある。ド・ジッター宇宙は4 次元時空という超球の次元の違いしかない。両宇宙とも空間の係数 g_ii (i= 1〜3) が周辺で大きい。両宇宙とも中心からある方向、x^i に離れると g_ii は、最初、距離の2乗に比例して大きくなり、さらに距離 a に近付くと分母が 0 に近付き発散する。g_ik は時空の間隔(又は剛体)の不変量の 式 ds^2= g_ik dx^i dx^k の係数だから、両宇宙とも宇宙の果てには奥行き方向に(距離の2乗に反比例以上に)薄くなった殻のような周辺世界をもつ。

ド・ジッター宇宙は、時間軸を虚数 (x^4= ict) にして球状でなく擬球状である。斥力項λの働きは反発であり物質がないため収縮要素がない。過去と 未来の時刻 t の半径 √(a^2 + c^2t^2) は、現在の半径 a より大きく、中心から距離 a を通過する直線上の点との距離のようである。無限大から 現在 a に縮まり反発し、また無限大に拡大するハイパーボリック(双曲的)な宇宙であり、これほど動的な宇宙を静的宇宙というのは、 5次元ユークリッド空間中の4次元超球という時空の一様性の解だからである。

アインシュタイン宇宙が3次元空間に射影したと同じく、ド・ジッター宇宙は4次元時空(x1,..,x4)に射影する。時間tを虚数軸にする(x^4= ict) この式の時間計量 g_44 は普通の計量の符号のような -1 の近辺でなく、1 の近くである。 g_44= 1 - (ct)^2/(a^2 +(ct)^2 - r^2) は、質点の周り のポテンシャルφ= 1/2 c^2 (g_44 -1), g_44 = 1 + 2φ/c^2 で表すと、φ= -1/2 (ct)^2/(a^2+(ct)^2-r^2) の分母から、空間的遠方 r には上に凸 の 3 次元逆パラボラ底のように、端で落ちる散逸壁のポテンシャルをもつ。但し、普通φは、g_44 と 1 次の関係ではなく、√g_44 と 1 次の関係 である。そして時間経過は、√g_44 に関係する(*)。

(1) 光で見る時刻 t の点の距離を r= ct (光円錐)と近似すると、単純な分母一定の g_44= 1 - (ct/a)^2、 g_44＜1 となり、1 との 差が t^2 に比例するから、時間経過√g_44 の逆数 1/√(1-(ct/a)^2)= 1+z の赤方偏移 z も、t^2 に比例する。距離に比例でなく 距離の 2 乗に比例する赤方偏移となる。ct= +- a の時刻は特異であり g_44= 0。これは、始まりと終りをもつ宇宙である。

(2) 時間的領域((ct)^2 ＞ r^2) では分母が大きく赤方偏移の程度が小さい。宇宙の半径、√(a^2 + c^2t^2) は、過去未来で大きく、 現在は最小の a である。つねに収縮し反発し膨張に転じる宇宙である。

(3) 空間的領域は、r が √(a^2 + c^2t^2) に近付くと分母が小さくなり、分数は大きくなる。r^2＝ a^2 + c^2t^2 で特異である。 その外側 r＞a は、g_44＞1 であり、そこからの光が中心に届くなら青方偏移する。

ド・ジッター宇宙の赤方偏移が距離の2乗比例というのは、俗説の可能性がある。J.A. Peacockによると Weyl(1923)が線形と明らかにしたという。もしそうなら、これはド・ジッター宇宙に対する永き誤解であったことになる。虚数時間の幾何学は 理解が難しく、 「奇妙な」という形容詞で揶揄され、 貶されてきた。

(*) g_44が時間の2次関数でφが時間比例なら、時間経過速度は時間に比例し、遠方の赤方偏移は時間的距離に比例できるだろうか。できない。 時間経過√g_44 と (ct/a) とは、2乗和一定の関係にある。g_44 + (ct/a)^2 = 1

(**) 局所で特殊相対論が成立し、特殊相対論を説明できるのはド・ジッター宇宙であり、アインシュタイン宇宙では人工的な設定である。

２.１ アインシュタイン宇宙とド・ジッター宇宙の成立

R_hijk + α( g_hj g_ik - g_hk g_ij )= 0

これを縮約して、R_ik +(n-1)αg_ik= 0

さらに縮約して、R= -n(n-1)α

アインシュタインテンソル G_ik も超球上で、次の値をもつ。

G_ik= (n-1)(n-2)/2 α g_ik

超球の射影の g_ik をもつことで、超球上の等曲率を確保し、上の R_hijk + α( g_hj g_ik - g_hk g_ij )= 0 が成立する。 その縮約した上記の3式に n= 3 を入れれば、R_ik= -2αg_ik, R= -6α, G_ik= α g_ik. (α= 1/a^2) が出る。

G_ik - λg_ik = -κT_ik は、(α-λ)g_ik = -κ T_ik となる。αとλが同じ値をとるとき、 T_ik = 0 となる。 塵埃の質量運動量テンソル T_ik は、3次元においてすべて 0、T_44 = ρ、 T= -ρ を仮定すると、宇宙項は、αと一致させ、 λ = αとすると、R + 4λ = κT から α= 1/2 κρ、半径 a は密度の関数、a = √(2/κρ) となる。

また、上記の3式に n= 4 を入れると、R_ik= -3αg_ik, R= -12α, G_ik= 3α g_ik となり、G_ik - λg_ik = -κT_ik は、 (3α-λ)g_ik = - κT_ik となる。これに T_ik= 0, T= 0 とするための λ = 3αを入れると物質のないド・ジッター宇宙解がでる。

アインシュタイン宇宙解 (α-λ)g_ik = -κ T_ik の α-λ が 0 でないときと、 ド・ジッター宇宙解 (3α-λ)g_ik = - κT_ik の 3α-λ が 0 でないときとは、ともに T_ik が値をもつが、宇宙解を与えるだろうか。 4次元的 (3α-λ)g_ik = - κT_ik は、自然な解釈を許さないかを考えると、物質の圧力を導入し T_11= T_22= T_33= p とし、T_44= u (p, u ともに正) T= 3p - u から、3α-λ= κ(3p - u) を与える。アインシュタイン解の(α-λ)g_ik = - κT_ik は、 α-λ= κ(3p - u) を与えるがそれらが解と言えるか不明。

超球の G_ik と g_ik の関係は、一般座標において成立し、射影によるg_ikにも保たれる。平行射影以外の射影の宇宙の果ての g_ik は 違っても、同種の超球上の宇宙解である。自然に思う射影を使うだけであろう。

３. フリードマン宇宙

(R_ik - 1/2 g_ik R)+ Λ g_ik +κ T_ik = 0 ...(1)

"拡張された重力方程式の第二項、宇宙定数Λは、理論を複雑にし、論理的簡単さをかなり減ずるものである。物質の有限平均密度の導入が 避けられないことから起こる困難によってのみ妥当とされる。フリードマンはこのディレンマから逃れる方法をみいだした。"

”三次元に関して等方的な四次元空間”の章で、物質の平均密度ρと、計量場の一定を捨てる場合、空間的一様等方の前提は、 四次元的宇宙の中心を通る全ての測地線を軸とする回転について不変から、四次元的球対称と考える。通常の4つの座標でなく、 x^1〜x^3 が不変で、x^4 だけが変わる時間的な線、中心を通る粒子の測地線を、中心からの距離と時間とを等しいとし、

ds^2= (dx^4)^2 - dσ^2, 　dσ^2= γ_ik dx^idx^k　(i,k= 1〜3) ...(2)

γ_ik= γ_ik0 G^2

γ_ik は、時間による正の係数 G を除いて同じ三次元の定曲率の計量とする。さらに、線素がユークリッド的になるように x^1 〜x^3 を採り直して、

γ_ik0= A^2 δ_ik

ds^2= (dx^4)^2 - G^2 A^2 ( (dx^1)^2 + (dx^2)^2 + (dx^3)^2 ) ...(2)

と表す。G を時間 x^4 だけの関数。A を r だけの関数 (r^2= (x^1)^2 + (x^2)^2 + (x^3)^2) とする。

A= 1/(1+ z/4 r^2) (z= 1 球状、z= -1 擬球状、z= 0 ユークリッド空間) ...(3)

３.1 フリードマン解

G_{i,k}= (z/G^2 + G'^2/G^2 + 2 G''/G) G＾2 A＾2 δ_ik = 0 　　(i,k= 1,2,3)
G_{4,4}= -3(z/G^2 + G'^2/G^2) = -κρ .......(4a)
G_{i,4}= 0

G は、時間 x^4 の関数で、宇宙の質点間の計量的距離の相対的測度。z/G^2 は、ある x^4 の空間的曲率、G'/G がハッブル膨張を表す。

(z/G^2 + G'^2/G^2 + 2 G''/G) = 0 .....(5)
(z/G^2 + G'^2/G^2)= 1/3 κρ

辺々引いて、

G''/G + 1/6 κρ = 0 ...(5a)

Gとρは正であるから G"は負で減速膨張であることが分かる。G は、極小や、変曲点をもたず、ρが 0 でない限り G に定数解はない。

３.２ 空間曲率０の解

2h' + 3h^2= 0 ...(5b)
3 h^2= κρ

h からρを推定する。h= 432km/sec/Mpc = 4.71・10＾(-28)、κ= 1.86・10^(-27) から、ρ= 3h^2/κ= 3.5 ・10^(-28) g/cm^3 空間の曲率は、ρと h の関係のつぎの式で与えられる。

z/G^2 = 1/3 κρ - h^2 ...(5c)

空間曲率 0 のとき、ハッブル定数は時間に反比例する。h= 2/3t ...(6)

(アインシュタインの使ったハッブル定数は現在の10倍大きい。密度と宇宙の空間的曲率には、h^2 が関係し、h が10倍の誤差をもつとき 密度ρと曲率 z/G^2 の関係は 100 倍違ってくる。上のρの値は、G.C.マクヴィティ(1939)の "ρ＜10^-27 g/cm^3, おそらくρ〜 10^-29 g/cm^3" という推定より１桁大きい。アラン・サンディジのハッブル定数を使うと、ρ〜 10^-30 g/cm^3 と、さらに１桁小さくなる。)

ここでアインシュタインは、次のように述べる。" h の測定値からわれわれは、宇宙の現在までの存在期間として、1.5・10＾9年 を得る。 この年齢は、地殻に対してウランの壊変から得たそれとほぼ同一である。これは、種々の理由から、理論の妥当性に対して疑を起したひとつの 逆説的結果である。"

３.３ 空間曲率非０の解

z + 2GG" +G'^2= 0 ...(5d)

t を G の関数と考え u= G'= 1/t', G"= (1/t')'(1/t')=u'u (ここで t, u の'はGによる微分)。z + 2 uu'G +u^2 = 0 または、z + (Gu^2)'= 0 (ここで ' はGによる微分である)。これをGで積分し、zG + u^2G = G0 (G0は正の定数)ゆえに、

(dG/dt)^2= u^2 = (G0-zG)/G ... (5h)

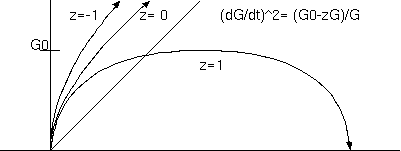
(5h)から、曲率が正 (z= 1) のときは、(dG/dt)^2= (G0-G)/G という、サイクロイドの微分方程式になる。曲率が0のときは、 (dG/dt)^2= G0/G から(*)、G= a t^(2/3), a= (9/4 G0)^(1/3)。宇宙年齢は、t= 2/3 (G/G')、ハッブル定数の逆数の 2/3 である。

曲率が負 (z= -1) のとき (dG/dt)^2= (G0+G)/G、Gは 0〜∞まで単調増加である。その中の ρ= 0 の極限は、(dG/dt)^2= 1、 曲率が消滅しユークリッド的、直線膨張に変わる。

(*) ((dG/dt)^2= G0/G は、dG/dt= a/√Gを変数分離し、√G dG= a dt、2/3 G^(3/2) = at + b、G= (3/2(at+b))^(2/3)+ c、 t=0 で G=0, t=1 で G=1 を使えば G= t^(2/3)である。)

ρとGの関係は、質量が保存されるなら ρ∝ G^-3 であるが、(G"= -1/6κρG は、G"∝-1/6κG^-2となる。) 宇宙論の場合、重力場の エネルギーは、質量と比較できるほど大きいため、そうとは限らないと思う。クリエーション場など無くても、空間が拡がっても薄まらない 斥力項がある場合のインフレーションではρ一定の膨脹すら考えることができる。

熱力学の断熱膨脹は、密集でエネルギーが高く、気体は、圧縮するのに仕事が必要である。ところが、重力による密集では逆に密集が エネルギーが低い状態であり、密集することによって仕事をさせることができる。断熱膨脹では粒子が稀薄になるだけで温度が下がるが、 それは粒子が外部壁に仕事をするからであった。物体がポテンシャルの高い場所に進むとき速度を失い粒子温度が下がる。これは、 ポテンシャルの空間的傾斜に仕事をしたのである。宇宙膨張では空間的な外部がないので外部壁はない、(ド・ジッター宇宙でないから) ポテンシャルの空間的傾斜もない。その体積だけが増大するとき温度と質量はどうなるのか。温度が下がる理由はないようにみえるが、 一般には温度が G に反比例するとされる。

フリードマン宇宙解について、アインシュタインの不満は、一定の大きさがないこと、その短期であることも問題だった。そして、最も 困るのが特異点だった。これについて、相対論の意味の"第2版への付録ー宇宙論的問題についてー" にならぶ各章をみて頂きたい。アインシュタインのこれらの問題に対する真剣さ、彼は三度条件を変えてその不可避を示した。なぜ、 それほどまで、特異点が問題でそれを避けたいか、現在では誰も理解しないだろう。殆どの人はそういうものと思い、暢気に神の つくりたもう宇宙には原初があるものと思うかも知れない。最近では物理学者がTVでそれについて"光あれ"などという創世記の言葉を口にする。 彼は、その軽さに気が付いていないのである。しかし、「相対論の意味」を読まずに相対論、宇宙論を分かった気にならないでほしい。 明らかに、アインシュタインはそういう態度ではない。時空の一点が解析的に解けないだけとみることもできたはずであるが、 そこに全ての矛盾を押し込めた特異点の存在を彼は、重く言えば宇宙論全体の失敗、軽く言えば未解決問題と考えていたように思う。

４. 一般相対論の宇宙

物差しと時計の係数である g_ik 自身は、その微分が現実の場である電磁気のポテンシャルのように、その値は任意の関数のgradを追加しても 現象に出ない仮想存在であった。時間計量g_44は、時間経過の速さを決める値で、局所検出できないことが明らかだが、その勾配は、重力として 表われ、2階微分は物質密度に比例しないといけない。そして、とくに空間計量g_ii(i=1-3)だけの変化は、間隔の変化としての局所測定が困難な ようである。重力波とフリードマン宇宙解はともに空間計量だけの変化として定式化され、とくに問題は膨張宇宙解の定式化にある。

一般相対論が重力現象だけを説明すると考えるのは、計量の意味の矮小化である。局所の計量(物差しの伸縮や時計の遅速)が局所の力学現象と して表われないのは、特殊相対論で物差しの短縮と時計の遅れが自らの慣性系で検出できないことに対応する。速度をもつ系の短縮はその系の 中では分からないこと、これが固有時、固有長の意味である(固有時、固有長は、系によらない)。それが可能なら絶対静止に対する絶対速度が 存在することになる。現在、自明に思えることを、ローレンツやフィッツジェラルドは、短縮を力学現象としてエーテルの圧縮で説明しようとした。 アインシュタインは、特殊相対論でそれがローレンツ変換という時空の座標変換であることを明らかにし、エーテルの存在を否定したのである。 そのとき、伸縮に伴う力を考えても無駄だった。短縮と力は系の中では存在しないからである。この特殊相対論の個別の慣性系に一般相対論で 対応するのは、計量の値をもつ局所である。

ポテンシャルと同じく、計量は局所測定に表われないが、その微分は現象として表われる。時間計量g_44の√g_44が重力ポテンシャルでその勾配 が重力になるが、空間計量g_ii(i=1-3)は、その時間微分が重力になるだろうか。これは、電場がスカラーポテンシャルの勾配と、ベクトルポテン シャルの時間微分との和からの類推だが、測地成分(アフィン接続)Γ^i_rs は、それに容易に対応する解釈はできない。

空間計量が伸縮するとき、現象は実際に力を及ぼし、硬い物体や重力で結合した惑星には影響が出ず、力の関係していない空間だけが伸縮する という考え方が多いが、空間計量の変化によって力が発生するメカニズムは不明である。剛体は現実にはないが、座標系ほどの剛体はない。 空間計量g_iiの変化は、時間計量g_44が特定の時計だけに関わるのでなく、全ての物理現象の時間経過を決めるように、その空間座標の目盛が 伸縮するとき、その場所の物差しを含めた全ての間隔が伸縮するだろう、そのとき、やはり力についてをいうのは無駄であろう。その力は硬い ものには強く、軟らかいものに弱く、最も軟らかい空間に浮かせた鏡の間には、殆ど発生しない必要がある。均一な間隔の変化には力が強度に 比例すべきである。しかし、局所には間隔変化もそれに伴う力も、存在しないのである。宙に浮かせた鏡に力は働かない。少し離れた別の局所 慣性系にあるもうひとつの鏡も同じだが、それとの間の間隔は、どちらかの局所慣性系を延長した物差しでは変化するかもしれない。しかし、 それを光の干渉計で測るのは難しい。2つの鏡間のどの場所の局所慣性系も同様に計量を打ち消し、途中の光の波長は同じだけ伸縮するからである。

時空が加速度を生み出す測地成分Γ^i_rsは、局所慣性系を基準にした g_ikから算出される。そのとき、測定器近傍の局所慣性系は完全に測地 成分を0とする。局所慣性系は自由落下系であり、その重力場の効果を完全に無くす。そして、局所慣性系との違いを生むのは、測定器の長さの 数km離れた2点の計量の違いである。それ以外は完全に力と加速度は打ち消され発生しない。

月と地球の近辺の空間計量が倍(相対的に局所からみる宇宙のサイズが倍)に増大するとき、遠方から見た月と地球の間隔がその方向に半分になり、 月と地球の間の空間だけが半分になるのではない。月と地球も共に半分に短縮する。短縮した距離の中に半分に楕円体になった月と地球があり、 局所の短縮した物差しで測ると月と地球は同じ38万kmの距離で、半分に縮小したことを知ることがない。なぜなら、物差しの伸縮には、全空間、 物体、間隔が伸縮する。個別の力によっては決して伸縮しない最も硬い剛体である座標系さえも伸縮しているのであるから。

それゆえ、上の議論は、極端にいうだけで、ある方向の計量g_iiが倍にもなり地球が平べったい楕円体になるような重大な計量変化のとき、局所は それを検知可能で、何らかの2次以上の非線型の重力現象が発生するが、2次以上では微小な計量変化は知り得ないだろう。計量変化の2次以上の 非線型は測定を困難にする。計量の時間変化は、まだそれほどの困難ではない。現代の重力波検出装置は、空間計量の 10＾-24 程度の変化を検知 しようとするが、そこまでの微小変化を検知するには外部基準を必要とするだろう。それなしに計量変動を局所検出できるというのは、楽観的である。 10＾-12の計量変動は、検出メカニズムが2次になるだけで10^-24になる。物差しの変動でなく潮汐作用のようなものが共鳴振動で初めて検出できる という説明もある。人工衛星のなかの離れた2点(例えば人間の頭と足)は、ほとんど同じ公転速度をもつが、どちらが中心天体に近いかによって重力 が少し違う、そのため2点には、質量に比例して伸長させる潮汐力が働く。これは重力ベクトルの空間微分ベクトルであり、時間計量の空間2階微分で 説明されるものであり、空間計量が2点間にこのような力を働かせるとは容易にはいえない。計量の2階微分は、2次ほどではないが測定を難しくする。 そうして、振動は計量変化から分離できるが、基本的に局所検出できない計量が介在する。局所の鏡に力は働かないから局所で振動も起きないだろう。

局所の間隔測定は、絶対速度測定でもなかっただけでなく、計量測定でもなかった。地球の公転速度(系の絶対速度)を測定しようとしたマイケルソン ・モーリー実験を模して巨大にしたようなLIGOなどの重力波測定装置は、局所の間隔の変動を同じ場所の光の波長で測定しようとする測定であり、 測定結果は決して出ないだろう。地上の時間計量(時間経過)の変化が、星からの光のスペクトル偏移や離れた場所へのメスバウワー効果から知ること が容易なように、空間計量の伸縮は、局所の物差しで局所の間隔の変化を知ることは困難だが、局所の外部との比較は違う。一定の遠方の計量を基準 にして局所計量の変化を知ることは可能である。そして、これが時間計量ならさらに容易であること、時間計量も光速伝播することを、我々は知る。

ds^2= g_ik dx^i dx^k

膨張宇宙論は、空間計量g_ii(i=1-3)の増大をそのまま宇宙膨張というが、計量と物差しの積和が不変量ds^2だから、g_iiの増大は遠方からみたこの 時空点の物差しdx^i dx^kの縮小である。物差しの縮小が宇宙膨張の意味になっている。これ自体を疑うべきだが(*)、これに疑問を持たない人はさらに 「塵の漂う系」は、塵にあたる銀河(局所慣性系)を結んだ系であり、局所慣性系とは空間的サイズが違い、その物差しが銀河間距離であることを思い 出そう。これを物質とともに動く「共動座標系」ともいう。膨張宇宙論は、銀河間距離を物差しとする共動座標系に空間計量 g_iiの増大をいうが、 物差しを増大させるには、g_iiの逆数を増大させるのが正しい。勿論、逆数でも宇宙サイズが変化することに変わりはないが、そのとき距離の縮小に 赤方偏移が伴うだろうか。ドップラー効果による説明はその逆の状況に使われた。さらに「最近の物差しの縮小が遠方過去の距離の増大を意味する。 現在の空間サイズは小さくなっても、我々が光でみる遠方過去の宇宙の果てがそれに比べて増大する。」という説に対して、過去の宇宙から出た光の 通過する時空の空間計量に合わせて光が波長を縮小する。だから現在の物差しから見て過去の物差し伸長は、光の波数には影響しない。 それ以外に不足距離の波数分だけドップラー効果で説明できるのは、説明すべき赤方偏移の逆の青方偏移である。

空間計量の増大と宇宙膨張には、設定した物差しが銀河間の距離であるのに、それ以外の別の物差しがあって、例えば、量子力学で定まる例えば原子 サイズを基準にして、相対的な銀河間の距離の増大が膨張宇宙を意味するという誤解を招く。縮小物差しが銀河間の距離の増大を意味するとは、つまり、 計量は単に重力に関わるような、巨大な天体の重力現象だけの物理であって、物差しは別にあると誤解させる。物差しが別というのは物差しの無効化 であり計量の否定である。膨張論は、物差しを逆数にして空間の膨張をいうことで、一般相対論と計量の意味を失なわせる。それは特殊相対論の意味 さえ捨てさせる。始まりのある宇宙、絶対空間と始まりからの絶対時間、CMBのような絶対静止空間のなかでの太陽系と地球の速度が存在すると考える マイケルソン・モーリー実験のようなダークマターの検出がなされる。局所慣性系のような概念が、エーテル概念を復活させ、相対論が構築した概念、 慣性系の対等、時間と空間の相対性の意味を失わせる。そんな心配は不要かもしれないが、よく見ればいつの間にか、我々は過去の誤謬に陥いる。 何が確かで何が仮説、何が観測で何が推測かを見極めることはますます難しくなっている。空間計量の変化に何もない空間だけが膨張するという考えは、 誤りと考える。

v^2= 2GM/r - z

式(2)の銀河間距離を物差しとする宇宙の大きさGがその逆数の銀河間距離、この式のrとなって、ニュートン力学を再現している。式(5h)の式は、Gが サイクロイドなどを描くのであり、Gの増大に伴うのは銀河間距離の縮小である。Gの増大に伴って増大する銀河間距離にするには、式(2)でGが逆数で あるべきだが、逆数のGはニュートン力学を再現しないだろう。しかし、代わりに1/Gの物差しの銀河間距離がニュートン力学のエネルギー保存を満たす ので、そのほうがより合理的に思う。式(2)の導出をそのまま正しいと仮定すれば、我々がいわゆる膨張宇宙(銀河間距離が収縮する収縮宇宙)にいるか、 現在が銀河間距離が増大する137億年後の(時刻0とする)発散に向かって負の時間の位相にいることを意味する。

(*)空間計量の変化は物体と空間を区別しない。宇宙が膨張するなら空間だけでなく物体も膨張すべきでないか。宇宙の膨張は物差しの縮小でなく膨張 として表されるべきである。物差しの縮小が宇宙の膨張では、アインシュタインの定常宇宙論の宇宙の周辺のように、現在点からみてそれが膨張でなく 縮小してきた網の目の間隔をイメージできる。空間計量の増大(物差しの縮小)がなぜ宇宙の膨張を意味するのか。「縮みの思想」の盆栽のようにそこに、 物差しは自ら縮小すれば、それを囲む宇宙が相対的に大きいという、誰も保証しない前堤を使っている。宇宙全体が一定でないなら、自らが小さくなる ことで宇宙が大きくなることはない。また、宇宙全体が一定なら宇宙が大きくなることもない。宇宙は物差しの集りである。物差しが縮小/膨張するとき、 宇宙も縮小/膨張するだろう。あの膨張するゴム風船の喩えでも風船の大きさは一定ではない。風船の上に書かれた銀河の絵と銀河の間隔が増大するに 伴って風船は膨張するのである。

大局の視点、物差しの縮小と宇宙の一定、または、局所の見解、物差しの一定偏見と経路距離の拡大(宇宙膨張)は、物体間の "空間"拡大という解釈を生む。 この解釈は力は質量には比例するが、質量の間の結合の硬軟には関係しないから、広がる間隔は空間に選択的で、硬く結合した質量間は膨張せず、結合 のない質量間の"空間"だけが膨張すると考える。確かに力が硬軟に関係する理由はないが、空間計量の変化とは物差しの変化である。物差しの変化による 間隔の変化は一様で、そこが物体によって占められていても、空間であっても同じ比率で伸縮する。そのため、もし力がそこにあれば、それは硬軟に 比例すべきだが、実際には局所に伸縮も力も存在しないのである。そして、遠方の距離だけが逆に伸縮してみえる。

物差し一定と宇宙膨張は、不変量dsを否定した局所の偏見である。さらに物差しは銀河間距離でありながら、空間計量g_ii(＝G^2 A^2)の増大を宇宙の 膨張という式(2)は、物差しが拡大しその係数も拡大し不変量dsを無視している。これがニュートン力学に整合するには(2)の後の式に逆転が必要である。 式(2)のGAをともに逆数にする、修正はそれだけで済む。

このような膨張宇宙論は正当かという認識論的疑問である。私は沢山ある相対論のパラドックスに捕まったのかも知れない。この疑問が長年放置された 筈はない。膨張宇宙論は、20世紀からの基本的世界認識である。何か思想的な尊厳を破壊するように思われるという理由もある。但、考えが到らない間、 それさえ分からない、唯、具体的に何がこの不可解さを招いたかを考え続け、今に到る。