相対論

1916年 12月 A. アインシュタイン

1952年 7月 9日 A. アインシュタイン

第 I 部 特殊相対論
I. 幾何学的な陳述の物理的意味
II. 座標系
III. 古典力学における空間と時間
IV. ガリレイ座標系
V. 相対性の原理 (制限された意味における)
VI. 古典力学において採られた速度加算の定理
VII. 相対性原理と光の伝播の法則が明白に両立しないこと
VIII. 物理学における時間の概念について
IX. 同時刻の相対性
X. 距離の概念の相対性について
XI. ローレンツ変換
XII. 動きのなかの測定棒と時計の振舞
XIII. 速度加算の定理、フィゾーの実験
XIV. 相対論の発見的価値
XV. 理論の一般的結果
XVI. 経験と特殊相対論
XVII. ミンコフスキーの 4 次元空間
第 II 部 一般相対論
XVIII. 特殊と一般の相対性原理
XIX. 重力場
XX. 相対性の一般仮説への議論としての慣性と重力質量の同等性
XXI. どの点において古典力学と特殊相対論の基礎が満足できないか
XXII. 相対性の一般原理からのいくつかの推論
XXIII. 回転する参照物体上の時計と測定棒の振舞
XXIV. ユークリッドと非ユークリッド連続体
XXV. ガウス座標
XXVI. ユークリッド連続体と考えられる特殊相対論の時空連続体
XXVII. 一般相対論の時空連続体は、ユークリッド連続体でない
XXVIII. 相対性の一般原理の厳密な定式化
XXIX. 一般相対性原理に基づく重力の問題の解
第 III 部 宇宙全体に対する考察
XXX. ニュートン理論の宇宙論的困難
XXXI. "有限" かつ "無境界" 宇宙の可能性
XXXII. 一般相対論による宇宙の構造
Appendix I. ローレンツ変換の簡単な導出 (XI 章への補足)
Appendix II. ミンコフスキーの 4 次元空間 (世界) (XVII 章への補足)
Appendix III. 一般相対論の実験的確認
Appendix IV. 一般相対論による空間の構造 (XXXII 章の補足)
Appendix V. 相対論と空間の問題

幾何学は、つぎのような確かな概念から出発する。"平面"、"点"、そして"直線"、それによって我々が 多かれ少なかれ確定した概念を連想することのできるものであり、確かな単純な言明(公理)から、 それは、それらの概念のお陰で、我々が "真"であると受け入れる傾向のあるものである。 そのとき、論理的な過程の基礎の上に、我々が受け入れざるを得ないように自ら感ずるような 正当化、全ての残りの言明は、これらの公理から導かれことが示される、すなわち、証明される。 ひとつの言明は、それが公理から理解された方法で導かれるとき、正しい("真")とされる。 個々の幾何学的言明の "真"への疑問は、公理の"真"のひとつに還元される。最後の疑問は、幾何学 の方法では答えることのできないだけでなく、それ自身、全く意味のないことであることは、 現在永く知られたことである。2 点を通る唯一つの直線が存在することは、真であるかどうかを我々は、 問うことができない。我々は、ただ次のように言えるだけである。ユークリッド幾何学は、"直線" と呼ぶものを扱う。それらの特性はそれぞれの 2 点がその上に位置するものによって一意に決定される 存在の特性に帰される。 "真"の概念は、純粋幾何学の言明に符合しない。なぜなら、"真" という言葉によって我々は最終的に 指名の習慣のなかで、常に"現実"の物体に相応させるからである；幾何学は、しかし、それに含まれる 概念の経験物体との関係に関与せず、これらの概念の間の論理結合だけに関与しているのである。

幾何学の言明を "真" と呼ぶのを我々が強制されて感ずることがどうしてかを理解することは、これにも関わらず、 難しくない。幾何学的な概念は、多かれ少なかれ自然の物体に対応していて、この最後のものは、疑いもなく これらの概念の起源の排他的原因である。幾何学は、その構造に最大限可能な論理的統一を与えるために、 そのような針路を差し控えて当然である。例えば、実際的剛体の上のふたつの印された位置に "距離" を調べる 習慣は、我々の思考の習慣のなかに何か深く停泊したものである。さらに我々は、我々の観測の位置が適切に 選択できて、それらのみかけの位置が単眼の観測に一致させることができるとき、 3 点を直線の上に配置されたものとみなすように習慣付けられている。

もし、我々の思考の習慣の追求のなかで、我々はいま、ユークリッド幾何学の言明にひとつの言明を補足する。 実際的に剛体の物体の上の2点はその物体に与えるどのような位置の変化にもよらず、つねに同じ距離 (線間隔)をもつというものである。そのときユークリッド幾何学の言明は互いに解けて、実際的剛体の 相対位置への言明となる(*1)。この方法で補足された幾何学は、物理の分野として扱うことができる。 我々は、幾何学的言明の"真"をこの方法で解釈して、いま合法的に問うことができる。一方、我々は、 これらの言明が幾何学的概念に関連付けられた現実の物事を満たすかどうか問うことで自ら正当化できる。 より正確でない言葉では、このことを次のようにいうことができる。この意味の幾何学的言明の"真"によって 我々は、定規とコンパスによる構築の有効性を理解できるのである。

もちろん、この意味の幾何学的言明の"真"の理解は、専らむしろ不完全な経験の上に打ち立てられたもの である。そのため、現在、我々は幾何学的"真"を仮定し、そして後の段階で(一般相対論のなかで)この "真"が制限されていることを見るだろうし、その制限の拡張を考察するだろう。

(*1)そのことから次がいえる。自然物体が直線と関連付けられていて、剛体の上に与える 3 点 $A,B,C$ が直線上であるのは、$A, C$ が与えられ、$B$ を次のように選択したときである。$AB$ と $BC$ の距離の和が 最小であるように。この不完全な示唆は、我々の現在の目的には十分である。

事象の情景の又は空間のなかの物体の位置の、どの記述も、その事象と又は物体と一致する、剛体 (参照物体)上の点の叙述に基づいている。これは科学的記述に適用されるだけでなく、毎日の生活に おいても適用される。もし、私が "ロンドンのトラファルガー広場"(*2) という場所の記述を分析すると、 私は、次の結果に到達する。それが参照する地球が剛体であり、その場所の記述；"ロンドンのトラファルガー広場" は、それによって空間内の事象が一致する(*3)名前が付与された、よく定義された点である。

この原始的な場所記述の方法は、剛体の表面上の場所を扱うだけでなく、この表面の互いに区別できる 点の存在によっている。しかし、我々は我々の場所の記述を替えることなしに、両者の制限から自らを 自由にできる。例えば、もし雲がトラファルガー広場の上に漂っているなら、その広場に垂直にその雲 に達するような棒を立てることで、我々は地球の表面に対してその位置を決定できる。標準測定棒によ って測定されたその棒の長さをその棒の足場の位置と結合して、完全な場所記述が我々に与えられる。 この描写を基礎にして、位置の概念の洗練を開発する手法をみることができる。

(a) 我々は、それによって場所記述が参照される剛体を想像する。それは、我々の要求する物体の位置に 完全剛体によって到達するという手法によって補足される。
(b) 物体の位置を特定するのには、参照の明示点の代わりに、数を使う。(ここでは、棒の長さを測定棒 によって測定した。)
(c) 我々は、雲の高さをいうのに、雲に達する棒をまだ立てられていないときでさえ使った。地上の異 なった場所からの雲の光学的観測の方法で、そして光の伝播の特性を考えにいれて、我々は、雲に到達 するためには、我々が必要としたに違いない、その棒の長さを決定する。

この考察から、もし、場所の記述のなかに、参照剛体の上の印し位置の存在(名前を持つこと)から 解放されるのには、数値的測定という方法が可能であるなら、それは利点があるだろうことが見える。 この測定の物理のなかで、それは、デカルト座標系の適用で達成される。

これは、剛体に硬く結合した、互いに垂直な 3 平面によって構成される。ひとつの座標系を参照して、 どの事象の光景も(主要な部分は)決定されるであろう。3 つの垂直な線の長さによって、 又は、事象の光景からそれら 3つの平面へ落とされる座標 $(x,y,z)$ によって。 これら 3つの垂直線の長さは、ユークリッド幾何学によって裏打された規則と方法に従って実行された 剛体測定棒を使った一連の操作によって決定可能である。

実際は、座標系を構成する剛体表面は一般に使用可能でない；さらに、座標の倍率は、実際には剛体棒 の構成によっては決定できない。しかし、間接的な方法で可能である。もし、物理と天文学の結果が これらの明快さを維持すべきなら、場所記述の物理測定は、常に上の考察(*4)に従うものと考えられる。

我々は、こうして、次の結果を得る：空間のなかの事象の全ての記述は、事象が参照されるべき剛体の 使用を含んでいる。結果としての関係は、ユークリッド幾何学の法則は、"距離" をもち、"距離"は、 剛体上の2つの印しの伝統的方法によって物理的に表現される。

(*1) ここで我々は、残りがないこと、すなわち、測定が数全体を与えることを仮定した。 この困難は、分割した測定棒の使用で克服でき、その導入は、何ら基本的に新しい方法を要求しない。
(*2) 私は、これを最初に参照されていた、"ベルリンのポツダム広場"よりは親しみやすいとして選んだ(R.W.L.)。
(*3) "空間における同時性" という表現の重要性をここでさらに研究する必要はない。この概念は、 意見の違いが実際の適用可能性によって起きることがほとんどないことを十分に明白に確認する。
(*4) これらの見かたの洗練と修正は、第 II 部で扱われる一般相対論によって扱われるようになるまで必要とならない。

"位置"と"空間"によって何をここで理解すべきかは、明確でない。私は、鉄道の均一に移動している客車の窓 のところに立っている、そして石を土手の上に落とす、投げることなく。そのとき、空気の抵抗の影響を無視 すれば、私は、その石がまっすぐな線で下がっていくのを見る。小道からその悪行を観察したひとりの歩行者 が石が放物曲線を描いて地球に落ちていくことに気がつく。そこで、私は、質問する：石の軌跡が "現実には" 直線なのか放物線なのかを"位置決め" せよ。さらに、"空間のなか" の動きとは何を意味するのか。以前の章 の考察から、答えは、自明である。最初の場所から、我々は、その中に"空間"という、あいまいな言葉を全体 として慎重に避けてきた。我々は、かすかな概念さえも形成できないと、率直に白状しなければならない。 そして、その代わり "参照の実際的剛体に対する動き" に置き換えた。参照物体(鉄道客車又は土手)に対する 位置は、前章ですでに詳細に定義された。"参照物体"の代わりに、我々は、間に"座標系" を挿入した。それは、 数学的記述に役立つ概念だった。我々は次のことをいう位置にいる：石は、客車に対して硬く結合した座標系 に相対的には、直線的に通過する、しかし、地面(土手)に対して硬く結合した座標系に相対しては、放物線を 記述する。この例の助けを借りて、次のことが明確になった。座標系に独立に存在する軌跡(lit."通過曲線"(*1)) のようなものはなく、特定の参照物体に相対的に軌跡は存在する。

動きの完全な記述を得るためには、その物体が時間とともに、どう位置を変えたかを明細に述べる必要がある。 すなわち、その軌跡の全ての点において、その物体がいつ、そこに存在し位置したかを述べなくてはならない。 これらのデータは、次のような時間の定義によって補完されなければならない。この定義のおかげで、これらの 時間の値が本質的には観測可能な(測定の結果の)大きさとして見なされるような。もし、我々が古典力学の基盤 の上に立脚すれば、次のような手法のなかに我々の描像への要求を満たすことができる。我々は同一の構成の ２つの時計を想像する；鉄道客車の窓にいる男がそれらのひとつを持ち、小道にいる男は他方を持つ。それぞれ の観測者は、彼自身の参照物体の上の、石によって占められた位置を、彼が手に持つ時計の各刻ごとに、決定する。 この話では、我々は、光の伝播速度の有限性に含まれる不正確さを、考慮していない。我々は、この事と、そして ここで優勢な 2番目の困難を後に詳細に扱う。

(*1) すなわち、その物体がそれに沿って動く曲線。

もし、$K$ がガリレイ系であるなら、他の全ての系 $K'$ も $K$ に関して均一な移動運動状態にあるならばガリレイ系である。 $K'$ に相対して、ガリレイニュートンの力学法則は、$K$ に関してと同様に、よく正確に保たれる。

我々は、一般化をさらに一歩進んで、このような信条を表現する：もし、$K$ に相対的に、 $K'$ が回転なく 均一に動く座標系であるならば、そのとき $K'$ に関して発生するすべての自然現象は、$K$ に関してと 正確に同じ一般法則に従って起きる。この言明を "相対性の原理" (制限された意味における) と呼ぶ。

全ての自然現象が古典力学の助けによる表現である資格があると確信するひとである限り、この相対性の 原理に疑いを持つ必要はない。しかし、より最近の電磁気学と光学の発展の視点のなかで古典力学は、 全ての自然現象の物理的記述として十分な基礎を与えないことは、ますます明白になってきた。 この危機にあたり、相対性原理の有効性の問は、議論に対する機が熟してきた。 そして、この問に対する答えが否定的であるかもしれないということが、不可能とは示されなかった。

しかしながら、その端緒の話で相対性の原理の有効性に非常に味方する 2 つの一般的事実があった。 古典力学は、全ての自然現象の理論表現としては、我々に十分に広い基礎を与えないにも関わらず、 依然、我々は、かなりの "真" の尺度として受け入れなければならない。なぜなら、それは天体の実際 の動きを与え、それには細々とした詳細な驚きの感受性を伴うからである。相対性の原理は、それゆえ、 力学の領域に偉大な正確さをもって適用するに違いない。 しかし、そのように広い一般性の原理がそのような正確性をもって現象のひとつの領域に成立していて、 それにも関わらず、他の領域には有効でないに違いないということは、先験的であり、あまり確からしくない。

我々は、いま、2 番目の議論に進み、そこにさらに後に戻って来る。もし、相対性の原理 (制限された意味における) が成立していないならば、そのときは、互いに相対的に均一な移動をしている、ガリレイ座標系 $K,K',K"$ などが、 自然現象の記述において "同等" でなくなる。この場合、自然法則が特別に単純な手法で定式化され得るという 信念に制限を受けることになる。そしてもちろん、ただひとつの条件で可能になり、我々の参照物体として、 全ての可能なガリレイ系の間から、特定の動きの状態の"ひとつ" ($K_0$) を選び出しておかなくてはならない。 我々は、そのときは、この系を "絶対静止系" と呼び、他の全てのガリレイ系を "動いている" とすることにおいて 正当化 (自然現象の記述のための、その利点を理由として) されなければならない。 もし、例えば、我々の土手が $K_0$ であるなら、そのときは、我々の鉄道の客車は、$K$ である。それを基にしては、 $K_0$ を基にするよりも、より単純さの少ない法則が成立することになる。この減少した単純さは、客車 $K$ が $K_0$ に対して (すなわち、"現実に") 動いていることを理由とするだろう。$K$ を参照として定式化された自然の一般 法則のなかに、客車の速度の大きさと方向が必然的に役割を果たすことになる。我々は、例えば、パイプオルガン から放射される音符がその軸が移動方向と平行であるときは、パイプの軸がこの方向に垂直であるとき放射された ものとは異なることを期待しなければならない。 いま、太陽を回る軌道上の動きのために、我々の地球は、毎秒約 30 km という速度の鉄道客車の移動と比べること ができる。もし、相対性の原理が有効でないとすると、そのときは、地球の運動方向がつねに自然法則に入り込む ことを期待しないといけなくなり、そしてまた、物理系がそれらの振る舞いにおいて、地球に対する空間中の方向 に依存するということになる。1年の軌道中の地球の回転の速度の方向の変化のために、地球は、1年間を通して 仮想的な$K_0$系に相対的に静止であり得ない。しかしながら、最も注意深い観測においても、そのような非等方 性の特性、すなわち、異なる方向における物理的な非同等性は、地球上の物理空間において、決して現れていない。 これが相対性の原理を支持する非常に強力な議論である。

手短に、光の速度 $c$ (真空中)の一定さの単純な法則を仮定しよう。それは正当に学校の子供によって信じられている。 誰が想像できよう、この単純な法則が良心的で思慮深い物理学者を最大の知的困難に陥らせたかを。どのようにこの困難 が起きたかを考察しよう。

もちろん、我々は、光の伝播の過程(他の過程においてもそうだが)を参照物体(座標系)に参照しないといけない。 そのような系としてもう一度我々の土手を選ぼう。その上の空気が取り去られたと想像する。もし、光線が土手ぞいに 送られるなら、上からみて、光のかけらが土手に対して速度 c で伝送されているだろう。ここで我々の客車が鉄道に そって速度 $v$ で再度移動していて、その方向は光線のそれと同じで、しかしもちろん、その速度はずっと小さいとしよう。 さて、客車に相対的な光の伝播速度について質問しよう。前章の考察が適用できることは明らかで、そこで、光線が男の 客室に対する歩みの部分の役割をしている。男の土手に対する速度 $W$ は、土手に対する光の速度に置き換わる。 $w$ は求める客室に対する光の速度であり、そして、我々は次を得る。 \[ w= c - v \]

客車に対する光線の伝播速度は、こうして c より小さいことが分かる。しかし、この結果は、V 章で前に出た相対性原理 に矛盾する。なぜなら、自然の他の一般法則と同じく、真空中の (in vacuo) 光の伝播法則は、相対性原理に従って、客車を 参照物体とするときとレールが参照物体であるときとは、同じでなければならないからである。しかし、以上の考察によって、 これが不可能であることが示された。もし、どの光線も土手に対して速度 c で伝播するのなら、そのとき、この理由から、 客車を参照するときは別の光の伝播法則が必然的に成立しなければならない。これは、相対性原理に反する結果になる。

この矛盾の情景のなかで、相対性原理と "真空中の"光の伝播の単純な法則以外の何も廃棄の対象でないと見えた。 これまでの議論を注意深く辿ったあなた方は、非常な自然さと単純さから、知性を納得させる相対性原理を、保持しなければ ならないと予想することがほとんど確かであろう。そのときは、真空中の光の伝播法則は、相対性原理を満たすことのできる より複雑なものに置き換えられなければならないだろう。しかしながら、理論的物理の発展は、我々がこのコースを追うこと できないことを示すのである。電気力学と動く物体に関連する光学現象について、時代を変える理論研究者、H.A.Lorents は、 この領域の経験が結論的な電磁現象の理論を導くことを示した。そのなかで真空中の光速一定は、必然的な帰結である。 それゆえ、輝かしい理論物理学者は、この原理に反する実験データは、何も見出されていないという事実にも関わらず、 相対性原理を拒絶する傾向にあった。

この危機に相対性の理論は、闘技場に入った。時間と空間の物理的概念の分析の結果として、このことが明白になった。 現実に、相対性原理と光の伝播法則には、まったく何も不整合はない。 そして、両者の堅固な系統的な成立によって これらの法則は、論理的に硬い理論へと到達することができた。この理論は、特殊相対性理論 と呼ばれる。我々が後に扱う その拡張理論と区別するために。後続のページで、特殊相対論の基本的概念を提示するだろう。

多分、しばしの後、次の答えがあなたに浮かぶだろう："その言明の意義は、それ自身明らかであり、さらに説明はいらない： もちろん、実際のケースで2つの事象が同時に起きたかどうかを、観測によって決定することを任務としたなら、それには、 いくらかの考察は必要とするだろう。" 次の理由で私は、その答えに満足できない。独創的な考察の結果としてある有能な気象 学者がつねに場所 $A$ と $B$ に同時に稲妻が落ちることを発見しようとしていると想像しよう。そのとき我々は、この理論的結果 が現実と整合しているかどうかをテストする作業に直面するに違いない。我々は、"同時"という概念が役割を果たす全ての物理 的言明において同じ困難に遭遇する。その物理学者にとって、実際の場面でそれが満たされているかどうかを発見する可能性を もつまで、その概念が存在しないのである。我々は、このように同時性の定義を必要とする。その定義が我々にそれによって、 現在の場合、彼がふたつの落雷が同時に起きたかどうかを機器によって決定する方法を与えるような同時性の定義を。 もし、私が同時性の言明に意味を付ける能力があると想像しているとき、この要求が満たされない間は、私は自らを物理学者 であると欺いていることになる (そしてもちろん、私がそうでない場合も同じく適用される)。 (私は読者に、彼がこの点を十分に納得できるまで、さらに、先に読み進まないように頼むだろう。)

その事をしばし考えた後、同時性をテストするための次の示唆を提案する。レールにそっての測定によって、$AB$ を結ぶ線分を 測定し、距離 $AB$ の中点 $M$ に観測者を置く。観測者には、ある器械(例えば 2つの鏡が90度をなして傾く) が供給され、$A, B$ のふたつの場所を同時に視覚的に観測することができるようにする必要がある。もし、その観測者がふたつの稲妻の光を同時に 知覚するなら、そのとき、それらは同時なのである。

私は、この示唆をとても喜んだが、にもかかわらず、物事が十分に落ち着いたとみることができず、私は次の反論を起さざる を得ないように感じる："あなたの定義は、確かに正しい。もし、それによって $M$ にいる観測者が稲妻のひらめきを知覚する 光が $A → M$ の長さに沿ってと$B → M$ の長さに沿ってとが同じ速度で旅するということを私が知りさえすれば。しかし、 この想定試験は、我々がすでに時刻を測定する方法を手中にもつときにのみ可能である。このようにそれは、我々がここに 論理的円環のなかを動くかの様相を示しているのかもしれない。"

さらに考察を経た後、あなたは、何か軽蔑のー確かにー眼差しを私に投げつけ、こう主張する： "私は、しかし、私の以前の 定義を保持する。なぜなら、それは、現実に、光について何も仮定しないからである。唯一つの要求は、同時性の定義を作る ことである。すなわち、現実のどの場合にも、それが、定義された概念が満たされているかどうかの実証的判定を与えないと いけない。私の定義がこの要求を満たすことは、議論の余地がない。光が $A → M$ 経路と $B → M$ 経路を同時間で通過する 必要があるということは、現実には光の物理的性質についての"推測"や"仮定"でなく、同時性の定義に到達するため、私が 私自身の自由意志で作ることのできる"規定"である。"

この定義がふたつの事象だけでなく、我々の選ぼうと思う数の事象の正確な意味を、事象の光景の位置と参照物体(*1) (ここ では鉄道の土手)に依らずに、与えることができることは明らかである。我々は、こうしてまた、"時間" の定義に導かれる。 この目的のために、同一の構成の時計を鉄道線(座標系)上の点 $A, B, C$ に配置すること、そしてそれらの指示の位置が (上の意味で) 同時で等しいことを想定する。このような条件で、これらの時計のなか、その事象に(空間上の)近隣の ひとつの時計の (針の位置を)読み取ってひとつの事象の"時間"を理解する。この方法で時間値は、本質的に観測する ことのできるどの事象にも付与される。

この規定は、さらなる物理的な仮定を含んでいる。その有効性が実証的な反対証拠なしには疑うことのできない仮定である。 全ての時計は、同一の構成であるなら、同じ速度で進む、ということが仮定されている。より正確にいえば： もし、ふたつの時計が参照物体の異なる位置に静止して配置され、ひとつの時計の指示の位置が(上の意味で)同時であり、 他の時計の指示の同じ位置をもつとき、そのときは、同一の "設定" がつねに(上の定義の意味で)同時である。

(*1) 我々はさらに、もし、異なる場所の 3 つの事象 $A, B, C$ が、$A$ と $B$ とが同時で、$B$ と $C$ とが同時である(上の定義の 意味での同時性) というような方法で起きるなら、事象 A, C の組の同時性の判定規準が満たされていると想定する。この仮定は、 光の伝播の法則についての物理的仮説である； 我々が真空中の光の速度の一定法則を保とうとするならば、それは、確かに 満たされなければならない。

ふたつの事象、(例えば、$A, B$ での落雷)鉄道土手を参照として同時であるものは、列車に相対しても同時だろうか。 我々は、直接にその答えが否定的でなければならないことを示す。

我々が落雷、$A, B$ が同時であると土手に関していうとき、我々は次を意味する：稲妻の起きた場所 $A$ と $B$ で放射された光線が 土手 $A→ B$ の長さの中点 $M$ において出会うことである。しかし、事象$A$ と $B$ はまた、列車上の位置、$A$ と $B$ に対応する。 点 $M'$ を、旅行している列車上の $A→ B$ の中点とすると、稲妻のひらめきがちょうど起きたとき(*1)の、この点 $M'$ は、点 $M$ に自然に一致する。しかしそれは、図では右向きに列車の速度 $v$ で移動する。もし、列車中の位置 $M'$ に座っている観測者が この速度を持っていなければ、そのときは、彼は永久に $M$ に残る。そして、稲妻のひらめき $A$ と $B$ からの光線は、同時に彼 に到達していただろう。すなわち、それらは、ちょうど彼が位置していた所で出会っただろう。 いま、現実には(鉄道の土手を参照として考察すれば)、彼は、$B$ から来る光のビームに対抗して、急いで行っている。一方、 それは、$A$ から来る光のビームの前方向に乗っている。それゆえ、その観測者は、$B$ から放射された光のビームを、 $A$ から 放射されたそれを見るよりも先に見るだろう。列車を彼らの参照物体として使う観測者は、それゆえ、稲妻 $B$ の方が稲妻 $A$ よりも先に発生したという結論に達しなければならない。我々は、こうして不可能な結果に到達した：

土手を参照として同時な事象は、列車を参照としては、同時でない。そして逆もまた真である(同時刻の相対性)。 どの参照物体(座標系)も、それ自身の特定の時間をもつ；我々がその時間に言及する言明の参照物体を告げられないなら、 事象の時刻の言明は、意味をもたない。

さて、相対性理論の到来の前は、時間の言明は絶対的な意味を持っていると、すなわち、参照物体の動きの状態によらないと、 つねに暗黙に物理学では仮定されていた。しかし我々はいま、この仮定がもっとも自然な同時性の定義とは両立しないことを 見た。もし、我々がこの仮定を捨てれば、そのとき、"真空中の" 光の伝播法則と、相対性の原理(VII 章で開発した)の衝突は、 消え去る。

我々は、VI 章の考察によってその衝突に導かれたが、もはや、それは、確固としたものではない。その章で、客車の中のその 男は、客車に対して毎秒、距離 $w$ を移動し、土手に相対しても同じ距離を時間の各秒に通過する。しかし、前述の考察に従えば、 客車を参照する特定のできごとに必要な時間は、土手から(土手を参照物体として)判断する同じできごとの継続時間とは、等しい と考えてはならない。それゆえ、歩くその男が距離 $w$ を鉄道線に対して土手から判断する1秒と等しい時間に移動すると主張する ことはできない。

さらに、VI章の考察は、まだ 2 番目の仮定に基づいていて、それは、相対論の導入よりさらに以前には、つねに暗黙になされた 仮定であるが、厳密な考察の光のなかで、任意な独断と判明したものである。

(*1)土手から判定して。

距離を鉄道線から判定しなくてはならないときは、違うことである。ここでは、次の方法が心に浮かぶだろう。もし、 それらの離れた距離が必要な列車上の 2 点を $A'$ と $B'$ で呼ぶなら、そのときは、これらの点の両方が速度 $v$ で土手に沿って 動いている。最初の場所で、我々が土手の $A$ と $B$ の点を決定する必要があったとき、それらは、土手から判定して特定の時刻 $t$ に 2 点 $A'$ と $B'$ によって、ちょうど通過されたものである。これらの土手の $A$ と $B$ の点は、VIII章で与えられた時間の 定義を適用して決定できる。これらの $A$ と $B$ との点の距離は、測定棒を土手に沿って繰り返し適用することで測定される。

この最後の測定が最初と同じ結果を供給するだろうことは、先験的にもはや確かでない。土手から測定された列車の長さは、 列車自体のなかでの測定で得られた長さから違ってもよい。この状況は、VI章の外見上明白な考察に対抗して提起されなければ ならない 2 番目の反論に我々を導く。すなわち、客車内の男がー列車から測定されたー単位時間に距離 $w$ をいくとき、 そのとき、この距離は、ー土手から測定されたものとしてはー 必ずしもまた $w$ に等しくないのである。

もし、これらの仮説を捨てれば、そのとき、VII章の矛盾は消える。なぜなら、VI 章で導いた速度加算の定理が無効になるからである。 真空中の光の伝播の法則は、相対性原理と両立できる可能性が自ら現れる。そして質問が持ちあがる：これらふたつの基本的な経験の 結果の間の明白な非合意を取り除くために、我々は、どのように VI章の考察を修正しないといけないのか? この質問は一般的なものを 導く。VI章の議論のなかで、我々は、列車と土手の両方に相対的に、場所と時間を扱わねばならなかった。鉄道土手に関して事象の場所 と時間を我々が知るとき、列車に関係してのその事象の場所と時間をどう見出せばよいのか? この問題に、光の真空中の伝送の法則が 相対性原理に反しないような性質をもつ考え得る答えが存在するのか。言葉を代えれば：我々は、個々の事象の場所と時間を両方の参照 物体に相対的に考えることができるだろうか? 土手に相対しても、列車に相対しても、どの光線も伝送速度 $c$ をもつようにして? この質問は、全く肯定的な答えとなり、ひとつの参照物体から他へ乗り換えるときの、事象の空間ー時間の大きさについての、完全に 確定した変換則を導いた。

我々は、これを扱う前に、次の付随的考察を紹介する。現在まで我々は、土手に沿って起きる事象だけを考察した。それは、数学的な 直線の関数の仮定をもつことである。II章に示した手法で我々は、この参照物体が横に垂直な方向に補完されることを想像でき、 棒の枠組の方法によって、どこに発生する事象もこの枠組で参照して場所特定できるようになる。同様に、我々は速度 $v$ で旅する 列車を全空間に広げて、どの事象も、どれだけそれが離れていても、2番目の枠組に関して位置決めできるように想像することができる。 どんな基本的誤りも犯すことなく、現実にはこれらの枠組が、その固体の貫通性のなさから、互いに絶え間なく妨害するであろうことを 無視することができる。そのようなどの枠組のなかにも、互いに垂直な 3 つの表面が区別されることを想像でき、それは、"座標面" ("座標系") と呼ばれる。ひとつの座標系 $K$ は、土手に対応し、座標系 $K'$ は列車に対応する。事象がいつ生起したかによらず、$K$ に関 して3つの垂直の $x,y,z$ の座標面によって、空間に固定され、時間に関しては時間値 $t$ によって参照される。同じ事象が $K'$ に相対して も時間と空間に関して、対応する $x', y', z', t'$ の値によって固定されるだろう。それらはもちろん、$x, y, z, t$ とは同じでない。 これらの値が物理測定の結果としてどのように扱うかを、すでに詳細に述べた。

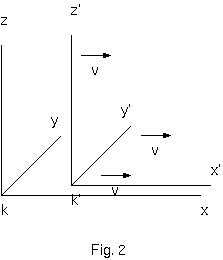
明らかに、我々の問題は、次の方法で正確に定式化できる。ある事象の $K$ に関する大きさ $x, y, z, t$ が与えられたとき、同じ事象の $K'$ に関する $x', y', z', t'$ の値は何か? である。関係は、真空中の光の伝送の法則は、ひとつと同じ光線、(そしてもちろん、どの線 についても) $K$ と $K'$ に関して満たすように選ばれている。座標系の相対的な空間の方向については、図.2 に示す。この問題は、次式に よって解かれた。 \[ \begin{align} x'&= {x-vt \over \sqrt{1-{v^2 \over c^2}}} \\ y'&= y \\ z'&= z \\ t'&= {t-{v \over c^2}x \over \sqrt{1-{v^2 \over c^2}}} \end{align} \] これらの式の系は、ローレンツ変換として知られる(*1)。

もし、光の伝送法則の代わりに我々が我々の基礎としてもつ、古い力学の暗黙の仮定を、時間と長さの絶対的な性格を表すもの とするなら、そのとき、上の式の代わりに、次の式を得るに違いない。 \[ \begin{align} x'&= x - vt \\ y'&= y \\ z'&= z \\ t'&= t \end{align} \] これらの式の系を、しばしば、"ガリレイ変換"といわれる。ガリレイ変換は、ローレンツ変換の式の光の速度 $c$ に無限に大きな 値を代入したとき得られる。

次の表示によって、ローレンツ変換に従えば、真空中の光の伝送速度の法則が、参照物体 $K$ と $K'$ の両方において満たしている ことを、すぐに見ることができる。光の信号が正の $x$ 軸に沿って送られ、この光の刺激が次の式によって \[ x= ct \] すなわち、速度 $c$ によって進んでいるとき、ローレンツ変換の式に従えば、この単純な式 $x$ と $t$ の間の関係は、$x'$ と $t'$ の関係を 含んでいる。実際に、ローレンツ変換の 1 番目と 4 番目の式の $x$ を $ct$ に代入して、 \[ \begin{align} x'&= {(c-v)t \over \sqrt{1-{v^2 \over c^2}}} \\ t'&= {(1-{v \over c})t \over \sqrt {1- {v^2 \over c^2}}} \end{align} \] それらから、割算をして、式、 \[ x'= ct' \] は、すぐに得られる。$K'$ 系を参照するとき、光の伝播は、この式に従って起きる。我々は、こうして、参照物体 $K'$ に相対して の光の伝送速度がまた $c$ に等しいことを見た。他のどの方向に進んでいる光線であっても、同じ結果が得られる。 もちろん、これは、驚くべきことではない。なぜなら、ローレンツ変換の式が、この視点を満たすように導かれたのであるから。

(*1) ローレンツ変換の単純な導出を付録 I に与える。

もちろん、この速度 $c$ の制限速度としての特徴は、ローレンツ変換の式から明確に出てくる。なぜなら、これらは、 もし、我々が速度 $v$ として $c$ よりも大きな値を選ぶと、意味をなさなくなるからである。

もし、反対に、1m の棒を $K$ に関して $x$ 軸に静止させることを考察すれば、そのときは、我々は、$K'$ から判定する棒の長さ が、 $\sqrt{1-v^2/c^2}$ になっていることを発見しなければならない。これは、我々の考察の基礎をなす、相対性の原理に全く合致 している。

先験的に、ローレンツ変換の式から測定棒と時計の物理的振舞を我々が何かを学ぶことができるに違いないことは、全く明らかである。 なぜなら、$x, y, z, t$ の大きさは、測定棒と時計という手段によって得られる測定結果よりも、多くもなく少なくもないからである。 もし、我々が考察の基礎をガリレイ変換に置くと、その動きの結果として棒の短縮は得られないだろう。

いま、 $K'$ の原点 $x'= 0$ に永久に置かれた 1秒をはかる時計を考察しよう。$t'= 0$ と $t'= 1$ がこの時計のふたつの継続する刻み である。ローレンツ変換の 1 番目と 4 番目の式は、これらふたつの刻みに対して、 \[ t= 0 \] と \[ t= {1\over\sqrt{1- {v^2 \over c^2}}} \] とを与える。$K$ から判定して、その時計は速度 $v$ で動いている。この参照物体から判定して、その時計のふたつの打刻の間は、 1秒ではなく、${1 \over \sqrt{1-{v^2 \over c^2}}}$秒であり、すなわち、いくらか大きい時間である。結果的に、動く時計は、 静止時よりもゆっくりと進む。ここでも、速度 c は、到達できない制限速度の役割りを果たしている。

VI章で、我々は一方向の速度の加算の定理を導いたが、それはまた、古典力学の仮説からの結果の形式をもっていた。この定理は、 また、ガリレイ変換(XI章)からすぐに引き出せる。客車のなかを歩く男の場所で、座標系 $K'$ に対して相対的に動く点を導入した。 次式に合致して、 \[ x'= wt' \] ガリレイ変換の 1 番目と 4 番目の式を使って、$x'$ と $t'$ を $x, t$ で表現でき、次式を得る。 \[ x= (v+w) t \] この式は、$K$ 系を参照した点の動きの (土手を参照する男の) 法則以外なにも表さない。我々はこの速度を記号 $W$ で表し、VI章と 同じく次式を得る。 \[ W= v + w \tag{A} \] しかし、我々は相対性の理論の基礎の上に同様の考察を実行することができ、次式のなかに、 \[ x'= wt' \] ローレンツ変換の 1 番目と 4 番目の式を使用し、$x'$ と $t'$ を $x, t$ で表す。式 (A)の代わりに、次式を得る。 \[ W = {v+w \over {1+{vw \over c^2}}} \tag{B} \]

それは、相対論に従った1方向の速度の加算の定理に対応する。これらふたつの定理のどちらがより経験に合うかという質問が いま出てくる。この点で、輝かしい物理学者フィゾーによって 50年以上前になされた最重要の実験によって我々は啓発された。 そしてそれは、その結果について疑いがあり得ないように、それからも、いくらかの最良の実験物理学者によって繰り返された。 その実験は、次の質問に関係している。光は、動きのない液体を特定の速度 $w$ によって旅する。液体が速度 $v$ で管を通って 流れるとき、どれほどの速度で光は、管 $T$ (付図. 3 参照)を矢印の方向に旅するのだろうか?

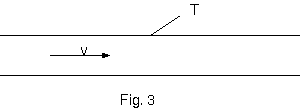
相対性の原理に従って光の伝播は、液体が他の物体に対して動いているかどうかによらず、"液体に対して" つねに同じ速度 $w$ であることを我々は確かに当然とみないといけない。光の液体に対する速度と、液体の管に対する速度は、知られている。 我々は、光の管に対する速度を要求されている。

我々が VI章の問題をもう一度目の前にもつことが、明らかである。管は鉄道土手又は座標系 $K$ の役割りを演じ、液体が客車 の又は座標系 $K'$ の役割りをもつ。最終的に光が客車に沿って歩く男の又はこの章の動点(?)の役割りである。もし、我々が 管に相対する光の速度を $W$ で記述するなら、そのときは、これは式 (A) か (B) によって与えられ、ガリレイ変換又は、 ローレンツ変換に従って、事実に対応するものである。実験(*1)は、相対論から導かれた式 (B) を支持するものであった。 その合致は、実に非常に正確であった。ゼーマン(Zeeman)による最新の最も優秀な測定によると、光の伝播への流れの速度 $v$ の影響は、1% 以内まで表式 (B) による。

しかしながら、我々は、いま、この現象の理論が H.A.Lorentz によって、相対論の言明よりもはるかに前に与えられていた ことに注意を引かなければならない。この理論は、純粋に電気力学的性質のもので、物質の電磁構造に対する特定の仮説によ って得られた。この状況は、しかし、少なくともその実験の相対論を支持する厳しいテストという結論性を減じるものではない。 なぜなら、Maxwell-Lorentz の電気力学は、その本来の理論が決して相対論に反対するものではないからである。むしろ、 相対論は、電気力学から開発されたものであり、電気力学がその上に作られた、前には互いに独立であった仮説達を、驚くほど 単純な結合と一般化にしたものであるからである。

(*1) フィゾー(Fizeau)は、$W= w + v(1-{1 \over n^2})$ を見出した。ここで、$n= {c \over w}$ は、その液体の屈折率。一方、${vw \over c^2}$ の 1 に 対する小ささのため、式 (B) は、最初、$W= (w+v)(1-{vw \over c^2})$ 又は、同じオーダの近似、$w+v(1-{1 \over n^2})$に置き換えることができ、 後者の式がフィゾーの結果に合致する。

光の伝播法則は、その受容は、我々の実際の知識によって正当化され、この思考の過程のなかで重要な部分を果たす。ひとたび、 ローレンツ変換をもつと、しかし我々はこれを相対性の原理と結合して次の理論に集積することができる：

どの自然の一般法則も、もし、我々がもとの座標系 $K$ の 時空変数 $x,y,z,t$ の代わりに、座標系 $K'$ の新しい時空変数 $x',y',z',t'$ を導入したとき、正確に同じ形式の法則によって変換されるように、構成されなければならない。これに関連して、 通常とその強調された大規模さとの間の関係をローレンツ変換が与えた。?? 要約していうと：自然の一般法則は、ローレンツ変換に対して共変である。

これは、相対論が自然法則に対して要求する確固とした数学的条件である。そして、このおかげで、その理論は、自然の一般法則を 探すときの価値ある発見的手法の助けとなった。もし、この条件を満たさない自然の一般法則が見出されるなら、そのときは、 この理論のふたつの基本的仮定のうち、少なくともひとつは反証されたことになるのである。いま、どのような一般的な結果を その理論がこれまでに明らかにしたかを検証しよう。

古典力学は、特殊相対論の要求に直面する前に修正を必要としていた。しかし、この修正の主要な部分は、物質の速度 $v$ が光速と 比較してあまり小さくない速い動きの法則にだけ影響した。そのような高速な動きの経験は、電子とイオンの場合の中に限定される； 他の動きは、古典力学の法則からの変化は、実験的に明らかになるには余りに小さい。星の動きについては、我々は、一般相対論に ついて述べるまで考慮しない。相対論に従えば、質量 m の質点の運動エネルギーは、もはや、よく知られた式、 \[ m {v^2 \over 2} \] では与えられず、次式である。 \[ {mc^2 \over \sqrt{1-{v^2 \over c^2}}} \] この式は、速度 $v$ が光速 $c$ に近付くと無限に近付く。その速度は、そのため、どれほど大きなエネルギーが加速に使われても つねに $c$ 未満に留まらないといけない。その運動エネルギーの式は、級数の形では、 \[ mc^2 + m {v^2 \over 2} + {3 \over 8} m {v^4 \over c^2} + .... \] もし、$v^2 \over c^2$ が 1 より小さいとき、3番目の項は、2番目の項よりつねに小さい。2番目の項が単独に古典力学で考えられたもので ある。最初の項$mc^2$は、速度を含んでいない。そのため、質点のエネルギーがどのように速度に依存するかの問だけを扱うときには、 考慮する必要がない項である。その本質的重要性は、後で話す。

特殊相対論が導いた一般的な性質の最重要の結果は、質量の概念に関係している。相対論の出現以前には物理学は、基本的に重要 なふたつの保存則を認識していた。すなわち、エネルギー保存則と質量保存則である；これらふたつの基本的保存則は、互いに全く 独立に現れていた。相対論によって、それらはひとつに統一された。いま、手短に、この統一がどうやって起きたか。そしてそれに 付随する意味について考察する。

相対性の原理は、エネルギー保存則が座標系 $K$ に関してだけでなく、$K$ に対して均一な移動の状態の、どの座標系 $K'$ に関しても、 短くいえば、どの "ガリレイ座標系"についても、成立することを要求する。古典力学と違って、ローレンツ変換は、ひとつのその ような系から、他の系への決定する要因である。

比較的単純な考察によって、これらの前提とこれに関連する Maxwell の電磁力学の基本方程式から、次の結論の導出される： 速度 $v$ で動く物体が放射の形のエネルギー $E_0$ の量を吸収して(*1)、その過程で速度変化を被らないとき、結果的にもつ、 エネルギー増加量は、 \[ E_0 \over \sqrt{1-{v^2 \over c^2}} \] 物体の運動エネルギーの上に与えられた式を考慮すれば、求める物体のエネルギーは、次になる。 \[ (m+{E_0 \over c^2})c^2 \over \sqrt{1-{v^2 \over c^2}} \] このように、その物体は、速度 $v$ で動く質量 $(m+ {E_0 \over c^2})$ の物体と同じエネルギーをもつ。それゆえ：もし、物体がエネルギー $E_0$を取得すると、そのとき、その慣性質量は、$E_0 \over c^2$だけ増加する。物体の慣性質量は、定数ではなく、物体のエネルギー変化 に従って変化する。物体系(複数の物体)の慣性質量は、そのエネルギーの尺度とさえ見なし得る。系の質量保存則は、エネルギー 保存則と同一となり、系がエネルギーを取得、放出しないときにだけ有効である。エネルギーの表式、 \[ {mc^2 + E_0 \over \sqrt{1-{v^2 \over c^2}}} \]

にある、これまで我々の注意を引いてきた、$mc^2$の項は、それが$E_0$を吸収する前に、物体がもっていたエネルギー(*2)に他ならない。

この関係と実験の直接の比較は、系に置くことのできるエネルギー変化$E_0$は、系の慣性質量の変化として感知できるほど 大きくないため、現在のところ不可能である。(1920；*注意を参照)${E_0 \over c^2}$は、エネルギー変化前に与えられた質量$m$と比べて 余りに小さ過ぎる。古典力学が質量保存則を独立に有効な法則として成功裡に確立できた理由は、この状況によるのである。

基本的な自然についての最終的所見を付け加えさせて頂く。遠隔電磁作用の Faraday-Maxwell 解釈の成功は、Newton 重力 タイプの (中間媒体なしの)即時遠隔作用のようなものがないことを物理学者が確信するようにさせた。相対論に従えば、 光速での遠隔作用がつねに、即時遠隔作用、又は、無限速度での遠隔作用の代わりをする。これは、この理論で速度 c が 基本的な役割りを演じていることと結合している。第 II 部では、我々は、どのような方法でこの結果が一般相対論において 修正されるかを見るだろう。

(*1) $E_0$は、その物体からは動いている座標系から判定したエネルギー取得。
(*2) その物体からは動いている座標系から判定したエネルギー。
*注意ー$α$粒子、陽子、重陽子、中性子、または$γ$線の砲撃によってもたらされる核変換過程の出現によって、 $E= mc^2$の関係によって表現される質量とエネルギーの等価性は、十分に確認された。砲撃粒子(又は光子)の 反応質量と運動エネルギーの等価質量の総和は、つねに結果の質量より大きい。その差は、発生粒子の運動エネルギー の又は放出電磁エネルギー($γ$光子)の等価質量である。同じく、自発分解する放射性原子は、つねに結果原子の質量の 総和より、発生粒子の運動エネルギー(又は光子エネルギー)の等価質量だけ大きい。核反応式と関連した核反応の放出する 線のエネルギー測定は、原子の重量の高精度までの評価を可能にする。(R.W.L.)

しかし、それ自身に、すなわち相対論の使用なしに、異質な予備的仮説を導入した Maxwell-Lorentz 理論だけで再現される これまで得られた、ふたつのクラスの実験事実がある。

陰極線と放射性物質から放射されるいわゆるβ線は、非常に小さな慣性と大きな速度をもつ負に帯電した粒子(電子)によって できている。電磁場の影響の下のこれらの線の曲がりを調べることで、我々は、これらの粒子の運動法則を非常に正確に研究 することができる。

これら電子の理論的取り扱いのなかで、我々は、電磁力学理論自身がそれらの性質の説明を与えないという困難に直面している。 １符号の電気質量(電荷)は互いに反発するから、これまでその性質が我々に知られない(*1)、それらの間に働く別の種類の力がない限り、 必然的に電子を構成する負の電荷がそれらの互いの反発力で飛散するだろう。もし、いま、電子を構成する電気質量の間の相対距離が 電子の運動によって変わらない (古典力学の意味での剛体結合) と仮定すると、我々は、経験に合致しない電子の運動法則に到達する。 純粋に形式的な視点に案内されて、H.A.Lorentz は、その運動の結果、電子の形が運動の方向に、式 $\sqrt{1-{v^2 \over c^2}}$だけ、 短縮を経験するという仮説を初めて導入した。どの電磁的事実によっても正当化されないこの仮説が、近年、偉大な精度で確認された、 あの運動の特定の法則を、そのとき、我々に供給した。

相対論は、電子の構造や振舞にいかなる意味での特別な仮説を必要とせずに、同じ運動の法則を導く。我々は、Fizeau の実験 について XIII 章に似た結論、その液体の物理的性質に関する仮説を描く必要なしに、相対論によって予言される結果に到達した。

我々が言及した 2 番目の事実は、空間中の地球の運動が地上の実験で知覚可能かどうか、という問に関係する。我々はすでに V 章 で、この性質の全ての試みが、否定的結果を導いたことを述べた。相対論が出される前には、この否定的結果を調停することは、 これから議論する理由によって、困難だった。時間と空間についての継承された偏見は、ひとつの参照物体から他のものに移るときの ガリレイ変換の最上の重要性に対して、どのような疑いも挙げることを許さなかった。いま、我々は、Maxwell-Lorentz 方程式が 参照物体 $K$ に成立していると仮定し、そのとき $K$ に対して均一に運動する参照物体 $K'$ に関しては、我々が $K$ と $K'$ の座標系の 間にガリレイ変換の関係の存在を仮定する限り、それが成立しないことを見出す。それは次のように現れる。全てのガリレイ座標系 のなかに、ひとつ ($K$) が物理的に唯一である動きの特定の状態に対応している。この結果は、空間にある仮想的なエーテルに対して $K$ が静止しているとみなすことで物理的に解釈される。一方、$K$ に対して動いている全ての座標系 $K'$ は、そのエーテルに対して 動いているとみなす。このエーテルに対する $K'$ の動き、($K'$ に対する"エーテルの漂い")に対しては、我々が $K'$ に相対して成立 すると思うものより、より複雑に扱われる。厳密にいえば、そのようなエーテルの漂いは、また、地球に相対して仮定されるべきで、 長い間物理学者の努力が、地球表面のエーテルの漂いの存在を検出する試みに、捧げられてきたものである。

これらの試みの最も注目すべきもののひとつのなかに、Michelson が工夫した方法、それが決定的に違いないかのようなものがある。 互いに反射面を向けているふたつの鏡の配置を想像されたい。全体の系がエーテルに対して静止しているならば、光線がひとつの鏡 から他へ通過して戻るのに、完全に確定した時間 $T$ を必要とする。しかしながら、もし、物体が鏡も含めてエーテルに対して動いて いるなら、この過程にわずかに異なる時間 $T'$ を必要とすることが計算によってわかる。そして、まだ、もうひとつの点がある： 与えられたエーテルに対する速度 $v$ について、物体が鏡の面に対して垂直に動くとき、動きが面に平行のときの結果から時間 $T'$ がわずかに異なることが計算で示される。推定されるこれらふたつの時間の違いは、極端に小さいにも関わらず、Michelson と Morley は、この違いが明確に検出されるに違いなかった干渉を含む実験を実行した。しかし、実験は、否定的結果をーー物理学者 を非常に混乱させる事実を、与えた。Lorentz と FizGerald は、エーテルに対する物体の運動が、運動の方向に物体の短縮を、 上で述べた時間の違いを補償するのに、丁度十分な量の短縮をつくり出す、という仮定によって、この困難から理論を救った。 XII 章の議論と比較すれば、相対論の立場からもこの困難の解が正しいものであることが示されている。しかし、相対論の基礎に 立った解釈の方法は、比較にならないほど、より満足できるものである。その理論によれば、エーテルの概念の導入の場合の "特別に有利な" (唯一の)座標系のようなものはなく、それゆえ、エーテルの漂いも、それを示そうとするいかなる実験もあり得ない。 ここでは、動物体の短縮は、理論のふたつの基本的原理から、特別な仮説の導入なしに結論される：そして、我々が見出したこの 短縮に含まれる主要な要素は、我々がどのような意味も付与できない動き自身にあるのでなく、特定の場合に選択した参照物体に 対する動きにある点である。このように、地球とともに動く座標系にとって、Michelson と Morley の鏡の系が短縮されたのではなく、 太陽に相対的に静止している座標系にとって短縮しているのである。

(*1) 一般相対論は、電子の電気質量が重力によって保持されているらしいとみる。

空間は、3次元連続体である。これによって我々は、点(静止の)の位置を3つの数(座標)$x,y,z$で記述することができるという意味で、 また、ひとつの点の近傍には無数の点があって、その位置は、座標で$x_1,y_1,z_1$のように表せ、それぞれの値を最初の点の座標 $x,y,z$にどれほど近くにも我々が選べるという意味である。後者の特性のおかげで我々はそれを"連続体"と呼び、3つの座標値が あることによって、それを"3次元"という。

同様に、Minkowski が"世界" と呼んだ物理現象の世界は、時空の意味で、4次元である。なぜなら、それは個々の事象で構成され、 それぞれは、4つの値で記述される。つまり、3つの空間座標$x,y,z$とひとつの時間座標$t$によって。世界はこの意味でまた連続体 である：どの事象にも、その座標値$x_1,y_1,z_1$を最初考えた$x,y,z,t$から不定に小さな値だけ異なるように我々が選択しようとする だけの数存在する (と実感する、少なくとも考え得る) "近傍"の事象がある。 この意味で世界を4次元連続体とみなすことに我々が慣れていないのは、物理学では、相対論の出現以前は、空間座標と比較して 時間が違ったもっと独立な役割りを果たしていたためである。それは、我々が時間を独立した連続体として扱うことに慣れていた ためである。実際、古典力学に従えば、時間は絶対的である。すなわち、それは位置と座標系の動きの状態とは独立である。 我々は、これがガリレイ変換の最後の式、$(t'= t)$ に表現されていることを見る。

相対論の世界の考察において、4次元流は、自然である。なぜなら、この理論では、時間は独立性を剥ぎ取られているからである。 これは、ローレンツ変換の 4 つ目の式に示されている。 \[ t'= {t-{v \over c^2}x \over \sqrt{1-{v^2 \over c^2}}} \] さらに、この式に従えば、$K'$ を参照とするふたつの事象の時間差 $Δt'$ は、$K$ を参照とする時間差が消えても一般に消えない。 $K$ を参照とするふたつの事象の純粋な "空間距離" が $K'$ を参照とする同じふたつの事象の "時間間隔" をもたらす。 しかし、Mikowsky の発見である、相対論の形式的開発の重要性は、そこにはない。それはむしろ、相対論の4次元時空連続体が その最も本質的な形式的特性として、ユークリッド幾何学の空間(*1)の3次元連続体との明白な関係を示す、という彼の認識の 事実のなかに見出される。しかし、この関係を明確にするために、通常の時間座標 $t$ をそれに比例する虚数の大きさの$\sqrt{-1}.ct$ に置き換えなくてはならない。これらの条件下で、(特殊)相対論の要求を満足する自然法則は、時間座標が空間座標と厳密に同 じ役割りを果たす数学的形式を仮定しているのである。形式的に、これらの 4 座標は、正確にユークリッド幾何学の 3 空間座標 に対応している。我々の知識へのこの純粋に形式的な付加の結果として、その理論は、否応なくはるかな清明さを得た。

これらの不適切な言明は、Minkowsky によって貢献された重要な概念についてぼんやりとした注意を与えるだけであろう。それなし では、続くページで基本的概念が発展させられる一般相対論は、多分、産着以上は、先に進めなかっただろう。Minkowsky の仕事は 疑いもなく、数学を経験しない誰もがそれに近付くことが難しいものであるが、しかし、一方この仕事を非常に正確に把握することは、 特殊又は一般の相対論のどちらかの基本的概念を理解するために必要というわけではないので、私はそれをここで現在離れて第 II 部 の最後頃にそれに戻る。

(*1) 参照. いくらかのより詳細な議論は、付録 II にある。

次のことは常に明快だった。その概念の視点から、それが我々に伝えることは、全ての動きは、相対運動としてだけ考えなければ ならないということである。我々が頻繁に使った土手と鉄道客車の描像に戻って、我々は、ここに実行される動きの事実を、等しく 正当化可能な、次のふたつの形式で表現できる。
(a) 客車が土手に対して相対的に運動している。
(b) 土手が客車に対して相対的に運動している。
動きの実行の我々の言明のなかで (a) では土手、(b)では客車が参照物体を提供している。もし、それが単に含まれる動きを検出 するか又は記述する質問であるなら、どの参照物体に対してその動きをいうかということは、基本的に重要でない。 すでに言及したように、これは自明である。しかし、それをずっと包括的な言明 "相対性の原理" と呼ばれる、我々が研究の基礎 としてとってきたものと混同してはならない。

我々がそれを保ち、使用した原理は、どの事象の記述のためにも、我々が客車と土手を等しく参照物体として選択してよいというこ とである(これも、また、自明である)。我々の原理は、また次を主張する：もし、我々が自然の一般的な法則をそれらが経験から得 られたように、
(a) 参照物体として土手、又は
(b) 参照物体として鉄道客車、
を使うことによって定式化するなら、そのときは、これらの自然の一般的法則(例えば、力学の法則とか、真空中の光の伝播の法則)は、 両方の場合で正確に同じ形式をもつ。これは、また次のように表現される：自然の過程の物理的記述は、参照物体 $K, K'$ のどちらも 他方と比べて唯一でない("特別に選択されない")。最初のと違い、この後者の言明は、必ずしも 先験的に成立しない； それは "運動" と "参照物体" の概念を含まない。そして、それらから導かれる；経験だけがその正しさ又は間違いを決定できる。

しかしながら現在まで我々は、自然法則の定式化に関して、すべての参照物体 $K$ の同等性を決して保守してきていない。 我々のコースは、次に述べる以上であった。最初の場所で、その動きの条件がそれに関してガリレイ法則が成立するような、 参照物体 $K$ の存在を仮定して開始した： ひとつ残され、他から十分に遠く離れた粒子は、直線上を均一に動く。 $K$ (ガリレイ参照物体)を参照して自然法則は、できるだけ単純であるとした。 しかし、$K$ に加えて全ての参照物体 $K'$ にこの意味の優先権を与えなければならない。そしてそれらは、自然法則の定式化において、 正確に $K$ と同等でなければならない、もしそれらの $K$ に対する動きが、"均一な直線上" の "回転のない運動" である限り；全ての これらの参照物体は、ガリレイ参照物体とみなされる。相対性の原理の有効性は、これらの参照物体についてだけであり、他に対して はない(例えば、別種の動きをもつもの)。この意味で、特殊相対性原理、特殊相対性理論という。

これに対して、次の言明、"一般相対性の原理" を我々は理解することを望む：それらの運動状態がどのようであっても、 全ての参照物体、$K, K'$ などが自然現象の記述(自然の一般法則の定式化)において同等である。 しかし、さらに進む前に、後の段階で明白になる理由によって、この定式化が、より抽象的な他のものに後に置き換えられないと いけないことを、指摘されなければならない。

特殊相対性の原理の導入が正当化されて以来、後の一般化に努力するどの知識人も、相対性の一般原理に向かった一歩を踏み出す 誘惑を感じたに違いない。しかし、単純で、明白に全く信頼できる考察は、次を示唆するかに見えた。現在、どの程度にもそのような 試みが成功する望みはほとんどないと。我々の古い友人の鉄道客車に我々が移されたことを想像しよう。それは、均一な速度で旅行 をしている。それが均一な運動である限り、客車の乗客は、その動きを感じることがない。そして、それが彼が気遅れなしに、この 場合の事実を、客車が静止し土手が動いていることを示す、と解釈できる理由である。さらに相対性の特殊原理によればこの解釈は、 物理的視点からも全く正当化できる。

もし、例えば、強力なブレーキの適用によって、客車の動きがいま不均一な動きに変化したとすると、そのとき、客車の乗客は、 それに相応して、強力な前方への急な動きを経験する。遅くなった動きは、客車のなかのその人に相対した物体の力学的な振舞に よって明示される。力学的振舞は以前に考慮した場合のそれと違う。この理由のために、静止又は均一運動をする客車を参照して 成立する同じ力学法則が非均一運動をする客車に相対して成立することは不可能であると示されるのかもしれない。全ての事象に おいて、ガリレイ法則が非均一に運動する客車に関して成立しないことは、明白である。このため、我々は現在の危機のなかで、 非均一運動には、一般相対性原理に反する絶対的な物理的現実を許すことの強制を感ずる。しかし、この後すぐに、我々は、 この結論を保つことができないことをみるだろう。

地球の石への作用は間接的に行われる。地球はその周囲に重力場を作り、それが石に落下の運動を作る。我々が経験から知るように、 石への作用の強さは、我々が地球から遠く進めば進むほど、全く確固とした法則に従って減少する。我々の観点から次を意味する： 空間中の重力場の特性を支配する法則は、働く物体からの距離と重力の作用の減少を正しく表すために、完全に確定したものに違いない。 それは、次のようなものである：物体(例えば地球)は、そのすぐ近傍に直接に場を作る；物体から離れた点の場の強さと方向は、 重力場自身が空間中の特性を支配する法則によって、そこから決定される。

電磁場との対比のなかで、重力場は最も注目すべき特性を示している。それは、次のような基本的な重要性をもつ。重力場の影響だけを 受けて動く物体は、加速を受けるが、それがその材質にも、物体の物理的状態にも、いささかもよらないことである。例えば、鉛の一片 も木の一片も(真空中の)重力場では、同じ静止から又は同じ初期速度から開始すれば、厳密に同じ方法で落下する。この法則は、最大限 の正確さで成立し、次の考察の光のなかで異なる形で表現できる。

Newton の運動法則に従って、

ここで、"慣性質量" は、加速を受ける物体の特性的な定数である。もしいま、重力が加速の原因ならば、

ここで、"重力質量" は、同様なその物体の特性的な定数である。これらふたつの関係から：

もしいま、我々が経験から見出すように、加速が物体の性質と状態から独立であるなら、そして、与えられた重力場が 常に同じであるなら、そのときは、重力的と慣性的質量との比は、同様に全ての物体で同じでなければならない。 単位の適切な選択によって、我々はこの比を 1 に等しくできる。そのとき我々は、次の法則をもつ： 物体の重力質量は、慣性質量に等しい。

この重要な法則は、これまで力学に記録されていたことは確かである、しかし、それが解釈されたことはなかった。 満足すべき解釈は、我々が次の事実を認識するときにだけ得られる："慣性" 又は "重量" ("重さ") は、状況に従って使われる 物体の同じ性質の明示である。続く章では、我々は、これがどこまで実際に成立するか、また、この問いがどうやって 相対論の一般仮説に結合するかを示す。

その箱の蓋の中央に外部からロープのついたフックがついている。そしていま、ある "存在" (どのような種類の存在でも我々には 重要でない)が一定の力で引っ張り始める。そのとき、箱は観測者とともに "上方に" 均一な加速運動によって動き始める。時間が 経つと、それらの速度は、前代未聞の値に達するだろう。我々がこれら全てを別のロープで引っ張られていない参照物体から見て いる限り。

しかし、どのように箱のなかの男は、その過程をみるだろうか? その箱の加速は、箱の床の反作用によって、彼に伝達されるだろう。 彼は、そのため、もし、彼が床に寝そべることを望まないなら、この圧力を彼の脚によって支えないといけない。彼は、そのとき、 箱のなかに立っていて、それは、我々の地球上の家の部屋のなかで誰もが立つのと正確に同じ方法である。もし、彼が手に持って いた物体を離すと、箱の加速はもはやこの物体に伝わらず、物体は、加速的な相対運動によって、箱の床に接近する。観測者は、 さらに、箱の床に向かう加速は、どのような種類の物体を実験に偶然使っても、常に同じ大きさであることを、確信するだろう。

その箱のなかの男は、彼の重力場の知識(前の章で議論したように)に頼って、彼と箱が時間に関して一定の重力場のなかにあると 結論するだろう。もちろん、彼は、しばし、なぜ箱が重力場のなかで落ちないのかと頭を悩ますだろう。しかし、すぐその後に、 箱の蓋の中央にロープのついたフックを発見し、その結果、箱が重力場のなかで支えられて静止しているという結論に達するだろう。

我々は、その男に微笑かけ、彼が結論を誤ったというべきだろうか? 我々が整合性を保つことを望むなら、我々はそうすべきとは 信じない； 我々は、状況把握の彼のやり方が、合理性も、知られる力学法則も犯していないことを、むしろ認めないといけない。 たといそれが、最初考えたように、"ガリレイ空間" に対して加速されていても、我々は、それにも関わらず、その箱が静止してい るとみなすことができる。このように、我々は、相対性の原理を拡張して、互いに関して加速されている参照物体を含めるための よい基盤を得た。そして結果的に、相対性の一般化された仮説に向かって、強力な論点を得たのである。

我々は、この解釈のやり方が、重力場の基本的特性である、全ての物体に同じ加速を与えること、又は、同じことになるが、 慣性質量と重力質量の等価性の法則に頼っている可能性について注意深くみる必要がある。もし、この自然法則が存在しなければ 加速箱のなかの男は、彼の周りの物体の振舞を重力場と推測することはできなかっただろう。そして、彼は彼の参照物体が "静止" しているという推測を経験の基盤の上で正当化できなかったであろう。

その箱のなかの男がロープを箱の蓋の内部に結合しロープの開放端に物体を付けることを想像しよう。この結果は、"垂直に" 下方向 に架けられているようにロープを引っ張る。もし、我々がロープの張力の原因について意見を尋ねると、この箱のなかの男はいう だろう："支えられた物体が重力場のなかで下方向の力を経験し、これがロープの張力とつり合っている；ロープの張力の大きさを 決めているのは、支えられた物体の重力質量である。" 一方、空間に自由に宙に浮いている観測者は、事の状態を次のように 解釈するだろう："そのロープは、箱の加速運動のなかで否応なしに役割りを果たしている。箱の動きをそれに取り付けられた物体 に伝えている。ロープの張力は、丁度その物体の加速に影響するだけの大きさである。ロープの張力の大きさを決めているのは、 その物体の慣性質量である。" この例に案内されて、相対性原理の我々の拡張が慣性質量と重力質量の等価性の法則の必要性 を意味していることを我々は見る。このようにして、我々は、この法則の物理的解釈を得た。

加速される箱の考察から、一般相対論が重要な重力法則を生み出さなければならないことを我々は見る。実際の所、相対論の一般的 な概念の系統的な追求は、重力場によって満足される法則を供給した。さらに進む前に、しかしながら、私は、これらの考察によって 示唆されるひとつの誤解に対して読者に警告しないといけない。重力場は、箱のなかの男にとって存在するが、最初に選んだ座標系 からはそのような場が存在しなかったという事実に関わらないのである。いま、我々は、容易に推測することができるかもしれない。 重力場の存在は常に単に外見的なものでしかないと。我々は、また、次のように思うかもしれない。ある種の重力場が存在して いるかもしれないにも関わらず、我々はつねに他の、それを参照すれば重力場が存在しない参照物体を選ぶことができると。 これは決して、全ての重力場において正しいわけではない。全く特別な重力場の場合だけである。例えば、そこから判定すれば、 地球の重力場を (全体として)消し去るような参照物体を選ぶことは不可能である。

我々は、いま、なぜ XVIII 章の最後に、一般相対性原理に反対して持ち出された、あの議論が十分納得できるものでなかったかを 正しく認識できる。列車の客車のなかの観測者がブレーキが適用されたとき、前方への急な動きを経験すること、そして彼が客車 の動きの非均一性(遅くなった動き)を認識することは確かに正しい。しかし、彼は、この急な動きが客車の "現実の"加速(減速) であるとみなすことを誰からも強制されていない。彼は、また、彼の経験を次のように解釈してもよいだろう："私の参照物体(客車) は、永久に静止している。それを参照することで、しかしながら、(ブレーキが適用される期間の間) 前方に向かう、時間によって 可変の重力場が存在する。この場の影響で土手は、地球とともに非均一に動き、それらの元の後方に向かう速度が連続的に削減した。"

しかし、思考の方法が論理的な人は誰も、物事のこの状態にずっと満足していられない。彼は、尋ねる："ある参照物体 (又はその運動状態)が他の参照物体(又は運動状態)より、優先されていることは、どこから由来するのか?" "このえこひいきの理由はなにか?"この質問で私が意味するものを明確にするため、ある比較をしよう。

私は、ガスレンジの前に立っている。そのレンジの上に並んで互いにとてもよく似て、他と見間違うような、ふたつのなべがある。 両方は、半分だけ水が入っている。私は、蒸気が一方のなべから連続して出ているが、他方からは出ていないことに注目する。 私はこれに驚く。ガスレンジもなべも以前に見ていないのにも関わらず。しかし、もし、私が青い色の明るい何かが最初のなべ の下にあって他方にないことに注目すると、私の驚きが止まる。私がそれ以前にガスの火を見たことがないにも関わらず。 私は、この青い何かが蒸気の放射を引き起こしているだろう、又は少なくとも多分そうしえるとしかいえないから。 しかし、もし、私が青い何かを両方に見付けず、しかも、一方は蒸気が連続して出ていて、他方はそうでないなら、そのときは、 私はまだ驚いていて、ふたつのなべの異なった振舞に原因を帰すことできる何かの状況を発見できるまで満足しないだろう。

それと同様に、私は古典力学(又は特殊相対論)のなかの参照系 $K$ と $K'$(*1) に関して考察した物体の異なる振舞に原因を帰すことのできる 実際の何かを無駄に探す。Newton は、この反論を見て、それを無効化しようと試みたが成功しなかった。しかし、E. Mach は、それを 誰よりも明確に認識し、この反論を理由として、彼は、力学が新しい基礎に置かれるべきであると主張した。それは、物理学の方法に よってのみ取り除かれ得るが、相対性の一般原理には合致できる。 なぜなら、そのような理論の式は、どの参照物体についても、その運動状態がどうであっても成立するからである。

(*1) その反論は、参照物体の運動状態がそれを保つのに外部的な代理を必要としない性質をもつとき、例えば、参照物体が均一に回転している場合 に、特により重要である。

例えば、$K$ (ガリレイの法則に従う)に関して均一な直線運動をする物体が、加速された参照物体 $K'$ (箱)に関しては、加速された一般には曲線 の運動を実行していることを我々は学ぶ。この加速又は曲がりは、広く普及している $K'$ に相対する重力場の運動物体への影響に対応する。 重力場が物体の運動にこの方法で影響することは知られていて、そのため、我々の考察は、何も本質的に新しいものを供給していない。

しかしながら、我々が類似の考察を光線に行ったとき、我々は基本的に重要な新しい結果を得るのである。ガリレイ参照物体に関して、その ような光線は、速度 $c$ をもつ直線的に伝達される。同じ光線の経路は、我々がそれを加速された箱(参照物体 $K'$)を参照として考察するとき、 もはや直線でないことは、容易に示される。このことから、我々は結論する。一般に、重力場のなかの光線は曲がって伝播することを。 ふたつの点からこの結果は偉大な重要性をもつ。

まず最初に、それは現実と比較することができる。その疑問への詳細な検討が、一般相対論の要求する光の曲がりは、実際に我々の自由になる 重力場に対しては、極端に小さくしかないことを示したが、その推定される太陽のそばをかすめる影響の光線の曲がりの大きさは、しかしながら 1.7 秒角である。これは、次のことによって自ら明示するはずである。ある恒星が地球から見て太陽の近傍にあることは、太陽の皆既日蝕の間 に観測できる。そのようなとき、これらの恒星は、太陽が空の別の部分にいる場合のそれらの空のなかの外見上の位置と比較して、その量を上 に示した分だけ、太陽から外側に変位して現れるはずである。この推論の正しさ又は否かの検証は、最大級の重要性の問題として、その早期の 解決が天文学者(*1)によって期待された。

2番目には、我々の結果が示すことは、一般相対論によれば、特殊相対論のふたつの基本的な仮定のひとつを構成し、それに対して我々は頻繁に 言及した、真空中の光の速度の一定性の法則が無制限な有効性を主張できない、ということである。光線の曲がりは、場所による光の伝播 速度の変化によってしか実現できない。この帰結として、我々は、次のことを考えるかもしれない。特殊相対論、そして、それとともに相対性 の理論全体が、ごみ箱に入るかもしれないと。しかし、現実にはこれはそうでない。我々は、特殊相対論が有効性の無制限な領域を主張できない と結論できるだけである； その結果は、我々が現象(例えば、光の)に重力場の影響を無視できる場合に限って成立する。

相対論の相手から、特殊相対論は一般相対論によってひっくり返されたということが、しばしば主張されるが、適切な比較という手段によって 現実の場合の事実を明確にすることが多分、賢明であろう。電気力学の発展の前に静電気の法則が電気の法則と見られた。現在、我々は、次の ことを知る。電場は、静電気の考察から、それは決して厳密に実現はしないが、電気的質量(電荷)が互いに対して、そして座標系に対して全く 静止する場合において正しく導かれる。この理由をもって、我々が静電気学が Maxwell の場の方程式によってひっくり返されたということは、 正当化されるだろうか? 少なくともそうでない。静電気学は、電気力学に包括され、制限された条件下のものである；静電気学の法則は、電磁 力学のそれらから、時間に関して不変な場の場合として直接に導かれる。いかなる物理理論も、より包括的な理論からそれを導出する方法が明 確にされ、制限された条件下に生き残るとされることより公平な運命を割り当てることはできない。

光の伝送の例だけを扱ったが、そのなかで我々が見るのは次のことである。一般相対論が我々に可能にするのは、自然の過程の軌跡に対する 重力場の影響を理論的に導出することである。その法則は、重力場のない場合には我々がすでに知るものである。しかし、最も興味を引く問題、 一般相対論がその鍵を与える解は、重力場自体の満たす法則の研究に関係したものである。少しの間、これを考察しよう。

我々は、適切に参照物体を選べば (近似的に) "ガリレイ的"に振舞う時空の領域、すなわち、重力場がない時空領域を知っている。 もし、いま、どのような運動をももつ参照物体 $K'$ に対するような領域に言及すれば、そのとき、$K'$ に相対して、空間と時間において変数の 重力場が存在する(*2)。この場の性質は、もちろん、選ばれた $K'$ の運動に依存する。一般相対論に従って、重力場の一般法則は、この方法 で得られる全ての重力場を満足させなくてはならない。全ての重力場がこの方法で作り出せるわけでは決してない。しかし我々は、重力の 一般法則がそのような特殊な種類の重力場から導き出せるという希望をいだくことができる。この希望は、最も美しい形で実現された。 しかし、目標に対する明確な洞察と、その現実的な実現の間には、重大な困難に打ち勝つことが必要であり、これが物事の根幹に深く横たわ るが、私は、あえて読者からそれを取り上げることをしない。我々は、我々の時空連続体の概念をさらに遠くまで拡張する必要がある。

(*1) 星野写真の手段によるふたつの遠征隊が Joint Committee of Royal and Royal Astronomical Societies によって編成され、理論が要求 する光の屈曲の存在が 1919 年 5 月 29 日の日蝕の期間に確認された (付録 III 参照) 。
(*2) このことは、XX 章の議論の一般化からくる。

我々は、我々が前に何度も使った、全く特別な場合から再び始める。動きの状態が適切に選ばれた参照物体 $K$ に相対的に重力場のない 時空領域を考えよう。そのとき、考慮中の領域に関して、 $K$ はガリレイ的参照物体であり、$K$ を参照して特殊相対論の結果が成立する。 $K$ に関して均一に回転している 2番目の参照物体 $K'$ によって参照されている同じ領域を考える。我々の考えを固定するために、我々は、 $K'$ が平坦な円形の円板であり、その中心の周りをそれ自身の平面内で回転していると想像する。円板 $K'$ 上の中心から離れて座っている 観測者は、半径方向外側に働く力を感ずることができ、そしてそれは元の参照物体 $K$ に関して静止した観測者からは、慣性の効果(遠心力) と解釈される。しかし、円板上の観測者は、彼の円板を "静止した" 参照物体と見ることができ、相対性の一般原理から、そうすることを 彼は正当化される。彼自身に、そして事実、その円板に相対的に静止した他のすべての物体にも働く力を、彼は、重力場の効果とみなす。 それにも関わらず、この重力場の空間-分布は、Newton の重力理論では可能でないだろう種類のものである(*1)。しかし、観測者は、 一般相対論を信じているので、これが彼を悩ませることはない；彼が重力の一般法則を、星々の動きを正しく説明するだけでなく、 彼に経験される力の場をも説明する法則を、定式化できることを信じているとき、彼は全く言い分が正しい。

その観測者は、時計と測定棒を使って、円板の上で実験を実行する。そうすることで、時間と空間のデータの記述の正確な定義に到達する のが彼の意図である。これらの定義は、彼の観測に基づくものである。この企てのなか、何を彼は経験するのだろうか?

まず最初に、彼は、ふたつの同じ構成の時計のうち、ひとつを回転する円板の中心に、もうひとつを円板の端に、それらが円板に静止するように置く。 我々はいま参照物体 $K$ の立場から、両方の時計が同じ速度で進むかどうかを、自問する。この物体からみると、円板中心の時計は、速度を持たない。 一方、円板の端の時計は、回転の結果として、$K$ に相対的に動いている。XII 章で得られた結果に従えば、こうなる。 後者の時計は、円板中心の時計よりも、永久に遅い速度で進む($K$ から観測して)。 円板の中心の時計のそばに並んで座る観測者を想像すれば、彼によっても同じ効果が分かることだろうことは、明らかである。 このように、回転円板の上は、又は場合をより一般化して、どの重力場でも時計は、置(静止)かれた場所によって、より速く又は遅く進むだろう。 この理由で、参照物体に関して静止して配置した時計を助けにして時間の合理的な定義を得るのは不可能である。同様な困難が我々の早期の 同時性の定義を適用しようとすると起きるが、この問いにさらに進むことを望まない。

さらに、この段階で、空間座標の定義も越えられない困難を表す。もし、観測者が彼の標準の測定棒(円板の半径より小さいとする)を、 円板の端に接線の向きに適用すると、XII 章に従って動く物体が運動方向に短縮を受けるから、ガリレイ系から判断してこの棒は1より短くなる。 一方、測定棒が半径方向に使われるなら、$K$から判断しての長さの短縮を経験しないだろう。もしそうなら、観測者が彼の測定棒で最初に円板の 円周を測定し、次に円板の半径を測定すれば、一方を他方で割って、彼はその商として、親しみのある数 $π= 3.14...$ という値でなく、 それより大きな値を得るだろう(*2)。一方、もちろん、$K$ に対して静止した円板ではこの操作は正確に$π$をもたらすのである。 このことは、回転円板の上では、ユークリッド幾何学の定理が、正確に成立しないことを証明する。そのことは、回転円板の上だけでなく、 一般に重力場のなかでもそうである。少なくとも、もし、我々が全ての場所の全ての方向のその棒に長さ 1 を割り当てるならである。 このゆえに、直線の概念もその意味を失う。それゆえ我々は、特殊理論のなかの議論で使われた方法を手段にしては、円板に相対して $x,y,z$ の座標を正確に定義するという位置にいない。そして、事象の座標値と時刻が定義されない限り、我々はこれらが起きることの なかの自然法則に正確な意味を付与することができないのである。

このように、全ての我々の以前の一般相対性に基づく結論は、疑問に付されることが明らかになっただろう。現実に我々は、一般相対論の 前提を正確に適用できるためには、ある巧妙な回り道をしなければならない。次の段落ではこれを読者に用意しよう。

(*1) 円板の中心で場が消え去り、中心から外側に進むと距離に比例して増加する。
(*2) この考察全体を通して、我々は、参照物体としてガリレイ(非回転)座標系を使わなければならない。なぜなら、我々は $K$ に相対した ($K'$ に相対すれば、重力場が優勢になる) 特殊相対論の結果の有効性だけを仮定してよいからである。

いま、我々は想像しよう。多くの小さな棒が同じ長さに作られている。それらは、大理石平板の大きさと比較して小さい。 私がそれらを同じ長さと言うとき、私は、ひとつを他のどれと重ねてもその両端がはみだすことがない、ことを意味する。 我々は、次に、これら小さい棒4つを大理石平板の上に置き、それらが4辺形(正方形)を形作り、対角線が等しい長さになるようにする。 対角線の等しさを確かにするために小さな試験棒を使う。この正方形に同様なものを最初のものに加え、それぞれの一辺が共通するよう にする。我々はそれぞれのこれら正方形を使って同様な手法で進み、最終的に大理石平板全体が正方形で敷き詰められるようにする。 その配置は、正方形の各辺がふたつの正方形に属し、各頂点が 4 つに属するようにする。

この仕事が大きな困難にならずに完遂できることは本当に驚きである。我々は、次のことを考える必要があるだけである。もし、何かの瞬間 に3つの正方形がひとつの角に出会うと、そのとき、4つめの正方形の 2 辺がすでに置かれて、そして、結果として、その正方形の残った 2 辺の配置がすでに完全に決定されている。しかし、私は、いま、もはや、4 辺形の対角線を等しく調整できない。もし、それらが自発的に等 しいなら、そのとき、これは大理石平板のそして小さな棒の特別な好意であり、それについて、私が感謝をこめて驚くしかないものである。 その建設が成功するものであるなら、我々は数多くのそのような驚きの経験を必要とするに違いない。

もし、すべてが順調に実際に完了してしまったなら、そのとき、私は、大理石平板の点は、 "距離"(線間隔)として使われる、小さな棒に関して、 ユークリッド連続体を構成する、と言う。ひとつの正方形の角を "原点" として選ぶことで、私は、正方形の角をこの原点を参照して 2 つの数 で特徴づけることができる。私は、考慮中の正方形の角に到着するためには、原点から始めて、"右に" 進み、そして "上に" 進み、どれだけの 棒を通過しなければならないか、だけを言えばよい。そのとき、小さい棒の配置で決定されるこれらのふたつの数を、デカルト座標系を参照した この角の "デカルト (Cartesian)座標" という。

この抽象的な実験の次の修正を使用することによって、その実験が不成功という場合もなければならないことを我々は認識する。我々は、その棒が 温度上昇に比例する量だけ "伸長する" ことを想定する。我々は、その大理石平板の中心を熱し、周辺はそうしない。その場合、テーブル上の 各点で我々の小さな棒のふたつがつねに一致させられ得る。しかし、我々の正方形の建設は、加熱のあいだ、必然的に乱されることになる。 なぜなら、テーブルの中心の領域は拡大するが、一方、外側の部分はそうでないからである。

我々の小さな棒を参照としてー単位の長さとしてー大理石平板はもはやユークリッド連続体でない。そして我々も、もはや直接にこれらの助けで デカルト座標を定義する位置にいない。なぜなら、上の構築がもはや完遂できないからである。しかし、その小さな棒への同様な手法がテーブル の温度による影響を (多分、全く) 受けない他のことがあるため、それは、全く自然に大理石平板が"ユークリッド連続体"であるという視点を保 つのである。これは測定又は長さ比較について、より巧妙な規定を作るという、ある満足な手法によってなされ得る。

しかしもし、非一様に熱された大理石平板の上にあるとき、どの種類の(すなわち、どの材料の)棒も同じ方法で、温度の影響で振る舞うとして、 そしてもし、我々が上で記述されたものに類似する実験での我々の棒の幾何学的振る舞い以外に温度の効果を検出する他の手段を持たないならば、 そのときは、我々の最上の計画は、我々の棒のひとつの端がこれらの 2 点に一致する限り、平板上の2点に1を割り当てることであろう； なぜなら、それ以外に、我々の進行が最上級の測定においてひどい任意になることなしに、どのような方法で我々は距離を定義するべきだろうか? デカルト座標の方法は、そのとき放棄され、剛体上のユークリッド幾何学を仮定しない、他のものに置き換えられなければならない(*1)。 読者は、ここで描写された状況が相対論の一般前提によって引き起こされたものに対応していることを知るだろう(XXIII 章)。

(*1) 数学者達は、次の形の我々の問題に直面してきた。もし、我々が表面(例えば楕円体の)をユークリッド3次元空間に与えられるなら、そのとき、 この表面には平面のときと同様に 2 次元幾何が存在する。Gauss は第 1 原理からこの 2 次元幾何を扱う仕事を実行した。彼は、表面が3次元の ユークリッド連続体に属している事実を使わなかった。もし、我々が表面のなかの剛体棒によって構成することを想像するなら(上の大理石平板 と同様な)、ユークリッド平面幾何の基礎にもたらされたものと違うこれらに成立する法則を見出すべきである。表面は、棒に関してユークリッド 連続体ではなく、その表面のなかにはデカルト座標を定義できない。Gauss は、それに従えば我々が表面のなかの幾何学的関係を扱うことのできる 原理を示した。そして、多次元非ユークリッド連続体を扱う Riemann の方法をこのように明確にした。このように、相対性の一般前提によって 我々が導かれるところは、数学者が遠い昔に形式的問題を解いたものである。

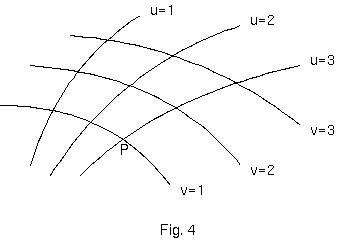
ここで、$g_{11}, g_{12}, g_{22}$ は、$u, v$ 上のある完全に確定した方法に依存する大きさである。大きさ $g_{11}, g_{12}, g_{22}$ は、$u$-曲線 $v$-曲線に相対し、 そしてまたテーブル表面に相対して、棒の振る舞いを決定する。そのなかの表面の点間が測定棒に関してユークリッド連続体をなす場合、しかし、 その場合に限って、次のような単純な方法によって、$u$ 曲線、$v$ 曲線を描き、それらに値を付化することができる： \[ ds^2 = du^2 + dv^2 \] これらの条件下では、$u$ 曲線と $v$ 曲線は、ユークリッド幾何の意味で直線であり、それらは互いに垂直である。ここでは Gauss 座標は、デカルト 座標である。Gauss 座標は、考慮中の表面点に関連するふたつの数の集合でしかなく、数値が微かにしか違わない場合に "空間上" 近傍点が対応 することが明らかである。

いままで、これらの考察は、2次元連続体に成立する。しかし、ガウスの方法は、3, 4, 又はそれ以上の次元の連続体にもまた適用できる。もし、 例えば、4次元連続体の想定が可能であるなら、我々はそれを次の方法で表す。その連続体のどの点にも、任意の 4 つの数、$x_1, x_2, x_3, x_4$ を関連させる。それらは、我々が座標として知る。隣接する点には隣接する座標が対応する。距離 $ds$ が隣接点 $P, P'$ に関連付けられるとき、 この距離が測定可能であり、物理的視点からよく定義されているとき、次の定式化が成立する。 \[ ds^2 = g_{11} dx_1^2 +2 g_{12} dx_1 dx_2 +...+ g_{44} dx_4 dx_4 \] ここで、大きさ $g_{11}$ 等は、連続体中の場所によって変わる値をもつ。連続体がユークリッド的であるときだけは、 次の単純な式をもつように、座標 $x_1.. x_4$ をその連続体の点に関連させることができる。

しかし、上で与えられた $ds^2$ の Gauss の取り扱いは、つねに可能というわけではない。それは、連続体の十分に小さな領域を考慮するときにだけ ユークリッド的な連続体であるとみなすことが可能である。ここのとは、例えば、テーブルの大理石平板と温度の局所変動の場合に明らかに成り立つ。 温度は、平板の小さな部分において実際的に定数である。そして、このように棒の幾何学的振る舞いは、ほとんどユークリッド幾何学の法則に従うはず である。それゆえ、以前の章での正方形の構築の不完全さも、この構築がテーブルの表面のかなりの部分に広がらないかぎり、明確に出てこないだろう。

我々は、これを次のようにまとめる：Gauss は、一般の連続体の数学的な扱いの方法を発明した。そのなかで、"大きさの関係" (近傍点間の"距離") が定義された。連続体のどの点にも連続体の次元の数だけの数(Gauss 座標)が割り振られる。これは、次のような方法でなされる。この割り当てには ひとつの意味しか付加されない。そしてその数(Gauss 座標の)が、隣接点には無限に小さな値だけ違うものが割り振られる。ガウス座標系は、デカルト 座標系の論理的な一般化である。それは、非ユークリッド連続体に適用できるが、"大きさ"とか"距離"の定義については、考慮される連続体の小さな 部分は、ユークリッド系により近似して振る舞い、注目する連続体の部分が小さければ小さいほど、近似する。

MInkowsky は、ローレンツ変換が次の単純な条件を満足することを見出した。 ガリレイ参照物体 $K$ に対する、それらの 4 次元時空連続体のなかの相対位置が空間座標 $dx, dy, dz$ 時間座標 $dt$ であるような、 ふたつの近傍の事象を考察する。2番目のガリレイ系を参照して、我々は、これらふたつの事象の対応する差 $dx',dy',dz',dt'$ を考える。 そのとき、これらの大きさは、つねに次の条件をみたす(*1)。 \[ dx^2 + dy^2 + dz^2 - c^2dt^2 = dx'^2 + dy'^2 + dz'^2 - c^2dt'^2 \] ローレンツ変換の有効性は、この条件からくる。我々はこれを次のように表現できる：
4 次元時空連続体の隣接する点に属する大きさ、 \[ ds^2 = dx^2 + dy^2 + dz^2 - c^2 dt^2 \] は、全ての選択された(ガリレイ)参照物体について、同じ大きさをもつ。もし、我々が $x,y,z,\sqrt{-1} ct$ を $x_1, x_2, x_3, x_4$ と置き換えれば、 我々はまた、 \[ ds^2 = dx_1^2 + dx_2^2 + dx_3^2 + dx_4^2 \] が参照物体の選択によらず、独立であるという結果を得る。我々は、大きさ ds をふたつの事象、又は4次元点の間の、離れた"距離"という。

このように、我々が時間変数として虚数変数$\sqrt{-1} ct$ を実数 $t$ の代わりにすると、時空連続体をー特殊相対論に従うーユークリッド4次元連続体 とみなすことができる。先行する章の考察からくる、ひとつの結果である。

(*1) 付録 I と II を参照。そこで座標自身に導かれた関係は、座標の差、そして座標の微分(無限に小さな差)にも正しい。

これらの考察の結果の視野のなかで我々はつぎの確信に導かれる。一般相対性の原理に従えば、時空連続体はユークリッド的とは考えられず、 ここで一般の場合として我々がもつ、温度局所変化のある大理石平板に対応し、それは、それによって 2 次元の連続体の例として 我々が知るものである。そこで、等しい長さの棒からはデカルト座標系を構成することができなかったように、ここでも、剛体の棒と 時計から系(参照物体)を作り上げることは不可能である。(座標系とは、) 測定棒と時計がひとつひとつ剛体的に配置され、直接に 位置と時間を表示しなければならないという性質のものである。そのようなことが、我々が XXIII章で直面した困難のエッセンスである。

しかし、XXV 章と XXVI 章の考察は、我々がこの困難を乗り越える道を我々に示している。我々は、任意の方法による 4 次元時空連続体、 ガウス座標を参照する。我々は時空連続体のどの点(事象)にも4つの数 $x_1, x_2, x_3, x_4$ (座標)を割り当てる、それには少しの物理的意味 もなく、確定的だが任意の方法で連続体の位置を数える目的に給するだけのものである。この配置は、我々が $x_1, x_2, x_3$ を"空間"座標、 $x_4$ を "時間"座標とみなさなければならないような種類である必要さえないのである。

読者は、そのような世界記述を全く不適切と考えるかもしれない。それらの座標自体に意味がないとき、事象に特定の座標 $x_1, x_2, x_3, x_4$ を割り当てるのはどのような意味があるのか。しかしながら、より注意深い考察は、この心配が根拠のないものであることを示す。 例えば、何かの種類の運動をもった質点を考えよう。もし、この点が瞬間だけ存在し継続がないとすると、それは時空のなかで単一の系、 $x_1, x_2, x_3, x_4$ で示される。そのように、その永久の存在は、無限に多数の値の系によって特徴づけられ、その座標値は、互いに密集し 連続性を与えるほどになる；質点に対応して、我々は、4 次元連続体のなかに (1次元の) 線をもつ。同様な方法で、連続体のなかの、そのような、 どの線も、多くの動く点に対応する。これらの点についての言明で現実に物理的な存在を主張できるものは、それらの遭遇についての言明である。 我々の数学的取り扱いでは、そのような遭遇は、問題の点の動きを表すふたつの線がひとつの特定の座標値の系、$x_1, x_2, x_3, x_4$ を共有する、 という事実のなかに表現される。成熟した考察の後、現実にそのような遭遇が時空の性質が物理的な言明に一致するという実際の証拠を構成する ということを、読者は疑いもなく受け入れるだろう。

我々がひとつの参照物体に相対して質点の動きを記述するとき、我々は、この点と参照物体の特定の点との遭遇以上の何も述べていない。 我々はまた、その物体の時計との遭遇、時計の針と目盛の特定の位置との遭遇の観察によって、時間の対応する値を決定できる。 そのことは、測定棒による空間測定においても全く同様であることは、少々の考察が示すだろう。

次の言明が一般に成立する：どの物理的記述もそれ自身を、それぞれが事象 $A$ と $B$ の時空一致をいう、いくつかの言明に分解できる。 ガウス座標によってそれぞれのそのような言明は、4つの座標値 $x_1, x_2, x_3, x_4$ の一致によって表現される。このように、現実に、 ガウス座標による時空連続体の記述は、参照物体の助けによる記述を完全に置き換える。後者の記述のやり方の欠陥を被ることなく； それは、表現しなければならない連続体の性質をユークリッド特性に縛りつけない。

我々は、この相対性の一般原理をまだ、もうひとつの形式で述べることができ、特殊相対論の自然な拡張の形式のなかよりも、さらに明快に 理解できるようにそれを描写する。特殊相対論に従って自然の一般法則を表現する式は、(ガリレイ)参照物体 $K$ の時空の変数 $x, y, z, t$ を 新しい参照物体 $K'$ 時空変数 $x', y', z', t'$ に、ローレンツ変換の使用によって置き換えるとき、同じ形式の式に素通りしないといけない。 一方、一般相対論に従えば、ガウス変数 $x_1, x_2, x_3, x_4$ の "任意の置き換え" の適用によって、ひとつのガウス座標系から他への移動に 対応するどの変換 (ローレンツ変換だけでない) についても、式が同じ形式の式に素通りしないといけない：

もし、我々が我々の"古風な"物事の 3 次元的視野に固執することを望むならば、そのときは、我々は一般相対論の基本的概念によって現在 実行中の発展を次のように特徴づけることができる：特殊相対論は、ガリレイ領域を参照とした。すなわち、そのなかに重力場の存在しない 領域である。これに関連してガリレイ参照物体は、参照の物体を提供する。すなわち、剛体で、 "孤立した" 質点の均一な直線運動のガリレイ の法則がそれに対して成立するようにその運動状態が選ばれているもの。

ある考察は、我々が同じガリレイ領域に "非ガリレイ参照物体" をも参照すべきことを示唆する。 これらの物体に関しては、特別な種類の重力場がそのときに現れる。(XX 章と XXIII 章)

重力場のなかでは、剛体とユークリッド特性とのようなものを持たない；そのように一般相対論には、仮想の剛体の参照物体がない。 時計の動きは、また、重力の影響を受ける。そして、時間の物理的定義が時計の助けによって直接に作られた特殊相対論においてのようには、 決して同程度のもっともらしさを持たない。

この理由によって、非剛体の参照物体が使われる。それは、全体として動いている、どのような方法においても、だけでなく、それは、動きの 間(即興)に形態の変化も被るのである。時計は、その動きの法則がどのような種類、不規則であっても、時間の定義を給する。 我々は、非剛体の参照物体上のある点に静止した、これらそれぞれの時計を、想像しなければならない。 これら時計は、ひとつの条件だけを満たす。それらの "読み出し"、同時に観測される隣接した(空間的)時計は、互いに無限に小さな量しか異ならない。 この非剛体の参照物体は、適切に用語して "参照軟体動物"は、任意に選ばれたガウス座標系というのと、ほぼ同等である。 "軟体動物"が与えるものは、ガウス座標系が形式的に空間座標が時間座標に対して分離した存在であることを形式的に保持している (全く正当化できない) ことと比較して確かに理解の容易さをもっている。参照物体が軟体動物と考えられる限り、軟体動物の上のどの点も空間として扱われ、 それに対して静止した全ての質点は静止しているとされる。相対性の一般原理は要求する。全てのこれらの軟体動物が参照物体として、 自然の一般法則の定式化において、等しい権利、等しい成功で使うことができることを； 法則自体は、軟体動物の選択とは独立である。

相対性の一般原理によって所持される偉大な力は、自然法則に課された概念的な制限の下にある。我々が上でみたように。

我々は、ガリレイ領域の考察から開始した。すなわち、ガリレイ参照物体 $K$ に相対して、そのなかに重力場のない領域である。 測定棒と時計の振る舞いは、$K$ を参照して特殊相対論から知ることができる。"孤立した" 質点の振る舞いと同じく； 後者は、均一に直線上を動く。

いま、この領域を無作為のガウス座標系、又は"軟体動物"を参照物体 $K'$ として参照しよう。そのとき、$K'$ に関して重力場 $G$ (特定の種類の) がある。 我々は、測定棒と時計、そしてまた、自由運動の質点の $K'$ を参照した振る舞いを、単純に数学的な変換によって学ぶ。 我々は、この振る舞いを、測定棒と時計、そして、質点が、重力場 $G$ の影響を受けた振る舞いと解釈する。 ここで、我々は、ひとつの仮説を導入する：測定棒、時計、そして、自由運動の質点への、重力場の影響は、 優勢な重力場がガリレイの特別な場合から、座標系の単純な変換によって導けない場合も、同じ法則に従って働き続ける。

次の段階は重力場 $G$ の時空での振る舞いを研究することである。重力場がガリレイの特別な場合から座標系の単純な変換によって導ける場合、 記述のなかに使われる参照物体(軟体動物)がどのように選ばれたとしても、この振る舞いは、法則に定式化されていて、それは常に有効である。

この法則は、まだ、重力場の一般法則ではない。なぜなら、考慮中の重力場は、特別な種類であるからである。重力の一般的な場の法則を見つけ出す ためには、上で見付けられたような法則の一般化を得る必要がまだある。これはしかし、気まぐれでなく、次の要求を考慮に組み入れることによって 得られる。

(a) 要求される一般化は、同様に相対性の一般仮説を満足しなければならない。
(b) 考慮下の領域に何か質量があれば、その慣性質量だけが、XV 章に従い、そのエネルギーだけが重要でその場を賦活する効果をもつ。
(c) 重力場と質量は、全体でエネルギー(そして運動量)の保存の法則を満足しなければならない。

最後に、相対性の一般原理は、重力場がないときの知られた法則、すなわち、それはすでに特殊相対論の枠組に組み入れられた法則、に従って 生起する全ての過程の軌跡に重力場の影響を我々が決定することを許す。これに関連して、我々は原理的に、測定棒、時計、そして自由運動質点 のためにすでに説明された方法に従って進んで行く。

この方法で相対性の一般仮説から導かれた理論は、その美しさだけによって秀でているのではなく； また、XXI 章で光を当てられた古典力学にあると考える欠陥を取り除いたことにあるのでもない。； また、慣性と重力質量の等価性の実証法則の解釈にあるのでもない； それはまた、天文学の観測のひとつの結果をすでに説明することにあるのである。それに対して古典力学は、無力である。

もし、我々がその理論の応用を重力場が弱いとみなせるところに制限するなら、そして全ての質量が光速と比較して小さい速度で座標系に対して 動くところに制限するなら、そのとき、我々は Newton 理論を第 1 近似として得る。そのように、ここに後者の理論が何も特定の仮定なしに得られる。 そこでは、Newton は、互いに引きあう質点の間にある引力は、それらの間の距離の自乗に反比例するという仮定を導入しなければならなかった。 もし、我々が Newton 理論からの逸脱を現れさせるために計算の精度を上げたとしても、それらの小ささによって、実際にはそれら全てが観測の テストを逃れてしまうに違いない。

我々はここで、これらの逸脱のひとつに注意を引きつけなければならない。Newton 理論に従えば、惑星は太陽の周りを楕円に動く。 もし、我々が恒星自身の動きと他の惑星の作用とを考慮から外すなら、その楕円は、固定した星からみてその位置を永久に保つだろう。 このように、もし、我々がこれらふたつの影響分を観測された惑星の動きから補正し、そして、Newton の理論が厳密に正しいなら、 惑星の軌道は、楕円であって、固定した星を参照としたそれは、固定している、ということを得るはずである。 この演繹は、偉大な精度でテストされ得て、現在達成できる観測の感度によって得られることのできる精度をもって、 ひとつを残して全ての惑星において確認されている。ひとつの例外は、水星、太陽の最も近くにいる惑星である。 リュービリ(Leverrier)の時代から、水星軌道に対応する楕円が、上述の影響を訂正されたあと、固定された恒星に対して静止せずに、 軌道運動の意味の惑星の平面内を、極端にゆっくりと回転していることが知られていた。楕円軌道のこの回転運動の得られた値は、 1 世紀あたり 43 秒角であり、その量は、数秒角以内に正しいと確認されるものである。 この効果は、古典力学では、ほとんど確かさのなくこの目的にだけ工夫された仮説を仮定したときに説明され得る。

一般相対論の基礎の上では、太陽の周りのどの惑星の楕円も必然的に、上に示されたように、回転することが見出された； 水星を例外として、全ての惑星については、この回転が現時点で可能な観測感度では検出するには小さ過ぎる； しかし、水星の場合は、1世紀あたり43秒角という量でなければならず、それは、観測に厳しく一致する結果である。

このひとつ以外には、これまで、理論からの演繹にはふたつだけ、観測によってテストされること許すものがある。 すなわち、太陽の重力による光線の弯曲(*1)、そして、大きな恒星から我々に届く光のスペクトル線が、地上で類似する手法 (すなわち、同種の原子による(*2)) で作られる光の対応する線と比べたときの変位がある。

(*1) Eddington と他によって 1919 年に最初に観測された。(付録 III 参照)
(*2) 1924 年に Adams によって確立された。(付録 III)

この見かたは、ニュートンの理論とは調和しない。後者の理論は、むしろ宇宙にある種の中心をもつこと を必要とする。その中心では星の密度が最大であり、我々がこの中心から外側に向かって進むに従って 星々の集団密度は低下するに違いなく、そして最終的には、大きな距離では空虚の無限の領域に続くのである。 星辰の宇宙は、無限の空間の海洋のなかにある有限の島であるべきなのである(*1)。

この概念は、それ自身、非常に満足できるものではない。それがさらにまだ不満足であるのは、星々によって 放射された光が、そしてまた、星系の個々の星が、永遠に無限の空間に向かって過ぎていき、決して帰らず、 自然の他の物体と相互作用をするために再び来ることがない、という結果に導くからである。そのような 有限の物質の宇宙は、次第にしかし、システム的に衰退することが運命づけられているだろう。

この矛盾を逃れるために、ゼーリガーは、ニュートン法則を修正することを示唆した。そのなかで彼は、 非常に遠方において、2つの質量の間の引力は、逆2乗則からの結果よりも、早く減少することを仮定した。 この方法で質量の平均密度は、宇宙でどこでも、無限に対してさえ、無限に大きな重力場をつくり出すことなしに 一定にすることができたのである。我々は、このようにして、物質の宇宙が中心の性質の何かをもつべきであるという、 不快な概念から自由になったのである。もちろん、上述の基本的困難からの我々の解放は、ニュートンの法則の 実証的または理論的のない修正と複雑さというという対価を支払ったのである。我々は同じ目的に助けとなる 数え切れない法則を想像することができ、どうしてそれらのうちのひとつが他よりもよいかの理由をいうこと のできないものである。すなわち、これらの法則のどれも、ニュートンの法則のようには、 より一般的な理論的原理によって基礎づけられていないだろうからである。

(*1) 証明ーニュートンの理論に従えば、無限からきて質量 $m$ に終わる"力線"の数は、質量 $m$ に比例する。もし、 平均として質量密度 $ρ_0$ が宇宙全体で一定なら、そのとき、体積 $V$ の球は、平均質量 $ρ_0 V$ をその中にもつ。 そのように、その球の表面$F$を通りその内部に通じる多くの力線の数は、$ρ_0 V$ に比例する。その球の表面の 単位面積あたりの球にはいる力線の数は、$ρ_0 {V \over F}$ 又は $ρ_0 R$ に比例する。このように、その表面の場の強さは、 球の半径 $R$ の増加に従って究極的に無限になる。これは不可能である。

最初のところで、我々は2次元空間のなかの存在を想像した。平坦な存在が平坦な機器をもって、とくに平坦な剛体 の物差しをもって、面内を自由に動くことができる。それらにとって、この面の外側はなにも存在していない： 彼らと彼らの平坦な"物事"に起き、観測するものは、全て彼らの平面内の内包的現実である。 特に、平面のユークリッド幾何学の構築は、棒を使って実行される。例えば、XXIV 章に考慮した格子構成。 我々と対比して、彼らの存在の宇宙は 2 次元である；しかし我々と同じく、無限に延びるのである。 彼らの宇宙のなかで無限数の棒によって作られた正方形のはいる余地がある。すなわち、体積(面積)が無限である。 もし、これらの存在が宇宙が"平面"であるというなら、その言明には意味がある。なぜなら、それは、かれらの棒を 使って平面ユークリッド幾何学を構築することができたことを意味するからである。これに関して、個々の棒は、 それらの位置によらずに、つねに同じ距離を表現している。

今度は、2番目の2次元存在を考えよう。けれども今度は平面上でなく球の表面の上にである。平坦な存在は、彼らの 測定棒と他の物体をもって、この表面に正確に一致していて、それを離れることができない。彼らの観測する全体の 宇宙は、その球体の表面を占有して広がっている。これらの存在は、彼らの宇宙の幾何学を平面の幾何学とみること ができるだろうか。そして彼らの棒を"距離"の現実化とみることができるだろうか? 彼らは、これをできない。 なぜなら、もし直線を実現しようとしても、彼らは曲線を得てしまうだろう。それは我々 "3次元存在" が大円と呼ぶ ものである。大円、すなわち、確定した有限長の自己包含線、測定棒の手段をもって測定できるものである。 同様に、この宇宙は、棒によって較正された正方形によって比較される有限の面積をもっている。この考察の大きな 魅力は、これらの存在の宇宙は、有限でありながら、かつ、限界がない という事実の認識のなかにある。

しかし、その球体の表面の存在は、ユークリッド宇宙にいないことを知覚するために、世界旅行を実行する必要はない。 彼らは、このことを、彼らの "世界"のどの部分にいても、納得することができる。もし、彼らがその余りに小さい一切れ しか使わないとき。ひとつの点から始めて等しい長さの、全方向に、多くの"直線"(3次元空間なかで円弧と判定される) を描く。それらの線の自由端が交差する線を彼らは "円" と呼ぶだろう。平面の表面にとって、円の周囲と直径の比率は、 両方の長さが同じ棒で測定されるなら、平面のユークリッド幾何学に従って、一定の値であるπに等しい。それはその円の 直径に依らない。彼らの球の表面では我々の平坦な存在は、この比率には次の値を見出すだろう、 \[ π{sin({r \over R})\over ({r \over R})} \] すなわち、これは、$π$よりも小さな値であり、その違いは、その円の半径が "世界球" の半径 $R$ と比較で大きくなれば なるほどより明確になる。その関係を用いることによって、球体の存在は、たとえ彼らの測定に、世界球の相対的に小さな 部分しか使えなくても、彼らの宇宙("世界")の半径を決定することが可能になる。しかし、もし、この部分がとても小さい なら、もはや彼らが、球状世界にいて、ユークリッド平面上にいないことを示すことができないだろう。なぜなら、球の 表面の小さな部分は、同じ大きさの平面の一片とは、微かにしか違わないからである。

そのように、もし、球体表面の存在が球状宇宙上の無視できるほど小さな部分を占める太陽系の惑星の上に住むならば、 彼らが有限又は無限の宇宙に住んでいるかどうかを決定する手段を持たないのである。なぜなら、彼らがアクセスする "宇宙の一片" は、いずれの場合も実際的に平面、ユークリッド的であるからである。この議論から次のことが直接導か れる。我々の球存在にとって、円の周囲は、半径の増加とともに最初、"宇宙の周囲" に達するまで増加して、それからは、 まださらに半径の値を増加しても、そのまま次第に零に減少するということがわかる。この過程を通して円の面積は、 ますます増加し続け、最終的に"世界球"の全体の領域と一致する。

多分、読者は、どうして我々の"存在"を、他の閉じた表面でなく、球の表面に置いたかに疑問を抱かれるであろう。 しかし、この選択は、つぎの事実によって正当性をもつ。全ての閉じた表面のなかで、球面は、その上の全ての点が 同等であるという特性によって独自性をもつのである。円の周囲 $c$ と円の半径 $r$ の比率は $r$ に依存するということは 認めるが、与えられた $r$ の値にとって "世界球" の全ての点は、同等である。； 言葉を替えれば、"世界球"とは、 "一定曲率の表面"である。

この 2 次元球状宇宙に対して 3 次元のアナロジーである Riemann によって発見された 3 次元の球状空間がある。 その点は、同様に全て同等である。半径で決定される有限の体積をもつ ($2π^2 R^3$)。球状空間を想像することは可能 だろうか。空間を想像するということは、我々の"空間"の経験の縮図を想像することに他ならない。我々が剛体の体の 動きをそのなかでもつことができる経験であり、この意味で球状空間を想像することができるのである。

一点から全ての方向に多くの線を描き、又は紐を引き伸ばし、測定棒によって距離 r のこれらのそれぞれに印を付ける ことを想像してみよう。これらの長さの自由端の全てが球状空間上にある。測定棒が作る正方形によってこの表面に特別 に領域 ($F$) を測定することができる。もし、空間がユークリッド的であれば、そのとき、$F= 4πr^2$； もし、それが球状 であれば、そのとき $F$ は、$4π r^2$ よりもつねに小さい。$r$ の値を増加させるに従って、$F$ は零から"世界半径"に よって決まる最大値まで増加するが、さらに $r$ の値を増加するなら、その領域は次第に減少して零にまでなる。最初、 開始点から放射する直線はどんどん発散するが、後にそれらは互いに近接し、最終的にそれらは開始点の対衝点において 再び交差する。そのような条件では、それらは球状空間全体を横切ったのである。その3次元球状空間は、全く2次元球の 表面のアナロジーとなっている。それは有限(つまり、有限体積)であり、境界を持たない。

まだもうひとつの種類の曲がった空間の存在に言及することができる：それは "楕円的空間" である。中の 2 つの"対衝点" が同等である(互いに区別できない)。楕円宇宙は、中心対称性を持った弯曲宇宙のいくらかの拡張と考慮することができる。

述べてきたことから言えることは、限界のない閉じた空間は、認識可能であるということである。これらの事どもから、 球状空間(と楕円空間)は、その上の全ての点が同等であるから、単純さにおいて勝っている。この議論の結果、最も興味 深い質問が、天文学者と物理学者とに対して提起された。それは、我々の住む宇宙が無限であるかどうか、又は球状宇宙の ありかたで有限であるかどうか、である。我々の経験は我々がこの質問に答えることを可能にするためには十分というには、 程遠い。しかし、一般相対論は、中程度の確かさをもって、それに我々が答えることを許す。この結果、XXX 章で言及 した困難はその解答を見出したのである。

我々は、すでに以前の議論から、測定棒と時計の行動が、重力場すなわち物質の分布、の影響を受けることを知っている。 これは、それ自身、ユークリッド幾何学の厳密な有効性の可能性を排除するのに十分である。しかし、次のことは知覚できる。 我々の宇宙がユークリッド的な宇宙から僅かにしか異なっていない。それは、この意見が、なおさらあり得るように見えることである。 一方、計算は次のことを示す。周りの空間の計量が、それが我々の太陽の規模でさえ、質量から影響を受けるのは極端に小さな 程度であることを。我々は次のように想像してもよいかも知れない。幾何学に関しては、我々の宇宙は、個々の部分が不規則に 曲がった表面を模して振る舞うが、決して平面から感知できるほどは外れてはいないということである。：それはさざなみの立つ 湖の表面のように。そのような宇宙は、疑似ユークリッド宇宙と呼ぶにふさわしいかもしれない。その空間を考慮するとき、 それは、無限かもしれない。しかし、計算は示す。疑似ユークリッド宇宙にあって物質の平均密度は、必然的にゼロかもしれない。 このように、そのような宇宙は、いたるところ物質に住まわれていない。：それは、XXX 章で不満足な描像を描いた我々にとって は、プレゼントかも知れない。

もし、我々が宇宙で物質の平均密度が零から異なるなら、その違いが小さくても、そのときは、宇宙は、疑似ユークリッド的 ではあり得ない。反対に、計算の結果がもし、物質が均一に分布していることを示すなら、宇宙は、必然的に球状(又は楕円状) かもしれない。一方、現実には物質の詳細の分布は均一でないから、現実の宇宙の個々の部分は球状の宇宙から外れていて、 すなわち、宇宙は、疑似球状であろう。しかし、それは、必然的に有限であろう。事実、その理論は、宇宙の空間の広がりと 物質の平均密度の間に簡単な関係(*1)を与えている。

(*1) 宇宙の "半径"を $R$ として、我々は次の式を得る。
\[ R^2 = {2 \over κρ}. \] この式に C.G.S.系を使い、${2\over κ}= 1.08 x 10^27$。 $ρ$は、物質の平均密度。$κ$は、ニュートン重力定数に関係する定数。

$x$ 軸の正に沿って進んでいる光信号は、次の式に従って伝送されている。 \[ x = ct \] 又は、 \[ \tag{1} x - ct = 0 \] 一方、同じ光信号は、$K'$ に相対的に速度 $c$ で伝送されていなければならない。 その $K'$ 系に相対的な伝播は、類似の表式で表され、 \[ \tag{2} x' - ct' = 0 \] (1)を満たす時空点(事象)は同時に、(2)も満たさなければならない。 明らかにこれは、一般に次式が満たされる場合である。λは定数として、 \[ \tag{3} (x' - ct') = λ(x - ct) \] なぜなら、(3) に従って、$(x - ct)$ の消滅は、$(x' - ct')$ の消滅も含意する。

もし、我々がx軸の負の方向に沿って伝送される光線に同様な考察をすると、次の条件を得る。 \[ \tag{4} (x' + ct') = μ(x + ct) \] 式 (3)と(4)との加算(又は減算)によって、また、便宜のため定数 a,b を導入し、定数λ,μを代えて、 \[ a= {(λ + μ)\over 2} \] と \[ b= {(λ - μ)\over 2}, \] とすると、次の式を得る。 \[ \tag{5} \begin{align} x'&= ax - bct \\ t'&= act - bx \end{align} \]

我々の問題の答えは、$a,b$ が知られるとき、与えられるだろう。次の議論からこれらは結果する。

$K'$ の原点は、永久に $x'= 0$ であるから、(5)の最初の式に従って、 \[ x = {bc \over a}t. \] もし、我々が $K'$ の原点が $K$ に対して動くときの速度を $v$ と呼ぶと、そのとき、 \[ \tag{6} v = {bc \over a} \] もし、K' 上の別の点の K' に関する速度、又は、K の点の K' に対する(x軸の負の方向の)速度を計算するとき、 同じ値 v が式 (5) から得られる。つまり、我々は、v でふたつの系の相対速度を示すことができる。

さらに、相対性原理が我々に教えることは、 $K$ から判定する $K'$ に相対的に静止する単位測定棒の長さは、 $K'$ から判定する $K$ に相対的に静止する単位測定棒の長さに厳密に等しくなければならない。 $x'$ 軸の点が $K$ からみてどのように見えるかは、我々は $K$ から $K'$ の "スナップショット" をとるだけでよい； これは $t$ ($K$ での時間)に特定の値(例 $t= 0$) を我々は入れなければならない。そのとき、我々は、この $t$ の値に (5)の最初の式から次の値を得る。 \[ x'= ax \] $x'$ 軸上の $K'$ 系で計った距離 $Δx'= 1$ だけ離れたふたつの点は、我々の同時写真では、距離、 \[ \tag{7} Δx= {1 \over a}. \] だけ離れている。

しかし、もし、そのスナップショットが $K'$ から($t'= 0$) 撮られれば、(5)式から $t$ を消去し、(6)を考慮して、我々は、次式を得る。 \[ x' = a (1-{v^2 \over c^2}) x. \] このことから、$x$軸上の($K$に相対で) 1 だけ離れたふたつの点の距離は、我々のスナップショットでは、次の距離で表現されるだろう。 \[ \tag{7a} Δx' = a(1-{v^2 \over c^2}) \] しかし、言われたことから、ふたつのスナップショットは、同一でないといけない：(7) の $Δx$ は、$Δx'$ と等しくないといけない。 そこで、我々は次を得る。 \[ \tag{7b} a^2 = {1 \over (1-{v^2 \over c^2})} \]

式 (6) と (7b) は、定数 a と b を決定する。これら定数を(5)に入れることで、我々は、XI 章に与えられた式の1番目と4番目を得る。 \[ \tag{8} x'&= {(x-vt)\over \sqrt{(1-{v^2 \over c^2} }\\ t'&= {(t-{vx \over c^2})\over \sqrt{1-{v^2 \over c^2}}.. \] このようにして、我々は x 軸の事象のローレンツ変換を得た。それは、次の条件を満たす。 \[ \tag{8a} x'^2 - c^2t'^2 = x^2 - c^2t^2 \] この結果の拡張は、x軸の外の事象で起きる事象を含めるために、(8)式を保持し、次の関係を補うことで得られる。 \[ \tag{9} y'&= y \\ z'&= z \] この方法で、我々は、任意の方向の真空中の光速の一定の前提が、$K$ 系と $K'$ 系の両方で満たす。これは、次の方法で示されるだろう。

我々は、$K$ の原点から時間 $t=0$ に送られた光信号を考える。それは、次の式に従って伝播する。 \[ r= \sqrt{x^2+y^2+z^2} = ct, \] 又は、この式の自乗である次式に従って伝播する。 \[ \tag{10} x^2+y^2+z^2-c^2t^2= 0 \] 相対性の仮定と関連して、光の伝播の法則によって、次が要求される。問題の信号の伝送は、ー$K'$ から判断してー対応する次の表式に従う。 \[ r'= ct', \] 又は、 \[ \tag{10a} x'^2+y'^2+z'^2-c^2t'^2= 0 \]

式 (10a) が式 (10) の結果であるためには、我々は、次式を持たなければならない。 \[ \tag{11} x'^2+y'^2+z'^2-c^2t'^2=σ(x^2+y^2+z^2-c^2t^2) \] 一方、$x$ 軸上で式 (8a) が成立しなければならないから、我々はこうして、$σ= 1$ をもつ。 ローレンツ変換が実際に式(11)の $σ= 1$ において満たすことは、容易に見て取れる； なぜなら、(11) は式 (8a) と(9) の、それゆえまた、(8) と (9) の帰結である。 我々は、こうして、ローレンツ変換を導いた。

(8)と(9)によって表されるローレンツ変換は、一般化される必要がまだある。 明らかに、$K'$ の座標軸が空間的に $K$ と平行に選択されることは、重要ではない。 また、$K'$ 系の $K$ に相対的な速度が $x$ 軸方向でなければならないことも、本質的でない。 単純な考察で、我々は、一般的な意味のローレンツ変換が、ふたつの変換、すなわち、 特別な意味のローレンツ変換と純粋な空間的な変換、直交座標系の軸を交換して軸が他の方向を向いた 新しい系に置換に対応する変換、との組合せで構成できることを示すことができる。

数学的に、我々は一般化されたローレンツ変換を次のように特徴づけることができる：

それは、 $x,y,z,t$ の線形一様関数によって $x',y',z',t'$ を表わす式で、次の関係が一定に保たれるものである。 \[ \tag{11a} x'^2+y'^2+z'^2-c^2t'^2= x^2+y^2+z^2-c^2t^2 \] すなわち：もし、左辺の $x',y',z',t'$ を $x,y,z,t$ の表示に置き換えれば、そのとき、(11a)の左辺は、右辺に一致する。

(12)から我々が読み取れることは、虚数時間座標 $x_4$ は、空間座標 $x_1, x_2, x_3$ と正確に同じ変換の条件となったことである。 それは、次の事実による。相対論に従えば、"時間" $x_4$ は、空間座標 $x_1, x_2, x_3$ と同じ形式の自然な法則に参入するのである。

座標、$x_1, x_2, x_3, x_4$ で記述される 4 次元連続体は、Minkowsky によって "世界" と呼ばれた。彼はまた、点事象に "世界点" という言葉を使った。3次元空間の "できごと" から、物理学は、まるで 4次元の "世界" の "存在"になろうとしている。

この4次元的な "世界" は、(ユークリッド)解析幾何学の 3次元の "空間" に近い類似性を保持している。もし、我々が 3 次元空間に、 同じ原点をもつ新しいデカルト座標系($x'_1,x'_2,x'_3$)を導入するなら、そのとき、$x'_1,x'_2,x'_3$ は、$x_1, x_2, x_3$ の線形一様 関数であり、次の不変式を満足する。 \[ x'_1^2 + x'_2^2 + x'_3^2 = x_1^2 + x_2^2 + x_3^2 \] 式(12) との類似性は完全である。Minkowsky の "世界" は、その形式的な手法において、4 次元ユークリッド空間(虚数の時間座標をもつ) とみなすことができる；ローレンツ変換は、4次元世界の "回転" に対応する。

しかし、この視点は、決して実際の過程の全てを包括するものでない；なぜなら、それは正確な科学の発展のなかで直観的及び演繹的思考 によって果たされる重要な部分を見逃しているからである。科学が現れたすぐのその初期段階から、理論的進展はもはや、配置の過程だけ によって達成されたものではない。実証的データに案内されて、むしろ研究者は、一般に、公理という少数の基本的な仮定から論理的に築 き上げられた考えの体系を開発するのである。我々は、そのような考えの体系を、"理論" という。理論は、多くの個別の観測の相関させる 事実のなかに、その存在の正当性を探し求め、そして、ここにしか理論の"真"は、存在しない。

実証データの同じ複雑さに対応して、ひとつひとつ考慮しえる程度まで異なるいくつもの理論が存在できる。しかし、テストされ得るその 理論からの演繹に関しては、理論間の合意は完全で、どの演繹もそのなかにふたつの理論の互いの違いを見出すことが難しいほどである。 例としては、一般的な興味がもたれる場合が、生物学の分野の、生存競争のなか選択による種の発展の Darwin の理論のなかと、そして、 獲得形質の遺伝的伝送の仮定に基づく発展の理論のなかにある。

もうひとつの遠隔の合意の例は、Newton 力学を一方とし一般相対論をもう一方とする、ふたつの理論からの演繹の間にある。この合意は、 遠く達成され、ふたつの理論の基本的仮定の間の深遠な違いにも関わらず、現在に到るまで、相対論以前の物理学がまたそれを導かず、 我々が調査し得るものとしては、いくつかの一般相対論からの演繹しか見出すことができなかったのである。 以下に、これら重要な演繹を再度考察し、現在までに得られたものに関して、実証的な証拠についても議論する。

Newton 力学と Newton 重力の法則に従って、太陽を巡る惑星は太陽の周りに、より正確には太陽と惑星との共通の重心の周りに、楕円を描く。 そのような系では太陽又は共通重心は、惑星年のなかで、太陽惑星間の距離が最小から最大まで増加し、再度最小まで減少するような様子をもつ、 楕円軌道の焦点のひとつにある。Newton の法則の代わりに、我々が何か異なった引力の法則を計算にいれると、我々は、この新しい法則に従えば、 まだ、太陽惑星間の距離が周期的な変化を示すような様子であるが、しかし、この場合は、そのような周期 (近日点ー太陽への最接近ーから 近日点までの) の期間の太陽惑星を結ぶ線によって示される角度は、360 度から違ってくる。軌道の線は、閉じず、軌道面の環状の部分を、 すなわち、太陽から惑星の距離の最小円と最大の円の間を、埋めつくす。

一般相対論に従っても、それはもちろん Newton 理論と違うのだが、惑星の Newton-Kepler 運動からの小さな変異は、軌道に起きるべきで 次のようになる。近日点からその次までの、太陽惑星の動径が描く角度は、ひとつの完全な回転に対応する角度を次に与えられた量だけ超えて いるべきである。 \[ + {24 π^3 a^2 \over (T^2 c^2 (1-e^2))} \] (注意：ひとつの完全な回転は、物理の絶対角度測定の習慣のなかでは角度 $2π$ に対応する。上の式は、ひとつの近日点と次の近日点との間の期間 に太陽惑星の動径がこの角度を超える量を与える。) この式のなかで $a$ は楕円の長軸、$e$ はその離心率、$c$ は光速、$T$ は惑星の回転周期を表す。 我々の結果は、次のようにも述べられる：一般相対論に従って、楕円の長軸は、太陽の周りを惑星の軌道運動と同じ意味で回転する。理論は、惑星 水星ではこの回転が 1 世紀あたり 43 秒角という量であること、太陽系の他の惑星ではその量が小さく必然的に検出を逃れることを要求する(*1)。

事実の点で、天文学者は、Newton 理論が現在達成できる観測の感度に対応する精度において、水星の運動観測には十分でないことを見出した。 他の惑星から水星に働く全ての摂動の影響を考慮した上で、説明がつかずに残された水星の近日点移動が上で言及された1世紀あたり 43 秒角 という量とほとんど違わないことが発見された(リュービリ Leverrier 1859 そして ニューコム Newcomb 1895)。実験結果の不確かさは数秒角だけである。

この結果は、太陽の皆既日蝕中の星の写真的記録の手段によって実験的な検証を許す。どうして我々が皆既日蝕を待たなければならないか、の唯一 の理由は、他のときには、大気が強く太陽からの光で照らされ、太陽円板の側にある星を見えなくさせるからである。予測される結果が付図から明確 に見ることができる。太陽($S$)のないときには、実際的に無限遠の星は地球から見たとき方向 $D_1$ に見える。しかし、太陽による星からの光の曲がり の結果、$D_2$ の方向に見える。すなわち、その現実の位置よりも、太陽の中心から、いくらか、より大きな距離の場所に見える。

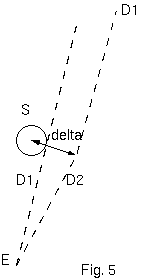
実際にこの疑問は、次の方法でテストされる。日蝕中の太陽の近傍の星々の写真が撮られる。それに加えて、同じ星々の 2 番目の写真が太陽が空の 別の位置にあるとき撮られる。すなわち、数ヵ月前とか後に。その標準の写真と比べて日蝕の写真上の星々の位置は、角度 $a$ に対応する量だけ、 半径方向に外側に(太陽中心から離れて)、変位して現れるはずである。

我々は、この重要な推論の調査において王室協会(Royal Society)と王室天文協会(Royal Astronomical Society)に対して恩恵を受けている。 戦争とそれによって引き起こされた物質的と心理的性質の困難にひるまず、これらの協会は、ふたつの遠征隊を組織した。ーソブラル (ブラジル)と プリンシプ島(西アフリカ)へのーそして数人の最も名高い英国の天文学者(Eddington, Cottingham, Crommelin, Davidson)を 1919 年 5 月 29 日の 日蝕の写真を得るために送った。日蝕中に得られた天体写真と比較写真、総計たった数 100 mm の間に、相対的な不一致が期待された。写真の撮影 とその後の測定には大きな精度が必要だった。

測定の結果は、全く満足する方法で理論を確認した。観測の垂直成分と、星々の計算された変位(秒角)が次の結果の表のなかに示される。

星の番号 最初の座標     2 番目の座標
        観測    計算    観測    計算
11      -0.19   -0.22   +0.16   +0.02
5       +0.29   +0.31   -0.46   -0.43
4       +0.11   +0.10   +0.83   +0.74
3       +0.20   +0.12   +1.00   +0.87
6       +0.10   +0.04   +0.57   +0.40
10      -0.08   +0.09   +0.35   +0.32
2       +0.95   +0.85   -0.27   -0.09

いま、円板から判断して、後者がポテンシャルΦの重力場にいて、それゆえに、我々の得た結果が重力場に全く一般に成立するだろう。 さらに、我々はスペクトル線を発する原子を時計とみなすことができ、次のことが成立する：

原子は、それが設置された場所の重力場のポテンシャルに依存する周波数の光を吸収又は放射する。

天体の表面に位置された原子の周波数は、自由空間に位置する(又はより小さい天体表面上の) 同じ元素の原子の周波数よりも、いくらか少ない。 いま、$Φ= -K{M\over r}$ ここで $K$ は、 Newton の重力定数、そして $M$ は、天体の質量。こうして、星々の表面で作られたスペクトル線の赤い方向 への偏移が実行されるはずである。地球上で作られた同じ元素のスペクトル線と比べ、この偏移の量は、次の値である。 \[ {ν_0 - ν \over ν_0 }= {K \over c^2} {M \over r}. \] 太陽においては、理論の予測する赤方偏移は、波長の約 50 万分の 1 である。信頼できる計算は、星々の場合には可能でない、なぜなら、 一般に、質量 $M$ も半径 $r$ も知られていないからである。

この効果が存在するかどうかは、未解決問題である。そして、現在(1920)、天文学者は解決に大きな熱意をもって働いている。太陽の場合は、 その効果の小ささによって、それが存在するという意見を形成するのは困難である。一方、Grebe と Bachem (ボン)は、彼ら自身の測定と、 青酸化物バンドの Evershed と Shwarzschild の結果としてその効果の存在を疑いを超えたとしたが、他の研究者、特に St. John は、彼らの 測定の結論として反対意見を導いた。

恒星の統計的研究によってスペクトルのより(赤い?)端への平均的な偏移は、確かに明らかにされている；しかし、現在まで、入手可能なデータ の検証は、現実にこれらの偏移が重力の効果であるか否かにおいて、確定した決定に到達することを許していない。観測の結果は集められ、 我々のここの注意に結び付く質問の立場から E. Freundlich の "Zur Prufung der algemeinen Relativitats-Theorie" (Die Naturwissen- schaften, 1919, No. 35, p. 520: Julius Springer, Belin) に詳細に議論されている。

とにかく、ここ数年以内に確定した決定が到達されるであろう。もし、重力ポテンシャルによるスペクトル線の赤方偏移が存在しないなら、 そのときは、一般相対論が欠点のあるものになろう。一方、スペクトル線の赤方偏移の原因が重力ポテンシャルであると確定的に追跡される なら、この偏移の研究は、天体の質量に対する重要な情報を我々にもたらすだろう。

(*1) 特に次の惑星、金星は、ほとんど正確な円軌道をもつので、近日点を精度よく位置決めすることを難しくする。

Note:ースペクトル線のスペクトルの赤い方向への偏移は、1924 年 Adams によって、その効果が太陽のそれの約 30 倍あるシリウスの高密度 伴星の観測から、決定的に確立された。(R.W.L.)

私のこの主題に対する元々の考察は、次のふたつの仮説を基礎としていた。
(1) 宇宙全体に物質の平均密度があって、どこでも同じで0でない。
(2) 宇宙の大きさ(半径)は、時間に独立である。

これら両方の仮説が一般相対論に従って、整合することが証明されたが、それは、ひとつの仮説的な項を場の方程式に付け加えた後においてだけである。 その項は、理論によってそうであることが必要とされず、理論的な視点からも自然にみえない("場の方程式の宇宙項")。

仮説 (2) は、そのとき私には避けられなく現れたが、なぜなら私は、もし人がそれから離れると、その人は底無しの推測に落ちいると考えたからである。

しかしながら、すでに 20 年台にはいって、ロシアの数学者 Friedman が、純粋に理論的視点から、別の仮説が自然であることを示した。彼は、 もし人が仮説(2)を捨てるつもりになれば、より自然でない宇宙項を場の方程式へ導入することなしに、仮説 (1) を保持することができると悟った。 すなわち、元々の場の方程式は、"世界半径"が時間に依存する(拡大する空間)解を許すのである。その意味で、人はいうことができる。Friedman に従って 理論が、宇宙の拡大を要求していると。

数年後、Hubble が銀河系外星雲 ("天の河達") の特別な調査によって、スペクトル赤方偏移が星雲の距離に従って規則的に増加することを示した。 これは、現在までの我々の知識に関する限り、ドップラー(Doppler)の原理の意味のなかにのみ解釈でき、大きな星々の系の拡大の動きとしてー Friedman に従って重力の方的式に要求されたものである。Hubble の発見はそれゆえ、ある程度は、理論の確認であると考えられる。

しかし、そこには奇妙な困難が持ちあがっている。Hubble によって発見された銀河の線シフトの解釈である膨張という解釈 (それは、理論的視点からは、 疑うことが難しい)は、"たった" 約 10 億年前にある拡大の原点を導く。一方、天体物理学者は、個別の恒星、恒星系の発展がそれよりかなり長い時間 を必要とすることが確からしいことを明らかにした。この不調和がどのように克服されるべきかは、知られようがない。

私はさらに、次のことを注意したい。宇宙の膨張理論は、天文学の実証的データとともに、(3 次元)空間の有限又は無限の特性について、どの決定も到達 すべきものとして許さない。一方、もともとの"静的な"宇宙の仮説は、閉じた(有限)の空間をもたらしていた。

空間一般をとくに空の空間を、物理的な現実性とみなさなければならない、というのは本当に厳しい要求である。何度も何度も昔から哲学者は、 そのような推定に抵抗してきた。デカルト(Descartes) は、これらの線上に何かを議論した：空間は、拡張と同一である。 しかし、拡張は物体と結合している；こうして物体なしの空間はなく、それゆえに空の空間はない。この議論の弱さは、第 1 にそれに続く結論にある。 拡張という概念は、その起源を固体接触への配置又は導入の我々の経験にもつことは、確かに正しい。しかし、このことから拡張という概念が、 この概念の形成を引き起こさなかった場合に正当化されないだろうと、結論することはできない。概念のそのような拡大は、実験的結果の理解への 価値によって間接的に正当化され得る。拡張が物体に制限されるという主張は、それゆえ、それ自身、確かに根拠がない。しかしながら、後に我々は、 一般相対論がデカルトの概念を遠回りに堅固にすることを見るだろう。デカルトが彼の注目すべく魅力的な見方にもたらしたものは、確かに次の感性だった。 それを強制する必要性なしには、人は、現実性を "直接に経験"(*1)されることのできない、空間のようなものに帰するはずがないということである。

空間の概念、又はその必要性の心理学的起源は、我々の思考の通例の習慣の基礎の上にあると現れるような明白なものからは、遠い。古い幾何学者は、 概念的物体(直線、点、表面)を扱ったが、本当には空間をそのようには、後の解析幾何学で扱われたようには、扱わなかった。しかしながら、空間の 概念は、ある原始的な経験によって示唆されている。 ひとつの箱が組み立てられたと想像しよう。箱は一杯になるようにと、物体が箱の内側に何かの方法で配置される。そのような配置の可能性は、物体 である"箱"の特性である。そのような何かは箱とともに与えられ、"内部の空間"は、箱によって与えられる。これは箱が違えば、異なる何かであり、 どの時点でその箱にどの物体があるかどうかに独立であると本当に自然に考えられる何かである。もし、箱のなかに物体がないなら、そのとき、 その空間は、"空" と現れる。

いままでのところ、我々の空間の概念は、箱と関連づけられてきた。しかしながら、箱の空間をつくる蓄積可能性は、箱の壁の堅さとは独立である ことが分かる。この堅さは、結果として箱の "空間" を失わずに、0 まで削減できないのだろうか。そのような極限の過程の自然さは明白であり、 そして、いまそこには、その箱なしの我々の空間想起が残され、自明なものとなる。依然としてそれは、この概念の起源を忘れたときには、とても 非現実的に見える。物体と独立として、物質なしに存在し得るものとして、空間を考えることは、デカルトにとって嫌悪すべきことだったことを、 ひとは理解できる(*2)。(同時に、このことは、彼の解析幾何学のなかで彼が空間を基本概念として扱うことを妨げなかった。) 水銀気圧計のなかの真空への注目の集中が、最後のデカルト派を確かに武装解除させた。しかし、この原始的な段階においてさえ、不満足な何かが 空間の概念に、又は独立した現実のものとしての空間思考に、執着することを否定できない。

空間(例えば、箱)のなかに物体が詰め込まれる方法は、3次元ユークリッド幾何学の主題であり、その公理論的構造はいつでも我々を欺き、それが 現実化できる状況を言及していることを忘れさせる。

もしいま、空間の概念が上で概略を示された方法で形成され、そして箱の "充填" についての経験からに従っているなら、そのときは、この空間は、 第 1 に境界化された空間である。この制限は、しかしながら、本質的とは見えない、なぜなら明白に、より大きい箱で小さい箱を取り込むものを常 に導入できるからである。この方法で空間は、境界を持たないものになる。

私はここで、概念が3次元ユークリッドの空間の性質が、どうやって、相対的に原始的な経験に逆追跡されるかを考えない。そうでなくて、私はまず、 他の視点から、物理学的思想の発展のなかで空間概念の役割りについて考察する。

もし、より小さな箱 $s$ が、より大きい箱 $S$ の虚ろな空間のなかに、相対的に静止して設置されるなら、そのとき、$s$ のうつろな空間は、$S$ のうつろ な空間の一部であり、同じく"空間"は、それらふたつの箱に属するそれらを含む。しかし、もし、$s$ が $S$ に関して動きのなかにあれば、その概念は、 より単純でなくなる。人はそのとき、$s$ がつねに同じ空間を含むが、$S$ の可変の空間を含むと考えがちである。そのときそれは、その特定の空間を 各箱への配分することが必要となり、空間は、境界を持つものでなく、これらふたつの空間が互いに対して動きをもつと仮定するのである。

人がこの複雑さを意識するようになる前に、空間は、無境界の媒体として又はそのなかで物体が泳ぎ回れるコンテナとして現れる。しかしいま、 互いに関して動きにある無限の数の空間があることが思い出されなくてはならない。客観的に存在し物事に独立な何かとしての空間の概念は、 前科学の思考に属しているが、互いに相対的に動きをもつ無限の数の空間の存在の概念は、そうでない。後者の概念は、実に論理的に避けられないが、 科学的な思考のなかにさえ、かなりの役割を果たしたといえるものからは、遠い。

しかし、時間の概念の心理学的起源についてはどうだろう? その概念は、疑いもなく "心に想起する" という事実に関連するだけでなく、 経験の感覚とこれらの回想との区別にも関っている。経験感覚と回想(又は単純な再現)との間の識別が何か我々に直接に心理学的に与えられたもの であるということは、それ自身の疑いがある。誰もが、あることを彼の感覚で実際に経験したのか、それについて単に夢を描いたのか疑いのなかに いた経験がある。多分、これらの代替物を区別をする能力が、心の活動性の結果としての創造性の要求の最初にくるのである。

経験は、"回想" と関連づけられ、"現在の経験" と比べて "以前に" あると考えられる。これが回想された経験への概念的な順序原理であり、 その完成の可能性が客観的概念の時間、すなわち、その個人の経験の配置に対して述べる時間の概念、を生起する。

時間の概念に客観性を与えることによって、我々は、何を言いたいのだろうか? ひとつの例を考えよう。ある人 $A$ (私) が "稲妻が光っている" という経験をもつ。人 $A$ は、同時にまた経験する。人 $B$ の行動が、彼自身の "稲妻が光っている" という経験と関連をもたらす、そのような $B$ の 行動を経験する。人 $A$ にとって "稲妻が光っている" という経験に他の人も参加しているという考えが起きる。 "稲妻が光っている" は、もはや 排他的な個人経験でなく、他の人々の経験(又は結果的に単に "潜在的経験")として解釈される。こうして "稲妻が光っている" には解釈が起き、 最初には "経験"として意識に入ってきたものが、いままた、(客観的な) "事象" として解釈される。それは単に、我々が "現実の外部世界"という ときに意味する全事象の総てである。

我々が見たように、我々が我々の経験に時間的配置を自ら付けなければならないと感じるのは、何か次のようである。もし、$β$が$α$より後で、 $γ$が$β$より後なら、$γ$は$α$より後である("経験のシーケンス")。いま、経験に関連する"事象"に伴う、この点の、この位置とは何だろうか。 最初に見たときは、事象の時間的配置は、経験の時間的配置に一致して存在することが、明らかな仮定であると思えた。一般に無意識にこれが行われた。 懐疑的疑いが自ら感じさせるまでは(*3)。客観世界という考えに到達するために、追加的に構築する概念がまだ必要なのである：事象は、時間に 局在するだけでなく、空間にも局在するという。

以前の段落で、どのように空間、時間、事象の概念が心理学的に経験に関係するかを記述しようと我々は試みた。論理的に考えて、それらは人間 の知性の自由な創作物であり、この方法でそれらがよりよく概観されるように、経験を相互の関係に持ち込む目的に役立つ、思考の道具である。 これらの基本的な概念の実証的な源を意識的にすることの試みは、我々がどの程度、これらの概念に実際に縛られているかを示すべきである。 この方法で我々は、それが必要な場合に、良識のある使い方をすることがつねに難しいことである、我々の自由を意識するようになる。

空間-時間-事象(心理学的な領域からの概念と対比して、より短く "空間的" と呼ぶ。)概念の心理学的起源に関連したこのスケッチに付け加える 本質的なものが、我々にはまだ何かある。我々は、箱を使ってそのなかに物体を配置する経験に空間の概念が結ぎ止められている。 このように、この概念形成は、すでに物体の概念(例えば、"箱")を前提している。また、これに関連して、同じように、時間の客観的概念の形成 を導入されなければならない人にも、物体の果たす役割が存在する。私には、それゆえ、物体の概念の形成が時間と空間の我々の概念よりも先行する べきことが現れている。

これら全ての "空間的" 概念は、すでに前科学思考に属し、それらは、心理学の領域からの苦痛、目標、目的、等、のような概念と並んでいる。 いま、物理学のそして同じく自然科学一般の思考の特徴であるのは、それが努力して原理的に "空間的" 概念とともに "だけ" で、それらの助けに よって表現しようと努めるのは、法則の形態をもつ全ての関係である。物理学者は、色と音を振動に還元することを探し、生理学者は、思考と苦痛 を神経過程に還元する。そのような方法で物理的要素が、そのように存在の原因結果の連鎖から消去され、そしてどこにも原因結果関連のなかに、 独立な繋がりが起きないようにする。それは、疑いもなくこの態度であり、全ての関係の包括が "空間的"概念だけの排他的使用によって原理的に 可能と考える、それは現在、"物質主義"という言葉で理解される。("物質" は基本的概念としてはその役割を失っているが。)

オリンピアの高原から自然科学の思考の基本的概念をひきずり落とし、そして地上の系統を明らかにすることの必要性は、なぜなのか? 答え：それらに付け加わったタブーをからこれらの概念を自由にするため、考えや概念の形成においてより大きな自由を達成するためである。 それは、D. Hume と E. Mach の不死の信頼に対するものである。彼らは他者以上に、この臨界的概念を導入した。

科学は、前科学思考から概念、空間、時間、そして物体(そして特別な場合に、"固体")を引き継いだ。そして、それらを修正し、それらにさらなる 正確を与えた。その最初の重要な達成は、ユークリッド幾何学の開発であり、その公理論的定式化が我々をその経験的起源(固体の配置又は並置の 可能性) に盲目にすることを許してはならないものである。特に、空間のユークリッド的性質だけでなく3次元的な性質は、実証的起源をもつもの である(それは、全体を"立方体"のような構成で充填できる)。

空間概念の難解さは、完全な剛体が存在しないことの発見でさらに強化された。全ての物体は柔軟に変形可能であり、その体積も温度変化によって 変化する。構造、その可能な合同性は、ユークリッド幾何学によって記述されるべきものであるが、それゆえ、物理的概念から離れては表示できない。 しかし、一方、物理が結局、その概念の設立に幾何学を使わざるを得なくなり、幾何学の実証的内容は、全て物理学の枠組のなかだけで述べられ、 テストされる。

これに関連して、原子論もまた想起されなくてはならない。そしてその有限の分割可能性の概念を； 原子以下の空間拡張は、決して測定できない。 原子論は、また我々に、鋭く静的に定義された境界表面をもつ固体という考えを強制的に放棄させる。厳しくいえば、マクロな領域においてさえ、 可能な互いに接する固体の構成において、 "厳密な" 法則というものはない。

これにも関わらず、誰も空間という概念を諦めようという考えをもたない。なぜなら、それは顕著に成功を収めた自然科学全体系のなかで不可欠と 現れているからである。Mach は、19 世紀に真面目に空間概念の除去を思った唯一の人であった。そのなかで彼はその置き換えを探し求めた。 全ての質点間の遠隔同時統合性を記述することによって(彼は、この試みを慣性の満足な理解に到達するために行った)。

場

Newton 力学では、空間と時間は対で役割を演じる。まず最初に、それらは、物理学で起きる物事の運搬者又は枠組の役割を果たし、それらを参照 した空間座標と時間座標によって、事象が記述される。原理的に、物質は、その動きが物理的な出来事を構成する、"質点" によってできていると 考えられる。物質が連続的なものと考えられるときは、まるでそれが仮であるかのように、人が離散的な構造を望まない又は記述することができな いところの場合において行われる。この場合、物質の小さな部分(体積の要素)が質点と同様に扱われ、少なくとも、これまで我々が関係したものは、 単に運動だけであり、そのときのそれの生起ではない。それは、不可能又は役に立つ目的、運動の属性を提供することができない(例えば、温度 変化、化学的過程)。空間と時間の2番目の役割は、ひとつの "慣性系"であるということであった。全ての考え得る参照系から、慣性系は、それを 参照すれば、慣性の法則が有効であると主張できることに特長があると考えられる。

このなかで、本質的なことは、次のことである。"物理的現実"、それを経験する主体から独立した存在としての考え、が構成されると、少なくとも 原理的には、考えられる。一方には空間と時間によって、もう一方には、永久に存在する質点があって、空間と時間のなかを運動するものによって。 空間と時間の独立した存在の考えは、次のこの方法で徹底的に表現される：物質が消え去ると、空間と時間は、背景に残る (物理的な出来事の一種 の舞台のように)。

この立場を乗り越えることは、そのひとつの進展から結果された。最初は、空間-時間の問題には、何もしないように現れた、すなわち、"場の概念" の登場である。その最終的な要求は、原理的には、粒子の概念(質点)の置き換えである。古典的な物理学の枠組のなかで、場の概念は、付随的概念 として現れ、その場合、そのなかでは物質が連続体として扱われる。例えば、固体の熱の伝導の考察において、物体の状態は、物体の全ての点の全 ての決めた時刻の温度を与えることで記述される。数学的には、このことは、温度 $T$ は、空間座標と時間 $t$ の数学的な表式(関数)によって表され るということである(温度場)。熱の伝導の法則は、局所的な関係式 (微分方程式)によって表され、それが熱伝導の全ての特別な場合を包括する。 ここで、温度は単に場の概念の例でしかない。これは、量(又は量の複合)であり、座標と時間の関数である。もうひとつの例は、液体の運動の記述 である。全ての点の全ての時刻に速度があって、それは量的に、ひとつの座標系の軸に対応する 3つの "成分" によって記述される (ベクトル) 。 ある点の速度の成分(場の成分)は、ここでまた、座標$(x,y,z)$と時間の関数である。

ここで言及された場の特徴として、それらが重さのある質量のなかにだけ起こることである；それらは、この物質の状態を記述することだけを助ける。 場の概念の歴史的な発展に従って、物質の存在しない場所には、場も存在しない。しかし、19 世紀の最初の 4 半世紀に次のことが示された。光の 干渉と運動の現象は、光が波の場であると見なされるときに、驚くべき明晰さを伴って説明できるということが。それは、完全に、弾性のある固体 のなかの機械的振動の場と類似していた。こうして、場は、重さのある物質のない、"空の空間" のなかにもまた存在し得るものとして導入される ことが必然的に思われたのである。

物事のこの状態は、パラドキシカルな状況を生み出した。なぜなら、その起源に従えば、場の概念は、重さのある物体の内部状態の記述に限定して 登場した。これは、はっきりいって、次の最大限の確信がもてるようにみえる。つまり、全ての場は、機械的解釈ができる状態とみなすべきで、 このことは、物質の存在を前提としている。これまで空とみた空間にさえ、物質のある形態の遍在を仮定することを、こうして、人は強制される ように感じた。それは、"エーテル" と呼ばれた。

場の概念の機械的な運搬者との関連の仮定からの解放は、物理学の思想の発展のなかで心理学的にもっとも興味をひく事象のひとつとなった。 19 世紀の後半を通じて Faraday と Maxwell の研究と関連し、さらに更にはっきりしてきたことは、場の言葉による電磁過程の記述は、質点の 機械概念に基づく扱いよりも、ずっと優れていたことである。電気力学への場の概念の導入によって、Maxwell は、電磁波の存在を予言すること に成功し、その電磁波の光との本質的な同一性は、それらの伝播速度が等しいことから、疑いようがなかった。この結果として、原理的には光学は、 電気力学に吸収された。この巨大な勝利のひとつの心理学的影響は、場の概念が古典力学の機械的枠組に対して、しだいに大きな独立性を勝ち得た ことである。

それにもかかわらず、最初に当然と認められたのは、電磁場がエーテルの状態と解釈されなければならないというものだった。そして、これらの 状態を機械的なものによって説明することが、熱狂的に探し求められた。しかし、これらの努力がつねに裏切りに出会うかように、科学は、次第に そのような機械的な解釈を否認する考えに慣れてきた。それにもかかわらず、電磁場がエーテルの状態に違いないという確信は、まだ残っていた。 そして、これが世紀の変わり目の位置であった。

エーテル理論は、それに問いをもたらした：機械的観点から、重さのある物体に関して、エーテルはどのように振る舞うか? それは、物体の運動に 役割を果たすだろうか、又は、その部分は、互いに静止の状態を続けるのだろうか? この問いに決定を下すために、多くの精巧な実験が実行された。 これに関連して、次の重要な事実が言及されなければならない： 地球の年周運動の結果としての恒星の "光行差"と、"ドップラー効果" すなわち、 知られた放射の周波数についての恒星から我々に届く光の周波数への恒星の相対運動の影響である。全てのこれらの事実と実験の結果は、ひとつ Michelson-Morley 実験を除き、H. A. Lorentz による仮定、エーテルは、重さのある物体の運動に役割を果たさない、エーテルの部分は、互いに 関して全く相対運動を持たない、によって説明できた。そのようにエーテルは、まるで空間が絶対的に静止であることの具現のように現れていた。 しかし、Lorentz の研究は、まださらに達成した。それは、電場への物質の影響ーとその逆ーが物質の構成粒子が、粒子の運動を分担する電荷を 担うという事実だけによる、という仮定の上に、重さのある物質中のそのとき知られた全ての電磁、光学過程を説明した。Michelson と Morley の実験に関して、H. A. Lorentz は、得られた結果が少なくとも静止エーテル理論に反しないということを示した。

これら全ての美しい勝利にも関わらず、理論の状態は、まだ全体として満足できるものでなく、そして、次の理由で。古典力学は、それが近い近似 として成立することを疑えないことは、全ての慣性系、又は慣性"空間"の自然法則の定式化のための対等、すなわち、ある慣性系から他への移行に 関する自然法則の不変、を教える。電磁と光学の "実験" は、かなりの正確さをもって同じことを教える。しかし、電磁理論の基礎は、特定の慣性系、 すなわち、光エーテルが静止する慣性系が偏愛を与えられなければならないことを教える。理論的基礎の視点は、大いに余りに不満足であった。 古典力学と同様に、慣性系の対等(特殊相対性の原理)を支持するような、修正はあり得ないのか?

この質問への答えは、特殊相対性理論である。これは、Maxwell-Lorentz 理論から空の空間での光速一定の法則を引き継いでいる。 慣性系の対等(特殊相対性原理)と調和させて、これを持ち込むためには、同時性の絶対的な性質を放棄しなければならなかった； ひとつの慣性系から他への移行のためには、さらに、時間と空間座標の Lorentz 変換が続く。特殊相対論の全体の内容は、次の言明に含まれる： 自然の法則は、Lorentz 変換に関して不変である。この要求の重要なことは、それが可能な自然法則を確定的な手法で制限するという事実のなかにある。

空間の問題に関する特殊相対論の位置は、何か? まず最初に、我々は、現実の4次元性がこの理論で最初に導入された、という意見に対して防御し ないといけない。古典物理においてさえ、事象は4つの数、3つの空間座標と時間座標によって局在化された。物理的な"事象"の全体性は、こうして、 4次元の連続的な多様体のなかに埋め込まれたものと考えられる。しかし、古典力学の基礎の上の、この4次元連続体は、1次元の時間と3次元の空間 の部分に客観的に分割し、その後者だけが同時的な事象を含んでいる。この分解は、全ての慣性系で同じである。ひとつの慣性系を参照するときの ふたつの確定した事象の同時性は、全ての慣性系を参照するときの、これらの事象の同時性を含む。これが古典力学の時間が絶対的であると我々が いうときの意味するものである。特殊相対論に従えば、それは違ってくる。ひとつの選択した事象に同時であるような数多くの事象が存在する。 それは正しい。ひとつの慣性系に関しては、である。しかし、もはや慣性系の選択に独立ではないのである。4次元連続体は、いまや、もはや客観的 に部分に分解できない。その部分の全て事象が同時性をもつような； "いま" は、その空間的に拡張された世界においてその客観的な意味を失った。 空間と時間が 4 次元連続体であると考えなければならない理由は、それが客観的に分解可能でないからである。もし、不必要な伝統的な任意性なし に、客観的である関係の趣旨を表現しようと望むならば。

一方、特殊相対論は、全ての慣性系の物理的な対等性を明らかにした。それは、静止したエーテル理論の欠点が多いことを証明した。 それゆえ、電磁場が物質の運搬体の状態であるとみなされるべき、という考えは放棄されることが必要である。場は、こうして、これ以上還元 できない物理的記述の要素となり、それは、Newton 理論での質量概念と同じ意味で、還元できないものとなった。

これまで、我々が見出そうと注意を振り向けたのは、空間と時間の概念のどの点が特殊相対論によって "変更" されたか、であった。 ここで、どのようなものを、この理論が古典力学から引き継いでいるか、に注意を集中しよう。ここでもまた、自然法則は、慣性系が空間時間の記述 の基礎として取られているときにだけ有効性を主張する。慣性の原理と、光速の一定性の原理は、慣性系に関してのみ有効である。場の法則も、意味 と有効性とをもつと主張できるのは慣性系に関してだけである。 このように、古典力学と同じように、ここでもまた、空間は、物理的現実の表現の独立した成分である。もし、我々が、物質と場が取り除かれること を想像すれば、慣性空間、又は、より正確に、この空間と付随する時間は、背景に残る。4次元構造 (Mikowsky 空間) は、物質と場の運搬体として 考えられる。慣性の空間とそれらの付随する時間は、線形の Lorentz 変換によって互いに繋がった、唯一つの特権的な、4次元座標系である。 この4次元構造にはもはや "いま" を代表する部分を客観的にもたないので、物事の発生と生成の概念は、確かに完全に留保されず、より複雑になる。 それゆえ、物理的な現実をこれまでのように 3 次元存在の "進化" ではなく、4 次元存在と考えるのが、より自然であることが明らかになる。

特殊相対論のこの剛体4次元空間は、ある程度、H. A. Lorentz の剛体 3 次元エーテルの 4 次元的な類似である。なぜなら、この理論でも次の言明は 有効であるから：物理的状態の記述は、空間が初期に与えられ、独立な存在であることを前提として要求する。このようにこの理論でさえ、デカルト の独立な、又確かに、"先験的" な空の空間の存在の困難を追い払わないのである。ここで与えられた要素的な議論の本当の目的は、どこまで、 これらの疑いが一般相対論によって克服されたか、を示すことである。

一般相対論のなかの空間の概念

4次元的に考えて、 4 つの座標の非線型の変換が $S_1$ から $S_2$ への移行に対応する。いま、問いが上がる：どのような種類の非線型変換が許されるのか。 又は、どのように Lorentz 変換は一般化されるのか? この問いに答えるために、次の考察が決定的である。

我々は、前の理論の慣性系にこの特性を与えた：座標の差は、静止した剛体の測定棒によって測定され、時間の差は静止した時計で測定される。 最初の仮定は、もうひとつで補足される。すなわち、静止した測定棒との相対的な配置と合致のためにユークリッド幾何の "長さ" の定理が成立する。(??) 特殊相対論の結果から、そのとき、要素的な考察によって、座標のこの直接の物理的解釈は、慣性系($S_1$)に対して加速する参照系($S_2$) に対しては、 失われることが結論される。しかしもしその場合、座標は、単に"隣接"の次数や階数を、そして、それゆえにまた、空間の次元の等級を表すものとなり、 その計量の特性を何も表さないものとなる。我々は、こうして、その変換を任意の連続変換(*4)への拡張へ導かれたのである。 これは、一般相対性の原理を意味する：自然の法則は、座標系の任意の連続変換に関して共変でなければならない。この要求(法則の最大限可能な単純 さのそれに繋がる)は、特殊相対性の原理よりも比較にならない位、さらに強力に、関係する自然法則を制限するのである。

この思考の列車は、独立な概念としての場に、本質的に基づいている。なぜなら、$S_2$ に関しての、優勢な状態は、重力場が存在すると解釈される。 この場を作りだす質量の存在の問いが持ち出されることなしに。この考えの列車のお陰で、なぜ純粋に重力場の法則が一般的な種類の場(もし、例を 挙げるなら、電磁場がある)の法則よりもっと直接的に一般相対論の概念に結び付くか、も把握することができる。 我々は、すなわち、自然法則のなかで、可能な特別な場合、事実、最も単純な特別な場合を代表する "場のない" Minkowsky 空間、 を仮定するのに、よい基盤を得たのである。我々は、参照とするその計量的な性質、そのような空間が $dx_1^2 + dx_2^2 + dx_3^2$ が空間的間隔 の自乗である事実によって特徴付けられる。間隔とは、単位物差しで計られ、ふたつの無限小の近傍点の 3 次元"空間的"な対角線(ピタゴラスの定理) であり、一方、$dx_4$ は時間的間隔、適切な時間物差しで計られた、$(x_1,x_2,x_3)$ を共通にするふたつの事象の時間間隔である。 これら全ては単純に、客観的な計量的な重要な値が次の量で与えられることを意味する。 \[ \tag{1} ds^2 = dx_1^2 + dx_2^2 + dx_3^2 - dx_4^2 \] Lorentz 変換の助けによってすぐに示せるように。数学的には、この事実は、$ds^2$ が Lorentz 変換に関して不変量であることの状態に対応している。

もし、いま、一般相対性の原理の意味で、この空間(式(1)参照)が座標系の任意の連続変換を受けるなら、そのときは、客観的に重要な量 $ds$ は、 新しい座標系のなかで、次の関係式によって表される。 \[ \tag{1a} dx^2 = g_ik dx_i dx_k \]

それらは、その添字の i と k との全ての結合に渡って 11,12,..,44 まで、累加算される必要がある。項 $g_{ik}$ は、定数ではなく、座標の関数である。 それらは、任意に選んだ変換によって決められる。しかしながら、項 $g_{ik}$ は、新しい座標の任意関数ではなく、式 (1a) が式 (1)に 4つの座標の連続 変換によって、変換されて戻るような関数というだけである。これが可能であるためには、関数 $g_{ik}$ は、ある一般共変方程式の条件を満たさなければ ならない。それは、一般相対論の定式化の半世紀以上も前に B. Riemann によって導かれた (Riemann 条件)。もし、関数 $g_{ik}$ が Riemann 条件を満た すとき、等価原理によって、(1a) は、一般共変形のなかで特別な種類の重力場を記述する。 これは、一般の種類の純粋の重力場の法則が Riemann 条件が満たされたとき、満たされなければならないことに続く； しかし、それは Riemann 条件 より弱い、又はより制限の少ないものでなければならない。この方法で、純粋な重力場の法則は、実際に完全に決定される。その結果は、ここでは さらに詳しくは正当化されないだろう。

我々はいま、一般相対論への移行が空間の概念をどこまで修正したかをみる位置にいる。古典力学に従っても、特殊相対論に従っても、空間(空間と時間) は、物質又は場から独立した存在であった。ともかく、空間を埋めるものすべて、座標、時空、又は慣性系に依存し、その計量的特性と共に、いちどきに、 あるがままに、考えられなくてはいけない。そうでなければ、"空間を埋めるものすべて" の記述は、無意味である (*5)。 一方、一般相対論の基礎の上では、"空間を埋めるもの" の対抗として空間は、座標に依存して、分離した存在をもたない。こうして、純粋の重力場が 重力方程式の解として、$g_{ik}$ (座標の関数としての) の言葉で記述されてよいのである。もし、我々が重力場を(すなわち、関数 $g_{ik}$)取り除くことを 想像するなら、そこには、式(1)型の空間は、残らない。そこは、絶対的な "無" であり、"位相空間" もない。(*訳注) 関数 $g_{ik}$ は、場を記述するだけでなく、同時にまた、多様体の位相幾何学的、そして計量的な構造特性を記述する。式(1)型の空間は、一般相対論の 立場から判断すると、場なしの空間ではなく、$g_{ik}$ 場の特別な場合である。なぜならその、ー使われた座標系にとって、それ自身なにも重要性のないー 関数 $g_{ik}$ は、座標に依らない値をもつ。空の空間のようなものはない。すなわち、場なしの空間。空間時間は、それ自身の存在を主張せず、場の構造 的性質としてだけある。

このように、デカルトは、彼が空の空間の存在を排除しなければならないと信じたとき、真実からそれほど遠くにはいなかった。その意見は確かに 不合理であるように見えるが、物理的現実は、排他的に重さのある物体のなかにしか見られないのであるから。現実の再現としての場の概念が必要 であり、一般相対性原理との繋がりにおいて、デカルトのアイデアを真の核心を示せば； "空の場" であるような空間はない。

重力の一般化理論

その特定の場の法則への問いは先行する一般的考察のなかで 2 度目のものである。 現在、主要な問いは、ここで熟慮されているようなその種の場の理論が、そもそも目標に導くだろうかどうかである。 これによって意味するものは、ひとつの場による物理的現実を 4 次元を含めて徹底して記述する理論である。 現在の世代の物理学者は、この質問に否定的な答えをする傾きがある。量子論の現在の形式に従えば、系の状態は直接指定できず、 系に達成できる測定結果の統計の言明によって間接的な方法でのみなされると信じている。現実性の概念のそのような弱体化によっては、 実験的に確認された自然の双対性(粒子と波の構造) だけが現実と確信される。私は、そのような、遠隔の理論的な否認は、 現在の実際の知識から正当化されるべきでないと、そして人は相対的場の理論の経路の目標への追求を止めるべきでないと信じる。

(*1) この表現が取られる cum grano salis。
(*2) Kant は、空間の客観性を否定することによって困難を取り除こうとする試みをしたが、しかしながら、真面目に受け取ることが難しい。 箱の内部空間に固有な梱包の可能性は、箱自身、又、箱の内部に詰められる物体と同じ意味で、客観的である。
(*3) 例えば、音の手段によって得られる経験の時間順は、視覚的に得られる順序と異なってよい。 そのため、人は単純に経験の時間順を事象の時間順と一致させることはできない。
(*4) この不正確な表現の様式は、多分、ここでは十分である。
(*5) もし、我々が、空間を埋めるものすべて (例：場)を取り除くことを考えるなら、そこにはまだ、式(1)に従った計量の空間が残る。 それは、またそこに導入したときの試験物体の慣性的振る舞いを決定するだろう。
(訳注) 本文と(*5)との明らかな違いの原因は、本文が宇宙項を導入した重力方程式の結論であり、物質(と場)のない空の空間は $g_{ik}$ 自体が 0 になる。 そこには時計も物差しも存在しない。一方、(*5)は、その後の宇宙項のない重力方程式によるため、空の空間は、式 (1) の Minkowsky 空間である。
(*6) 一般化は、次の方法で特徴づけられる。空の Minkowsky 空間からのその導出に従って、関数 $g_{ik}$ の純粋な重力場は、対称の特性が与えられる。 $g_{ik}= g_{ki} $($g_{12}= g_{21}$ 等)。一般化場は、同種のもので、対称性をもたないものである。その場の方程式の導出は、純粋重力の特別な場合のそれに 完全に類似する。