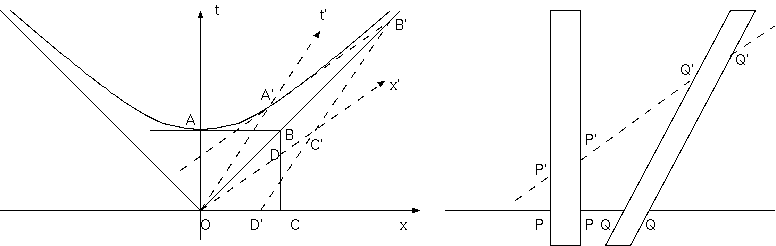
Fig. 1.
目次
I. Newton 方程式の不変量とその 4次元空間表現
II. 世界仮説
III. 連続体中の運動表現
IV. 新しい力学
V. 1 個又は 2 個の電子の運動
私があなた方の目前に示そうと希む、空間と時間との見かたは、実験的物理の土地から飛び出してきて、そこにその力を示している。 それらは、根本的である。これからは、空間自体、時間自体はただの影に消え去る運命とされ、両者の一種の結合だけが独立した現実 として保持されるだろう。
最初に、私は、どのようにそれが現在の受け入れられた力学から、純粋な数学的な思考の線にそって、出発することが可能であったか、 そして変化した空間と時間の概念に到達することができたかを示す。Newton 力学の方程式は、2 重の不変性を示している。最初に、もし、 我々が基礎にする系の空間座標に対して、任意の "位置の変化" を行っても、その形式は不変に保たれる;次に、もし我々が運動状態を変化しても、 すなわち、どのような "均一な平行移動の運動" を与えることによっても。さらに、時間のゼロ点は、役割をあたえられていない。 我々は、幾何学の公理にはそれがすでに終了し手が離れたようにみる習慣がある。我々が力学の原理に機が熟したと感じるとき、その理由のため、 ふたつの不変性は、一緒に言及されることが多分ほとんどない。両者ともそれ自身、力学の微分方程式にとってある変換の群を意味する。 最初の群の存在は、空間の基本的特性とみることができる。2 番目の群は、好んで特別な軽蔑をもって扱われる。まるで、我々、問題に直面しない心が、 静止と仮定された空間が結局は均一な平行移動状態でありえないことを、決して物理現象から決定できない困難に打ち勝てるかのようである。 このように、ふたつの群は、互いにそれらの生活を全体として分離している。それらの全く異種の性質は、それらを結合しようとするどんな 試みをも意気消沈させただろう。しかし正確には、それらが複合されたとき、全体として完全な群を我々に与えると考えられる。
我々は、物事の状態を図形的方法によって視覚化しようと試みるだろう。$x, y, z$ を空間の直交する座標値とし、$t$ は時間を示すとする。 我々の知覚の対象は、常に場所と時間の組合せを含んでいる。誰もある場所を時間なしに、又は場所なしの時間を示さない。しかし、 私はまだ、空間と時間とがともに独立な重要性であるという独断を尊重する。時間の1点における空間の1点の、それは値 $x, t, z, t$ の系を私は世界点(world-point)と呼ぶ。全ての考え得る $x, y, z, t$ の値の系の多様性を我々は、世界(world)と命名する。この最も 勇敢なチョークの一片とともに、黒板の上に4つの世界軸を拡げることができる。たったひとつのチョークの軸であっても、そのように すべてのドキドキする分子が構成し、さらに宇宙のなかの地球の運動に役割を果たし、それは我々に抽象の十分広い視野をすでに与える; 数字 4 に繋がる何かそれ以上の抽象は、数学者にとって苦ではない。退屈な空虚のどこにも逃げることなく、どこにもどの時にも我々 が何か知覚できるものがあると想像しよう。"物質"とか"荷電性"とかいうことを避けて我々はこの何かに"実質"という言葉を使う。 我々は、注意を世界点 $x,y,z,t$ にある実質点に集中して、他の全てのときも我々がこの実質を認識できると想像する。この実質点の 空間座標の変化を$dx, dy, dz$とし、時間要素 dt に対応する。そのとき、我々は、イメージとして、いわば、実質点の永遠に残る経歴、 世界の中の曲線である世界線(world-line)、その点が一意にパラメタ t によって $-∞ $から $∞ $ まで参照できるものを得る。宇宙全体が 同様な世界線に分解され、そして私は喜んで自身参加して、次のように私の意見をいうだろう。それらの世界線の間の相互の関係として、 物理法則は、その最も完全な表現を見出すだろうと。
空間と時間の概念は、$x, y, z$ の座標と $t= 0$ とその両側 $t>0$ と $t<0$ に落ち分かれる。もし単純性のために空間と時間のゼロ点を残す ならば、最初に言及した群は、力学のなかで、我々が $t=0$ の $x, y, z$ 軸を、我々が選ぶどのような回転もその原点の周りに与えることが できることが、次の表式が一様な線形変換に対応することを意味する。 \[ x^2 + y^2 + z^2 \] しかし、2 番目の群は、我々がーまた、力学の法則の表式を変化することなくー $x, y, z, t$ を $x-αt, y-βt, z-γt, t$ に置き換える ことができることを意味する。どのような一定値 $α, β, γ$についても。こうして、時間軸には世界の上半分 $t>0$ に向かう、我々が選 ぶどのような方向をも与えることができる。いま、上方向のなかの時間軸のこの完全な自由さとともにある、空間の直交性の要求は、何 がもつのか?
結合を確立するために、正のパラメタ c をとり、次の図形的表現を考察しよう。 \[ c^2t^2 - x^2 - y^2 - z^2 = 1 \] それは、 $t= 0$ によって分離したふたつの表面を構成する。 2 枚の双曲面のアナロジーである。$t>0$ 領域の面を考え、いま、$x, y, z, t$ を 4 つの新しい変数 $x', y', z', t'$ にする一様な線形変換をとるとき、新しい変数のなかでこの表面の表式は、同じになる。 原点の周りの空間の回転がこれらの変換に関係する(属す)ことは明らかである。それら変換のひとつ、$y, z$ が変化しないものを考慮し て残りの全ての理解を得る。この面と $x, t$ の平面との交線、ー双曲線 $c^2t^2 - x^2 = 1$ の上側部分と漸近線を描く(図 1)。 原点からこの双曲線の部分の任意の動径ベクトル $OA'$ を描き、双曲線の $A'$ での接線が漸近線と右 $B'$ で交わる。平行四辺形 $OA'B'C'$ を 完成させ、最後に後で使うため $B'C'$ を延ばし $x$ 軸を $D'$ で切るようにする。いまもし、$OC'$ と $OA'$ を斜めの座標値、$x', t'$ とし、その 測定を $OC'= 1, OA'= 1/c$ とすると、その双曲線の部分は、再び、表式、$c^2t'^2 - x'^2 = 1, t'>0$ を得る。$x, y, z, t$ から $x', y', z', t'$ への移行は、問題とした変換である。これらの変換に、空間と時間の任意のゼロ点の移動を付随させて、それによって変換群を構成する。 それは、また明らかにパラメタ $c$ に依存する。この群 I を $G_c$ と記述する。

もし $c$ を無限に増加させ、そしてそれゆえ $1/c$ を 0 に向かって収束させるなら、図からみて双曲線のこの部分は、さらに $x$ 軸に向かって 曲り、漸近線の角度はさらにもっと鈍角になる。そして、その極限ではこの特殊な変換は、$t'$ の軸がどの上方向を向いた軸でもよくなり、 一方、$x'$ 軸は、$x$ 軸にどこまでも正確に近付くようになる。この見かたでは $G_c$ は $c= ∞ $のときの極限で$G_∞ $ になり、それは、Newton 力学に適切な完全群に他ならないことが明らかである。 これがそうであり、一方、$G_c$ は $G_∞$ よりも数学的により明瞭であるから、それは、その考えはいくらかの数学者を打ったかもしれないが、 無邪気なものにみえた、それは、結局は、事実として、自然現象は $G_∞$ 群の不変性をもつのではなく、むしろ$G_c$ の群をもつのである。 なぜなら、$c$ は有限で確定的だが、普通の測定単位では、極端に大きいからという考え。そのような予感は、純粋数学にとっての極端な勝利 であったかもしれない。確かに、数学は、いまは途中段階の知恵を示すだけにも関わらず、事後の賢明さの満足をもち、遠い地平への妨害な き視野によって感覚の鋭い幸せな先行者のお陰で、我々の自然の概念のそのような変態の、遠い帰結を即座に把握することができたのである。
私は、同時に我々が最終的に扱う $c$ の値について述べる。それは空の空間(真空)中の光の伝播速度である。空間であることと空であることを 両方いうのを避けるために、我々はこの量を別の方法で定義できる。電気学の電磁気単位と静電気単位との比であるとして。
群 G_c に関連する自然法則の不変量の存在は、そのときこの方法で取られなくてはならない:ー
自然現象の全体性から、逐次に増強された近似によってさらにさらに正確に $x, y, z, t$ の参照系を導くことが可能である。空間と時間は、 それを手段としてこれらの現象は、確定した法則に合致して、それら自身を表示する。しかし、これがなされるとき、この参照系は、現象 によって決して一意に決定されない。 自然法則の表現を変化させずに、$G_c$ 群の変換を満足する参照系に何らかの変化をすることはまだ可能である。
例えば、上述した図に対応して我々は、時間 $t'$ を示すことができる。しかし、そのとき必然的にそれに伴い、3 つのパラメタ $x', y, z$ の 座標による空間を定義しないといけない。その場合、$x, y, z, t$ によるのと正確に同じ方法で $x', y, z, t'$ で物理法則が表現される必要が ある。そのとき我々は、もはや空間でなく、3 次元空間のなかの無数の平面のアナロジーで、無数の空間を持つべきである。3 次元幾何は 4 次元物理の章になる。なぜ私が最初に、空間と時間とは影に消え去り、ひとつの世界だけがそれ自身存続するだろうといったかを、いま読者は 知るのである。
いま問いは、我々に空間と時間の概念のこの変更を強いる環境とは何か?である。それは実際に経験に反論されないのか?そして、最終的に 現象を記述するのに有利なのか?
これらの質問に進む前に、私は重要な注意をしなければならない。もし我々が、何れにしても、個別の空間と時間をもつなら、静止した実質点 に対応する世界線として、$t$ の軸にに平行な直線をもつということである;均一な運動をする実質点に対応しては、$t$ 軸にある角度をもった直線; 変化する動きの実質点に対しては、何らかの形の曲線の世界線をもつ。もし、どの世界点 $x, y, z, t$ にもその点を通る世界線をとり、上述の 双曲面の任意の動径ベクトル $OA'$ に平行なものを見つけるならば、その世界点の関係する実質を静止とするように与えられた、空間と時間の 新しい概念をもつものとして、新しい時間軸として $OA'$ を導入することができる。我々はいま、次の基本原理を導入する:ー
どの世界点にある実質もつねに、空間と時間の適切な決定を伴えば、静止と見なし得る。
その原理は、次のことを意味する。任意の世界点にある次の表式、 \[ c^2dt^2 - dx^2 - dy^2 - dz^2 \] は、つねに正の値をもつ。又は、同じことだが、どの速度 $v$ もつねに $c$ より小さいと証明される。従って、$c$ が全ての実質の速度の上限としてあり、 そしてそれは正確に、$c$ の大きさのより深い意味を明らかするだろうものである。この 2 次形式にあるその原理の第 1 印象は、全く喜ばしくない。 しかし、我々が心に留めるべきは、そのなかにこの微分の 2 次の表式の平方根が現れる力学の修正された形式は、速度が光速を超える場合が、 幾何学において虚数の座標をもつ図形のそれのような、ある役割だけを今後は果たすというその方法をいま作るであろう、ということである。
いま、群 $G_c$ を仮定することの衝撃と真の動機は、真空中の光の伝播のための微分方程式が、その群 $G_c$ をもつという事実から来ている(*)。 一方、剛体の概念は、群 $G_∞$ を満足する力学のなかにだけ意味をもつ。もし我々が、 $G_c$ を伴う光学理論をもち、そしてもし他方に剛体をもつならば、 $G_c$ と $G_∞$ に適切なふたつの双曲面によって、ひとつで同じ方向をもつ $t$ が区別されなくてはならないことを容易に示すことができる。 そして、これはさらなる帰結をもち、我々は、実験室のなかに適切な剛体の光学機器を使用することによって、地球の運動方向に対しての 方向が変化したとき、現象のなかに何らかの変化を検知することができなければならないということである。しかし、この目的に向かって 方向づけられた全ての努力、とりわけ有名な Michelson の干渉実験は、否定的結果を持ったのである。 この失敗を説明するために H.A. Lorentz は、仮説を立てた、その成功は、群 $G_c$ の光学のなかの、このまさに不変性のなかにある。 Lorentz によれば、どの運動物体も運動方向の短縮を受けなければならない。速度 $v$ をもつとき、短縮の比率は、 \[ 1: \sqrt{1 - v^2/c^2} \] この仮説は、極端に空想的に聞こえる。なぜなら、その短縮は、エーテル、又は、何かその種のもの、の中の抵抗の結果とみなすべきでもなく、 単純に上からの贈り物、ー運動の周辺への共同する環境のようであるから。私は、いま、我々の図によって、Lorentz 仮説は、空間と時間の 新しい概念と完全に同一であり、それは、実に、仮説をずっと明瞭にすることを示そう。もし単純さのために $y, z$ を無視し、1次元空間の世界 を想像するなら、平行な帯で $t$ の軸に同じく正確に上向きのものと、もうひとつは、$t$ 軸に対して傾いているもの(図 1. 参照)が、それぞれ、 静止物体と均一運動の物体との履歴が、どちらも一定の空間的長さを保つことを示している。もし、$OA'$ が 2 番目の帯に平行であるなら、 我々は $t'$ を時間として、$x'$ を空間座標として導入でき、そして、そのとき、2 番目の物体が静止を示し、最初のものが均一運動にある。 我々はいま、最初の物体を静止と見て、長さが $l$ と仮定する。すなわち、最初の帯の $x$ 軸上の交差線 $PP$ は、$l.OC$ に等しい。ここで、$OC$ は、 $x$ 軸上の物差しの単位を示す; そして他方、2 番目の帯に静止を見るとき、同じ長さ $l$ をもち、それは、2 番目の帯の $x'$ 軸に平行に計った 交差線 $Q'Q'$ が $l.OC'$ に等しいことを意味する。我々はいま、これらふたつの物体のなかに、ひとつは静止し、もうひとつは均一な運動の、 ふたつの等しいローレンツ電子のイメージをもつ。しかしもし、我々がもとの座標 $x, t$ を保持するなら、我々は、2 番目の電子の大きさとして、 その帯の $x$ 軸に平行な交差線を与えねばならない。いま、$Q'Q'= l.OC'$ から、明らかに、$QQ= l.OD'$ である。もし、2 番目の帯の $dx/dt$ が $v$ に 等しいなら、簡単な計算で、 \[ OD'= OC \sqrt{1 - v^2/c^2} \] それため、また、$PP:QQ= 1: \sqrt{1-v^2/c^2}$ である。しかし、これが運動する電子が短縮する Lorentz 仮説の意味である。もし他方、2 番目の 電子を静止と見るなら、それに伴って、$x', t'$ の参照系を採用し、最初の帯の長さは、$OC'$ に平行な交差線 $P'P'$ で表さねばならない。そして、 我々は最初の電子が2番目のそれと比べて正確に同じ比率で短縮するのを見なければならない;図のなかで、 \[ P'P':Q'Q' = OD:OC' = OD':OC = QQ:PP \] Lorentz は、$x, t$ と結合した $t'$ を、均一運動のなかの電子の "局所時間" と呼んで、短縮の仮説のよりよい理解のために、その概念の物理的 構築を申し出た。しかし、ひとつの電子の時間は、丁度他と等しいこと、いわば、$t$ と $t'$ とが対等に扱われるべきことを最初に明確に認識した 功績は、A. Einstein(+) に属する。このように、現象によって一意に決定される概念としての時間は、その高い席から初めて降ろされた。 Einstein も Lorentz も空間の概念には攻撃しなかったが、多分、その理由は、そこで $x',t'$ 平面が $x,t$ 平面と重なる、上述の特別な変換にあり、 ある解釈が、空間の $x$ 軸がその立場を保持するということを可能にするからであろう。ひとは、より高い数学の部分で別の傍若無人の行為のように 判断される対応する空間概念の違反を見付けることを期待してもよい。それにも関わらず、このさらなる段階は、群 $G_c$ の真の理解において不可欠 である。そしてそれが採られるとき、群 $G_c$ の不変性の要求への "相対性の前提" の言葉は、私にとって非常に無力に思える。なぜなら、その仮説は、 空間と時間のなかに 4次元世界だけが現象によって与えられる、しかし、空間と時間への投影は、まだある程度の自由をもつことが許される、 という意味をもつことになるからである。私はそれを、"絶対世界の仮説" (又は短く、"世界仮説") と呼ぶことを好む。
世界仮説は、4 つの座標 $x, y, z, t$ に同一の扱いを許す。この方法によって、私がいま示すように、物理法則が表される形式が明瞭 さにおいて優れて表示される。とくに加速度の概念は、明晰な特性を獲得した。
私は、幾何学的な表示の仕方を使う。もし我々が $x, y, z$ の3者のうち、z を暗黙に無視すれば、それは、すぐに心に浮かぶからである。 私は、任意の世界点 O を時空の原点にとる。頂点 O をもつ円錐、$c^2t^2 - x^2 - y^2 - z^2 = 0$ は、ふたつの部分から構成される(図 2)。 ひとつは値 $t<0$、他方は値 $t>0$ である。前者は、O の前方円錐であり、いわば、"Oに光を送る" 全ての世界点である。後者は、後方円錐 であり、"Oから光を受ける" 全ての世界点である。前方円錐で囲まれた内部だけを、O "以前"と呼んでよく、後方円錐は、O "以降" と呼ぶ ことができる。すでに議論された、次の双曲面は、O 以降 にある。 \[ F = c^2t^2 - x^2 - y^2 - z^2 = 1, t>1 \] 円錐の間の領域は、全ての一定の正の値 $k$ について、次の一枚つなぎの双曲面形、によって埋められている。 \[ - F = x^2 + y^2 + z^2 - c^2t^2 = k^2 \] 我々は、とくに、後の図にある、O を中心とする双曲面に興味がある。これら双曲面の単独部分を短く、中心 O をもつ内部双曲面と呼ばれる だろう。これらの部分のひとつは、世界線と見なすと、$t= -∞$ から $t= ∞$ までの光速 c に漸近的に立ち上がる運動を表している。
もしいま、空間中のベクトルのアナロジーで、$x, y, z, t$ の座標系のなかの方向をもつ長さをベクトルと呼ぶなら、O から面 $+F = 1, t>0$ への時間性のベクトルと、O から面 $-F = 1$ への方向をもつ空間性のベクトルとを区別しなければならない。
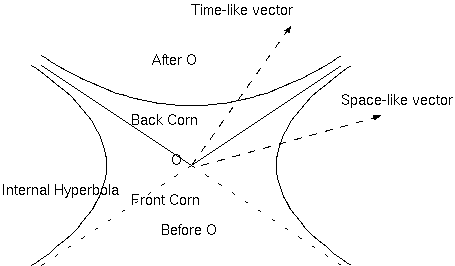
時間軸は、前者のベクトルのどれに平行に走ってもよい。前方円錐と後方円錐の間のどの世界点も座標系を配置して、Oと同時であるとする ことができ、それだけでなく、O よりこれだけ前、又は後であるとすることもできる。 O の前方円錐のなかの世界点は、必然的につねに O より以前であり; O の後方円錐のなかの世界点は、必然的につねに O より以降である。$c$を極限、$c=∞ $ に持っていくことに対応して、 完全な平坦化が起き、円錐の間のクサビ形の領域から、平面の座標面 $t= 0$ になる。図のなかでこの領域は意図的に異なった幅で描かれている。
我々は、我々の選んだ任意のベクトルを分解する。例えば、O から $x, y, z, t$ へのそれを、$x, y, z, t$ の成分にする。もし、ふたつの ベクトルの方向が、それぞれ、O から $-+F= 1$ の面のひとつへの動径ベクトル $OR$ のそれであり、もうひとつが同じ面の接線ベクトル $RS$ のそれであるとき、ベクトルは、互いに垂直という。このように、成分 $x, y, z, t $ と $x_1, y_1, z_1, t_1$ とをもつ両ベクトルが互いに 垂直である条件は、 \[ c^2 tt_1 - xx_1 - yy_1 - zz_1 = 0. \] 異なる方向のベクトルの測定のために空間性ベクトルでは、O から $-F= 1$ は、つねに大きさ 1 とし、時間性のベクトル O から $+F= 1, t>0$ では、つねに大きさは、$1/c$ に割り当てることで、物差しの単位を固定するとする。
もし、我々が実質点の世界線が世界点 $P(x, y, z, t)$ を通過することを想像するなら、その線に沿って離し置かれた時間性ベクトル $dx, dy, dz, dt$ に相当する大きさは、それゆえ、 \[ dτ= {1 \over c} \sqrt{c^2dt^2 - dx^2 - dy^2 - dz^2}. \] である。
世界線にそって採られた任意の固定の始点 P_0 から可変の終点 P までの、この量の積分、$∫dτ= τ$ を、我々は、実質点の固有時と呼ぶ。 世界線の上で、$x, y, z, t$ ーベクトル $OP$ の成分ーを、我々は、固有時$τ$の関数と見なし;$τ$に関する 1 階微分係数を $x', y' z', t'$ と $τ$ に関する 2 階微分係数を $x", y" z", t"$ と書く。そして、適切なベクトルに名前を与える。ベクトル $OP$ の $τ $ に関する導関数を速度ベクトル、 この速度ベクトルの$τ$ に関する導関数を $P$ における加速度ベクトルと呼ぶ。こうして、一方、 \[ c^2 t'^2 - x'^2 - y'^2 - z'^2 = c^2, \] から、次を得る。 \[ c^2 t't" - x'x" - y'y" -z'z" = 0, \] すなわち、速度ベクトルは、時間性の単位長ベクトルであり、P で世界線の方向をもつ。 加速度ベクトルは、速度ベクトルに垂直であり、それゆえ、つねに空間性ベクトルである。
いま見られるように、世界線上の P 点に共通する無限に近傍の 3 つの点をもつ確定的な双曲線があり、その漸近線が "前方円錐" と"後方円錐" を作りだす(図 3)。この双曲線をPの曲率の双曲線と呼ぶ。もし、M がこの双曲線の中心であれば、ここにMを中心とする内部双曲面をもつ必要が ある。$ρ$をベクトル MP の大きさとすると、そのとき我々は、P において加速度ベクトルが MP 方向をもつ大きさ、$c^2/ρ$ であることを知る。
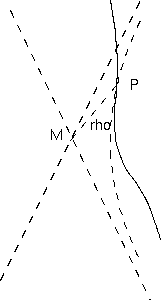
もし、$x", y", z", t"$ がすべて 0 であれば、曲率の双曲線は、世界線にPで接触する直線に還元し、我々は $ρ= ∞$ としなければならない。
物理法則への群 G_c 仮定が決して反論を導かないことが示すことは、この仮説の上に物理全体の改訂が実行されることは、避けられない。 この改訂の実行は、すでにある程度成功裡に行われた。熱力学と熱放射の問題(*)、電磁過程、そして最終的に、質量概念の維持を伴った 力学(+)においてである。
この物理の最後の分野において、次の質問を上げることは、基本的な重要性をもつ。ー空間の各軸に平行な $X, Y, Z$ の成分をもつ力が、そこの 速度ベクトルが $x', y', z'$ である座標点 $P(x, y, z, t)$ において作用する。参照系が変わるとき、我々は、何をこの力であるとすべきか? 現在、群 $G_c$ が疑いもなく認められる場合、電磁場のなかの動電力については、ある合意された言明が存在する。これらの言明は、単純な規則 に導く:ー座標系が代った場合、問題の力は、変換し、新しい空間座標のなかの力になる。$t'X, t'Y, t'Z, t'T$ の成分をもつ適切なベクトルを とるという方法によって。ここで、 \[ T= {1 \over c^2} ({x' \over t'} X + {y' \over t'} Y + {z' \over t'} Z) \] は、その世界点にその力によってなされる仕事の c で割った仕事率で、不変に残る。このベクトルは、つねに P 点の速度ベクトルに垂直である。 P 点の力に対応するこの種類の力ベクトルは、"動力ベクトル" と呼ぶべきものである。
私はいま、P を通過する一定の力学的質量 $m$ をもつ実質点の世界線を記述しよう。速度ベクトルに質量 $m$ の積は、"運動量ベクトル" と呼ぼう。 そして、加速度ベクトルと質量の積は、P点にある運動の "力ベクトル" である。これらの定義をもって、質点の運動法則と上記の動力ベクトル とは、次のようになる。:ー(**)運動の力ベクトルは、動力ベクトルに等しい。 この主張は、4つの軸に対応する成分の 4 つの方程式を満足 する。そして一方、両方のベクトルは、先験的に速度ベクトルに垂直であるから、4 番目の方程式は他の 3 式の帰結とみることができる。 上の T の重要性に従って、4 番目の方程式は、疑いもなくエネルギー法則を表している。それゆえ、運動量ベクトルの t に沿う成分は、c を 乗算されて、質点の運動エネルギーであると定義されるべきである。この表式は、 \[ mc^2 {dt \over dτ} = mc^2/\sqrt{1 - v^2/c^2}, \] すなわち、付加的な定数 $mc^2$ を引いた後、$1/c^2$ のオーダーの大きさまで Newton 力学の ${1 \over 2} mv^2$ である。どのようにエネルギーが座標系に 依存するかは、この方法で非常に明確になった。しかし、$t$ 軸は、どの時間性のベクトルの方向にも置くことができる、一方でエネルギー法則は、 全ての可能な参照系に枠組され、運動方程式の全ての系をすでに含んでいる。すでに述べた c= ∞への極限の移行において、Newton 力学の原理的 な構造の重要性をこの事実が保持し、I. R. Shütz (++)によってこの意味ですでに認識されたものである。
我々は、あらかじめ、長さと時間の単位の比を、速度の自然の限界が、c= 1 になるように決定することができる。もし、我々がそのとき、さらに、 $√-1 t= s$ を $t$ の代わりに導入すれば、微分の 2 次の表式、 \[ dτ^2= - dx^2 - dy^2 - dz^2 - ds^2 \] は、$x, y, z, s$ において完全に対称的になる; そして、この対称性は、世界仮説に反しない全ての法則に伝わる。このように、この仮説の本質は、 次の秘伝的式のなかに、非常に意味深長な仕方で数学的に包まれているのかもしれない。 \[ 3.10^5 km = \sqrt{-1} secs. \]
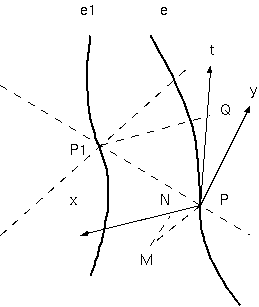
世界仮説によって与えられる利点は、Maxwell-Lorentz 理論に従ういかなる種類であっても運動する点電荷から起きる効果を示すこと によって、多分、最も衝撃的に例証される。そのような電荷 $e$ をもつ点電子の世界線を想像し、そこに任意の初期点からの固有時$τ$ を導入する。任意の世界点 $P_1$ にその電子によって引き起こされる場を見出すために、我々は、$P_1$ に属する前方円錐を構成する(図 4)。 その線の方向は、どこにおいても時間性ベクトルの方向であるから。円錐は明らかに単独点 $P$ において世界線に出会う。我々は、 $P$ 点での世界線の接線を引き、$P_1$ を通るこの接線への垂線 $P_1 Q$ を構成し、その長さを $r$ とする。そのとき、前方円錐の定義によって、 $PQ$ の長さは、$r/c$ でなければならない。いま、$PQ$ の方向をもち、大きさ $e/r$ のベクトルが、$x, y, z$ の軸に沿う成分によって表わすものが、 $c$ 倍したベクトルポテンシャルである。そして、$t$ の軸に沿う成分が、$e$ によって世界点 $P$ に賦活された場のスカラーポテンシャルである。 このなかに、A. Liénard と E. Wiechrt によって定式化された基本的法則がある(*)。
そのとき、その電子によって作りだされる場の記述のなかに、我々は、その場の電気的と磁気的力への分離が、基礎にする時間軸に関して 相対的なものであることをみる;ふたつの力を一緒に記述する最も洞察的な方法は、力学のねじりとのあるアナロジーにあるものである。 アナロジーは完全ではないが。
私は、動く点電荷の別の動く点電荷への動電力の作用を記述する。世界点 $P_1$ を通過する電荷 $e_1$ の2番目の点電子の世界線を想像しよう。 我々は、$P, Q, r$ を前と同様に定義し、$P$ の曲率の双曲線の中心 $M$ を構成し(図 4)、そして最終的に、$M$ から、$P$ を通り、$Q P_1$ に平行な 想像される直線への垂線 MN を構成する。$P$ を始点として、座標系を次のように決定する:ー $t$ の軸を $PQ$ の向きに、$x$ の軸を $Q P_1$ の 向きに、$y$ の軸は $MN$ 方向に、そこで最後に $z$ の軸の方向を $t, x, y$ の軸に垂直にする。 $P$ における加速度ベクトルを $x", y", z", t"$ とし、 $P_1$ における速度ベクトルを $x'_1, y'_1, z'_1, t'_1$ としよう。 最初の動く電子 $e$ から 2 番目の動く電子 $e_1$ への $P_1$ に 働く動力ベクトルは、いま、次の式を取る。 \[ - ee_1 (t'_1 - {x'_1 \over c})R, \] ここで、ベクトル ${\bf R}$ の成分 $R_x, R_y, R_z, R_t$ は、次の 3 つの関係式を満たす。 \[ c R_t - R_x = {1 \over r^2}, R_y= {y" \over c^2r}, R_z = 0, \]
そして、ここで、4 番目に、このベクトル $R$ が $P_1$ の速度ベクトルに垂直であり、この状況を通して、後者の速度ベクトルから独立である。
我々は、この言明を以前にされた、ひとつが他の動く点電荷に作用する動電力の同じ基本的な法則の定式化(*)と比較するとき、我々は、ここで 取られた考慮される関係が、全くの単純にある内部存在を明らかにしているものが、4 次元のなかだけであること、そして、我々がその上に いることが強制される 3 次元空間へは、それらは非常に複雑な投影だけを投げていることを受け入れざるを得ない。
世界仮説に従って改革されるときの力学のなかにあって、Newton 力学と現代の電磁力学との間の調和の憂慮すべき欠如は、それ自身の調和 のなかに消え去る。結論の前に Newton の引力の法則のこの仮説への態度について少し触れたい。私は、次を仮定する、ふたつの質点 $m, m_1$ が世界線を描くとき、$m$ による動力ベクトルが $m_1$ に働く。その正確に同じ形式で、電子のとき与えられたものと、違うのは、$-e e_1$ が $+m m_1$ に置き換わらなければならないだけである。我々はいま、特別に考慮するのは、$m$ の加速度ベクトルが一定のゼロである場合である。 そのとき、$m$ が静止であるして、$m_1$ だけが $m$ から与えられた動力ベクトルの下に運動する、そのような方法で $t$ を導入しよう。 もし、我々がいま、この与えられたベクトルに第1段階として $t'^{-1} = \sqrt{1 - v^2/c^2}$ の要素を付加することによって、それは、$1/c^2$ の オーダーまで、1 に等しいとすることで、次のことが見て取れる(++)。$m_1$ の位置、$x_1, y_1, z_1$ にとって、そしてそれらの時間変化にとって、 我々が正確に Kepler の法則に再び到着しなければならないのである。但し、$m_1$ の固有時$τ_1$ を時間 $t_1$ の代わりにする以外はである。 この単純な所見から、次のことも見て取れるであろう。提案された引力法則が新しい力学と結合して、天体の観測を説明するのにおいて、 Newton の引力法則が Newton 力学と結合したよりも、よく適合しないことはないことを。
重さのある物体のなかの電磁過程の基本的方程式もまた、世界仮説と完全に適合する。私が別の所で示すように、電気の理論の概念からこれら 基本的な方程式を導出を放棄することは、公平でなくいずれにしても必要でない。Lorentz によって教えられ、それらを世界仮説に適合させる ためにしたように。
世界仮説の例外のない有効性は、私は思いたい、世界の電磁的イメージの真の核である。それは Lorentz によって発見され、さらに Einstein によって明らかにされ、いま昼の光の下に完全に開いた。その数学的な帰結の開発のなかに仮説の実験検証への十分な示唆があるだろう。それは、 純粋数学と物理の間の未確立な調和の概念よって、古く確立した見かたの放棄が無情で苦痛である者にとってさえ十分な慰めになるであろう。