最初の一歩の前進は、光源の位置の(負の)重力ポテンシャルによるスペクトル線の赤方偏移の存在の結論的な表示である (p.92を見よ)。この実証は、その平均密度が水の 10^4 倍のオーダーを超える、いわゆる "矮星" の発見によって可能になった。そのような星 (例えば、シリウスの暗い伴星) では、質量と半径とが決定でき(*)、この 赤方偏移は、理論によって太陽での約 20 倍の大きさと期待され、そして実際に期待された範囲にあることが実証された。
次の一歩の前進は、短く言及するが、重力物体の運動法則に関係する。理論の初期の定式化のなかでは、重力を受ける粒子の 運動法則は、重力場の方程式に追加する独立の基本的な仮定として導入されたー式 90 をみよ、それは、重力粒子が測地線を 運動することを主張する。これは、ガリレオの慣性法則の "本物" の重力場が存在する場合への仮説の移行を構成する。 任意の大きな重力的質量の場合に一般化された、この運動法則は、空の空間の場の方程式だけから導くことができることが示された。 この導出に従えば、運動法則は、場がそれを発生する質点の外側のどこにも特異性のない条件を含められることになる。
3番目の歩みは、いわゆる "宇宙論的問題" に関係し、ここで詳細に考察されるだろう。ひとつには、その基本的重要性からであり、 部分的にはまた、これらの質問の議論が決して終結しないからである。また、現在のこの問題の扱いのなかには、最も重要な基本的 な視点が十分に強調されていないとの印象を私が逃れられない事実によって、私は、より正確な議論の必要を緊急に感じるのである。
その問題は、次のように大まかに形式化できる:恒星に対する我々の観測のおかげで我々は十分に次のことを確信している。すなわち、 恒星の系は、無限の空の空間に浮かぶ島に類似してあるものではなく、存在する質量の全体量の重力中心のようなものが存在するもので もない。むしろ、我々は次のことを確信する必要を緊急に感ずる。空間にある物質の平均密度が存在し、それがゼロではないことである。
それゆえ、問いはもち挙がる:この仮説、経験から示唆される仮説は、一般相対論とどのように和解するのか?
上記の条件は、その問題を確定的なものにするには、決して十分ではない。最も単純かつ最も根本的な特殊化は、次の条件であろう: (自然に測定された)物質の密度$ρ$は、(4 次元的)空間のどこでも同じである。計量は、適切な座標選択によって、$x_4$ に独立で、 $x_1, x_2, x_3$ に関しては、一様であり等方である。
私が最初に最も自然な理想化された大規模な物理空間の記述であると考えたのはこの場合である;それはこの本の 103 -108ページに扱われている。この解への反論は、負の圧力の導入が必要であることであり、それには物理的正当性が存在しない。 その解を可能にするために、私は、独自に方程式に新しい項を導入し、上述の圧力の代わりにした。それは相対性の視点からは許されるものである。 重力の方程式は、こうして拡張された: \[ (R_{ik} - {1 \over 2} g_{ik} R) + Λ g_{ik} + κ T_{ik} = 0 \tag{1} \]
ここで、$Λ$は、宇宙的な定数("宇宙論的定数") である。この第2番目の項の導入は、理論の複雑さを構成し、論理的な単純さを深刻に減損する。 その導入は、ほとんど避けられない物質の有限の平均密度の導入によって作られる困難によってだけ正当化できる。 いずれにしても、我々が注目できるのは、ニュートン理論にも同じ困難があることである。
数学者フリードマンは、このディレンマ(*)を逃れる方法を見出した。彼の結果は、その後、ハッブルによる星系の膨張(距離に伴って均一に増大する スペクトル線の赤方偏移)という驚くべき確認を見出すに至った。次下は、本質的に、フリードマンのアイデアの表出以外の何ものでもない:
我々は、いま、宇宙が空間的にいって、どこでも等方的である状態に数学的な形式を見出さなくてはならない。(4次元的)空間の 全ての点 P を通して粒子のある経路が存在する (それは以降、短く "測地線" と呼ばれるだろう)。 P と Q をそのような測地線の無限に近いふたつの点としよう。我々は、そのとき、場の表式が P と Q とを固定する任意の座標系の回転に 関して不変であることを要求しなければならない。これは、どの測地線のどの要素についても有効であるだろう(*)。
上の不変の条件は、測地線全体が回転軸上にあることと座標系の回転にその2点が不変に残ることを意味する。これは、測地線の3重の無限の 周りの全ての座標系回転に関して解が不変であることを意味する。
簡潔さのために、この問題の解の演繹的な導出に私は立ち入らない。しかしながら、直感的に明らかであるのは、3次元空間にとって、 線の2重の無限の周りの回転のもとに不変である計量は、本質的に (適切な座標選択によって) 中心対称の型のものであろう。 そこでの回転軸は、動径の直線であり、その対称性の理由は測地線である。一定半径の表面は、そのとき、一定の(正の)曲率の表面であり、 それは、どこでも(動径の)測地線に垂直である。こうして我々は、不変の言語によって次を得る:
測地線に直交する表面の類が存在し、これらの表面のそれぞれは、一定の曲率の表面である。これら測地線の類のどのふたつの表面の間に 含まれる切片も等しい。
注意 このように直感的に得られた場合、類の表面が一定の負の又はユークリッド的(ゼロ曲率)であり得る限り、それは一般的なものでない。
我々が興味のある 4 次元の場合も、全く類似している。さらには、計量空間の慣性の添字が 1 であるとき、本質的な違いは存在しない; 唯一の違いは、時間性として、動径方向を選ばなくてはならないこと、それに対応して、類の表面内の方向は、空間性であることである。 全ての点の局所の光円錐の軸は、動径線上にある。
その上の $x_1, x_2, x_3$ が一定で $x_4$ だけが可変である時間性の線として、我々は、粒子の測地線を、中心対称の形態のなかで中心を通 る直線に選ぶ。$x_4$ を、さらに、中心からの計量距離に等しいとしよう。そのような座標のなかで、計量は次の形式をとる: \[ ds^2= dx_4^2 - dσ^2\\ dσ^2= γ_{ik} dx_i dx_k (i,k= 1,2,3) \tag{2} \] $dσ^2$ は、球状超平面のひとつの上の計量である。異なる超平面に属する$γ_{ik}$ は、そのとき、(中心対称性から)全ての超平面の上で、 $x_4$ だけに依存する正の係数以外は、同じ形式をとるだろう: \[ γ_{ik} = γ0_{ik} G^2 \tag{2a} \] ここで、$γ0$ は、$x_1, x_2, x_3$ にだけ依存し、$G$ は $x_4$ だけの関数である。そのとき、我々は次をもつ: \[ dσ0^2= γ0_{ik} dx_i dx_k (i,k= 1,2,3) \tag{2b} \] は、3次元のなかで正の曲率の確定した計量であり、全ての $G$ において同じである。
そのような計量は、次の方程式で特徴付けられる: \[ R0_{iklm} - B(γ0_{il} γ0_{km} - γ0_{im} γ0_{kl})= 0 \tag{2c} \] 我々は、座標系 ($x_1, x_2, x_3$) を線要素が同形的にユークリッド的になるように選ぶことができる: \[ dσ0^2= A^2(dx_1^2 + dx_2^2 + dx_3^2) すなわち、γ0_{ik}= A^2 δ_{ik} \tag{2d} \]
ここで、$A$ は、$r (r^2= x_1^2 + x_2^2 + x_3^2)$ だけの正の関数。方程式に代入して、我々は、$A$ に次のふたつの方程式を得る。 \[ -{1 \over r} ({A' \over Ar})' + ({A' \over Ar})^2 = 0\\ -{2A' \over Ar} - ({A' \over A})^2 - B A^2 = 0 \tag{3} \]
最初の式は、次によって満足し: \[ A= {c_1 \over c_2 + c_3 r^2} \tag{3a} \] ここで、定数は、さしあたり任意である。
$c$>0 (球状空間)
$c$<0 (擬球状空間)
$c$=0 (ユークリッド空間)
座標の相似変換($x_i' = a x_i $ここで、$a$ は定数)によって、我々はさらに、最初の場合に $c= {1 \over 4}$, 第2の場合に $c= -{1 \over 4}$ を得る。
3つの場合それぞれに、我々は次を得る: \[ A = {1 \over 1 + {r^2 \over 4}}; B= +1,\\ A = {1 \over 1 - {r^2 \over 4}}; B= -1,\\ A = 1; B= 0 \tag{3d} \] 球状の場合、単位空間($G=1$)の "円周" は、$∫_{-∞}^{+∞} {dr \over 1 + {r^2 \over 4}}= 2π $であり、単位空間の "半径"は、1 である。 3 つ全ての場合で時間の関数 $G$ は、2質点間の (空間断面で測った) 距離の時間変化の尺度である。 球状の場合、$G$ は、時間 $x_4$ の空間の半径である。
要約 我々の理想的な宇宙の空間等方性の仮説は、次の計量を導く: \[ ds^2= dx_4^2 - G^2A^2(dx_1^2 + dx_2^2 + dx_3^2) \tag{2} \] ここで、$G$ は、$x_4$ だけ、$A$ は、$r (r^2 = x_1^2 + x_2^2 + x_3^2)$ だけに依存する。ここで、 \[ A= {1 \over 1 + {ζ \over 4} r^2} \tag{3} \] そして、場合の違いは、それぞれ $ζ= 1, ζ= -1, ζ= 0$ によって特徴付けられる。
だけが 0 でない成分である。添字を下に下げて、$T_{ik}$ の唯一の非消滅の成分は、 \[ T_{44}= ρ \tag{4d} \] これを考慮して、場の方程式は、次になる: \[ {ζ \over G^2} + {G'^2 \over G^2} + 2 {G'' \over G} = 0\\ {ζ \over G^2} + {G'^2 \over G^2} - {1 \over 3} κρ=\\ \tag{5} \] ${ζ \over G^2}$ は、空間断面$ x_4 = const$ の曲率である。$G$ は、どの場合も、時間の関数であるふたつの物質粒子の計量距離の相対的尺度。 ${G' \over G}$ は、ハッブル膨張を表す。$A$ が式から抜け落ちる。要求される対称性の型の重力の方程式の解があるべきため、そうでなければならない。 両式を引算し、我々は次を得る。 \[ {G'' \over G} + {1 \over 6} κρ= 0 \tag{5a} \] 一方、$G$ と$ρ$は、どこでも正でなければならないから、$G''$ は、$ρ$が消滅しない場合、どこでも負である。$G(x_4)$は、このように、 最小値も、変曲点も、持ち得ない;さらに、$G$ が定数という解は、存在しない。
この値は、大きさのオーダーにおいて、天文学者の推定(質量と可視恒星、恒星系の視差を基にしている)と何かの一致をもつ。 私は、ここに例として、G. C. マックビティー(McVittie) を引用する。(Proceedings of the Physical Society of London, vol. 51, 1939, p. 537) "平均密度は、確かに $10^{-27}$ g/cm$^3$ より大きくなく、そして、より確からしいのは $10^{-29}$g/cm$^3$ のオーダーである。"
この大きさの決定の非常な困難さのために、私はこれをさしあたりの満足な一致と考える。一方、量 $h$ は、$ρ$ より正確に決定されるから、 観測できる空間の構造の決定が $ρ$ のより正確な決定と連携されるという主張は、多分、誇張はない。なぜなら、(5) の第2式のために、 空間曲率は、一般の場合、次式で与えられるからである:
我々が空間曲率を無視する場合、(5b)の第1式は、$x_4$ の初期値の適切な選択の後、次式となる。 \[ h= {2 \over 3}・{1 \over x_4} \tag{6} \] この式は、$x_4= 0$ に特異性がある。そのため、そのような空間が負の膨張をもち、時間が $x_4= 0$ の上に制限されるか、又は、 それが正の膨張をもち、$x_4= 0$ から存在を開始するかである。後者の場合が我々が自然のなかに実感を見出すものと一致する。
測定された $h$ の値から、我々は、世界の今までの存在の時間 $1.5・10^9$ 年を得る。この年齢は、地球の地殻についてのウラニュウム の崩壊から得たものとほぼ同程度である。これは、パラドックス的な結果であり、それによって理論の有効性に疑いを起こす、ひとつ の理由以上のものである。
次のような問いが起きる:現在の困難は、現実的には無視できる空間曲率という仮定のもとに起きたものである。 それは、適切な空間曲率の導入によって除去できるのだろうか? ここに、 $G$ の時間依存を決定する (5)の最初の式が使用されるであろう。
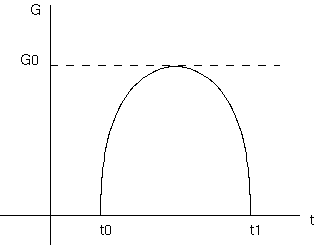
$G$ は、$0 ≦ G ≦ G_0$ の区間に残る。$G$ は、次のようなスケッチによって、量的に与えられる:

半径 $G$ は、0 から $G_0$ まで立上り、そして再び連続的に 0 に落ちる。空間断面は、有限 (球状) である。 \[ {1 \over 3} κρ - h^2 >0 \tag{5c} \] (b) 負の曲率をもつ空間 \[ ({dG \over dt})^2 = {G_0 + G \over G}. \tag{5h} \] $G$ は、$t$ に伴い $G= 0$ から $G= +∞$ まで増加する (又は、$G= ∞$ から $G= 0$ まで行く)。このゆえに、${dG \over dt}$ は、単調に $+∞$から1まで、次のスケッチに描かれたように減少する:
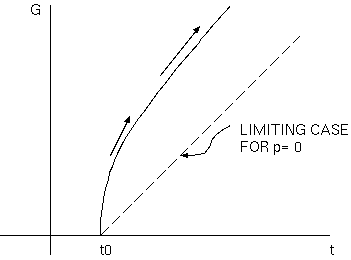
これは、そのとき、収縮なしの連続的な膨張の場合である。空間断面は無限であり、我々は次をもつ。 \[ {1 \over 3} κρ - h^2 <0 \tag{5c} \] (訳注: (c) 曲率のない空間)
平坦な空間断面の場合、以前の章で扱われた、ふたつの場合の間に位置し、次の式に従う: \[ ({dG \over dt})^2 = {G_0 \over G}. \tag{5h} \]
この非消滅曲率の場合の研究の結果は、次のことを結果としてもたらす。すべての非消滅("空間")曲率には、消滅曲率の場合と同じく、 そこで膨張の始まった $G=0$ である初期状態が存在する。このゆえに、これは、そこでは密度は無限であり、場は特異である、断面である。 そのような、新しい特異性の導入は、それ自身、問題と思える(*)。
さらには、空間曲率の導入による膨張の開始からの時間間隔への影響と、固定値 $h= {G' \over G}$ への低下は、大きさのオーダーにおいて無視 できることが明らかになった。この時間間隔は、(5h) から初等的計算によって得られるが、我々はここでそれを省略する。 我々は自身を、ρ消滅の膨張空間の考察に制限しよう。これは、前述のように、負の空間曲率の特別な場合である。(5) の2番目の式は、 次をもたらす(最初の項の符号の反転を考慮して)。 \[ G'= 1 \] このゆえ、($x_4$ の適切な初期点によって) \[ \begin{align} G&= x_4 \\ h= {G' \over G} &= {1 \over x_4} ... \end{align} \tag{6a} \] こうして、この極端な場合も、膨張の継続期間において空間曲率の消滅する場合(式(6)をみよ)と係数が1である以外、 同じ大きさのオーダーの結果をもたらす。
式 (6) に関連して言及した疑い、すなわち、現在観測できる星と星系の開発に、これがそのような驚くべき短い継続時間を与えることは、 それゆえ、空間曲率の導入によって除かれない。
人は、例えば、その粒子が互いに静止した塵から、ガスの分子のように互いに相対的なランダム運動をする粒子の塵に、置き換える ことができるだろう。そのような物質は、断熱的な圧縮に抵抗をするだろう。それはその圧縮に伴って増加するだろう。 これが無限の圧縮の生起を妨げることができるのではないだろうか? 我々は、次に、そのような物質の記述の変更が上の解の主要な性質を、何も変化させることができないことを示す。
この式に関連し、我々は、ローレンツ系の時間軸を選び、$T^{14}= T^{24}= T^{34}= 0$ とすることができる。さらに、系の空間回転によって、 $T^{12}= T^{23}= T^{31}= 0$ とし、さらに、粒子ガスを等方的にすることができる。これは、$T^{11}= T^{22}= T^{33} = p$ を意味する。これは、 $T^{44}= u$ と同様に不変量である。次の不変量: \[ J= T^{uv} g_{uv} = T^{44} - (T^{11} + T^{22} + T^{33}) = u - 3p \tag{7b} \] は、このように $u, p$ によって表現される。
$T^{uv}$ の表式から、$T^{11}, T^{22}, T^{33}$ そして $T^{44}$ は、全て正であることが出る; それゆえ、同じことが $T_{11}, T_{22}, T_{33}$ そして $T_{44}$ にも真である。
重力方程式は、いま、次になる: \[ 1 + 2GG'' + G'^2 + κT_{11} = 0 \\ -3G^-2(1 + G'^2) + κT_{44} = 0 \tag{8} \] 最初の式から、ここにもまた ($T_{11}>0$から)、$G''$がつねに負である。そこでは、$T_{11}$ 項は、$G$ と $G'$ が与えられたとき、$G''$ を減少させる ことしかできない。
このことから、質点のランダムな相対運動の考慮は、我々の結果を基本的に変化させない。
(2) 宇宙への空間的 "等方性" の要求だけがフリードマンの形式を導いている。それは、それゆえ、疑いもなく一般的な形式であり、 宇宙論的問題に適している。
(3) 空間曲率の影響を無視して、人は平均密度とハッブル膨張の関係を得る。大きさのオーダーについて、経験的に確認される。
人はさらに、膨張の開始から現在までの時間について $10^9$ 年の大きさのオーダーの値を得る。この短い時間は、恒星の発展の 理論のそれと一致しない。
(4) 後者の結果は、空間曲率の導入によっても変化しない; 星と星系の互いのランダム運動の考慮によっても、それは変化しない。
(5) スペクトル線のハッブルの偏移をドップラー効果以外の方法による説明を幾人が試みている。しかしながら、既知の物理的事実 のなかに、そのような概念の支持はない。そのような仮説に従えば、ふたつの星、$S_1, S_2$ を剛体棒で結合することができる。もし その棒に沿った光の波長の数が、時間に伴ってこの方法で変化すべきならば、単色の光を $S_1$ から $S_2$ へ送り、そして反射して $S_2$ に戻すと、異なる周波数($S_1$ の時計で測定して) で到着できることになる。これは、局所で測定される光速が時間に依存することを意味し、 それは、特殊相対論にさえ反することになる。(訳注1) さらに、$S_1$ と $S_2$ の間を行き来する光信号は、"時計" を構成することになるが、 $S_1$ にある時計(例えば原子)と一定の関係にないことを注意すべきである。これは、相対性の意味での計量が存在しないことを意味する。 これは、相対性がもたらした全てのそれらの関係の理解を失うことを意味するだけでなく、それは、また、ある種の原子的形態は "相似" に関係するものではなく、"合同" に関係しているという事実に一致しない (鋭いスペクトル線、等)(訳注2)。
上記の考察は、しかしながら、波の理論に基づいており、そして、いくらかの上記の仮説の支持者は、光の伸びの過程を全体として波の 理論に従ってでなく、コンプトン効果に類似する仕方にあると想像している。散乱なしのそのような過程を仮定することは、我々の現在 の知識の視点からは正当化できない仮説を構成する(訳注3)。それはまた、元の周波数から相対的な周波数シフトの独立性の理由付けも 失敗する。このゆえに、人は、ハッブルの発見を星系の膨張と考える以外ないのである。
(訳注1) すでに一般相対論は、特殊の結論をいくつか克服した。例えば、同じ系のなかの異なる場所の時計の時計の進行は自由になった。
$S_1$と$S_2$を往復する光による局所の時計が "$S_1$ にある原子時計と一定の関係にない" というのは理由のない憶測であり、局所の時計の進行
は一致するだろうから、それは、"相対性の意味での計量" を否定しない。さらに、同じ系のなかの異なる時間の時計の進行は自由であろう。
特殊相対論でも、時計を移動させるとき、時計の速度に合わせて時計の進行は変化するだろう。計量の時間係数 $g_{44}$ の時間的変動があれば、
"局所で測定される光速が時間に依存し、特殊相対論にさえ反する" ことになるが、それを理由にして否定することはできないと思われる。
(訳注2) フリードマン宇宙の計量は、$g_ii (i=1,2,3)$ の時間的変動だから、"合同"でなく、"相似" に関係するようである。
(訳注3) コンプトン散乱は、散乱角が 0 のとき、電磁波の波長の変化を見ない。$Δλ= λ(1-cosΘ)$。もし、$Θ= 0$ で $Δλ $が少しでも
あれば、光は、荷電粒子に正面衝突するときもエネルギーを低下することになる。
理論的疑いは、膨張の始まりの時に、計量が特異に、密度ρが無限になるという事実に基づいている。これに関連して次を注意すべきである: 現在の相対論は、物理的現実を計量場(重力)を一方とし電磁場と物質を他方にする分割に基にする。現実には空間は、恐らく均一の性質をもち、 現在の理論は、制限された場合にだけ有効なのであろう。場と物質の大きな密度の場合、場の方程式とそれらに入る場の変数さえも現実の意味を もたないであろう。人はそれゆえ、場と物質の非常な高密度には方程式の有効性を仮定してはならず、人は "膨張の始まり" が数学的な特異性を 意味しなければならないと結論してはならない。我々が認識すべき全ては、方程式がそのような領域まで連続してはならないことである。
この考察は、しかしながら、"世界の始まり" が、現存する星と星系の発展の視点から、それらの星と星系がまだ個別の実体として存在しなかった、 始まりを現実に構成するという事実を変えるものではない。
(7) しかしながら、理論に要求される動的な空間の概念を有利にする、いくらかの実証的な議論がある。その比較的高速な崩壊にも関わらず、 そして、ウラニウムの創成の不可能性が認識できるという事実にも関わらず、どうしてウラニウムは、まだ存在するのか? なぜ、空間は、夜の空を 白熱する表面にみえさせるだけの放射に満たされないのか? これは、現在まで静的な世界の視点からは満足な解答を見出せない古い問いである。 しかし、この型の問いに立ち入ることは、議論を余りの遠くへ導いていく。
(8) 与えられた理由により、我々は、その短い "人生" にも関わらず、膨張宇宙を真面目に受け取らなければならないように見える。 もし、人がそうしたとき、主要な問いは、空間が正又は負の空間曲率をもつかどうかになる。これに対して我々は、次の注意を付け加える。
実証的観点からは、判断は煮詰まって、表式 ${1 \over 3} κρ - h^2$ が正(球状の場合) か負(擬球状の場合) かの問いになる。これは、最重要の問いと 私にはみえる。実証的な判断が、現在の天文学の状態において、不可能とは見えない。$h$ (ハッブル膨張) は、比較的よく知られている一方、 全ては、可能な限り高い正確さをもつ$ρ$の決定に懸かっている。
世界が球状であるという証明が与えられることは想像可能である(それが擬球状であると人が証明できることは、想像しにくい)。これは、 人がつねに$ρ$の上限でなく下限を与えることができるという事実による。これは、天文学的に観測できない(非放射の)質量が$ρ$のどれだけの 比率を占めるかについて、我々がほとんど意見形成できないためである。これを私は、いくらか、さらに詳細に議論したい。
我々は、多くの個別の星を含み、十分な精度で静止した系であるとみなせる天文学的な物体、例えば、((年周)視差が知られた)球状星団を 考察する。スペクトルから観測できる速度から人は重力の場を(蓋然的仮定の下に)決め、それによって、この場を発生する質量を決めること ができる。そうして計算された質量と星団の可視星のそれを比較でき、それらの重力を発生する質量が星団の可視星の質量をどれだけ 超えているかの少なくとも粗い近似を見出すことができる。人は、こうして特定の星団について ${ρ_d \over ρ_s}$ の推定を得ることができる。
一方、非放射星は、平均的に放射星より小さいから、それらは、星団の星との相互作用によって、平均的に大きな速度をもつ傾向がある。 こうして、それらは、大きな星よりも、星団からより速く"蒸発"するだろう。そのため、小さな天体の相対頻度は、星団内部ではその外部 と比較して小さいであろうと期待できる。人は、それゆえ、$({ρ_d \over ρ_s})_k$ (上記の星団の密度の関係)のなかに、空間全体の ${ρ_d\over ρ_s }$ の下限を得ることができる。人はそれゆえ、空間の質量の全体平均密度の下限を次によって得る。 \[ ρ_s[1+({ρ_d \over ρ_s})_k] \] もし、この量が ${3h^2\over κ}$ より大きければ、人は空間が球状の性質をもつと結論できる。他方、私は、合理的に信頼できる$ρ$の上限決定を 考えることができない。
(9) 最後に重要なこと:宇宙の年齢は、ここで使われた意味で、放射性鉱物から見出された地球の堅い地殻の年齢を確かに超えなければならない。 これら鉱物による年齢の決定は、あらゆる側面で信頼できるから、ここで提示した宇宙論的理論が、もし、それらの結果に何か反論を見出すなら、 それは、反証されたのである。この場合、私は、何も合理的な解を見ない。