慣性系では物体が円運動するには、中心からその物体を引く力、向心力が必要である。これは、ニュートン力学の惑星運動では "現実" の力、重力、万有引力である。振り回すひもが物体を引く(作用)とき、物体からひもを引く慣性力(*)(反作用)を伴う。 慣性力は、質量が加速度をもつために必要な力である。この現象を回転系からみると、向心力はそのままあり、物体は回転系に静 止しているので、向心力とつり合う遠心力が必要になる。遠心力は、系の回転から生じる "みかけ" の力である。回転系では自由 物体は、初め静止していても遠心力の加速を受けて、中心から離れる遠心方向の運動を始めるが、それは慣性系からみると等速直 線運動のままである。遠心力は、物体の静止/運動によらずに受ける。コリオリの力は、日常生活ではあまり意識されないが、速度 をもつ物体が回転系内で受ける力である。物体の速度と系の回転とに比例して、速度と回転軸との両者に垂直な方向に力を受ける。 コリオリの力も回転系による "みかけ" の力である。
遠心力は、局所的には軸に向う加速系で受ける力に似ている。その加速系は、局所的には遠心方向の加速度を与える場を与える。 遠心力の原因は、回転系内の静止点が慣性系から見た回転の中心に向う加速度である。回転系はその符号反転した加速度を与え る場をみせる。回転系と加速系との違いは、回転系の各点が局所的にも回転していることである。場所に依らない局所的な回転 がコリオリ力を生んでいる。遠心力の大きさは、場所に依存し、中心軸からの距離に比例するが、コリオリ力は、場所によらない。 さらに、遠心力の大きさは、回転系の角速度の2乗(w^2)に比例するが、コリオリ力は、角速度の1乗(w)に比例するという違いも ある。両者は、このように違った性質をもっている。
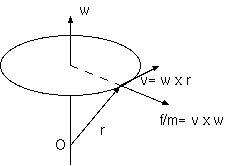
回転は軸をもち、軸の方向と回転の大きさを示す角速度ベクトルで表される。回転系は、回転軸が通る点を始点とするベクトル w によって表現される。w を軸にして回転する系の性質は、w 方向には一様であり、軸からの距離だけによる軸対称性をもつ。軸上に原 点 O をとり、回転系内静止点の原点からの位置ベクトルを r とすると、慣性系からみたその点の速度は、v= w x r である。(原点の w 座標は外積 w x r によって関係しなくなる。) そのとき遠心力場は、F/m= v x w であり、慣性系からみた回転系内点の加速度 w x v の符号反転である(下図参照)。速度 V の w 成分に w x V は関係せず、遠心力は軸から外に向き、コリオリの力は、回転面内にある。

(*) 物体が加速度をもつための慣性力を仮定して、動力学につり合いを見る方法。慣性系からみて円運動する物体にはひもからの向心 力と慣性力がつり合っている。これを仮定しなければ、バランスの崩れた力が加速度を生むというだけである。円運動に同期する回転 系からみると、この慣性力に対応する遠心力が存在して、向心力とつり合って静止している。
この説明を聞いて、何かおかしく感じる人が大半だろう。ひとつは、"遠心力は運動によらず V= -v も V= v も同じ大きさの外側向き の力 v x w を与える" ということだろう。"回転系上で逆向きに走る乗員は、回転を減らしているのに遠心力が増えると考えるのか。 回転系上で回転を増やすのと減らすのに片方は遠心力が増えるのよいとして、もう一方は減るのではないか"、ということだろう。 これは、つねに慣性系だけから見る習慣で、w が増えれば遠心力が増え、w が減れば遠心力は減る。遠心力は rw^2 に比例する。そう いう見方が一番分かりやすく思うからだろうが、こういう意見が多いと思う。もうひとつは、ディスカバリー号のデッキの回転と逆向 きにジョギングする乗員が浮遊するのにコリオリの力と遠心力がつり合わないがそれでよいのか、という疑問だろう。コリオリの力の 大きさは、測定されてきたから、その大きさを疑うことをせず、2V x w とすると、もとの遠心力の2倍だから、明らかにつり合わない。 浮遊でなく内側に落ち込む強さである。この宇宙のコリオリの力の大きさが2倍に狂っていて、本当は V x w でちょうどつり合って乗 員は浮遊するのではないかとすると、それなら遠心力はどうなったのかである。いや遠心力はすでに無くなっているではないかとも思う。 こんな半端な思考ではこの宇宙に住むことはできない。回転と同じ方向に走行する乗員は、どうやって4倍の遠心力を得るのか。回転 速度が2倍だから遠心力は4倍、これは答えであって、それにどう到達するかである。コリオリの力を使って、4倍の遠心力と浮遊乗員と を説明しなければならない。
半径 10m 程度 (9.8m)の円筒の側面を床にすると、遠心力が地上の重力加速度 1g = 9.8 m/sec^2 と等しい人工重力を与える回転は、 rw^2= 9.8 から w= 1。w=2πf から 6.28 秒で 1 回転である。v^2/r= 9.8 からは v= 9.8 m/sec。遠心力は v x w である。浮遊時の コリオリの力は 2V x w = -2v x w = 2w x v で中心に向かって遠心力の2倍の大きさで、つまり、遠心力の打ち消しはできない。 遠心力とコリオリの力とがつり合って浮遊することは、不可能なのである。毎秒 9.8 m という速度は、100mを10.2秒の速度で、健康な 人が出せる限界の速度と思うが、その速度を一瞬でも出せれば、我々は、この筒のなかでずっと浮遊して完全に休むこともでき、または、 逆に体を鍛錬するために、体重を4倍までにして走り続けることもできる。浮遊時は、床の下には星空が一面に停止していて、後方の 大陽の光の角度も変わらずにいるだろう。そのときはただ、この宇宙船のなかの風の音を楽しめばよい。静かで物音ひとつしない船内 の鼓動を聞けばよい。もちろん、それは、まだ核融合でしかない、この人類のエネルギー源の静かな鼓動である。実際の窓は、採り入 れる光のための窓は小さく一部にしかない。ここは機器に包まれた機械室の狭い通路のような、細長い部屋である。天井は高いが軸が あって、その先には考えたくもないが、床に人が逆さに立っている。廊下には無限の長さがある。床が透明な部分を持つわけでもない。
その速度に達しないなら、完全な浮遊はない。回転系からみたその乗員の経路の円軌道の半径がこの部屋の半径より大きいなら、すぐ に弯曲した床と交差する。体の重心が下がるまでの少しの間は、宙に浮くこともできよう。しかし、その速度出すまでに体重が減り、 床との抗力が減少して、床を蹴るときの摩擦を十分利用できないから、その速度を出すことも難しいのである。完全に浮遊する直前に、 最後に床を蹴る力が重心を交差していないと、体は軸を横にした前のめりか宙を仰ぐ回転に入るから、この最後の動作は、慣れるまで は難しい。このときまだ我々はすぐに来る、HALの反乱を知らない。そして木星への数ヵ月の旅の途中にあって、我々の本当の使命も 聞かされていない、平和なときである。この永遠に続くように思えるような時間は、ひとときだけなのであるが。それを知っている私 は映画のストーリーを知っているだけであって、現実のこの部屋のこの今日の数時間の作業を思い返しながらの休養の時間に、あの古 い映画が既視感にように甦ってきて軽い病的発作を生むのである。これらすべてのことをあの映画は用意していたと思いながら。
遠心力場は、重力と同様にその勾配が力場を与えるスカラーのポテンシャルによって表すことができる。中心軸から外れた物体が外に 向かって滑り落ちるような、回転軸を軸とする逆放物面をもつポテンシャル場である。F/m = -gradφ= rw^2、φ(r)= -1/2 r^2w^2 = -1/2 v^2 これは、回転系内の静止点を慣性系からみた運動エネルギーの符号反転である。ニュートン重力中のポテンシャルと区別して、 回転系のポテンシャルは、"実効ポテンシャル" と呼ばれる。
実効という言葉に取り立てて意味はなく、正しくもないが、ポテンシャルに近いからそういうだけであろう。地球軌道を離れてからは、 地球同期の回転系もあまり意識しなくなる。我々は滑り落ちるだけでなく、無理矢理に推進してその高みを離れてきた。それはじつは、 高みであると思ったのが、低さであって、遠方の惑星領域からみれば、井戸の底に近かった。微妙で弱く感ずることもできるかできな い程度の数週間の高温の水素推進、それは床に側面からの傾斜を与える方向だったが、そのあと、全く不意に静けさに戻った。これか ら2ヵ月間は、推進がない。それは、全く騒音がないということである。小型原子炉はしばらく核融合の火を止める。動力が停止する ことでそれがもとの振動がなくなり、少しの観測がスケジュールされているが、乗員にとくにする仕事はない。そして、時間だけは十 分に与えられている。そのようなとき音楽を聞くこともでき、地球の最新のニュースを見ることもできる。しかし、地上の風景を嫌っ てここに就いたのであるから、ニュースに深い興味があるはずもない。作業とするものがないとき、作業員はできるだけ休養のために 長期睡眠をとることが予定されている。この長いバカンスは、多くの精神的な疾患の回復が期待されている。無重力状態の長期休眠は、 小児時代のトラウマからの開放と、そして老化の恐怖からのそれが期待される。まだ誰もそれを明確に示していないだけのことである。
(1)回転系では PE + KE は一定でない
ニュートン力学の地上での物体の運動エネルギーと位置エネルギーの和が一定と整合して、回転系での運動エネルギーと位置エネルギ
ーの和も一定が成立するだろうか。答え:成立しない。
回転系の静止点の速度を v とし、系内速度を V とすると、慣性系から
みた運動エネルギーは、KE= 1/2 (V+v)^2 である。系内の PE= -1/2 v^2、 KE= 1/2 V^2 であるとすると PE + KE = 1/2 (V^2 - v^2)。
これは V と v との大きさに依存する。
すべての自由物体は、回転系ではその速度に比例した半径をもって同期した円軌道を描く。ほとんど静止した物体は小さな円を描く。 重力も考慮した "実効ポテンシャル" は、その傾きが0である5つのラグランジュ点を作り、それらは山か峠であり、谷底はない。 自由物体は実効ポテンシャルの傾斜によって円軌道の中心を徐々に移動させる。小惑星の集まるトロイ点L4とL5は広い丘だが、どうして 山に集まるのだろう。普段は傾斜を下るが、一度円軌道が山の頂点を巡ると、逃れることができないのかもしれない。円は小さくなる だけであるから。
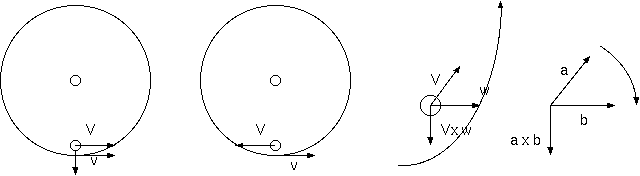
回転系では、速度 V をもった外力なしの質点は、速度 V に比例しそれと垂直な力 F/m= 2V x w を受け、これを遠心力に対抗し、さら に向心力をもって速度に比例した半径の円軌道を描く。円軌道の向心加速度は、速度に比例するが、時間積分した軌道の周期は、速度 に依存せず一定であり、当然、回転系の周期と一致する。(v が 2 倍で、r は 2 倍、mv^2/r = mrw^2 は 2 倍。w は一定。)
コリオリの力の元になるベクトルポテンシャル B= rot A の A は、一意に決定されないが、中心からの距離 r と w に比例する A= v= w x r という軸対称解 A= (-y, x, 0) がある。rot v = 2w であるから、回転系の速度場 v を コリオリの力のベクトルポテンシャル とすることができる。 電磁気の A は、rot B = dE/dt + i の電流によるが、回転系の w は一様であり rot w = 0 から電流に相当す るものはないと考えられる。
F(r)/m = v x w + 2V x w = (2V + v) x w
である。この式で、遠心力とコリオリ力は区別されない。この区別のない仕組みは本質的であり、みかけの力は、速度(2V + v)全体に 掛かり、物体の速度から、その系内点の v を引いた系内速度 V に関するものをコリオリ力といい、v に関するものを遠心力という。 回転系の原点に対する物体の速度があり、物体速度と回転の外積が遠心力とコリオリの力の和を作ることをこの式は意味している。 そのうち、(V + v) x w の部分は、原点からみた速度 V+v と w との外積であり、これは、回転系内の座標 r によらず、回転軸の位置 に依らない。回転系には軸があって、外部世界との速度を反映するが、その座標の軸方向の成分は、w との外積で効果が消える。 (V + v) が (2V + v) になっても、回転系の静止点速度と系内速度で出来ていることは変わらない。遠心力とコリオリの力は、 もともとの発生的原因は、回転系からみた物体の速度 V+v と w の外積であり、両者は、区別してできたものではない。 速度を系速度 v と系内速度 V に分解して遠心力とコリオリの力に分けただけである。
遠心力が v x w 、コリオリの力が 2V x w で、みかけの力全体が F/m= (2V + v) x w なら V= -v では遠心力と同じ大きさの向心力を 作り、V= v では遠心力の丁度 3 倍の遠心重力を作る。
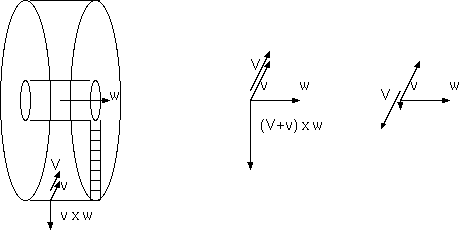
軸から r の点での遠心力 v x w (v= w x r) は、そこを軸にする同じ w をもつ回転系からみると、r= 0 から、もはや遠心力はなく、 v が系内速度 V に移され、みかけの力 (2V + v) x w 、は大きさを変えるがコリオリの力となる。また、その系内速度 V を系の速度 v に置き換える軸の位置をさがしてその回転系からみると、みかけの力全体が遠心力と現れる。性質が全く異なる回転系のふたつのみかけ の力は、回転系の並進選択による違いでしかない。
コリオリの力があまりなじみがないのは、普通、それが遠心力より小さいためだろうが、回転系のその点の接線速度程度の速度で遠心力 と同程度の力を受ける。地球の自転速度程度の速度で地球の自転の遠心力程度のコリオリの力が働くだろう。日が東から昇る地球の回転 w は北極星を指すベクトルである。北半球で地球の回転の上向き成分をwとするとはそれは緯度の正弦に比例し、速度 V に向かって V x w は右に働く。北半球では弾丸は常に右にそれる。これは台風の渦の風が左にそれるのとは逆だが、流体力学は、さらに難しいのである。
(a) 静止系からみる回転系の静止点: 静止系からみた円運動は、それに同期する回転系からみると物体が静止するために、 向心力につり合うみかけの力、"遠心力" が必要である。これは、回転系では "現実" の力である。
(b) 回転系からみる慣性系の静止点: 慣性系上の静止点は、回転系 w からみて -w で円運動をするから、遠心力に対抗する もうひとつのみかけの力、系内速度に比例する "コリオリの力" が必要となる。これも、回転系 w では "現実" の力である
しかし、このとき、回転系 w の力、遠心力とコリオリの力だけでつり合いが成立するのではなく、静止系、すなわち、回転系 w からみて 回転系 -w の遠心力を含めてつり合いが成立すると考える。これは、(b) が (a) の回転相対であることを意味する。なぜなら、 もともと (a) は、ひとつの系のなかの "現実" の力のつり合いでなく、それと別の系の "みかけ" の力のつり合いであったからである。
コリオリの力の大きさについて、旧版では、(b)の状況で慣性系に静止する -w の回転に向心力が不要と考え、回転系 w 内部の力だけで つり合うことを仮定し、コリオリの力を V x w とした。ここでは、(b) の -w の円運動をするためには、回転系 w においても、慣性系に おいてと等しいその系のなかの現実の力による向心力が必要であると仮定する。そうすると、遠心力に対抗して慣性系の円運動と等しい 現実の向心力を生むためには、遠心力のちょうど 2 倍の反対符号 2V x w のコリオリ力の大きさが必要となる。そのとき、w 系内に力の つり合いを求めず、その代わり、w 系からみた -w 回転系 (静止系) に遠心力の存在を仮定する。-w 回転のコリオリの力は、乗員と -w 系との間に速度がないから考えなくてよい。
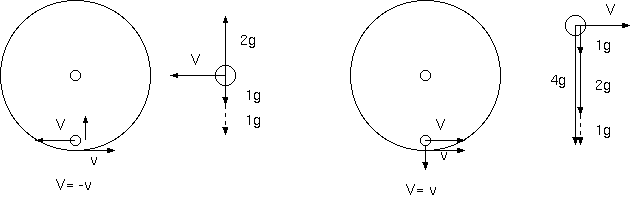
回転する円筒型の室内で円筒の側面を床として、回転系の速度 v とは逆方向に系内速度 V= -v で乗員が走行するとき、床から浮遊する。 これは、(b) の状況である。床の速度 v を前方とし、回転 w は v に向かって右とし、コリオリ力は中心(上)に向かう。乗員が慣性系に 戻るから浮遊する。逆に床と同方向に系内速度 V= v で乗員が走るなら、コリオリ力は、下に(外に)床に向かい、乗員は慣性系からみて 2 倍の回転をし、遠心力は w^2 に比例するから 4 倍の抗力を床から受ける。これらは、コリオリの力の大きさを 2V x w とする場合と、 V x w とする場合、どちらが整合するだろうか。コリオリ力が V= -v で力 0、V= v では力 4 倍を与えなければならない。
コリオリの力を V x w とする場合、V= -v で走行する場合、回転系 w からみて、系内速度 V の生み出すコリオリ力 V x w が中心(上)に 向かい、回転デッキ内の遠心力 v x w とでちょうどつり合う。しかし、デッキの回転方向と同方向の走行をする場合(V= v)、遠心力と コリオリ力の和は、2 倍の遠心力となり 4 倍を説明できない。
"w系の遠心力" + "-w系の遠心力" - "w 系のコリオリの力"= 0 (1g + 1g - 2g= 0)
また、デッキの回転と同方向の走行 V= v の場合、
"w 系の遠心力" + "+w 系の遠心力" + "w系のコリオリの力" (1g + 1g + 2g= 4g)
w 系の現実の遠心力、コリオリの力と物体系 +w のみかけの遠心力の和は、丁度 2w 系の遠心力 4g と等しい。回転系内の "現実" の力には、 つり合いを求めず、相対回転には必ずみかけの力が伴う、合成回転系を静止系にする相対回転においてさえ遠心力が伴うとするのである。
(Va + Vb) x (Wa + Wb) = Va x Wa + Vb x Wa + Va x Wb + Vb x Wb
の右辺第1項は、Wa の遠心力、第2,3項は、等しく加算してコリオリの力 2 Vb x Wa = 2 (Wb x r) x Wa になるが、第4項に回転 Wb の遠心力 Vb x Wb がある。遠心力とコリオリの力は、Wa 系では "現実" の力であるが、それに "みかけ" の力 Wb 系の遠心力を補って、 回転和 Wa + Wb の遠心力になる。
ベクトルの外積は角が垂直のとき代数的な積として記述でき理解しやすい。遠心力とコリオリ力の和、a^2 + 2ab は、b^2 を補って、回転和 a+b の遠心力 (a+b)^2 になる。b^2 は、回転系 a からみた付加的回転 b の遠心力である。コリオリ力は、2ab であり、回転 a と、b の元 となる系内速度 V とに比例する。浮遊の場合、b= -a で 0 になることに対応する。
コリオリ力の大きさが V x w であるなら、遠心力とコリオリ力の和 (V + v) x w が場所によらず一定となるが、コリオリ力が 2V x w なら、 遠心力とコリオリの力は、回転系の取り方によって、両者は互いに行き来する特性があるとはいえ、それらの和 (2V + v) x w は一定でない。 回転系の選択において一定なのは、v_a + v_b であり、これは v + V に対応する。(2V + v) ではない。
コリオリの力が、2V x w であるとき、付加的な回転の遠心力を補って、一般的な回転和の遠心力が説明できた。回転系 w のコリオリの力が 別の回転系 -w または +w の向心力になり、みかけの遠心力を補って回転和の遠心力となることは、遠心力とコリオリの力の和に w 系から みた V のもたらす付加的回転の遠心力 V x Wb を補った (2V + v) x w + V x Wb が、ある回転系から他の異なる回転系Wbへの移行において 不変量であることを示す。このとき、Wb は、Wa と同じ方向を向いた回転でなくてもよく、V と r によって Wb は決まる。また、付加的回転 Wb が回転 Wa に比べて小さいとき、V≪v のとき、2次の第4項は消え、遠心力とコリオリの力の和が不変になる。
三角関数が回転を表すことは、斜辺の長さ 1 である直角三角形の他の辺が cosΘ, sinΘとして表せ、原点と(1,0)とを結ぶ単位長の線分を、 Θだけ回転した位置が (cosΘ, sinΘ) として表せることから来ている。Θは、回転による角度で、wt として時間に比例するとすると、 (cos wt, sin wt)である。これを 2 次元の位置ベクトルとすると、その時間微分は、(-wsin wt, wcos wt)である。時間微分が 90 度の位相 進みを伴って、sin が cos になり、cos が -sin になること、回転角速度 w(= 2πf) が乗算されることを工学はよく使い、1次元又は2次元 等の任意の波形を扱う数学的手法がフーリェによって開発され、現代 20 世紀後半からの我々はそれを固定の計算的道具を使って意識せずに 利用し回転を三角関数で扱う扱いは慣れている。しかし、三次元回転を扱う記述は、物理の外積を使わないと何もできない。3次元の剛体の どこか 1 点の回転は、軸を例えば z 軸に固定すればもちろん、2 次元回転である。
回転の方向と大きさの両方を表す3次元ベクトルで、回転の軸の方向を向いた、角速度の大きさをもつベクトル、1文字 w で回転を表し、通常 の3次元位置ベクトル r のように扱うなら、3 次元内部の回転の表記を全て扱うことが出来る。軸の方向は、地球の回転が北極星を指すように、 又、図に例を示すように右回り(反時計周り)で上を指す。回転系の位置 r のもつ速度は、w x r によって表せ、加速度は、w x (w x r) である。 これらが、2次元の回転を含んでいることは、w= (0, 0, w), r= (cos wt, sin wt, 0) の w x r を考えれば、外積 a x b = (a_y b_z - a_z b_y, a_z b_x - a_x b_z, a_x b_y - a_y b_x) に代入してみれば、w x r = (-wsin wt, wcos wt, 0) となって、2次元回転を含んで扱っていること が分かる。さらに、どの方向を向いた w においてもそれに垂直な面内でこれが再現されるということを認め、我々は回転に 3 次元ベクトルの 外積記述を使う。
剛体を x 軸の周りに w_1 で回転させておいて、それ全体を y 軸の周りに w_2 回転させても、結果は、w_1 + w_2 というベクトルの和の方向を 向いたひとつの軸の回転によって表されることは、オイラーの定理と呼ばれる。複数の回転は、1つの回転に統合できる。また、有限の大きさの 角度をもった回転は、加算において交換できないが、無限小の角度と角速度は、加算において交換法則がなりたつ。
回転に相対性はないと真っ先に否定される。とくにニュートン力学においては、それは明確であると思われている。ニュートン自身がバケツの水面 が上昇することをいって絶対静止空間の証拠としたとされ、マッハは、遠方の質量がこれを決めているかもしれないとこの物理の根底にある物質 でない不確かな存在を疑った。そのような考えを無意味な哲学扱いしたファインマン(*)は、コリオリの力を説明するのに、メリーゴーランド のように回転する円板の中心 r= 0 から半径方向に等速直線運動する物体が円板からどうみえるか、という状況を使った。 "ファインマン物理学"、坪井忠二訳、岩波書店、力学 I p.271。 ここで、太郎は地上にいて、次郎は回転系にいる。"次郎はなにものかをこの線にそって半径方向に動かす。" (以下引用) 角運動量は、
L= m v_tan r= m ω r・r = m ω r^2
(中略(角運動量保存から)) r を大きくするにはトルクを働かさなければならない。必要なトルクは m が半径方向に動くとき、L が時間的に変化する 割合である。m が半径方向ににだけ動くとすると、ωは一定だからトルクは、
τ= F_c r= dL/dt = d(mωr^2)/dt = 2mωr dr/dt
であって、ここに、 F_cは、コリオリの力である。我々が求めたいのは、m を v_r = dr/dt の速さで動かすのに、次郎はどれだけの横の力を出 さなければならないかということである。これは、F_c = τ/r = 2mωv_r である。
(以上引用) ここで、ファインマンは、力のモーメント F_c r が、スカラー化された角運動量 L= wωr^2 の時間微分に等しいとし、 それを r による微分と dr/dt= v_r との積とすることで、コリオリの力の大きさを導いた。 p.279 には、ベクトル記述で 2m V x w と書くこともしている。
(*)第16章、pp. 223-226 参考。
F_r= - m v^2_a/r = - m v^2_b/r - 2m v_b ω - m ω^2 r
太郎のみる求心力は、次郎のみる求心力(第1項)、回転系に静止する物体に働く求心力(第3項)、コリオリの力(第2項)の和とする。 ここで、ファインマンは、"次郎は第1項を感じるだろうか?" と問い、答えを描く。""感じます"と次郎はいうだろう。 "私が回転していなかったとしても、円に沿って v_b の速度で走ると、求心力はあるはずです。"これは次郎に生ずる求心力であって、 これは回転とは関係がない"と。
回転系上であろうとなかろうと円運動に必要な向心力がこの第1項であるように書かれているが、この第1項は、我々の式の第4項の 付加的回転 -w 系の遠心力に対応する項であり、回転系内速度 v_b を別の回転として発生する力である。第1項と第3項は、つねに 同符号だから一方を遠心力、他方を向心力とはできない。円運動に必要な向心力は、この第1項でなく第2項のコリオリ力が供給するのである。 そして、第1項を次郎が感ずるということは、遠心力とコリオリの力以外を感ずるということになるから、このファインマンの指摘は、 誤りというべきかもしれないが、次のように多少の理由がある。
我々は、 +w 回転系から -w 回転系へ移る (静止系に戻る) ときに静止系に属するみかけの力、遠心力を計算にいれた。これによって、 コリオリの力の 2V x w の大きさが回転系の物理として整合することを見た。注意すべきは、この遠心力は、この回転系からみても 現実の力ではなく、みかけの力であり、それを元の系からみると、2 重のみかけの力であることである。そして、相対的な回転において 発生し、それが静止系にもあることは驚くべきことである。また、この系で物体が静止しているため発生しなかったコリオリの力においても、 相対回転によって起きることは同じであろう。
静止系にもみかけの力があるということは受け入れがたい。みかけの力が系間にあるとしなければ、静止系には多値のみかけの力が決定 なく存在するという矛盾を招く。しかし、系の間に系があるわけではない。回転系のみかけの力は、相対回転に属するという認識によって、 我々は "回転には相対性はない" という立場から、すこし後退すべきことを知る。つまり、相対回転によって次の系の遠心力とコリオリの力が 存在する。静止系と回転系とでみかけの力の関係は違わない。ただし、だからといって、ある系が静止系かどうかを系内で判断できない わけではない。静止系は、回転系のなかのひとつで単にその回転が 0 であり、そのなかで物体が外力なしに静止又は等速直線運動をする。
"+w 系からみて -w 系であるから、静止系にも -w 回転による遠心力が存在する" というとき、遠心力が静止系に現実の力としてあるか といえば、これは、系を移るときの計算上の都合のようである。むしろそれは、もとの回転系 +w 系(次郎) に属しているとすれば、 多値性の問題が消え、静止の絶対性は確実である。こうして辻褄は合わされる。しかし、これは、次郎が w 系に感じるみかけの力ではない。 これが回転系 w の現実の力であるなら、遠心力とコリオリの力以外にみかけの力があることになるが、聞いたことがない。 それは、その回転系の回転 w (w_a 又は v) ではなく、別の回転 w_b (又は v_b)に関係するものである。