慣性系では物体が円運動するには、中心からその物体を引く力、向心力が必要である。これは、ニュートン力学の惑星運動では 重力の "現実" の力、万有引力であった。振り回すひもが物体を引く(作用)とき、物体からひもを引く慣性力(反作用)を伴う。 慣性力は、質量が加速度をもつための力である。この現象を回転系からみると、向心力はそのままあり、物体は回転系に静止して いるので、向心力とつり合う遠心力が必要になる。遠心力は、系の回転から生じる "みかけ" の力である。回転系では自由物体は、 初め静止していても遠心力の加速をを受けて、中心から離れる遠心方向の運動を始めるが、慣性系からみると等速直線運動のままである。 コリオリの力は、日常生活ではあまり意識されないが、回転系で物体が速度をもつとき、磁場の中の電荷がうける力のように、 速度と回転軸との両者に垂直な方向に力を受ける力である。これも回転系での "みかけ" の力である。
遠心力は、局所的には中心方向の加速をもつ加速系と類似する。それは、局所的には遠心方向の加速度を与える場である。 遠心力の原因は、回転系内の静止点を慣性系から見た中心に向う加速度である。その符号反転した加速度が回転系では、場から生じるとみえる。 回転系と加速系との違いは、回転系の各点が局所的にも回転していることである。局所的な回転がコリオリ力を生んでいる。 遠心力の大きさは場所に依存し、中心軸からの距離に比例するが、コリオリ力は、場所によらない。さらに、遠心力の大きさは、 回転系の角速度の2乗に比例するが、コリオリ力は、角速度の1乗に比例する。両者は、このように違った性質をもっている。
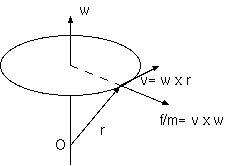
回転には軸があり、軸の方向と回転の大きさを示す角速度ベクトルで表される。回転系は、回転軸が通る点と、回転のベクトル w によって表現される。z を軸に回転する系の場の性質は、z 方向に一様であり、z 軸からの距離だけによる軸対称性をもつ。 軸上に原点 O をとり、そこからの位置ベクトルを r とすると、慣性系からみた回転系内点の速度は、v= w x r になる。 そのとき遠心力場は、F/m= v x w であり、その系内静止点の慣性系での加速度 w x v の符号反転である。

半径 10m 程度 (9.8m)の円筒の側面を床にすると、遠心力が地上の重力加速度 1g = 9.8 m/sec^2 を与える回転は、rw^2= g から w= 1。w=2πf から 6.28 秒で 1 回転である。v^2/r= g からは v= 9.8 m/sec。遠心力は v x w 。浮遊時のコリオリの力は V x w = -v x w = w x v で中心に向かう。
遠心力場は、重力と同様にその勾配が力場を与えるポテンシャルによって表すことができる。回転軸を軸とする逆放物面をもつ ポテンシャル場である。F/m = -gradφ、φ(r)= -1/2 r^2w^2 = -1/2 v^2 これは、(なぜか)回転系内の静止点を慣性系からみた 運動エネルギーの符号反転になっている。
(1)PE + KE は一定でない
ニュートン力学の地上での物体の運動エネルギーと位置エネルギーの和が一定と整合して、回転系での運動エネルギーと
位置エネルギーの和も一定が成立するだろうか。答え:成立しない。
系の点速度 v とし、系内運動速度を V とすると、慣性系からみた運動エネルギーは、KE= 1/2 (V+v)^2 である。
系内の KE= 1/2 V^2 、φ= -1/2 v^2 であるから、系内の KE + φ = 1/2 (V^2 - v^2) となり、
これは、V と v との大きさに依存する。
ニュートン重力中のポテンシャルと区別して、回転系のポテンシャルは、"実効ポテンシャル" と呼ばれる。
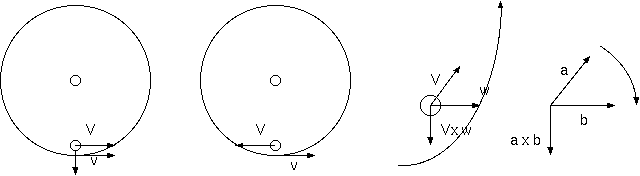
回転系では、速度 V をもった外力なしの質点は、速度 V に比例しそれと垂直な力 F/m= V x w を受け、速度に比例した半径の 円軌道を描く。円軌道の向心加速度は、速度に比例するが、時間積分した軌道の周期は当然、速度に依存せず一定であり、 回転系の周期と一致する。(v が 2 倍で、r は 2 倍、mv^2/r = mrw^2 は 2 倍。w は一定。)
コリオリの力の元になるベクトルポテンシャルを考えることができる。rot B= A である A は、一意に決定されないが、 中心からの距離 r と w に比例する A = v = -r x w という軸対称解 A= (-y, x, 0) がある。電磁気の A は、ソレノイドの 周囲の電流に相当するような rot B = dE/dt + i があるという原因によって起こっている。
F(r)/m = v x w + V x w = (V + v) x w
である。(V+v) x w は、慣性系からみた速度 V+v と w との外積であり、遠心力とコリオリ力は、ここでは全く区別されていない。 この区別のない仕組みは本質的であり、見掛けの力は、速度 (V+v) 全体に掛かり、慣性系の速度からその系内点の v を引いた 系内速度 V に関するものをコリオリ力といい、v に関するものを遠心力というのである。回転系は、ある速度をもっていて、 その回転系からみる物体速度と回転の外積が遠心力とコリオリの力の和として見えることをこの式は意味している。 回転系には軸があるということは、外部世界との速度を反映してよいのであるが、その座標の軸方向の成分は、w との外積で効果が消える。 遠心力とコリオリの力は、もともとの発生的原因は、回転系からみた物体の速度 V+v と w の外積であり、 両者は、区別してできたものではない。人間が分類しただけである。
遠心力が v x w 、コリオリの力が V x w で、みかけの力全体が (V + v) x w なら V= -v で遠心力を丁度打ち消して浮遊し、 V= v では遠心力の丁度 2 倍の人工重力を感ずるのは至極、当然のことである。
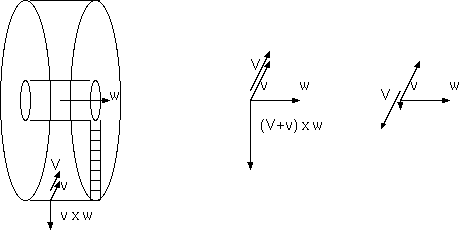
軸から r の点での遠心力 v x w (v= w x r) は、そこを軸にする同じ w をもつ回転系からみると、r= 0 から、もはや遠心力はなく、 v が系内速度 V に加算され、みかけの力 (V + v) x w 、全てがコリオリの力となる。また、その系内速度 V を系の速度 v に置き 換える軸の位置をもつ回転系からみると、みかけの力全体が遠心力として現れる。性質が全く異なる回転系のふたつのみかけの力は、 回転系の選択による違いでしかないのである。
コリオリの力があまりなじみがないのは、普通、それが遠心力より小さいためだろうが、回転系のその点の接線速度程度の速度で 遠心力と同程度の力を受けるのである。それは、地球の自転速度程度の速度で地球の自転の遠心力程度のコリオリの力が働くこと とも呼応している。日が東から昇る地球の回転 w は北極星を指すベクトルである。北半球で w が真上を向いているとし速度 V を前方とすると V x w は右に働く。北半球の弾丸は右にそれる。これは台風の渦の風が左にそれるのとは逆である。流体力学は、 さらに難しいことがあるのである。