1 赤方偏移は、宇宙膨張かドプラー効果か
2 ゴム膜の上の虫
3 光エーテルの復活
4 曲る光のハッブル定数
5 遠方のハッブル定数
6 局所慣性系と速度をもった場
7 閑話休題
8 閑話休題つづき
9 フリードマン解の空間曲率0のときの光エーテル的回帰について
10 ブルータス、...
11 曲って戻る光?
12 g_ik からの光速を使うと
13 場と速さ
14 背景輻射自体、存在できるのか
15 光の廻廊
16 光が戻る計量
17 光速が0になる計量
18 光速が0になる計量(続き)
19 G,A ともに逆数でないと意味をなさない
20 逆数のままで意味を取ると
宇宙の果てとその光の廻廊について考える。宇宙とそのなかの光の経路を微分方程式を使って扱う。微分方程式は、瞬間の一点の力学、 ダイナミックス、動的関係式であるのに、そのようなものが宇宙全体の時空の有様を示すのである。局所の法則を仮定して宇宙全体を記述する。 そのとき、単純な数式は何のためかといえば、単純な宇宙モデルは、宇宙の全体を包含するという複雑さを持たない。 そのため、宇宙の特徴のひとつを捉えればその役割を十分果たしたのである。単純な式で宇宙を表す同一化の所作は、有効性をつねに疑ってよい。
もし、光の赤方偏移を空間膨張による波長の拡大で説明するなら、現在の宇宙の果てに見える過去の物体は静止し、光が飛んでいる間に 膨張して赤方偏移したのである。その場所は、近傍から宇宙の果てまで移動したのではなく、最初からその遠方にあったことになる。 これは、膨張を否定するわけではなく、その広さが最初からあったことを意味するだけであり、その点はそこから膨張して今はその2倍 近く遠くをほぼ光速で遠ざかりつつあるとしてよい。これは、また有限宇宙を否定するわけでもない。宇宙の果てより宇宙の半径が十分 大きければ、問題ない。しかしこの解釈は、フリードマン宇宙は、初速がゼロの膨張でないことから反論を受けると思う。

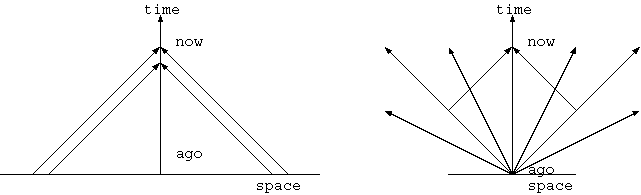
それに対して、赤方偏移をドップラー効果とし、今見える宇宙の果てがほぼ光速で遠ざかる物体のドップラー映像とするなら、もし、今 見える宇宙の果てが最初から遠方にあってほぼ光速で遠ざかっていたとするなら、ハッブル定数が、始りからの時間の逆数ではなくなり、 フリードマン宇宙(または膨張宇宙)の原則と矛盾するようだ。そこで、それらの物体がここの近傍からほぼ光速で広がり、宇宙の果てに 到達してからここまで光が届くなら、この場所の宇宙の始めの原点から広がる、膨張による事象の地平線の光円錐と、この場所の現在の 観測点に収斂する光円錐の交わる円(実は球面)が宇宙の果てであり、この場所の宇宙年齢は、宇宙の果てからの光の到達時間の 2 倍 となり、普通に言う、宇宙年齢が宇宙の果てからの光の到達時間に等しいこととは、異なる結論になる。これは、”簡単に宇宙年齢を2 倍にする方法”である(21.7, 30)。 (杉本大一郎氏は、現在の地平線が 2ct の距離にあるとするが、年齢を 2 倍にはしない。("間違いだらけの物理概念"(丸善)参照。))
佐藤文隆氏は、宇宙膨張で時間的に見える領域が拡大し、宇宙の果てに外から物質が入り込むという説明を TV で話されたことがある。それは、 そこで彼が上図左で図示されたように最初から遠方の宇宙が存在し、時間とともにその観測可能な領域がちょうど光速で広がるとするのだろうか。 もしそうなら、それは少なくとも彼のいわれるようにその場所が最初、この1点にあって、ある時期にはここから 数 cm にあった、というものでは ないと思われる。一点からの膨張では宇宙の始めから広がる光円錐領域である宇宙の果ては、時間的に変化しないからである。(直線的膨張なら、 宇宙の果てには、いつまでも同じ模様が見えているはずである。減速膨張なら外から物体が境界を越えて入ってくるかも。いや、氏は単に始まりからの 時刻が経てば観測空間が拡がらないといけないという意味で言われたのだろう。)
それらは、宇宙に光速一定を適用した宇宙と光の議論である。特殊相対論的な宇宙の像である。そこでは光は直進する。これを一度、 放棄してみよう。過去には物差しが小さく、光速が遅かったとするとどうなるか。まず、光速が宇宙の始まりからの時間に比例するとき、 光経路 x(t)を求めたい。
dx/dt= c(t)= at
距離をx、時刻をt(始0で、現在1)とし、光速c(t)はxの時間微分、境界条件を x(1)= 0, c(1)= -1 とすると、光の経路は、x(t)= -1/2 t^2 + 1/2 と簡単にでる。xは光の経路であって、宇宙の果てのようでもある。xとは t^2 に比例する放物線で2乗拡大する宇宙、パラボリック宇宙になり、 宇宙の果てからの光の到達時間は、直線の光の 2 倍かかる。宇宙の果ては最初から遠方にあり、見える領域が時間とともに拡大する宇宙である。 ハッブル定数は、時間に反比例し、その逆数の 2 倍が宇宙年齢になる。そして、この宇宙では光は戻らず、背景輻射がない。
次に単純な関係、宇宙のサイズ x に光速 c(t)が比例するとすると、微分が元の関数に比例する指数関数である。x は光の経路でもある。
dx/dt= c(t)= ax
x= exp(at) とおくと dx/dt= a exp(at)= ax
宇宙が一定の比率だけ拡大するのに一定の時間がかかり、宇宙は、無限の過去からの指数拡大のインフレーションになる。ハッブル定数は、 文字どうり時間的定数である。いつ見ても宇宙は同じように膨張している「定常膨張宇宙」である。この宇宙も光が戻らず背景輻射がない。 両者とも宇宙の年齢を延ばすが、まだまだ粗雑で、これを宇宙とはいえないだろう。これらは、光速を宇宙年齢と宇宙のサイズに比例させ 光速が大きい理由を説明するだけで、微分方程式に仮定した c(t)= at, c(t)= ax の物理的根拠や現実性が見えないからである。
(*) 前の20章のように、光が飛んでいる間に波長を伸ばすのは、宇宙の塵を結んだ膨張する各点を静止とする共動座標でのことで、 通常の物差しの変化しない座標系に変換するとドップラー効果になるだけの話だという説明がある。 "Interpretation of the cosmological metric" http://arxiv.org/abs/0803.2701
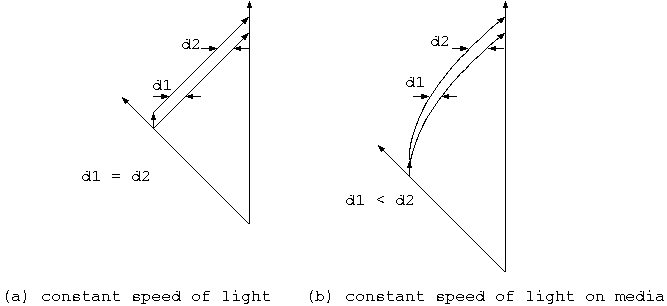
しかしこの描像は、膨張するゴム風船上を虫が這うのとは、まだ異なっている。相対論 FAQ のいう、”2匹の虫が同じところから時間を おいて同じ方向に出発すると、その間隔が時間とともに広がる”という性質がない。(FAQ によると、これが宇宙の膨張による光の赤方偏移であり、 ドップラー効果による説明は、その1次近似という。この説明も訳の分からないもので、光の膨張とドップラー効果は採る座標系が違う という説明が必要なのだが。)つまり、この虫の這うイメージは、光速一定でなく、光速が光の媒体に対して一定である。 これを図示したのが下図の右(b)である。遠方の光速は媒体の広がる速度が差し引かれ遅い。近傍で45度の傾きになるためには、 虫のスタート時点は、昔に遡る必要がある。
しかし、ゴム風船を芋虫が這う、光速度が媒体に対して一定は、特殊相対論以前の光である。どの慣性系から見ても光速一定が特殊相対論であり 系の中で光速を時空の関数とするのが一般相対論である。光エーテルの復活が、この膨張宇宙論に本当に必要かどうかは、疑問である。 そうすると系によって光速が違い、局所においても特殊相対論が成立しないように思うが、それでよいのかどうか。FAQの答えを書かれた かたは、マイケルソン・モーリー実験をどう解釈し直すのだろうかと、腑に落ちない。
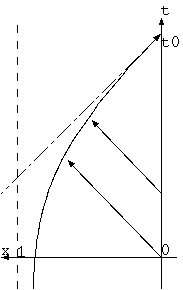
FAQ に従って、宇宙の果ての光の出発時点は、更に古い可能性がでる。風船上の虫の光の経路は、現在のこの場所を (x、t)= (0, t0)とし、 距離 x に比例する空間膨張で光速が低下するような、光エーテルを考えてみよう、後退を正とし、空間膨張速度 x から光速 1 を引き、
c(t)= dx/dt= x - 1
とする微分方程式は、
x(t)= 1 - exp(t-t0), c(t)= -exp(t-t0)
光の経路は、下図になる。距離 1 からの光の到達には、無限の時間がかかり、宇宙の始まりからある程度膨張してから虫(光)がスタート したとしても、どの程度過去からの光か特定できない図になる。しかしこれは、距離による光速低下を固定した定常的な空間構造であり、 膨脹宇宙とは、まだ、かなり違う。
x/t
によるものである。なぜなら、原点から初速vを保存して発散する点の座標 x は、x_i = v_i t であるから、v_i= x_i/t (i= 1,2,3))。 膨脹宇宙の各点の位置 x で速度が決まるのではなく、x/t でその速度が決まるとする。光速 c(t) を媒質速度引く1、x/t - 1 として、
c(t)= dx/dt= x/t - 1
この微分方程式は (u= x/t とおき、dx= u dt + t du を、dx= (u - 1)dt へ代入。du= -dt/t から、u= -log|t|+C、x= -t(log|t|+C)。 x(1)= 0 から、C= 0)、
x(t)= - t log |t|
という解をもつ(下図)。
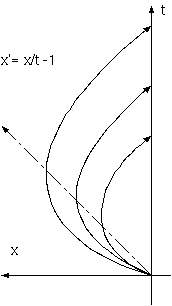
光は、時間に対して、ぐるりと曲って来る。光線は、原点(t,x)= (0,0)から発し、広がってまたもとの位置、x= 0 の t 軸に戻る。 これが我々が見る光である。宇宙の果てと見ているものは、この場所の、どこの場所でもある原点の光である。光は、一度その宇宙の果て より外側まで行って、外側から地平線を越えて入ってきて、そのあと原点に帰って来る。光は、この曲線上の途中から発生してもよい。 それは、最初からの光と重なってくるだろう。
宇宙の果てに x(t)= t という地平線があり、その外側は媒質速度が光速以上であり、粒子はこちらに向かえない。それらの粒子からの 光は、最初しばらくは、こちらに向いたまま、向うに進むことになる。x= t では、媒質速度がちょうど光速を打ち消し、ここからみる 光速は 0 となる。すべての光の曲線の頂点は、x= t に乗っている。地平線を光が通過するのは、地平線が粒子的地平線であり、粒子は それを越えられないが、光にとっては違うからである。向うに向かっていた光は、一瞬、停止し、地平線が光速で逃げ過ぎるのを待って、 こちらに向かい始める。宇宙の果ては、現在の 1/e の時刻の t= x= 1/e の大きさである。
この光の経路は、現代の膨脹宇宙の考え方に最も近いようだが、このモデルは単純に宇宙の各点は一点から直線的に膨脹するとするニュ ートン的な膨脹宇宙である。x/t の 1 以上、光速以上の膨脹も最初から存在する。粒子的領域は地平線を越えては来ないが特異な原点 以外では一度も関係のない光が地平線から入ってくるため地平線問題が存在する。この宇宙モデルも、現代的な膨脹宇宙に近く、その 問題点も備えているようだ。
宇宙の果てと宇宙年齢の関係がこのモデルでは明確で、宇宙年齢を150億年として、宇宙の果てはその 1/e (e=2.71828182..)約50数億光年先である。 光は、少なくともそれより近い図の曲線経路上で発したのである。その地平線は、今はさらに遠くに膨脹し、ちょうど150億光年先にある。しかし、 もし、宇宙の果ての地平線が 150 億光年先なら、今は宇宙年齢 400 億年であり、現在の地平線は、400億光年さきである。これは”簡単に 宇宙年齢を e 倍にする方法”である。ハッブル定数(速度/距離)の示すのはどちらなのだろうか。距離推定が正しければ、それは 宇宙の果てが150億光年であり、宇宙年齢が400億年である。年齢推定が正しいなら宇宙年齢が150億年で距離は50億光年である。 宇宙の果ての距離と宇宙年齢に同一の数字を使うのは、何か考えがあるのだろうか。球状星雲の年齢などから、宇宙年齢が〜150億年のほうが正しい のだろう。距離を宇宙の果てまで明確にいう方法はない。この2倍やe倍の関係は、聞いたことがないが、何か間違ったのだろうか。 頂点の最大距離を目でみる方法はないし、曲がる光(方向と速度の変わる光)には、光速*時間=距離の関係もないだろう。
光経路上で、速度 x/t と距離 x は、現在から昔に遡ると、地平線までは線形ではないが単調な対応で、速度と距離はともに上昇する。しかし、 地平線は x の最大点であり、そこから外側では、t→0 で x→0、x/t= -ln|t|+C →∞ であり、距離は下がり速度は増えるので、ハッブル定数 は、地平線付近からさらに増加する。このハッブル定数の時間遡及による変動は、光線経路に沿うための見掛の変動であり、膨脹の時間的変動 ではない。
もしも、現在の近傍でハッブル定数を正しく求められるなら、その逆数は正確な現在の宇宙年齢を示すだろう。しかし、銀河の固有運動のために 赤方偏移は、近傍では正確でなく、遠方ほど精度が向上するという性質をもつ。一方、距離の測定は、事情が逆で、セファイドの周期、Ia型超 新星の明るさ等、絶対等級を知る道具は、当然、それが見える範囲しか測定できない。そこで、できるだけ光度の大きい現象の標準光源によって 遠方まで測定する。そのため距離と速度の両者を使うハッブル定数は、適当な距離で固有運動を超える赤方偏移が明確に存在するほど遠く、 距離推定の方法と組み合わせられるほど近い必要がある。
ハッブル定数は、赤方偏移と距離の一定の関係として、それが測定できる距離よりも、さらに遠方に適用できると考えられた。しかし、深宇宙の 赤方偏移までハッブル定数が使えるという自信は、多くの天文学者は持たない。大規模構造の考え方では、数十億光年まで距離と赤方偏移の線形 関係が成立すると考えているようであるが。
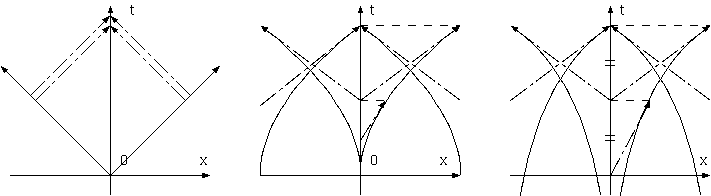
例えば、見えている光が過去であることを全く考慮しないハッブル定数(点線)と、宇宙の果てから直線的に来る光のモデル(一点鎖線)と、この モデル(実線)との 3 者はどれほど違うかを考えよう。見えているものを現在とするハッブル定数は、現在 t0= 1 とすると H= 1/t0= 1 であり、 速度は距離に比例する(v= x)。宇宙の果てからの 45度の光経路(光速一定)では、時刻 t= 1-x の過去の期間を測定する。v= x/t= x/(1-x) は、 x に比例するよりも遠方で大きい。
さらに、曲った経路モデルは、もっと過去の大きなハッブル定数を測定する。ハッブル定数が 1/t であること、H= v/x = 1/t は変わらないから、 この空間(点線)測定に比べ、45 度直線光モデル(一点鎖線)は、地平線までの遠方で 2 倍まで大きなハッブル定数、そして、この曲った経路の モデル(実線)は、e (=2.71828182..)倍まで大きなハッブル定数を測定することになる。
もしも、現実がこの曲線モデルであって、それを空間方向の測定とか宇宙の果てからの直線光と誤認しているなら、ハッブル定数の測定値は、 実際より大きく(宇宙年齢を実際より短く)誤認していることになる。これの補正は、宇宙年齢との矛盾を多少とも緩和する方向である。
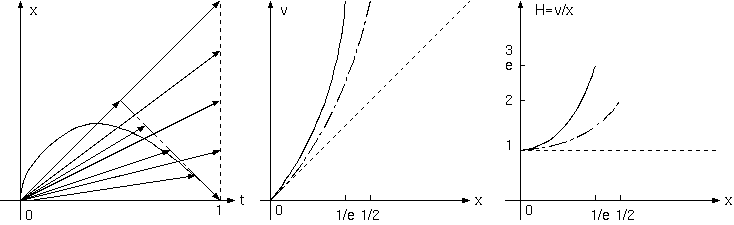
ハッブル定数の逆数は、距離を速度で割った時間を表し、それは、膨張を始めてからの時間、宇宙年齢である。そのため過去のハッブル定数は、 現在より大きい。ハッブルの "定数" は、時間の関数であり、はるかな深宇宙では速度が距離に比例しない。それは、単純な理由である。 速度 v と距離 x の比であるハッブル定数は、見られる側の時空点の(過去の)時刻 t に関係し、みる側の(現在の)時刻 1 ではないからである。
ここから遠方まで宇宙が膨張した遠方をみることは、過去の遠方からここまで光が戻ってくることである。光が -45 度の x= 1-t の経路 をやって来るとする直線光モデル(前項の図の一点鎖線)では、遠方銀河の距離 x と速度 v をプロットすれば直線から外れていく。 時空の各点で、x= vt の直線的膨張をするとき、過去の光円錐上 (x= 1-t) では、速度 v、x、t、H は互いに次のように表せる。
時刻 t= 1-x = 1/(v+1)
距離は、x= 1-t = v/(v+1)、
速度は、v= x/(1-x)= (1-t)/t。
ハッブル定数は、H= v/x = v+1 = 1/t = 1/(1-x)
直線の光では地平線の無限大の赤方偏移 v= 1 は、t= x= 1/2 にある。このとき、速度 v と特殊相対論のドップラー効果の赤方偏移(1+z) には、v= ((z+1)^2-1)/((z+1)^2+1)と、1+z= √((1+v)/(1-v))の関係がある。
2006年6/28、ビッグバン(放送大学 進化する宇宙('05)) (杉山直氏) は、ハッブルの測定した距離の 100 倍(z= 1、赤方偏移による波長の 延びが (z+1)= 2倍、v/c= 0.6)程度の距離まで直線に乗ることを強調し、"ハッブルは正しかった" と発言をされたが、(この言葉は2重に 間違って元に戻っている。そもそも1929年のハッブルは、赤方偏移が距離の2乗に比例するド・ジッター宇宙を意図していた。その後も彼は、 宇宙膨張説、後退仮説を取らなかった。) ここでの話は、もっと遠方で直線から外れるという話である。時刻の逆数であるハッブル定数は遠方ほど大きい。この要素を無視すると、 直線膨張であっても過去ほど膨張が激しいという見かけの減速膨張を見てしまう。また、距離 x= v/(v+1) は、x= v より小さいので遠方 銀河が明るくなる方向である。
これは z= 1 程度までの測定で、遠方銀河が暗すぎるという方向の観測と、過去に速度が小さかったとして宇宙項の存在による解釈がなさ れることとは、整合しない。(銀河の M/L 比からは遠方が逆に明るいという結果もある) 逆に、遠方まで厳密に ハッブルの法則が成り立つためには、次の(1)〜(4) のいずれかであればよい。
(1) 光速が無限大で光は即時に来ている。遠方も t= 1 ならハッブル定数は 1 になるが、光速の有限性が確認されて数百年もたつ。光速は 高い精度で測定されてきたから、この説は除外してよいだろう。
(2) 光速が有限かつ一定で、観測がすべて過去の光円錐であること x= 1-t を認め、その上で距離 x に比例する速度 v (x= v) を仮定すると、 v= 1-t、速度が時間だけの関数となる。距離に比例するように見えた後退速度 v は、実は、時刻 t だけによって変化していて、宇宙全体が 一様に最初光速で後退し、それから宇宙年齢によって後退速度は線形に減退し、現在 0 である。これは、時間加速説に近い。
(3) 遠方までハッブル定数が一定 (v= Hx が H= 1) を満たし、dx/dt= v - 1 なる光エーテル速度場の光経路は、v を x で置き換えた dx/dt= x - 1 という微分方程式(境界条件 t= 1 で x= 0, x'= -1)から x(t)= 1 - exp(t-1) であり、 21.2 に図示 した指数的経路である。光の経路が指数的な宇宙では、光が出発点に戻らないから背景輻射が存在しない。ハッブル定数は、文字どおり時 間的定数であり、宇宙の年齢との関係はない。
(4) 共動座標の計量 ds^2= dt^2 - a(t)^2 dx^2 を認め、a(t)= t (直線的膨張) であるなら、光経路xの微分である光速は dx/dt= -1/t から光経路は、x= -log(t) になり、外に曲がる(光が直線よりも遠方から来る)曲線だが、a(t)dx を dx' に置き換え ds^2= dt^2 - dx'^2 の計量に移る宇宙的座標変換をすると、光経路 x に t が掛かり、x'= xt に、光エーテル論が導く経路と全く同じ光経路 x'= - t log(t) になる。媒体速度は、v= x'/t = a(t)x/t = x、速度は距離に比例し、ハッブル定数は宇宙の果てまで定数である。しかし、v= x になるのは、 a(t)= t の直線膨張だけであり減速膨張ではできない。(間違いのようだ。v = x' でないとハッブル定数が定数ではないようだ。)
光源の速度が光速に加算されないことは、色々な光源からの光も、遠方からの光も局所で同等であるという必要があったからであった。 光の遠方での速度は、それほどは重要ではなく、それを統一する必要はないとする考えかたがあるのも事実である。それなら、光は遠方 では、光源ではないが光の媒体の速度が光速に加算されるとするのは、正しいことだろうか。これは、正しいとも間違っているとも実証 されていない。遠方では、光速一定は実証されていないとすべきだろう。
いや逆に、場所によって速度なしに時計の進みの違うことが実証されているといった方がよい。時間の進みが異なれば、光速も違って当 然である。しかし基本的にエーテルの存在が無意味になった後で、同じような空間に属性を持たせるものは、局所においても光は媒質に 対して速度をもつとする考えを復活するのではないか。そうすると、特殊相対論は、根拠を失い、その損失は大きい。これは、大きさの 違いではない。局所と宇宙に違う法則が働くこと自体が疑問である。天体と地上が同じ法則で動くことをニュートンは見出したのである。
アインシュタインは、"エーテルと相対論"で、この新しい(計量)エーテルについて、速度の概念はこれには 適用できないといった。宇宙膨脹では、計量(メトリックテンソル) g_ik の場に速度の概念を適用したことにおいて、"我々はただ、動き の状態をエーテルに帰属させることから自らを防御しなければならない。" という彼の考えから逸脱し、誤りを発展させたのかもしれない。
宇宙の果てからの直進光、この宇宙の果ては、原点から時間が経っていないこと:
宇宙の果ては原点から光の速度に近い速度で飛び去っている。その場所は、宇宙の始まりの時刻を止めている。だからそこに至る時間を
考えなくてもよい。という反論。特殊相対論を膨脹宇宙に適用しようとするのは、めずらしく貴重である。しかし、光の速度に近い速度
で移動する物体は歳をとらないが、それをみる我々が歳をとるのである。原点から宇宙の果てまで物体が移動するのに必要な宇宙年齢の
1/2 の時間は、宇宙の中心から眺めるこちら側に存在する経過時間である。 (特殊相対論には同時刻が定義できる。A-B-Aと光を往復させ
て、Bで光が反射する時刻と同時刻なのは、光がAを出てからAに帰るまでの中央の時刻とする。宇宙の果てと同時刻になるのは、ここの宇
宙年齢の 1/2 の時刻である。*)
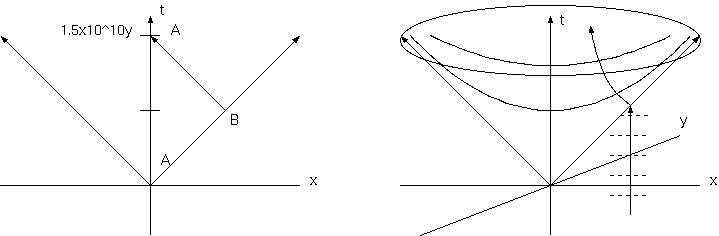
膨脹宇宙の泡の中では、空間は双曲面をしている。泡の中の空間は無限ということについて:
1999 年の 4 月の日経サイエンス、佐藤勝彦氏訳の Martin.A.Bucher、David.N.Spergel の "Infration in Low-Density Universe" は、
新しいインフレーション理論、オープン・インフレーションの考えを紹介している。その中で、擬真空から眞の真空に変る、2段階目の
インフレーションを行う、光速で膨脹する泡の中の空間が無限という話である。泡の膨脹開始時点からの経過時間は、膨脹の円錐に
そって時間が経たないから、同じ経過時間を結んだ双曲面が空間になる。それは、無限の広さをもつ負の曲率の空間になるという。
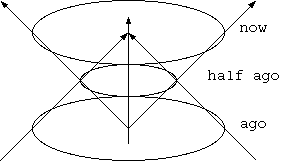
これは、宇宙の果ての特殊相対論的な議論と解釈でき、不思議な感動を与える。膨脹宇宙の周辺での宇宙膨脹からの局所経過時間をτとする。 v= x/t, γ=1/√(1-v^2), τ= t/γ= t√(1-v^2) = √(t^2-x^2), τ^2= t^2 - x^2 から、 局所経過時間τ一定をむすんだ超曲面は、負の曲率の双曲面をなし無限の広さをもつ。
過去の閉ざされた方向には現実に地平線があったように見えても、実際的に空間が無限というのは、光に近い速度で飛んでも 空間に限界や周期性をもたないことである。この未来の方角への光線は、膨脹宇宙では、もとより無限であった。 原点から同時刻を結んだ双曲面が無限空間とは、どういう意味があるのかは難しい。その意味を体験できるのだろうか。 ここで真直と考えている座標軸は、遠方では膨脹宇宙の円錐に沿って曲っているかもしれない。 内部の時間は外からその泡に入ってからの経過時間であり、外からみると各時点で有限の泡であり、外から入ることができるが、 出ることができないというから、少なくとも、光エーテルによる曲った光のモデルではないようだ。
この泡、光速で広がる暗い泡を爆発させてビッグバンを体験させるというこの最終兵器が原理的にも可能でないことを祈る。 この描像は、少し怖いことかもしれない。この宇宙が 2 度目のビッグバンというのだろうか。それは、実証可能な仮説だろうか。 外から入ってきた物質が短期間の高温を経験して生き残れるのだったら、それは、実証可能である。ビッグバン以前の物質の存在が その実証になる。そして、もし実証されたなら、このビッグバンは、自然現象だったかもしれないが、誰かの最終兵器だったかも しれないことになる。人工的なビッグバンは、作った本人もその場から逃げ出すことができないから、兵器というよりは、宇宙の近隣を 光速で拡大しながら破壊する自爆装置である。それは、宇宙の殆んどすべてを捨て周りの迷惑を顧みない自暴自棄も極端な話である。 そこから宇宙は真っ新の様相で始まるのである。人類は、単細胞生物を 30 億年経験し、多細胞になって 6 億年にしかならない。 みずからそこまでの破壊を受けたと理解することはまずないだろう。そういうひとときの幻想を導く話である。
速度 v= x/t で移動する宇宙の周辺の経過時間τの1/γの短縮の比率は、周辺宇宙の奥行のローレンツ短縮の比率と同じである。 その逆数γを距離 x にある間隔 dx に掛算して積分すると、∫γdx= ∫1/√(1-(x/t)^2) dx= ∫t/√(t^2-x^2) dx これは x<t では、 arc tanh(x/t)= 1/2 ln((t+x)/(t-x)) であり、t が x に近づくとどこまでも大きくなる。 これが、特殊相対論的膨脹宇宙の周辺短縮、宇宙の果てに無限の物体が薄くなって畳み込まれているという描像である。
dx/dt= c(t)= rx/t - 1
x'= rx/t - 1 を解くには u= x/t とおくと、もとの式は、x'= ru - 1、dx/dt= ru-1、 dx= (ru-1)dt、になり、 x= ut、dx= udt + tdu をつかうと (ru-1)dt= udt + tdu、変数分離し、 ((r-1)u-1) dt = t du、dt/t= du/((r-1)u-1)、ln|t|= 1/(r-1) ln|u- 1/(r-1)|+c、 u= c t^(r-1) - 1/(1-r)、x= ut= ct^r - t/(1-r)、これは、すでに x(0)= 0 をみたす。x(1)=0 から c= 1/(1-r)。
x= 1/(1-r) (t^r - t)、
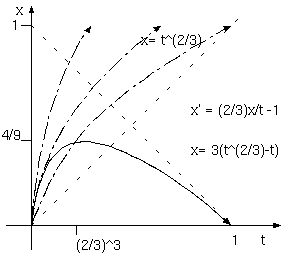
時間微分、x'= r/(1-r) t^(r-1) - 1/(1-r) は、 x'(1)= -1 をみたす。 r= 2/3 では、x= ct^(2/3) - 3 t、x(1)=0 から c= 3 をいれ、光経路は、
x= 3(t^(2/3) - t)
時間微分は、x'= 2 t^(-1/3) - 3 となる。
地平線で光が止まる光の頂点は、dx/dt= 0 から、x/t= 1/r をつかい、t^(-1/3)= 3/2, t= (2/3)^3 となる。x= 3(t^(2/3) - t) に代入すれば、佐藤文隆の"ビッグバン"での "膨脹因子 a(t)= 4/9 での引き返し" という説明と一致する。
"量子と実在"、ニック・ハーバート著、はやし・はじめ訳、白揚社 p.23からの引用。
"イギリスの指導的物理学者、かの高名なウイリアム・トムソンのちのケルビン卿が、マイケルソン・モーリーの実験の数年後に語った 次の言葉は、物理学者の一般的な態度を示すものであった。 "私たちにとって確実なことが一つある。それは、光エーテルの実在性と 物質性(substantiality)である。""
この言葉は、当時の学者にどれだけ先見性がなかったかを示す逸話であるが、これが膨脹宇宙論では文字通りの復活を果している。
曲って戻る光は、空間的な曲がりではない、時間と距離の図での曲がりは、速度変化である。石を真上に投げ上げ、真直に落ちてくるように、 時間軸を横に取った図の曲線は、対称的な抛物線とちがい、登りよりも墜ち方が緩やかである。向うへ進んでいた光がこちらに向かいだす、 方向転換かともとおもうと、それも方向転換ではなく、光速より速い物体からのこちら(内側)向きの光が、しばらくは向うに引っ張っていかれて いたのが、空間(?)が光速以下になると、こちらに向かい出すのである。
この光の引き返し現象は、本当にあるのだろうか。例えば、ニュートリノに質量があれば、それを追い越す系があるから、右巻き左巻きのスピンの 2種類ができると習った。光だけは、系が追い越せないものだった。系とは、特殊相対論で速度の違う慣性系の意味である。異なる場所に行くこと を、系を次々乗り替えるというのは、まるで速度をもった慣性系がその空間に所属してるようだが、 系の乗り換えであるから、粒子は、遠方に行っても加速されるわけではないようだ(*)。
光は、系に対する速度を変えず、エネルギーと運動量を波長を延ばして下げる。それがどこまで下がっても、到達するというのは、どうしてだろう。 ブラックホールの事象の地平線のように、光が越えられない境界でないのはなぜだろうか。それは、どこでも系に対する速度が光速という仮定 だから、少なくとも少しは系を乗り換えて、何とかはい上がってやって来ることができる、ということだろうか。 ブラックホールの事象の地平線の内部から外に向かった光が引き返すのと、仕組はどう違っているのか。
粒子がその場所に行っても系の乗り換えだから加速されないなら、宇宙膨脹の中で、ある場所から光速に近い速度で飛びだした宇宙船は、 周囲との相対速度を徐々に落し、そのうち停止するということのようだ。粒子は、停止してしまうとそのあとは、系を乗り換えられない。 なぜなら、停止しているからである。その場に停止したままである。これでは、まるで速度に比例する抵抗のようだ。 粒子の性質がそれなら、もし、ニュートリノに質量があるなら、粒子の地平線を越えられず、光の背景輻射はあっても、 それ以前のニュートリノの背景輻射は存在しないということか。
(*) 測地線の物理にあるように加速の項は存在する(2017 6/8)。
光速は、g_ik 自体から計算できる。膨脹宇宙の各時点の g_ik から、各時点の光速を使えば、光エーテル的描像よりもましな方法で、 曲った経路の光が計算できるかもしれない。それが同じ結果になるか調べる必要がある。そう思って、やってみると全く逆の結果になった。
ds^2= dt^2 - (GA)^2 (dx^2+dy^2+dz^2)
フリードマン宇宙の計量の式に空間的間隔 dl= √(dx^2+dy^2+dz^2)を使い、ds=0 をいれると、dl/dt= 1/(GA) が光速。 空間的曲率が 0 のとき、G の従う微分方程式、(dG/dt)^2= G0/G から、G∝ t^(2/3) である。 光速は、c(t)= t^(-2/3) とすると t= 1 で c(t)= 1 を満たす。光速 c(t) から光の経路 x(t) の求出は、単純に dx/dt= -c(t)= -t^(-2/3)、 x(t)= -3t^(1/3) + C である(C は任意定数)。 光が現在この場所に来ていること x(1)= 0 を使い、
x(t) = 3(1 - t^(1/3))
となる。この光の経路は、45度の線に見える距離の 3 倍の距離から来る逆方向に曲った光の経路である(下図)。この光の経路は、フリードマン宇宙の 計量の時間変化、G の増大を字義どおり使用し、光速の時間的変化としたもので、宇宙膨脹という解釈を必要としないし、物差の縮小という 解釈もいらない。なにより光エーテルを使用しない。しかし、膨張宇宙的結論とは、全く違う結果になっている(*)。 この経路は、直線的な距離よりも遠い所から来ているため、光の減衰が多くなる現象を説明することができるかもしれない。
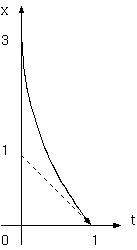
(*) 物差しの縮小の解釈には合致している。光速が昔大きかったから、光は、光速一定の場合の距離より 3 倍遠方から来る。 当時の物差しで測れば違うが、それは計量変化を無視する系である。
ある時空点の g_ik 場を速度をもった系だとするのは、電磁気で力線を物質的実在とみて、電磁場の速度を考えるのと同様に、 怪しい方法であろう。ある系で磁力線があって、それを速度 v で横切る電荷の系では、磁力線が速度 -v で横切っているとみるわけではない。 電荷は電場を見ているのである。電磁場は観測系によって変換されるから、場の速度とは、一種、混乱した概念である。 g_ik 場も観測系によって異なるから、それに速度を与えるのは同様の問題がある。 電磁場が系によってローレンツ変換されるように、g_ik もローレンツ変換される訳ではない。 g_ik は変換方法を表す不変式の係数である。 しかも、局所慣性系では、g_ik は、g_00= 1, g_11= g_22= g_33= -1 というミンコフスキー時空の標準値である。
物質の移動は、光円錐の中だけで、光の移動ですらこのように制限されるという光円錐を、曲がる光の膨張宇宙に書き込めば、 次のようになる(下図)。それらの光円錐は、媒体の速度によって、吹き流しのように、色んな方向を向いている。 時空点に、小さな光円錐を描くのはすべて、一般相対論の光エーテル的理解であるといって良いのかもしれない。
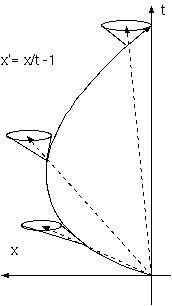
ある時空点を通過する光は、均一でどこから来た光も等しい性質をもつ。その時空点の全ての局所慣性系は、その光とは光速の関係にあるが、 互いに光速までの全ての速度をもつ。それゆえ、その系の速度をその点の光の速度(これを遠方から知ることができるとして、)から光速を 引いて与えることはできない。その時空点に唯一の速度を与え、その時空点の標準的な静止系を設定するのは、特殊相対論的に誤りである。 (それは、その時空点の全ての局所慣性系は、大きな速度の可変性があるのに、唯一であること、この見方では全ての局所慣性系からみて光速一定 は成立できないだろうと思われる点である。)
光エーテルを認めるなら、特殊相対論を否定することになり、マイケルソン・モーリー実験を説明できなくなり、物理は一からやり直しになる。 2種類の曲がった光経路の光エーテル的描像、dx/dt= rx/t - 1 (r= 1, 2/3) では、ある時空点の光速を、その時空点の媒体速度 rx/t と 光速 1 の差で与えている。光速 1 は、この場所からみた光速をそのまま、遠方の局所に適用している。 順序としては、媒体速度を先に与え、光の経路がそのあとに求まる。
そうではなく、遠方過去の光速を g_ik 自体から先に与え、光経路を求めたのが、dx/dt= -c(t)= -t^(-2/3)、x(t)= 3(1 - t^(1/3))である。 それは、全く反対の性質の光経路になる。より遠方の空間からの光の経路にみえる。しかし、これが宇宙の膨張や収縮を表している訳ではない。 光エーテル的概念では、光経路 x(t) があると媒体速度は、dx/dt + 1 になるが、光経路 x(t) の微分 dx/dt に先与の光速 c(t) を加算した 媒体速度 dx/dt + c(t) は常に 0 である。局所光速は 1 だが、ここから見るその時空点の光速は 1 ではなく、計量から直接に求まる。
光が曲って戻って来ているとするとき、最遠の距離は、宇宙年齢の 1/2 の距離よりも短い。直線的膨張 x= vt において光の経路は、 x= -t ln|t| であり、dx/dt= 0 の時刻と距離は、1/e である。これは、50.4 億光年になる。減速膨張 x= t^2/3 では、光の経路は、 x= 3(t^(2/3) - t) となり、光が曲る頂点は、t= 8/27, x= 4/9 である。137億年にいれると 60.89 億光年の場所になる。
最初光は、光速より速い後退場所からこちら向きに出て、こちらに向かっても向うに進んでいて、あるとき速度を失いこちらに向かい出す。 虫が膨張する風船の上を進むように光が媒体に対して速度をもち、媒体が x/t の速度をもつという考えは、特殊相対論以前の 光エーテル論 である。物質は光速に制限されても慣性系は光速に制限されないという考え方は、光を追い越す系を容易に設定する。その系からみると 光が逆進するということさえ使っている。光の運動量が系によって逆転するためには、光速の系から見た止まった光のエネルギーが 非ゼロでないといけない。この考え方はほとんど無謀な、特殊相対論の成果のすべてを放棄する試みである。ここからみると遠方の光の 速度は、一度止まりこちらに向かう、その地平線の近傍の系からみると問題がないが、ここからみたその停止した光とは一体、何だろうか。
特殊相対論的にみれば、この光の経路の頂点 x/t= 1 (又は x/t= 3/2)は、現在の我々から光速で飛び去っていた場所であり、そこからの ドップラー効果が無限大である。光速にどこまでも近い場所では時間経過がなく、そこよりも先からの光は、来ることができない。 光の経路は、(一般相対論で仮に曲ったとしても、) そこで途切れその先を考えることができない。その外からは光だけでなく全ての影響 のない因果の地平線である。その場所に僅かな質量でも存在させるのには無限大のエネルギーが必要であるから、それは仮に有限宇宙 とすると有限の質量しかもたない宇宙全体を使っても不可能なことであり、有限宇宙には存在しえないなにかの幻影であろうといえる。
重要なことは、現在の 1/1000 程度の時刻の晴れ上がり時点の背景輻射が見えるためには、原点近辺の光が戻ることが必要なことである。
そのような計量の場所の例として、例えば、ブラックホールの事象の地平面がある。ブラックホールの半径方向の計量は、∞になり、 時間方向の計量は 0 になる。そこでは、半径方向の物差しは長さが 0 になり、時間の経過は無限に遅くなり、光速度が 0 になる。 しかし注意すべきは、光がそこで方向転換はしないことである。光が方向転換をする計量とは一体あり得るのだろうか。 全くないのでないか、そのために必要なことは何か、について考える。
その時点以前とその時点以降で時間の経ちかたが逆転すること。その場合、その時刻で時間軸が折れ曲がる必要があり、 一般座標変換が折れ曲がりのない滑らかな写像であるという原則を崩す。g_ik の時間微分が連続でないということになる。 また、それは、空間軸についても言え、空間軸に折れ曲がりを必要とするものも存在しないと考えてよい。 ある場所までの空間が折れ返すと、光は、そこで反射するように戻ってくるだろうが、その時空の一点において、 光の逆転を期待するのは、g_ik の微分可能性から排除できる。光がそのまま戻って来るというのは、ブラックホールの地平面が そうであるように時空の特異面であるが、それよりもさらに存在し得ない特異性を要求するのである。
折れ曲がりでなくて、光は、時空を使ってぐるっと回って来ているのであり、ある時空点による反射ではない、ということでは ないだろうか。それでは、光がぐるっと回って来るためには、その場所の時空は、計量はどうであればよいのだろうか。
光円錐がそこでは、ある時刻より前では、外側に向かっていて、ある時刻ではちょうど円錐の近い側面がこちらの時間軸と平行 であって、それからすこし時間が経過すると光の円錐はこちらに向かい、光は時間空間図の上でぐるっと回って来る。それが、 膨張宇宙説の光の回廊の描像であろう。そこに必要なものは、時空のゆっくりとした傾斜だけであり、特異性は必要でないよう に考えられる。近くから発した光がある地点より先に届かないという意味では特異であるが、局所に特別なものは不要である。 そこでは、ds= 0 という光の経路は、時空間の座標変換によって、こちらの時間軸に平行であるだけである。光の進路の空間軸 と時間軸だけの2次元 (dx, dt) を考え、局所からミンコフスキー時空 (dx', dt') への変換において、
dx'= a dx + b dt
dt'= c dx + d dt
とし、変換後の ds^2 を
ds^2= dx'^2 - dt'^2
として上の変換を代入して、
ds^2= (a^2-c^2) dx^2 + 2 (ab - cd) dxdt + (b^2-d^2) dt^2
g_11= a^2 - c^2, g_14= 2(ab - cd), g_44= b^2 - d^2 である。dx,dt が 0 でなく ds^2= 0 なら光が存在すると考え、例を探す。
a = c, かつ b = d は、g_ik を恒等的に 0 とし、ds^2= g_ik dx^idx^k という不変式を成立させない。物差し、時計の存在 できない時空であるから、除外してもよいだろう。
b = d で、a != c なら、g_ik が恒等的に 0 ではなく、計量として存在し得るのではないか。g_44 = 0 であれば、光速が 0 になる。 これは、特殊相対論で慣性座標系が光速度をもつローレンツ変換に相当し、(γ= 1/√(1-v^2) を除外した疑似)ローレンツ変換、
x'= x - vt
t'= t - vx
に v= 1 をいれると
x'= x - t
t'= t - x
となり、a= 1, b= -1, c= -1, d= 1 の上の変換に相当する。それはあり得ないローレンツ変換であるが、一般の局所の変換として 何ら問題のない変換ではないか。時空の変換は場所、時間とともに徐々に滑らかに変化していって、局所の変換が光速の慣性系に 相当するローレンツ変換でもよい。しかし、 g_11= a^2 - c^2= 0 になるので、光速 √(-g_44/g_11) は 0/0 の不定であり、0 ではない。 これは、局所慣性系が光速で飛び去る時空である。そこでの時間と空間は、ミンコフスキー時空に変換後に同じものの符号違いになる。 ということは、そこには時計と物差しの区別のないものしか存在しないことを意味し、それは、この変換に対して疑いを抱くに十分である。
は、光速 u= dx/dt= 0 をもつには、b= +-d であればよい。
(a^2 - c^2) u^2 + 2 (ab - cd) u + (b^2 - d^2) = 0
は、a^2= c^2、ab != cd なら 1 次方程式、解は、u= -(b^2-d^2)/2(ab-cd)。a^2 != c^2 なら 2 次方程式、解は、 u= (cd - ab +-|bc - ad|)/(a^2 - c^2)、u= (d - b)/(a - c) 又は -(b + d)/(a + c)。u= 0 を満たす a,b,c,d は、あり得る。
v を残して、上の疑似ローレンツ変換の光速を求めると、a= 1, b= -v, c= -v, d= 1 であるから、v!= 1 では a^2 - c^2 = (1-v^2) != 0 になり、bc-ad= v^2 - 1 であるから、v<1 では bc-ad<0, v>1 で bc-ad >0 である。u= +-|v^2-1|/(1-v^2)= +-1、 疑似ローレンツ変換の局所光速は+-1 である。v= 1 のときに光速不定。γは、v= 1 で無限大になるから、γを含めた局所ローレンツ変換、
dx'= γ(dx - v dt)
dt'= γ(dt - v dx)
は、dx' dt' の両方が無限大になる。この数学的な特異性は、ここからみた地平面にだけにある。しかし、地平面で光が反射する とはまだいえない。こちらから地平面に進んでいった光がそのまま先に行き、向うからの光がこちらに来るだけかもしれない。 光速で飛ぶ地平面を文字どうり事象の地平面とするなら、向うからなにも来ないから、光はこちらから進んで反射するか、地平面 は完全黒体面でないといけない。局所慣性系の速度になんら制限がなく、地平面は事象の地平面ではないという立場をとるなら、 光は地平面を越えて行き来する。計量の場に局所慣性系の速度を関連付ける光エーテル理論なら、地平面が飛び去る向うからの光 を受け入れるだろう。
しかしながら、この議論で抜け落ちているのは、実際のフリードマン宇宙の計量が、それを満たしているかどうかである。それは、 実に怪しい。それは例えば電磁場を自由に配置してよいなら可能なことも現実に物理的に存在を決めるマックスウエル方程式の解か どうかによって現実性をみる必要があるようにである。
空間計量 g_11 は、G^2 A^2 が相当するが、G は時間の関数で時間とともに増大するもの、A は空間の関数であり、
A= 1/(1+ zr^2/4), (z= 1(球状), -1(擬球状), 0 (ユークリッド的平坦))
となっている。時間的計量 g_44 には固定的値 -1 が取られていて、それが 0 になることはない。ゆえに、光速を 0 にするためには、 空間側の係数 g_11 が ∞ になる必要があるが、それは、A が擬球状であるときの r= 2 の場所である。そのとき空間的計量 g_ii は ∞になる。宇宙は周辺短縮し、r がそれを越えると A は符号が反転するが、A^2 しか計量にはでてこないので、問題があるわけではない。
その場合、宇宙の周辺で光速が 0 になる条件が満たされているが、それが光の廻廊になっているかどうか怪しい。むしろ、宇宙の原初 の光の回帰は、光エーテル的解釈に依る、とみるほうが理解が容易である。もともと、フリードマン宇宙の計量の式は、物差しの縮小 する式であり、宇宙膨張の式ではないから、その式をまともにとっても得るところは少ないのかもしれない。
A の球状、擬球状も逆転しているようにみえる。宇宙がある大きさの限界をもつものを球状と呼ぶのは、通常の習慣である。A の大きさに おいて限界を持つのを球状、∞にするのを擬球状としている。AとGは空間計量をその2乗に比例させ(g_11, g_22, g_33= A^2 G^2)、AとGは、 物差しのサイズの逆数を意味している。G の増大は、空間の物差しの縮小である。 A が∞になるとき(擬球状(z=-1)でr= 2 のとき) 周辺空間の物差しの微小化によって空間的限界を与えるのである。それに反して、 球状の場合の-∞〜∞までの∫ A dr が 2πを与えることが示されるがこれは、物差しの大きさに積されるものであるから、 G と A とともに、その逆数でないと、その意図するものにはなっていない(*)。
そのような計量の意味の取り違えによって GA がその逆数でしかないとき、時間的関数 G がどのようになるか、例えばそれが空間的曲率 が正のとき、サイクロイドの微分方程式を与えるなどを議論してもさほどの意味のない議論である。
(*) このことは、 "ポアンカレ宇宙" のR^2-r^2 に "どの定規の長さも" 比例する宇宙の式と、 G=1, z= -1 の A^2 が一致することを考察すれば理解できる。"この仮想の世界では、大きい球に閉じ込められていて"、という言葉で始まる ポアンカレ宇宙は、有限の半径 R 内に無限の体積のある宇宙である。
(1) Gの増大は収縮宇宙を意味し、ハッブル定数が測定できるはずもないが、仮に138億年とすれば138億年前に無限大から収縮してきた宇宙、 という解釈ができる。または、
(2) 振動宇宙の条件を満たす臨界密度を超える密度なら、Gが現在、減少位相にあるため膨張宇宙、という解釈もあり得る。そのとき、 過去が無限か有限かは密度によるが、未来は138億年後に無限の大きさに発散する宇宙である。最後に、
(3) G,Aの逆数を忘れた計量の理解そのままで、膨張宇宙という解釈が現代まで続くフリードマン宇宙がある。
様々な解釈は、いずれも矛盾をもつが、 (3)は(1)(2)と違い基本的誤りである。それがどう変化するかの問題に、少なくとも宇宙のサイズは、 銀河間の距離= 物差し比例で、1/Gであり、Gではない。銀河間のサイズを物差しの逆数に見ている。空間間隔は物差しのサイズであり、 その逆数の G = √g_ii ではない。ds^2= g_ik dx^i dx^k は不変量である。楕円の a^2 x^2 + b^2 y^2 = r^2 (a>b)のaが大きいx座標は 短縮している。