エラー訂正コード(ECC)の話
1ビットエラー訂正・2ビットエラー検出 (SEC/DED) のエラー訂正コードについて、その理論と具体的な設計上の留意点を解説したものである。
現在ではパソコンのメモリにも使用されているECCについてはご存知のかたが多いでしょう。
しかし、ECCの回路自体を設計することはあまり経験することがなかったかも知れません。
ここではHamming Codeとして知られる1ビットの誤りを訂正するECCについて、その実際の設計方法について解説します。
1.ECCの簡単な歴史
情報理論の創始者とも言われる米国のクロード・シャノンによって符号伝送は遅延を許容するならば品質の悪い伝送路でもいくらでも正確に伝えることができることは理論的に示されたのですが、その具体化を最初に提示したのは1952年に当時Bell研在籍のハミング(Hamming)でした。
彼は従来のパリティビットを拡張することで1ビットの誤り位置を検出する符号を考案しました。
パリティビットが1ビットの誤りの存在を検出(Detect)するのに対して、この符号はその誤り位置を検出するのでバイナリ符号であればそれを訂正(Correct)することができるのです。
これによってデータはディジタル化によって品質を劣化させることなく伝送・保存が可能になることが示されその後に衛星通信などから実用が始まります。
Hammingのエラー訂正符号の成功はその後の多くのエラー訂正技術に発展し、コンピュータのメモリの微細化・大容量化により必然的に発生する誤りの自動修正、磁気記憶装置における誤り訂正機能を用いた大容量化、CD・DVDへの適用による大容量メディアの安価・量産など情報産業の基本技術として大きな発展を遂げつつあります。
Hammingは符号を構成する各要素の間の距離(distance)をそのビット列の各々の違いの総和で定義し、1ビットの誤り訂正のためにはその最小値(minimum distance)が3以上であることが必要十分であることを示しました。
この「距離」は数学上での距離の3原則を満たしておりHamming距離と呼ばれます。
距離の3原則とは?
数学で言う距離(Metric)とは空間上の任意要素(x、y)の相互で定義される値M(x,y)が以 下の性質を満たすことである。
・M(x,y) ≧ 0 (0になるのは x=yのときに限る)
・M(x,y) = M(y,x) (反射律)
・M(x,y)+M(y,z)≧M(x,z) (三角律:三角形の2辺の和は他の一辺より大きい)
また符号生成のための生成マトリックスの考えを示し、これがこの後の多くの符号理論の元になりました。
この後に誤り訂正符号は大きな進歩を遂げ、様々な符号が考案され実用化されました。
一例をあげると
・隣接した複数ビットの誤りの訂正機能
これは例えば4ビット、8ビットから成るチップの障害に対応するものです。
・小さなパケットに適当な複数ビット誤り訂正のボーゼ・チャウダリ・ハンチントン(BCH)符号
・磁気ディスク装置に用いられるFire符号など
レコード内の複数ビットがファームウェアなどで訂正できます。
・大きなバーストエラーを訂正できるReed-Solomon符号など
これによってCDやDVDが実用化されました。
2.誤りを検出、訂正する原理
ここで対象になっているのは、例えば通信回線を通じて伝送されるデータとかメモリに書き込むデータのように送り手と受け手があって、その間でデータが変化してしまう可能性のあるものです。
簡単のためにデータの長さは一定で送り手、受け手で了解があるものとします。
伝送路の上での雑音などの原因で、データの一部が変化して例えば1から0に、またはその逆に変わるものとし、抜けたり余分に入るようなことはないものと仮定します。
このモデルの最も簡単なものはデータが1ビットまたは2ビットから構成されているものです。
これを具体的に見えるように表現して見ましょう。
2進の数字0と1で表される2つの状態があるとします。この値が途中で変化してしまったことを検出するためには、もう1ビット追加して状態を(0,0)と(1,1)の2個の状態で表現することが適当でしょう。もちろん(0,1)と(1,0)の2個でも同じですが。
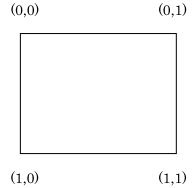
この図のように(0,0)から1ビットの誤りが発生しても他の正常な状態(1,1)にならずに実際には定義されていない状態(0,1)または(1,0)になり、誤りが発生したことが認識できます。
では、2ビットから成る4個の状態(0,0)、(0,1)、(1,0),(1,1)の場合はどうでしょうか?
この場合に更に1ビットを追加して3ビット構成として、追加した1ビットを全体の個数が偶数になるように決めます。
つまり(0,0,0)、(0,1,1)、(1,0,1)、(1,1,0)とするのです。
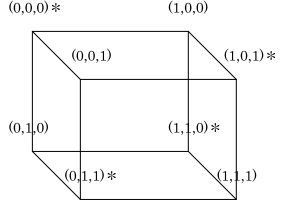
図から判るように正常な状態(*で示したもの)はほかの正常な状態と隣接していません。
従って1ビットのエラーでは必ず未定義の状態になりエラーの発生が検出できます。
次にエラーの訂正について考えます。
2個の状態の場合には、それぞれ(0,0,0)と(1,1,1)に正常の状態を割り当てます。
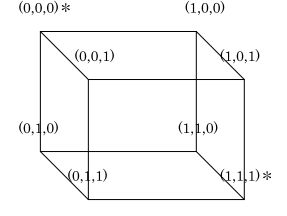
この図で正常な状態以外の各状態は(1,0,0)、(0,1,0)、(0,0,1)の3状態が(0,0,0)の状態が1ビット誤ったものとして、(0,1,1)、(1,0,1)、(1,1,0)の3状態が(1,1,1)の状態の1ビット誤りとして処理されることにより、1ビットの誤りが訂正できます。
これ以上の状態が大きな場合については図で示すのは困難であるので、これを符号空間のベクトルとして表すことにします。
例として4ビットから成る符号 (0,0,0,0)、(0,0,0,1)、(0,0,1,0)、、、(1,1,1,0)、(1,1,1,1)について述べます。
このままでは最初の2個(0,0,0,0)と(0,0,0,1)についてみても、最後の項しか違いがなく1ビットの誤りで違うものになってしまうことが明らかです。
これを両者の間の符号間距離(値の異なる項の数の和)が1であると定義します。
これに誤り検出や訂正の機能を持たせるには更に何ビットかを追加してこれを次元の高いベクトル空間の中に配置し、それが互いの間に隙間を持つ(つまり符号間の最小距離を大きくする)ことができるようにするのです。
まず1ビット追加して、最後の項は全体の1の数が偶数になるようにします。
つまり(0,0,0,0,0)、(0,0,0,1,1)、(0,0,1,0,1)、、、(1,1,1,0,1)、(1,1,1,1,0)とするのです。
このようにして作られたデータは互いに少なくとも2個所異なっており、符号間最小距離は2となっています。(実際には距離は全て偶数です)
従ってどこか1ビット間違えても正しい符号と識別することができ、1ビットの誤りを検出する機能を持ちます。
それでは、さらに1ビット追加したら誤り訂正機能を持たせられるでしょうか?
これが不可能なことは簡単に示せます。
仮に6ビットの符号として最初のものを(0,0,0,0,0,0)としてみます。
するとこの符号が1ビット誤るときには(1,0,0,0,0,0)、(0,1,0,0,0,0)、、(0,0,0,0,0,1)の6個の可能性があります。同様にして他の15個の符号もそれぞれ6個づつの1ビット誤りの符号に囲まれます。
1ビットの誤りが訂正できるには元の符号を合わせて7個づつのこれらの符号が全て異なるものであることが必要条件で、都合7x16=112個の符号が存在できなければならず、26=64しか組み合わせのない6ビットの符号では不足なのです。
今度は付加するチェックビットの側から考えてみましょう。
3ビットのチェックビットがあれば、8個の異なる状態が表現できます。
誤りのない状態と2進数で表現された7桁の数値のどれかが反転しているか否かを表現できる可能性があります。
実際にこのような組み合わせを作ることが可能であり、これがHamming Codeとなったのです。
これを拡張すると、4ビットの付加で11ビットまで、5ビットの付加で26ビットまで、6ビットの付加で57ビットまで、7ビットの付加で120ビットまでの1ビット誤りが訂正できます。
3.符号の作り方
皆さんの中には昔こんな種類の数当てゲームを経験したひとがいるでしょう。
例えば6枚の紙にそれぞれいろいろな数字が並べてあって、そのうち一つの数字が載っている紙を選ぶとその数字を当てると言うものです。
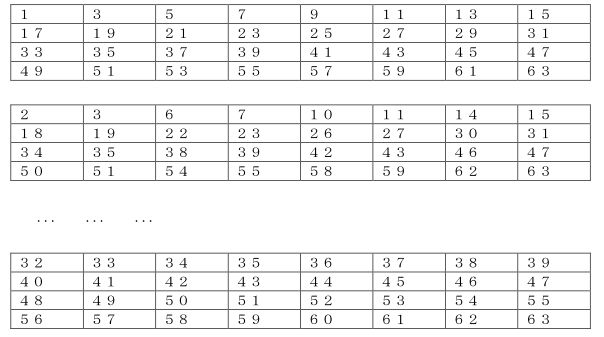
原理はとても簡単でそれぞれの紙には20、21、、、、、、25に対応する値が1である数字が書いてあるので、それを合計すれば共通の数字がすぐに計算できるのです。
Hammingの考案した方式もこれと全く同じ原理で誤りの発生した位置を「計算」することができる方式でした。
4ビットのデータに3ビットのチェックビットを付加することを考えてみましょう。

とすると1、2、3はいわゆる単位行列となっています。
4ビットの符号に対して表の●の部分に対応してExclusive-Or演算を行った結果が1、2、3に対応してチェックビットとなります。
読み出した値に対しても同様の操作を行うと、その違いに対応する1、2、3の値の和から違いのある場所が計算できるのです。(実際には3と4は入れ替えてあるので、位置は入れ替え前のもので示されます。
折角ここまでしたのだから、更に2ビットの誤りがあることは位置の指定は無理でも検出できると便利です。
このためには符号間の最小距離が4以上であることが必要十分なのです(考えて下さい)。
ところが符号の距離を偶数にするにはとても簡単な方法があるのです。
それはパリティチェックビットを付加することです。
パリティビットを付加するとそれぞれの符号の中の1の数は全て奇数(または全て偶数)となるので、その間の距離は全て偶数になります。
従ってデータの4ビットにHammingチェックの3ビット、更にパリティチェックの1ビットを付加した符号は全ての1ビットエラーを訂正し、更に2ビットエラーの発生を検出することができます。

4.実際の実装の手法
ここまでの話は古典的な原理に基づくものですが、実際のECC回路はこのような形では設計されていません。
一番の問題は最後の行のパリティの演算が段数が多くてこれが演算速度のクリチカルパスになることです。
そこで、これらの行が一次独立であることを利用して1、2、3行の和を最後の行に加えた(演算はExclusive-Or)結果

を用いても同じ効果が得られるのでこの形を採用します。
ところで、この●の位置を見て気づかれたことがあると思います。
全ての列パターンは異なっており、●の数は奇数になっています。
実は単位行列を含みかつ各列が異なっていることのみがエラー訂正を可能にするために本質的なことであり、各列が奇数であることが2ビットエラー検出のための条件なのです。
実際の多くの応用では訂正には論理回路を用います。
この場合、計算によって算出するような綺麗な形よりも少ないハードウェアにより高速に演算できる回路を作れることが条件になります。
その場合●の数ができるだけ少なく、かつ各行で均等であることが望ましいことになります。
例えば16ビットのデータに6ビットのチェックビットを付加する場合には6C3 = 20であることから各列を全て●が3個の列とすることができます。
古典的方法では

これから列を入れ替えて

を作り、これにパリティビットを追加して

とします。
これをパリティビットの行だけを上の5行のExclusive-Orを加算して修正すると

となり一番多い行では●が10個となりチェックビット(右側の6ビット)の演算には10入力のExclusive-Or演算が必要となります。
これは各行での●の数が不均等であることと、●が5個ある列のを用いていることが原因になっています。
このままでもビット6からビット21までの16ビットをデータビットとし、先頭の6ビットをチェックビットとしてECCシステムとしての利用は可能ですが、実用のためには更に改善の余地があります。
まず●の数が最小でしかも各行に均等であることを条件にして生成してみましょう。
6C3=20であることから、16個の列は全て3個以下の●で済み、しかも偶数行であることから対称性を利用すれば均等に割り当てが可能なことが予想されます。
以下にその20列を全部並べると

ここで20列は不要なので対称性のある*の4列を外して残りにパリティビットの6列を加えると

これにより、各行は8入力でパリティが生成でき、例えば2入力E_OR/E_NORゲートを3段で済みます。
この結果、例えば4桁の16進数(16ビット構成)の0x55AA (B'0101010110101010')に対しては、各行の●の位置にある1から生成されるチェックビットはB'100111'となり、全体のビットはB'1001110101010110101010'となります。
仮にこの最後のビットが誤って読み出された(0が1になった)とすると、これをチェックビットも含めて演算した結果はB'001011' となります。
これがエラーの症状(Syndrome)を表すもので、簡単に言えばエラーの発生している列のうちで●がある行に対応します。
ハードウェアではこれを各列のパターンとの一致を調べ、一致しているものがあれば(この例では最後の列 ○ ○ ● ○ ● ●)その列に対応するビットの1ビット誤りとして訂正(ビットの反転)が行われます。
もしSyndromeが全て0でなくて、しかも一致するものがなければこれは複数ビットのエラーで訂正できないものとして処理されます。
もちろん3ビット以上のエラーが発生した場合にはSyndromeは全て0になったり、他の1ビットエラーのパターンに一致したりしてエラーの見逃しや誤訂正が発生する可能性がありますが、これは本訂正回路の守備範囲外のことです。
このようにしてECC回路が構成されるのですが、実際にはこれでも完全ではありません。
例えばメモリシステムにおいては定義外や未実装または障害によってチェックビットを含めた全ビット障害と言うパターンが発生する可能性があります。
これは本来の検出・訂正の範囲外ですが、特定のエラーパターンであるのでエラーとして検出できることが望ましいのです。
実際、装置の出荷試験時にアドレスを実装範囲を超える番地としてアクセスしたときにエラーとして検出されないことが問題になった事例がありました。
これは全て0および全て1のパターンのSyndromeをエラー無し、または1ビットエラーのパターンに一致しないようにすることで可能となります。
これに関しては必要十分条件が理論的に求められていますが、そこから詰めるまでもなく多くの場合には各チェックビットを偶数パリティと奇数パリティを適当に混在させることで実現可能です。
それでどうしても駄目な場合には列を別のビットパターンに入れ替えて再度試みることになります。
ちなみに先の例は全て偶数パリティとして議論してきたので、この場合には全て0のパターンは正常データと見なされてしまいます。
全て1のパターンは各行の重みが全て偶数であるので、本来のチェックビットは全て0となり、Syndromeは訂正不能データとなります。
この場合にはどこか2個所の行を奇数パリティとすれば全て0、全て1の両パターンとも訂正不能データとできることは容易に解るでしょう。
5. その他の拡張について
ECCに関する改善はいろいろ提案されています。そのうちのいくつかについて。
・複数ビットエラーの訂正
これには離散した複数ビットの訂正を目指すものと、隣接した(複数ビットから成るグループ内の)複数ビット訂正を目指すものがあります。
前者の例としては先に少し触れたボーゼ・チャウダリ符号などがありますが余り効率が良くないのと、語幅が大きいとハードウェアでの対応が大変なので(結果としてメモリなどではアクセス速度が落ちる)通信などの用途にしか用いられないようです。
後者は例えばメモリの4ビット(nibble)や8ビット(byte)の単位で発生しうる複数ビットのエラーに対応するもので、これはHammingの方式が2進の値を扱うのに対して例えば16進数のガロア体(Galois Field)に拡張して考えたものです。
以前にIBMのD.ボッセン氏が熱心に研究し、富士通でもMシリーズの2次キャッシュに使用した例があります。
しかし、最近ではむしろ訂正よりも複数ビット誤り検出のほうに主力が注がれているようです。
6. 関連技術
メモリの場合にECCにより1ビットの誤りを訂正しても、誤りの発生原因が読み出し経路のマージン不足等による一時的なものでない限り誤ったデータはメモリ上に残っている可能性があります。
以前にはメモリの内容が放射線などの外部要因でランダムにエラーが発生する可能性があることが指摘されました。
このために誤ったデータに対しては訂正書き込みを行うとともに、メモリの使用されていない時間を利用して周期的に全メモリの内容を順次再書き込みすることが行われたこともあります。
また、メモリの1素子に恒久的な障害を検出した場合、ランダムに発生するエラーと合わせて訂正不能エラーとなることを防止するために、この素子に関連するデータを予備の素子に変換する手段を持たせたこともあります。
これもメモリの速度が論理素子に近くなるにつれて難しくなり、O/S側での再マッピングで対応できるので行われなくなっていると思います。
7. 最後に
ECCは高級な装置において信頼度を向上させるための技術と受け取られて、民需製品にはあまり関係がないと考えて関心が少ない向きもありますが、これは大きな認識間違いです。
ディジタル製品と言えどベースになっているのはアナログ技術であり、アナログデータをどれだけのマージンでディジタル化できるかが性能とコストを決定するのです。
ECC回路の付加によってメモリなどのLSIの加工精度、回路のノイズマージン、伝送路のノイズマージンなどをもっと小さくすることが許容できれば一層の高集積化と製造コストの低減の可能性が広がります。
従ってECCの技術はアナログ技術の最後の一滴を絞り取ってコストダウンを行う手段だとの認識が必要となります。
市販のまたは既存回路のECC回路の利用できる分野は限定されていますが、以上に示したような手法によって誰でも自分の設計する回路に好きなビット幅のECC回路を組み込むことは可能であり、その場合の増加する設計量やコストは回路全体に比較するとはるかに小さなものです。
ここに示したルールを使用する限り市販のECC回路に比べても遜色ない回路が作れるのです。
これは私が実際の設計現場で遭遇した経験に基づいてのことですが、全ビット障害と言う想定外のケースが起こり得るとの考察と、それから対応方法を検討して実装にこぎつけるまでの思考の広げ方は実際のハードウェア設計者にとって非常に重要なことだと考えます。
実際にそこまで辿り着くためには考えられない事態まで想像する思考の広げ方と、それに対処する手法の発見との二段階となりますが実際に発生する障害を「想定外」と言い訳する見苦しさよりも一手先を先読みする思考が常に要求されているものと認識することの大切さを常に心に留めていたいものです。