慣性の原理を物理の要石とみなす限り、この立場は、確かに正当化される唯一のものである。しかし、普通概念のふたつの深刻な批判が存在する。 第1番目には、それは、それ自身作用するが、作用されることのない、あること(時空連続体)を思考する科学の思想の様式に反している。 これが、E.マッハ(Mach) が力学のシステムにおいて、空間を作用の原因として除去しようと試みをすることを導いた理由である。 彼に従えば、物質粒子は、非加速的な運動を空間に相対してするのではなく、宇宙の他の全ての質量の中心に相対してする； この方法で、ニュートンとガリレオの力学に対比して、力学的な現象の原因の系列は閉じられる。 媒体を通した作用の現代理論の制限のなかにおいて、この概念を開発するために、慣性を決定する時空連続体の特性が、電磁場に類似する 空間の場の特性と見なされなければならない。古典力学の概念は、これを表現する方法を与えない。この理由のため、その解として E.マッハの試みは、現在の所、失敗している。我々は、後にこの観点に戻って来るだろう。 第 2 番目として、古典力学は、互いに非均一な運動をする参照空間への相対性の原理の拡張を直接に求める欠乏症を呈している。２物体の 質量比は、力学では互いに基本的に異なるふたつの方法によって定義された；最初には、それらの間に同じ動機の力が与えられるときの互い の加速の比として(慣性質量)、次には、同じ重力場のなかでそれらに作用する力の比として(重力質量)。 全く異なって定義された、これらふたつの質量の等価性は、事実、非常に高い精度の実験によって確認された(エトベッシュ(Eötvös)実験) が、古典力学は、この等価性に何も説明を提供しない。しかしながら、この数値的一致がこれらふたつの概念の現実の性質の等価性に 還元され割り振られた後にだけ、科学は正当性を完全にすることは明らかである。

(慣性質量)・(加速)= (重力場の強さ)・(重力質量)

加速が物体の性質から独立であることは、慣性と重力質量の間に数値的一致があるときだけである。いま、$K$ を慣性系としよう、 互いにまた他の物体から十分遠い質量は、そのとき、$K$ に関して加速から解放されている。我々はまた、これらの質量を、$K$ に関して 均一に加速している座標系 $K'$ に参照させる。$K'$ に相対的には、全ての質量は等しく平行な加速をもつ； $K'$ に関しては、それらは、 あたかも、重力場が存在し、$K'$ が加速されていないかのように行動する。 いまのところ、そのような重力の "原因" についての問いを俯瞰すれば、それは後に我々を占有するだろうが、この重力場が現実のもの であると我々が考えることを妨げるものはない。すなわち、$K'$ が "静止" していて、重力場が存在するという考えは、$K$ だけが "許される" 座標系であって重力場はないという考えと同等に考え得るものである。 座標系 $K$ と $K'$ の完全な物理的等価性の仮定を、我々は "等価性の原理" と呼ぶ。この原理は、明らかに、慣性と重力質量の同等性の法則 に深く結合していて、互いに非均一的運動をする座標系への相対性の原理の拡張を意味している。 事実、この概念を通して、我々は、慣性と重力の性質の統合に到着する。なぜなら、それを見る我々の方法に従えば、同じ質量が慣性だけ の作用のもとにある($K$に関して)、又は慣性と重力の結合した作用のもとにある($K'$に関して)、のいずれとも表れることができるからである。 慣性と重力のそれらの性質の統合によって数値的な等価性を説明できる可能性は、私の信ずるところによれば、遭遇する全ての困難も、 この進歩と比較すれば小さいと考えなければならないような、そのような古典力学の概念に対する優越性を相対性の一般理論に与える。

等価原理は、ガリレイ領域を扱うのに、我々が等しく非慣性系、すなわち、慣性系に相対して加速と回転から自由でないような座標系、 を使用してよいことを要求する。もし、我々が、さらに、ある座標系への選別に客観的な理由についてのいらいらする問いから完全に 離れようとするなら、そのときは、我々は、任意に運動する座標系の使用を許さなければならない。この試みを真面目にしようとする とすぐに、我々は、特殊相対論によって我々がそこに導かれた時間と空間のあの物理的解釈との相克に出会うことになる。 なぜなら、$K'$ をその z'軸が $K$ の z 軸と一致して、後者の軸の周りに一定の角速度で回転している座標系としよう。$K'$に相対的に静止 する剛体の構成は、ユークリッド幾何学の法則に従うだろうか？ 一方、$K'$は慣性系ではないので $K'$ に関する剛体の構成の法則を、また、 自然法則一般についても、我々は、直接には知らない。しかし、我々は、慣性系 $K$ に関して、これらの法則を知っている。そして我々は、 それゆえ、$K'$に関しての式を推定できる。 $K'$ の $x'y'$ 平面の原点の周りに円とこの円の直径を描くことを想像しよう。さらに、我々が 互いに等しい多数の剛体棒を与えられていると想像しよう。我々は、これらを $K'$ に相対的に静止している円の円周と直径にそって順次 直列に並べることを想定する。もし、$U$ を円周にそったこれらの棒の数、$D$ を直径にそった数とすると、そのとき、もし、$K'$ が $K$ に相対的に 回転していないなら、我々は次をもつ。 \[ {U \over D} = π \] しかし、もし、$K$' が回転するなら我々は違う結果を得る。$K$ の確定した時間 t において我々は全ての棒の端を決定することを考えよう。 $K$ に関して、円周上の全ての棒は、ローレンツ短縮を経験する。しかし、直径上の棒は、この短縮(それらの長さにそった！)を経験しない。 それゆえ、次式が出てくる。 \[ {U \over D} ＞ π \]

我々が考察してきた場合は、表面の2次元的扱いで説明した場合と類似する。後者もまた、単純な計量的意味をもつ表面(例えば楕円体の表面) の座標系を導入することは、不可能である。一方、平面上でデカルト座標、$x_1, x_2$ は、単位測定棒によって測られた長さを直接に意味する。 ガウスは、彼の表面の理論のなかで、この困難を乗り越えた。連続の条件を満たす以外は全く任意な曲線座標を導入し、そして、その後にだけ、 これらの座標値が表面の計量的特性に関係しているとすることによって。 類似の方法によって、我々は、一般相対論に任意の座標値、$x_1, x_2, x_3, x_4$ を導入する、時空点を一意に数値化し、隣接する事象が隣接 する座標値に関連する；それ以外、座標値の選択は任意である。もし我々が、そのようなどの4次元座標系にも有効である形式を法則に与える なら、すなわち、法則を表現する方程式が任意の変換に関して共変であるなら、我々は、その最も広い意味において相対性の原理に忠実である。

(*訳注)この文を意訳。原英文: "もし、我々が $K'$ に関して、全体として不自然な方法で (すなわち、$K'$に関して時間に明示的に 依存する法則のような方法で)、時間を定義しなければ、同じことが $K'$ から判断しても実行されなければならない。"

物理学の4次元時空連続体のなかに類似の関係がある。重力場のなかで自由落下する観測者の直近傍において、重力場は存在しない。 我々は、それゆえ、つねに、時空連続体の無限小の領域をガリレイ的とみることができる。そのような無限小領域には、それを参照すれば、 特殊相対論の法則が有効であると我々がみなすべき、慣性系(空間座標 $X_1, X_2, X_3$ と時間座標 $X_4$ をもつ)が存在する。 我々の単位測定棒と時計によって直接に測定可能な量、 \[ dX_1^2 + dX_2^2 + dX_3^2 - dX_4^2 \] または、その負の、 \[ ds^2= - dX_1^2 - dX_2^2 - dX_3^2 + dX_4^2 \tag{54} \] は、それゆえ、ふたつの隣接する事象(4次元連続体のなかの点)に対する一意に決定される不変量である。持ち寄り重ねるとき互いに等しい 測定棒と、持ち寄るときその速度の等しい時計とを、我々が使用するならばである。このなかには、ふたつの測定棒の相対的な長さ、ふたつの 時計の相対的な速度は、それらの以前の履歴から原理的に独立である、という物理的な仮定が不可欠である。しかし、この仮定は、確かに経験 によって保証されている；もし、それが成立しなければ、鋭いスペクトル線はあり得ないだろう。なぜなら、同じ元素の単独原子は、確かに同 じ履歴を持たない。そしてなぜなら、ー単独原子の以前の履歴に依存する相対的可変性を仮定してーこれら原子の質量または固有の周波数が かつてずっと互いに等しかったと想定することは理屈に合わない。

以上述べたことに従って、一般相対論の定式化には、不変量の理論とテンソルの理論の一般化が必要であることが明らかである； 任意の点変換 に関して共変である方程式の形成についての問いが持ちあがる。テンソルの一般化された計算は、相対論よりもずっと以前に数学者達によって 開発された。リーマン (Riemann) は、ガウス (Gauss) の任意次元の連続体の一連の考察を最初に拡張した； 予言的視点をもって、ユークリッド (Euclid) 幾何学の一般化の物理的な意味を見た。そして、とくにリッチ(Ricci) とレビ・チビタ(Levi-Civita) とによって、テンソルの計算の 形式での理論の開発が続いた。ここで、このテンソル計算の最も重要な数学的な概念と演算を短く提示する。

テンソルは、線形直交変換の不変量理論と同様に、添字の性質を保存して、乗算によっても形成できる。例えば、 \[ A_μ^ν B_{στ} = C^ν_{μστ} \tag{60} \] 証明は、変換の規則から直接に出てくる。

テンソルは、異なる性質のふたつの添字に関する縮約によって形成できる。例えば、 \[ A^μ_{μστ}= B_{στ} \tag{61} \] $A^μ_{μστ}$のテンソル性質は、$B_{στ}$ のテンソル特性を決定する。証明ー \[ A^{μ'}_{μστ} = {∂x_α \over ∂x'_μ}{∂x'_μ \over ∂x_β}{∂x_δ \over ∂x'_σ} {∂x_t \over ∂x'_τ} A^β_{αδt} = {∂ x_δ \over ∂x'_σ} {∂x_t \over ∂x'_τ} A^α_{αδt} \]

これによって、テンソルの代数的な特性に対する全ての本質的なことは、言い終えた。

基本テンソル $dx_ν$ の任意選択における $ds^2$ の不変性から、(55)に整合する対称性の条件と関連して、 $g_{μν}$ が 対称共変テンソル(基本テンソル)の成分であることが出る。様々な $g_{μν}$に対応して $g_{μν}$ の行列式 $g$ を作り、そしてまた、 余因子を $g$ で割ろう。これら余因子を $g$ で割ったものは、$g^{μν}$ で記述し、そして、その共変の性質は、まだ知られていない。 そのとき、我々は、次をもつ。 \[ g_{μα} g^{μβ}= δ_α^β= 1 (if α=β), 0 (if α≠β) \tag{62} \] もし、我々が無限小の量(共変ベクトル)を形成するなら、 \[ dξ_μ= g_{μα} dx_α \tag{63} \] $g^{μβ}$を掛け、$μ$に渡り総和して、(62)を使って、次を得る。 \[ dx_β= g^{βμ} dξ_μ \tag{64} \] $dξ_μ$の比は任意であるから、そして、$dx_β$ も $dξ_μ$ と同様にベクトルの成分であるから、$g^{μν}$ は、反変テンソルの成分(*) (反変基本テンソル)であることが出てくる。δ_α^β (混合基本テンソル)のテンソル性質は、それゆえ、(62)によって続いてくる。 我々は、基本テンソルによって、共変添字の性質のテンソルの代わりに、反変添字性質のテンソルを導入したり、その逆もできる。例えば、 \[ A^μ= g^{μα} A_α \\ A_μ= g_{μα} A^α \\ T^σ_μ= g^{σν} T_{μν} \]

(*) もし、我々が (64)に$∂x'_α \over ∂x_β$を掛け、$β$に渡り総和し、$dξ_μ$をアクセント付きの系に変換することによって置き換えるなら、次を得る。 \[ dx'_α= {∂x'_σ \over ∂x_μ} {∂x'_α \over ∂x_β} g^{μβ} dξ'_σ \] 上でなされた言明は、これから出る。なぜなら、(64)によって、我々はまた $dx'_α= g^{σα'} dξ'_σ$ を持たねばならず、両式は、 どの $dξ'_σ$ の選択にも成立しなければならないからである。

それにも関わらず、一般の場合のテンソルの不変量の微分演算は、最も満足に認識される、次の方法でレビ・チビタ(Levi-Civita)とワイル(Weyl) によって導入された。($A^μ$) を反変ベクトルとし、その成分が、$x_ν$ の座標系に関して与えられているとしよう。$P_1$ と $P_2$ を、 連続体のふたつの無限近傍点とする。点 $P_1$ を囲む無限小領域にとって、質量を考慮する我々の方法に従って、それに関して連続体が ユークリッド的な $X_ν$ の座標系 (虚数の $X_4$ 座標をもつ) が存在する。$A^μ_{(1)}$ を点 $P_1$ でのそのベクトルの座標値としよう。点 $P_2$ に ベクトルを引き、$X_ν$ の局所系を使って、同じ座標値をもつ ($P_2$を通る平行なベクトル) ことを想像せよ。そのとき、この平行ベクトル は、$P_1$ にあるベクトルと移動とによって、一意に決定される。我々は、この操作を、その一意性は後に示すが、ベクトル ($A^μ$) の 無限近傍点 $P_2$ への平行移動と呼ぶ。もし、我々が $P_2$ 点でのベクトル ($A^μ$)と $P_1$ から $P_2$ への平行移動によって得るベクトルと のベクトルの差を作れば、我々は、ベクトル ($A^μ$) の与えられた変位 ($dx_ν$) に対する微分と見なすことのできるベクトルを得る。

量 $g_{μν}$ は、連続体の全ての計量特性を決定するから、$Γ^ν_{αβ}$ をも決定しなければならない。 もし、ベクトル $A^μ$ の不変量を考えるなら、すなわち、その大きさの2乗、 \[ g_{μν} A^μ A^ν \] が不変量であり、これは、平行移動によって変化しえない。我々は、それゆえ、次をもつ。

これはワイルが１階の反変テンソル密度(*)と呼ぶ量である。そこから、 \[ Ａ= {∂Ａ^μ \over ∂x_μ} \tag{74} \] は、スカラー密度であることが出る。

(*) この表式は、$A^μ \sqrt{g} dx= Ａ^μ dx $ がテンソルの特性をもつことのなかで正当化される。どのテンソルも$\sqrt{g}$ で乗算されるとき、 テンソル密度に変わる。我々は、テンソル密度には大文字のゴシック文字を使う。(訳注：全角文字を使用した。)

形成の一般法則は、いま、明らかになる。これらの式から、理論の物理的応用において興味のある他のいくつかを導こう。

もし、$A_{στ}$が反対称であるなら、我々は次のテンソルを、 \[ A_{στρ}= {∂A_{στ} \over ∂x_ρ} + {∂A_{τρ} \over ∂x_σ} + {∂A_{ρσ} \over ∂x_τ} \tag{81} \] それは、全ての添字の対に反対称であるが、周期的交換と加算によって得る。

$A^{στ}$ が反対称の場合、我々は (80) から、$τ$と$ρ$に関する縮約によって、次を得る。 \[ Ａ^σ= {∂Ａ^{στ} \over ∂x_τ} \tag{82} \] 一般の場合、(79) と (80) から、$τ$と$ρ$に関する縮約によって、我々は、次の式を得る。 \[ Ａ_σ= {∂Ａ^α_σ \over ∂x_α} - Γ^α_{σβ} Ａ^β_α \tag{83} \] \[ Ａ^σ= {∂Ａ^{σα} \over ∂x_α} + Γ^σ_{αβ} Ａ^{αβ}. \tag{84} \]

≪＝BACK　TOP∧　NEXT＝≫

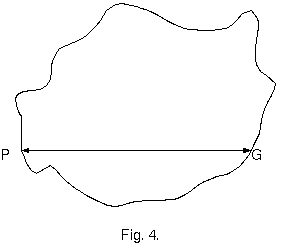
リーマンテンソル もし、我々が連続体の点 P から点 G に伸びる曲線が与えられたなら、そのとき、P に与えられたベクトル $A^μ$ は、平行移動によって G までその曲線に沿って動かすことができる。もし、連続体がユークリッド的 (より一般的に、座標の適切な選択に よって $g_{μν}$ が一定である) ならば、そのとき、その移動の結果として G に得られるベクトルは、P と G を結ぶ曲線の選択に依存しない。 しかし、そうでないとき、結果は移動の経路に依存する。この場合は、それゆえ、ベクトルは、もし、それを点 P から閉じた曲線に沿って運び、 再び P に達するならば、$ΔA^μ$ (その方向に、その大きさでなく) の変化を被る。我々は、いま、このベクトルの変化を計算する。 \[ ΔA^μ= §δA^μ \] 閉曲線の周りのベクトルの線積分へのストークスの定理のように、この問題は、無限小の線の大きさをもつ閉曲線の周りの積分に還元できる； 我々は、この場合に限定しよう。

我々は、最初に、(67) によって、 \[ ΔA^μ= -§ Γ^μ_{αβ} A^α dx_β \] このなかで $Γ^μ_{αβ}$ は、積分経路上の可変点 G にあるこの量の値である。もし、我々が次のように置き、 \[ ξ^μ= (x_μ)_G - (x_μ)_P \] P における $Γ^μ_{αβ}$ の値 を $\overline{Γ^μ_{αβ}}$ で表すと、そのとき、我々は、十分な精度をもって、次をもつ。 \[ Γ^μ_{αβ} = \overline{Γ^μ_{αβ} }+ {∂\overline{Γ^μ_{αβ}} \over ∂x_ν }dξ_ν \] さらに、$A^α$を $\overline{A^α} $から P から G への曲線に沿った平行移動によって得られた値としよう。いま、(67)によって、容易に証明できるのは、 $A^μ -\overline{A^μ}$ が1次の無限小であり、一方、曲線が1次の無限小の大きさをもつから、$ΔA^μ$ は、2次の無限小であることである。それゆえ、 もし、我々が次のように置いても、2次のオーダーの誤差しかない。 \[ A^α = \overline{A^α} - \overline{Γ^α_{στ}} \ \overline{A^σ} \ \overline{ξ^τ} \] もし、我々がこれらの値、$Γ^μ_{αβ}$ と $A^α$ を積分に導入して、我々は、2次より高次の全ての量を無視して、次式を得る。 \[ ΔA^μ= -({∂Γ^μ_{σβ} \over ∂x_α} - Γ^μ_{ρβ}Γ^ρ_{σα}) A^σ §ξ^α dξ^β. \tag{85} \]

(*) 曲線上の隣接点の方向ベクトルは、考慮中の各点の方向ベクトルから、線要素 ($dx_β$) に沿った平行移動によってもたらされる。