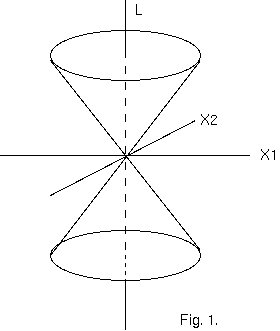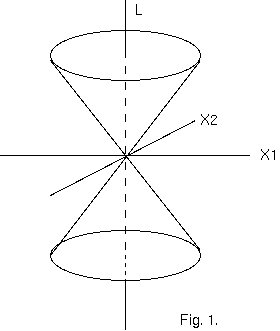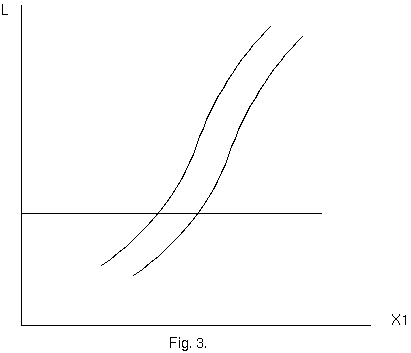≪=BACK TOP∧ NEXT=≫
特殊相対性の理論
剛体の構成に関する以前の考察が基づいたのは、ユークリッド幾何学の有効性の仮説に無関係に、空間の全ての方向、又は全ての
デカルト座標系の構成が物理的に同等であるという仮説であった。我々はこれを、"方向に関する相対性の原理" と表すことができ、
この原理に従って、テンソル計算の助けによって、どのように方程式(自然の法則)が見出されるかを示した。我々はいま、参照空間
の運動状態に関して、相対性があるかどうかを問う; 別の言葉では、物理的に同等である、互いに相対的な運動状態の参照空間が
あるかどうかである。力学の立場からは、同等な参照空間が存在することは現れている。なぜなら、地球上の実験は、我々が太陽に
対して毎秒約 30 km の速度で運動しているという事実を何も言わない。他方、この物理的な等価性は、任意の運動をする参照空間に
成立するとは見えない; なぜなら、力学的効果は、揺れる鉄道の列車のなかの物理法則が、均一な速度の運動をするそれのなかと
同じ法則をもたらすとは思えない; 地球の回転は、地球に対する運動の方程式を書き下すのに考慮しなければならない。それゆえ、
それに参照するなら、力学法則が (より一般的に物理法則が) 最も単純な形式によって表示できる、デカルト座標系、いわゆる慣性系
があるかもしれないと思えることが明らかになる。我々は、次の言明の有効性を推量してよい: もし、$K$ が慣性系であるなら、
そのとき、$K$ に相対して回転なく均一に動く全ての他の系 $K'$ もまた慣性系である; 自然法則は、全ての慣性系に一致している。
この言明を我々は、"特殊相対性の原理"と呼ぶ。我々は、この "平行移動の相対性" の原理から、方向の相対性に対して我々がすでに
行ったように、ある結論を引出す。
≪=BACK TOP∧ NEXT=≫
これを行うことを可能にするために、我々は、最初に次の問題を解かなくてはならない。もし、我々が、ある事象のひとつの慣性系 $K$ に相対する
デカルト座標 $x_ν$ と時間 $t$ を与えられるならば、同じ事象の、$K$ に相対的に均一に平行移動する慣性系 $K'$ に相対する座標、$x'_ν$ と時間 $t'$ を
どのように我々は計算できるだろうか? 前相対論の物理では、この問題は、無意識に次のふたつの仮説を作ることによって解かれた:ー
1. 時間は絶対的である; 事象の $K'$ に相対する時間 $t'$ は $K$ に相対する時間と等しい。もし、即時的信号を遠方に送ることができるならば、
そして、もし、人が時計の運動状態がその速度に影響を受けないことを知るならば、そのとき、この仮定は、物理的に正当と認められるだろう。
なぜなら、そのとき、時計は、ひとつひとつが類似で、同じく規制され、$K$ と $K'$ 系に渡って分布でき、それらに静止して、それらの表示は、
系の運動状態から独立しているだろう; ひとつの事象の時間は、そのとき、その直ぐ近傍の時計によって与えられるだろう。
2. 長さは絶対的である; もし、間隔が $K$ に相対的に静止して、長さ $s$ をもつなら、そのとき、それは、 $K$ 系に相対的に運動する $K'$ 系に
相対しても同じ長さ $s$ をもつ。
もし、$K$ と $K'$ の軸が互いに平行であるなら、これらふたつの仮定に基づく単純な計算が、変換の方程式を与える。
\[
\begin{align}
x'_ν&= x_ν - a_ν - b_ν t\\
t'&= t - b
\end{align}
\tag{21}
\]
この変換は、"ガリレオ変換(Galilean Transformmation)"として知られる。時間で 2 回微分して、我々は、次を得る。
\[
{d^2 x'_ν \over dt^2} = {d^2 x_ν \over dt^2}
\]
≪=BACK TOP∧ NEXT=≫
さらに、ふたつの同時的事象には、(訳注:空間間隔が系によらない。)
\[
{x'}_ν^{(1)} - {x'}_ν^{(2)} = x_ν^{(1)} - x_ν^{(2)}
\]
2 点間の距離の不変性は、2乗と加算からの結果である。このことから容易に、ニュートンの運動方程式のガリレオ変換(21)への共変性がでる。
こうして、物差しと時計に関するふたつの仮説を作るなら、古典力学が特殊相対性の原理へ合致するようになる。
しかし、このガリレオ変換への平行移動の相対性を建てようとする試みは、電磁現象に適用されるとき失敗する。マックスウェル・ローレンツ
(Maxwell-Lorentz) の電磁方程式は、ガリレオ変換に関して共変でない。特に我々は、(21) によって、$K$ を参照する光線がもつ速度 $c$ をもつ
ことは、参照する $K'$ の方向に依存して、異なる速度をもつことに注目する。$K$ の参照空間は、それゆえ、その物理的特性によって、それ
(静止エーテル) に相対運動するその他の全ての参照空間と区別される。しかし、全ての実験は、参照物体とする地球に対して相対的な電磁現象
と光の現象が地球の移動速度による影響を受けないことを示した。これらの実験の最も重要なものは、マイケルソンとモーリー(Michelson and
Morley) の実験であり、知られていることを想定する。特殊相対性の原理の有効性は、電磁現象に関しても、疑いをもつことは難しい。
他方、マックスウェル・ローレンツ方程式は、運動物体中の光学の問題の扱いにおいて、その有効性を証明した。他の理論は、光行差、運動物体
中の光伝播(フィゾー(Fizeau))、二重星の現象観測(ド・ジッター(De Sitter)) の事実を満足に説明しなかった。マックスウェル・ローレンツ
方程式の帰結、真空中に光は速度 $c$ で伝播すること、少なくとも確定したひとつの慣性系 $K$ に関しては、証明されたと見なされなければならない。
特殊相対性の原理に従って、我々は、この原理の真実性を、全ての他の慣性系についても、また仮定しなければならない。
≪=BACK TOP∧ NEXT=≫
これらふたつの原理から、何かの結論を引出す前に、我々は、最初に、"時間"と"速度"の概念の物理的意味を復習しなければならない。
前に行ってしまったものから次のことは来る。慣性系に関して座標値は、測定と剛体の助けを伴う構成とによって、物理的に定義される。
時間を測定するために我々は、$K$ に相対して静止してどこかに存在する時計 $U$ を想像した。しかし、我々は、この時計では、時計からの
距離が無視できない距離にある事象の時間を時間を確定できない。なぜなら、事象の時間ととこの時計の時間とを比較するために我々が
使うことのできる "即時的信号" がないからである。時間の決定を完了させるために、我々は、真空中の光の速度の一定性の原理を採用できる。
我々は、類似する時計達を $K$ 系に相対的に静止して、次の状況に従って規制して、置くことを想像しよう。光線が時計のひとつ $U_m$ から
それが時刻 t_m を示す瞬間に送出され、真空の距離 $r_{mn}$ を通して旅行して、時計 $U_n$ に到達する; この光線が時計 $U_n$ に出会う瞬間に
この時計は $t_n = t_m + {r_mn \over c}$ を示すように時刻設定される(*)。光の速度の一定性の原理は、そのとき、この時計合わせが反論を導かない
ことをいう。時計のそのような調整を伴い、我々は、それらのどの側で起きる事象にも時間を割り振ることができる。この時間の定義は、$K$ 系
にだけ関係するものであることを注意することは不可欠である。我々は $K$ 系に相対的に静止した時計達を使っているからである。時間の絶対的
な特性をもつ前相対論の物理で作られた仮定 (すなわち、慣性系の選択から時間が独立であること) は、この定義からは決して出てこない。
(*) 厳しく言えば、最初に同時性を何か次のように定義することの方がより正確であろう: $K$ 系の点 A と 点 B にあるふたつの事象は、
間隔 AB の中点 M において観測されるとき、それらが同時に現れるならば、同時刻である。そのとき、時間は、$K$ に静止する類似の時計
の表示の組であり、それらは、同じ時刻を同時に記録する。
≪=BACK TOP∧ NEXT=≫
相対性の理論は、しばしば、次のように批判される。理論の中心的な役割を光の伝播に正当化なしに与えることを、それが光の伝播法則の上
に時間の概念を建てることを。状況は、しかしながら、次のようなものである。時間の概念に物理的な意味を与えるためには、異なる
場所の間に関連を打ち立てることを可能にする、ある種の過程が必要とされる。そのような時間の定義のために、人がどのような過程を選択
するかは重要でない。しかしながら、我々がそれに関して何か確かなことを知る過程だけから選択することは、その理論にとって長所となる。
これは、"真空中の" 光伝播において、考え得る他の過程より高い程度に成立する。マックスウェルと H. A. ローレンツの研究に感謝する。
これらの考察の全てから、空間と時間のデータは、物理的現実であり、単なる架空でない重要性をもつ; 特にこれは、座標系と時間がはいる
全ての関係に成立する。例えば、(21)の関係である。それゆえ、ひとつの慣性系 $K$ からそれに対して動く別の $K'$ へ我々がそれによって移る
真の変換方程式は何かと問うという意味だけでなく、それらの方程式が真か偽かを問うという意味もある。これが光速一定の原理と特殊相対性
の原理によって、独特に設定されることを示されるだろう。
この目的に向かい我々は、空間と時間とは、すでに示された方法で、ふたつの慣性系 $K, K'$ に関して、物理的に定義されたと考える。さらに、
K のひとつの点 $P_1$ から別の点 $P_2$ へ真空を通して光線を渡す。もし、$r$ が 2 点間の測定された距離ならば、そのとき、光の伝播は、次式を
満たさねばならない。
≪=BACK TOP∧ NEXT=≫
\[
r= c.Δt
\]
もし、我々がこの式を2乗し、$r^2$ を座標差 $Δx_ν$ で表せば、この式の代わりに我々は次のように書ける。
\[
Σ(Δx_ν)^2 - c^2 Δt^2 = 0
\tag{22}
\]
この式は、$K$ に相対する光の速度の一定性の原理を定式化する。光線を発する源の運動が何であれ、成立しなければならない。
同じ光の伝播は、$K'$ に相対的に考察できる。その場合も、光速一定の原理が満たされねばならない。
それゆえ、$K'$ に相対的に我々は、次式をもつ。
\[
Σ(Δx'_ν)^2 - c^2 Δt'^2 = 0
\tag{22a}
\]
式、(22a) と (22) とは互いに、$K$ から $K'$ への変換に関して相互に整合的でなければならない。これをもたらす変換を、ローレンツ変換
(Lorentz Transformation) と呼ぶ。
≪=BACK TOP∧ NEXT=≫
これらの変換の詳細に考察する前に、空間と時間について少し一般的な所見を述べる。
前相対論の物理では空間と時間は、分離した実体であった。時間の指定は、参照空間の選択から独立していた。
ニュートン力学は、参照空間に関して相対的であった、そのため、例えば、同じ(訳注:異なる?)場所にふたつの非同時的事象が生起するという言明は、
客観的意味 (すなわち、参照空間からの独立性) をもたなかった。しかし、この相対性は、理論の構築に役割をもたなかった。
人は、空間点についてを時間の瞬間と同じ様に述べた。あたかも、それらが絶対的現実であるかのように。
真の空間-時間の指定の要素が 4 つの数 $x_1, x_2, x_3, t$ で指定される事象であることは、観察されなかった。
何かが起きるという概念は、つねに 4 次元連続体のそれであった; しかし、これの認識は、前相対論の時間の絶対的な性格によって妨げられていた。
時間の絶対的な性格、とくに同時性のそれ、の仮説を放棄をすれば、時空概念の 4 次元性は、すぐに認識される。
物理的現実性をもつのは、そこで何かが起きる空間のなかの点でもなく、時間のなかの瞬間でもなく、事象それ自身だけである。
空間のなかに絶対的(参照空間から独立)な関係はなく、ふたつの事象間の時間のなかに絶対的な関係はなく、後に明らかになるように、
空間と時間の絶対的(参照空間から独立)な関係がある。
4 次元連続体の 3 次元の空間と 1 次元時間連続体とへの客観的合理性のある分割がないという状況は、
自然法則が 4 次元時空連続体のなかの法則として表現されるとき、論理的に最も満足する形式を呈することを示している。
これによって、相対論がミンコフスキーに負う方法における偉大な進歩がある。
この立場から考察すれば、我々は、$x_1, x_2, x_3, t$ を事象の 4 次元連続体のなかの 4 座標値と見なさなくてはならない。
我々は、4次元連続体のなかの関係を自身に描くのは、3 次元ユークリッド連続体と比較してずっと成功しない;
しかし、ユークリッド3次元幾何学の中でさえ、その概念と関係は、我々の精神の抽象の性質だけのものであって、我々の視覚と我々の接触の
感覚を通して形成されるイメージとは、決して同じではない。事象の 4 次元連続体の非分割性は、しかしながら、決して空間座標と時間座標
の同等性を含むものではない。反対に、我々は時間座標が物理的に全体として空間座標から違って定義されることを思い出さなければならない。
(22) と (22a) の関係式は、引用したとき、ローレンツ変換を定義し、さらに、空間座標から時間座標の役割の違いを示している;
なぜなら、項 $Δt^2$ は、空間項 $Δx_1^2, Δx_2^2, Δx_3^2$ とは反対の符号をもつ。
≪=BACK TOP∧ NEXT=≫
ローレンツ変換を定義する条件をさらに分析する前に、我々は、時間 $t$ の代わりに光の時間 $l= ct$ を導入する。定数 $c$ が後に開発する式に
明示的に入らないようにするためである。そのとき、ローレンツ変換は、最初に次の式を共変の方程式にするような方法で定義される。
\[
Δx_1^2 + Δx_2^2 + Δx_3^2 - Δt^2 = 0
\tag{22b}
\]
すなわち、もし、ふたつの与えられた事象(光線の放出と受容)を我々が参照する慣性系でそれが満足すれば、全ての慣性系に関して方程式
が満足するということである。最終的に、ミンコフスキーとともに我々は、実数の座標値 $l= ct$ の代わりに、虚数の時間座標を導入する。
\[
x_4= il= ict, (\sqrt{-1} = i)
\]
そのとき、光の伝播を定義する方程式は、ローレンツ変換に関して共変でなければならないが、次になる。
\[
Σ_{(4)} Δx_ν^2 = Δx_1^2 + Δx_2^2 + Δx_3^2 + Δx_4^2 = 0
\tag{22c}
\]
この条件は、つねに満足する(*)。もし、我々がより一般的な次の条件を満足していれば。
\[
s^2= Δx_1^2 + Δx_2^2 + Δx_3^2 + Δx_4^2
\tag{23}
\]
(*) その場合、この特殊化が理に適うことは、後に明らかになる。
≪=BACK TOP∧ NEXT=≫
は、変換に関して不変量でなければならないという条件である。この条件は、線形変換、すなわち、次の形の変換によってだけ満足される。
\[
x'_μ= a_μ + b_{μα} x_α
\tag{24}
\]
ここで、$α$に渡る総和は、$α= 1$ から $α= 4$ までに拡張される。(23), (24) の式をみれば、もし、我々が、次元の数と実数性の関係を無視するとき、
ローレンツ変換は、ユークリッド幾何の平行移動と回転変換に恒等的に定義されていることが分かる、我々は、また、係数 $b_{μα}$ が次の条件を
満足しなければならないことを結論することができる。
\[
b_{μα} b_{να}= δ_{μν} = b_{αμ} b_{αν}
\tag{25}
\]
一方、$x_ν$の比が実数であるから、$a_4, b_{41}, b_{41}, b_{43}, b_{14}, b_{24},$ そして $b_{34}$ は純虚数、それ以外の全ての $a_μ$ と $b_{μα}$
が実数であることが出る。
特別なローレンツ変換 もし、座標値のふたつだけが変換され、そして、もし、新しい原点を決めるだけの $a_μ$ が消滅するなら、我々は、
(24) と (25) の形の最も単純な変換を得る。そのとき、我々は、添字 1, 2 について、(25) の関係が与える 3 つの独立な条件のために、次式を得る。
\[
\begin{align}
x'_1&= x_1 cos Φ - x_2 sin Φ\\
x'_2&= x_1 sin Φ + x_2 cos Φ\\
x'_3&= x_3\\
x'_4&= x_4
\end{align}
\tag{26}
\]
これは、x_3 軸周りの(空間)座標系の空間のなかの単純な回転である。前に学んだ (時間の変換のない) 空間のなかの回転は、ひとつの特別な場合
として、ローレンツ変換に含まれる。添字 1, 4 については、我々は同様な仕方で、
\[
\begin{align}
x'_1&= x_1 cos Ψ - x_4 sin Ψ\\
x'_4&= x_1 sin Ψ + x_4 cos Ψ\\
x'_2&= x_2 \\
x'_3&= x_3
\end{align}
\tag{26a}
\]
≪=BACK TOP∧ NEXT=≫
その実数性の関係のために、$Ψ$は、虚数にとらなくてはならない。これらの式を物理的に解釈するために、我々は、虚数の$Ψ$の代わりに、
実数の 光時間 $l$ と $K'$ の $K$ に対する速度 $v$ を導入する。我々は、最初に、次の式をもち、
\[
\begin{align}
x'_1&= x_1 cos Ψ - il sin Ψ\\
l'&= -ix_1 sin Ψ + l cos Ψ
\end{align}
\]
一方、$K'$ の原点、すなわち、$x'_1= 0$ については、$x_1 = vl$ でなくてはならないから、これらの最初の式から、
\[
v= i tan Ψ
\tag{27}
\]
そして、また、
\[
\begin{align}
sin Ψ&= {-iv \over \sqrt{1 - v^2}}\\
cos Ψ&= {1 \over \sqrt{1 - v^2}}
\end{align}
\tag{28}
\]
そうして、我々は、次を得る。
\[
\begin{align}
x'_1&= {x_1 - vl \over \sqrt{1 - v^2}}\\
l' &= {l- v x_1 \over \sqrt{1 - v^2}}\\
x'_2&= x_2 \\
x'_3&= x_3
\end{align}
\tag{29}
\]
これらの式は、よく知られた特殊ローレンツ変換を形成する。それは、一般的な理論では 4 次元座標系の虚数角の回転と表現するものである。
もし、我々が通常の時間 $t$ を光時間 $l$ の代わりに導入するなら、そのとき、(29)のなかで、$l$ を $ct$ に、$v$ を ${v \over c}$ に置き換えなければならない。
≪=BACK TOP∧ NEXT=≫
我々は、隙間を埋めなければならない。光速一定の原理から、次の式、
\[
ΣΔx_ν^2 = 0
\]
が、慣性系の選択に独立である重要性をもつことが出る; しかし、$ΣΔx_ν^2$ の量の不変性は、これから決して出てこない。
この量は、係数を伴って変換されるかもしれない。これは、(29)の右辺に係数$λ$が掛かるかもしれないことによるのであり、その$λ$は $v$ に依存できる。
しかし、我々がいま示すように、相対性の原理は、この係数が 1 から異なることを許さない。我々は、その軸の方向に運動する剛体の丸い円筒をもつ
ことを想像しよう。もし、その半径が静止状態で単位の測定棒で測定されて、$R_0$ に等しいとするとき、運動中の半径 $R$ は、$R_0$ と異なるかもしれない。
相対論は、参照空間に関する物体の形態が、その参照空間に相対的なその運動に独立であるとは仮定しないからである。しかし、空間の全ての方向は、
互いに同等でなければならない。$R$ は、それゆえ、速度の大きさ $q$ に依存してよい、しかし、その方向に依存してはならない;
$R$ は、それゆえ、$q$ の偶関数でなければならない。もし、円筒が $K'$ に相対的に静止しているなら、それの側面の方程式は、
\[
x'^2 + y'^2 = R_0^2
\]
もし、我々が(29)の最後の2式を一般化して書くならば、
\[
x'_2= λx_2 \\
x'_3= λx_3
\]
そのとき、円筒の側面は、$K$ を参照して次の式を満足する。
\[
x^2 + y^2 = {R_0^2 \over λ^2}.
\]
要素λは、それゆえ、円筒の側方向の短縮を表し、このように、上から $v$ の偶関数だけであり得る。
≪=BACK TOP∧ NEXT=≫
もし、我々が第3の座標系 $K''$ を導入して、$K'$ に対して $K$ の $x$ 軸の負の方向に速度 $v$ をもって動くとすると、我々は、(29)を 2 回適用して次を得る。
\[
\begin{align}
x''_1&= λ(v)λ(-v)x_1 \\
&.... \\
&.... \\
l''&= λ(v)λ(-v) l
\end{align}
\]
いま、$λ(v)$ は、$λ(-v)$ と等しくなければならないから、そして、我々は全ての系で同じ測定棒を使うことを仮定しているから、
$K''$の $K$ に対する変換は、恒等変換でなければならないということが出てくる (一方、$λ= -1$ である可能性は考える必要がないから)。
(訳注:$λ(v)= 1$ という言明が省かれている。)
これらの考察において、不可欠であることは、測定棒の行動がそれらの以前の運動の履歴に依らないという仮定である。
運動する測定棒と時計 確定した $K$ の時間 $l= 0$ において、整数 $x'_1= n$ で与えられた点の位置は、$K$ に関して $x_1= n \sqrt{1 - v^2}$
で与えられる;これは、式 (29) の最初の式から出てきて、"ローレンツ短縮" を表わす。$K$ の原点 $x_1= 0$ に静止する時計、その鼓動が
$l= n$ で特徴付けられるものは、$K'$ から観察されたとき、次の式によって特徴付けられる鼓動をもつだろう。
\[
l'= {n \over \sqrt{1 - v^2}};
\]
これは、式 (29) の2番目から出てきて、その時計は、$K'$ に対して静止した場合よりも、ゆっくりと進むことを示す。これらふたつの帰結は、
必要な変更を加えれば(mutatis mutandis)、全ての参照系にとって成立し、独創的なローレンツ変換の物理的な内容を形成する。
速度の加算定理 もし、我々が相対速度 $v_1$ と $v_2$ をもつ、ふたつの特殊ローレンツ変換を結合するならば、そのとき、
ふたつの分離したローレンツ変換の代わりをする単独のローレンツ変換の速度は、(27) に従って、次で与えられる。
\[
v_{12}= i tan(ψ_1 + ψ_2)= i{tan ψ_1 + tan ψ_2 \over 1 - tan ψ_1 tan ψ_2} = {v_1 + v_2 \over 1 + v_1 v_2}.
\tag{30}
\]
≪=BACK TOP∧ NEXT=≫
ローレンツ変換とその不変量の理論についての一般的な言明 特殊相対論の不変量の理論の全体は、(23) の不変量 $s^2$ に依っている。
形式的には、それは、4次元時空連続体のなかで、前相対論の物理のなかの 3 次元ユークリッド幾何学の不変量 $Δx_1 + Δx_2 + Δx_3$ と同様
な役割をもつ。後者の量は、全てのローレンツ変換に関しては不変量でない;式 (23) の量 $s^2$ がこの不変量の役割を呈している。
任意の慣性系に関して $s^2$ は、測定によって決定できる; 物差しの単位を与えられ、任意の事象対に関して、それは、完全に確定する量である。
不変量 $s^2$ は、次元の数を軽視しても、対応するユークリッド幾何学の不変量から、次の点で異なっている。ユークリッド幾何学のなかでは $s^2$ は、
必然的に正である; それは、関係する 2 点が一緒になるときだけ消滅する。一方、次の式の消滅から、
\[
s^2= ΣΔx_ν^2 = Δx_1^2 + Δx_2^2 + Δx_3^2 - Δt^2
\]
そのふたつの時空点が一緒になると結論することはできない; 量 $s^2$ の消滅は、ふたつの時空点が真空中の(in vacuo)光信号によって
結合できるという、不変な条件である。もし、P が 4 次元空間のなかで $x_1, x_2, x_3, l$ によって表現される点(事象)なら、そのとき、
光信号の手段で $P$ と結合できる全ての "点" は、$s^2= 0$ の円錐上にある (図 1. と比較せよ、図は、次元 $x_3$ が抑圧されている)。
"上" 半分の円錐は、$P$ から光信号を送れる点ででき; "下" 半分の円錐は、そこから光信号を $P$ に送れる "点"を含むだろう。
円錐表面によって囲まれた内部の点 $P'$ は、$P$ とともに、負の $s^2$ を与える; $P'P$ と同様に $PP'$ もミンコフスキーに従って時間性である。
そのような間隔は、速度が光速よりも小さい運動の経路になり得る要素を表す(*)。この場合、慣性系の運動状態を適切に選ぶこと
によって、$l$ 軸を $PP'$ の方向に引くことができる。もし、$P'$ が "光円錐" の外部にあれば、$PP'$ は、空間性である; この場合、慣性系の
適切な選択によって $Δl$ を消滅させることができる。
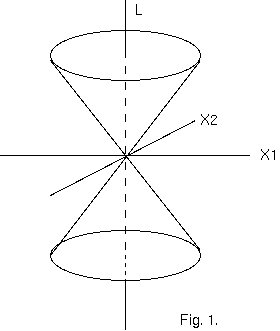
(*) 光の速度を超える物質の速度は、特殊ローレンツ変換 (29) の根号表式 $\sqrt{1 - v^2}$ から、可能でない。
≪=BACK TOP∧ NEXT=≫
虚数の時間変数 $x_4= il$ を導入することによって、ミンコフスキーは、ユークリッド空間の 3 次元連続体の不変量の理論に完全に類似する、
物理現象の4次元連続体のための不変量の理論を作った。それゆえ、特殊相対論の 4 次元テンソル理論は、3 次元空間のテンソル理論から、
次元数と実数性の関係だけが異なっている。
任意の慣性系のなかにある $x_1, x_2, x_3, x_4$ の 4 つの量で指定される物理的実体、$A_ν$ は 4 元ベクトルといって、成分 $A_ν$ をもつ。
もし、$A_ν$ がそれらの実数性と変換特性との関係で、$Δx_ν$ に対応するならば;それは、空間性か時間性である。16 の量 $A_{μν}$ は、
そのとき、2 階のテンソルの成分を形成する。もし、それらが次の方法に従って変換するならば。
\[
A'_{μν}= b_{μα} b_{νβ} A_{αβ}
\]
このことから、$A_{μν}$ が変換特性と実数性特性に関して、ふたつの 4 元ベクトル $(U), (V)$ の成分 $U_μ, V_ν$ の積と同様に振舞うこと
が出てくる。全成分は、添字 4 を一度だけ含むと純虚数であり、それ以外は実数である。3 階と高階のテンソルも同様な方法で定義される。
これらのテンソルの加算、減算、乗算、縮約、そして微分の演算は、全体として、3 次元空間のテンソルの対応する演算に類似している。
≪=BACK TOP∧ NEXT=≫
テンソル理論を4次元時空連続体に適用する前に、我々は、特に反対称テンソルをさらに検討する。2階のテンソルは一般に $16= 4.4$ の成分を
もつ。反対称テンソルの場合、ふたつの等しい添字をもつ成分は、消滅する。そして、等しくない添字の成分は、等しく反対符号で対をなす。
それゆえ、電磁場の場合そうであるように 6 個だけ独立成分が存在する。事実、我々がマックスウェルの方程式を考察するとき、それらが
テンソル方程式であると見なすことは、我々が電磁場を反対称テンソルとみなす場合に限って、可能であることが示される。さらに、3 階の
反対称テンソル(全ての添字対について反対称)が 4 つだけ独立な成分をもつことは明らかである。3 つの異なる添字の組合せが 4 つしかない
からである。
我々はいま、マックスウェル方程式 (19a), (19b), (20a), (20b)に戻って、次の記述法を導入する(*):
\[
Φ_{23}, Φ_{31}, Φ_{12}, Φ_{14}, Φ_{24}, Φ_{34}\\
h_{23}, h_{31}, h_{12}, -ie_x, -ie_y, -ie_z
\tag{30a}
\]
\[
J_1, J_2, J_3, J_4 \\
{1 \over c} i_x, {1 \over c} i_y, {1 \over c} i_z, iρ
\tag{31}
\]
そして、$Φ_{μν}$は、$-Φ_{νμ}$ に等しくなければならないとする慣習に従うなら、そのとき、マックスウェル方程式は、次の式に繋げられる、
\[
{∂Φ_{μν} \over ∂x_ν} = J_μ
\tag{32}
\]
\[
{∂Φ_{μν} \over ∂x_σ } + {∂Φ_{νσ} \over ∂x_μ } +{ ∂Φ_{σμ} \over ∂x_ν }= 0
\tag{33}
\]
(30a) と (31) から代入によって容易に検証できるように。
(*) 混乱を避けるためにこれ以降、3 次元の空間添字には $x, y, z$ を $1, 2, 3$ の代わりに使用し、数字の添字 $1, 2, 3, 4$ を 4 次元時空
連続体に予約する。
≪=BACK TOP∧ NEXT=≫
もし、我々が仮定するように$Φ_{μν}, J_μ$がテンソルの性質をもつならば、 (32), (33) は、テンソルの性質をもつから、ローレンツ
変換に関して共変である。その結果、これらの量をひとつの(慣性)座標系から他へ変換する法則に許されるものは、唯一に決定される。
電磁力学が特殊相対論に負うところの方法論的進展は、原理的にこのなかにある、つまり、幾つかの独立な仮定が消えることである。例えば、
我々が (19a) を、我々が上でしたように、方向の相対性の立場だけから見れば、我々は、それらが 3つの論理的に独立の項をもつことをみる。
これらの式に電気的強さが入ってくる仕方は、それらに磁気的強さが入って来る仕方とは、全体として、独立であるように現れている;
我々が、もし、$∂e_μ \over ∂l$ の代わりに、例えば $∂^2e_μ \over ∂l^2$ をもつ、又は、この項がなくても、それは、驚くべきことではないだろう。
他方、式 (32) にはただふたつの独立な項が現れている。電磁場は、ひとつの形式的な単位として現れ、電場がこの式に入ってくる仕方は、
磁場が入ってくる仕方によって決定されている。電磁的な場以外には、電流密度だけが独立な実体として現れている。この方法論的進展は、
運動の相対性を通して、電場と磁場が分離した存在を失う、という事実から起きている。ひとつの系から判断して、純粋に電場として現れている
ひとつの場は、他の慣性系から判断したとき、また磁場の成分をもつ。変換の一般法則は、電磁場に適用されたとき、特殊ローレンツ変換の
特別な場合として、次の式を与える。
\[
\begin{align*}
e'_x&= e_x, &h'_x= h_x\\
e'_y&= {e_y - v h_z \over \sqrt{1-v^2}},&h'_y= {h_y + v e_z \over \sqrt{1-v^2}}\\
e'_z&= {e_z + v h_y \over \sqrt{1-v^2}},&h'_z= {h_z - v e_y \over \sqrt{1-v^2}}
\end{align*}
\tag{34}
\]
もし、$K$ に関して磁場 ${\bf h}$ だけが存在して電場 ${\bf e}$ がないとき、$K'$ に関しては ${\bf e}'$も存在して、$K'$に相対的に静止した電荷
に作用するだろう。
$K$ に相対的に静止した観測者は、この力を、ビオ・サバール (Biot-Savart) 力または、ローレンツ (Lorentz) 電動力と呼ぶ。それは、
それゆえ、あたかも、この電動力が電場の強さと融け合って、単独の実体になったかのように現れるのである。
≪=BACK TOP∧ NEXT=≫
この関係を形式的に見るために、次の電気性の場の単位体積に働く力の表式を考察しよう。
\[
{bf k}= ρ{\bf e} + {\bf i} \times {\bf h}
\tag{35}
\]
ここで、$i$ は光速を単位とする、電気性の速度ベクトルである。もし我々が、(30a), (31) に従って$J_μ, Φ_{μν}$ [訳注: $Φ_μ$を修正]
を導入すると、我々は、その表式の第1成分として次を得る。
\[
Φ_{12} J_2 + Φ_{13} J_3 + Φ_{14} J_4
\]
テンソル $(Φ)$ の反対称性のために、$Φ_{11}$ が消滅することをみれば、$k$ のその成分は、4次元ベクトルの最初の3つの成分は、次によって、
\[
K_μ= Φ_{μν} J_ν
\tag{36}
\]
そして、第4番目の成分は、次で与えられる。
\[
K_4= Φ_{41} J_1 + Φ_{42} J_2 + Φ_{43} J_3= i(e_x i_x + e_y i_y + e_z i_z) = iλ
\tag{37}
\]
それゆえ、単位体積あたりの力の4次元ベクトルが存在し、その最初の 3 成分 $k_1, k_2, k_3$ は、単位体積あたりの動質力(ponderomotive force)
成分であり、その4番目の成分は、単位体積あたりの場の仕事率に$\sqrt{-1}$ を掛けたものである。
(36) と (35) の比較は、相対性の理論が形式的に電気性場の動質力 $ρ{\bf e}$と、ビオ・サバール力又はローレンツ力${\bf i}\times {\bf h}$
とを統合することを示す。
≪=BACK TOP∧ NEXT=≫
質量とエネルギー
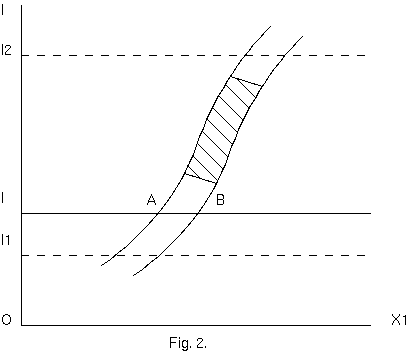
4元ベクトル、$K_ν$ の存在と意味から、重要な結論を描くことができる。電磁場がしばらくの間その上に作用する物体を想像しよう。
象徴的な図(図. 2)では、$Ox_1$ は、$x_1$ 軸を表すと同時に、3 つの空間軸 $Ox_1, Ox_2, Ox_3$ の代わりをする;$Ol$ は、実数の時間軸を表す。
この図のなかに有限の広がりの物体が確定した時間 $l$ に間隔 $AB$ によって表現されている; 物体の全体としての時空存在は、帯で表現されていて、
その境界がどこも$l$軸に45°未満傾いている。時間の断面$ l= l_1$ と $l= l_2$ との間にあって、それらまでは拡がらない帯の部分を影付けしている。
これは、時空多様体の部分を表していて、そのなかで電磁的な場が物体に作用する、又はそのなかに格納された電荷に作用しそれらへの作用が物体に
伝達される。我々はいま、この作用の結果として、物体の運動量とエネルギーにおいて実行される変化を考える。
我々は、その物体において運動量とエネルギーの原理が有効であることを仮定する。運動量変化、$ΔI_x, ΔI_y, ΔI_z$ エネルギー変化、$ΔE$ は、
次の式で与えられる。
\[
\begin{align*}
ΔI_x&= ∫_{l0}^{l1} dl∫k_x dxdydz &= {1 \over i} ∫ K_1 dx_1 dx_2 dx_3 dx_4 \\
&...&... \\
&...&... \\
ΔE&= ∫_{l0}^{l1} dl∫λ dxdydz &= {1 \over i} ∫ {1 \over i} K_4 dx_1 dx_2 dx_3 dx_4
\end{align*}
\]
4 次元体積要素が不変量であり、$(K_1, K_2, K_3, K_4)$ が 4 元ベクトルをなし、影付きでない部分の積分が何も貢献しないから、境 $l_0$ と $l_1$ の間
の積分がそうであると同じく、影付き部分以上に拡がった 4 次元積分は、4元ベクトルとして変換する。それゆえ、$ΔI_x, ΔI_y, ΔI_z, iΔE$ は、4元
ベクトルを形成することになる。それらの量自身はそれらの増分と同じ方法で変換されると予期できるから、我々は、4つの量の総計、
\[
I_x, I_y, I_z, iE
\]
自身が、4元ベクトルの性質をもつと推定する; これらの量は、物体の瞬間的な状態(例えば、$l= l_1$)に対するものである。
≪=BACK TOP∧ NEXT=≫
この4元ベクトルは、また物質粒子と考えられる物体の質量 $m$ と速度 $v$ によって表現できる。この表現を式にするために、最初に次式、
\[
-ds^2= dτ^2 = -(dx_1^2 + dx_2^2 + dx_3^2) - dx_4^2 = dl^2(1 - q^2)
\]
が、物質粒子の運動を表す4次元線の無限に短い部分に対する、不変量であることを注意する。不変量 $dτ$ の物理的重要性は、容易に与えられる。
もし、我々の考える接線方向をもつように時間軸が選択されるなら、又は他の言葉では、もし我々がその質点を静止に変換すると、$dτ= dl$ である;
これは、それゆえ、質点と同じ場所に静止した光秒時計によって測定されるだろう。我々は、それゆえ、$τ$を物質粒子の固有時と呼ぶ。
$dl$ とは違って、$dτ$は、それゆえ、不変量であり、光速と比べて小さい速度の運動では、実際的に $dl$ と同等である。こうして我々は、
\[
u_σ= {dx_σ \over dτ}
\]
が、$dx_ν$と同様に、ベクトルの性質をもつことを見る; 我々は、$(u)$ を速度の 4 次元ベクトル(短く、4 元ベクトル)と呼ぶ。
その成分は、(38)によって、
\[
Σu_σ^2 = -1
\tag{40}
\]
の条件を満たす。
我々は、その通常の記述では次式であるこの4元ベクトルが、
\[
{q_x \over \sqrt{1-q^2}}, {q_y \over \sqrt{1-q^2}}, {q_z \over \sqrt{1-q^2}}, {i \over \sqrt{1-q^2}}
\tag{41}
\]
3次元では次式で定義される、物質粒子の速度成分から形成できる唯一の4元ベクトルであることを見る。
\[
q_x= {dx \over dl}, q_y= {dy \over dl}, q_z= {dz \over dl}
\]
我々は、それゆえ、
\[
(m {dx_μ \over dτ})
\tag{42}
\]
≪=BACK TOP∧ NEXT=≫
が、その存在を我々が上で証明した、運動量とエネルギーの 4 元ベクトルと等しくされる、あの 4 元ベクトルでなければならないことを見る。
成分を等しいと置いて、我々は次の 3 次元の記述を得る。
\[
\begin{align}
I_x&= {mq_x \over \sqrt{1-q^2}}\\
&..... \\
E&= {m \over \sqrt{1-q^2}}
\end{align}
\tag{43}
\]
我々は、事実、これらの運動量の成分が、光のそれと比べて小さい速度では古典力学のそれらに一致することを認識する。
大きな速度では運動量は、速度に線形よりも速く増え、光速に接近するとき無限に大きくなるように増加する。
(43)の最後の式を静止した($q= 0$)物質粒子に適用すれば、静止した物体のエネルギー $E_0$ がその質量に等しいことを見る。
我々が秒を時間の単位にとるならば、次を得るだろう。
\[
E_0 = mc^2
\tag{44}
\]
質量とエネルギーは、それゆえ、本質的に似たものである;それらは、単に同じことの違う表現である。物体の質量は定数ではない;
そのエネルギー変化とともに変化する(*)。我々は、(43) の最後の式から $q$ が 1 の光速に接近するとき $E$ が無限に大きくなることを見る。
もし、我々が $E$ を $q^2$ の累乗に展開するなら、我々は次を得る。
\[
E= m + {m \over 2} q^2 + {3 \over 8} mq^4 + ....
\tag{45}
\]
この展開式の第 2 項は、古典力学の物質粒子の運動エネルギーに対応する。
(*) 放射性過程のなかのエネルギー放出は、原子の重さが整数でないことと、明らかに繋がっている。式 (44) で表現される、
静止質量と静止のエネルギーの等価性は、近年に到るまで多くの場合で確認されてきた。放射性の分解では、結果質量の和が、つねに
分解前の原子の質量より小さい。その差は、解放された放射性のエネルギーだけでなく、発生した粒子の運動エネルギーの形で現れる。
≪=BACK TOP∧ NEXT=≫
物質粒子の運動方程式 (43)から我々は、時間 $l$ で微分することによって、そして、運動量の原理を使って、3 次元ベクトルの記述の
次を得る。
\[
{\bf K}= {d \over dl} ({m{\bf q} \over \sqrt{1-q^2}})
\tag{46}
\]
この方程式は、電子の運動のために H. A. ローレンツによって以前に採用され、β線の実験で偉大な精度で正しいことが証明されたものである。
電磁場のエネルギーテンソル 相対性の理論の開発の前、エネルギーと運動量の原理は、電磁場について微分形式で表現できることが
知られていた。これらの原理の4次元形式は、エネルギーテンソルの重要な概念を導き、それは、相対論のさらなる開発のために重要である。
もし、単位体積あたりの力の 4 元ベクトルの次の表式のなかで、
\[
K_μ= Φ_{μν}J_ν
\]
場の方程式、(32) を使って、$J_ν$ を場の強さ $Φ_{μν}$ を使って表して、いくらかの変形の後、場の方程式 (32) と (33) を繰り返し適用して、
次式を得る。
\[
K_μ= -{∂T_{μν} \over ∂x_ν}
\tag{47}
\]
ここで、我々は、次の書き方をした(*)。
\[
T_{μν}= - {1 \over 4} Φ_{αβ}^2 δ_{μν} + Φ_{μα} Φ_{νβ}
\tag{48}
\]
(*) 添字$α$と$β$について総和されるもの。
≪=BACK TOP∧ NEXT=≫
式 (47) の物理的意味は、この式の代わりに次の記述を使って明確になる。
\[
\begin{align}
k_x&= -{∂p_{xx} \over ∂x} - {∂p_{xy} \over ∂y} - {∂p_{xz} \over ∂z} - {∂(ib_x) \over ∂(il)}\\
&......................\\
&......................\\
iλ&= -{∂(i s_x) \over ∂x} - {∂(i s_y) \over ∂y} - {∂(i s_z) \over ∂z} - {∂(-η) \over ∂(il)}
\end{align}
\tag{47a}
\]
または、虚数を消去して、
\[
\begin{align}
k_x&= -{∂p_{xx} \over ∂x} - {∂p_{xy} \over ∂y} - {∂p_{xz} \over ∂z} - {∂b_x \over ∂l}\\
&......................\\
&......................\\
λ&= -{∂s_x \over ∂x}-{∂s_y \over ∂y}-{∂s_z \over ∂z}-{∂η \over ∂l }
\end{align}
\tag{47b}
\]
後者の形式に表現したとき、我々は、最初の3式が運動量の原理を述べることをみる; $p_{xx} ... p_{xz}$ は、電磁場のマックスウェルの歪であり、
$(b_x, b_y, b_z)$ は、場の単位体積あたりのベクトル運動量である。(47b) の最後の式は、エネルギー原理を表現し、
${\bf s}$ がエネルギーの流れのベクトル、$η$は、場の単位体積あたりのエネルギーである。事実、我々は、(48) から、場の強さの実数成分を
導入することによって、電磁力学からよく知られる次式を得る。
\[
\begin{align}
p_{xx}=& -h_x h_x + {1 \over 2} (h_x^2 + h_y^2 + h_z^2) \\
& -e_x e_x + {1 \over 2} (e_x^2 + e_y^2 + e_z^2) \\
p_{xy}=& - h_x h_y - e_x e_y \\
p_{xz}=& - h_x h_z - e_x e_z \\
&.................... \\
&.................... \\
b_x=& s_x = e_y h_z - e_z h_y \\
&.................... \\
&.................... \\
η=& + {1\over 2} (e_x^2 + e_y^2 + e_z^2 + h_x^2 + h_y^2 + h_z^2)
\end{align}
\tag{48a}
\]
我々は、(48) から、電磁場のエネルギーテンソルが対称であることに注目する;これと次の事実は、結合している。
体積あたりの運動量とエネルギーの流れは、互いに等しい (エネルギーと慣性の関係である)。
≪=BACK TOP∧ NEXT=≫
我々は、それゆえ、これらの考察から、単位体積あたりのエネルギーは、テンソルの性質をもつことを結論する。これは、直接には電磁場だけに
証明されている、我々は、その汎用的有効性を主張してもよいにも関わらず。Maxwell 方程式は、電荷と電流の分布が知られるときに電磁場を
決定する。しかし、我々は、電荷と電流を支配する法則を知らない。我々は、実に、電気が要素的粒子(電子、正の核子)からなることを知る。
しかし、理論的視点からは、我々は、これを理解できない。確定した大きさと電荷の粒子のなかの電気性の分布を決定するエネルギー要素を
知らない。そして、この方向に理論を完成させようとする全ての試みは、失敗した。そのとき、仮にも我々が Maxwell 方程式を少しでも基礎を置く
ことができるのは、荷電粒子の外側だけについて知られる電磁場のエネルギーテンソルについてである(*)。これらの領域のなかで、荷電粒子の外側、
我々がエネルギーテンソルの完全な表式をもつと信じることのできる唯一の領域には、(47)によって、次式をもつ。
\[
{∂T_{μν} \over ∂x_ν} = 0
\tag{47c}
\]
保存原理への一般的表式 我々には避け難く、全ての他の場合もエネルギーの空間分布は、対称テンソル $T_{μν}$ で与えられ、この完全な
エネルギーテンソルがどこでも (47c) の関係をみたすという仮定を作ることになる。少なくとも我々は、この仮定によって積分型エネルギー原理の
正確な表式を得るのをみるであろう。
空間的に制限のある閉じた系を考えよう、4 次元的にその外部で$T_{μν}$が消滅する帯で表すことができる。(47c) の空間的断面に渡る積分をとる。
$T_{μν}$ が積分の境で消滅するから、${∂T_{μ1} \over ∂x_1}, {∂T_{μ2} \over ∂x_2}$ そして ${∂T_{μ3} \over ∂x_3}$ の積分が消滅して、我々は、次を得る。
\[
{∂ \over ∂l} \{∫T_{μ4} dx_1 dx_2 dx_3\} = 0
\tag{49}
\]
括弧の内部は、全体系の運動量の表式であり、i 倍されて、系の負のエネルギーと一緒にして、(49)が積分形式で保存原理を表すようになる。
これが正しいエネルギーの概念と保存の原理を与えることは、次の考察からみることができる。
(*) この知識の欠如を救済する試みが荷電粒子を固有の特異点として考慮することによってなされた。しかし、私の意見では、これは物質構造の
本当の理解の放棄を意味する。外見だけの解に満足するよりも、我々の現在の不可能性を受け入れるほうが、私にはずっとよいと思える。
≪=BACK TOP∧ NEXT=≫
物質のエネルギーテンソルの現象論的再現
水力学的方程式 我々は物質が電気的な荷電粒子によって出来ていることを知っている。しかし、これらの粒子の構成を支配する
法則を知らない。力学的問題を扱うのに、我々は、それゆえ、古典的力学のそれに対応する、物質の不正確な記述を使用せざるを得ない。
物質の実質の密度$σ$と水力学的圧力とは、その上にそのような記述が基づく基本的概念である。
$σ_0$ は、物質に対して動いている座標系を参照して推定する、ある場所の物質密度としよう。そのとき、静止の密度$σ_0$ は不変量である。
もし、我々が任意の運動をする物質を考え、圧力を無視するなら(真空中の塵、粒子のサイズと温度を無視して)、そのとき、エネルギーテンソルは
速度成分 $u_ν$、と $σ_0$ にだけ依存するであろう。我々は、次のように置き、$T_{μν}$ のテンソル特性を保存する。
\[
T_{μν}= σ_0 u_μ u_ν
\tag{50}
\]
ここで、$u_μ$ は、その3次元表現を(41)で与えた。事実、(50)から、$q= 0$ については、$T_{44}= -σ_0$ (単位体積あたりの負のエネルギーに等しい)
であることが出てくる。それは、物質とエネルギーの等価原理に従い、上に与えたエネルギーテンソルの物理解釈に従わねばならない。
もし、外部の力(4次元ベクトル $K_μ$)がその物質に作用するなら、運動量とエネルギーの原理から、次式が成立しなければならない。
\[
K_μ= {∂T_{μν} \over ∂x_ν}
\]
我々は、この式が、すでに得られたと同じ物質粒子の運動法則を導くことを示す。空間に無限小の拡がりをもつ物質を想像しよう、すなわち、4次元
のひもである; そのとき、ひも全体を、空間座標 $x_1, x_2, x_3$ に関して積分することによって、我々は次を得る。
\[
∫ K_1 dx_1 dx_2 dx_3
= ∫{∂T_{14} \over ∂x_4} dx_1 dx_2 dx_3
= -i {d \over dl} \{∫σ_0 {dx_1 \over dτ} {dx_4 \over dτ} dx_1 dx_2 dx_3\}
\]
≪=BACK TOP∧ NEXT=≫
いま、$∫dx_1 dx_2 dx_3 dx_4$ は、不変量であり、それゆえまた、$∫σ_0 dx_1 dx_2 dx_3 dx_4$ も同じである。我々は、最初、我々が選んだ慣性系
に関して、次に、物質がそれに相対的に速度 0 をもつ系に関して、この積分を計算する。積分は、そのひもの線を覆うように拡げられ、
$σ_0$ が断面全体で定数とみなせるようにする。ふたつの系に関する線の空間体積がそれぞれ $dV$ と $dV_0$ であるなら、そのとき、我々は次式をもつ。
\[
∫σ_0 dV dl = ∫σ_0 dV_0 dτ
\]
そして、それゆえ、また、
\[
∫σ_0 dV = ∫σ_0dV_0 {dτ \over dl} = ∫dm \hspace{2mm} i {dτ \over dx_4}
\]
もし、我々が右辺側を前者の積分の左辺に置き換え、${dx_1 \over dτ}$ を積分記号の外に置けば、次を得る。
\[
K_x = {d \over dl} (m {dx_1 \over dτ}) = {d \over dl} ({m q_x \over \sqrt{1-q^2}})
\]
我々はそれゆえ、エネルギーテンソルの一般化された概念は、我々の以前の結果に一致することを見る。
≪=BACK TOP∧ NEXT=≫
完全流体のオイラー方程式 現実の物質の行動に近付くために、我々は、エネルギーテンソルに圧力に対応する項を付加しなければ
ならない。最も単純な場合は、完全流体のそれで、そのなかでは、圧力はスカラー $p$ によって決定される。接線方向の歪 $p_{xy}$ 等は、
その場合消滅し、エネルギーテンソルへの貢献は、式 $pδ_{μν}$ でなければならない。それゆえ、我々は次を置かなければならない。
\[
T_{μν}= σ u_μ u_ν + pδ_{μν}
\tag{51}
\]
静止では、物質の密度、または、単位体積のエネルギーは、この場合、$σ$ではなく、$σ - $p である。なぜなら、
\[
-T_{44}= -σ{dx_4 \over dτ} {dx_4 \over dτ} - pδ_{44} = σ - p
\]
他に力のない場合、我々は次をもつ。
\[
{∂T_{μν} \over ∂x_ν}= σu_ν{∂u_μ \over ∂x_ν} + u_μ{∂(σ u_ν) \over ∂x_ν }+ {∂p \over ∂x_μ} = 0
\]
もし、我々がこの式に $u_μ (= {dx_μ \over dτ})$ を掛け、$μ$ の総和をとれば、(40)を使って我々は次を得る。
\[
-{∂(σ u_ν) \over ∂x_ν} + {∂p\over ∂τ} = 0
\tag{52}
\]
ここで、我々は、${∂p \over ∂x_μ} {dx_ν \over dτ} = {∂p \over ∂τ}$ とした。これは、連続の方程式であり、古典力学の式から${dp \over dτ}$ だけ異なる。
それは、実際的には、消滅するように小さい。(52) を観察して、保存原理は次の式をとる。
\[
σ {du_μ \over dτ} + u_μ{dp \over dτ} + {∂p \over ∂x_μ} = 0
\tag{53}
\]
その式の最初の3添字については、明らかにオイラー方程式に対応している。(52), (53) の式は、古典力学の水力学の方程式に1次近似で
対応することは、一般化されたエネルギー原理のさらなる確認である。物質(またはエネルギー)の密度は、テンソル特性をもつ(とくに対称
テンソルを構成する)。