回転系には遠心力と、コリオリの力があるが、性質が違うように見えるそれら2つのみかけの力が、同じものという議論である。
<目次>
1. はじめに
2. コリオリの力の原因は何だろうか
2.1 回転デッキ
3. 回転系の実効ポテンシャル
3.1 回転系では PE + KE は一定でない
3.2 回転系での質点の運動は、磁場中の電荷の運動に類似する
3.3 速度 V+v は、系内点速度 v と系内速度 V に分離される
3.4 みかけの力が遠心力とコリオリ力に分離される
4. 回転系からみた静止系
5. 浮遊の力学
6. 回転系の合成
7. 回転の表記について
8. 回転の相対性について
9. 回転の相対性
10. 回転系からみた直線運動
11. 慣性系との運動エネルギー(KE)差による導出
12. 微分演算子によるコリオリ力の導出

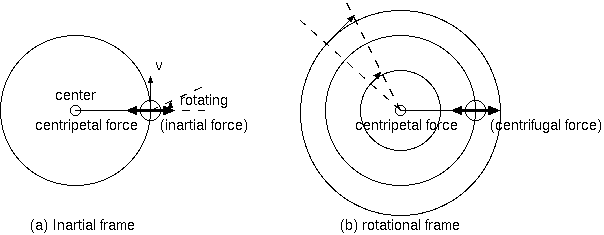
物体が回転系で受ける2つのみかけの力は、遠心力とコリオリの力である。遠心力は、軸に向う局所加速系が遠心の加速度をみせるのと同じく、 慣性系から見た回転系内の静止点の向心加速度が原因である。遠心力は、遠心方向に軸からの距離rに比例し回転系の角速度wの2乗に比例する 力mrw^2又は、回転する点が速度v(= rw)の2乗に比例し半径に反比例する力mv^2/rである。系内点には局所の加速以外に、さらに各点に局所の 回転がありコリオリ力を生む。コリオリ力は、角速度wと系内速度Vとに比例し、場所によらない。両者は全く性質が違うようにみえる。
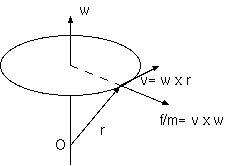
回転は、回転軸の方向を向く角速度のベクトルで表すことができる。wを軸にする回転系の性質は、軸方向に一様で、軸からの距離だけによる 軸対称である。軸上に原点をとり、原点から系内点への位置ベクトルを r とすると、原点を共有する慣性系からみた回転系内の静止点の速度は、 v= w x r で表される。(rのw方向成分は外積w x rによって関係しない。) 系が原因のみかけの力は、質量に比例する力を発生する加速度場である。 そのとき遠心力場 F/m は、v x w であり、慣性系からみた回転系内点の加速度 w x v の符号反転である(下図参照。外積 x の前後交代は符号反転)。 遠心力は軸から外方向をもち、コリオリの力 2V x w は色々な方向をとるが、系内速度Vとwの両方に垂直で、軸wに垂直な面内でVに垂直である。 (Vのw方向成分は外積 2V x w によって関係しない。) 遠心力は系点速度vとwとの外積、コリオリ力は物体の系内速度Vとwの外積の2倍である。 両者はともに速度とwの外積である。
(*) 物体の加速度から慣性力を仮定して動力学につり合いを見る考え方。慣性系で円運動する物体のひもからの向心力と慣性力とつり合いは、 回転系では向心力と遠心力とのつり合い。慣性系での慣性力を仮定しないとき、作用と反作用のバランスの崩れた力が加速度を生むと考える。
(**) 慣性系に静止して浮遊する物体は、回転系からみると現実の力なしに円運動する。つまり、慣性系での円運動の向心力は現実の力だが、 回転系ではみかけの力でありえる。現実とみかけの区別は不明確である。作用と反作用は、物体間の相互に働く力で、AからBに作用が働くとき、 BからAに反作用が働く。慣性系からみたとき両方の力は大きさが等しく方向が逆である。回転系など非慣性系からみるとき力と加速度が慣性系 とは違ってみえるのである。つり合いは、1物体に働く複数の力の和が0をいう。
コリオリの力の原因は何だろうか。 慣性系に静止した点は、回転系からみて円運動をする。その円運動にも向心力を与える必要がある。例えば、 回転する円筒型の室内で速度 v をもつ円筒の側面を床として乗員が走るとき、部屋の回転と逆方向に系内速度 V= -vで走る乗員は、浮遊すると 想像できる。逆に、床と同じ方向に走行する系内速度 V= v の乗員は、慣性系からみて 2w の回転するための向心力の増加が必要で、床から4倍 の抗力を得ないといけない。回転系の遠心力は運動によらず V= -v にも V= v にも同じ大きさの外側向きの力 v x w を与えるのに対して、 片方は回転系の回転と逆向きに浮遊して円運動し、他方は回転系と同じ向きに円運動して4倍床に押しつけられる。この走行方向による違いを コリオリ力 2V x w が与えるのである。
この説明を聞いて、おかしいと感じる人が多いだろう。ひとつは、"遠心力は運動によらず V= -v にも V= v にも同じ大きさの外側向きの力 v x w を与える" ことだろう。「回転系上で逆向きに走る乗員は、回転を減らしているのに遠心力が同じなのか。回転系上で回転を増減する のに遠心力が等しいのはおかしくないか?」ということだろう。これは、いつも慣性系だけから見る習慣で、w が増えれば遠心力が増え、w が減れば遠心力は減る、遠心力は rw^2 に比例する、という素朴な見方によるからだろう。ところが、遠心力は回転系wに付随するもので、 系内の物体の運動によらないと考えてこの言い方になる。もうひとつは、「円筒形デッキの回転と逆向きに走る乗員の浮遊にコリオリの力 と遠心力がつり合わないがよいのか」という疑問だろう。浮遊は遠心力とコリオリ力のつり合いと考えるのはとても一般的である。 コリオリ力が V x w なら遠心力とつり合うが、2V x w ではつり合わない。浮遊でなく内側に落ち込む強さである。
しかし、遠心力とコリオリ力がつり合うなら、回転系からみる回転には向心力は必要ないのか。静止した浮遊乗員に向心力も遠心力もないように 見え、「なぜなら、回転していないから」と言われそうだが、回転系では浮遊乗員は円運動している。それに遠心力と向心力はないのか。 こんな中途半端な思考ではこの宇宙を理解できない。そしてそれなら、回転と同方向に走行する人は、どうやって4倍の遠心力を得るのだろうか。 コリオリ力 V x w が外向きに遠心力に加勢しても 2倍の遠心力になるだけである。そのとき「角速度が2倍なら遠心力は4倍に決まっている」 というのは、答えを先に与えるだけだ。回転系の力学で正しくそれにどう到達するかである。
(結論は、回転系で順回転する点には、回転系の遠心力にコリオリ力から2倍の力が加勢し、新たな順回転の遠心力が加算して4倍の遠心力になる。 向心力は床から得る。 そして、回転系で逆回転する点には、回転系のコリオリ力から逆回転の向心力が2倍与えられ、回転系の遠心力と逆回転の遠心力の和に釣り合って浮遊する。)
浮遊時は、床の下に星空が一面に停止していて、後方の大陽の光の角度も変わらずにいるだろう。そのときはただ、この宇宙船のなかの空気の風の 音を楽しめばよい。静かで物音ひとつしない船内の鼓動を聞けばよい。もちろんそれは、2001年にはまだ核融合でしかない、この人類のエネルギー 源の静かな鼓動である。外を見るための実際の窓は、小さく一部にしかない。ここは機器に包まれた機械室の狭い通路のような、細長い部屋である。 天井は高いが間に操縦室にいく軸が遮り、その軸までの梯子が伸びている。その先にはあまり考えたくもない、この上に弯曲した廊下はそのまま天 井に続き、天井に人が逆さに立つ。それゆえ、廊下の長さには限りがない。この回転する床が透明な部分を持てば、外の星の配置を見ることもでき るが、床は透明でないので、外の回転する宇宙を意識し続けることもない。床に立って動かないとき、地上と同じような重力だが、動けば何か違和 感を感じる程度の疑似重力である。そして、走れば、地上とは少し違う目眩いの感覚を伴う。
その速度に達しないなら、完全な浮遊はない。回転系からみたその乗員の経路の円軌道の半径がこの部屋の半径より大きいなら、すぐに弯曲した床 と交差する。体の重心が下がり足が再び床を踏むまでの少し間、宙に浮く。しかし、その速度を出す前に体重が減り、床との抗力が減少して、床を 蹴るときの摩擦を十分利用できなくなるから、その速度を出すことは難しい。完全に浮遊する直前に、最後に床を蹴る力が体の重心を交差していないと、 体は軸を横にした前のめりか宙を仰ぐ回転に入るから、この最後の動作は慣れるまで難しいだろう。このときまだボーマンは彼にすぐ来る、HALの反乱と プールの長い宇宙遊泳、そしてHALを殺す必要も知らない。そして木星(又は土星)への数ヵ月の旅の途中にあって、本当の役割も知らない平和な時である。 この永遠に続くように思える時間はひとときだけなのだが。それを知る私は映画のストーリーを知るだけであって、現実のこの部屋のこの今日の数時間 の作業を思い返しながらの休養の時間に、あの映画が既視感にように甦ってきて軽い病的発作を生むかのような、これら全てをあの映画は用意していた。
車輪の中をハムスターになって走る分には、コリオリの力 2V x w は、遠心力と同じく上下方向でそれを増減するだけだから、まだ、奇妙ではないが、 弯曲した床をもつ広いロビーが遠方まで見える宇宙ステーション内の情景で、様々な方向に動き回れば、走る方向による視覚と運動の違いによって、 ここが地上の重力でないことを思い知るだろう。バスケットボールやサッカーの長方形のコートは、w軸方向にゴールを置くのがよいかもしれない。 その方向へのボールの運動は、まだコリオリ力が小さい。しかし、単なる予想だが、一般に球技はほとんど不可能なのではないか。球の速度は、人 の最高速度36km/h の何倍も出る。野球は150km/hの球速のボールが扱われる。
コリオリ力は、系内速度Vに比例した加速度を出すから、それによってピッチャーからキャッチャーまでの距離Lを一定として、ボールが受ける 横方向の加速度と速度と変位を考えると、ボールが飛んでいる時間をtとして、ボールの速度は V=L/t、コリオリ加速度 2Vxw (ここでwはVと 垂直としてベクトルの外積を大きさの積にする) 一定としてtだけ経つと速度2Vwt= 2Lwの速度になる。つまり、速度Vに比例するコリオリ力の 起こす速度変位はtによらない、つまり速度Vによらない横向きの速度を与える。さらに、コリオリ力による変位は、時間tの間に速度が0から 2Lwまで増加する3角形の面積 Lwt であり、Lwt= LwL/V= wL^2/V であり、速度Vに反比例する。Vが小さいほどぶれは大きい。ストライクから の外れ方は遅い球ほど大きい。
こう考えると、コリオリ力の下のスポーツ、球技は、不可能ではないかもしれない。一定距離Lでなく一定時間tのコリオリ加速度、速度、変位 は、加速度はVに比例し、速度もVに比例し、変位もVに比例する。これは、重力の下での球技のボールが下にぶれることと、さほど変わらない。
回転系の静止点の速度を v とし、系内速度を V とすると、慣性系からみた運動エネルギーは、KE= 1/2 (V+v)^2 である。系内の PE= -1/2 v^2、 KE= 1/2 V^2 であるとすると PE + KE = 1/2 (V^2 - v^2)。(Vとvを同じ直線上に限定して考え) これは V の大きさに依存する。 PE+KE= 1/2 (V+v)(V-v) は、変数 V= v と V= -v で0。-v <V< +v では負であり、その外側では正である。V=0 がポテンシャル極小で安定である。 そしてこれは、回転系上に静止することである。
回転系に静止した点の慣性系からみる速度vは、軸からの距離に比例する。最初軸上で静止した質点が軸から外れると、遠心力によって 外向きの系内速度Vを増やすだろう。それはVが-vに近付くことだろう。系内点に接触しないなら、慣性系からみた物体は静止または等速 直線運動をする。それを回転系からみると、V = -vを保つということだろう。PE + KE = 1/2 (V^2 - v^2) は、0を保つのであり、PE+KE は保たれるのではないか。軸から離れていけば、Vは大きくなるが、その分、v も大きい場所に移動していく。少なくとも単純な放物面 ポテンシャルをすべり落ちる運動は、そういえる。しかし、そういう運動ばかりではない。V+vが0でない最初から慣性系で速度をもった 一般の運動は、慣性系の速度 V+v を変えないから、V^2-v^ は変わる。上の例は V+v=0 だから V^2-v^2 (= 0)を変えない特別な例である。
すべての自由物体は、回転系ではその速度に比例した半径をもって同期した円軌道を描く。ほとんど静止した物体は小さな円を描く。(?) いや、慣性系で直線運動する物体は、回転系でも円運動と直線運動の合成した運動をするだろう。<ー未確認。慣性系では速度は保存される (V+v)が、回転系では系内速度Vは保存されない。物体が場所を移動すれば v は変わるから、Vも変わる。重力のある慣性系にあったような、 速度とポテンシャルの関係がある。さらに、後述するが、運動エネルギー差がポテンシャルと考えられる。
重力も考慮した "実効ポテンシャル" は、その傾きが0の5つのラグランジュ点を作り、それらは山か峠であり、谷底はない。自由物体は 実効ポテンシャルの傾斜によって円軌道の中心を徐々に移動させる。小惑星の集まるトロイ点L4とL5は広い丘だが、どうして普段は傾斜 を下る物体が、山に集まるのだろう。円軌道が山の頂点を一度巡ると、逃れられないのかもしれない。円は小さくなるだけであるから。
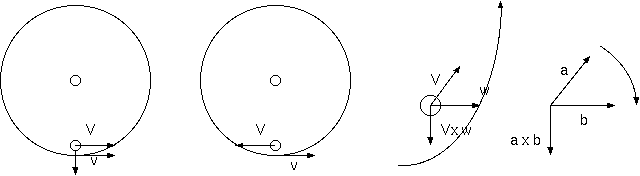
回転系では、速度 V をもった外力なしの質点は、速度 V に比例しそれと垂直な力 F/m= 2V x w を受け、これを遠心力に対抗し、さら に向心力にして速度に比例した半径の円軌道を描くのである。円軌道の向心加速度は、速度に比例するが、時間積分した軌道の周期は、 速度に依存せず一定で、回転系の周期と一致するのではないか。(v が 2 倍で、r は 2 倍、mv^2/r = mrw^2 は 2 倍。w は一定。)。
コリオリの力の元になるベクトルポテンシャル (B= rot A の A) は、一意に決定されないが、中心からの距離 r と w に比例する A= v= w x r という軸対称解 A= (-y, x, 0) がある。rot v = 2w であるから、回転系の系点速度 v は、コリオリ力のベクトルポテンシャルであり得る。 しかも、コリオリ力の不思議な "2" まで再現する。電磁気の A は、rot B = dE/dt + i の電流によるが、剛体回転系の w は一様であり rot w = 0 から電流 i に相当するものをもたない。
F(r)/m = v x w + 2V x w = (2V + v) x w
である。この式で、遠心力とコリオリ力は区別されない。この区別のない仕組みは本質的であり、みかけの力は、速度(2V + v)全体に 掛かり、物体の速度 V+v から、その系内点の v を引いた系内速度 V に関するものをコリオリ力といい、v に関するものを遠心力という。 回転系の原点に対する物体の速度があり、物体速度と回転wの外積が遠心力とコリオリの力の和を作ることをこの式は意味している。 そのうち、(V + v) x w の部分は、原点からみた速度 V+v と w との外積であり、これは、回転系内の座標 r によらず、回転軸の位置 に依らない。回転系には軸があって、外部世界との速度を反映するが、その座標の軸方向の成分は、w との外積で効果が消える。 遠心力とコリオリ力の和は (2V + v) であっても、回転系の静止点の速度vと系内速度Vでできていることは変わらない。遠心力とコリオリの力は、 もともとの発生的原因は、慣性系からみた物体の速度 V+v と w の外積であり、両者は、区別してできたものではない。 速度を系点速度 v と系内速度 V に分解して遠心力とコリオリの力に分けただけである。
遠心力が v x w 、コリオリの力が 2V x w で、みかけの力全体が F/m= (2V + v) x w なら V= -v では遠心力と同じ大きさの向心力を 作り、V= v では遠心力の丁度 3 倍の遠心重力を作る。
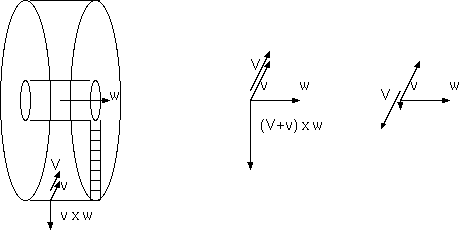
軸から r の点での遠心力 v x w (v= w x r) は、そこを軸にする同じ w をもつ回転系からみると、r= 0 から、もはや遠心力はなく、 v が系内速度 V に移され、みかけの力 (2V + v) x w は2倍に大きさを変えるがコリオリの力となる。また、その系内速度 V を系の速度 v に置き換える軸をさがしてその回転系からみると、みかけの力全体を遠心力にすることもできる。性質が全く異なる回転系のふたつの みかけの力は、回転系の並進選択による違いでしかない。
日が東から昇る地球の回転wは北極星を指すベクトルである。北半球で地球の回転の上向き成分をwとするとはそれは緯度の正弦に比例し、 速度 V に向かって V x w は右に働く。北半球では弾丸は常に右にそれる。逆に台風の渦の風は左にそれるが、流体力学はさらに難しい。 コリオリ力が圧力勾配に対抗してつり合う向き、等高線にほぼ平行に空気は流れるとされる。
(a) 静止系からみる回転系の静止点: 静止系からみた円運動は、それに同期する回転系からみると物体が静止するために、 向心力につり合うみかけの力、"遠心力" が必要である。これは、回転系では "現実" の力である。
(b) 回転系からみる慣性系の静止点: 慣性系上の静止点は、回転系 w からみて -w で円運動をするから、遠心力に対抗する もうひとつのみかけの力、系内速度に比例する "コリオリの力" が必要となる。これも、回転系 w では "現実" の力である
しかし、このとき、回転系 w の力、遠心力とコリオリの力だけでつり合いが成立するだけではなく、回転系 w からみた -w の回転系である 静止系にも、遠心力を含めてつり合いが成立すると考える。これは、(b) が (a) の回転相対であることを意味する。なぜならもともと (a) は、 ひとつの系のなかの "現実" の力のつり合いでなく、それと別の系の "みかけ" の力のつり合いであったからである。
コリオリの力の大きさについて、旧版では、(b)の状況で慣性系に静止する -w の回転に向心力が不要と考え、回転系 w 内部の力だけで つり合うことを仮定し、コリオリの力を V x w とした。ここでは、(b) の -w の円運動をするためには、回転系 w においても、慣性系に おいてと等しいその系のなかの現実の力による向心力が必要であると仮定する。そうすると、遠心力に対抗して慣性系の円運動と等しい 現実の向心力を生むためには、遠心力のちょうど 2 倍の反対符号 2V x w のコリオリ力の大きさが必要となる。そのとき、w 系内に力の つり合いを求めず、その代わり、w 系からみた -w 回転系 (静止系) に遠心力の存在を仮定する。-w 回転のコリオリの力は、乗員と -w 系との間に速度がないから考えなくてよい。
回転する円筒型の室内で円筒の側面を床として、回転系の速度 v とは逆方向に系内速度 V= -v で乗員が走行するとき、床から浮遊する。 これは、(b) の状況である。床の速度 v を前方とし、回転 w は v に向かって右とし、コリオリ力は中心(上)に向かう。乗員が慣性系に 戻るから浮遊する。逆に床と同方向に系内速度 V= v で乗員が走るなら、コリオリ力は、下に(外に)床に向かい、乗員は慣性系からみて 2 倍の回転をし、遠心力は w^2 に比例するから 4 倍の抗力を床から受ける。これらは、コリオリの力の大きさを 2V x w とする場合と、 V x w とする場合、どちらが整合するだろうか。コリオリ力が V= -v で力 0、V= v では力 4 倍を与えなければならない。
コリオリの力を V x w とする場合、V= -v で走行する場合、回転系 w からみて、系内速度 V の生み出すコリオリ力 V x w が中心(上)に 向かい、回転デッキ内の遠心力 v x w とでちょうどつり合う。しかし、デッキの回転方向と同方向の走行をする場合(V= v)、遠心力と コリオリ力の和は、2 倍の遠心力となり 4 倍を説明できない。
"w系の遠心力" + "-w系の遠心力" - "w 系のコリオリの力"= 0 (1g + 1g - 2g= 0)
回転系からみた静止系のつり合いは、第2項の"-w系の遠心力"が回転系で円運動をする物体から出る慣性力ともいえる。 また、デッキの回転と同方向の走行 V= v の場合、
"w 系の遠心力" + "+w 系の遠心力" + "w系のコリオリの力" (1g + 1g + 2g= 4g)
w 系の現実の遠心力、コリオリの力と物体系 +w のみかけの遠心力の和は、丁度 2w 系の遠心力 4g と等しい。回転系内の "現実" の力には、 つり合いを求めず、相対回転には必ずみかけの力が伴う、合成回転系を静止系にする相対回転においてさえ遠心力が伴うとするのである。 また、同様に第2項の"+w系の遠心力"は、回転系からみて円運動をする物体の加速度からでる慣性力ともいえる。
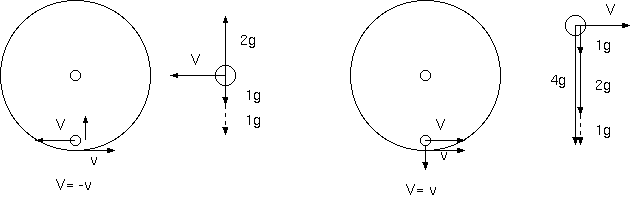
部屋の速度を前方として、回転 w の軸が右方向とすると、 V= v の運動ではコリオリ力、2V x w は、遠心力と同じ外向きの力で、床から4倍 の抗力が対抗して、1倍の回転の向心力を作る。逆方向 V= -v の運動ではコリオリ力は遠心力の2倍の向心加速であり、遠心力(v x w)を打ち消し 円運動に必要な1倍の向心力を与え円運動し浮遊するのである。
(Va + Vb) x (Wa + Wb) = Va x Wa + Vb x Wa + Va x Wb + Vb x Wb
の右辺第1項は、Wa の遠心力、第2,3項は、等しく加算してコリオリの力 2 Vb x Wa = 2 (Wb x r) x Wa になるが、第4項に回転 Wb の遠心力 Vb x Wb がある。遠心力とコリオリの力は、Wa 系では "現実" の力であるが、それに "みかけ" の力 Wb 系の遠心力を補って、 回転和 Wa + Wb の遠心力になる。
ベクトルの外積は角が垂直のとき代数的な積として記述でき理解しやすい。遠心力とコリオリ力の和、a^2 + 2ab は、b^2 を補って、回転和 a+b の遠心力 (a+b)^2 になる。b^2 は、回転系 a からみた付加的回転 b の遠心力である。コリオリ力は、2ab であり、回転 a と、b の元 となる系内速度 V とに比例する。浮遊の場合、b= -a で 0 になることに対応する。
コリオリ力の大きさが V x w であるなら、遠心力とコリオリ力の和 (V + v) x w が場所によらず一定となるが、コリオリ力が 2V x w なら、 遠心力とコリオリの力は、回転系の取り方によって、両者は互いに行き来する特性があるとはいえ、それらの和 (2V + v) x w は一定でない。 回転系の選択において一定なのは、v_a + v_b であり、これは v + V に対応する。(2V + v) ではない。
コリオリの力が、2V x w であるとき、付加的な回転の遠心力を補って、一般的な回転和の遠心力が説明できた。回転系 w のコリオリの力が 別の回転系 -w または +w の向心力になり、みかけの遠心力を補って回転和の遠心力となることは、遠心力とコリオリの力の和に w 系から みた V のもたらす付加的回転の遠心力 V x Wb を補った (2V + v) x w + V x Wb が、ある回転系から他の異なる回転系Wbへの移行において 不変量であることを示す。このとき、Wb は、Wa と同じ方向を向いた回転でなくてもよく、V と r によって Wb は決まる。また、付加的回転 Wb が回転 Wa に比べて小さいとき、V≪v のとき、2次の第4項は消え、遠心力とコリオリの力の和が不変になる。
回転の方向と大きさの両方を表す3次元ベクトルで、回転の軸の方向を向いた、角速度の大きさをもつベクトル、1文字 w で回転を表し、通常 の3次元位置ベクトル r のように扱うなら、3 次元内部の回転の表記を全て扱うことが出来る。軸の方向は、地球の回転が北極星を指すように、 又、図に例を示すように右回り(反時計周り)で上を指す。回転系の位置 r のもつ速度は、w x r によって表せ、加速度は、w x (w x r) である。 これらが、2次元の回転を含んでいることは、w= (0, 0, w), r= (cos wt, sin wt, 0) の w x r を考えれば、外積 a x b = (a_y b_z - a_z b_y, a_z b_x - a_x b_z, a_x b_y - a_y b_x) に代入してみれば、w x r = (-wsin wt, wcos wt, 0) となって、2次元回転を含んで扱っていること が分かる。さらに、どの方向を向いた w においてもそれに垂直な面内でこれが再現されるということを認め、我々は回転に 3 次元ベクトルの 外積記述を使う。
剛体を x 軸の周りに w_1 で回転させておいて、それ全体を y 軸の周りに w_2 回転させても、結果は、w_1 + w_2 というベクトルの和の方向を 向いたひとつの軸の回転によって表されることは、オイラーの定理と呼ばれる。複数の回転は、1つの回転に統合できる。また、有限の大きさの 角度をもった回転は、加算において交換できないが、無限小の角度と角速度は、加算において交換法則がなりたつ。
L= m v_tan r= m ω r・r = m ω r^2
(中略(角運動量保存から)) r を大きくするにはトルクを働かさなければならない。必要なトルクは m が半径方向に動くとき、L が時間的に変化する 割合である。m が半径方向ににだけ動くとすると、ωは一定だからトルクは、
τ= F_c r= dL/dt = d(mωr^2)/dt = 2mωr dr/dt
であって、ここに、 F_cは、コリオリの力である。我々が求めたいのは、m を v_r = dr/dt の速さで動かすのに、次郎はどれだけの横の力を出 さなければならないかということである。これは、F_c = τ/r = 2mωv_r である。
(以上引用) ここで、ファインマンは、力のモーメント F_c r が、スカラー化された角運動量 L= mωr^2 の時間微分に等しいとし、 それを r による微分 2mωr と速度 dr/dt= v_r との積とすることで、コリオリの力の大きさを導いている。 p.279 には、ベクトル記述で 2m V x w と書くこともしている。
(*)第16章、pp. 223-226 参考。
F_r= - m v^2_a/r = - m v^2_b/r - 2m v_b ω - m ω^2 r
太郎のみる求心力は、次郎のみる求心力(第1項)、回転系に静止する物体に働く求心力(第3項)、コリオリの力(第2項)の和とする。 ここで、ファインマンは、"次郎は第1項を感じるだろうか?" と問い、答えを描く。""感じます"と次郎はいうだろう。 "私が回転していなかったとしても、円に沿って v_b の速度で走ると、求心力はあるはずです。"これは次郎に生ずる求心力であって、 これは回転とは関係がない"と。
回転系上であろうとなかろうと円運動に必要な向心力がこの第1項であるように書かれているが、この第1項は、我々の式の第4項の 付加的回転 -w 系の遠心力に対応する項であり、回転系内速度 v_b を別の回転として発生する力である。第1項と第3項は、つねに 同符号だから一方を遠心力、他方を向心力とはできない。円運動に必要な向心力は、この第1項でなく第2項のコリオリ力が供給するのである。 そして、第1項を次郎が感ずるということは、遠心力とコリオリの力以外を感ずるということになるから、このファインマンの指摘は、 誤りというべきかもしれないが、次のように多少の理由がある。
我々は、 +w 回転系から -w 回転系へ移る (静止系に戻る) ときに静止系に属するみかけの力、遠心力を計算にいれた。これによって、 コリオリの力の 2V x w の大きさが回転系の物理として整合することを見た。注意すべきは、この遠心力は、この回転系からみても 現実の力ではなく、みかけの力であり、それを元の系からみると、2 重のみかけの力であることである。そして、相対的な回転において 発生し、それが静止系にもあることは驚くべきことである。また、この系で物体が静止しているため発生しなかったコリオリの力においても、 相対回転によって起きることは同じであろう。
静止系にもみかけの力があるということは受け入れがたい。みかけの力が系間にあるとしなければ、静止系には多値のみかけの力が決定 なく存在するという矛盾を招く。しかし、系の間に系があるわけではない。回転系のみかけの力は、相対回転に属するという認識によって、 我々は "回転には相対性はない" という立場から、すこし後退すべきことを知る。つまり、相対回転によって次の系の遠心力とコリオリの力が 存在する。静止系と回転系とでみかけの力の関係は違わない。ただし、だからといって、ある系が静止系かどうかを系内で判断できない わけではない。静止系は、回転系のなかのひとつで単にその回転が 0 であり、そのなかで物体が外力なしに静止又は等速直線運動をする。
"+w 系からみて -w 系であるから、静止系にも -w 回転による遠心力が存在する" というとき、遠心力が静止系に現実の力としてあるか といえば、これは、系を移るときの計算上の都合のようである。むしろそれは、もとの回転系 +w 系(次郎) に属しているとすれば、 多値性の問題が消え、静止の絶対性は確実である。こうして辻褄は合わされる。しかし、これは、次郎が w 系に感じるみかけの力ではない。 これが回転系 w の現実の力であるなら、遠心力とコリオリの力以外にみかけの力があることになるが、聞いたことがない。 それは、その回転系の回転 w (w_a 又は v) ではなく、別の回転 w_b (又は v_b)に関係するものである。
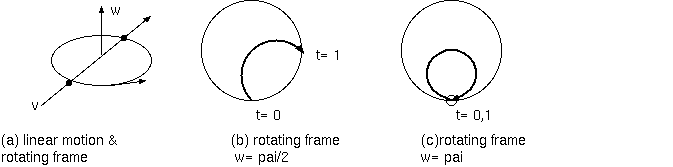
速度2の等速直線運動を回転系(w=π/2とw=π)からみるとどう見えるか。半径1の円を横断するのに1秒かかる。そのとき、円は90度と180度回転する。 90度回転する系は、w=π/2であり、180度回転する系は w=πである。直線運動が円を交差して再び交差するまでに90度回転した系からみると、 直線運動は、ほぼ半円のような経路を描き、180度回転した系からみると、ほぼ円のような経路を描く (正確には円でなく、始まりと終わり の交差点は尖っている)。大まかに、これらの経路を半円と円と考えて、平均の系内速度の大きさ v は、期間が1秒だから半円と小円運動の経路 長に一致し、√2/2π と π である。コリオリ力 v * w はそれぞれ、√2/4 π^2 とπ^2 とである。これらは、半円(w=π) と小円運動(w=2π) の向心力 rw^2、それぞれ、√2/2 π^2 と 2π^2 の半分にあたる。つまり、系内速度による平均コリオリ力の大きさは、系内円運動に必要な 平均向心力の半分である。これは、刻々のコリオリ力と遠心力と向心力ではなく、時間平均の話である。
しかし、なぜ2倍なのか。遠心力が系点速度の2乗に比例する v^2/rである、V^2 系内速度の2乗に比例する何かがあって系内速度で微分すると2Vが出る。 これが2の元か。rot(v)= 2wであるから、回転が2次元の平面上だからか。そして、最も基本的な問い、なぜコリオリ力が存在するのか。
回転系上の任意の静止点には慣性系からみると局所回転がある。速度の空間微分と速度の乗算は、速度の時間微分、つまり加速度として表われる。 速度に比例する力、コリオリ力は、回転系上の静止点の(慣性系からみた)速度の空間的な違いによる。それが系内速度によって加速度と表われる。 この考え方は、成功すれば、コリオリ力を導出するが、次式は、目的の加速度の項以外の項を生み出すように思え、思考は未完である。 w軸をz方向とし、Vはx,y面内に限定する。
v=wxr、
rot(v)= 2w
rot(v)_z = v_y/dx - v_x/dy
F_coriolis= V x 2w = V x rot(v) = (dx/dt, dy/dt) x rot_z(v)
= (dx/dt, dy/dt) x (d^2y/dtdx - d^2x/dtdy)
= [- dy/dt (d^2y/dtdx - d^2x/dtdy), dx/dt (d^2y/dtdx - d^2x/dtdy) ]
= [ -d(dy/dt)^2/dx + d^2x/dt^2, d^2y/dt^2 - d(dx/dt)^2/dy ]
= [ d^2x/dt^2 - d(v_y)^2/dx, d^2y/dt^2 - d(v_x)^2/dy ]
もっと基本的なコリオリ力の説明方法がある。物体が系内速度Vをもつとき、物体の軌跡が、ある微小時間内に、ある微小角度を得ることを使う。 この角度変化の速度は、角速度wであり、物体の系内速度Vとは実は全く関係ない。ところが、これを見えない力による、とか加速度場によるとみる とき、コリオリ力であり、系内速度Vに比例する大きさをもつ加速度になる。ある微小時間dtに、ある微小角度dΘを得るとき、w=dΘ/dt という 角速度wをもつ。系内速度Vの物体がその軌跡(の進行方向)をdΘ(《1)だけ変更するには、その運動量を質量で割った、Vsin(dΘ)= VdΘの変化が 必要である。それを微小時間 dt で行うには、2VdΘ/dt の加速度が必要である。ここで 2 は、底辺 dt の三角形が面積 VdΘ をもつには、 長方形で形成するのに比べて高さが、2倍必要だからである。加速度から角度変化 dΘ を得るには2階の時間積分がある。それゆえ、コリオリの力は、 2V x wである。この説明では、2は、時間積分によって発生した。
PE(rot)= KE(rot) - KE(int) = -V・v -1/2 v^2
PE+KE=一定は、物体の運動における物体の速度と位置のエネルギー和の一定をいい、系を移るとき不変という意味はない。一般に慣性系を変えると KEが変化する。回転系と慣性系の系間での運動エネルギーとポテンシャルの関係は、PE - KE = 一定という仮定に基づく。
PE(rot) - KE(rot) = PE(int) - KE(int)
これは、慣性系での運動エネルギー一定からくる。慣性系の運動量と運動エネルギー保存は、回転系では満たされない。 回転系は、軸をPEの高みにして物体に遠心加速を与える、回転放物面(∝ -r^2)ポテンシャルである。公式、
grad(v・A)= (A・∇)v + (v・∇)A + v×(rot A) + A×(rot v) ....(0)
のAにvを代入し、
grad(1/2 v・v)= (v・∇)v + v×(rot v) = W×v + v×2W = v×W ....(1)
-grad(-1/2 v・v)= v×W .....(2)
と遠心力を導く。静電場EとスカラーポテンシャルΦの関係では場がポテンシャルの勾配(例:E= -gradΦ)で、a点からb点までの物体移動のエネルギー 差が経路によらず、任意の閉路一巡で線積分が0、つまり、場に回転がない。それに対し磁場の閉曲線一巡は、閉曲面内のrot B=i。電流があれば、 一巡のBの線積分は0でない。Bに沿って磁荷は加速され一巡し異なる速度で始点に戻るから磁気のポテンシャルは存在しない。電場もdB/dtがあれば rot Eは0でなく、電場はスカラーポテンシャルの勾配にベクトルポテンシャルの時間微分の加算になる(E= -gradΦ -dA/dt、rotA= B)。
回転系中で質点が受ける力 F=m(v×W + 2V×W)は、磁場中で電荷が受けるローレンツ力 F=q(E + V×B)と同じ形であるが、コリオリ場2Wは電磁場と 同様にベクトルポテンシャル v (rot v = 2W) を考慮しなければならないと考える必要はない。なぜなら、回転系の磁場にあたる2Wは一様でその回転 は0である。-dA/dt= -dv/dt= -W×v は遠心力であり、-grad(-1/2v^2) - dA/dt では、= v×W - W×v = 2v×W 遠心力が実際の倍になる。
速度Vの質点がみるスカラーポテンシャル -V・v の勾配としてコリオリ力があると考えると、系内速度と系点速度との内積 V・v は、V・v>0 なら 遠心力と同じく遠心方向の下り勾配であり、V・v<0なら向心方向である。確かにコリオリ力は V・v>0のとき、系の速度vと同方向のVでは遠心方向 で、V・v<0 のとき向心方向を満たし、V= -v や V= v のときコリオリ力が遠心力の倍という大きさも正しく表わす。公式(0)のAにVを代入し、
grad(v・V)= (V・∇)v + (v・∇)V + v×(rot V) + V×(rot v) .....(3)
(V・∇)v= W×V
(v・∇)V= -W×V
v×(rot V)= 0
V×(rot v)= V×2W
第1-3項の和は0、第4項 2V×W だけが残り、コリオリ力が出る(?)。
-grad(-v・V)= 2V×W ......(4)
Vとvとは和が一定で dV= -dv とすると、対称的な(1)が0以外の値をとることは難しいのではと思うが、Vは質点の速度であって、空間に分布する ベクトル場ではないから、上のような非対称な答えがあり得るだろう。質点以外はV=0で第2項と第3項は0だが、第1項も0でないと、またもコリオ リ力が半分になる。ポテンシャルが -(Vv + 1/2 v^2) だけでも十分な説明だが、その勾配が遠心力とコリオリ力になることも確かめたい。 (2013/07/22)
この方向の考えは間違いかもしれない。ひとつ不安なことに気が付いた。vとVの内積v・Vをポテンシャルの勾配がコリオリ力ならVがvと垂直のとき v・V=0だからコリオリ力=0になるが、回転系Wの軸に向かう又は軸から離れる半径方向のVは、vと垂直だが、コリオリ力は働かなければならない。 これは矛盾である。(2013/08/11)
これへの反論。v・V=0 でも、その0でない勾配は可能だから、これによってコリオリ力=0とはいえない。回転系W軸に向かう又は離れる方向のVのとき、 その場所のポテンシャルは0でも勾配はあり得る。(2013/08/29)
Vが空間に分布する系内速度でそれらが全て半径方向なら、ポテンシャルV・vは到るところ0でコリオリ力は存在できない。これは事実に反する。 そもそもVとは質点速度であり、空間に分布しないから、それによる空間属性のポテンシャルを定義するのは、混乱のもとである。Vが質点の 系内速度なら、質点以外の場所の値を定義しないから、その勾配をいうことも rot V を考えることも誤りである。誤りの前提に立つ議論は、 どのような結論も真にできる。そこから正しい結論を導くことはできないし、できたとしたも偶然である。しかも、望むのは実在するコリオリ力 の導出である。結果を知る者のする議論は疑わしい。
議論の前提に気に入らない点を見出して、議論を全て無意味とする批判は、手法が巧妙で恣意的である。前提を認めないなら、もともと議論の必要 もない。疑わしい前提は、避ける方法を考え正しい議論に戻すためにある。全否定は何も生まない。疑わしいものを得ないことは、正しいことを 得ることではない。疑わしいことを排除すれば全てを失う。 (2013/08/31)
X' = X’ + w x X ....(1) X''= X'’+ w x X' .....(2) X''= (X’ + wxX)’ + wx(X’+ wxX) .....(3) = X’’+ (wxX)’+ wxX’+ wx(wxX) = X’’+ 2wxX’ + wx(wxX)(1)のu_i= u_r + W×r_iは正しいが、(2)を X''= X’’+ w x X'と考える a_i= a_r + W×u_i は正しくなく、4項のうち第2項を見落す。 (3)の右辺第1項は(du_i/dt)_r であり、a_r= (du_r/dt)_r ではない。系内速度 V = X’と系点速度 v = wxX を使うと、第2項は、 系点速度vの回転系での時間微分v’になり、これが0でなく、系内速度Vに比例するコリオリ力の半分 wxV になる。
(V+v)'= (V + v)’ + wx(V + v)
= V’+ v’ + wxV + wxv
= V’+ wxX’+ wxV + wxv
= V’+ wxV + wxV + wxv
= V’+ 2wxV + wxv
また、これは、線形の時間微分の演算子 ()' = (()’ + wx()) の座標Xへの2回の作用を示す。2回の微分演算の交差項、前からwを外積するwxと
回転系の時間微分’の順が違う (wx())’と wx()’とがw一定下で等しいことにより、コリオリ力 2wx()’を導く。(2013/11/18)
()''= (()’+ wx())^2 = ()’’ + 2wx()’ + wx(wx()))