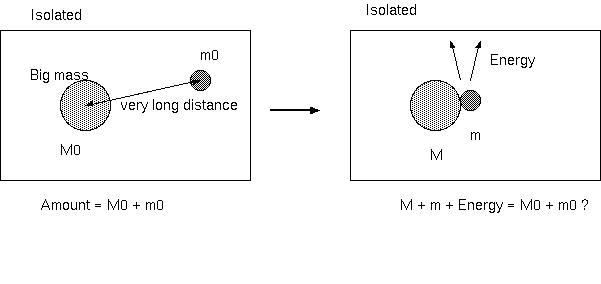
図 1. 孤立系が全体の質量・エネルギーを変えないとすると、静止質量は、場所によって変わる必要がある。
1. はじめに
2. 動質量が質量に反映すると
3. それの逆を考える
4. ニュートン重力と慣性
5. ニュートン重力のバネ
6. ニュートン力学とポテンシャル
7. ポテンシャルと質量の関係
8. "光の伝播への重力の影響について"について
9. あとがき
10. ポテンシャルと計量

一般相対論は、質量が原因となって場所によって計量が違い、同一座標系内の場所と時間の違いによって、時間の経過と物差しの 大きさが変化する。ある地点からみた遠方の姿は、その場所がみる姿とは異なる。その間の一般的な時空の写像を一般座標変換という。 それは、重力方程式を使って、局所の計量を微分的変換として大局的な一般座標変換を求める、ブラックホールの時空を説明したり、 宇宙解を求めたりする。そこにおいて"時間と空間とは相対的だが、質量はそうでない、質量は不変でどこに置いても同じ" と考える べきだろうか。場は物質から決まり、物質は場からその運動だけ影響を受け、その質量自体は、影響を受けないのだろうか。
時間経過の遅い、ブラックホールの周辺の時空を遠方から見るとスローモーションになる。そこの人間は、一言喋るのにこちらの 一年を要するかもしれない、ほとんど動かない彫像と化している。それをある瞬間に同じ力で叩いてもその彫像は、すばやく変化 できない。それは質量が大きくなったと言わないのだろうか。質量もテンソルで場の影響で方向によって大きさの違うものでは ないだろうか。光速も物差しも方向によって大きさが違うのである。物差しの短縮と時間経過は、物体の速度に反映すると考えられる。
特殊相対論の横方向の速度は、時間経過の比率で緩やかになり(1/γ)、加速度は、さらに小さい(1/γ^2)。加速度は、力/質量の比 であり、力が 1/γ倍に小さく横質量がγ倍に大きくなっている。しかし、時間経過に k 倍の遅れなら速度は 1/k 倍、加速度 1/k^2 倍といのは、一般的ではない。ローレンツ変換に横方向の短縮がないためである。時間経過が k 倍に延び、物差しが j 倍になれば、 速度は、j/k 倍、加速度は、j/k^2 倍になる。
この時間経過の遅れは、質量の増加ではないかと考えて、次のような考えをしてみた。宇宙論のポテンシャルの発散の問題も 解決できるかもしれないからである。
m= m0(1 + GM/rc^2) ...............(1)
m0GM/rc^2 の項は、そのポテンシャルエネルギーを質量換算(c^2 で割った)したもの。(1)を、ニュートン重力の式 F= GMm/r^2 にいれると、
F= GMm0/r^2 + (GM)^2m0/r^3c^2 ....(2)
となって M^2/r^3 の項が付け加わる。(2)を r で積分して、重力のポテンシャルΦ= -GM/r は、
Φ= -GM/r - 1/2 (GM/rc)^2 .......(3)
となり、-1/2 (GM/rc)^2 の項が加わる。重力ポテンシャルΦとFの関係は、F= -grad Φ、 F= -(dΦ/dx, dΦ/dy, dΦ/dz) であるからΦの r^-2 の項が Fでは、r^-3 になる。しかし、ρ一定の宇宙の重力ポテンシャルの積分可能性は、これによって 解決されるとは思えない。符号が同じであるから、ポテンシャルがさらに積み重なるだけである。それゆえ、これは重力の遮蔽 ではなく、質量の相乗効果になる。
もし、重力のポテンシャルがΦ= -(GM/rc)^2 だけなら、厚さ d、密度ρ、半径 r の球殻の質量が 4πdρr^2 なら、そこから のポテンシャルへの寄与は、 4πdρ/c^2 という一定になる。積分はまだ発散するし、重力 F が r^3 に反比例してしてしまう という大きな問題が残る。 (3)の式は、GM/r= x とおくと Φ= -x が Φ= -x -(x/c)^2 になっている。 r が大きくなると関係 ないが、r の小さいところでは、これは大きな差になる。(2003 Aug 15)
2 体の等しいシュバルツシルト・ブラックホールを合体させるとき、29% までの質量が失われる。これは、単にブラックホール の面積の非減少則からの限界である。2 つの質量が合体するとき、合体後の面積からの限界を 2 とすると質量=半径は、√2 倍 以上であり、取り出せるエネルギーは、最大、(1-1/√2)= 0.29 である。多くのブラックホールを順次合体させれば、100 % ま で質量をエネルギーに変化できる。その質量の合体によるエネルギーへの変換を考えるとき、次の疑問がでる。もし、重力によ る結合が静止質量を変えないなら、得られるエネルギー分だけ全体質量を増やすことになる。重力による結合も、核反応と同じ く質量欠損を起こすのではないか。重力だけ例外ということはなさそうだ。ポテンシャルの低下に伴って質量も減少する必要がある。
前章の議論を反転して考える。ポテンシャルが質量を減少させると考える。総量のエネルギーが不変であり、物質がポテンシャル の低い場所に移動するとき、その変化で運動エネルギーが発生した分、静止質量は減少すると考えるのである。このとき(1)は、
m= m0(1 - GM/rc^2) ................(1)
であり、第2項の符号が反対になる。ニュートン重力の式、F= GMm/r^2 の m に入れると、
F= GMm0/r^2 - (GM)^2 m0/r^3c^2 ....(2)
となって - M^2/r^3 の項がでてくる。重力のポテンシャルは (2)の F/m0 を r で積分して、
Φ= -GM/r + 1/2 (GM/rc)^2 ........(3)
となり、1/2 (GM/rc)^2 が加わる。r の小さい近傍に働く重力の遮蔽効果になる。遠方のポテンシャルを違わせるものでない。
m= m0 (1 + φ(r)/c^2)
m を r の関数とするとき、φ(r)m(r) が通常の φ(r)m0 の代わりをする。これが -GMm0/r であるなら、
-GM/r= φ(r)(1 + φ(r)/c^2)
から、φ(r) を求めることもできよう。φ(r)m(r) の r による微分 (φ(r)m(r))' がニュートン重力 GMm0/r^2 であるなら、 (φ(r)m(r))'= φ'(r)m(r) + φ(r)m'(r) から
GM/r^2= φ'(r) + 2 φ(r)φ'(r)/c^2
というφ(r)の微分方程式から φ(r) の関数形を求めることも可能であろう。しかし後述するが、それらも疑わしい。
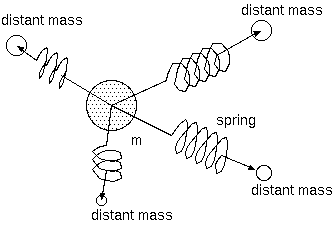
遠方からの重力を受けている物体は、多くのバネによって四方八方から繋がれている。そのことが、慣性を説明するのだろうか。 慣性は、遠方の質量が作るポテンシャル場の影響かもしれない。しかし、重力を空間の性質として説明するポテンシャルは、 遠方の影響が強い。太陽系の端に出たぐらいでは、その違いが測定でき、実験的に示されるとは思わないのである。
地球から出て地球の半径の10倍、100倍に離れたとしても慣性は、全く変化しないことを我々は測定し確認するだろう。 そのとき我々の体は、地球から繋がったバネを失い、距離の2乗に反比例するそのバネの引力は、1/100、1 万分の1に弱まる。
それに対してポテンシャルは、バネのようにある方向に力を与えるものではない。それはある高み(*)を空間に考えることで、 その傾き、勾配が重力を与えるものとして、空間に特性として与える。その大きさは無限遠を 0 とするときマイナスであり、 質点からの距離に反比例し、地球の半径の10倍、100倍離れても、地球の影響は 1/10、1/100にしか弱まらない。遠方の影響が大きい。 太陽地球間の 2000 億倍も遠いアンドロメダ銀河の質量は、2000 億の太陽より大きいが、その地球への影響の方が太陽よりも大きい。 これは、物理的な実体が効果と乖離している症状であり、ポテンシャルは本当に物理的な実体か、物理量なのか、と疑がわれる。
地球上で暮らす我々は、地球の表面の一定の重力を受けることに慣れている。しかし、宇宙空間に出て行って、無重力状態の衛星で 生活をするとき、その重力を感じることがなくなるが、慣性はまったく影響なく残る。気をつけることは、体の速度を変えるときに、 はっきりと力積がいることである。体の速度を変えるとき、方向転換のときには地上と同じだけの衝撃を伴うのである。 重力が 1/6 の月の上では、物体は、落下加速度が 1/6 であり、6 倍の秒数で同じ速度になる。6 倍の高さで同じエネルギーを蓄える。 2 mの高さから落ちることを地球上で警戒するなら、12 mの高さを警戒する必要がある。重力はなくなり、慣性は残る。 誤解を招く表現をあえて採ると、慣性質量の大きさと重力質量の大きさは同じでないのである。(慣性質量=重力質量とは、同じ 重力場において、重力が物質の種類によらないことをいう。)
だが、本当にそうだろうか。上の考え方はニュートン力学なのである。無重力状態で慣性が消え去ることはないだろう。しかし、 重力の係累から解放されたときの質量は、地上の質量と少しは違っていてもよいのではないだろうか。 問題はそれが測定にかかるかどうかだろうか。それが時間経過の重力効果と同じ程度なら測定されるだろう。 そして、それが増えるのか減るのかという符号がまず重要である。
(*) ポテンシャルを "高み" で比喩することは、地上の生活習慣によるだろう。一様な重力が考え方に及ぼす影響は大きい。 質量 m が h だけ高い所にあることが、mgh のエネルギーをだす潜在能力(ポテンシャル)を秘めている、gh がポテンシャルである。 空間にスカラーのポテンシャルを考え、その傾き、勾配ベクトルを重力とする。そのことは、まだ理解しやすいが、3 次元の中 の電荷や質量に安定点のないことを表すラプラスの方程式は、実感し難い。空間にはくぼみや丘がなく、すべてサドルであるとは。
理想的な引っ張りバネの特性は、平衡点からの変位に比例する引力を与える。両側からバネで引っ張られた物体は、両側からの 引力の和の合力を受ける。a, b の物体を結ぶ線分の中点に c 点があり、バネ(バネ定数 1 kg重/cmとする)で結ばれているとき、 c 点を a 側に 1cm ずらすと a からの引力は 1 kg重減り、 b からの引力は 1kg重増える。合力は、b 方向に 2 kg重増える。 微小な変位に対して復元力が働く安定性がある。通常のバネとかゴム紐の途中に物体がある場合の安定である。
a が原点(0,0)に b が (1,0)にあり、c が(r,0) あれば、理想的なバネのとき、 (右を正とする) 力が変位に比例し、 a からの力が -r 、b からは (1-r)、合力は、 -r + (1 - r)= 1 - 2r であり、中央 r= 1/2 で力が 0 になる。 中央より少し右では、1-2r は負、少し左では 1-2r が正であり、中央の点を外れても復元力がある。
これを力の空間的積分であるポテンシャルでみると、バネの場合 r^2 に比例する。a 点と b 点から伸ばされたバネの中点の ポテンシャルは、r^2 + (1-r)^2 = 1 - 2 r + 2 r^2= 2(r-1/2)^2 +1/2 となって2次式の放物線となり、r= 1/2 に極小点がある。
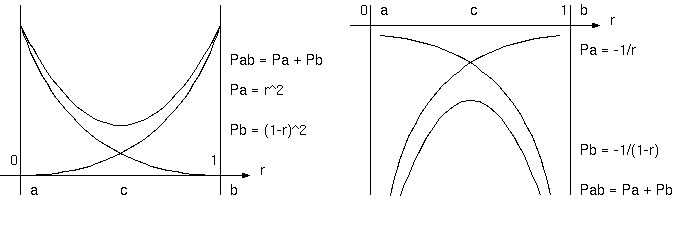
ニュートンの重力は、それとはすこし違う。距離の2乗に反比例する力をもつので、a, b 2 つの天体からの引力が、 物体 c を引っ張っているとき、c が a, b の中点から b 側に少し移動すると、b 側の引力が強まり a 側の引力は弱まる。 物体 c は、ずれた方向にさらにずれるという不安定さをもつ。これはバネやゴム紐とは違う引きかたである。
a からの引力は -1/r^2、b からは 1/(1-r)^2、合力は、 -1/r^2 + 1/(1-r)^2 = (2r-1)/r^2(1-r)^2、r= 1/2で 0 となる。 r < 1/2 のとき負、r > 1/2 で正となるから不安定である。ニュートンポテンシャルは、a 点から -1/r、 b 点から -1/(1-r) である。両者の和、-1/r -1/(1-r) = -1/r(1-r) は、r= 1/2 で極大であり、上に凸になる。(不安定点は上に凸、安定点は下に凸 のポテンシャルをもつ。) 万有引力は、2 天体を結ぶ線上で不安定である。宇宙のすべての物体は、この不安定性をどのように 扱っているのだろうか。線から外れる方向の変位については安定である。
ただし、天体的規模の万有引力は、もしバネとしても、バネ定数が負で(?)その絶対値は非常に小さい。地上では重力は一様と するのが第1近似である。重力は、上に行けば弱まるが、質量 1 kg に働く重力は、上下に 1 m 移動して重量の変化を測定 するには精密な重力計でなければ分からない程度である。地球の半径が 6500km だから 1m は、その 1/650万であり、1 m の高低差による重力の違いは、距離の 2 乗に反比例の式から、650万分の1の2倍、0.3 mg重であり、7桁の精度が必要である。
理想的なバネで物体が結合されているとき、物体に変移を与えると、物体は抵抗して移動を拒み、正のバネ定数をもって平衡点 に戻る方向の力を場から受ける。それは、慣性とはかなり異なる性質である。現実の物体にバネ定数の痕跡はないし、万有引力 で結合した物体間に負のバネ定数も確認できない。そこには、慣性は加速度への抵抗、バネは変位への抵抗という違いがある。
物体と遠方周囲の巨大な物体との重力的結合が、両者の間に部分的な剛体性を与え、加速度に抵抗する力を与える必要がある。 上の議論では、万有引力源が不動点に固定されているという考えに囚われている。周囲の巨大な質量も力に反応する質量 M であり、 それとバネ定数 k で結合した質量 0 の物体は小さな質量 m の動きをすることが説明できればよい。質量 0 の a 点を力 F で押すと、バネ定数 k が働き、そのとき a 点は、F/k だけ力の方向に移動する。バネを通して同じ大きさの力 F が b 点の 質量 M に働く。b 点は F/M の加速度をもち、それがバネを通して a に影響を戻す。k が大きくバネが剛体棒なら、m = M となるが、k が小さいとき小さな質量の姿をするか。バネに結合した点の時間の関数 x をばね方向の座標とすると、力と運動 の関係は、x= F/k +∫∫ F/M dt^2 である。バネが質量を生むことはないと結論して間違いなさそうである。
しかし、ポテンシャルというスカラー値が空間に分布し、その勾配を万有引力とすることは、考えや計算を単純にする。 多物体から受ける重力での物体運動を計算するのに、万有引力では、N-1 個からの物体間の距離 r_i を使って、引力を受ける 側の質量 m も掛けて、引力のベクトルを N-1 個加算し、物体の質量 m で割算して加速度を出すが、
F = G Σ M_i m / (r_i)^2、a = G Σ M_i / (r_i)^2
もともと重力による加速度を求めるのに受ける側の質量 m は、不要であった。引力ベクトルの加算は、3個の成分の加算である。 それに比べてポテンシャルは、-1/r に比例するスカラーの加算でその場所のポテンシャルを出し、その勾配から加速度がでる。 N が大きいとき、 N-1 個からの引力をベクトル加算するよりは、スカラー加算したほうが計算量が小さい。ポテンシャルの 空間的微分(勾配) grad = (d/dx, d/dy, d/dz) はベクトルで、質量を掛ければ力となる。φの x 方向の変化率を x 成分、 y 方向の変化率を y 成分、z 方向の変化率を z 成分とする。万有引力は、それ以上説明のできない遠隔力であったが、 ポテンシャルは、場である。
φ= -G Σ M_i / r_i、 a= -grad φ
ポテンシャルとはその場所に単位質量を置くのに必要なエネルギーであるが、どこからそこに置くかの任意性があり、ポテンシャル に確定値を求める事は、本質的にできなかった。例えば、電気的なスカラーポテンシャルは、その差しか意味を成さない"電圧"である。 そのような仮想の値を使うのは、計算上の必要だけだっただろうか。そうではなく、新たにポテンシャルを物理量とし、ポテンシャル が従う物理に切替えることが必要だったと理解すべきであろう。それが一般相対論である。そこでは、ポテンシャルの不確定が 一般座標の不確定に置き換えられている。
高さ h に gh のポテンシャルがある。そこに質量 m を置くのに必要なエネルギーが位置エネルギー mgh である。 そこから物体を落とすと運動エネルギー 1/2 mv^2 に変わる。v^2= v0^2 + 2gh 重力が受ける質量に比例し、 ポテンシャル・エネルギーが受ける質量に比例するため、場の概念となる。電場が電荷に対して力を与えるように F= q E、 重力場は質量に対して力を与える場である。重力場を g として F= mg、と書いても F = ma から、g= a である。 つまり重力場は、質量比例の力を与える力場というよりも、質量に関係なく加速度を与える場である。
電場がスカラーポテンシャルの勾配である E= -grad φ のと同じ意味で、重力場は、ポテンシャル場の勾配である。 a= -grad φ 質量 M の質点から r の距離の重力場は、GM/r^2 の大きさの中心に向かうベクトルであり、ポテンシャルは、 -GM/r のスカラーである。ポテンシャルと質量 m の積がエネルギーであり、その r による微分がニュートンの万有引力である。 質点周囲のポテンシャルは、球対称で半径に依存し、-GM/r という値をとる。その勾配は、最も急な坂を昇る方向をもつ、 中心から外向きのベクトルであり、大きさは GM/r^2 となる。符号を逆転した -grad ベクトルが重力場であり、 ポテンシャルの最急降下ベクトルである。
ニュートンの万有引力が遠隔力であるのに対して、ポテンシャル場の考え方は、近接力である。特殊相対論から重力が即時的 伝達をすることは考えられないから、電場と磁場とが光速で伝達する電磁気のポテンシャルを使う考え方との類推から、 重力の伝達も光速ということは、一般相対論においても持つと思われるが、ニュートン重力の即時伝達に伝達時間を考慮する と間違いになることも知っておく必要がある。電磁気でも同じ仕組があって、等速直線運動をする電荷の出す電場は、 常に即時的な現在の電荷の方向を指すのである。
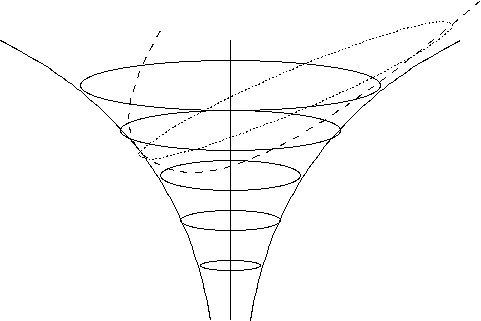
ある質点からの距離 r の点の高さが -1/r になるような漏斗面を考え、ポテンシャルを模擬して理解の助けにすることがある。 3 次元空間上のポテンシャルを、2次元の面の高さとして表している。ニュートン力学での物体の円軌道、楕円軌道、方向転換 しかできない双曲軌道がその曲面上の物体運動として可能らしいことが分かる。しかしこれは、それ以外の運動が可能かなど 議論できない程度の粗雑なモデルである。 ポテンシャルの凹みは、中心質量 M に比例し、距離 r に反比例するから、遠方の大きな質量の窪みは、近傍の小さな窪みと 同じ程度の深さになる。いろいろな規模の凹みの分布する宇宙の星々の間の航海の路線を想像することができる。近傍の太陽は、 ピンで突いたような窪み、アンドロメダ銀河からは、その2000億倍巨大なスケールの坂道だが、低下は同じ程度である。
2物体 M と m とが重力で関係し m が無限遠から近付き、仕事 W (W>0)をして M から r の距離に静止したとき、r 点での m の静止質量 m は、無限遠での質量 m0 より小さい。質量エネルギーの保存則から、r 点での質量 m と仕事 W の和は、m0 に等しいからである。
m + W/c^2 = m0 .........(1)
仕事 W は、ポテンシャルφ(r)<0 (φ(∞)=0)の低下量とその点での質量の積に等しい。
W= -φ(r)m ..........(2)
仮にこれを次のように質量 m0 によるとすると、
W= -φ(r)m0 ..........(2)'
ここでもし(2)' を (1) にいれると、
m = m0(1 + φ(r)/c^2) .........(3)
最も一般的に使われる式になる。弱い重力ポテンシャル場では、この式の精度が問題になることはない。しかし、極限的に強い 重力ポテンシャルのとき問題である。この式では、φ/c^2 → -1 とする極限で、m → 0 となる。それに対して、質量が変化する と考える (2) を (1) にいれると、
m= m0/(1 - φ(r)/c^2) .........(4)
となり、(4) は、(3) とは、異なる式の形になる。弱い重力ポテンシャル -φ(r)/c^2 ≪ 1 では一致するが、強い重力では違ってくる。 (4) は、φ/c^2= -1 でも、m= m0/2 にしかならず、φ(r)/c^2 が→ -∞ で初めて m → 0 になる。
物体に自由落下とか軌道運動をさせる場合、運動エネルギーが動質量になって質量に加算され、ポテンシャル低下による静止質量の減少 を補って、質量は無限遠と違わないと考えられる。ブラックホールの地平面では、ポテンシャルはどうなっていて、質量はどうなのだろう。 時間経過は、ポテンシャルの低下と直接に関係する。地平面のすぐ外での時間経過 dt' と無限遠での時間経過 dt との比は、 dt'/dt = √ (1-2GM/rc^2) である。ブラックホールの時空は、dt^2 の係数 g_44= -(1-2GM/rc^2), dr^2 の係数 g_11= 1/(1-2GM/rc^2) であり、光速は、ds^2= 0 から、dr/dt = c√(-g_44/g_11) になる。(地平面の外で g_11 ≧ 1 から、物体は r 方向に短縮している。)
ニュートンポテンシャルをφ= -GM/r とすると、g_44 との関係、φ= -1/2 c^2 (g44 + 1), g44 = -1 - 2φ/c^2 も出る。 地平面で g11 = ∞、g44= 0 になり、φ= -1/2 c^2 となる。ポテンシャルの比 (1+φ/c^2) は、無限遠の 1/2 に下がっている。 φは、ある距離で -∞になるのではなく、距離を 0 に近づけてやっと -∞ になる。 (4) では、地平面で質量の方が 1/2 になる。 両者はどう折り合いをつけるのか。
(2) 式について、不正確な考え方を訂正する。質量 m を r の関数にするだけでなく、ポテンシャルの式と、質量の式をともに変更する のであれば、両者の任意性がある。W= -φ(r)m(r) というとき、仕事と質量の概念を既定として、質量を単に変数にしたが、もとの ポテンシャル概念は、質量一定を仮定している。(4) を導いた (2) のように、その点の m でポテンシャルとエネルギーを決めている。 それはたしかに、m に比例するだろうが、仕事は、力の∞〜rの積分であり、力は、重力場 g と途中の各点での m の積である。 (g= -dφ/dr,または、ベクトル g= -gradφ)
r_0
W= -∫gm dr .............(5)
∞
力の線積分 W を経路途中の m でなく始点の m0 や 終点の m で割ってポテンシャルとしたのは不正確であり、(3),(4)を再考できる。 (5)を微分形式で書き、
dW/dr= gm .............(6)
であり、(1)から、
dm/dr= -1/c^2 dW/dr .............(7)
(6),(7)から得られるのは、
dm/dr= -1/c^2 gm という、m と g の関係式である。これに g= -dφ/drをいれると、
dm/dr= 1/c^2 m dφ/dr
dm/m = 1/c^2 dφ
両辺を積分し、φ(∞)= 0 で m= m0 を使うと、
ln(m)= φ/c^2 + ln(m0) から、
m= m0 exp(φ/c^2) .............(8)
となる。(3),(4) よりも (8) 式が確かそうである。(8) の m は、(3),(4) の間((3) < (8) < (4)) になる。この式は、m と φの 関係であり、r との関係は、φ(r)= -GM/r のままでよいのだろうか。φの空間微分が重力という関係は保っている。しかし、(8)は、 φ=c^2 ln(m/m0) というポテンシャルの新たな定義ともとれる。質量とポテンシャルの片方の r の関数形が定まれば他方も定まるが、 関数形を決めるには条件不足である。
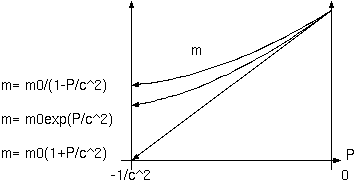
否定的に言えば、このポテンシャルと質量との関係は、両者の意味を変えているのだから、ほとんど意味はない。両方の意味とも確か でないから、確かなものがなにひとつないのである。
しかし、確かなことが全くないかとさがせば、無限遠での質量、これは、エネルギーである。これがMの近くに落ち込むことで取り出せ るエネルギーは、m0c^2 以上は、望めないだろう。ニュートン力学では、質量は変わらず、-GM/r のポテンシャルであるなら、物体 m を物体 M に限りなく近づけるだけで、どこまでもエネルギーを取り出せる。ところが、相対論は、E= mc^2 という式ができ、静止質量 のエネルギーという、信じられないほどの大きなエネルギーが質量に付随することを明らかにした。その代わりに、静止質量 m0 に対応 するエネルギー以上を取り出すことを期待できなくしたのである。
無限遠で、m0 であった質量が、M の近傍に落ち込むことで取り出せるエネルギーの最大が、m0c^2 であるなら、距離 r= 0 では、質量は 0 になる必要がある。(8) 式では、これは、r→ +0 でのポテンシャルφ(r) → -∞ であることが必要である。そうでないと m→0 には できない。静止質量 m0 のエネルギーを取り出すためには、r=0 で m= 0 を式 (8) から、φ(0)= -∞ である必要がある。 ニュートンポテンシャル φ(r)= -GM/r は r→0 において、φ(r) →-∞ であることでは条件を満たしている。
この部分には混乱がある。物体 W は、質量 M をもって下の点 S1 にいて、エネルギー E1 を受け取って M' の大きさに変わり、 Eγh/c^2 = M'γh - Mγh 又は、 M'- M = E/c^2 ...(1b) と書かれると、当然、M' ≧ M であるが、E/c^2 は、S2 から E2 として放射され、S1 で E2 として受け取られた放射エネルギーE1 = E2(1+γh/c^2)) の差 E2 - E1 であり、それが物体 W の質量に (差だけが) 付加することもおかしいし、物体 W の上昇時の機械的仕事 Mγh 又は M'γh となにか関係するものではない。 物体 W が下(S1) で受けとるエネルギーが E1で、受け取る以前の質量が M なら、M'= M + E1= M + E2 +E2γh/c^2 である。
仮りに、M を S1 でエネルギーE1 放出前の物体 W の質量と定義し直すなら、物体に付加して下降と上昇時の機械的エネルギー差 M'γh - Mγh がエネルギー単独の上下の差と等しいと理解できるが、エネルギーが上下するとき大きさが変わるのに、 質量が上下しても (付加したエネルギーの変化分以外は、) 何も変化しないことになる。質量も上下で変化するなら、 上で質量 M が下で質量 M'のとすると、上下で静止質量が変化せず機械的エネルギー付加分だけ下で総質量が増加するなら、 M'= M + Mγh/c^2とするべきであり、(静止質量が M と M' というなら M'= M である。) 機械的エネルギーを放出した分だけ 下では静止質量が減るとすると、M'= M - Mγh/c^2 だろう。
重力井戸の中で質量がどうなるかという問題を明確にすることは、難しい。下で局所的には、放射エネルギーが増加するように、 質量も仕事の放出分増加して見えるが、上から見ると質量とエネルギーは変化しないと理解すべきではないだろうか。 放射も上からみると周波数を変えない。時間の経過が遅くなっている下の局所時間のためにエネルギーが増加して見えるのである。 同様に、下の局所で測定した静止質量は変化せず、上からみた質量が時間経過緩慢分だけ、減少しているというのが本当かもしれない。 その減少分は、放出する機械的エネルギーとも等しい。下で静止質量が上にあるときと変化していないように見えても、 質量がすべてエネルギーに変換されて上に運ばれる場合を考えれば分かるように、それは時間経過の緩慢分だけ上の基準では減っている。
この問題には客観的判定方法がある。二物体間の重力で質量を計るなら、二物体の間の引力をバネで測定できる。その距離を リンク機構で回転に変え目盛をもった表示をすれば上でも下でも同じく目盛が正しく見える。こうして局所の重力質量、(局所の引力) をポテンシャルの異なる遠方から測定できる。重力定数がポテンシャルの影響を受けない限り、重力質量は、グローバルな測定ではないか。
質量を放射エネルギーに変換したときそれを上方で受けると減少することを考えれば、質量の相対性は明らかである。しかし、 静止質量が局所で変化せず、遠方からは変化するというのは、上記の道具からみると矛盾するように見える。 重力定数がポテンシャルの関数でないといけないことになる。それでは、ポテンシャルの定義も崩れるのではないか。 そうではない。上記の道具は、局所の測定を遠方から見ているだけである。物体のバネ定数は、グローバルではあり得ない。 なぜなら、力はグローバルではなく、変換されるものだからである。
もうひとつ考慮すべきことがある。E= mc^2 の c は局所の光速かもしれない。グローバルな光速というものはなく質量エネルギー関係は、 場所の関数とするのである。平坦遠方からみて光速が低下した質量近辺では、質量が低下せずともエネルギーは低下できる。 質量は逆に増大しても、光速 c の低下比率の2乗が大きければエネルギーは低下できる。質量の相対性は明らかである、とは言えない。 1次近似だけの議論でエネルギー低下を時間経過比率とし E= E0(1+Φ/c^2)、光速の低下率を c= c0(1+Φ/c^2) とするなら、質量の増加比率は、 m= m0(1-Φ/c^2)になる。また、ブラックホール解から r 方向の光速を c= c0(1+2Φ/c^2) とするなら、質量増加は大きく m= m0(1-3Φ/c^2) になる。 局所慣性系の光速 c0 の存在をたよりにして、この考慮を打ち切るべきかもしれない。しかし、光速の大きさが方向によるとき、c^2 は何を意味するか、 光速がベクトルの成分なら、c^2 は、ベクトルの大きさの2乗となる。光速が方向によって大きさの変わるベクトルとするなら、c^2 も方向によって 大きさの変わるスカラーである。ある点の質量エネルギー変換の比とすることは難しい。 (Jan 9 2005)
質量がポテンシャルに依存するという論文は、Harihar Behera による、"The contribution to the perihelion advance of Mercury arising out of the dependence of mass on gravitaion potential" (arXiv astro-ph/0410401) があった。
質量がニュートンポテンシャルに比例するとした m* = m0 (1 - GM/c^2r) を使って、水星の近日点移動を説明しようとしたもので、一般相対論の ケプラー結合問題のハミルトニアンへの項は ΔH = -h_e/r^3 である。h_e= kl^2/(m^2c^2), k= GMm ポテンシャルエネルギーへの修正は、 U= -k/r -h_e/r^3 である。質量のポテンシャルへの依存は、U* = -k/r -h/r^2 -h_e/r^3 と r の -2 次の項を追加することになり、結果、 -w_e/3 の効果になるという。一般相対論の修正分の -1/3 だけの効果があって、無視できないというものである。つまり、42.98 arcsec/centry に -14.326 arcsec/centry の効果となる。彼は、一般相対論の様々な効果を質量のポテンシャル依存で説明できるとするが、これだけは、残念ながら 符号が違ったのである。
私がこの論文に気がついたことは、質量のポテンシャル依存をいうべきなのは静止させた物体であり、水星のように軌道を描く物体の質量は、 ポテンシャル依存の質量の減少分は、丁度、運動エネルギーに変化し、質量のポテンシャル依存による効果は、軌道運動する天体には元もと存在しない のではということである。 (July 18 2005)
重力方程式の質量は右辺にまとめられている。もし、それが左辺の計量によって変化するというのは、隠れた仕組によって式が制御され、 重力方程式の概念が成立しないという反論がありえる。しかし、重力方程式自体が離れた時空点の質量を記述していると期待も可能では ないか、と考える。また、遠方からどう見えるかは、基本的に時計と物差しであり、質量ではないのではないかという疑いもある。 これには、重力方程式と計量の場は重力を扱うためのものであり、離れた場所の質量の影響は真っ先に重力である。計量場とは重力の場 であると答えたい。
計量の局所観測性は、その勾配である重力は容易に観測できるのに比べて時間経過と物差しの延び縮みの変化は小さく、計量は基本的に 計測が難しい。計量は原理的に一点では観測できない。物体を移動するだけでその慣性質量が変化するなら、重力質量も変化し重力計測 できると考えるべきだろう。ただ、孤立系の質量エネルギー保存は、むしろ他への重力が変化しない方向である。質量が変化せずに運動 エネルギーが無から発生するほうが、他への影響を与えるだろう。
エネルギーは、時間経過に直接に比例するものである。例えば E= hνである。ポテンシャル低地からの光は、高地において赤方偏移する。 これが放射エネルギーがポテンシャルと関係する仕方である。放射は移動するとエネルギーを失う(または獲得する)。このことがエネルギ ーの別の形である質量においても成り立つのではないかと考える。ポテンシャルの g_44 との関係は、g_44 は、dt^2 の係数だから、時間 経過は √-g_44 と比例でありエネルギーが時間経過に比例するなら、ポテンシャルも √-g_44 比例であり、g_44 に比例でない。遠方から みて g_44 が 1/4 の時空点は、時間が 2 倍ゆっくりと経過するのである。
ポテンシャルを φ= -GM/r とするとき、質点の側の計量 g_44 との間には g_44= 1-2φ、φ= (1-g_44)/2 という線形関係がみえるが、 dt'/dt= √(1-2GM/rc^2)、(dt)^2 の係数は g_44= -(1-2GM/rc^2)、dr^2 の係数は g_11= 1/(1-2GM/rc^2)である。1-2GM/rc^2 は、 ポテンシャル比率 (1+φ/c^2) の 2 倍変化する。古典的な (1+φ/c^2) に近似されるのは、√-g_44= √(1-2GM/rc^2) である。 この 1-2GM/rc^2 は、g_44 と g_11 の両方に出る。ポテンシャルは、その勾配が重力であるから、g_11 も関係しているのではないか。
ポテンシャルφは、その勾配が重力を与えるスカラーである。 ニュートン力学の万有引力の重力場よりポテンシャル場が説明を 単純にし、場の従う力学を考えることができる。距離の 2 乗に反比例する重力場は、遠隔的で場としての説明性がない。それに 比べ、ポテンシャルφは、物質の質量密度ρとの関係がある。時空の2階微分が物質密度であるという、4 次元のダランベール 方程式 □φ=ρ、それを静的にした 3 次元ポアソン方程式、△φ=ρ (△はφの 3 次元の 2 階微分の和 grad div がスカラー にもどりこれが質量の空間密度ρを意味する。) さらに、密度ρ= 0 ではラプラス方程式 △φ=0 がそれである。これらは、 ニュートンから始まる古典力学のポテンシャル場の方程式、重力理論といえるものであろう。
それは、電磁気において電場と磁場が従うマックスウエル方程式自体より、電磁ポテンシャルのほうがより基本的に思えるのと 同様である。しかし、電磁ポテンシャルもニュートンポテンシャルも最初から仮想の存在であった。物理量ではなく単に計算を 簡単化する存在であり、ポテンシャルには確定値が存在しないことがその本質的でありゲージ変換であるという理解もされてきた。 そのような重力ポテンシャル仮想論に対して、"ポテンシャルは実在し、この重力方程式に従う" というのがアインシュタインの 一般相対論の言明である。スカラーであったポテンシャルは、計量と名を変え、独立 10 変数をもつ 2 階の対称テンソルとなった。
その計量場と質量とを等価とし、=で結ぶニュートン力学のポテンシャル理論の式の形式は、重力方程式に引き継がれている。 場に曲がった時空を与える計量場を扱うことが違うが、2 階の曲率リッチテンソル R_ik とスカラー曲率 R でできたアインシュ タインテンソル G_ik (= R_ik + 1/2 g_ik R) がそのままエネルギー運動量テンソル T_ik と等しい。計量場のある曲率を表す 2 階のテンソルが質量密度に比例する、これは、時空の 2 階微分□φが質量密度ρであるという古典的なポテンシャル理論の 基本形式をもっている。G_ik= -κ T_ik (これに宇宙項をいれると、G_ik - λ g_ik = -κ T_ik) である。
現在は、計量で議論すればよいから、スカラーポテンシャルは、もはや無理な形式という批判もありえるが、ポテンシャルが計量 にスムーズつながると思っていてもそうではない。なれ親しんだニュートンポテンシャルが、計量との間にどのような連関があって、 そしてこの間にはどのような問題があり、どれほど計量と齟齬するかを知ると、我々は計量にそれほど慣れていないことを自覚する のである。そのことをあまり意識されたことのない人に、次のことは新鮮かもしれない。
(1) 質点のそばで g_44= 1 - 2GM/rc^2、 g_11= 1/(1 - 2GM/rc^2) である。ニュートンポテンシャルを φ= -GM/r とすると、 g_44= 1 - 2φ、φ= (1-g_44)/2 である。φと g_44 は線形関係である。
(2) g_44 は、時間の係数、dt^2 の係数であるから、時間経過は、√-g_44 に比例する。たとえば、時間が 2 倍ゆっくりと 経過する場所の g_44 は 1/4 である。ポテンシャルがエネルギーなら √-g_44 に比例する。これは、(1)と矛盾する。
(3) g_11の次元は、長さの -2 乗、g_44 の次元は、時間の -2 乗である。それゆえポテンシャルは、g_44/g_11 比例である。 これは、(1)とも(2)とも異なる。エネルギーが時間経過に比例し、そしてそれが、なぜか長さの次元をももつ。ポテンシャルは、 その勾配が重力であるから、計量の時間係数 g_44 だけと関係をがあるだけでなく、空間係数 g_11 も関係する。その次元から、 時間と空間の両方をもち、それと質量との積がエネルギーである速度の 2 乗であり、φ/c^2 が無次元であり、その勾配が加速度 であることからも、加速度と長さの積、速度の 2 乗の次元をもつ。
(4) E=mc^2 という特殊相対論の式と、E=mφ を考えあわせると、φは、その場所の光速の 2 乗(c^2) ではないだろうか、について。 一般相対論では光速は、時空の関数である。そのため、光速とポテンシャルの近縁関係を示唆する。しかし、これには矛盾が伴う のではないか。場所によって光速は異なるだけでなく、方向によっても異なるから、ポテンシャルは光速の 2 乗によって表される ことはない。逆に、ポテンシャルが方向に依存するという性質を獲得すればよいのかもしれないが。
(5) 質点のそばの計量では、ポテンシャルは、空間係数 g_11 とも関係する。 g_44= 1 - 2φから、φ= (1-g_44)/2 と同時に g_11= 1/(1 - 2GM/r)から、φ= (1- 1/g_11)/2。つまり、時空は、互いに深く関係し g_11 と g_44 が互いに逆数である。
ニュートンポテンシャルが確定値をとれない性質は、計量は、座標依存であることとつながる。座標は特殊相対論の座標系ではなく、 曲線座標系を考えるから、ここの時空の任意の一点からみる遠方がすべて違う座標系になりえ、ある運動する点からみた遠方も、 同じ点の別の運動からみる遠方と違っている。例として、平坦時空で、加速系からみた計量は、g_ik が座標の関数となってくる。 双子のパラドックスで、地球の兄と弟のロケットがあって、弟の時間経過が遅く、同時に、弟からみて兄の時間経過も遅くなければ ならないが、再会したとき非対称になる理由。弟の加減速のとき加速系のみる時空が違い、地球の時間が急速に経過するからである。 弟の加速系でみる地球は、g_44 が大きく時間経過が速い。非対称の理由は、加減速だけであり、加速が自分の加速度と座標の積に 比例する g_44 をみせるのはないか。(Sep. 16 2007)