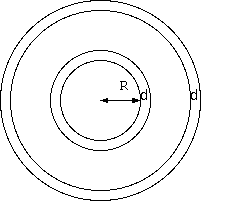

定常で無限の宇宙では、夜空は無限の輝度になるという話がある。星の密度を一定とすると星の数は、体積に比例する。 ある半径 R の先の一定の厚さ d (d は R より十分小さいとする d≪ R)の球殻を考え、球殻の体積 v は厚さ d 一定から 球殻の面積 S= 4πR^2 に比例するが、放射は、距離 R の 2 乗に反比例するから、両者の影響は打ち消され、 球殻からここに届く放射が距離によらず一定になる。これを無限遠まで積分すれば無限大になる。 膨張宇宙論の入門書で、よくこの説明が使われ、これを使って宇宙の膨張の証明とする。(例えば佐藤文隆氏の"ビッグバン"。)
この話は、何かが間違っていることを教えるパラドックスである。定常でなければ無限大にならないし、宇宙に端がある有限宇宙 でも放射が無限大になることはない。しかし、それで宇宙には始まりがあるか、または有限と結論するのは早計である。そこには 数学的な間違いがある。まず、この無限大は、物質の立体角を 0 とすることから起きている。これは、さきほどの簡単な数学に 抜け落ちた部分である。星には大きさがあり、透明でない。それが遠方の光を遮る。そのため、宇宙の明るさが無限大になることはない。 せいぜい全天が星の表面輝度で埋めつくされ、夜空は、その明るさになるだけである。これは、無限大とは全くちがう。無限大で なくても、星の表面温度の輝度では、夜空が暗いという現実と合わないのではないか、と考える人には、次の説明が必要だろう。 つまり、星の表面輝度ではなく、全天が物質の平均温度輝度で埋めつくされるのである。宇宙が無限の大きさでどこも同程度に星 が占めて、今と同じ宇宙が永遠の過去から続いていても。
宇宙の塵埃(チリ)のために夜空が暗いという考えはこう否定される。宇宙が透明でなく途中に遮る物質があっても夜空が無限大 (又は星の輝度)になることを妨げない。光を遮るチリ物質は、定常が無限の過去からであれば、それがいずれは温度を上げ、 そのうち星と同じ温度になるからであると。それは、一部は正しい一方的な議論である。それは、星の表面温度のままではない。
もし、夜空が無限の輝度なら、一瞬でチリは無限の温度になる。温度が一ヶ所に集中することは、物理的な系ではあり得ない。 そのことだけから、先の簡単な数学にどのような間違いが入り込んでいるか、分かってもよいのである。太陽の表面温度の輝度 で全天が覆われるなら、チリはそのうち太陽表面温度になる。それは難しい理屈でなく温度の平均化過程である。しかしチリが 温かくなると同時に星が冷める。チリが暖まる永遠の時間を考えるなら、その間に太陽もチリの温度になるだろう。 つまり、宇宙全体で物質がどの程度の平均温度を持つかを考えたほうがよいのである。
それは、決して太陽表面温度の 6000 度ではなく、絶対温度 2.7 度程度である。宇宙は、星のように温度の高い光る物質だけで できているのでなく、暗い物質、チリのように光らない物質の方がずっと多く、それらが物質の大半を占めることが昔から知ら れている。全天がその平均輝度になるとは、全天が 2.7 度の黒体輻射に満たされることである。そうすると、オルバースの話は 定常宇宙を否定するためのパラドックスでなく、宇宙の背景輻射をも定常宇宙で説明する話であることに気が付いてよいのである。
有限宇宙で、宇宙に空間的な端があるという考えは、すでに余りにも優雅でないため、誰もが拒否するものとなっている。 一様等方の概念がそれに代わる。それに比べて定常性の概念は、どうしてこれほど簡単に捨て去ったのか。 それは、一般相対論の解が定常性を十分与えないからであった。アインシュタイン自身、定常解を捨てた。空間的な端に比べ、 時間的な端には、我々の批判力が十分であるとは思えない。あるとき突然、宇宙が始まったとする膨張宇宙論は、一見容々と未来が 開けるようにみえるために、受け入れやすい。もし、時間軸を逆転し 150 億年後には宇宙が一点に収縮してなくなると言われると、 両者になにも違うものがなくても、それは間違いだと反論してしまうだろう。最近は、宇宙が 2 度目の加速膨張を始めたといわれても、 さほど嫌な感じはしないが、それがもし、加速収縮が減速を始めたというと、気持が悪いものであろう。 しかしそれは、人類的視点からは、その逆とほとんど違いがないのである。
1758年生まれのドイツの物理学者・天文学者、ハインリッヒ・ウイルヘルム・オルベルスのグループは、火星と木星の間に惑星を探していた。 小惑星セレスの発見は、1801年イタリアのジュゼッペ・ピアッツイに先を越されたが、彼は、当時のガウスによる最小二乗法による見失った セレスの再発見 (1802年) を行った。1826年のこの人の議論によって、その名を冠する "オルバースのパラドックス" は歴史上、その時代の 考えを鼓吹するために使われてきた。特殊相対論の出たときは、これがオルバースのパラドックスを説明するとされたし、現在優勢な膨張 宇宙論は、有限時間とそれから来る有限の観測できる空間がこれを説明するとしている。(それが唯一の解であって、それ以外にこれを説明 できるわけがないように人々は流行の病に冒されていう。赤方偏移は事実であるが、それが宇宙膨張のドップラーシフトによる赤方偏移で あるという証拠はない。後退仮説は、赤方偏移の説明のための仮説でしかない。定常宇宙にある赤方偏移は無限宇宙の永遠性を復活するだろう。)
なお、無限空間でなくても、周期的な境界条件でも同様な結果になる。境界条件が熱的な反射壁なら小さな有限の閉鎖空間でも、 無限空間と同じである。それが無限の輝度を生むはずはなく、体積あたりの(有限の)エネルギー密度で満たされるだけである。 アインシュタインの定常宇宙解のような無境界有限空間は、無限の過去からの放射が回り込むので、オルバースの問題を逃れるわけではない。
私の夜空を眺める習慣は途絶えてしまったが、天の河はたんに美意識で眺めるものではない。多くの星が実は太陽のようなものであり、 太陽地球間の距離(1億5000万km)と隣りの恒星までの距離(1.3pc)の比率が約20万倍である。pc(パーセク)という単位が太陽地球間を 基線にして角度の 1 秒の距離として定義されている。夜空には多くの星があって、肉眼で 6000 個ほど見える。星々はまとまって、 天の河をなしている。それは立体的には円盤形をなし、我々の銀河系というものを構成していた。それ以外の部分は空虚と思われていた 時期があったし、たくさんの星雲は、他の銀河系であるという説が認められたのは、20世紀に入ってしばらく経ってである。 隣りの恒星までの距離とアンドロメダ銀河という隣りの銀河系までの距離の比率が100万倍もある。
隣りの銀河までの距離は、太陽地球間の距離の20万倍と100万倍の積で、2000億倍の距離がある。これはほとんど想像を絶する距離の 比率である。太陽の光は、昼の明るさをつくりだし、星々のすべての光の量を合わせたよりずっとずっと明るいものであるが、 それは、地球が平均的な恒星間の距離の中にいないからだろう。もしも地球が平均的な恒星間距離にいれば、太陽からの光と、 その他の全ての星の光とは、ほぼ同程度か、他の方が大きいことになるだろうからである。 他の銀河系からの光は、もっとも近いアンドロメダ銀河だけが肉眼で観測できる銀河であり、その他の銀河がそれよりも暗いことも、 我々が銀河系の平均距離の中にいずに、銀河系にどっぷり浸かっているからである。 もし銀河間のただ中にいれば、われわれの銀河系からの光量と他のすべての銀河系からの光量は、 やはり同程度か他の方が多いということになるだろう。
遠方の物体は、影響が少なくなるが、その分、数が多くなるのである。銀河系の中の星の数は、さきほどでた 2000億という数字と 一致する数が使われている。隣りのアンドロメダ銀河も我々の銀河とほぼ規模が同じと考えると、そこからの星の光量は、2000億倍し、 そして太陽までの距離の 2000 億倍なので、影響は、2000億倍の2乗に反比例するから、太陽からの光量の 2000億分の1になる。 これでは遠方は影響がないように考えるほうが正しいようにみえるだろうが、これが正しくない理由は先に説明した。 重力も、光量も距離の2乗に反比例する。距離の2乗に反比例する星の輝度と重力では、近傍と遠方の影響は、同程度である。 しかし、力をポテンシャルの空間微分ととらえる重力ポテンシャルの式 -GM/R でみれば、地球への太陽の影響とアンドロメダ銀河の影響 とは同程度になる。
遠方は近傍と同程度以上の働きをする。均一な密度で分布する星(その数は R^2に比例する)のポテンシャル(1/Rに比例する)への影響は、 遠方ほど大きい。一般相対論の g_ik の場も重力ポテンシャルをその44成分とする量であるから、同様の性質をもつ。重力方程式は (静的な)ポアソン方程式∇^2 φ = ρ、(又は動的なダランベール方程式 □^2 φ = ρ)の形を踏襲している。重力方程式の左辺の G_ik は、 一種の 2 階微分であり、右辺の運動量エネルギーテンソル T_ik は、i= k= 4 のとき物質密度ρとなる。 地球に対する太陽とアンドロメダ銀河の影響が同程度とは、パラドキシカルであるが正しいのである。g_ik というポテンシャルを 物理量として、それが従う方程式、それが重力方程式である。ポテンシャルは、確定値を持ち得ないという任意性があるが、 ポテンシャルの任意性は、一般座標の任意性に置き換えられている。重力方程式は g_ik の確定値を出すわけではなく、 座標系を指定することで g_ik が確定するのである。
ニュートンの万有引力をポテンシャルを使って表すことは、重力という遠隔力のベクトルを使わず、空間に存在するスカラーですむ というだけでなく、物質との関係が微分方程式 ∇^2 φ = ρ に表せ、それをポテンシャルが従う方程式とみなすことができるからである。 電磁気のスカラーポテンシャルと電荷の関係は、まさにこの式を満たしている。特殊相対論ができたときニュートンの万有引力は、 何者も光速を超えられないという特殊相対論の法則に違反しているので、重力の影響の光速化が必要であった。 リエナール・ヴィーヘルトの式φ= ∫ρ(x)dx/R(x,t-r/c) のように、重力もある点からの過去の光円錐の時空点にある質量によって ポテンシャルを計算することができると思われた。ポアソン方程式と、質点の運動方程式、加速度がポテンシャル勾配に比例する、 d^2r/dt^2= - grad φをローレンツ不変な形式に書き換えることが要請された。 しかし、それは予想以上の書き換えになり、その作業にアインシュタインは、10年を要し一般座標変換に不変な重力方程式を導いた。
この物理での力学的記述からポテンシャル記述への移行は、上に述べたような、パラドックスを招来する。 それは、普通に言うオルバースのパラドックス以上のパラドックスである。ポテンシャルは距離の 1 乗に反比例するからである。 (May. 5 2007)
次元との関連、保存量の流れ
オルバースのパラドックスは、次元と関係している。3 次元空間であるから、球殻が半径 R の 2 乗に比例する面積をもつのである。 2 次元空間の上の境界は円をなしその広さは R に比例する。そのような 2 次元空間では、オルバースのパラドックスは、どうなる のだろうか。
これは、なぜ光や重力が距離の 2 乗に反比例(逆2乗則)であるのかという疑問と関係している。光や重力が水や熱などの流れである ようにある所の源から流れでて、流れの途中を遮る面に流れの密度が考えられる。流れの面の広さ、球の面積が距離の 2 乗に比例するから、 流れの密度は距離の 2 乗に反比例するのである。という答えができる。ある点での発散(空間的に外に向かう)が、その点の密度のマイナス の時間変化になるという保存則である、と解釈できるのである。そのとき、光や重力は何が流れていて保存されているのかということになるが、 光で保存されるのは光量であり、それはそのままエネルギー保存則でもあり、保存量には実体があるように感じられる。そして、 光を吸収するものがないことが必要なことも、それによって得心できる。それに対して、重力にはそのような保存される実体がないのが不思議である。 また、それを物質が吸収するということもない。この保存量の流れという考えによれば、次元が変わって影響するのは逆 2 乗則であって、 オルバースのパラドックスの方ではない。次元でなく宇宙の曲率が違っても、恐らくこれは同じだろう。
距離の 3 乗に反比例でも発散
球殻の厚さ d が一定のとき、球殻の体積は半径の2乗に比例 v(R)∝ R^2 する。放射が距離の -r 乗に比例するとき、天体の密度ρを一様、 (Rによらない) とすると、ρ v(R) R^-r ∝ R^(2-r) であるから a0〜∞ の定積分∫R^-n dR は、 n>= -1 では発散するが、n= -2 では 発散しない。∫_a0^∞ 1/R dRは発散するが、∫_a0^∞ 1/R^2 dRは発散しない。つまり、r<= 3で発散、r=4 は発散しないとなる。
厚みは一定である必要があるのか
この中の仮定を違えることができる。まず、球殻の厚さ d を一定にとる必要はないと考えてみる。
d が R に比例 (d∝ R) であっても、無限遠までの空間を球殻に分割できる。そのような比例的球殻でもオルバースのパラドックスを考える ことができ、そのとき、個々の球殻の体積が距離の 3 乗に比例 (v ∝ R^3) するから、厚みの均等な球殻の場合より、発散しやすい。 r<=4 で発散、r= 5 は発散しない、となる。逆 4 乗則も発散する。
それなら逆に、球殻の厚さを距離の逆数に比例 (d ∝ 1/R) させてみよう。これでも (ある距離より無限遠までの 1/R の積分が発散するから) 球殻は無限遠まで到達できる。そのとき r<=2 が発散し、r= 3 は発散しない。発散条件は多少緩やかになるが、逆 2 乗則 r= 2 が発散する ことは変わらない。さらに、厚みを半径の 2 乗に反比例 (d∝ R^-2) とすると r= 2 も発散しないが、球殻自体が無限遠まで到達しない、 有限宇宙になる。そのため、d ∝ R^-2 以上(n<=-2)を除外する。 つまり、逆 2 乗則は、球殻の厚みを距離に依存して変えても発散するぎりぎりの条件であった。
このような結論は、一体どういうことだろう。何かの間違いが矛盾へ導いたのである。無限遠までの球殻の厚みの取り方を変えるだけで、 逆 r 乗則が発散したり、しなかったりするのは、なにかおかしい。厚みを R の n 乗とすれば、r<=n+3 のどのような逆 r 乗則も発散できる。 これは、何かしくじったのである。球殻の厚さ d とは R の微分 dR であり、それが距離 R に比例することは、dR=R dR' の R'という 距離への置き換えであり、ある量 (ここでは球殻からの放射) の R の無限大までの積分と R' の無限大までの積分とがこの球殻の厚みに よって違ってはならない。これ自体、積分の変数変換であり、dR にふくまれた R は被積分関数に含める必要があるのである。(Dec. 13 2007)
球殻の厚みを距離に比例させる dR=R dR' は、dR/R = dR' から log R = R' + C、対数距離 R' への変換、厚みを距離に逆比例させる dR =1/R dR' は、R dR=dR'、1/2 R^2 = R' + C という 2 乗距離への変数変換のようだが、v(R) は、R' で表されていないから、変数変換 でもない。そのため、直上の段落はむしろ誤りで、最初の考えの方が正しく、逆 3 乗則が均等厚みで発散、1/R 比例厚みでは発散しないのは、 そのまま受け取るべきだろう。球殻の厚みを R 比例にすることと同様に、球殻の厚みを 1/R に比例させることも、なんら不可能な操作ではない。 そのとき球殻の体積は、R 比例であるから逆 2 乗則は、発散し、逆 3 乗則は、ある距離の外側で発散しない。 (Jan. 3 2008)
距離Rに反比例するポテンシャル(φ,A)が与えられ、その時間的、空間的微分として、実効性のある力場、重力、電場、磁場が使われる。 スカラーの空間的な微分である勾配 -gradφ、時間的な微分の -dA/dtとして、それら仮想であった背後場が実在し、1/Rに比例するなら、 物理に空間的な局所性がないという問題を含むことは、オルバースのパラドックスが最も問うことである。距離の2乗に反比例する光やエネルギーは、 当然、このパラドックスの問いに答えないといけないが、ポテンシャルと同様に、一般相対論の計量場 g_ik にもこの問いは投げかけられている。 なぜ、このような宇宙的に無理のある背後場を使用して、その微分として実効性のある力場が最も現実的に説明できるのであろうか。 それは、何を期待し、何を犠牲にしたのであろうか。まずは、現実の実効場の相互の関係を知ることができたことがある。電場と磁場の関係は、 その最たるものである。相対論が両者の関係を明らかにした。相対論は電場、磁場を個別にローレンツ変換(速度による座標変換)するよりも、 現実の場をその微分としてもつ原始関数として存在する背後場(ポテンシャル)のローレンツ変換として表す方が明確で単純だった。しかし、 それはなぜこれほど現実の場でないのか。そして、それはオルバースのパラドックスを極端に受けるのである。なぜ、2階のテンソルと、2次の速度積 によって加速度が表され、なぜ、それらがニュートン理論よりも精密に物理を表すのだろうか。そういう基本的な枠組みを考えないといけない。 それは、誤差が宇宙的になるから精密に表されるのだろうか。 (2020 9/18)