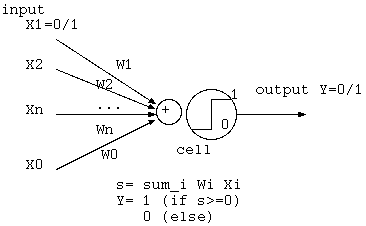
図1. パーセプトロンの細胞
コンピュータは、フォン・ノイマンによるプログラム内蔵型コンピュータによってプログラムをデータとして扱う基本構造の能力に頼っている。 コンピュータの基本構造、新たな処理構造は、考えられているだろうか。CPUが処理速度を上げることは良いのだが、プログラムは一度に一つのデータを操作する命令しか 処理しない。それなら、単一命令が同時に複数データを扱えばよい(SIMD)。能力は数倍になるだけだろう。プログラムの実行に命令をフェッチするサイクルが必ずかかる。 それなら、複数の命令を同じアドレスに並べた非常に長い命令語(VLIW)マシンにすればよい。これも能力を2倍にするだけだろう。 又は、組み込みマシンなら、ハーバード・アーキテクチャ、命令とデータのバスを分離すればよい。しかし、これはプログラム内蔵型の利点を全て捨てる。
CPUが扱うメモリーのアドレスがどこまでも増えることは、一度に処理するデータの比率がどこまでも減ることである。メモリーの殆どのセルは何もしないことに費やされる。 だから、データのコピーや移動にかかる時間は、処理速度が向上しても、同程度にデータの量が増えれば、同程度の時間がかかる。これはどうすればよいのか。 これらは、コンピュータが逐次的な処理によって動作する仕組みから来ている。それならば、単一CPUをやめて、マルチCPU(多数の処理ユニット)が並列動作すればよい。 処理は殆どが多くのデータに同じ処理をかけることに費やされるか、又は、ひとつのデータに同じ処理を繰り返し行うループに費やされるものであるから。
複数のデータに同じ処理をするとき、データを単に分担して複数PUが並列処理する。これにはデータの分割と処理後の統合がいる。 又は、処理過程を区切って複数PUがパイプライン処理(1処理が終わると次のPUにデータを渡す)をする。しかしこのときマルチCPUの制御は、通信だけでつながる疎結合、 共有メモリーを持つ密結合があり、どちらも扱いが不便で、単純な命令の並びの逐次的処理ではない。 疎結合では分担処理の終了とデータ送信、次のデータの待ち受けと受信がいる。密結合ではデータ通信はないがメモリー帯域を分け合い、 データ毎に処理段階を示しセマフォー(排他制御)がいる。配列数とPU数が違うとシストリックアレイ記述が必要。複数の処理の流れマルチスレッドを扱うOSと、 それを記述する言語なら可能とはいえ、煩雑でN個の処理装置で高速化はN倍までであって、N倍の高速装置に勝てない。それらは既に現在の普通の技術であるが、 応用毎に設計を必要とする。そのようなコンピュータは、数字を計算し書類や画を作成する道具であり、人間の助けをする事務機械であるが、 違いを見つけて区別をし、類似性を見出して概念統合するような人間の能力の代わりではない。
コンピュータ基礎論のなかで、多くの神経回路モデル(多値論理、閾値論理、遅延を含む論理、等)は、通常の論理素子によるCPUとメモリーを使用する コンピュータに不得意な処理を行うことができるとして研究された。フォン・ノイマンによる自己複製マシンの研究から始まったセルラーオートマトン (グリッド状に可変の論理関数を用意して上下左右の場所間を連結する仕組みで FPGAの原型) 又は、セル状の隣接を入力として状態をもつオートマトン、 例えば、ライフゲームは、各セルが8近傍に1個以下又は4個以上では0に消滅, 2個で保持, 3個で誕生というルールで状態変化するだけのオートマトンで、 万能性がある(Wikipediaによい説明がある)。
閾値論理は2値論理のAND,OR,NOT等を1素子で実現できる。1入力では重み1と閾値0.5でバッファ。負の重み-1と閾値-0.5でNOTになる。 2入力で重み1と閾値1.5でAND、閾値0.5でORになる。論理 A~B は、A入力の重み1、~をもつB入力の重みを-1、閾値は1下げて0.5でできる。 and を or に換えた論理 A+~B は、閾値をさらに1下げて-0.5でできる。3入力で多数決論理 A(B+C)+BC が1素子で重み1と閾値1.5でできる。 負の重みの実現は、not出力をもつだけでよい。
多値論理も2値論理に比較して素子数を減らす。位取り記数法で数Nをn進数で表すのに log_n(N) のn進数素子がいる。これの構成要素をnとし、 N一定の下、総要素数 nlog_n(N) の最小値は、 (xlog_x(N))'= 0 から、n= eである。3値論理素子が最も近い。閾値論理や多値論理は、耐雑音性が低下し、 3値論理には2値論理の2倍の耐雑音性がいる。1個の閾値は0/1の線に対応するが重み後は多値である。2閾値で0/1/2を表す出力に2本線を使う素子も考えられる。 信号が多値なら、積和と閾とを素子とみると、ニューラルネットワークに近い。パーセプトロンから始まる並列分散処理(PDP)は、パターン認識を行う学習機械であり、 最も工学的な意図をもったものだった。その他、多くの素子が統計的な互いの入出力関係をもつボルツマンマシンなどがある。
y= (W・X ≧ 0)

W += c Xp (Xp∈ A), -c Xp (else)
この学習方法によって、カテゴリAが線形分離可能なとき、カテゴリA内の全入力サンプル (類似の文字) で1を出力し、 カテゴリA外のパターンでは0を示すように収束できる (ローゼンブラットによるパーセプトロンの収束定理)。 証明は省略するが、学習時正解のとき重み修正なし、不正解のときだけ修正で行われた。重みの初期値は任意である。
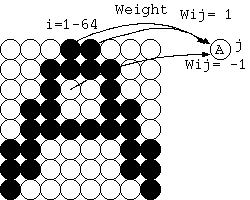
パターン識別は、多次元空間の分離である。例えば、図3のように 8x8 画素のパターン認識は、64次元空間の2領域への分離である。 パターン認識の一般的特徴として、文字の幅が大きいときは、文字が少々ずれても正解する。画素が少し欠けても多くても正解する。 多数の入力画素と重みとの積和(内積)で結果を得ているから、入力画素が少々違っても結果に影響しない。 もちろん、パターンによっては AをAと正解しないことも、別のBをAと答えることもあり得る。そこで自分がAとするカテゴリという考え方をする。
入力パターンXは入力の画素数+1次元の多次元空間の点であるが、入力画素に結合しない線もすべて重み0が存在するとして、同次元の重みの多次元空間の 点Wが存在すると考える。同空間に配置すると、認識とは入力と重みとの内積の符号判別である。カテゴリ内の入力点ごとに識別関数は重みに正の結果を要求し、 重みの点を移動させることが学習である。カテゴリ識別がすべて正解を出すなら学習は終了である。 これは、ベクトル量子化のカテゴリ代表点を重み点とみなせば、入力点の提示ごとにカテゴリ代表を入力点に近づける逐次的な平均化処理であり、学習に必要な 提示回数は、重みの初期値に依存する。学習時、不正解のときだけ、カテゴリ内は重みを入力に近づけ、カテゴリ外は重みを入力から遠ざける "誤り訂正型学習"もある。 学習のための入力パターンあたり1回の提示だけで完了する(近づける比率cを毎回変える必要があるが)"絶対学習" も存在する。方法が学習速度や結果に関係する。
単層のパーセプトロンのある細胞の重みを学習し、その白黒反転パターンに正確に反応する重みをもつ細胞を作るのは容易である。 そして両方の細胞のいずれかが1を出すとき1になるOR細胞を第2層に作ると、元のパターンと白黒反転パターンの両方に正解できる。 同様に、任意のパターンに汎用の白黒反転、上下反転、左右反転に対応する重みをもつ細胞を形成することができると推測できる。
非線形識別を行うものは、区分線形マシンや、入力の積項の並び x, x^2, x^3,...又はx, x^2, xy, xz, ...を用意してその後に通常のパーセプトロン の線形識別する"Φマシン" があった^[2]。この層は固定で学習しない。
多層パーセプトロンは、単層を超える能力をもつが、多層パーセプトロンには、一般的な学習アルゴリズムがなかった。パーセプトロンの層状結合は、 層の細胞は前の層の細胞の出力だけを入力にし、層状マシンは入出力が区別される。入力層は、セルを持たない。
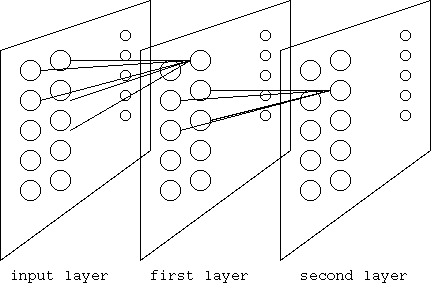
多層パーセプトロンは、認識問題に特有な閾値によるステップ関数(識別関数)が、学習の考えを難しくした。閾値関数の両方の出力レベルで傾きが0で 閾値で無限大のため、微分が関数を通過しない。閾値関数を微分可能な区分線形関数、シグモイド関数 y= 1/(1+exp(-x)) に換えれば傾きが伝播する。 シグモイド関数の微分は、 y'= exp(-x)/(1+exp(-x))^2 = y^2(1/y - 1) = y(1 - y) であるが、伝播において線形細胞と仮定するとき y(1-y)を無視する。
逆伝播は誤差を通常MSE(入出力の画素値差の2乗和)として、全ての重みを誤差に関係させ、全ての重みの、誤差への寄与率に比例した修正である。 そのとき誤差が層を逆方向に伝播することから逆伝播学習という。パターンp入力時の修正は勾配への比例である、
ΔWp= c ∂Ep/∂Wp,
これを各層の各細胞において行うには、最終層の細胞jでは、
Ej= 1/2 d_j^2, d_j= t_j - y_j
y_jは出力値、t_jは訓練値。
e_j= d_j*y_j(1 - y_j).
ΔW_j= c x_j e_j または c x_j d_j
c は正の係数。その前層の細胞kでは、後層の細胞jの値誤差の重み和である。
t_k= sum_j W_jk e_j または sum_j W_jk d_j
ΔW_k= c x_k (y_k-t_k)*y_k(1-y_k)
逆伝播は重み空間での最急降下法であり、初期値に依存する局所解に導き、全体の最適解を保証しないが、 これは未解決/非存在によって解に導かないからそう名付けられる多くの最適化問題の一般的な性質である。それでも多くの応用で支障にならない。 学習の係数cの大きさ、変化に慣性を与えるなどの工夫によって対処される。 さらに、全ての可能な写像が3層のニューラルネットワークで実現できるという証明がなされた。
画像圧縮への応用:逆伝播学習は、もとは認識問題の出力に Yes/No の正解を与える "教師あり学習" の仕組みであった。これを画像自体を 入力でありかつ出力への教師信号とし、中間層のセル数を制限して、機械が画像自体を "教師なし学習" する画像圧縮伸長ができる。 これは、画像符号化に特徴的な、解釈に基づくあらゆる個別の人為(ヒューリスティックス)を避けることができる。 層状マシンは即時的で遅延なしであるが、遅延画像を入力に併用すれば時間方向処理も行える。
多くのニューロンモデル(多値論理、閾値論理、遅延を含む論理、等)は、普通の論理素子によるプログラム内蔵型コンピュータに不得意な処理を容易に行うことができる。 そのなかで最も工学的なパターン認識の学習機械であったローゼンブラットによる層状マシン、パーセプトロンは、多数の0/1入力に重みを掛けた積和にしきい値を使い 0/1出力をする細胞の並ぶ層である。層の細胞は前の層の細胞の出力だけを入力にする。入力層にAという文字を与え、類似の文字が正解になるようある細胞を学習する。 文字が少々ずれても、画素が欠けても正解するようだ。白黒反転パターンを正解する細胞の学習も可能である。入力に(学習で変化する)定数の重みを掛けた入力の線形和 に閾値を使用するから、単層では多次元空間を超平面で区切るだけで、EXORができない、多層では学習アルゴリズムがないという欠点が知られていた。非線形判定を行う ものは、区分線形マシンや、入力同士の積項の並びを用意して線形加算するΦマシンがあった [2]。 マービン・ミンスキーは "パーセプトロン"という本で、これが領域の "連結" という基本的な特徴を判別できないことを証明して、ニューラルネットの第1回の研究流行を止めた。それを離散的でない網膜で論じた。その条件ではどのような 賢い判定も連結判定はできないだろう。
大阪大学の基礎工、生物工学でセルラーオートマトン(グリッド状に可変の論理関数を用意して上下左右の場所間を連結する仕組みでFPGAの原型)の研究者であった私の先生は ミンスキーに同調して層状マシンには否定的だった。ミンスキーは、地球の裏側の学生の人生にも影響を与えた。私は、民間の会社に移籍。70年代にルーメルハートによって 閾値関数の代わりに滑らかなシグモイド関数をもつ多層マシンに対して可能な学習アルゴリズム、バックプロパゲーション(逆伝播)アルゴリズムが開発され全ての可能な写像 が3層のニューラルネットワークで実現できるという証明がなされた 2回目の流行時に、Cottrell 等による3層の砂時計型画像圧縮が示され、非線形写像による次元削減の画像 圧縮が圧縮側に入力層を含め3層、伸長側に3層、の全5層のニューラルネットワークによって行われることを私は示した。それは、非線形な次元削減をデータだけによって行う。
その目標を理解するより先に人は批判をする。(1) 東大生研の最初の会合で、原島先生は、機械学習は技術の放棄であると述べられた。私がニューラルネットは使用可能な 技術のひとつであり技術放棄とは考えない、これを使う目的は相関による変換の学習であると答えると、例えば2次元に円状分布する入力パターンは2次元が無相関である。 これの符号化は変換では難しいがVQなら可能である、と問われた。私はその後、2次元の円状分布を与えた5層網(2-n-1-n-2)で、円に巻き付く線を入出力関数にする学習結果 を発表した。学習には手助けが必要で、中心を通る線に収束するのを人為的に線を中心から外せば曲がっていき、円を包んで交差できる。同時期、ATRの豊玉さんが3次元中の 球面の学習結果を示された。球を包む曲面は交差できないだろう。 (2) 基本的でない非線形に依存する無意味な画像圧縮である。画像を画素数より少ない次元、例えば1次元表現するのは最初、相関抽出で複数次元では固有関数抽出だが、 1次元での非線形性は、画像の学習点をつなぐ曲線の学習であり、これは無意味な過学習を招くだけである。 (そうではない(1)の結果をみよ。) (3) 符号化の観点からは、次元削減よりも、値の削減によって、ビットを減らすことの方が、必要かつ有効であろう。(そのようなことは、例があるのか?) (4) 通常の符号化のように、十分な符号量を与えれば原画像に漸近する性質なしに実用にならない。次元削減はその方向に繋がらない。(そうだが、どうすればよいのか?) (2)-(4)は共同研究者や、他の学者の意見であった。
我々はよく識っていると思うことも、工学において理学のような不可能証明をして、意地悪な学者として歴史に名を残すべきでない。不可能性は、何らかの条件に依存して、 その条件を変えて回避すべきである。不可能性の証明よりも、可能な条件を見出すほうが、ずっと有益な正しい姿勢である。素子の識別関数を滑らかな微分可能関数にして 多層マシンで逆伝播学習できるようになった。3層によって任意の非線形写像が実現できる。次に離散画素上の画像認識では、連結判定は特別に難しい問題ではない。 これがミンスキーによる否定を解決し無意味にする。逆伝播は重み空間での最急降下法だから、局所解を導き、最適解を保証しないという、よくある否定も賛成できない。 これは多くの最適化問題の一般的な性質である。未解決/非存在によって解に導かないからそう名付けられるだけである。それでも多くの応用で支障にならない。 逆伝播は、パーセプトロンの問題を一般的な最適化問題のレベルにしてくれたのである。
私がコンピュータ基礎論を学んだのは [3] による。今、この本を顧みて、彼のパーセプトロン批判以外、彼のこの分野についての意見は全て正当である。神経回路網が 本当にコンピュータの実現に関わる基礎的研究と信じる、彼の実用的な深い理解は、誰にとっても常に学ぶべきものである。
[1] DAVID E. RUMELHART, JAMES L. McCLELLAND, AND THE PDP RESEARCH GROUP, "PARALLEL DISTRIBUTED PROCESSING", 1986
[2] ニルソン、"学習機械" 訳 渡辺茂、コロナ社.
[3] MINSKY, "計算機の数学的理論", 金山裕、近代科学社
近年、画像認識や人物特定に利用されているニューラルネットは、特徴抽出に砂時計型の次元削減と逆伝播学習を使う。画像再現を特徴抽出の認識に利用する。 ニューラルネットがVQと比べて優位かは不明であるが、VQがあまり非線形を意識しないのに対し、神経回路網は非線形写像をそのまま実現させる優位さがある。 しかし、その重みの学習は、VQの代表点の作成と比べて、例示パターンの重みへの採用方法が不明確である点でVQもまだ可能性があるかもしれない。VQ出力は 普通、複数の代表点から、最近傍の代表点の符号を画像部分の符号に用いるが、距離尺度、例えばユークリッド距離の使用はこの空間への非線形性の導入である。 どの代表点に近いかのボロノイ分割は、空間を非線形に分割する。VQの1代表点は、線形空間での1セルの重みに対応する。
多層ニューラルネットに対応して多段VQを考える。各層の複数の代表点は、複数の特徴抽出セルに対応する。代表点の最近傍による選択から前段の代表点毎の 出力を類似性に一般化し、代表点数がそのまま次段の入力の次元数になる。多層ネットの逆伝播学習に対応するものは、多段VQの逆方向学習である。 各層の学習(代表点の移動)は、LBG法かk-meansでよい。学習は、後方層から前層へ変化させる。(大まかに選択された代表点座標を減算した誤差を次段の 入力にする多段VQとは別の話である。)
学習とは例示による認識系の形成である。完全な結果を得るかの問題は、それが人間の任意な(例外を与えるような)パターン分離に従うだけと考えるなら、 機械がそれを模擬することはあまり意味をなさない。機械に求めるものは、人間以上に正確な認識であるから。それを達成する構造が重要である。 それは自己組織化であり、教師なし学習である。人間が行うとされる概念統合と概念分離を同時に行うことを可能にするのは、 どのような仕組みが可能かを基本に戻って考える必要がある。
(2018/7/31)
ニューラルネットの意味は、均一な素子の非線形の利用であり、それが線形素子では層状であれランダム結合であれ、どのような結合も入力の線形結合しか得ない ことである。非線形素子にして初めて複雑な結果を得ることができる。これがある種の問題を解くことができるということは、人工知能の又は計算問題、アルゴリ ズム問題、コンピュータ基礎論のひとつの成果であるといえるだろう。素子を単純に均一にして、又は問題に合わせて層状に結合し、一般的な学習方法を与えること は、どのような問題もこれで解くことができるのではないかと思わせる。つまり、それが目標にしているのは自動プログラミングであり、解法の探索の放棄であり、 思考の放棄であり、我々が最後には恐れる人工知能なのである。コンピュータ科学のなかにはそういう遠い目標も存在することを知り、現在ある程度は使用され、 一部は解決されていることを知れば、数個〜数100個程度の細胞の結合のシミュレーションが何を導くだろうか?と疑問をもつ方も、この問題の意味を理解するだろう。
我々の意識が存在する器である脳の神経細胞がイオン透過性を使いK,Caイオンを内部に保持し膜内外にイオン濃度を違えて、それが脱分極により興奮を周囲に伝達し、 パルスの即時性又は密度変調PDMでもって信号伝達する事を知っても、それが次世代計算機の模型となると多くの人は信じないだろうが、神経回路網研究はマカロック とピッツによる人工ニューロンが論理演算や記憶の機能を実現できることを示すことから始まった。現在の計算機、AND,OR,NOTのブール代数による論理素子によって 構成された高速なCPUの単純な命令実行操作と膨大なメモリーの組み合わせの限界を突破する計算機の探求である。ヒトの意識の仕組みは、膨大な神経回路網とその 記憶の仕組みだけでできているとまだ信じられるから、高速な神経回路網素子を膨大に用意し学習できたときに何が起き得るかを知ることである。(2018/11/13)