
反射光を都市の照明に利用する衛星を考える。この衛星は、太陽エネルギーの少しを都市に反射することで、都市の夜をほとんど 無くすことができる。都市の照明の電力が不要になる。そして、これは現実性のない未来の技術を使わなくてすむ。
これは、光のままで直接に地上の都市を照明する。衛星軌道上で太陽光発電して、地上にマイクロ波で送電するような何段階 かのエネルギー変換を行う必要がなく、全体としての効率の高さが利点である。夜間の都市の照明に使われた電力を他の目的 に使用することができるのでエネルギー利用に便利な発電と同じ利点がある。また、光のまま地上に送るほうが、マイクロ波 で地上のアンテナに送電するよりも安全ではないかと思う。
太陽の等級;-26.8
満月の等級;-12.6
5等級差が100倍、14等級差の明るさは40万倍で 14.2 等級差の太陽の明るさは満月の約50万倍である。満月は1等星の40万倍明るく、 太陽は1等星の2000億倍明るい。月の反射率は、7%(地球は40%、金星は85%)である。満月は0.25lx 太陽は10万lxである。
我々の文明は、19世紀の終わりから電気を発明して都市は夜を追い出してきた。夜の暗さは人間の活動を制限してきたことは明らか だからである。地球は、近くに異常に大きな衛星、月をもつのに、どうして、これほど地球の夜は暗いのだろうか。たった地球の影 に入るだけであるのに。
地球の側にあって太陽と対にして扱われる月は、その素材が黒板より黒い。さらに月の素材は光を正面にだけ反射する性質があって、 満月と半月は、-13等級と -10等級とで、16(15.85)倍の明るさの違いをもつ(半月は満月の6.3%の明るさ)、つまり、半月は、太陽の 790万倍も暗い。それは太陽と同じサイズに見える衛星としては異常な暗さである。
月を空に40万個並べることはできない。1方向に100個並べ、それをそれと垂直な方向に100個並べると、うまく詰め込んで1万個である。 それでほぼ60°の視角になる。月の表面に立ったアポロの宇宙飛行士たちは、見渡す限り(180°の視角)に月の表面を見ただろうが、 月面上の日陰は、地球上の半月の明るさの大雑把に1万倍程度とすると、それは太陽の 1/1000 の明るさ 100lx で、夜の室内照明程度 である。日向の10万lxと日陰の明暗のコントラストは極端で激しい。月の風景は空には雲と青空がなく昼も空は暗黒で、さらに土も黒い。
もし、月が普通の雪又は雲に覆われた衛星であったなら、地球上からみる満月は現在の満月の10倍明るく、0.25 lx は、2.5lxになる。 そして、正面にだけ光を返す月の素材の性質がなかったら、半月がこの満月の数分の1の明るさ(1lx)になり、半月は現在の80倍明るくなる。 それは現在の満月の4倍明るく、ひと月のうち約半分の月の見える夜でその明るさになる。
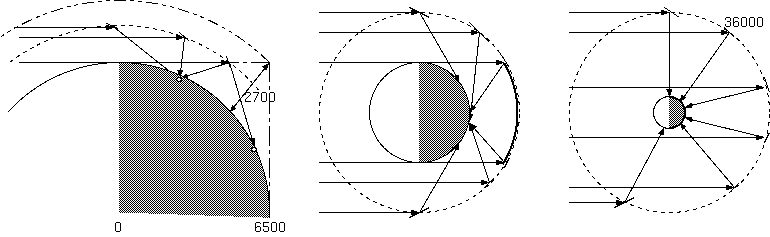
太陽と月とは、ほぼ等しい視直径0.5°をもつ。(月の軌道は楕円(離心率0.0549)で、月の距離は約11%変動するから皆既日蝕と金環日蝕が起きる。) 1mで1cm程度(8.73mm)、距離の100分の1の直径である。大雑把に太陽は月の400倍の距離、1億5000万kmの距離に直径140万km。月は38万kmの距離に 直径3500kmである。これは衛星軌道の高度を100kmとするとき1km程度である。直径1kmの鏡を高度100kmに置くと、鏡に照らされた地域の中心は、 ほぼ真昼の明るさになる、そのことを、我々は十分に知って来たのだろうか。
光の中心から離れるにつれ空の照明は暗くなり、鏡の半径だけ離れて明るさは約1/2になる。照明される地域の大きさは鏡の大きさと高さに関係する。 これを10倍の大きさにするには、鏡を10倍の直径10kmにすればよいが、鏡の面積が100倍になり、現在の技術での実現性が下がる。 鏡の高度を10倍にすれば、照明地域の大きさは10倍、その面積は100倍になるが、照度が1/100になる。
地上の都市の中心から100km先の1kmの直径の鏡を見れば、太陽像が鏡にちょうど重なる像をみるだろう。その地域の中心から外れると太陽像と 鏡の二円がずれて重なる形の部分日蝕になる。500m離れ、太陽は半分だけ顔を覗かせ、1km外れて太陽像は鏡から外れ、その外のコロナの部分 をみることになり明るさは急に下がる。要するに、鏡が大きければ広い範囲で完全な太陽像を見、逆に小さな鏡では太陽の一部分をみることになる。
さらに小さい鏡では、太陽像をピンホールを通して覗くようになる。しかし、小さな穴が太陽像に架かり、背景に太陽の光球をもつなら、 地上の照明地域の明るさは鏡の面積に比例すると考えられる。直径400mの鏡で約1/6。直径200mの鏡で1/25である。直径100mの鏡で太陽光の1/100。 これでも満月の5000倍明るい。直径50mの鏡で1/400。満月の1250倍明るい。312lxは机上読書の明るさである。直径25mの鏡で1/1600で、満月の312倍の 明るさ(78lx)の薄明、夜の室内照明である。
小さな鏡の照明地域のパターンは、中心の明るさが弱まって拡がり、境界はくっきりとなる。つまり、小さな鏡は、ピンホールカメラのように 地上に太陽像を投影するのである。映された太陽の光球像の縁で明るさは大きく変化し、その外の地域は暗いだろう。
2010年5月に太陽風と光子の帆船として 12月に金星フライバイをして航行中というJAXAの太陽帆、イカロスは、14mx14mであった。イカロスの14mx14m =200m^2 は、16m直径の円の面積で、100km高度で完全な鏡であれば、直径1km程度の地域は1km鏡の太陽光の1/4000の明るさ=満月の125倍の明るさ 31.25lx になる。イカロスの膜の素材は、7.5ミクロン(μm)厚のポリイミド膜にアルミ蒸着という。昔読んだ、クラークのSFでは、それを宙に放り 上げると決して落ちて来ないような膜であった。現実にはもっと実用的な厚みの膜でよかったのである。食品用ラップが20μm程度のようだ。
500°Cにも耐える強度の高い素材ポリイミド (密度1.43) の 7.5μm厚の膜は約 10.7 gr/m^2 であり、1km四方の面積の質量は 11t になる。 地球近辺の光の反射による光圧9.2μPa (Pa=N/m^2) の1km四方への推力は9.2Nであり、重力加速度の約1万分の1である。加速度は膜の質量/面積 比だけにより面積によらない。(9.2μN /10.7g= 0.86 mm/s^2)。これは 1時間で 3m/s の加速であり、周回速度8km/sを脱出速度11km/sに変える 3km/sの加速を約1000時間(40日)(さらに (衛星の全質量)/(膜質量) 倍)で与えることになる。
直径1km鏡で10t、10km鏡1000t、100km鏡10万t、360km鏡100万t、重量を大気圏外まで上昇させる重量あたりの価格(1kg数100万円)が実現性を制限し、 現在は1km鏡以外無理と思われる。そのためにも軽く強靭な素材が望まれる。カーボンナノチューブの側面を開いたような膜(方向による導電性? 金属光沢?黒鉛のように黒い?透明?)なら、nmオーダになり重量が現在の1/1000以下になる可能性もある。
クラークの「太陽からの風」を読みかえせば、2平方マイル (最大10ポンド推力)の一人乗り太陽帆ヨットの話である。アルミ蒸着したプラスチック という現実的な素材だった。1平方マイルで1トン、5ポンドの輻射圧。1/1000Gの加速という、加速から判断するとイカロスの1/10程度の厚さ(0.5〜 1μm程度)のようだが、「1インチの数100万分の1の厚み」という記述(0.01μm)とは合致しない。もし、これほど薄い膜なら、単原子膜に近いだろう。 自然界によくある非常に薄い膜の現象、シャボン玉の膜がしばらく経つと部分的に完全な透明になって残りが球形を保つことをみる、そのとき、 見えなくなった単原子シャボン膜は、空気を通さず、その強さが通常のシャボン玉の膜の強さに比べてさほど低下しないことを表している。 薄い膜は強度が伴えば太陽帆船に最も適した素材である。厚さが1/1000の膜が使えるなら 1/1000G は 1G にもなり得るだろう。 しかし、鏡面又は黒い膜でもよい(光圧は1/2)が、透明でないことが必要である。そして薄さによる加速は、太陽帆船には重要だが、鏡衛星には 地上を照らす期間に加速をつねに考慮する必要があるから、適度であるほうがよいかもしれない。
これには、まだ考慮すべきことが多くある。軌道が地球の影に入ると全く働かないから、高度は100kmでなく、それより少々上げる必要がある。 低軌道の人工衛星は、92分で地球を1周するから、うまく制御して都市に向ける鏡の方向制御が完全であっても、短時間しか投光の明るさは連続 しない。1km鏡を実用するには多少高度を上げて利用できる時間を長くし、しかも、複数の鏡を使わなければならないだろう。多くの衛星を次々 と続けざまに利用する必要がある。これは大変だ。10個程度ならまだよいが、数10個から100個以上もあれば、収拾がつかない。
高度100kmでは、地上の1点を+-30°の範囲で照らす軌道上の距離は350km程度であり、その間を人工衛星は毎秒8kmで44秒で通過する。 高度100kmからみる地平線までの距離は h=1, R=65, √(2Rh)= 1140km、両側だからこれの2倍、約2000kmの距離は 250秒= 6分程度である。 高度400kmで12分なら8個の衛星でカバーでき、高度1600kmでは25分で4個程度である。
衛星の高度が高いと、距離の2乗に反比例して暗くなる代わりに、照明地域は距離の2乗で面積が増えるだけでなく、照明の持続時間と自由度が上がる。 高度数100kmでは、今のISSが朝方か夕方の空をゆっくり横切るのと同じである。高度を上げれば、この地球の影にはいらない時間帯の制限は少なくなり、 衛星の移動もゆっくりになる。しかし、高度が1000kmでも太陽の反対地点を照らすことはできない。これは、地球の形と大きさが原因であるから変更の しようがない。思い切って高度が10000kmなら、恐らく2個の衛星で夜の間中を照明することが可能だろう。そして、照明範囲は直径100kmになり、 首都圏の人口密集地域の大半をカバーできるだろう。しかし、距離が100倍では明るさは1万分の1(10lx)である。それでは効果が期待できないかもしれない。
そのため、1km鏡の間は、より地球の近くの軌道で試すほうがよいのだろう。高度100km〜数100kmでは1kmの鏡は十分明るく、金星のように夕方と明け方 の空にあって地上を照らし、野外で本が読める明るさにできれば十分であろう。しかし、これは冬の真夜中を照らすことができない。それよりも高い、 地球の半径6500km*(√2ー1)= 2700km以上の高度で太陽の反対地点を照らすことができ、それは北欧の夏の白夜のように水平線、地平線からの照明で、 丁度4個の衛星で夜の都市をカバーできる。この3000km程度の高さでは規模をかなり上げる(30倍の直径、900倍の面積) 必要があるように思うかも知れ ないが、完全な10万lxの明るさでなくても十分役に立つ。例えば、1km鏡のままでも直径30kmの範囲への1/900の明るさ(111lx)の供給は暗闇と比べると 明確に利点があるのではないか。
照明範囲を大きくするには、衛星高度を高くする必要があるが、高くして照明地域の面積が増える代わりに、同じ鏡では暗くなるから、衛星の規模を 大きくする必要があるというトレードオフである。2700km程度までの低高度軌道の1km鏡を過ぎれば、第2段階は、地球の半径 6500km 程度の軌道に 10km直径程度の鏡をのせることだろう。そうすると軌道の大半が利用可能である。
それは、結構高い角度からの夜間照明になるが、ビルの谷間を十分照明できるだろうか。夜を無くし、犯罪は本当に減り、人々は活動的になるだろうか。 小さい鏡は、太陽や月よりも光源の視角は小さい、10km鏡は薄明を与えても、物の落とす影はくっきりとしているだろう。夜の空は明るいわけではなく 暗黒で、超新星が太陽系の近くで光ったように、強い星のような光源である。星の観測は不便になるかもしれないが、まだ遮光しやすい光源であろう。 しかし、メリットもある。人工的な衛星であるから、必要性がないとき有害なときは、それを止めることができる。有効性を確認して使用できるのである。
日本人に特有の夜空と月をみる習慣を壊すから、その情緒的影響が大きい可能性はある。現在の衛星放送のアンテナで行っている放射パターンの調整 と同様に、すこし鏡の膜の形を変形して、日本列島を列島の形のままに照明できるかもしれない。また、他国にもサービスすべきかどうかは、国際交渉 すればよい。360km鏡は規模の点で明らかに未来技術である。今、それを始めるのは早過ぎ、1km鏡や、10km鏡ならそれに比べてまだ容易である。
ところが、衛星が地球の影に入ることには対策があるのである。この照明衛星の軌道面は、地球の赤道面上の必要はないし、地球の公転軌道面の必要 もない。夜に日本頭上に上がって、昼間は南半球上に下がる軌道にもできる。放送衛星には完全な固定アンテナが使えるように地球の自転からみて 静止する必要があったが、これにはそういう制限がないのである。重要なのは、自転同期である。赤道上の静止軌道でなく、地上からみて衛星が南北 (東西)に振れる軌道を採ればよい。温帯の日本では季節によって必要度が違い、冬には都市照明に誰も文句を言わないだろうが、夏には評判が悪くなる だろう。そのため、冬の夜には日本の頭上に来て、夏の夜には地平線からの角度の低い軌道にする。しかし、季節的な軌道修正は必要なときすればよい。 何と言ってもこれは宇宙船なのだから。
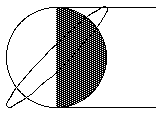
地球公転面に傾斜(上図は45°)した軌道にすれば全く地球の影に入らない軌道ができる。これは低高度軌道でも可能である。つまり、影の問題は、 赤道面上の軌道を考え過ぎていただけであった。低高度軌道は「夕方と朝方の空に金星のように」と考える必要もなかったのである。極地方に近付く、 地球公転面に対する傾斜が大きい(90°に近い)軌道だと、低高度でも地球の影に入らない軌道にできる。そして、それは常に夜の都市を照らすこと さえできる。日本が昼間でも日本以外の他の都市を照らせば良いのである。
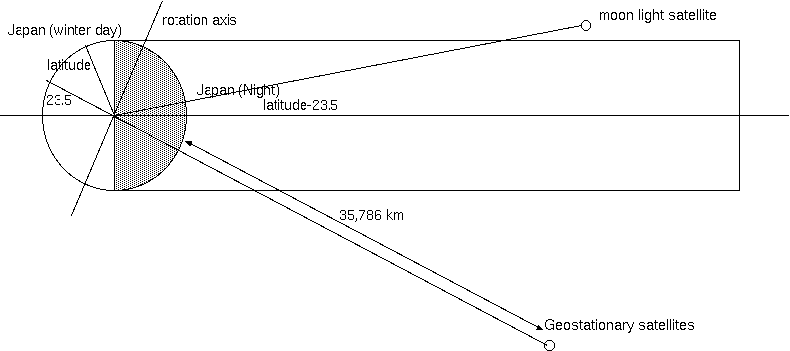
楕円同期軌道にも意味がある。楕円は長径が周期を決めるから、軌道を細くできる。周期が1日だが、楕円軌道では円形の同期軌道と違って、 ケプラーの面積速度一定の法則から楕円の焦点から衛星までの扇型の面積が定速変化し、地球の近くで速く遠方でゆっくり回る。そのため、 楕円のうち地球の夜側の部分の面積にあたる軌道上の大半の時間を遠方で安定して過ごし、短時間だけ地球へ接近して低高度で保守をすることができる。
さらに、自転同期でなくてもその1/2, 1/3, ...の周期の軌道も有効である。衛星は1日に軌道を2,3 回転し、地球の昼側に行っている時間は照明が 消えるが夜側に大半の時間存在する。明るさの変動は好ましくないが軌道の規模が小さいので、10km鏡や1km鏡でも有効かもしれない。 1/2周期は2/3距離、1/3周期は1/2距離程度として、明るさは、2倍と4倍になる。1km鏡で1.5lxと3lx、10km鏡で150lxと300lxである。
近地点は鏡の高度と速度の調整に少ないエネルギーで速度変化が可能という利点がある。但し、少なくとも地上数10km程度の大気圏に入らない注意 が必要である。質量に比べて面積の巨大な鏡衛星は、薄い大気も大きな抵抗になり、軌道調整どころではなくなる。そして、特に大きな鏡は、毎日、 地上に近付くとき、空が落ちてくるという昔の杞憂、今、現実の恐怖を与えないようにすべきだろう。
このような巨大な鏡の衛星の制御はどうするのだろう。少なくともヨットの制御は、風を受ける帆だけでなく、船体と海の抵抗を利用するから、 風上にも進めるのであるが、この膜ヨットにはそれにあたるものがない。太陽からの光と風だけで制御するのである。しかし、衛星は重力に拘束され、 円や楕円の軌道上を運動しているという特性が利用できる。鏡のうける力と加速度の方向は、鏡の角度を変えて広く変化できる。 軌道速度を打ち消す加速は地球や太陽に近付かせ、軌道速度を増加させる加速は中心天体から遠ざかせる。この方法で太陽系内航行を制御するのは、 太陽帆ヨットに限らず、太陽系内の移動の基本だろう。
例えば、最も単純な、円軌道から速度の方向を変えず速さだけ変化させる例では、太陽中心で現在の速度の方向に加速すれば、円軌道はそこを近地点 とする楕円軌道に移ることになり、逆に減速すれば、そこを遠地点とする楕円軌道に移行する。鏡の方向を斜め前方にして反射光を前に投射すると 減速し、逆に反射光を後方に投射すると加速になる。
そして軌道が楕円なら、太陽に近付いていく期間には、太陽に垂直に帆を向けて太陽に光を反射すれば、軌道速度の減速を受けるが、逆に太陽から 遠ざかる期間が必ずあって、その期間に太陽に光を反射すれば、軌道速度を加速できる。そして膜面を太陽光に平行にして、全く加減速を受けない 状態にも、いつでもできる。光を都市に向ける仕事を中断すればであるが。
しかし、巨大な太陽帆ヨットは、鏡の方向を変化させるだけでも容易ではないだろう。それを光圧で行うには、膜面の部分的遮蔽に依らないと できないのではないか。角運動量保存を意識して、回転の開始と終了には逆の行動が必要である。もちろん、帆を広げるために遠心力を利用して、 円形の鏡が円周方向に回転していたら、問題をさらに難しくさせる。回るコマが倒れないように、自転軸方向の安定があるのはよいが、その自転軸 を変えようとするとそのトルクが、別の方向(自転軸とトルクと両方に垂直な方向)へのトルクを生み出すからである。
鏡衛星は、鏡の角度を制御して、都市に光をむける主目的の仕事があり、さらにそれに追加して、自らの軌道を修正していく必要がある。 地上への光の投入は、自らの軌道確保と両立させにくいだろう。大きな加速がないことは、制御の遅さになるが、安定性でもある。 軽い素材を望み過ぎると、衛星の主目的の鏡の仕事を行うだけで軌道を外れていく加速が大きいことになる。そして、小さな加速だからと間違って 放置すると、鏡は放物線や双曲線を描いて太陽系から加速しながら出発する最も容易な方法になってしまう。
ロケットと比べた、重量を上に運ぶための軌道エレベータの安さ (体重を軌道に上げるのに家庭の数日分の電気代) は気を失う程であるが、 強くて軽い繊維の大量生産は難航するだろう。最初、クラークの「楽園の泉」ではダイヤモンドのホイスカー、最近はカーボンナノチューブ と想像された素材の、そのマクロな繊維をまだ私は見たことがない。現在、市場に存在しないものを、静止軌道上で何10万トン(何万km)も 製造する話は未来に属する話である。それよりもロータベータという、周回軌道速度(8km/s)を衛星の回転する紐の接線速度が打ち消して、 サイクロイド曲線を描き、大気圏に真上から突入してくる、回転する数100km〜数1000kmの紐のような回転衛星による上昇方法が規模(数100分の1) の妥当さをもち、素材への密度あたりの強度(k/ρ)の要求の程度が低いと思う。それでも数100〜数1000tの重さになるだろう。
照明衛星は、軌道に上昇するためでなく、エネルギーの技術である。地球温暖化を防ごうというときに、太陽光をさらに集めることが本当に 役に立つかと言うと、夜には光が、冬や寒冷地には熱が、役に立つだろう。この簡便な技術は、自己増殖するフォン・ノイマン・マシンによって 木星を太陽化するような「2010年」の未来の(外来の)技術を使わない。それなしに、地上の一部の夜を同程度に無くすことができる。
これを心配する理由は、人工的に夜を無くすことが、生物環境にどのような破壊をもたらすかを我々が知らないからであると思う。いくらか の生物の日周性を狂わせるかもしれない。しかし、すでに都市には本当の夜はなく、いくらかの生物の代表(ヒト)の日周性は狂っている。 だからこれが都市だけを明るくするのなら影響は小さいだろう。そう、弱い光は許容されるべきだろう。人類は、夜にも昼ほどではないが 弱い光を必要としてきた。そして、どれだけの電力が、都市の照明に冬の暖房に使われているかを考えてみたまえ、といえばよいかもしれない。
日本よりむしろ、光をこい慕う北欧の都市は、これをすでに計画しているかもしれない。1km直径の太陽光の全エネルギーは、1GW (1MkW) 程度であり、ほぼ現代の発電所1基分である。発電所が膜ひとつで出来ることには驚かないだろうか。構造の単純さは、制御の容易さに つながるものである。
この人工日蝕は、都市冷房に使用できるかもしれない。しかし、照明は鏡の角度調整で持続時間を長くできるが、遮蔽は長くする方法がない。 照明には小さな鏡もそれなりに有効であったが、遮蔽には十分な大きさが必要である。部分的な遮蔽は意味をなさない。 また、地上からみて太陽の位置に静止するのではなく、太陽を追尾して移動する必要がある。つまり遮蔽衛星は、照明衛星よりも難しいのである。
そして、この話には、まだ何か、落し穴があるのではないかと思う。つまり、上空からの武器としての使用法が疑われるのである。 例えば、直径数10km〜数100kmの膜は、制御さえ十分に行えば、光以上に速いものはないから、ミサイルより高速な、防げない都市爆撃の 脅迫の道具立てになる。そのため人工衛星として許可されない(又は公表されない)可能性もある。それでも、規模が小さい間は、 武器として疑われる可能性もない。何といっても、直径1km程度では都市を焼き尽くす能力はないことは明らかである。
凸レンズと同じ働きをする凹面鏡になれば、違うのではないかと思うかもしれないが、そうでもない。ピンホールに類する小ささでは、 どのようなレンズをはめても大きな効果はない。十分に大きな鏡の一部に太陽像がみえる関係になれば、凹面鏡の効果が出てくる。100km よりも遠方の1kmの鏡が凹面鏡であってもピンホールであることは同じであるが、1km鏡を20kmに高度を下げると地上からみる太陽像は鏡の 一部になり、鏡の1/5の大きさになる。これも、同じく1kmの地域を照らすが、中心だけでなく1kmの範囲でほぼ同じ太陽の明るさになる。
そのとき、(20kmの高さなら) 鏡の膜の面を僅かに凹面鏡に変形すると、1kmの地域から200mの地域の狭い範囲まで光を絞ることが可能である。 完全にピントのあったレンズでも、太陽の視角によって地球近辺では焦点距離の1/100以上に光を絞ることはできない。これで、直径200mの範囲 で太陽光の25倍の光熱密度になる。その場所からみて太陽像は鏡一杯に拡がり、1m^2に1.366kW の太陽光の25倍、1m^2に34kWを得ることになる。 つまり、1km鏡は100kmより近くに来ない限り、絶対に安全である。自然の太陽光以上にならないからである。そして、近付いて来る光子帆船は 危険である。何100km径の鏡はそれだけで危険である。薄い膜で出来た鏡は、円環に膜をピンと張った平面状態で使うが、光反射の光圧によって つねに凹面の放物面になるだろう。鏡を推進して加速度を与えることによっても凹面は起きるだろう。
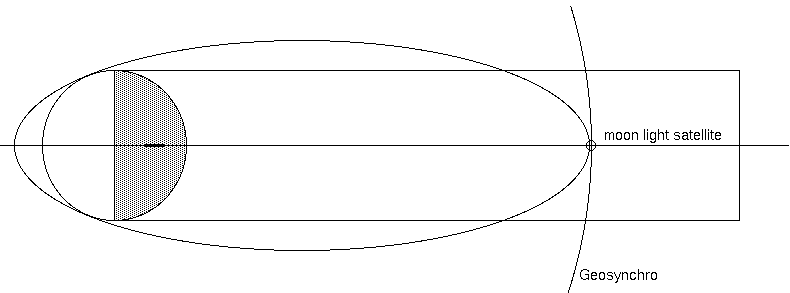
しかし、リング鏡は焦点距離をもつ。無限遠には放物面、近傍には楕円と違って球面には収差があるが光を焦点近くに集中させる。静止軌道の 約1/2の高度に焦点ができ、宇宙船はそこを避けて航行する必要がある。また、高度6500kmのリングは、焦点位置が地表にくる不都合がある。 このリングの焦点を利用して集光の働きで効率よく夜を照らし、焦点を地面よりかなり下にして焦点を結ばず、夜を均等に照らす最適な高度 があるだろう。それは単純な数学である。6500km高度ではリングは地上よりも速く回転するが、リングは一様であるから固定的である。リング の回転は、その高度の軌道速度であれば張力がなく、軌道速度を少し超えることによってリングに沿う方向の張力を与える。これはリングの 形を保つのに必要である。リングは多少の工夫をして光と熱が熱帯を避け、極地方に向かうようにしたり、気象の制御をすることもできるだろう。
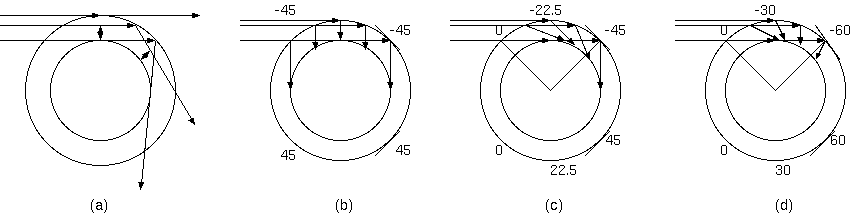
真夜中を照らしできるだけ使用範囲を広くするには、夕方衛星には、0〜45°まで鏡回転させ、明け方衛星には-45〜 0°まで回転させる(図2(c))。 夕方、0 〜60 まで回転させ、明け方は、-60〜0 まで回転させる(図2(d))などがある。(c)は衛星は地球の影で 90°回転させる必要があるが、 (d)は60°であり、影の回転速度を使用時の回転速度に合わせたものである。欠点は、夜9時過ぎから朝3時前まで本当の夜になることである。
2700kmまでの低高度軌道で高緯度のリングは、地球の夜を照らすのに便利がよい。低高度軌道で周期が90分とか2時間までであっても、 リングは一様だから、常に地球の夜側を照らすことができ、地球の自転同期軌道ほど遠方でなく、1桁以上地球に近いから規模の問題が少ない。 北半球だけでなく南半球用と2本のリングが必要だから、ちょうど明暗境界線にあるリングの内面にテーパを持たせれば、両半球を兼ねること になって地球の夜側のある角度の円形領域を広く照らすことができる。この照明領域を広げることが難しいなら、高度を変えて何重にも多重化して 繊細な土星の環のように平面化したリングとなって、常に太陽を向く自転をしてもよい。
リングによらない場合、自転同期軌道が最終の形ではない。地球の暗側面を一様に照らすには、自転に同期しないほうがよい。つねに太陽の反対側 にいる軌道がある。第2ラグランジェ点 L2 は、公転同期点で、つねに太陽の反対側で地球の影の中にいて、地球による皆既日蝕をみる位置である。 そのL2を少しだけ外れて地球の影に入らないように周回することは、可能である。それは月の高度の4倍程度遠い150万kmで、地球の暗側面を一様に 照らすのに適している。鏡を置けば 1万5000km程度の直径の太陽像が地上に映り、これは地球の直径(13000km)とほぼ同じである。150km鏡で満月の 40倍の明るさ 10lx を地球上の全ての夜に与えることができる。
もちろん、その中間的規模として、月面上への鏡設置が考慮できる。3800km径 (月サイズ)の(380km鏡で1000lx、38km鏡で10lx)の太陽像を地球に 投影する。方向制御装置の月面設置は軌道上よりも容易だが、地球上の1/6もの大きな重力が膜面を凹面にするから鏡の平面保持のために分割鏡 が有利だろう。
1km鏡を容易と思うのは全くの誤りかもしれない。それを今考えても全くだめかもしれない。これはイカロスの14mx14mの面積の4000倍である。 その違いは大きい。10tと思うから小さいように思うだけである。そしてそれが無人で制御できるということもクラークはSFにしていない。 膜の「のたうち」による破壊など巨大な膜の性質の扱いは難しい。私は、現在のイカロスの成功した結果をそれがどれだけの問題を乗り越えたか を全く知らずに、我田引水しているだけである。そして、照明のための衛星も私の初出のアイデアではない。どのSFだったかをいま明確にいえない が、SFでは何度か読んだアイデアである。そしてそれが武器になることも誰かのSFにあった。継続した弱い加速が我々の知る最大の速度を得る方法 になることも。小型のコンピュータによる制御も。SF作家は普通の人の50年先を予見していた。クラークの「太陽からの風」は、1963年5月である。
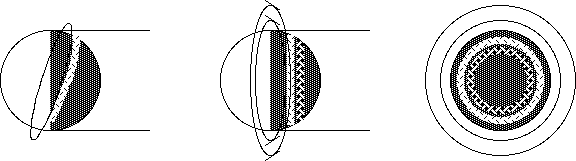
それでは、次に完全な球形鏡の明るさを考える。これは、全く違う話であり、どうやって解答に近付けばいいか。平面鏡の月には太陽が鏡の全面に 映るが、球形鏡には太陽は小さくしか映らない。正面から光があたる満月には、満月の真中にだけ小さく光る太陽像をみるだろう。横から光があたる 半月には、太陽像は半月の明るい側のなかの楕円光点であろう。地球からみる月の球形の鏡は、月からみた宇宙を映している。
満月の真正面の中心に 0°の位置があり、そこから90°の位置が満月の端である。その縁にある鏡は丁度正面の真向いの180°の位置を映す。つまり、 鏡はいつもその鏡の角度を2倍した角度の位置を映すという性質がある。+-180°の宇宙の全景を +-90°までの半球鏡が映すのである。地球からみて 直径0.5°の太陽は、月からみても 0.5°だろう。そこで、0.5/360 を2回かければ半球鏡の月の中の太陽像の面積を大体言うことが出来そうである。 (1/720)^2 は、約 2x10^-6である。月の反射率7%を掛ければ1.4x10^-7だが、反射率を掛ける前に、満月が太陽の50万分の1の明るさという答えにな ってしまった。ま、それぐらいのいい加減な計算である。
光の当たる点から鏡は1方向に光を返すが、散乱は半球状の立体角に等しく光を散乱する。太陽光の反射の例では、球鏡面からは球鏡面中の小面積 (1/720)^2=2x10^-6の部分の反射しか見ないが、球散乱では光を受けた半球面全体からの光を見るのであり、結局、球散乱面の最大の明るさは 球鏡面と等しいのだろう。球鏡面はその球面に入った光をマクロな構造によって、最大限、均等に周囲に散乱している。そして、球鏡面の明るさは 球のサイズによらない。球面に入った光を、球面の外に返すだけである。球散乱面は、散乱をミクロ化して実行している。ミクロ化で付け加わる要素は、 光の反射と通過による局所の反射率である。例えば雲が反射率が80%のとき、20%は熱に消失したエネルギーである。
2π∫ A(θ) Rsinθ cosθ dθ = 2π∫A(r) r dr これを最大化するには、A(θ)∝sinθ だろう。
月は、正面からの光の反射で完全散乱面と比較する幾何アルベドで 0.12、ボンドアルベドは 0.11 である。それ以外の反射率7%はどういう数値か。
月の軌道と静止軌道は、ケプラーの第3法則(T^2:L^3 周期比の2乗が軌道半径(長径)比の3乗に比例することをよく表す。静止衛星軌道は、地上から 3万6000kmであり、月軌道半径 38万5000km の約1/10である。月の周期は29.5日である。2乗して1000になる周期比の30と、3乗して1000になる軌道比 の10は覚えやすい。さらに、低高度人工衛星の軌道周期約90分から、24時間/90分=16、(16)^(2/3)= 6.3, 42000/6.3= 6,666km と地球の半径がでる。