はじめに
1.なぜ磁気浮揚か
2.静磁場で磁気浮揚
3.アーンショーの定理
4.剛体の安定性
5.磁気ではどうか
6.反磁性の安定浮揚
7.そしていま
写真では、磁石の極を水平に置いているようで、前から見たら円筒形の磁石が円に写っている。その下に5個のパチンコ玉らしき 鉄球が水平に列を作っている並んでいる。その列の真中の下に、宙に浮いたパチンコ玉が上の列から 1 mm ぐらい離れて浮いている。
磁石のそばのパチンコ玉はそれ自身磁石になり、同じ方向に磁化された横にある玉は、お互いに斥力を及ぼす。それで、 上の列の玉から斥力を受け、上の磁石からの引力と、重力と上の列の真上の玉からの斥力とがつり合っていると書かれている。 静的な磁場で物体を安定に宙に浮かせる現象は、初めてである。アーンショーの定理にも、言及されていた。 高校生の発見と言う。どうしてこれほど簡単な実験で出てきそうな現象が見落とされていたのか。パチンコ玉は、 浮いた玉の周囲の磁場を再現するためには6個は必要だろう。
家で手持ちの数個のパチンコ玉4個と種々の磁石で色々再現しようとしてやってみて、これは実は、記事から読み取るだけでは、 そうそう再現できない現象かもしれないと思い出した。できるだけ多くが(3個が)磁石に近付こうとして一列に並ぼうとはしない。 3個を一列に並べるためには、玉の直径を使った制限が必要である。その宙に浮く現象は、 5個が一列に並んだ場合にだけ起こるのかもしれない。3個では、整列させてもその下に浮く点は発生しないのかもしれない。 さらに、写真では磁石の強さがわからない。磁場の強さが普通でなく強いのかもしれない。巨大なネオジウム鉄磁石かもしれない。 だとすると、それまでのフェライト磁石や、アルニコ磁石では、発見しようにもできなかった現象であり、 それほど簡単な話ではない。手持ちの直径4、5cm厚み1cm位の円筒形のフェライト磁石4、5個、 ネオジウム鉄の磁石(D22mmx10)2個とかで試す。
(*) 岩手高校の佐々木修一教諭と生徒たちの発見による磁気浮揚の論文 [3] を参照。
毎秒1000回という回転数は、6 万 rpmであり、一般的ではない。まず、軸受が問題になる。通常の軸受は使えない。 ボールベアリングの規格を見ると、小型のものに 4000 rpm とか書いてある。大型のものは、もっと低い。 磁気軸受というものも世の中には存在し電気的に制御する軸受であり、数万 rpm まであるが、それは、もっと大がかりなモータである。 回転鏡に力はほとんどかからないから、軸受というほどのことはなく、何かに浮かす必要があるだけである。 多角形の断面をもつ物体を空気中で回転させると風切り音が出て振動の原因になる。真空中に浮かす必要がある。
回転鏡の強度も必要で、小さい必要がある。半径 5mm で、毎秒 1000 回の回転をさせると接線速度は、毎秒 31.4 m/sec になる。 その遠心力は、rω^2 = 0.005*6*6*10^6= 2 x 10^5 m/sec^2 約 2万g (g= 9.8m/sec^2)である。表面の1グラムの物体は、20 kg重 の力で外に引かれる。1/10 に小型化し、直径 1mm にすると 1/10 の 約2000 g である。1g に 2kg 重 の力、それで千切れない 必要がある。レーザーの光の束(RGBの3本要るだろう)を反射させるための 0.数 mm 程度の鏡面なら大丈夫かもしれない。 垂直同期の走査は遅いからそんな問題は無く、もう少し大型で水平走査の後でやるとよいと思われた。
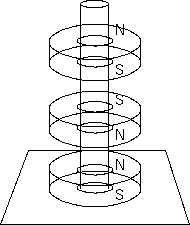
磁石での物体支持は、次元が制限されていると容易である。アクリルのパイプの中に円盤形の軸方向磁化されたフェライト磁石 を重ねるか、ドーナツ型フェライト磁石の穴にアクリル棒を通してもよい(下図)。NS を毎回逆向きすると圧縮ばねができる。 平面内のある位置に物体を安定させることも容易である。板の裏から磁石で引いてやれば、鉄球はそこに安定する。 しかし1 次元、2次元内の安定は、必ず物体との接触が伴う。欲しいのは完全に3次元で安定に浮かすことである。

一点以外は外部物体に接触する必要がなく、回転できる玩具も"王様のアイデア"店にあった(下図)。 これは、あり合わせのボールペンほどの小穴の開いた円盤型磁石、長方形磁石、ボールペンとアクリル板工作で作成可能だった。 同じ向きに磁化した磁石どうしの反発を利用して上に浮かせ、それを対にすることで、円筒形の中心安定を得る。 あとは、ボールペンの軸の先の平面に向かって斥力を及ぼすように、円盤型磁石の位置を調整するだけである。 ペンの先端とアクリル板(又は鏡)は先端の摩擦や窪みに頼らないことを表している。 先端の平面の抗力を磁石の斥力に置き換えれば完全な浮揚だが、それでは軸の中心安定性を損ねるのだろうか。 しかし、その問題は棒の長さを長くすれば任意に削減できる。これは中心安定性の問題でなく斥力の性質かもしれない。
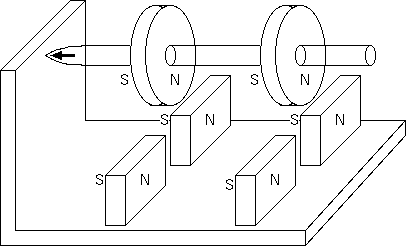
ふつうの磁石での吸引支持には、ボールペンなどを逆さにつり上げる一点支持をよく見掛ける。 ペンの頭に付けた小磁石か鉄片をその上の磁石が持ち上げない程度に引く。1次元に垂直な面内での安定性を利用して、 ペンの頭が倒れるときペン先を中心にした球面内を移動するが、これを磁石の引力が安定化する。
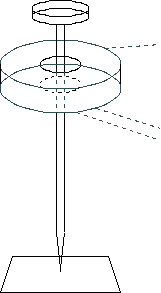
大きめのドーナツ型磁石とそれより小さな円盤型磁石で、一点支持でコマのように回ることができる玩具ができる(下図)。 ドーナツ型磁石は机の端に木片か何かで支持する。小磁石には、接着剤で適当な長さの竹串などの棒を付けておく。 小磁石を反発する向きに近付けると、ある距離までは、(1)斥力で、中心安定性がない。それより近付けると、 全体とは逆のドーナツの穴の磁場の影響で、(2)軸方向は安定でないが斥力、中心安定性がある領域がある。 さらに近付けると(3)軸方向引力で、中心安定性があるようになる。これらの(2)又は(3)の状態の中心安定性を使って、 台の上に一点支持する。(3)の両方の磁石の引力を使うと真横支持でもでき、逆さ支持もできる。 小磁石に付けた竹串をドーナツの穴の中を通して、両磁石の引力を外向きの力にする。 (逆に小磁石を吸引する向きに近付け、遠方からある距離までの引力かつ中心安定性を利用した一点支持もできる。) 通常の磁石では、引力のとき中心安定性あり、斥力のとき中心安定性なしであるが、 ドーナツ型磁石は、斥力かつ中心安定を作ることができる。
ひもを引っ張る形で安定させるものでは、下図は、磁石に引かれて宙に浮いた糸のついた針が回転する (紙の小片を付ければ よく見える) ものである。針の距離からくる引力の強さを反映して、糸の張力が大きくなると糸のよじれを解く向きに回転し、 少し離せば引力がへり、よじれの力が勝ち逆方向に回転する、一種の計りである。ネオジウム鉄合金の強力な磁石では、 数センチ以上も遠方に浮かせることができる。
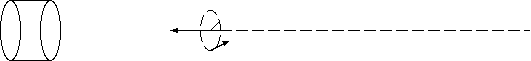
ここからは、実現できないかもしれない。磁気で浮かせる軸受は、中心軸への安定性と斥力がいる。その両方を単純なしくみ で実現するには、円錐形などの凸凹界面で斥力を使うことであろう(下図)。

円錐形であれば、中心安定性も斥力も共に実現するのではないだろうか。中心から外れると、すき間の狭くなる斜面が斥力を増やし、 すき間の大きくなる方は斥力を減らす。それで中心軸からのずれから戻す力を得る。軸方向の安定性は、1次元斥力の話、 アクリルパイプの例で説明した。界面を円錐形にすることで、多少弱まるかも知れないが、安定性を保つのではないだろうか。 両者の安定性があれば、軸受に必要な用件は満たしている。軸の両端にこれを使えば軸を宙に浮かせることができるように見える。 本当に可能だろうか。円錐端面をもつ永久磁石は売られていない。鉄材を旋盤を使って作るしかないから、いまだに実験できない。
磁石の斥力で 3次元物体を安定浮揚させるのは、立方体の 8 頂点の近くでそれぞれ 3 面に小型磁石の反発を与えればよいとまず思う。 それができれば 2 重箱の内側の箱を浮かせられる。そんなことが可能だろうか。頂点の部分だけでは 3方向に安定して斥力を与えそう であるが、立方体全体ではあり得ないように思う。理解しにくいから、物体浮揚にその場所は8箇所必要でなく向かい合う2箇所に単純化 し3角錐を円錐にする。そうしてできる円錐軸受は、中心軸へ向かう安定性と軸方向の斥力とが両立する。しかし、ふたつの斥力によっ て中間の物体を安定に支えるかが問題である。その斥力は普通の磁石の斥力のように少し離れれば弱まる斥力でないかもしれない。 つまり、一方へ少し動けばその方の斥力が増え他方の逆向きの斥力が減るなら、両方の斥力の和はつねに安定点に向いて安定できるから、 この性質がないのかもしれない。これができるなら、立方体の頂点ひとつ (3個の磁石対)だけで浮くように思える。円錐軸受ではないが、 軸方向磁化のドーナツ磁石の穴に別の同じ軸方向に磁化した磁石を埋めると、中心安定性とともに軸方向の斥力をもつが、その斥力は、 中央で0で両側に飛び出す性質をもち、少し離すと斥力は強まるのである。
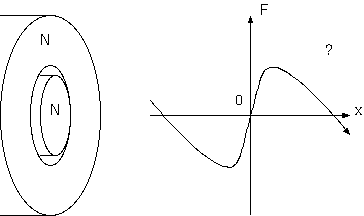
一点の電荷を安定浮揚させることができないのは、ガウスの定理の言い替えである。電荷が空間に安定であるためには、 ある空間点からずれると、そこに引き戻す力が働く必要がある。かりに電荷が正で、その空間点で力なしに浮いているなら、 それは、電場ベクトルがこの点を中心として、内側を向くことである。それを電場の(負の)発散 div E= dEx/dx + dEy/dy + dEz/dz (各成分の成分方向の微分和) という。 そこに単位電荷を置けば働く力のベクトル場を考えるなら、安定浮揚には力の負の発散 div F < 0 が必要である。 1点の正(負)電荷を安定にするには、電場の負(正)の発散が存在しなければならない。
電荷を安定させるためには、電場の発散が必要である。ガウスの定理 div E=ρ は、電場の発散は、電荷密度ということである。 真空中には電荷が 0、つまり発散が 0 であるから、その点に外部電荷なしにその点を安定にする方法はない。 そのことは逆に、その場所を取り立てて避けるように不安定にする方法もないという事ではある。 ここで、外部電荷という言い方をしたが、力を受ける側の電荷の発する場をそれには勘定しない。 一点の電荷は自分の出す電場の影響を受けないし(*1)、物体の安定の場合も、物体内の電荷の場は、物体内の電荷には 内部的な力、内力を与えるだけで、内力は作用反作用の原理から物体全体では0となり、物体が外から受ける力、 外力には寄与しないからである。ある場所に電荷を安定にするには、その場所に外部電荷として符号が逆の電荷が 存在しなければならない。
静的な電場内の電荷は、ある点から別の点まで移動させるとき、移動経路によらずその仕事が一定である。 異なる経路を一巡しても仕事を得ることも失うこともない。 (回転が0である場である。) このような場はポテンシャルをもつ。 そのとき、3 次元上にスカラー値 φ(x,y,z) を考え、それの空間的な微分、勾配 (gradient) が力になると考える。
3次元でなく2次元の上に高さを張る面 φ(x,y) では、斜面の傾き (dφ/dx, dφ/dy) が2 次元の力を与える。 3 次元上のφ(x,y,z) のスカラーポテンシャルでは、(dφ/dx, dφ/dy, dφ/dz) の力が電荷に働らくと考える。 そのときポテンシャルは、電荷がその場所にあるための位置エネルギーである。
(*1)これは変な表現だが、"電荷はそこにあるではないか、その電場は現実のものではないか。" という疑問に対して、 これは、電磁気の線型性を使った電荷と場の分離のための手法であるといって納得できるだろうか。
∇^2φ= Δφ= d^2φ/dx^2 + d^2φ/dy^2 + d^2φ/dz^2
これは、勾配(負が電場 E= -grad φ)をとり、さらに発散(div E)をとることにあたる (∇^2= div grad)。ポアソン方程式、
∇^2φ= -ρ
は、電荷密度ρが正ならポテンシャルが上に凸、∇^2φ<0 であり、そこに負の電荷が安定するし、ρ<0 で ∇^2 φ>0 下に凸 であればそこに正の電荷が安定する。電荷密度ρ= 0 の空間でポテンシャルが従う式をラプラスの方程式といい、
∇^2φ= 0
ポテンシャルの2次微分の和は 0 であり、ある方向にポテンシャルが下に凸なら別の方向には上に凸になっている(サドル)。 電荷密度のない空間(電荷の側の空間もこれによって表される) ではポテンシャルはつねに極小をとらず、電荷は安定に停留しない。
なお、極小点は、2次微分が0でないだけでなく、1次微分も0でないといけないが、1次微分は、より大きいスケールの重力を 打ち消すために、つねに0が望まれるわけではないので、強調しない。また、rot E = -dB/dt から、動的な電磁場では rot E が存在する。そういう場合は、電荷は経路の一巡において速度を得るので上記の議論は、違って来る。この場合も スカラーポテンシャルは存在するが、動的な電場は、しばしおく。 アーンショーの定理の、電場における点電荷の非安定性は、以上のように理解できる。
距離が変わらないように連結した 2 電荷があってそれを全体として剛体(硬い形の変わらない物体)として考える。 それぞれの電荷の位置のポテンシャルは、安定でないとする。2 質点を連結した物体の運動は平行移動と回転運動に分類できる。 いま、運動を平行移動だけに制限すると、6 変数の関数だったものが、平行移動という拘束条件によって自由度が 3 になる。 そこで、それぞれの現在の位置を中心とする、ひとつの座標による連結したポテンシャルφ_cを考えることができる。
φ(x1, x2) = φ_c(x) (x1、x2、x= x1-x01 = x2-x02 は、位置ベクトル)
その連結した平行移動物体は、各点が受ける力を加算して受け、連結ポテンシャルφ_cは、2点のポテンシャルの加算に比例する。
φ_c(x) = κ(φ(x1)+φ(x2))
いま、各点のポテンシャルが極値を持たず安定でないから連結ポテンシャルは、安定でない。 これは、平行移動という拘束条件によって自由度を制限したポテンシャルであり、回転運動も許せば安定になるかというと、 一般にそうではない。一般に拘束条件を外すと不安定になる。例えば、サドル(峠)の峰方向は、下に凸であるが、2次元を許すと、 峠の道の方向が許され、下に凸でない。
この 2 点は、容易に n 点に拡張できるから、電荷の分布した(導体でない)剛体の安定もない。 剛体の自由度は 3n 自由度から、6 自由度に制限される。それを平行移動だけにして 3 に制限したとき安定でないなら、自由度 6 でも安定でない。
そのため、磁荷と静止磁場との関係は、電荷と静止電場との関係と非常に類似する。磁石を整列した0でない小さな距離の磁荷ペアの 分布で近似し、その内部で反対の磁荷どうしが打ち消し、磁石の極にだけ磁荷が表れると考えるなら、磁石は磁荷の分布する物体と みなせる。磁荷の静止磁場における振舞は、電荷の静止電場における振舞と同じであり、磁場には、昔から磁石の極の表面に磁荷が 分布しているとし、磁石や電流の外側の空間には磁気的ポテンシャルを考える手法があり、この磁気ポテンシャルのラプラシアンが 0 であるから、磁場のなかで磁荷は安定に留まらないのである。
一点の磁荷が安定しないなら、これを磁荷の分布する物体に拡張できる。電荷の分布する物体が電場で安定に浮遊できないように、 磁荷の分布した物体も磁場内で安定しないことになる。そのため、電場または磁場で物体を安定に浮かせることは、原理的に不可能 になる。 (しかし、物体が導体で電荷が移動する場合、物体が磁性体で磁化が変化する場合は違う。) そして、ニュートン重力も 電磁気と同じく、ラプラスの方程式を満たすから、アーンショーの定理は全てを満たしてしまい、電磁場と重力場によって、電荷 または磁荷を帯びた質量を安定に浮揚させる方法がないことになる。
それに対して、磁荷の非存在、スカラーポテンシャルの非存在、場がどう作られたかなどは、実は関係ないのではないか、空間の磁場には 回転がないのでポテンシャル場を考えることができ、磁場に発散がないことは、それだけで磁荷が安定浮揚ができないということを表して いるではないか。起源とは関係なく、振舞を決める式が同じなら違いをいうべきでない。発散の定義と安定性はじつは同義の関係である、 という反論ができる。
しかし、力を与える方も受ける方の磁荷も非存在のとき、その力の有り様をいうことにどれだけの意味があるのだろうか。磁場中で磁石や 鉄の受ける力は、本当に磁場から磁荷が受ける力だろうか。"仮に磁荷が存在し、磁荷が磁場の向きに力を受けるとき、磁場の発散が 0 であるから安定性はない。" そして、"仮にラプラスの方程式に従うスカラーポテンシャルが存在するなら、その極小極大は発散 0 だから 存在しない。" これら、ふたつの言明は、つねに真である。前提が偽のときは何をいう言明も真である、という意味においてである。 磁場のアーンショーの定理は、力を受ける磁荷と磁気的ポテンシャルとが存在してラプラスの方程式に従うとき、磁荷は安定でない というのであり、電磁気では磁荷は存在せず、磁気的ポテンシャルは、磁荷の存在するときに磁石の外部空間に仮想可能な場である。
しかし、それは、1997年のことである。今度は、回転する磁石でなく、静止した鉄球である。その衝撃は、大きい。 電磁気は一体、こんな事さえ、知らなかったのだ、いう驚き。それ以上の複雑なことは、すべて嘘に近い。 どうして、高校生に発見され学者の発見でなかったのか。それは、目の多さではない。事実を見ようとしない者には、 事実は見えないのである。反磁性体の安定浮揚、今回のような現象が決して存在しないという証明をしたはずの アーンショーの定理は、どのような基本的な捨象による誤りがあったのだろう。それを明確にすることが必要である。 更には、このような否定的な定理がもつ、研究への有害性を意識すべきかもしれない。
磁気双極子が力を受ける場は、磁場自体ではない。磁場ベクトル B の磁気双極子ベクトル U の方向微分係数
(U・∇)B = (U_x d/dx + U_y d/dy + U_z d/dz) B = U_x dB/dx + U_y dB/dy + U_z dB/dz = ((U・∇)B_x, (U・∇)B_y, (U・∇)B_z)
ベクトルによって力を受けるとする。磁気双極子が任意の方向を向くことのできるとき、磁気双極子は、もっとも楽にできる 磁場の向きをとり、B の B 方向微分係数、(B・∇)B という力を受ける。ベクトルの公式から、
(B・∇)B = 1/2 grad B^2 - B x (rot B)
右辺の第2項は、Maxwell 方程式から電流密度のない静的電磁場で 0 だから、力の場は、1/2 B^2 をポテンシャル場とすることになる。 磁気双極子が B の方向を向く常磁性体は、B^2 の大きい方向に力を受け、B の逆方向を向く反磁性体は、B^2 の小さい方向に力を受ける。 この磁気双極子に力を与える 1/2 B^2 のポテンシャル場は、存在しない磁荷の受ける力、磁場 B によるものではなく、ラプラスの方程式 には従わない。そのため真空中にも極大、極小点が存在でき、磁気双極子の安定浮揚が可能である。
物体を磁荷の分布と見るのではなく、磁場の向きを向く磁気双極子の分布と仮定すると、その勾配によって力を与えるポテンシャル場は、 磁場の2乗になり、ラプラスの方程式には従わない。このように反磁性体において、 "磁場中において磁荷の分布する物体が安定浮揚しない" という磁場のアーンショーの定理は乗り越えられたのかもしれない。磁場のアーンショーの定理は、反磁性体の安定浮揚を説明できない。 むしろ、磁気浮揚は、アーンショーの定理で説明すべき現象ではなかった。
磁気浮揚を示す事実が見出されなかったことも重要である。その事実が見出されるまでは、つねにそれを原理的に否定する "定理"が勝利する。 反例がないことによって我々は惑わされる。超伝導体の完全反磁性による物体浮揚の動画像を見て、我々はこの不思議な現象の存在を知った。 液体窒素によって冷却された超伝導体の上で、ふつうの磁石が滑り落ちることなく安定に浮かび、軸方向に磁化された円筒型磁石は軸を中心に 抵抗なく回転することを見た。超伝導体から磁力線が排除される説明ではその場所に安定して離れないことを説明できず、磁力線が穴にピン止 めされる説明では、磁石の軸方向の回転に抵抗がないことを説明できないように思う。これは見たことのない異常な現象である。"カムイ伝" のある場面で河原では磁鉄鉱が宙に浮いていたという。常温超伝導体ができれば、我々はそれが当り前の風景になるだろう。
磁性浮遊コマ以前、反磁性体の安定浮揚は、知られていた。円筒型の強力な電磁石の上での蛙の安定は、軸方向では下に増える B^2 の斥 力による重力との打ち消しと安定、あまり長くないソレノイド(円筒型コイル)は、中心軸よりもソレノイドに近付く方が磁場が強いから、 半径方向は中心軸上での極小性による安定と思われる。詳しくは、[1] を参照。
しかし今回は、反磁性体ではなく、鉄球という単純な形の強磁性体の安定浮揚が示されたのである。B^2 の極大での安定であろうか。私は、 磁場が電流をソースにすることからB^2の極大の存在を疑ってきた(*1)。しかし、B^2 の極大での安定であるなら、強磁性体の砂鉄などが 浮揚することになるが、そうではなさそうである。アーンショーの定理は、磁化を扱わない。近傍に同じ向きに磁化された鉄球が必要なら、 それは、微小な磁気双極子でなく、ある大きさの鉄球の磁化の現象かもしれないし、それならば、B^2 のポテンシャル場という反磁性体の 安定浮揚の説明とは、異なる説明を要するかもしれない。
(*1) 蛙の浮揚の論文[1]では、磁気モーメントmと磁場Bの内積、m・B をエネルギーとして、m が B の方向を向くことから B^2 の項が出る。 磁場 B を渦なし非圧縮の流体の速度の場のようにみて、太洋中の水の速度のように、どの点も周囲の速度より大きくなれず、速度は境界で 最大であるから、常磁性体や強磁性体の安定浮揚は、不可能とされている。
[1] "Of flying frogs and levitrons" M V Berry, and A K Geim, Eur. J Phys. 18 (1997) 307-313
[2] "Spin Stabilized magnetic levitation",Martin D. Simon, Lee O. Heflinger, S.L. Ridgeway American Journal of Physics MS8229
[3] Sasaki Shuichi, Yagi Ichimasa and Murakami Masato, "Levitation of an iron ball in midair without active control", JOURNAL OF APPLIED PHYSICS, Vol.95, No. 4(2004) p2090-2093, ( http://hdl.handle.net/10140/1918 ) jap-v95n4p2090-2093.pdf
関連? Youtube Incredible Magnet Invention