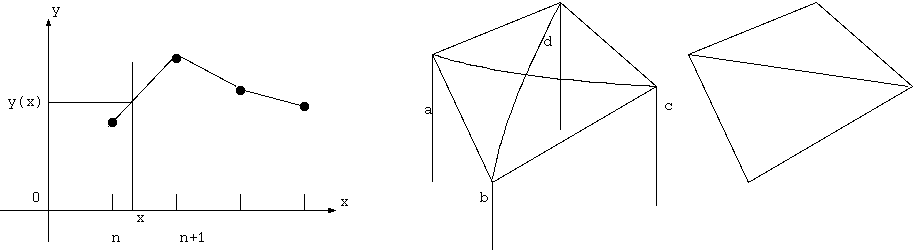

(2) 2 次元標本では、双一次内挿 (Bi-linear interpolation) がよく使われる。 z(x,y) (0<=x<=1, 0<=y<=1) を x, y それぞれに線形な関数 z= Axy + Bx + Cy + D として、次の 4 点での値を定めると z(0,0)= a, z(1,0)= b, z(0,1)= c, z(1,1)= d z の式に代入して a= D, b= B+D, c= C+D, d= A+B+C+D. から、A= a+d-b-c, B= b-a, C= c-a, D= a のように A,B,C,D が求まり、
z= (a+d-b-c)xy +(b-a)x +(c-a)y +a
になる。z の x による偏微分を y の 1 次関数とし、y による偏微分を x の 1 次関数とする。4 点を通る双曲面である。
dz/dx= (a+d-b-c)y +(b-a)
dz/dy= (a+d-b-c)x +(c-a)
d^2z/dx^2= 0
d^2z/dy^2= 0
d^2z/dxdy= a+d-b-c
(4)1次元信号の内挿式
二点(0,a),(1,b)が決める線形内挿は、y= (b-a)x +a である。三点(0,a),(1,b),(-1,c)が決める二次式は、
y= Ax^2 + Bx + C とおいて、y(0)=a, y(1)=b, y(-1)=c を解くと、C= a, A+B+C= b, A-B+C= c, から
B= (b-c)/2, A= (b+c-2a)/2。四点が決める 3 次式 y= Ax^3 +Bx^2 +Cx +D は、 y(-3), y(-1), y(1), y(3)
がそれぞれ a,b,c,d として、
a= -27A + 9B -3C +D
d= 27A + 9B +3C +D
b= -A +B -C +D
c= A +B +C +D
から解くことができるが、次第に解くのが困難になることがわかる。n+1 点が決める n 次式を一般的に扱う ラグランジュの第1補間式がある。
L_n,k = Π_{i=0 i!=k}^n (x-xi)/(xk-xi)
(x- x0)(x -x1)..(x -xk-1)(x -xk+1)..(x -xn)
= -------------------------------------------
(xk-x0)(xk-x1)..(xk-xk-1)(xk-xk+1)..(xk-xn)
L_n,k は、分母が定数、分子が x の n 次式になる。x= xi (i!=k) で分子のどれかが 0 となって 0 となり、
x= xk では分母子は同じ式となり、1 になる。そこで、y(x)= Σ_k L_n,k yk は、y(xk)= yk を満たす、n+1 点
の (xk, yk) を通る n 次の補間式となる。
ラグランジュの第1補間式自体は、一般に標本が不足したときそれを増加するのにはあまり使われていないと思う。 n が増えればそれに比例して次数が上がるということが納得ができない。補間式が n 点を全て通る必要など元々ない。 それでは、10000点の信号の補間には、10000 次の補間を必要とするのか、という疑問である。普通、補間には式が単純で 誤差が小さいことが望まれる。 n 点は普通、非常に大きく、補間の点数はもとの標本点数の数倍しか必要としない。 例えば、オーディオ信号のサンプル周波数変換や画像拡大において元の信号の性質を壊さず、元の標本に含まれている信号 の性質を十分に取り出すことができればよい。元のサンプルに含まれた情報を十分引き出すことを望むだけである。
通常のオーディオではどうするかというと、サンプル数の増加には、まず、0 点を必要なだけ挿入する。例えば、5倍の サンプル周波数にしたければ、1 個のサンプル間に 4 個の 0 を挿入する。そして、多くの次数をもつ鋭い肩をもつ LPF を通す。 その場合のディジタルフィルタは、FIR フィルタまたは IIR フィルタのよい設計が望まれるが、そのカットオフ周波数は、 元の標本のサンプル周波数の 1/2 の周波数に対応する周波数はできるだけ通し、それ以外をできるだけ落とすフィルタを使う。 フィルタの処理は、単純でありサンプル点あたりタップ数倍の積和を要するだけである。ラグランジュの補間を使う実用的な ディジタルフィルタは、ないのではないかと思う。
それなら、歴史的価値以外にこれがどうして意味があるかというと、内挿補間のひとつの理想を体現しているからである。 標本された信号から元の信号を推定する方法として、それ以外に重要そうなものとしては、ナイキスト補間である。