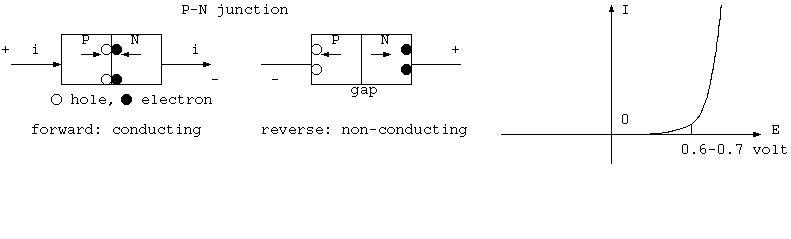
P-N conjunction and diode
PN 接合、ダイオード
P型とN型の半導体を接合するとダイオードになる。P型を+にN型をーにするとホールと電子は、接合面で互いに接近し消し、両極から
補充され電流が流れる。逆にP型ホールをーにN型の電子を+にすると両者は互いに離れ、間に空隙ができ、電流が流れない。これは、
電気を1方向にだけ流すダイオード特性になる。電流iは電圧vの指数関数 i(v)= I_0 exp(v/V_0) で、 広い電流範囲で電圧V_0は、
シリコンSiで約0.7V、ゲルマニウムGeで0.3Vである。真空管では熱した又は電子放出しやすい物質で覆われたカソード(陰極)から、
アノード(陽極)へ真空中の電子の流れの1方向性を使う。PN接合以外にも、針電極をGeに刺した点接触ダイオードもあった。

半導体を使う増幅回路では、電力の振幅を増大させるトランジスタ(以下Tr)を能動素子といい、コイルL, コンデンサC, 抵抗R を受動素子という。 アクティブな能動素子Trは、電圧又は電流によって電力を増幅する。電流を、電流で制御するバイポーラ Tr と、電圧で制御するユニポーラ FET がある。
バイポーラTr
バイポーラ Tr は、サンドイッチ構造で3端子の真中をB(ベース), 端の一方をE(エミッタ)、他方をC(コレクタ)という。
N型とP型半導体によりNPNとPNPとがある。Bは薄くE,C通過速度で素子速度が決まるから、一般にNPNは、PNPよりも高速である。
BE間電圧V_BEによってベース電流I_Bを流し、その h_FE倍のコレクタ電流I_Cが流れる電流増幅である。
電圧V_BEに対する電流I_BEは指数型のダイオード特性であり、広い電流範囲でV_BEは0.6-0.7Vである。ベースは薄く、エミッタからの電流の一部が ベースに流れ、大半はコレクタに向かう結果、I_BEによってコレクタ電流 I_CE が制御される。電流増幅率 h_FE = I_CE/I_BE は、ほぼ一定で、 Trの特性(I_CやV_CE)によって数10〜100倍をもつ。信号には微分増幅率 h_fe= ∂I_CE /∂I_BEが働く。
増幅回路 電流または電圧の増幅機能は、電力の増幅機能をもつ。Trの回路には、エミッタ接地、コレクタ接地、ベース接地の回路がある。
エミッタ接地回路
エミッタを接地して、ベース(入力)とコレクタ(出力)が信号によって変動する最も一般的な回路。入力電圧とバイアス電圧に抵抗Rinを介した
電流をベースに与え、電源電圧Vccから負荷抵抗Rlを介してコレクタV_Cに繋がり、ベース電流のh_FE倍のコレクタ電流に負荷抵抗Rlを掛け、
電源電圧VccからRl*Icを引いてコレクタ電圧V_Cになる。ベース電流からコレクタ電圧への変換とみると、電流が増え電圧が下がる反転増幅である。
入出力抵抗(R_in, Rl)によって電圧増幅になる。
Vout= Vcc - (Vin+V_bias)/Rin * h_FE * Rl
コレクタ接地回路(エミッタフォロア)
コレクタを接地し、ベース(入力)とエミッタ(出力)を変動させる。ベースに入力電圧Vinを与え、エミッタ電圧は0.6-0.7V(NPNでは)下の電圧が出るよう
に負荷抵抗Rlが付くから、V_E = Vin - 0.7v - I_BE * (1+h_FE) * Rl 例えば h_FE が 100 のときエミッタ電圧変動は、ベース電圧変動の99%になる。
エミッタがベースに追従するエミッタフォロアともいう。ベースエミッタ電圧V_BEは、ベース電圧変動の残りの1%で、I_BE= (V_in - 0.7v)/((1+h_FE)*Rl)
高インピーダンス(周波数の関数としての抵抗)から低インピーダンスへの変換回路で、電圧は増幅しないが、電流を約h_FE倍に増幅する。
ユニポーラ電界効果Tr(FET)
FET素子は、ソースに対するゲート電圧Vgsでドレイン電流Idsを制御する。キャリアが電子の N-ch (Nチャネル)とホールの P-ch (Pチャネル)がある。
一般にP型よりもN型が高速である。
真空管と同様、入力のゲート電圧が出力ドレイン電流を制御する。Ids/Vgs は、相互コングスタンスという増幅率である。 3極管は定電圧、5極管は定電流型のプレート電流電圧特性をもつが、FETは、5極管特性をもたせることが多い。
FET素子には高速性と低電力性が望まれる。ゲートに接合ジャンクション型(J-FET)と金属酸化物(MOS)の絶縁を介した電場で制御するMOS-FETがある。 論理素子にはMOS-FETが使われる。キャリアが電子の N-MOSとホールのP-MOSがあり、P-MOSよりも N-MOS の方が速いが、ともに、 ソース接地では統計的に約半分の ON時にドレインソース間に電流を流し電力を消費する。
負荷抵抗の代わりに逆型のMOSを使用するソース接地回路が、相補型 Complementary MOS (C-MOS) である。ON時には負荷側の素子がOFFになり電源アース間 に定常電流がなく、状態変化時に入力ゲートのコンデンサへの充放電電流しか流れない。そのため、C-MOS は、P-MOS, N-MOS よりも圧倒的に低消費電力である。
但し、一方の素子がONからOFFになってから、他方の素子がOFFからONにしないといけない。両側がONの瞬間には電源からGNDへ電流が貫通し、熱による素子破壊が 起きるため、両側の素子がOFFの入力電圧範囲を持たせる。このOFF電圧幅が大きいとON-OFFの遷移が遅く、小さいとOFF幅が0を越え、両側ONの危険が起きる。
エンハンスメントN-MOS: ドレイン電流がONになるVgs が正の(負のものをディプレッション)N-MOS。C-MOSでは閾値は電源電圧の半分未満(<Vdd/2)か、 相補 Vgsの和が Vdd 未満を要す。
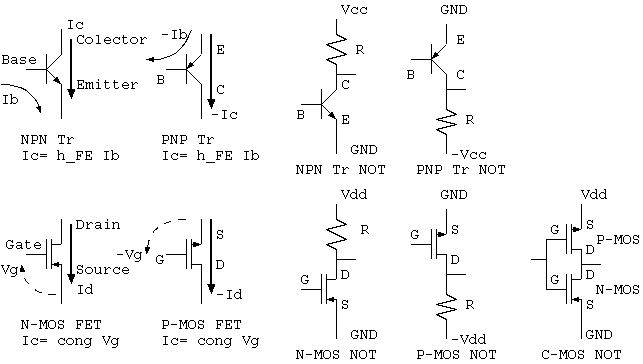
NOT, AND, OR 論理
ブール代数の論理は、入出力ともに 1 または 0 の値をとり、1入力のNOTと2以上の入力のAND, ORとの組み合わせで全て記述できる。 n入力 AND 論理は、入力が全て1のとき出力が1で、その他で 0であり、n入力 OR 論理は、入力のどれかが1のとき出力が1になりその他は0である。 1入力 a の NOT論理は ~a、a, b のANDは、a ^ b, OR は、a | b と書く。3入力以上の AND, OR もある。o= a ^ b ^ c のような 3入力 ANDは、a,b,c が全て1のときだけ1になる。

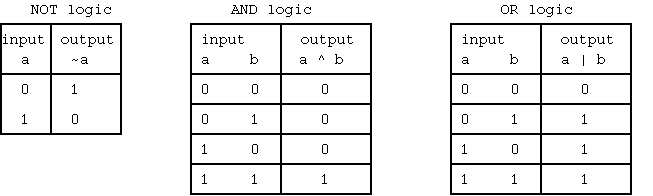
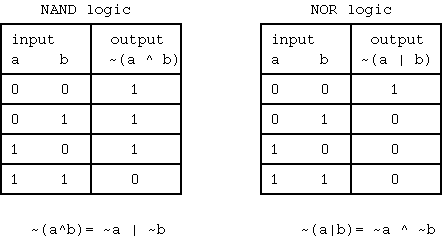
NAND, NOR 論理
AND の後に NOT をとる論理 ~(a^b) を NAND という。OR の後に NOT をとる論理 ~(a|b) を NOR という。
ド・モアブルの法則から NAND は、~(a^b) = (~a | ~b) であり、NOR は、~(a|b) = (~a ^ ~b) である。
NOTは、抵抗を介したベースに結合したエミッタ接地、2入力のNAND,NORは、各抵抗を介しベースに結合したエミッタ接地でできる。 そのため Tr, FET, C-MOS でも NOT機能をもつ NAND か、NORが基本である。3入力以上も同じ。これは閾値が NAND と NOR とを区別する閾値論理ともいえる。例えば、3入力の閾値が2.5のときNAND, 0.5 では NOR になる。 閾値が1.5では(a^b)|(b^c)|(c^a)という、3入力の内、2入力が1という条件で1を出力する。
完全性
NAND 論理 ~(a^b) は、a = b とすると NOT になり、NAND に NOT を後続すると AND になる。NAND に NOT を前置 ~((~a)^(~b)) すれば、
OR 論理 ~((~a)^(~b))= a|b になり、それに NOT を後続すれば NOR になる。すなわち、NANDだけで全論理を構成できる。
これを論理の完全性という。NOR も同様に完全性をもつ。
排他的論理和 EXOR、一致論理 EXNOR
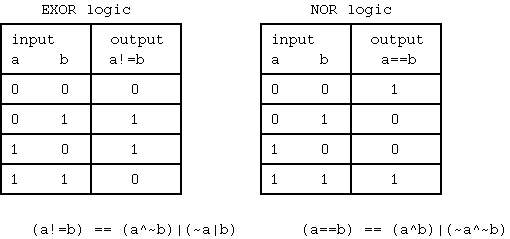
排他的論理和(EXOR)は、(a^~b) | (~a^b) で表される。その反転、一致(EXNOR)論理 a==b は、(a^b)|(~a^~b) である。EXOR論理は、
出力= (b==1なら)~a, (b==0なら)a であり、条件反転である。EXOR または EXNOR は、AND または OR を作成できないため、完全性がない。
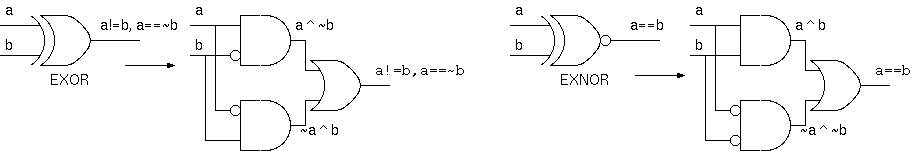
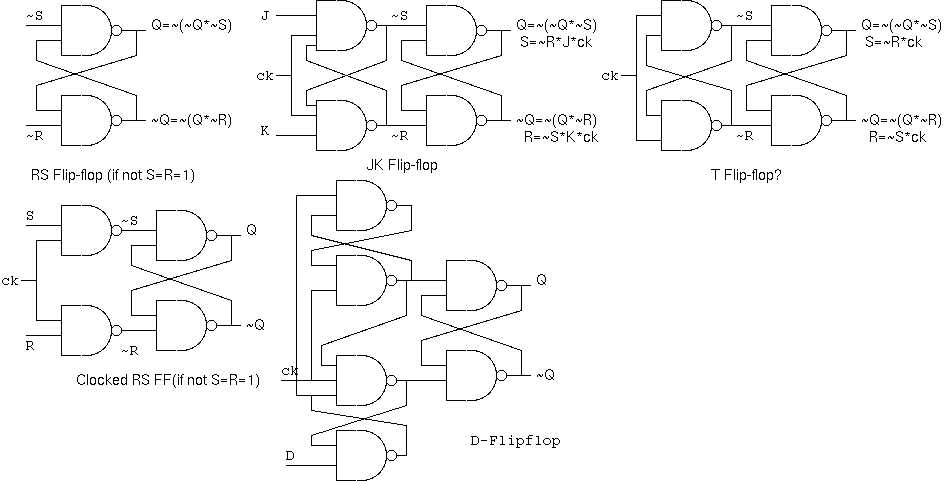
RS flip-flop: 状態をセットしリセットするflip-flop。 ~S = 1, ~R = 1 では変化なし。 ~S = 0 でセット、~R = 0でリセットする。 S= R= 1 なら、Q、~Q ともに1になる。
clocked RS flip-flop: クロック付きRSflip-flop。clock時、~S=0 でセット、~R=0でリセットする。
JK flip-flop: clock時、R でなく J で(ck 同期で) セット、S でなく K で(ck同期)リセット。J=K=1 で T flip-flop。
T flip-flop : クロック毎にQ,~Qが反転。
D flip-flop : クロック立ち上がり(clock↑ )時の入力DをQにコピー。その前のセットアップ時間、その後のホールド時間が必要。
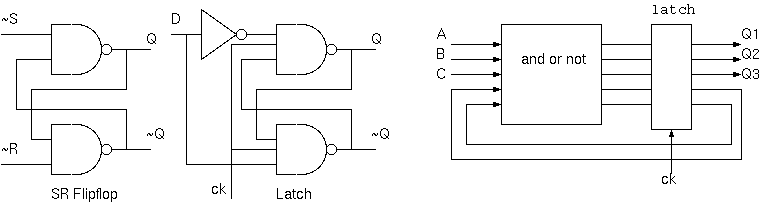
組み合わせ論理と内部状態
組み合わせ論理(combinational logic)とは、AND,OR,NOTの組み合わせだけで構成する瞬時的な(時間に関係しない、フィードバックのない)論理回路をいう。
内部状態をもつ論理回路は、より複雑な動作ができる。クロック毎、外部入力とラッチされた内部状態とを入力にして、出力と内部状態とを変化する。
入力に対する要求: クロック(例えばD-flipflopのck立ち上がり)毎に値を知るにはsetup (事前に入力値が保持される時間)と、 hold (事後に入力値が保持される時間)が必要。さらに、組み合わせ論理(多段のAND,OR,NOT回路)の遅延への考慮が必要である。 組み合わせ論理の遅延は、setupの余裕を減らし、 hold の余裕を増やす。(setup= setup_0 - delay_combi, hold= hold_0 + delay_combi.)
記号による記述、スキマティックス
論理回路の記述を記号で書く。線は値に 0 または 1 をとり、論理回路が AND, OR, NOT の記号で扱うことができ、それをスキマティックスという。
より複雑な論理設計は、ハードウエア記述言語(HDL) (製品例 Verilog) によって書かれる。現在、ほとんどのハードウエア記述は、HDLによる。
テストベクター
クロック毎の全入力列と LSI 内部の全てのD-FFに、直列ビット列を与えて初期設定し、任意クロック後の全出力と内部D-FF値を引き出すことができる。
それによって、チップとシミュレーションとの一致を確認する。設計側が用意したテストベクターによってチップはテストされ、
テストを通過したチップだけをファンダリーが出荷する。この仕組みが歩留まり率を確保させる。
微細化
セルベースのLSIには、設計単位の大きさを表わす、"ルール"というものがある。例えば、0.18μ(180 nm)ルールのTr設計は、その1/√2 の
0.13μ(130 nm)ルールに移行すると約2倍の面積密度が得られ、微小化による速度が√2倍向上する。電源電圧を下げることで速度はさらに√2倍
向上し、2倍の速度になる。微細化 1/√2 による性能向上は、密度と速度の積では 4倍になる。半導体のファブ(後工程)は、このルールを
10年間以上、1年または1.5年で1/√2にしてきた。この微細化による性能向上は、何処までも可能ではなかった。
2006 年ごろ、微細化による電源電圧の削減にリーク電流による限界が現れ、そのため、微細化による性能向上は2倍程度に制限された。
この重大な問題が、どう解決されたか、私は知らない。2022年現在、TSMC のファブで 5nm ルール、3nm ルール等が可能という。
微細化による性能向上は、各自調査されたい。
内部CPU
巨大なLSIをコントロールするには、LSIに組み込むCPUを使う。ウインボンド・エレクトロニクスでは2002年、MPEG-2エンコーダの設計にARM社の
ARM9という組み込み用CPUのライセンスを受けて使用した。ARM9 は〜150MHz で動作する汎用レジスタをもつ32bitCPUで、命令バスとデータバスが分離
したハーバード・アーキテクチャで、1クロックでフェッチと実行サイクルをもつ。NTSC ビデオの 54 MHzの倍までの使用で、108MHzで動作させた。
内部CPUには内部プログラムをダウンロードする必要があり、内部CPUに外部から指示を与えるデータパスが必要になる。
しきい論理によるNAND,NOR
しきい論理は、入力の値がしきい(閾)値より少ないか大きいによって0,1を出す。通常、Tr などの回路では否定型が単純で、
しきい値を変えると、NANDとNORは、変化できる。2入力A,B のとき、A+B >= θで、 θ= 0.5 ならNOR、θ= 1.5 なら NAND になる。
3入力でも、多数決論理は容易に作成できる。(a^b)|(b^c)|(c^a) = (a+b+c)>=θ、θ= 1.5 で多数決論理である。
n-入力でも同様に利点があるが、多入力の多数決は、雑音に弱いという欠点がある。
FET スイッチ論理
if(gate==1) Out= IN 記述。else 記述がないことの不便。例えば、if(G) O= I else O= ~I なら、O= GI | ~G~I で、O= (G==I)。
NOTとFET1つで一致回路ができる。また、SWの直列は、AND、並列は OR になる。if(G1) O1= 1. if(G2) O2= O1, if(G3) O3= O2,
は、O3= G3^G2^G1 といえそうだが、else がない。 if(G) O= I1, else I2 なら、選択回路である。
2入力セレクタ: I1,I2 に各 FET を付け、G1,G2(=~G1) で選択する。
4入力セレクタ: I1-I4 ではG=G1,G2をデコードして、O= I1 (G=00), I2(G=01), I3(G= 10),I4(G=11) 。
2-4デコーダで排他的な4選択子をgateでFETを結合(or)だけでセレクタができる。