目次
ポアンカレ宇宙
1 ポアンカレの寓話宇宙
2 内部は無限
3 物体(定規)のサイズが場所による
4 時空の変形(=計量)と不変量
5 宇宙の果ての見え方
6 宇宙と幾何学
7 宇宙の内部でこの構造を知ることができるか
非ユークリッド幾何学の話は、平行線が唯一つ存在する、存在しない、又は無数に存在するユークリッド幾何学、ロバチェフスキー幾何学、 そしてリーマン幾何学を対比し、それらの依って立つ公理は、いずれが正しいかどうか判定できず、それらはただ便利さのうえで選ばれる。 それらが現実の宇宙のなかでいずれか検証することはできないという考え。そこで、星の視差による検証可能性の議論が否定的にでてくる。
宇宙の空間的曲率の判定が恒星程度の距離によって可能でないことは、現在の後知恵として明らかであるが、彼は、それを原理的な不可能性 として議論している。この本のなかにアインシュタインの "幾何学と経験" の議論のもとではないかと思われる考えがあった。 第 2 部第 4 章空間と幾何学の "非ユークリッドの世界" にある球状有限宇宙の話である。
(勿論、ポアンカレは、特殊相対論と一般相対論に大きく貢献をしただけでなく、その他の多くの分野、特に最近は複雑系、カオスの学問に 業績を残したことが知られるようになった、当時の最高の知識人であった。)
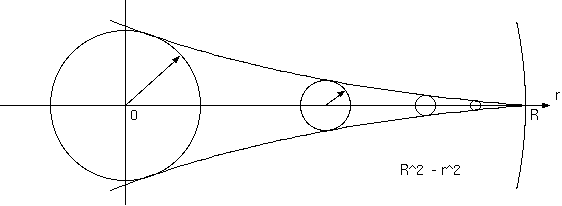
この仮想の世界では、大きい球に閉じ込められていて、この世界は温度は一様でなく、中心がもっとも温度が高く、 中心から遠ざかるにつれて温度が下がり、この世界を包む球面に達すると絶対温度が 0 になる。
この温度の変化する法則は、限界をなす球面の半径を R として、中心からの距離を r とする場所の絶対温度は、 R^2 - r^2 に比例する。
そこではあらゆる物体は、等しい膨張係数をもつ。どの定規の長さも絶対温度に比例する。 物体は、そこに置かれるとすぐにその温度に熱平衡になる。
これらの仮説は、矛盾しないし、想像できないものはない。そうすると、運動する物体は、限界の球面に近付くと しだいに小さくなるに違いない。
この世界は我々の用いる幾何学の見地からは有限であるが、この世界のなかにいる住人にとっては、 無限の広がりをもった宇宙になる。
(中略)
さらに、この世界の光は、その屈折率が R^2 - r^2 に反比例してさまざまに屈折する媒質の中を通過すると仮定しよう。 この条件のもとでは、光線は、直線ではなく、円弧となることがわかる。
(引用終了)

まず、どうして R^2 - r^2 という 2 次なのか。例えば、R - r という 1 次式に物差しのサイズが比例する場合、この世界の住人に とって宇宙は無限にならないのかもしれない、との予想は外れた。限界球面 R までの距離 x = R - r に物差しが比例する 1 次式 であっても、住人にとっての限界球面までの距離、∫dx/x の 0 から R までの定積分は、無限大に発散する。
R
∫ dx/x ⇒∞
0
物体が中心から遠方にいくに従って 2 次元的な占有面積は、より速く 2 乗で減少し 0 に漸近するし、物体の体積は、 3 乗で 0 に近付く。そのため、その面積、体積をもとに計測する宇宙の体積は、より速く発散するだろう。 R^2 - r^2 に物差しが比例する 2 次式では、さらに容易に発散するだろう (∫_0^R dx/x^2 ⇒∞)。 しかし、住人が無限の宇宙を感ずる有限宇宙のために物差しのサイズの変化が 2 次である必要はないのである。
ds^2 = dx^2 + dy^2 + dz^2
そして、特殊相対論のローレンツ変換が知られ、速度をもった剛体の変形の法則、ユークリッド距離の式に、時間間隔の 2 乗 を引いたものが、ローレンツ変換によって変わらない不変の時空間隔であるとするミンコフスキーによる定式化があった。 そしてそれは、時間が虚数軸なら 4 次元ユークリッド空間になる。
ds^2 = dx^2 + dy^2 + dz^2 - dt^2
ミンコフスキーの時空間隔をもつ特殊相対論の扱う時空は、一様等方な、平坦な時空であり、それは、時空が重力によって変形した、 平坦でない時空の幾何学では異なることを理解する必要があった。曲った時空での幾何学として、非ユークリッド幾何学が必要となる。 そこでは平坦な時空と何が違うのかというと、最も基本的な不変の時空間隔、ユークリッド距離が成り立たないことから始まる幾何学の 再編である。そこでは、剛体は変形なしに平行移動もない。この世界の住人にとって中心から遠方に移動することは、縮小を伴うのである。
つまり、相対論は、物差と時計の変化、時空の変形を表す法則である。時空(=剛体)の変形、弯曲、膨張、縮小を 記述することが相対論の目的である。特殊相対論によって速度をもった時空が変形を受け、物差の縮小や、時計の 間隔の変化が起きた。それは一般的な常識からは遠く想像もつかないものであった。(しかし、基本的な事象間隔は、 虚数の時間を追加しただけの 4 次元ユークリッド距離だった。) 同様に一般相対論では時空の変形が質量の存在から起き、 それが重力の本当の姿というのである。
特殊相対論の座標系中の時間測定、座標系中の長さ測定が他の系からどう眺めても変えられないように、 剛体と時空間隔は、固有時、固有長の存在に置き換えられる必要があった。一般相対論において不変量は、 時空のある一点の事象が、他の点からどのように非線型に写像され変形しても保存される量であり、 それは遠方からの観測によらない局所の事象間隔であり、曲がった時空での剛体の移動の法則である。
ds^2 = g_ik dx^i dx^k
ポアンカレのこの球状有限宇宙は、アインシュタインの "幾何学と経験" で応答されたように思える。 そして彼の定常宇宙にとって重要なヒントだったのではないだろうか。 次に述べる、アインシュタインの球状有限の定常宇宙は、R^2 - r^2 を計量 g_ik の平坦 δ_ik からの偏差の分母にもつ。 ただし、g_ik が R^2 - r^2 に反比例するとき、物差しの長さはその 1/2 乗に反比例するから、 このポアンカレの宇宙の半分程度の歪である。 そして分子側に、x^ix^k があって、それが物を奥行き方向に平坦化させるのであるが(*)。
(*) アインシュタイン定常宇宙の計量、g_ik= δ_ik + x_i x_k/(R^2-r^2) から、その宇宙の中心からの累積距離は、x= r/R とし、 ∫_0^R √g_11 dx= ∫_0^R √{1 + x^2/(1-x^2)} dx = ∫_0^R dx/√(1-x^2) は、発散しない。
それを知るためには中心以外にいればよい、という意見は当たらない。宇宙を見る位置としては中心以外の地点はないからである。 球状の有限宇宙というとき、それは宇宙を外から見ることではない。宇宙を外から見ることは不可能である。住人の視点は、つねに 中心の視点であり、宇宙を外から見る視点は、ありえないものである。
宇宙を我々が見るとき、中心に我々の銀河系があって、中心から外れた所に遠方の銀河がある。その遠方銀河からみると、そこを中心 とする宇宙がみえて我々の銀河系は、遠方にあるだろう。しかし、見え方の様相は、ここから見た宇宙と基本的に違うものではない と思われる。宇宙の任意の一点から眺めた宇宙の像は、どこから眺めても多少の偶然的な違いはあっても基本的にはほとんど同じ像 であろう。
1992年、ブラジルのリオから南に少しいったアングラ・ドス・ライスという観光地での MPEG 会議に参加したとき、激しい一週間の 会議の終わりの週末に真っ暗な静かな内海の海辺にでて夜空を眺めた。しばらくすると目が慣れてきて南半球の星ぼしが見えてくる。 そこで見たのは全くなじみのない星座である。ここはブラジルで日本とは地球の反対側だから人間が逆さに立っているだけではない。 星空さえも違うのである。それは、まるで遠方の星系にいって迷ったかような幻想を抱かせる。 そして友人が持参した小さな双眼鏡で眺めた南半球でしか見えない球状星団は、それまで一度も経験することのなかったものであった。 その夜空は、多少きらめく星団と星雲が多いように見えるが、北半球の夜空と同程度に暗いのだろう。宇宙原理と仮定すべき一様性と 等方性。それは、宇宙を数学的に扱うための方法である。そして問題は、3番目のそれを我々が捨て去ったと思っている定常性なのである。
ポアンカレの宇宙で、この歪を測定しようと移動して自らのサイズ変化を測定しても無駄である。観測者は、つねに宇宙 の中心にいる。しかも、持ち運んだ物差で測定しても結果は変わらない。宇宙の有様は、遠方の見え方によって判断する 以外の方法はない。宇宙はこの図のように、遠方に歪みを持つことが基本的に起こりえる。この静的宇宙では宇宙を同時刻 の空間で切断した像と、宇宙の果てを光でみる像が同じであるから、この宇宙の住人は、この図そのままの宇宙を見るのである。 この宇宙では一様に分布する遠方の銀河が平坦な空間よりも多く小さく見え、距離と面積の2乗、距離と体積の3乗の関係 からの偏りがあるだろう。
この宇宙では不変の空間間隔は、ds^2= (R^2/(R^2-r^2))^2 dr^2 であろう。中心から r の場所の計量、g_ii(i=1〜3)= (R^2/(R^2-r^2))^2 であって r が大きくなると、g_ii (i=1〜3) がともに同じく大きくなり、物が平坦化でなく等方的に 小型化する。そして、r → R で、g_ii → ∞に発散し、物体は無限小になる。
さて、この宇宙の直接の距離 r を測定する方法がない場合も、この宇宙の様子を知ることができるだろうか。 dx= R^2/(R^2 - r^2) dr のとき、距離 r までの物差の累積距離 D(r) は、
D(r)=∫_0^r dx= ∫_0^r R^2/(R^2 - y^2) dy = R/2 ln |(R+r)/(R-r)|
である。(D(r)>r、r→R で D(r)→∞である。)この宇宙の住人が、r を知らず、D しか知らないとき、この宇宙が遠方で 歪んでいることを知ることができるだろうか。D を半径とする球面の面積 4πD^2 は、D の増大が緩いので、S(r)の g_ii 倍 よりも小さい。そのため、r を知らなくても、この宇宙の様子を知ることができる、と考えることができる。 これは、ポアンカレに反論できたのかもしれない。