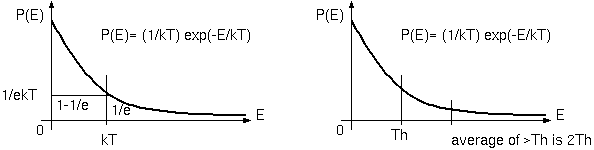
太陽コロナは、太陽表面温度(5780K)に比べて遥かに高い100万度を越える温度をもち、その加熱の仕組みには謎が残るとされる。気体粒子の運動 エネルギー分布は温度によるから、太陽重力の大きな脱出速度を超える粒子は、軽い電子で多く陽子で少ない。高速な電子が放出すれば太陽表面 を正に帯電させ、電子放出自身を抑制し陽子放出を促して太陽風に含まれる電荷をバランスさせ帯電を一定にする過程が考えられる。この静電的 な陽子の加速は、太陽コロナの高温の主要因となり得るだろうか。
太陽表面は、その厚みが半径の1/100以下の 5780K の温度をもつ境界面をもつ。その内部は高い気圧の不透明なプラズマで、その外側は気圧が低 く透明である。伝導と対流によって上昇してきた熱は、ここから先は光熱の放射と粒子の放散によって移動する。陽子と電子からなる気体は、重 力と電磁気の影響だけを受ける自由粒子である希薄な太陽風となり、皆既日蝕のときに太陽からその直径の数倍にも拡がるコロナを見ることがで きる。コロナの温度は、鉄などのスペクトル線の拡がりから 100万度を超えるとされる。
自然は高温と低温を中間的な温度にして、逆に中間的な温度を高温と低温に分離することをしない。熱力学の第2法則の「エントロピー増大」であ る。しかし、粒子速度を見分け粒子の通過を制御する「マックスウエルの悪魔」の門があれば、気体を一方に高い温度、他方に低い温度に分離でき、 これにはエネルギーがいらないという逆説がある。太陽の上空にあるコロナは、この逆説を実現するかのように、太陽の表面温度より遥かに高い温 度をもつ。その仕組みを最も単純に、重力と電気力によって説明したい。この場合最初にある仕組みとして、高速粒子だけが重力ポテンシャルの高 い場所に来ることができることは、「マックスウエルの悪魔」の速度の選別であるが、重力ポテンシャルを登ると、物体はその位置エネルギー分の 運動エネルギーを失い、結果的に上空の温度を変えないのである。このコロナの高温には電子放出とそれによる陽子の電気的加速が必要である。
地球の大気圧は地表から5.5km上空で1/2になる。太陽表面では重力が地表の27.8倍もある。この比率を使えば、太陽表面の境界層はじつに200m で1/2という極端に薄い層になるが、地球の大気(窒素分子(分子量28)80%と酸素分子(分子量32)20%で平均分子量29)と違って水素プラズマ気体は1 で軽いため、地球大気組成の29倍の厚みが必要であり、これが先の重力の比率と近いから、地球の大気圧と同じく高さ5.5kmで1/2になる。太陽と 地球の5780/300=19.3倍の温度の比は、気圧と密度の関係を19.3倍に変えるが、この指数関数には影響しない。この気圧2倍を10回繰り返すと、 55km下で1024気圧になる。
地球大気1リットル1.2グラムは、約1000倍に圧縮して水の密度(1cm^3 で1g)になる。気体を圧縮して発生した熱をよく冷却すると大抵の気体分子 はある温度以下で液体になる。それがこの辺りの気圧である。冷却すれば液体窒素、液体酸素、液体水素が実現する。もう少し圧縮すれば、それ らは固体にもなるがヘリウムは例外と思われていた。液体や固体の水素は金属だろう。しかし、温度が高い太陽表面では水素やヘリウムのプラズ マは圧力だけでは明確に液体や固体に変化せず圧縮性が残ったままだろう。
この指数関係は、気圧2倍が仮に20回続けば、110km下で100万気圧になる。地球では穴の中では重力が中心からの半径に比例するように減少するが、 地球の中心の気圧は、この辺りの値である。大気の下に6500kmの縦穴があれば、重力の減少を考慮して、気圧がその上の気体の密度と重力の積の積 分であるから、温度は常温のままで、密度と気圧が比例するなら、地球の中心気圧は、地表から中心までの積分は3角形の面積、重力一定時の半径 の1/2の深さの気圧である。しかし、6500kmの半分、3250kmの深さまで 5.5kmで気圧2倍が続くとする気圧 2^591 は現実的でない。地下の温度は高 く、またどこかで大気は圧縮性を失う。圧力と密度の比例関係が崩れると、気圧と深さとの指数関係がなくなるのである。
太陽では半径70万kmに比べて数千km程度は重力も温度も一定とみなせるが、110kmのさらに2倍の220km下では1兆気圧(10^12)にもなる。これは大きい がまだ金属水素の10^3気圧と比べて10^15倍の原子核同士が接してしまう気圧 10^18 には6桁も及ばない。しかし、その限界もあと少し下(1気圧の下 330km)で起きる。指数関数は現実には続かず、原子核圧力が関係するようになる。太陽で現実的な気体は数100kmまで長くて数千kmで温度や性質が変 わるだろう。そのような大きな気圧変化が薄い境界層で起きる結果、輪郭のくっきりとした白い光球が見られるのである。もし太陽の質量がそのまま でその半径が10倍大きく、太陽表面重力が今の1/100なら、境界層は100倍に間延びして、現在の太陽にない周辺減光のあるボーとした光の球体になっ てもよいのである。太陽表面が固体か液体の表面のようなくっきりした単純な白い球体に見えるのは、この高度と圧力の指数関係があると考えられる。
電子の脱出速度の温度は、m_e v_esc_sun^2 /k= 2.52 x10^4K 2.52 万度。その約1/4である太陽表面温度 5780K では電子の平均速度は、v_e= 29.6 x 10^6[cm/s] =296[km/s] 陽子は、v_p= 69.07 x 10^4 [cm/s]= 6.91[km/s] であり、電子の上下平均速度は、脱出速度の約半分であるが、粒子エネ ルギーは指数分布をしているから、脱出速度以上をもつ電子の割合が少しある。それに対して陽子は、脱出温度が 4.62 x 10^7K 約4620万度で太陽 表面温度の約1万倍も高い。その比率は、ほとんど0である。
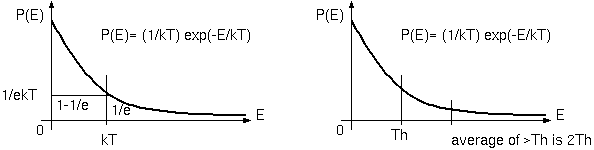
エネルギーに対する粒子の存在確率は、指数関数の肩の上に(ー運動エネルギー/温度)をもつボルツマン分布、exp(-mv^2/(2kT))に比例する。上下 の平均速度が脱出速度をもつ温度の気体では、上下の運動エネルギーが kT 以上の粒子の比率は、1/e=0.3679 である。これが半分より少ないのは、 粒子の大半が低いエネルギーで、かつどこまでも高速な粒子が少しあるという分布の偏りによる。脱出温度の1/2では、exp()の中が-2になり、存在 確率は2乗(1/e^2= 0.135)になる。1/4 の温度で -4乗で 1.8% である。それが太陽表面で電子が上下に脱出速度以上をもつ比率であり、上向き速度 をもつ粒子はその1/2だから、太陽表面で電子のつねに0.9%が上向きの脱出速度以上を持ち、周囲が真空で止めるものがなければ、すぐにでも飛び 出してそのまま遠方に向かうのである。
運動エネルギーがポテンシャル落差に等しい、1/2 v^2= GM/x は、dx/dt= √(2GM)/√x という位置xの微分方程式になる。変数分離し、√x dx= √2GM dt 両辺を積分し、2/3 x^(3/2)= √2GM t これから、 x= (3/2 √2GM t)^(2/3) である。最初に脱出速度ちょうどをもって上昇する粒子は、 その後ずっと全ての場所でその場所の脱出速度ちょうどを持ち、 dx/dt= √(2GM)/√x を保つ。このとき、x^3= 2GM (3/2 t)^2 空間的サイズと時間 の3:2の乗数関係は、ケプラーの第3法則「惑星の公転周期の2乗は、軌道の長半径の3乗に比例」にもある。また、x ∝ t^(2/3)は、平坦 (空間曲率 0) を保つ膨張と同じである。
脱出速度ちょうどの粒子は、最初の1/2の重力ポテンシャル地点、(1)太陽半径R=70万kmと同じ高さに24分足らずで到達する。そこでの速度は最初 の1/√2である。(2)次の1/2の地点に2R=140万km上昇し(表面から3R=210万km)には約67分、(3) 次に4R=280万km登って7Rの高さ490万kmに3.16時間、 (4)次は9時間で8R=560万km上昇し15R=1050万km、(5)1日で2170、(6) 3日で 4410、(7) 8日で8890、(8)24日で 255R=17850万km、途中で地球の公転 軌道 1億5000万kmを通過する。重力ポテンシャル1/2までの工程ごと距離2倍、速度1/√2、時間2√2倍に比例的に減速しながら、ずっと遠方に向かう。
もちろん、脱出速度より速い粒子は、これより早く遠方に行くし、脱出速度未満の粒子は、途中で引返す。低い運動エネルギーの粒子は多く、高い 運動エネルギーの粒子は少ない。粒子がエネルギーを獲得する確率は、単純な指数の肩に(ーエネルギー/温度)をもつ指数型分布であり、温度は平均 エネルギーだから、その平均との比の指数に比例するだけである。
P(x>0)=∫_0^∞ a exp(-ax) dx = [-exp(-ax)]_0^∞= 1
P(x>z)=∫_z^∞ a exp(-ax) dx = [-exp(-ax)]_z^∞= exp(-az)
ある閾値 z 以上の存在確率が e^(-az) になる。z= 1/a のとき 1/e である。平均エネルギーは、エネルギー値 x とその存在確率 P(..)との積、 ax exp(-ax) で表され、全体の平均エネルギーは、1/a になる。
E*P(x>0)=∫_0^∞ a x exp(-ax) dx = [exp(-ax)/a (-ax -1)]_0^∞= 1/a
E*P(x>z)=∫_z^∞ a x exp(-ax) dx = -[x exp(-ax)]_z^∞ - ∫_z^∞ exp(-ax) dx = exp(-az)(z + 1/a)
閾値 z 以上の粒子の平均エネルギーは、exp(-az)(z + 1/a) になる。例えば z= 1/a のとき 2/ae、平均以上の粒子の平均エネルギーは、平均の 2倍である。閾値 z 以上の粒子の平均エネルギーを各エネルギーの存在確率で割り、粒子あたりの平均エネルギーは、z + 1/a、粒子が上空に来て 速度 z を失い、上空の平均運動エネルギーは、元の平均運動エネルギー 1/a である。ある速度を超える粒子だけが脱出できるという重力による 速度選別された粒子は、その位置エネルギー分の運動エネルギーを失って上空にきて元の温度になる。上空の温度は、上昇も下降もしない。
マックスウエルの悪魔の穴は、z以上のエネルギーを持った高速粒子だけを通過させるが、そのとき粒子をzだけ減速させる穴は、穴の元の部屋の 温度を下げるけれども、粒子の移動した先の部屋の温度を元の部屋の温度から変えない。上空の温度が変わらないのは、粒子の速度分布と重力脱 出だけで考えるからである。実際の天体の大気には上空の温度には変化がある。地球の大気圏では高度とともに温度が下がっていってその先は一 度温度が高くなり、それもまた下がり最後に非常に小さな値に収まる。地球の大気中の水素分子の上昇分離は、粒子速度の分布と重力脱出だけで 説明されるが、温度エネルギー分布と重力だけでは温度分離はできない。
その過程を量的に把握するために、抑圧された電子放出と加速された陽子放出との確率の一致によって、電気的ポテンシャルを求めよう。これは 上空に電子脱出温度2.52万度と陽子脱出温度4620万度との中間の温度、両者の幾何平均である108万度を導く。電気的ポテンシャルxは、陽子には、 粒子温度Tに対するxのエネルギー加算を与え、
Pp(Θp)= 1/kT exp(-Θp/(kT + x))
に存在確率を増加する。陽子の加速は、温度 T への x/k の加算のように働くが、全粒子への加速なので、係数の 1/kT を変化させない。電子に は、放出に必要な運動エネルギーΘeをxだけ増加し、
Pe(Θe+x)= 1/kT exp(-(Θe + x)/kT)
に存在確率を減少する。両方の存在確率が等しい Pp(Θp)= Pe(Θe+x) として、
exp(-Θp/(kT + x)) = exp(-(Θe + x)/kT)
xをΘe単位にして、
(Θp/Θe)*(kT/Θe)= (kT/Θe + x)*(1 + x)
Θp/Θe=1836.1 であり、太陽表面温度Tは、kT/Θe= 0.25 だから、
(x+1)*(x+0.25)= 1836.1*0.25
幾何平均 x〜0.5*√1836.1=21.42 は、x の概略値を与える。正確には方程式 x^2+1.25x-458.775= 0 を解き、
x= -0.625 + 0.5*√(1.25^2+1835.1)=(√1837.66-0.625)/2=21.12
x=21.12 は概略値と比べて少し小さいだけである。Θe=2.56 x 10^4 K を使い、qΦ=21.12* 2.56 x 10^4 K=54.07 x 10^4 K。幾何平均の108万度 の半分である理由はkT/Θe= 0.25 による。電気的ポテンシャルxが陽子に運動エネルギーを与え、電子と混合した太陽風プラズマの温度を与える。
Pp(E)= 1/kT exp(-E/kT), E= Θp-x
Pe(E)= 1/kT exp(-E/kT), E= Θe+x
両者の存在確率を等しいとすると、指数関数の肩のなかが等しい。
E= Θp-x= Θe+x
x= (Θp-Θe)/2,
E= (Θp+Θe)/2
E は、陽子脱出温度の1/2、2310万度である。電気的ポテンシャル x との加減算で、E+x で陽子の放出エネルギー、 E-xが電子の放出エネルギー になる。逆に言えば、x は、大きい方(Θp)を引き下げ、小さい方(Θe)を押し上げ両者の中間のエネルギーE 2310万度の存在確率にする。 E は、 表面温度の5000倍も高い温度で、存在確率は低いが、コロナは、非常に希薄な太陽風である。電気的エネルギーは 2000eV 程度であり、電子にと っては脱出エネルギーの 1000 倍もの壁で抑圧される。陽子はその同じエネルギーを与えられても脱出エネルギーの 1/2 であって、残りの速度を 最初から持っていた比率だけが脱出する。電気的エネルギーは、太陽表面温度で、電子と陽子が存在確率を等しくさせる。
電子放出による電荷は蓄積して太陽表面を正に帯電させる。帯電はこの電子放出を抑制し、電子と陽子の放出を同程度にする 2000V 程度の電圧で ある。あたかも、熱エネルギーで放出する電子は、細い糸をもって陽子と結合していて、陽子を引き上げる。陽子と電子を結ぶその糸は1対1ではな く、1個の陽子は多くの糸で重力井戸から引き上げられる。脱出電子による電気的エネルギーは、電子の重力脱出と陽子の重力脱出の平均であり、こ れが電子脱出と等しい陽子脱出にする。
ここで説明に電気だけにして磁気を使わないのは、大枠を示すためである。磁場なしに現象の骨格は説明できる。重力と電場は荷電粒子の速さを 変え、粒子にエネルギー注入削除し、加熱冷却する場であるのに対して、磁場の作用は磁場と粒子速度との外積であり、荷電粒子の方向を変える だけでその速さを変えず、粒子運動へのエネルギーに直接関与しない。磁場は、粒子速度に比例する抵抗のように荷電粒子の軌道を磁力線に沿わ せ、粒子の存在分布に2次的に影響しえる。
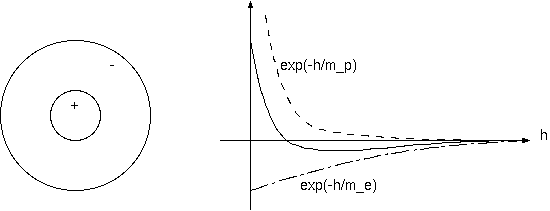
これは、高度における圧力の指数関数を陽子と電子にあてはめた図である。陽子高度は低く電子高度は高い、その高さ比率は1836.1倍である。 この極端な乖離は、電子と陽子の電荷が電場を各高度にもたらし、電子放出を抑制し陽子放出を導出して遥かに平滑化されるが、電子が陽子より 多い上空の負の電場は、両者が等量放出されるために必要である。