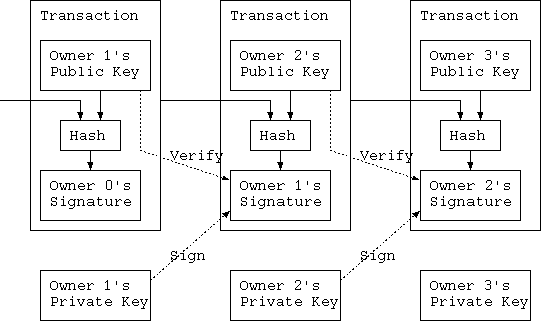
必要なものは、信用の代わりに暗号の証明に基づく電子支払いシステムで、第3者の信用の必要なしにどの望む2団体も互いの 直接取引を許すものである。取引が反転することが計算量的に実際的でないことが、売人を詐欺から防御し、預託メカニズムの 手続きが、容易に買人の防御を実装できるだろう。この論文では、我々は2重消費問題に対して、P2Pの分散タイムスタンプサーバー を使った、取引の時間的順序の計算論的な証明を生成する解答を提案する。正直なノードが集合的に、 攻撃者ノードのどの協力グループよりも多くのCPUパワーを制御する限り、システムは安全である。

もちろん問題は、受取人が何れかの所有者がコインを2重消費しなかったことを検証できないことである。共通の解は、全ての取引に 2重支払いをチェックする、信用される中央権威者、造幣局の導入である。各取引の後、コインは造幣局に新コインを発行するために、 返却されないといけない。造幣局から直接発行されたコインだけが2重支払いがないと信用される。この解の問題は、全てのお金の システムが造幣を行う会社に頼っていて、どの取引も銀行のようなそれらを通さなければならないことである。
我々は、受取人が以前の所有者がどの取引かで署名しなかったことを知るための方法を必要とする。我々の目的のために、 我々が後の2重支払いの試みについて考慮しないような、最も以前の取引をひとつ考慮する。取引の不在を確認する唯一の方法は、 全取引を警戒することである。造幣局ベースモデルでは、造幣局は全ての取引を警戒するなかで、最初に到達したものと決定する。 信用する団体なしにこれが達成されるには、取引は公に案内されなくてはならない[1]、そして、それらが受け取られたなかで、 順序の単独の歴史について参加者が合意するシステムを必要とする。受取人は、各取引の時刻に最初に受け取ったということについて、 ノードの過半数が合意したという証明を必要とする。
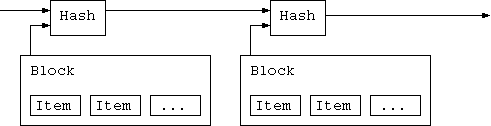
我々のタイムスタンプネットワークにとって、我々はブロック内のノンス(*)を値がブロックのハッシュが要求されるゼロビットを与えるまで 増加することによって仕事証明を実装する。ひとたびCPU労力が仕事証明を満たすまで消費されると、そのブロックは、その仕事をやり直しなし には、変更できない。後のブロックはその後に連鎖されるから、そのブロックを変更する仕事は、その後の全てのブロックをやり直しを含むだろう。

仕事証明はまた多数決決定において決定代表の問題を解く。もし、多数決がIPアドレス一票ベースなら、多くのIPを割り振れる誰かによって転覆 できるだろう。仕事証明は、本質的に、1CPU1票である。多数決は最長のチェーンによって代表され、そのなかに投資された最大の仕事証明の労力 をもつ。もし、CPUパワーの大多数が正直なノードによって制御されるなら、正直なチェーンは最も早く育ち、どの競争者をも凌駕するだろう。 過去のブロックを修正するには、攻撃者はそのブロックとその後の全ブロックの仕事証明をやり直し、それから、正直ノードの仕事に追いつき 凌駕しなくてはならないだろう。我々が後に示すのは、後継のブロックが追加されるに従って、より遅い攻撃者が追いつく確率が指数関数的に 消滅することである。
ハードウェアの速度増加と、時間において動作ノードの興味の変化を補償するために、仕事証明の難しさは、時間あたりの平均ブロック数を 目標にした移動平均で決定される。もし、それらが余りに速ければ、難しさが増加する。
(*) [訳者注] 暗号通信で用いられる、使い捨てのランダムな値
1) 新しい取引が全ノードに放送される。
2) 各ノードは、新取引を集めてブロックにいれる。
3) 各ノードは、そのブロックに難しい仕事証明を見出す仕事をする。
4) あるノードが仕事証明を見出したとき、ノードはそのブロックを全ノードに放送する。
5) ノードらは、そのブロックのなかの全取引が有効で、すでに消費されたものでないときだけ、ブロックを受け入れる。
6) ノードらは、そのブロックの彼らの受容を表明する、次のブロックをチェーンに作成することに働き、以前のハッシュと同じく、
受容ブロックのハッシュを使う。
ノードは、常に最長のチェーンを正しいものと考え、それを伸ばすことを続ける。もし、2つのノードが次のブロックの別のバージョン を同時に放送しても、いくらかのノードは最初に一つを受信したり他を受けたりしてもよい。その場合、彼らは彼らの最初の受信で働き、 しかし、他の枝をそれがより長くなるなら保存する。次の仕事証明が見出されひとつの枝がより長くなるとき、結合は壊されるだろう; 他の枝に働いているノードは、そのとき、より長いものに切り替える。
新しい取引の放送は必ずしも、全ノードに到達する必要はない。それらが多くのノードに到達する限り、彼らはやがてブロックに投入するだろう。 ブロックの放送は、またメーセージの欠落にも耐性がある。もし、ノードがブロックを受け取らなければ、それは次のブロックを受けたとき、 ブロックの喪失を知り、それを要求するだろう。
動機はまた取引手数料によって資金を得られる。もし、取引の出力値がその入力値より少ないとき、その差は取引手数料であり、それは取引を包含する ブロックの動機値に加算される。ひとたび、予定した一定数の貨幣が流通に入ったとき、動機は全て取引手数料に転換でき、完全にインフレから自由になる。
動機はノードが正直にいることを勧める。もし、貪欲な攻撃者が全ての正直なノード以上のCPUパワーを集合することができたとしても、彼はそれを 彼の支払いを盗みとることで人々を詐取するために使用するか、新貨幣を生成することにそれを使用するかを選択しなければならないだろう。彼は、 ルールによって行動することがより利益を得ることを見出すべきだろう。ルールとは、システムと彼自身の冨の価値を覆すよりは、つながった他の 誰よりも新貨幣によって彼に好意的なルールである。
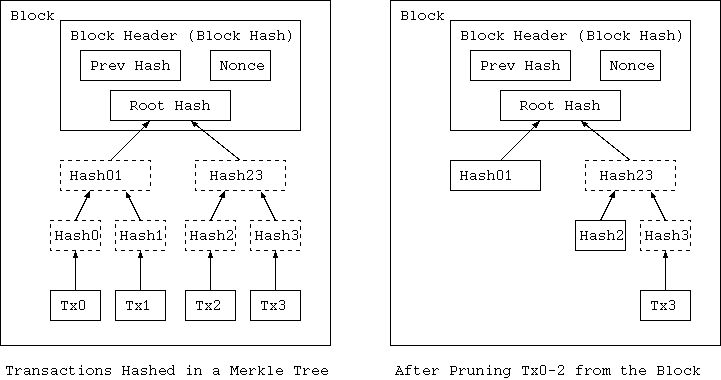
取引なしのブロックのヘッダは約80byteであろう。もし、我々がブロックが10分毎に生成されると仮定するなら、80bytes * 6 * 24 * 365 = 4.2 MB 毎年である。コンピュータシステムが典型的に2GB のRAMを2008年のように売られ、そして、ムーアの法則が 1.2GB 毎年の成長を予測するなら、 メモリにブロックヘッダが保持されなければならないとしてさえ、ストレージは問題にならないだろう。
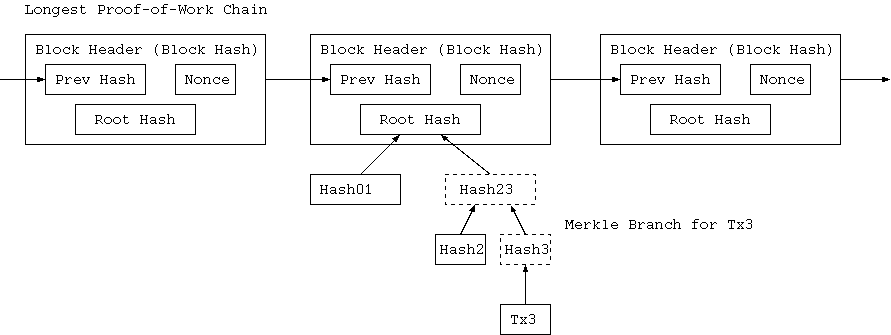
そのように、正直なノードがネットワークを制御する限り、検証は信頼できるが、攻撃者によってネットワークが圧倒されるなら、ネットワークはより 脆弱だろうか。ネットワークノードは取引を彼ら自身で検証できる一方、攻撃者が続けてネットワークを圧倒している間、単純化した方法は攻撃者の まやかしの取引で騙され得る。これに対抗して防御する1戦略としては、ネットワークノードが無効なブロックを検知した時、彼らからの警告を受け、 それに即応し、ユーザのソフトウェアがブロック全体と警告を受けた取引を不整合の確認をするためにダウンロードすることであろう。
(*) [訳者注] 最長仕事証明チェーン
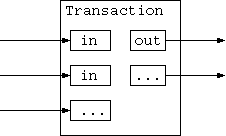
ファンアウト、取引が幾つかの取引に依存する場所で、さらにそれらの取引がより多数に依存するようなことは、ここでは問題ではないことに注意 しなければならない。取引の完全な単独の履歴の抽出は、決して必要ではない。
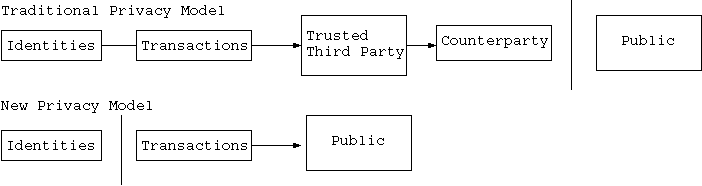
追加的なファイアオールのように、よく知られた所有者に繋げられることから取引を守るには、それぞれの取引に新しい鍵のペアが使われる必要がある。 幾らかの繋がりは、多数の入力の取引では避けられない。それは必然的にそれらの入力が同じ所有者によって所有されていることを明かす。リスクは もし、鍵の所有者が明らかにされると、同じ所有者に属する他の取引を繋がりが明らかにするかもしれないことである。
正直なチェーンと攻撃者のチェーンとの間の競争は、2項分布のランダムウオークとして特徴付けられる。 勝利の事象は正直なチェーンが1ブロックだけ伸長し、そのリードを+1だけ増加することで、そして、 失敗の事象は攻撃者のチェーンが1ブロックだけ伸長し、そのギャップを-1だけ減らすことである。
攻撃者が与えられた赤字からの追付きの確率は、ギャンブラーの没落問題に類似している。無制限の信用をもったギャンプラーが赤字から 開始して、負債解消に達することを試みる可能性として無限回の試みをすることを仮定する。我々は彼が一度負債解消に達し、攻撃者が正直な チェーンを追撃することの確率を計算できる[8]。
$p$= 正直ノードが次のブロックを見出す確率
$q$= 攻撃者が次のブロックを見出す確率
$q_z$= 攻撃者が$z$ブロックビハインドから追撃するだろう確率
\[
q_z= \begin{cases}
1 (p \le q),\\
(q/p)^z (p \gt q)
\end{cases}
\]
$p \gt q$という我々の仮定を与えると、確率は攻撃者の追撃しなければならないブロック数の増加の指数関数で低下する。彼に不利な勝算なことに、
もし彼が幸運な突撃を初期にしないなら、彼がさらに負けることで、彼のチャンスは消滅的に小さくなる。
我々はいま、新しい取引の受取人が、十分確かに送り人が取引を変更できなくなるまで、どれだけ待つ必要があるかを考察する。我々は、送り人 が、彼が彼に支払ったと暫く受取人を信じさせることを欲する攻撃者と仮定する、そのとき、幾らか時間が過ぎた後、彼自身に払い戻すようにする。 受信者はそれが起きたら警告されるだろうが、送り人はそれが間に合わないだろうことを望む。
受信者は、新しい鍵のペアを生成し、公開鍵を送り人に与え、すぐにサインさせる。これは、彼が幸運にもずっと前に間に合って、そのとき取引を 実行するまで連続的に仕事することで、送り人にブロックのチェーンを前もって用意することを防ぐ。一度、取引が送られると、不正直な送り人は、 秘密に彼の取引の別バージョンを含む並列的なチェーンの仕事を開始する。
受取人は、取引があるブロックに加えられ、zブロックがその後に繋がるまで待つ。彼は、攻撃者のした過程の正確な量を知らないが、正直なブロック が平均的にブロック当たりの時間をとると仮定して、攻撃者の可能な過程が次の期待値をもつポアソン分布になる: \[ λ = z{q \over p} \] 攻撃者が今まだ追撃しているかもしれない確率を得るには我々は、彼がその点から追撃できる確率によって彼が成し遂げる進展の各量として ポアソン密度を掛け: \[ \sum_{k=0}^∞ { λ^ k e^{-λ}\over k!}・ \begin{cases} (q/p)^{(z-k)} (k \le z),\\ 1 (k \gt z) \end{cases} \] 分布の無限の尾を総和を避けるため、再配置して、 \[ 1 - \sum_{k=0}^z {λ ^k e^{-λ}\over k!} ( 1 - (q/p)^{(z-k)} ) \] C コードに変換して、
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
走らせた幾らかの結果、我々は、z に指数関数的の確率が低下することをみる。
q=0.1 z=0 P=1.0000000 z=1 P=0.2045873 z=2 P=0.0509779 z=3 P=0.0131722 z=4 P=0.0034552 z=5 P=0.0009137 z=6 P=0.0002428 z=7 P=0.0000647 z=8 P=0.0000173 z=9 P=0.0000046 z=10 P=0.0000012 q=0.3 z=0 P=1.0000000 z=5 P=0.1773523 z=10 P=0.0416605 z=15 P=0.0101008 z=20 P=0.0024804 z=25 P=0.0006132 z=30 P=0.0001522 z=35 P=0.0000379 z=40 P=0.0000095 z=45 P=0.0000024 z=50 P=0.0000006Pが0.1%より小さい場合に解いて、
P < 0.001 q=0.10 z=5 q=0.15 z=8 q=0.20 z=11 q=0.25 z=15 q=0.30 z=24 q=0.35 z=41 q=0.40 z=89 q=0.45 z=340
References
[1] W. Dai, "b-money," http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, "Design of a secure timestamping service with minimal
trust requirements," In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, "How to time-stamp a digital document," In Journal of Cryptology, vol 3, no
2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, "Improving the efficiency and reliability of digital time-stamping,"
In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, "Secure names for bit-strings," In Proceedings of the 4th ACM Conference
on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, "Hashcash - a denial of service counter-measure,"
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, "Protocols for public key cryptosystems," In Proc. 1980 Symposium on Security and
Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, "An introduction to probability theory and its applications," 1957.